Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1

Подождите немного. Документ загружается.

просто получать из формул гидродинамики интересные математи

ческие соотношения.

Конечно, равенство (14.90а) справедливо при условии, что xv

являются корнями уравнения (14.74).

Равенство (14.90а) можно доказать строго математически, не

прибегая к физическим соображениям. Однако это математическое

доказательство достаточно громоздко — см. подробности такого

доказательства в монографии Хупера [863].

Учитывая равенства (14.90) и (14.90а), формулу (14.89а) можно

переписать в таком, несколько более простом виде:

Vc(t) = AnR2cb$* Ьр сух

су-

’ R,

4 R 2

Jo(xv)-J2i

г г кt

е *1

(14.906)

или же

У c(t) = V3an-4Tii??bP*ApeyX

X V D

^ ^С )

Jl{xv)-J\

( /? Y

\x ~ \

Л V n

I R <)\

2 Кt

е кс

(14.90в)

В статье [972] приедена таблица с результатами подсчета

безразмерной величины Vc, добытого количества (объема) жидкости

из скважищл за различные промежутки времени. Безразмерная

величина VCi используемая в статье [972] и монографии [863],

связана с размерной величиной V с следующим соотношением:

у Ус (14.90Г)

с 2nR^b^*Apcy‘

Аналогичным способом можно определить безразмерную вели

чину Узап упругого запаса жидкости в пласте; учитывая равенство

(14.90), получим

V -=

----------

-лгп-----------= .

мп 2%R2cb^*APcy

/зал

Более удобно было бы определять безразмерные величины, не

вводя множитель 2 в знаменатели формул (14.90г) и (14.90д).

Однако такое изменение малосущественно и поэтому в данной

работе решено было сохранить те обозначения безразмерных

величин, какие были приняты теми авторами, которые впервые

вывели соответствующие формулы.

Пользуясь равенствами (14.90г), (14.90д) и (14.27), формулы

(14.906) и (14.90в) можно переписать в безразмерной форме:

где параметр Фурье/о — «безразмерное время» определяется с по

мощью равенства (14.27).

Через боковую поверхность цилиндра радиуса г за все время

может быть добыто количество жидкости, которое равно ее

упругому запасу в объеме пласта между рассматриваемой боковой

поверхностью и внешней непроницаемой границей пласта, т.е.

Для облегчения подсчетов по формулам (14.82), (14.86), (14.86а),

(14.89), (14.89а) необходимо знать значения корней ху трансцен

дентного уравнения (14.74). В статье В. Д. Полянина [523] выпол

нены сведенные в таблицы подсчеты первых 15 корней этого

уравнения при многих различных значениях отношения — от 5

^ с

до 5000; некоторые результаты этих подсчетов воспроизведены

здесь в табл, 14.5.

Л С

(14.90е)

Ve(/o) = VMo -2 £

V / J

lV(r,t)]t=^ = n(R2k-r2)b^tApcy. (14.91)

Таблица 14.5

Первые 15 корней уравнения (14.77) при различных значениях —

R с

Номера

корней

Значения корней xv при

R с

100 1000 5000

0,1103

0,0072

0,0006

0,0001

2 0,4979 0,0429

0,0041 0,0008

0,8554

0,0755 0,0073

0,0014

4 1,2087 0,1077

0,0105

0,0021

1,5603

0,1397 0,0137

0,0027

1,9111 0,1717

0,0168

0,0033

7 2,2614

0,2036 0,0200

0,0040

2,6114

0,2355 0,0231

0,0046

2,9612

0,2674

0,0263

0,0052

10 3,3108 0,2993

0,0295

0,0059

11 3,6604

0,3311 0,0326 0,0065

4,0099 0,3629 0,0358

0,0071

13 4,3593 0,3948

0,0389 0,0078

4,7086 0,4266

0,0421

0,0084

15 5,0579

0,4584 0,0452

0,0090

На основе анализа табл. 14.5 можно сделать такие же замечания

по поводу закономерностей изменения величин корней, какие были

сделаны в двух предыдущих параграфах по поводу табл. 14.2 и

14.3.

В статье [972] авторы приводят лишь по 2 первых корня

уравнения (14.57), причем для значений только от 1,5 до 10.

Кс

Приведенные авторами величины корней хорошо совпадают с теми,

что приведены в табл. 14.5 по данным В. Д. Полянина. Например,

для —— = 10 авторы цитированной статьи указывают такие величины

R с

двух первых корней: 0,1104 и 0,4979.

Проведенный анализ выведенных в данном параграфе формул

позволяет схематично изобразить последовательные положения пье

зометрических линий в различные моменты, графики понижений

давления в различных точках пласта, графики изменения расходов и

количеств жидкости, перетекшей через различные боковые поверх

ности коаксиальных цилиндров. Все эти схематичные изображения

соответственно полностью повторяют те, какие были помещены на

рис. 13.12-13.15. Только обозначения координаты jc и длины пласта L

следовало бы заменить величинами радиуса-вектора г и радиуса Rk

внешней границы пласта; обозначение Г (первую букву слова галерея)

надо заменить на С (первую букву слова скважины).

Действительно, как и на рис. 13.12, все пьезометрические линии

в рассматриваемом здесь плоско-радиальном потоке должны

начинаться в одной точке на стенке скважины (на высоте,

соответствующей заданному забойному давлению рсу); все эти линии

должны заканчиваться на границе пласта (при г = Rk), причем на

этой границе касательные к постепенно снижающимся пьезомет

рическим линиям должны быть горизонтальны.

Как и на рис. 13.13 все линии графиков понижения давления

на разных расстояниях гь г2, г3... от возмущающей скважины

должны иметь точки перегиба и, снижаясь, асимптотически прибли

жаться к горизонтальной прямой на уровне постоянного забойного

давления рсу.

Как и на рис. 13.14 график изменения дебита скважины Qc(t)

должен быть представлен линией, имеющей одну асимптоту,

совпадающую с осью ординат, а другую — совпадающую с осью

абсцисс. Все остальные линии графиков расхода жидкости Q(t)

через боковые поверхности цилиндров радиусов

г {<г 2<г 3 ... cR к должны быть расположены под линией графика

для возмущающей скважины.

Как и на рис. 13.15 линия графика изменения количества

жидкости Vc(t\ протекшей через стенку скважины, должна

резко подниматься из начала координат, касаясь в этой точке

оси ординат, и затем асимптотически приближаться к горизон

тальной прямой на высоте У зап, соответствующей упругому запасу

жидкости во всем пласте — см. равенство (14.90) и рис. 14.7.

График изменения количества жидкости V (t), протекшей через

боковую поверхность цилиндра радиуса г, изображается линией,

которая располагается ниже графика Vc(t) и асимптотически

приближается к горизонтальной прямой, соответствующей упру

гому запасу жидкости в части пласта между боковыми поверх

ностями коаксиальных цилиндров радиусов г и Rk — см. ра

венство (14.91).

В табл. J4.6 приведены при Rk = 5RC значения безразмерной

величины Vc, определяемой формулой (14.90е); эти значения

заимствованы из обширной таблицы статьи [972]. [fo данным

табл. 14.6 на рис. 14.7 изображен график зависимости Vc от / 0. По

данным этой таблицы и по рисунку видно, что уже при/0>50

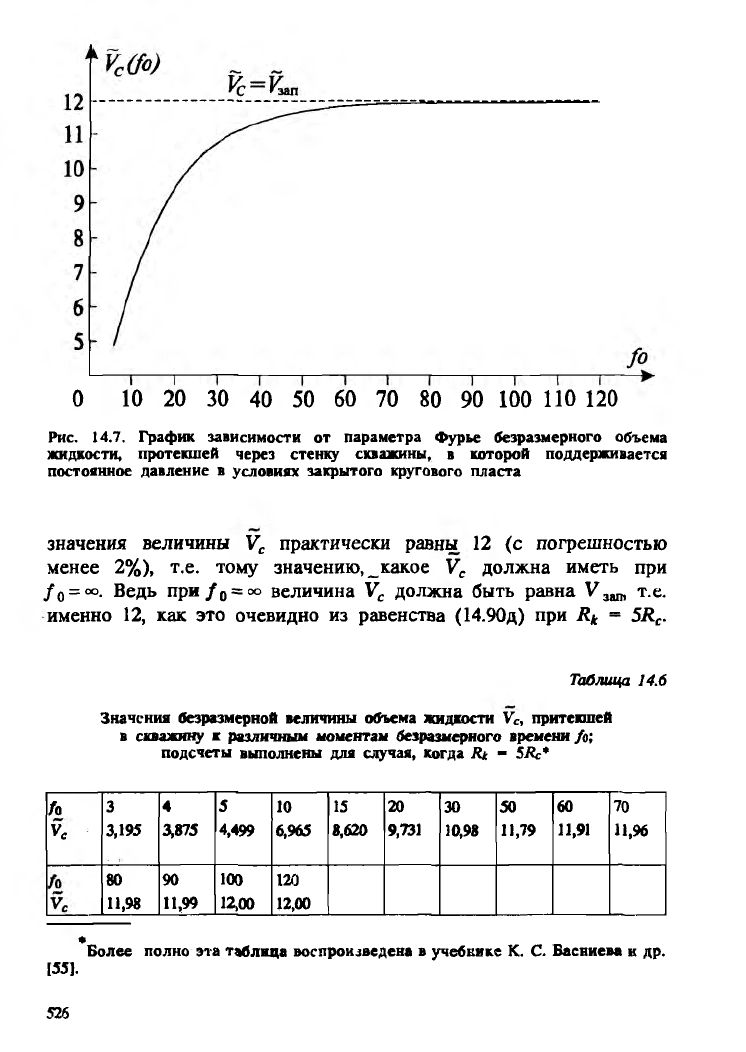
О 10 20 30 40 50 60 70 80 90 100 110 120

Рис. 14.7. График зависимости от параметра Фурье безразмерного объема

жидкости, протекшей через стенку скважины, в которой поддерживается

постоянное давление в условиях закрытого кругового пласта

значения величины Vc практически равны 12 (с погрешностью

менее 2%), т.е. тому значению, _какое Vc должна иметь при

/ 0 = °о. Ведь при / 0 = °о величина Vc должна быть равна V3an, т.е.

именно 12, как это очевидно из равенства (14.90д) при Rk « 5RC.

Таблица 14.6

Значения безразмерной величины объема жидкости VCf притекшей

в скважину к различным моментам безразмерного времени /о;

подсчеты выполнены для случая, когда Rt - 5Rc*

/о

3,195

3,875

4,499 6,965

8,620

9,731

10,98 11,79

11,91

11,96

11,98

11,99

100

12,00

120

12,00

Более полно эта таблица воспроизведена в учебнике К. С Басниева и др.

[55].

Приведенные в таблице данные, когда радиус Rk внешней

границы превышает радиус Rc скважины лишь в пять раз, прак

тически может соответствовать лишь случаю «укрупненной сква

жины», заменяющей собой, например, разрабатываемую залежь

нефти в ограниченном пласте (линзе).

см 2

Если принять, что к =104

-----

, Лс = 1км=105 см, то найдем

значение времени, соответствующее значению / 0 = 50, при котором

укрупненной скважиной из пласта оказывается отобранным почти

весь (с погрешностью менее 2%) его упругий запас; на основании

соотношения (14.27):

R 2

t = —~f0 = 10 8 с - 579 сут.

Примечание. Подробнее таблица величины Vc в функции

параметра/о для значений — от 1,5 до 10, составленная Ван

R с

Эвердингеном и Херстом [972], полностью воспроизведена в статье

[862] и книге [863] Хупера.

§ 5. Задание постоянного дебита скважины

при непроницаемой внешней границе пласта

Задача, которая исследуется в данном параграфе, отличается

от той, которая была решена в предыдущем параграфе, только

тем, что задано не постоянное давление на стенке скважины, а

постоянный (установившийся) ее дебит Qcy, как это было в условии

задачи в § 3. Однако, в отличие от § 3, здесь рассматривается

закрытый пласт с непроницаемой внешней границей, совпадающей

с боковой поверхностью цилиндра радиуса Rk — см. рис. 14.1.

Итак, требуется проинтегрировать дифференциальное уравне

ние пьезопроводности (14.1) при соблюдении начального условия

(14.3) (одинаковости давлений во всех точках пласта в начальный

момент), при соблюдении граничного условия (14.37) на стенке

скважины и при соблюдении граничного условия (14.57) на внешней

границе.

Задача решается тем же методом, какой был использован в

предыдущих параграфах данной главы. Воспользуемся готовым

решением, подробности которого можно найти в книгах Хупера

[863] и Маскета [439].

В результате интегрирования уравнения пьезопроводности при

указанных выше условиях, понижение давления в любой точке

пласта в любой момент определяется такой формулой:

___ QcyW

2 R\

4 R2 + ~R2

v о 7

(R2k-R 2c)2 + 2(Ri-R4c)-4Riln-^

2 ч 2

Rl-R2

cln^c

-*s-

v = 1

Ji(xv)Y0

9-L

I'l 0tv)

(14.92)

/?(jevW f

2 Kf

e XvJ2c

где xv — корни трансцендентного уравнения

( Rk1

Ji(xv)Yt

х —

VRC

-/1

\Х'Т С

K,(xv)-0. (14.93)

\ )

\ >

Полагая г ■ Rc

в формуле

(14.92),

определим понижение

давления Ар с ( t) в скважине в любой момент, упрощая выражение

под знаком суммы с помощью соотношения (П. 162а)*:

2R^ ( l Kt

4 + Rl

A i Ж \ Q СУ М- I

----------

APc(t)'2nbk\Rl-R2

(R}-R2c)2 + 2(Ri-Ri)-4Ri\n^

-2 1 -

\х ^

А V р

L К с /

•■К2

J\(xv)-J\

Г Rk ]

х *тс

\ >

2 Kt

e Rc

(14.94)

Формулы (14.92) и (14.94) впервые были выведены в статье Маекета {916], что

подчеркивается Хупером [863], метод изложения которого принят в данном пара

графе.

Если допустить, как это чаще всего бывает на практике, что

Rc« R h то формулы (14.92) и (14.94) несколько упрощаются и

принимают, соответственно, такой вид:

hpir't)~2nbk\2Rl + 2Ri 4

* /iC*v)y0

V = 1

X V п

к* - - + 1П — -

Kl(*v)

(14.95)

X у

л .

2 КГ

Qcy4 1 л ?

Kf 3

Д/>е(*) = ;™ Н T ^ + 2-i^-T + l n ^ -

2 reft* I 2 Д* 4

■ f

-2 S -

X V n

e ’*1

(14.96)

Чтобы найти разность (p - pc) давлений в любой точке пласта

и в скважине, вычтем равенство (14.92) из равенства (14.94):

а А С су Д [ 1

ДРс-ДР=Р-Рс = ^ Т 7 1 о „2 »2

2%Ък [2Л?-Л?

/? *

v = lJ2l(Xy)2~J 1

JC2

Л v

“ Jt-

/1(*у)Ув Uvjf- "/в

I'lUv)

(14.97)

2 Kf

A Xy R1

e Kc

Несмотря на громоздкость приведенных формул, их анализ

позволяет сделать ряд полезных выводов.

Как уже отмечалось, во всех предыдущих формулах величины

слагаемых под знаками сумм быстро стремятся к нулю с ростом

времени. В каждой из этих формул присутствует одно слагаемое,

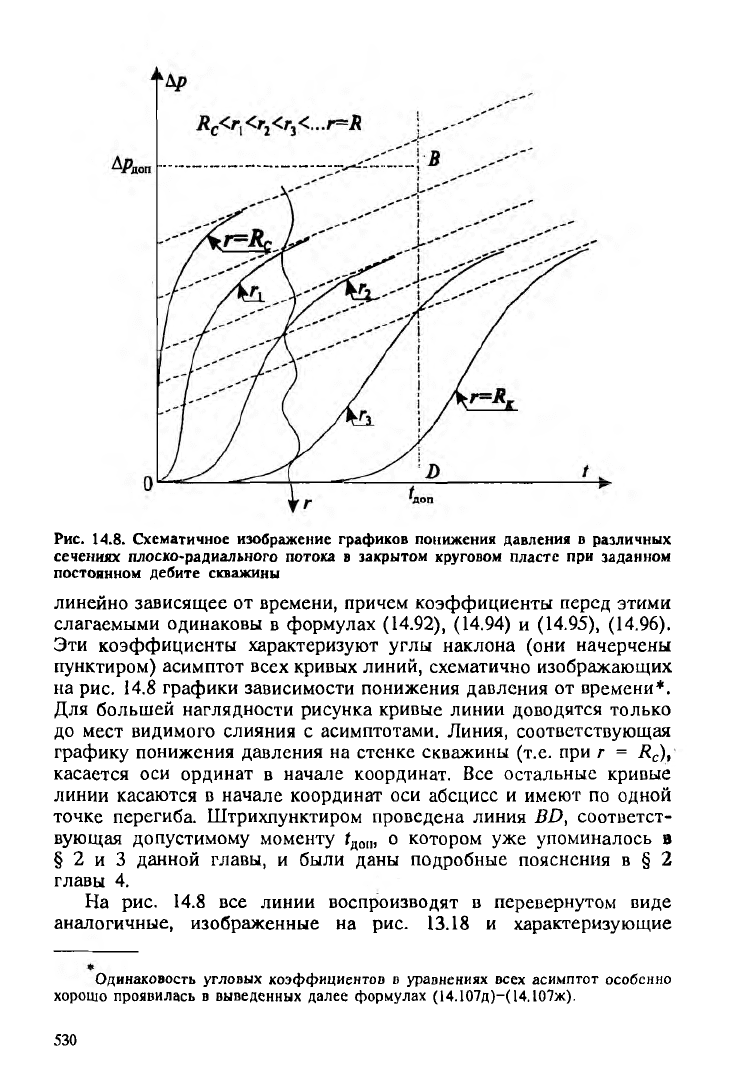
Рис. 14.8. Схематичное изображение графиков понижения давления в различных

сечениях плоско-радиального потока в закрытом хруговом пласте при заданном

постоянном дебите скважины

линейно зависящее от времени, причем коэффициенты перед этими

слагаемыми одинаковы в формулах (14.92), (14.94) и (14.95), (14.96).

Эти коэффициенты характеризуют углы наклона (они начерчены

пунктиром) асимптот всех кривых линий, схематично изображающих

на рис. 14.8 графики зависимости понижения давления от времени*.

Для большей наглядности рисунка кривые линии доводятся только

до мест видимого слияния с асимптотами. Линия, соответствующая

графику понижения давления на стенке скважины (т.е. при г = Rc)t

касается оси ординат в начале координат. Все остальные кривые

линии касаются в начале координат оси абсцисс и имеют по одной

точке перегиба. Штрихпунктиром проведена линия BD, соответст

вующая допустимому моменту ?доп, о котором уже упоминалось в

§ 2 и 3 данной главы, и были даны подробные пояснения в § 2

главы 4.

На рис. 14.8 все линии воспроизводят в перевернутом виде

аналогичные, изображенные на рис. 13.18 и характеризующие

Одинаковость угловых коэффициентов в уравнениях всех асимптот особенно

хорошо проявилась в выведенных далее формулах (14.107д)-(14.107ж).

графики изменения самого давления (а не понижения давления)

в сходных условиях замкнуто-упругого режима, но для прямоли

нейно-параллельного потока. Рис. 14.8 полезно еще сопоставить с

рис. 4.2 и 14.3.

Пьезометрические линии в условиях данной задачи такие же,

какими они схематично были изображены на рис. 13.19 для

аналогичных условий замкнуто-упругого режима в плоско-парал

лельном потоке. Следует только считать, что ось ординат проведена

по стенке скважины, а не по стенке галереи, что по оси абсцисс

откладываются значения радиуса-вектора г, а не координаты х;

расстояние ОА следует считать равным ( R к - R с ).

Итак, судя по формулам (14.92)—(14.96), понижения давлений

при больших значениях времени становятся линейно-зависящими

от времени. Полагая f = °о и Rc« R k из формулы (14.97)

обнаруживаем, что

Р-Рс =

2 nbk

Rc 2 R2k

(14.98)

Интересно сопоставить последнюю формулу с аналогичной

формулой для условий установившегося потока, когда окружность

радиуса Rt служит контуром питания:

ОсуИ. «1 (14.99)

’’-" ‘ • г f b i ,nRl-

В условиях замкнуто-упругого режима перепад давления ока

зывается, судя по формуле (14.98), меньшим по сравнению с

аналогичными условиями установившегося режима.

Судя по той же формуле, начиная с достаточно больших

значений времени разность давлений (р - р с ) перестает зависеть

от времени, становится величиной постоянной, что подтверждает

изображенную на рис. 14.8 параллельность практически прямоли

нейных участков графиков понижений давлений.

Такое движение жидкости было названо в книге [739] «равно

мерно неу становившимся».

Для определения расхода Q жидкости через любую боковую

поверхность цилиндра, коаксиального скважине, продифференци

руем по г равенство (14.92) и найденную производную подставим

в формулу, выражающую закон Дарси: