Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1

Подождите немного. Документ загружается.

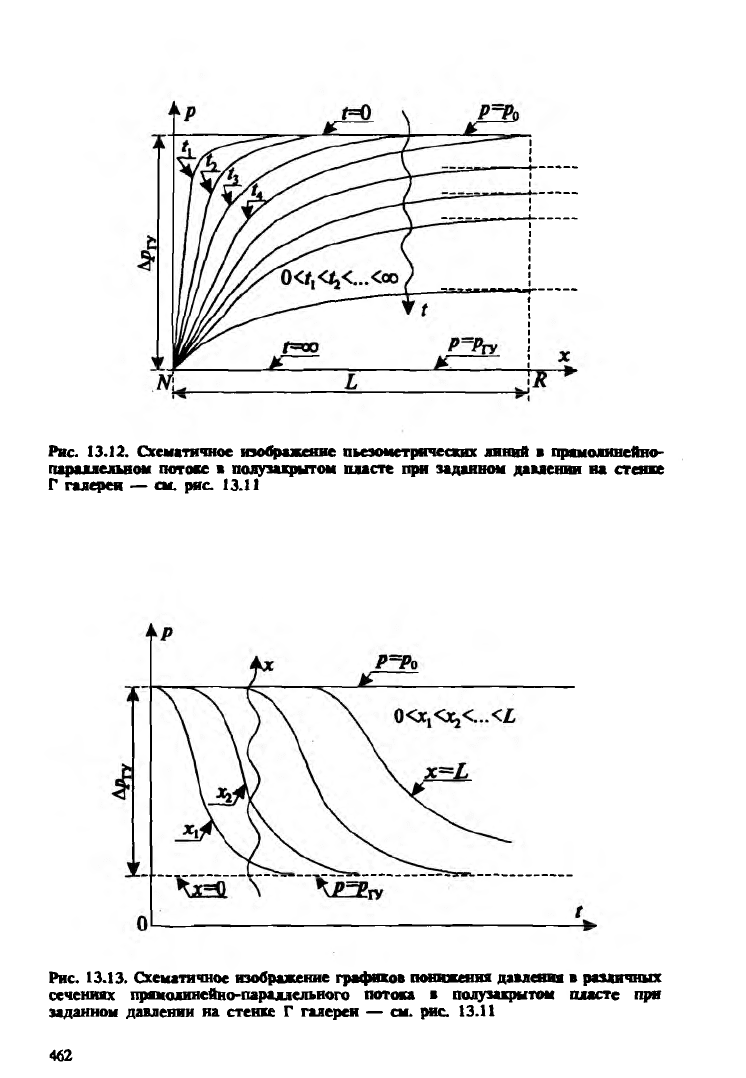
Ряс. 13.12. Схематичное изображение пьезометрических линий в прямолинейно-

параллельном потоке в полузакрытом пласте при заданном давлении на стенке

Г галереи — см. рис. 13.11

Рис. 13.13. Схематичное изображение графиков понижения давления в различных

сечениях прямолинейно-параллельного потока в полузакрытом пласте при

заданном давлении на стенке Г галереи — см. рис. 13.11

Следовательно, расход жидкости в любом сечении пласта

асимптотически приближается к нулю.

На основании выведенных формул (13.71)—(13.79) построены

рис. 13.12— 13.15.

На рис. 13.12 схематично изображены последовательно сни

жающиеся со временем пьезометрические линии. Все они начи

наются из одной точки, соответствующей величине постоянно

удерживаемого давления р^ в галерее; все линии имеют гори

зонтальные касательные на закрытой границе пласта и, сни

жаясь, со временем асимптотически приближаются к горизон

тальной прямой NR.

На рис. 13.13 схематично изображены графики понижения

давления в различных точках пласта с координатами

х = 0, хх, х2 •.. xL ; все эти линии, понижаясь, асимптотически

приближаются к горизонтальной прямой р = Ргу.

На рис. 13.14 схематично изображены графики изменения со

временем величин расхода жидкости в различных сечениях пласта

Для галереи, т.е. в сечении х » 0, соответствующая кривая имеет

своими асимптотами и ось ординат и ось абсцисс, так как в

начальный момент, при мгновенном снижении давления в галерее,

расход жидкости через ее стенку должен был бы быть бесконечно

большим. Все остальные кривые асимптотически приближаются к

оси абсцисс, имея по две точки перегиба и по одной точке,

соответствующей максимальному значению расхода жидкости через

данное сечение потока

На рис. 13.15 изображены графики изменения со временем

объема жидкости, перетекшей через данное сечение пласта до

момента t. В сечении х * 0, т.е. на стенке галереи, этот объем

монотонно возрастает и асимптотически приближается к горизон

тальной прямой, соответствующей полному упругому запасу жид

кости в пласте. Все остальные кривые имеют по одной точке

перегиба и асимптотически приближаются каждая к своей гори

зонтальной прямой, соответствующей величине объема упругого

запаса жидкости между данным сечением пласта и его закрытой

границей.

Заметим, что, учитывая равенство (13.78), формулу (13.77) можно

переписать еще так:

(2 у - 1)2 я 2 Kt "

4 I 2

• (13.80)

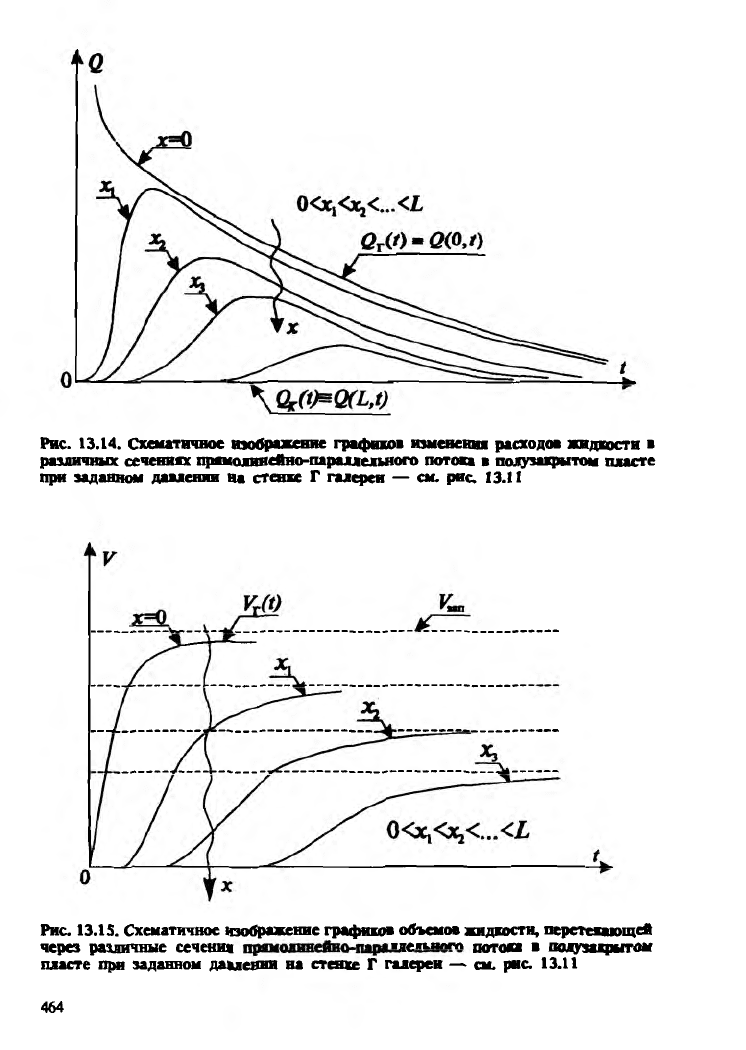
Рис. 13.14. Схематичное изображение графиков изменения расходов жидкости в

различных сечениях прямолинейно-параллельного потока в полузакрытом пласте

при заданном давлении на стенке Г галереи — см. рис. 13.11

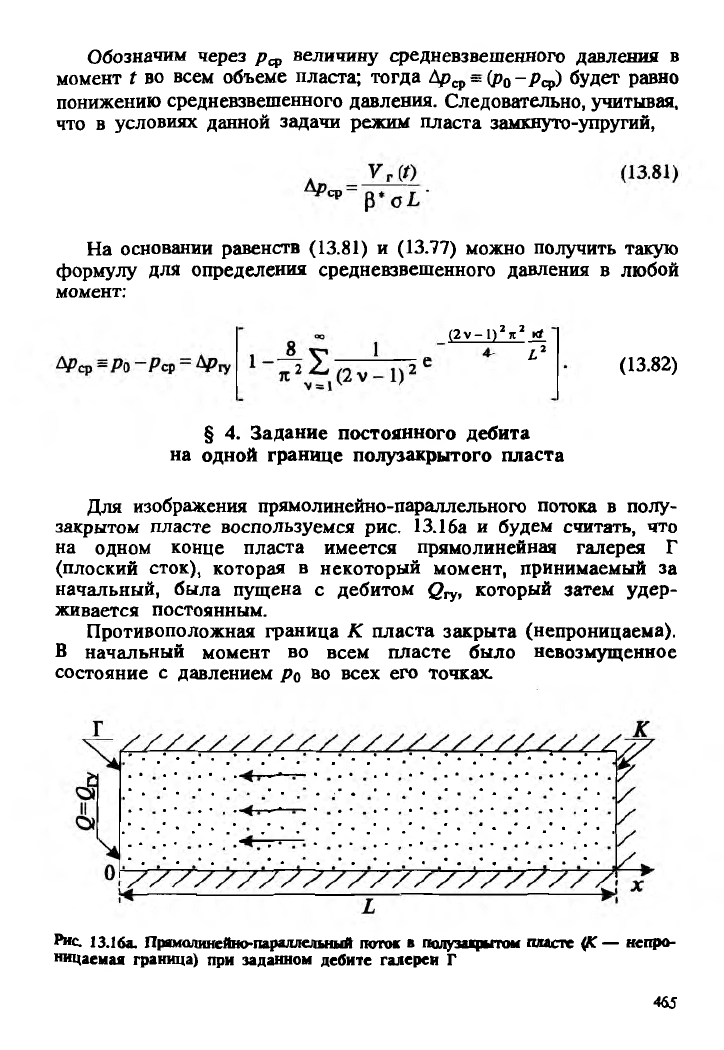
Обозначим через рср величину средневзвешенного давления в

момент t во всем объеме пласта; тогда ДРср = (pQ- Рср) будет равно

понижению средневзвешенного давления. Следовательно, учитывая,

что в условиях данной задачи режим пласта замкнуто-упругий,

На основании равенств (13.81) и (13.77) можно получить такую

формулу для определения средневзвешенного давления в любой

момент:

Для изображения прямолинейно-параллельного потока в полу

закрытом пласте воспользуемся рис. 13.16а и будем считать, что

на одном конце пласта имеется прямолинейная галерея Г

(плоский сток), которая в некоторый момент, принимаемый за

начальный, была пущена с дебитом QTу, который затем удер

живается постоянным.

Противоположная граница К пласта закрыта (непроницаема).

В начальный момент во всем пласте было невозмущенное

состояние с давлением

Ро во всех его точках.

Рис. 13.16а. Пртолинейно-параллельный поток в полузакрытом пласте (К — непро

ницаемая граница) при заданном дебите галереи Г

(2 у -1)2 к 2 Kt

(13.82)

§ 4. Задание постоянного дебита

на одной границе полузакрытого пласта

Данная задача от разобранной в предыдущем параграфе

отличается только тем, что теперь на границе Г считается

установленным не постоянное давление, а постоянный дебит £?гу*

Пуск галереи с постоянным дебитом вызывает неустановившийся

прямолинейно-параллельный поток жидкости в пласте. При сформу

лированных условиях удобно начинать исследование неустановивше

го ся потока не с определения давления р (х, t) в любой точке пласта

в любой момент, а с определения расхода жидкости Q (дс, t) через

любое сечение пласта в любой момент. Необходимо решить такую

краевую задачу: при заданных начальном и граничных условиях про

интегрировать дифференциальное уравнение расхода (12.2), которое

для прямолинейно-параллельного потока, т.е. при а = 0, имеет вид:

Начало координат помещено на границе Г — рис. 13.16а; длина

пласта опять считается равной L.

Постановка данной краевой задачи вполне аналогична той,

которая была рассмотрена в § 1. Действительно, дифференциаль

ные уравнения расхода (13.83) и пьезопроводности (13.1) одинаковы;

аналогичный вид имеют краевые условия (13.84)— (13.86) и (13.2)—

(13.4). Поэтому можно воспользоваться готовым решением, пред

ставленным формулой (13.19), но только в эту формулу надо

подставить Q вместо Ар и вместо 4Ргу«

Подставляя в формулу (13.87) значения х = 0 и х = L, сразу

убеждаемся, что граничные условия (13.85) и (13.86) удовлетворя

ются. Подстановка в эту же формулу значения t =* 0 обеспечивает

удовлетворение начального условия (13.84), так как из теории

рядов известно следующее равенство — см. формулу (1.441.1)

на стр. 52 [183]:

d2Q 1Э Q

дх2 к ЭГ *

О<x < L , f>0.

(13.83)

При£=0.... 6 = 0, 0<jc<L. (13.84)

Прих = 0— Q-Qry, t> 0.

(13.85)

(13.86)

(13.87)

V — 1

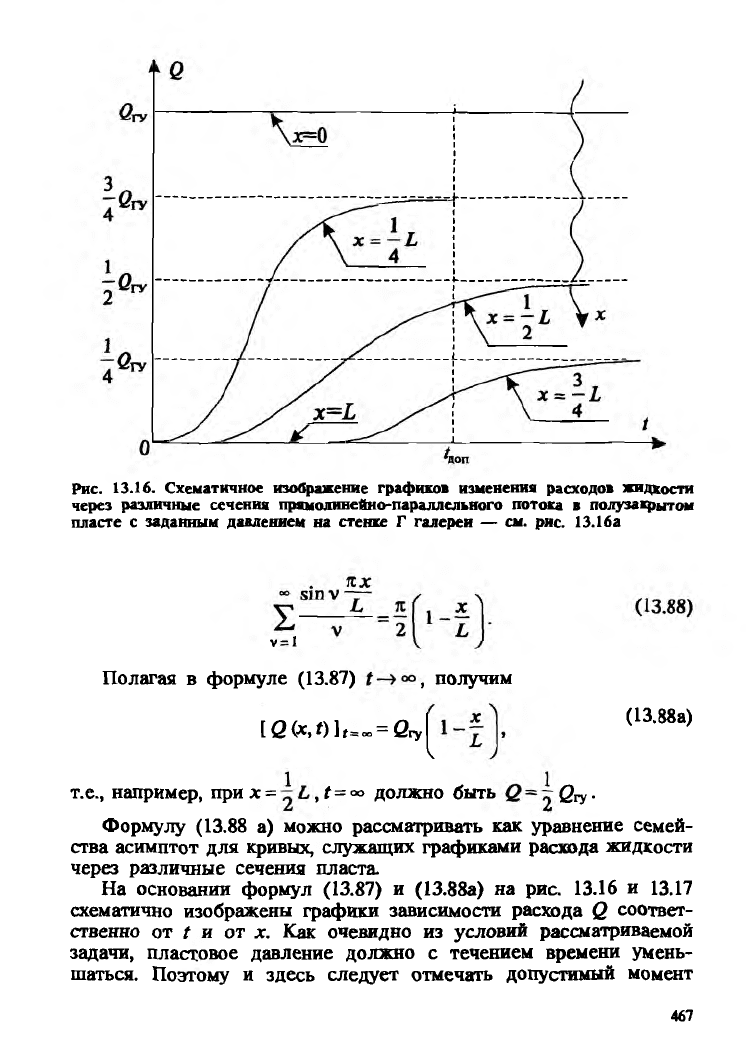
Рис. 13.16. Схематичное изображение графиков изменения расходов жидкости

через различные сечения прямолинейно-параллельного потока в полузакрытом

пласте с заданным давлением на стенке Г галереи — см. рис. 13.16а

v ~ 1

Полагая в формуле (13.87) , получим

[Q (M )h = » = Gry

(13.88а)

т.е., например, при х = , f=<» должно быть Qry •

Формулу (13.88 а) можно рассматривать как уравнение семей

ства асимптот для кривых, служащих графиками расхода жидкости

через различные сечения пласта

На основании формул (13.87) и (13.88а) на рис. 13.16 и 13.17

схематично изображены графики зависимости расхода Q соответ

ственно от t и от х. Как очевидно из условий рассматриваемой

задачи, пластовое давление должно с течением времени умень

шаться. Поэтому и здесь следует отмечать допустимый момент

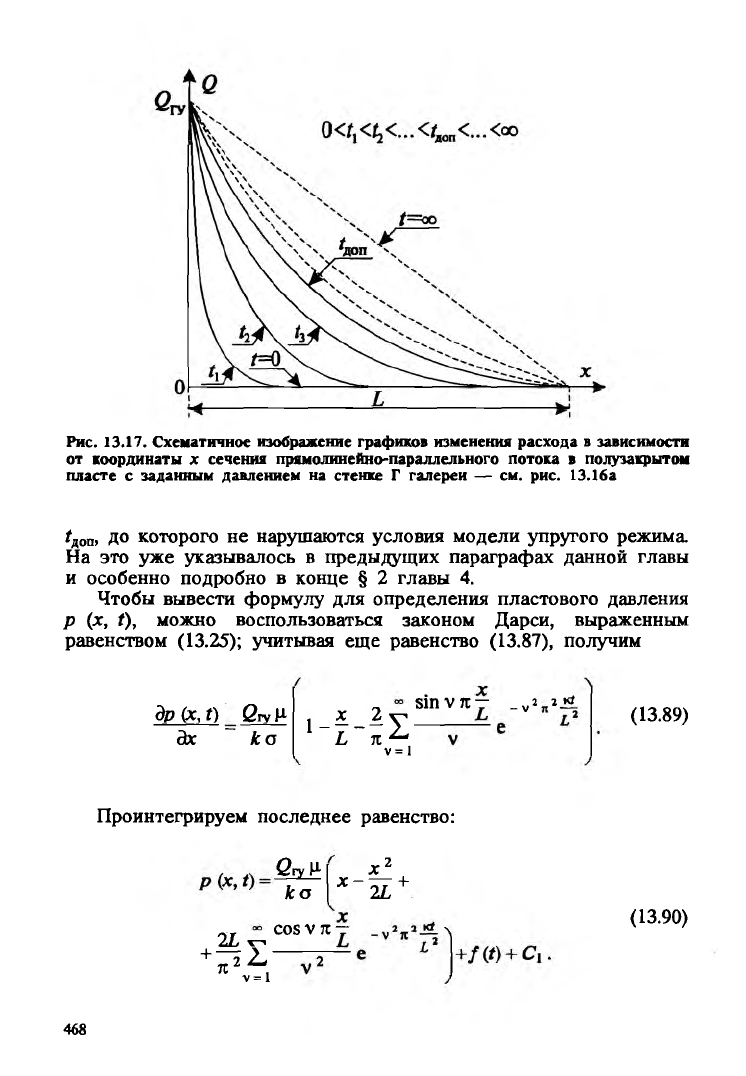
Рис. 13.17. Схематичное изображение графиков изменения расхода в зависимости

от координаты х сечения прямолинейно-параллельного потока в полузакрытом

пласте с заданным давлением на стенке Г галереи — см. рис. 13.16а

*Дот ДО которого не нарушаются условия модели упругого режима.

На это уже указывалось в предыдущих параграфах данной главы

и особенно подробно в конце § 2 главы 4.

Чтобы вывести формулу для определения пластового давления

р (х, t), можно воспользоваться законом Дарси, выраженным

равенством (13.25); учитывая еще равенство (13.87), получим

dp(x,t) _ 6гуЦ

Эх ка

‘- Н е

v = 1

sinvrc— _ v2 2_tf

(13.89)

Проинтегрируем последнее равенство:

О х »

ко

Х2

х~ и +

2L Vi

+ ^ 2 ,"

к .

v = 1

COS V К ~ ч

Для определения функции / (f), появившейся при интегриро

вании, подставим найденное значение р (х, t) в дифференциальное

уравнение пьезопроводности (13.1), откуда найдем, что

бгуЦ*

dt koL '

Следовательно,

(13.91)

Подставляя (13.91) в (13.90) и объединяя произвольные" посто

янные интеграции, получим:

х г кt

х 21 L +

V = I

+с.

(13.92)

Учтем начальное условие (13.2) и известное равенство — см.,

например, стр. 245 [547]:

(13.93)

v = 1

Тогда окончательная формула для определения понижения

давления в любой точке пласта и в любой момент примет вид:

бгу М*

ко

Kt • 1 х 2 _

L 2 + 2 L 2

. ~ COSV7C— _ v2 2jtf

*12^ L г2

—e ^

— — _j_ — _ — V*

L 3 яг2-

(13.94)

Полагая х » О, найдем понижение давления в галерее в любой

момент £

4Pr(0s />0-ft(0=-

С?гуЦ£

ко

К* 1

Z ^ + 3-

(13.95)

Судя по формулам (13.94) и (13.95), при достаточно больших

значениях времени t величины Др (jc, t) и Дрг (t) будут линейно

зависеть от времени, т.е. соответствующие участки графиков будут

прямолинейны и параллельны друг другу.

Для удобства проведения более полного анализа процесса

перераспределения пластового давления воспользуемся безразмер

ными величинами: параметром Фурье Fo, имеющим значение

безразмерного времени, безразмерной координатой х и безразмер

ным понижением давления Ар (х, Fo) .

Примем, что

F“= z5 ' * = Г' (13.%)

На основании этих определений формулу (13.94) можно

переписать так:

° ° ~ 2 2

^ 1

х 2 ж-4» cos v rex ^v я Л?

Ар(х,Ро)=Др + - - х + -^--Г г Е v 2 е • (13.97)

V = 1

Формулы (13.94) и (13.97) допустимо рассматривать как урав

нения семейства кривых: графиков зависимости понижения давле

ния от времени на различных расстояниях ;Гот галереи (от плоского

стока). На рис. 13.18 схематично изображены три таких графика

для сечений пласта; которым соответствуют следующие значения

безразмерной координаты:

jc = 0 — стенке Г галереи,

х = 0,5 — середине длины пласта,

х = 1 — непроницаемой границе К пласта

При достаточно больших значениях времени t и параметра Fo

величинами сумм рядов, входящих в формулы (13.94), (13.95) и

(13.97), можно пренебречь (как малыми величинами) и, например,

последнюю формулу переписать так:

Др (х, Fo) s Fo + - - X + — .

В математике известен стандартный прием, с помощью которого,

зная уравнение кривой, возможно найти уравнение ее асимптоты

(если кривая имеет асимптоту). Применяя этот прием к формуле

(13.97) как к уравнению семейства кривых, пришли бы к той же

самой формуле (13.98), которую таким образом можно рассматри

вать не только как формулу для приближенного определения

давления при больших значениях

t или Fo, но и как точное (если

сохранить знак равенства) уравнение семейства асимптот. На

рис. 13.18 асимптоты начерчены пунктирными линиями.

Полагая, например, х -0 или jT= 1 в формуле (13.98), получим

уравнения асимптот к кривым, представляющим собой графики

изменения со временем понижения давления соответственно на

стенке галереи (в стоке) или на закрытой границе пласта:

Д/Г (0, Fo) = /Ь + ^ , <13" >

bp(\,Fo)=Fo-\. (13.100)

Эти две асимптоты являются крайними из всего семейства

параллельных асимптот; у всех у них угловой коэффициент равен

1, т.е. все они наклонены к оси абсцисс под углом 45°. Начальные

ординаты асимптот, представленных формулами (13.99) и (13.100),

1 Г О

равны соответственно — и .

Найдя производную по времени от понижения давления

Арг (t) , определяемого формулой (13.95), нетрудно убедиться, что

величина этой производной при t = 0 равна бесконечности.

Следовательно, кривая понижения давления на стенке галереи в

начальный момент касается оси ординат. ^Все остальные кривые

графиков понижений давления, т.е. при 0 < jT< 1, касаются в начале

координат оси абсцисс. Все кривые, кроме графиков, ^соответству

ющих двум границам пласта (т.е. кроме значений х = 0 и х= 1),

имеют точки перегиба.