Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1

Подождите немного. Документ загружается.

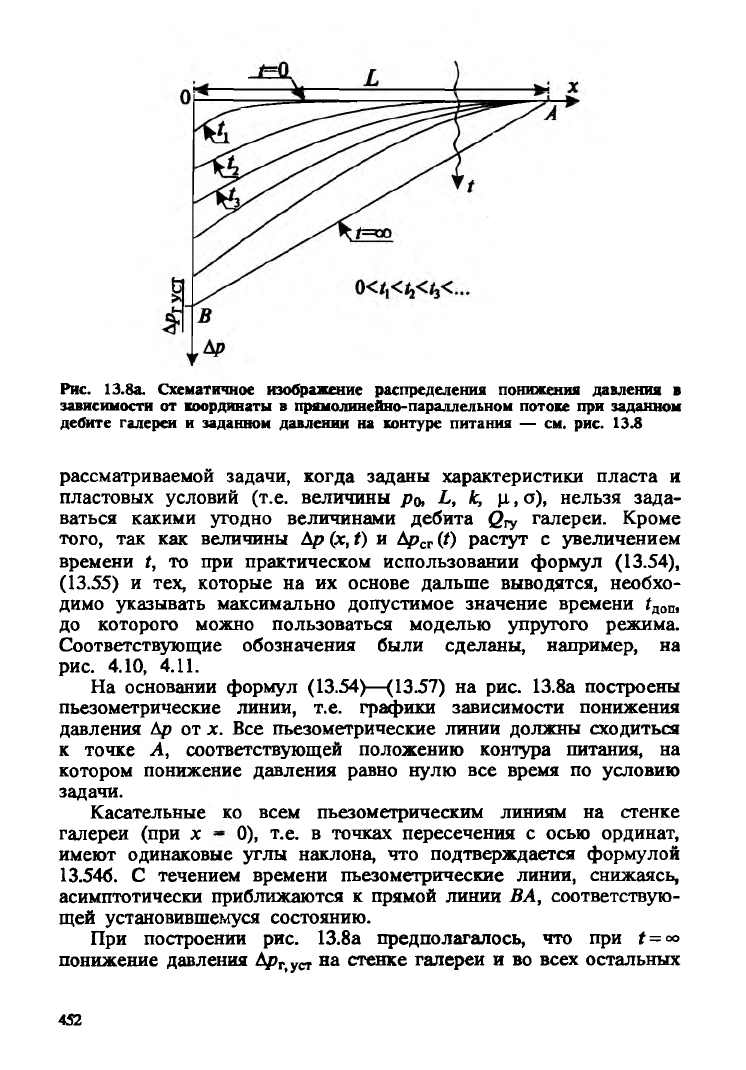
Рис. 13.8а. Схематичное изображение распределения понижения давления в

зависимости от координаты в прямолинейно-параллельном потоке при заданном

дебите галереи и заданном давлении на контуре питания — см. рис. 13.8

рассматриваемой задачи, когда заданы характеристики пласта и

пластовых условий (т.е. величины ро, L, к, ji,a), нельзя зада

ваться какими угодно величинами дебита Qry галереи. Кроме

того, так как величины Ар (х, t) и Арсг (t) растут с увеличением

времени t, то при практическом использовании формул (13.54),

(13.55) и тех, которые на их основе дальше выводятся, необхо

димо указывать максимально допустимое значение времени ?доп,

до которого можно пользоваться моделью упругого режима.

Соответствующие обозначения были сделаны, например, на

рис. 4.10, 4.11.

На основании формул (13.54)—(13.57) на рис. 13.8а построены

пьезометрические линии, т.е. графики зависимости понижения

давления Ар от х. Все пьезометрические линии должны сходиться

к точке А, соответствующей положению контура питания, на

котором понижение давления равно нулю все время по условию

задачи.

Касательные ко всем пьезометрическим линиям на стенке

галереи (при х - 0), т.е. в точках пересечения с осью ординат,

имеют одинаковые углы наклона, что подтверждается формулой

13.546. С течением времени пьезометрические линии, снижаясь,

асимптотически приближаются к прямой линии ВА, соответствую

щей установившемуся состоянию.

При построении рис. 13.8а предполагалось, что при t = °о

понижение давления АрГ)уст на стенке галереи и во всех остальных

точках пласта таково, что упругий режим нигде не нарушен. Бели

бы понижение давления Арт уст превзошло допустимую величину

для сохранения упругого режима, то на рис. 13.8 пришлось бы

ограничиться пьезометрической линией, соответствующей допусти

мому понижению давления на стенке галереи, соответствующей

какому-то моменту времени, который пришлось бы считать допу

стимым моментом ?доп, как это выше было пояснено.

Если воспользоваться параметром Фурье Fo (безразмерным

временем) и безразмерной координатой х у определенными равен

ствами (13.22), то, учитывая еще соотношение (13.57), формулы

(13.54) и (13.55) можно «деперсонифицировать», т.е. записать в

безразмерной форме:

АР | _ - 8 у

___

____

АРг.уст 712v" (2 v - 1) 2'

(13-58)

(2v- 1)яд:

х cos л

-----

г-*

----

_ (2v- 1)гя2,

(2у-1)*яа

АРсг = 1 _ у

------

е 4 F° Г13.59>

АРр.уст rt2v~ ( 2 v - l ) 2 * )

В § 2 главы 6 был исследован прямолинейно-параллельный поток

после пуска прямолинейного стока (галереи) с постоянным дебитом

в условиях полубесконечного пласта. Применительно к обозначениям

данного параграфа формулу (6.30), определяющую понижение дав

ления Пар (х, t) в любой точке (положение которой определяется

координатой х) в любой момент t, можно переписать так:

Др (х, t) = 2 Vitf г erfc .

(13.60)

Положив в формуле (13.60) х = 0 и учитывая соотношение

(П.35), получим понижение давления на стенке галереи:

2 {Згу М* I— (13.61)

Дра (t) S Др (0,0 = - j ^ - а/кГ .

Различие в постановках задач данного параграфа и § 2 главы 6

состоит лишь в том, что пуск галереи с постоянным дебитом Qjy

в данном параграфе рассматривался в условиях конечного пласта

длиной L с поддержанием начального давления на его конце (на

контуре питания); а в § 2 главы 6 пласт был бесконечным, т.е. не

было никакого контура питания и считалось, что начальное

пластовое давление могло сохраняться лишь на бесконечно

большом расстоянии от галереи (при х - «>).

Учитывая и сходство и различие в постановке задач данного

параграфа и § 2 главы 6, можно утверждать, что при не слишком

больших значениях времени и при не слишком большом удалении от

галереи можно с небольшой погрешностью пользоваться для опре

деления понижения давления в условиях конечного пласта формулами

(13.60) и (13.61), выведенными для условий полу бесконечного пласта

вместо более громоздких формул (13.58) и (13-59). Чтобы сделать

более очевидной возможность использования, например, формулы

(13.61), сначала несколько преобразуем ее, а затем введем в нее

параметр Фурье, определяемый тем же равенством (13.22):

Заметим, что левые части формул (13.59) и (13.63) содержат

формально совершенно одинаковые величины. Сопоставление

подсчетов позволяет утверждать, что использование для условий

конечного пласта простой формулы (13.63) вместо формулы (13.59)

вносит погрешность, не превосходящую 1% (точнее, даже не

превосходящую 0,8%) при Fo < 0,3; при Fo = 0,5 погрешность уже

немного превосходит 4%.

В пределах допустимой погрешности можно воспользоваться

формулами (13.63) и (13.64) и для построения графиков зависимости

понижения давления от времени или от параметра

Fo; каждый из

этих графиков имеет форму параболы.

Для дальнейших сопоставлений понадобится кроме формулы

(13.54) и другая формула для того случая, когда скорость прямоли

нейно-параллельного потока направлена в противоположную сторону,

т.е. когда начало координат помещено на контуре питания, а галерея

с постоянным дебитом находится на расстоянии L от этого контура,

т.е. р = рк при х =*= 0 и Q * Qry при х =* L. В этом случае в формуле

достаточно заменить х на (L - х) и в итоге получим:

(13.62)

или же

(13.63)

4с (М)

. (2v-l)«oc

х sm — г г 1— е

( 2 v - 1)2я2 Kt

Чтобы определить расход жидкости Q{x, t) через любое

сечение, перпендикулярное к направлению скорости прямоли

нейно-параллельного потока, изображенного на рис. 13.8, сле

дует воспользоваться законом Дарси, выраженным с помощью

формулы (13.25). Определим производную по координате х от

понижения давления, используя равенство (13.54), и подставим

значение этой производной в формулу (13.25):

G (M ) = Giy

. (2v- 1)жх

Xsm 2L *

( 2 v - 1 ) 2712 Kt

(13.65)

Полагая в равенстве (13.65) получим, что, как и

следовало ожидать, Q (jc , f)—>Gry> т.е. во всех сечениях потока

величина расхода жидкости стремится в пределе к величине

дебита галереи. Анализ этой формулы и полученных на ее

dQ d2Q ,

основе производных и позволяет судить о форме гра

фиков изменения расхода, схематично изображенных на

рис. 13.9 для различных сечений потока, т.е. при различных

значениях координаты х. В начальный момент t = 0 все

изображенные на рис. 13.9 кривые линии касаются оси абс

цисс; каждая из этих кривых имеет при t> 0 по одной точке

перегиба и все они асимптотически приближаются к горизон

тальной прямой Q = Qr* Смысл обозначения fflon выше уже

был пояснен.

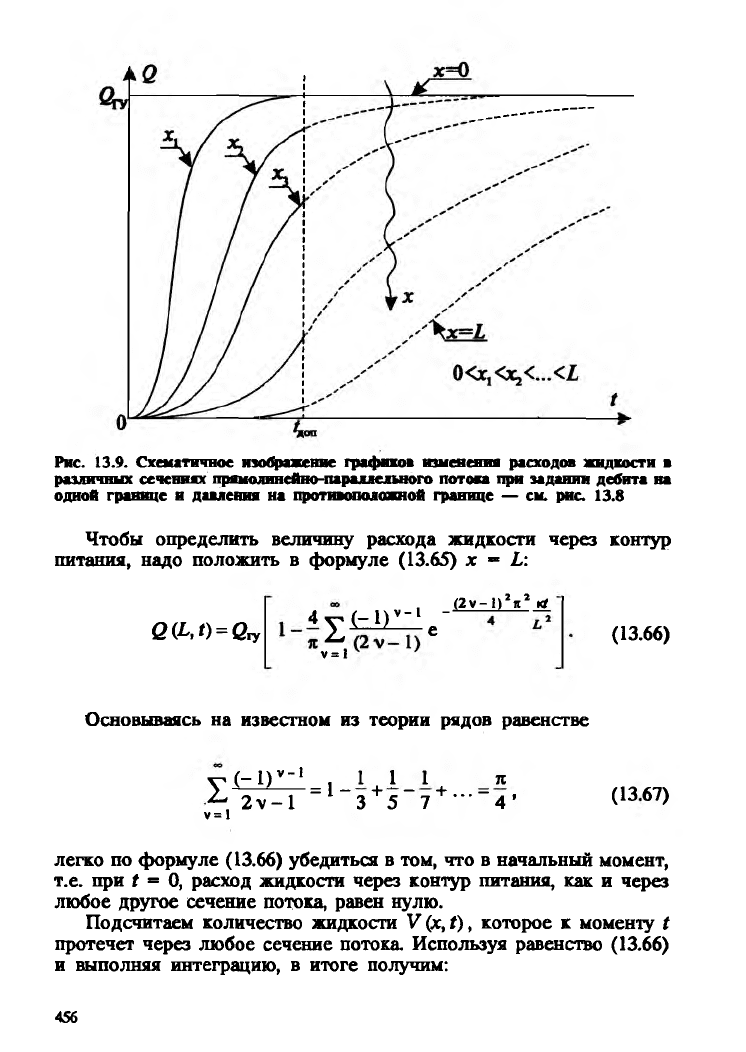
Рис. 13.9. Схематичное изображение {рафиков изменении расходов жидкости в

различных сечениях прямолинейно-параллельного потока при задании дебита на

одной границе и давления на противоположной границе — см. рис. 13.8

Чтобы определить величину расхода жидкости через контур

питания, надо положить в формуле (13.65) х *= L:

Q(L,t) = Qry

4Е Ы Ш е-

V = 1

(2v- 1)2я2 к1

(13.66)

Основываясь на извесгноы из теории рядов равенстве

V '(-D v_1 .111 п

£ Т Г Т =1~3 + 5‘ 7 + -" = 4- (1367>

V = 1

легко по формуле (13.66) убедиться в том, что в начальный момент,

т.е. при t - 0, расход жидкости через контур питания, как и через

любое другое сечение потока, равен нулю.

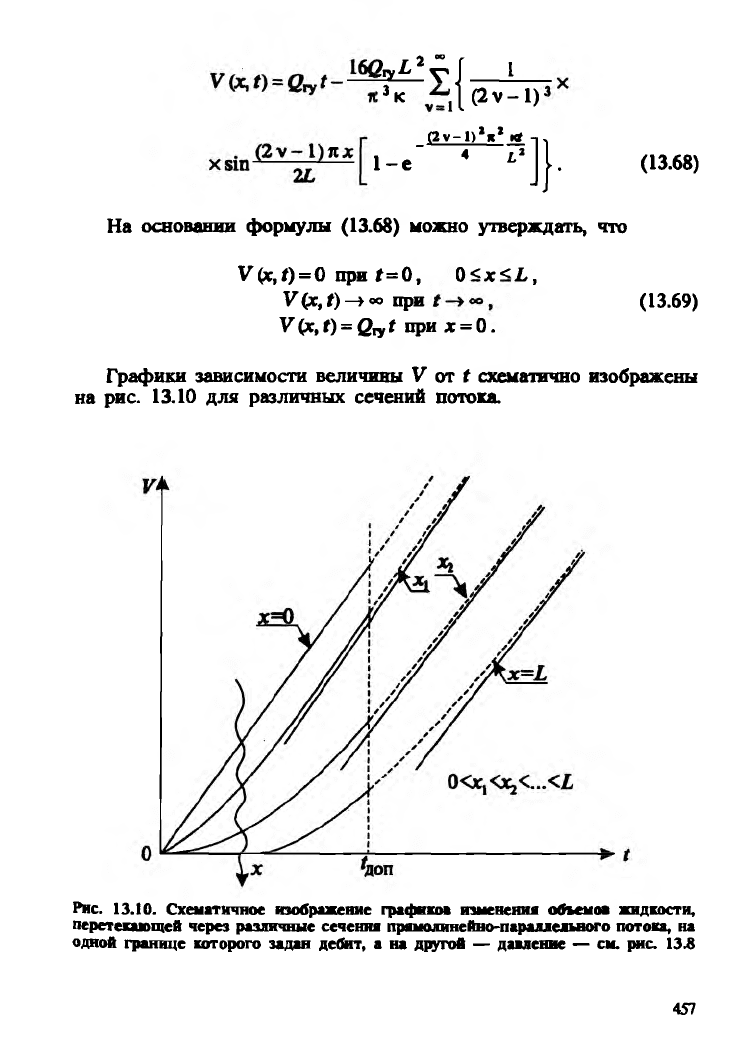
Подсчитаем количество жидкости V (х, t) , которое к моменту t

протечет через любое сечение потока. Используя равенство (13.66)

и выполняя интеграцию, в итоге получим:

k i f f j

___

:3к —Д (2v- 1)-

[

О » - ! )* » * rt

1-e" 4 **]j. (13.68)

На основании формулы (13.68) можно утверждать, что

V (x,f)=0 при /=0, 0 <х<Ь,

V (r ,t) ->«о при (13.69)

V(pc, t) = Q,y f при x = 0.

Графики зависимости величины V от t схематично изображены

на рис. 13.10 для различных сечений потока.

Рис. 13.10. Схематичное изображение графике» изменения объемоа жидкости,

перетекающей через различные сечения прямолинейно-параллельного потока, на

одной границе которого задан дебит, а на другой — давление — см. рис. 13Л

§ 3. Задание постоянного давления

на одной границе полузакрытого пласта

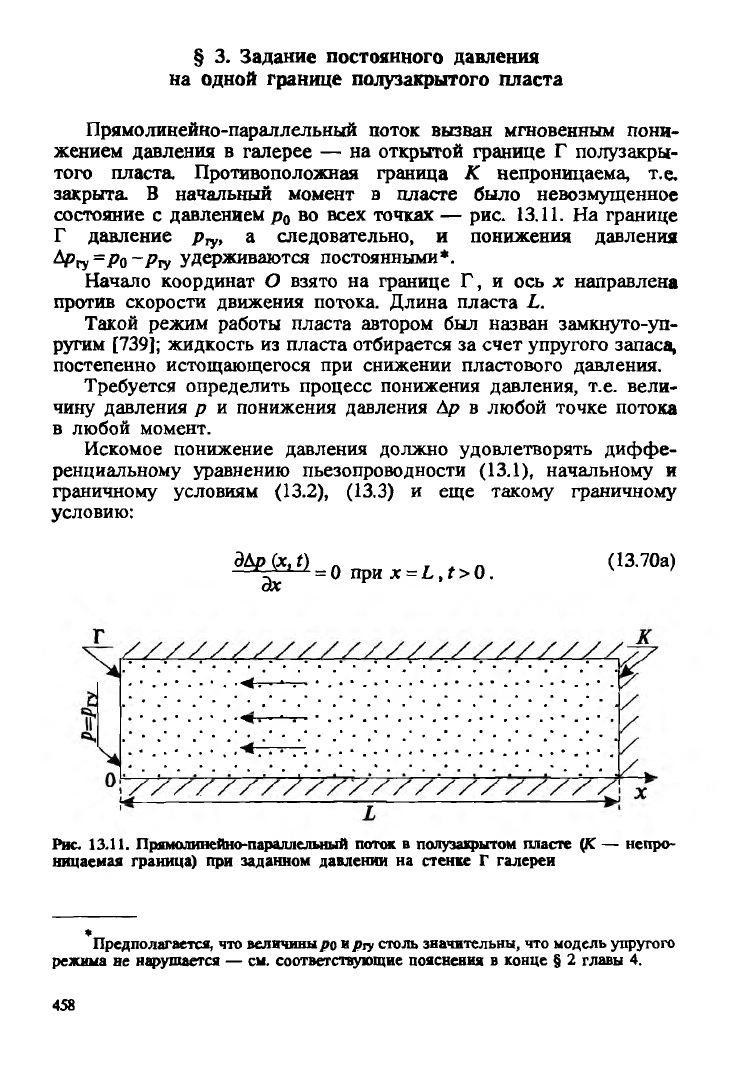
Прямолинейно-параллельный поток вызван мгновенным пони

жением давления в галерее — на открытой границе Г полузакры

того пласта Противоположная граница К непроницаема, т.е,

закрыта. В начальный момент в пласте было невозмущенное

состояние с давлением р0 во всех точках — рис. 13.11. На границе

Г давление р^ а следовательно, и понижения давления

АРгу =Ро ~Ргу удерживаются постоянными*.

Начало координат О взято на границе Г, и ось х направлена

против скорости движения потока. Длина пласта L.

Такой режим работы пласта автором был назван замкнуто-уп

ругим [739]; жидкость из пласта отбирается за счет упругого запаса,

постепенно истощающегося при снижении пластового давления.

Требуется определить процесс понижения давления, т.е. вели

чину давления р и понижения давления Ар в любой точке потока

в любой момент.

Искомое понижение давления должно удовлетворять диффе

ренциальному уравнению пьезопроводности (13Л), начальному и

граничному условиям (13.2), (13,3) и еще такому граничному

условию:

^ 4 = 0 при *=£ ,,>0. <’ 3-70а>

Рис. 13.11. Прямолинейно-параллельный поток в полузакрытом пласте (К — непро

ницаемая граница) при заданном давлении на стенке Г галереи

Предполагается, что величины ро и рту столь значительны, что модель упругого

режима не нарушается — см. соответствующие пояснения в конце § 2 главы 4.

Полученное методом разделения переменных решение диффе

ренциального уравнения пьезопроводности определяется равенст

вом (13.7). Подставив в это равенство граничное условие (13.3),

получим, как было пояснено в § 1,

^>(*,0 = Apn,+^i* + X-Avsm(Xv*)e * . (13.706)

v = l

Продифференцируем равенство (13.70 б) по координате х:

= A + S xv^v««(>-v*)e (13.70в)

Vs I

Учитывая граничное условие (13.70а), равенство (13.70в) позво

ляет сделать такие выводы:

(2 v - 1)аи* Kt

Поэтому вместо (13.706) получим

оо

___

, ..

. Т- .. .(2v-l)jtX~ 4 Г*

&pQc,t) = &pnr + 2^Av smi

-----

2^7— е • (13.70г)

V ~ 1

Подставляя в равенство (13.70г) начальное условие (132) и

используя для определения коэффициентов A v такой же прием,

какой был пояснен в § 1 и 2, найдем, что

л _ ^ (^Л О д)

(2 v -l)n ‘

Учитывая (13.70д), из равенства (13.70г) получаем окончательное

выражение для искомого понижения пластового давления:

n ^ -2 v -lX

V= 1

(2 v-!)»«* rt

. (2v-l)nx 4 F *

:sm i — — i — e

Используя обозначения (13.22), можно переписать последнюю

формулу в безразмерной форме:

~= Д ^ = 1_ 4 £ _ Ц . х

АЛу nv,,2v- 1

. (2v-l)rtJt 4

xsin-*

-----

^ — e

(13.72)

Продифференцировав равенство (13.71) и используя закон

Дарси, можем определить расход жидкости Q (рс, t) через любое

попереченое сечение потока в любой момент:

(2V-1)1»* *t

„ , Л ЗДртуко ^ (2v-l)n.x 4 г1

Q (* ’ ) = — uL X е08

----

2 L

----

е • ( 1373>

V = 1

Из формулы (13.73), полагая х - О, найдем величину расхода

жидкости QT (t) через стенку галереи:

'чл » 00 (2 у - 1)2яа к*

QT(t) = Q(0,t)=^ L ° £е 4

V = 1

(13.74)

Полагая х — L в формуле (13.71), получим величину понижения

давления АрК (t) на закрытой границе пласта:

Арк (0 = Ар (L, 0 = 4Лу

- , Ov- rt

1 _ 4 Y (- 1) 4 £*

2v - 1

(13.75)

Определим объем жидкости V о- (/), которая протечет через

стенку галереи за время t; для этого воспользуемся формулой

(13.74):

ОО

У — -— ■

v , , (2 v -1)2

ОО

~v? , (2 v - l) 2e

(2v - 1)1я2 Kt

* L*

Или же, учитывая известную формулу теории рядов

*(2 v -l)2 8 ’

(13.76)

окончательно получим, заменяя величину к его выражением с по

мощью равенства (1.41):

Vcr(0 = ApIy3*oL

V = 1

(2v- 1)аж2 Kt

rc*_“ (2 v -I)2

(13.77)

Формула (13.77) определяет, по существу, ту часть упругого

запаса жидкости, которая извлекается из пласта за время L

Положим в формуле (13.77) f=°o, тогда определится величина

У »,, полного упругого запаса жидкости в пласте:

V 3M = (V cr) /_ = p ‘oLAfl

iy ■

(13.78)

Заметим, что р* — коэффициент упругоемкости пласта, oL —

объем пласта, Др гу — понижение давления на стенке галереи,

которое при f=oo достигается во всем пласте. Действительно, из

формул (13.71), (13.73), (13.74) получается, что

Ap(x,f)-*4Pry,C(M)-»<),Gr(f)->0 при оо. (13.79)