Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1

Подождите немного. Документ загружается.

мерных потоках соответственно в пространстве одного, двух и трех

измерений:

( Ар ) а=0 = ^ е "4* - VjbTerfc

2а/:

4к* 4к*

= ^ ^ ie rfc ' / P _

2o/fc 4к? ’

(4.13)

(А Р )а =1 =

4я**

-E i

Н У

< ^2 >

Н -

4кЬк

4к*

V J

•■тж*

(4.14)

у А \ Gc^ f

<4р," 2 = Щ еГ,С

л/# Г

4к/ ‘

(4.15)

Определения, свойства и графики дополнительной функции

ошибок erfc х и кратной интегральной дополнительной функции

ошибок /erfc х см. в § 2 Приложения.

Определения, свойства и графики упрощенной интегральной

показательной функции [ -Ei ( -х ) ] и интегральной показательной

функции Е j (х ) см. в § 3 и 4 Приложения*.

Определим величину Qg расхода жидкости через «поперечное»

сечение потока 5 = const. Для этого в формулу (3.43) подставим

производную , полученную при дифференцировании равен

ства (4.9):

1 +а

а_ 1 г1

1 V2 >

а -1

<^2 >

^ е- ё '

2 1 2 ’ 4к*

V J

4к£

\ )

(4.16)

Формулу (4.16) можно упростить, если учесть следующее

соотношение, полученное с помощью равенства (П.99):

По поводу названий интегральных показательных функций смотреть специаль

ное примечание в конце § 4 Приложения.

На основании (4.17) формула (4.16) примет вид:

1+а

а + 1 V-

2 ’ 4кt

Для условий прямолинейно-параллельного потока в формулу

(4.18) надо подставить а = 0 и учесть равенства (П.9) и (П.109):

(

б| ) о=о — Qc erfc "\/ ^ •

(4.19)

Для условий плоско-радиального потока в формулу (4.18) надо

подставить а = 1 и учесть равенства (П. 8) и (П. 108):

(G | )a = l = Qce

(4.20)

Для условий сферического радиального потока в формулу (4.18)

надо подставить а = 2 и учесть равенства (П.9) и (П. 110):

(Q |)a = 2 = Q / erfcV ^ + ^ V £ "e 4|^

(4.21)

Количество Vg жидкости, которая к моменту t протечет через

сечение ^ = const потока, определится равенством (3.45), в которое

надо подставить величину Qg из (4.18):

Для вычисления интеграла в правой части равенства (4.22)

применим метод интеграции по частям и учтем равенства (П. 100)

и (П. 103):

vf=-

1+а

1 ± »

2 ’ 4к# | 4к *, 7|^ 4к#

(4.23)

В формуле (4.23) под знаком интеграла заменим переменную t

на и, приняв:

ьг Ь 2 Ъ 2

т~: = и, t = , dt = - , du

4кt 4ки 4ku 2

(4.24)

Vf = -

T + a l

1+a 11

2 ’ 4k*

_ OO

-¥ -\ u

a -3

-u

e rfu

4к*

(4.25)

По поводу формул (4.16), (4.22)—(4.25) следует учесть те же

замечания, какие выше были сделаны по поводу формул (4.7) и

(4.9). Поэтому, например, вместо формулы (4.16) предпочтительнее

пользоваться выведенной в § 4 данной главы формулой (4.126),

полагая в ней s = 0, что приводит к формуле (4.126 бис).

На основании равенства (П.67) интеграл в правой части можно

заменить обобщенной интегральной показательной функцией:

(4.26)

(4.27)

V У

l i

4кt

<£2 '

^2~ Е (

г ^2 ^

4кt

\ )

3^1

4к*

v* =

Учитывая (4.26), перепишем (4.25):

Qct

1+сО

Г 1+а

f l l '

1 + а

^ Р я

Г1 1 '

2 ’ 4кt

\ У

4кt

\ )

" 3-а

4к*

V )

Интеграл, входящий в формулу (4.25), можем выразить через

неполную гамма-функцию, используя соотношение (П.97):

v*=-

Qct

a+1

(a + 1

( 1 9“ 2 ^

а-1

2 ’ 4к1

\ J

4к*

\ )

2 ’ 4к*

V J

(4.27а)

Полагая a = 0 в формуле (4.27) и учитывая равенства (П.83),

(П. 109) и (П.9), получим величину (V g )a=0 для прямолинейно-па

раллельного потока:

(V |)a-oe <2cfferfc Vfe- 2

^ Щ ^

ierfc V ^ " l • (428>

На основании равенства (П.34) формулу (4.28) можно переписать так:

(V|)«=o = 4Gc t i 2erfc V g " . (4.28 бис)

Полагая в формуле (4.27) a = 1 и учитывая равенства (П.8),

(П.69) и (П.108), получим величину ( Vg )a = i для плоско-радиального

потока*:

(V|)a=1= e c^ 2

4кt

= Qct\ е

t 2

4к?

-Ei

.1 1 '

4к*

(4.29)

Полагая в формуле (4.27) a = 2 и учитывая (П.9), (П.ЗЗ), (П.82)

и (П. 110), получим величину ( Vg)a=2 для сферического радиаль

ного потока:

(V %)a=2 = Qct erfc

С + ierfc .

4к*

4к£

(4.30)

В формуле (4.29) выражение, заключенное в фигурные скобки, совпадает с оп

ределением СКИП-функции II рода

ж.

4к*

(см. формулу (П.367).

§ 2. Анализ формул, характеризующих одномерные потоки

к стокам с постоянными дебитами

Сопоставляя между собой три формулы (4.13)—(4.15) для

понижения давления Ар, три формулы (4.19)—(4.21) для расхода

жидкости и три формулы (4.28)—(4.30) для объема V g

перетекшей жидкости, можно подметить закономерность, которая

подтверждается, если еще для каждой из перечисленных величин

выписать формулы при последующих значениях а, равных 3, 4,

5, и т.д. Именно оказывается, что при всех четных значениях

а (включая нуль) структура формул иная, чем при всех нечетных

значениях а . При всех четных значениях а (включая нуль) в

формулы обязательно входит дополнительная функция ошибок

либо кратная интегральная дополнительная функция ошибок

При всех нечетных значениях а эти специальные функции в

формулы не входят, но зато входят упрощенные интегральные

показательные функции (не считая еще и обычных показательных

функций). Такая закономерность прослеживалась и в предыду

щем параграфе при исследовании воздействия мгновенного стока.

Математическое пояснение такого рода закономерности приво

дится в § 2 главы 5 и в § 11 Приложения.

Подмеченная закономерность указывает на некоторое родство

в математическом описании одномерных потоков в пространствах

нечетного числа измерений (при четных числах а) и на некоторое

отличие в их математическом описании в пространствах четного

числа измерений (при нечетных числах а).

Для условий одномерных нестационарных потоков характе

ризующие их гидродинамические величины ( Ар , Qg, Vg) явля

ются функциями только двух переменных —одной координаты

£, и времени t. Поэтому особенно важно и интересно выявить

раздельное влияние изменения координаты и времени на каждую

из трех перечисленных функций и, для полноты картины, на

частные производные этих функций I и II порядков по коор

динате и времени. Анализ частных производных каждой из

функций необходим, чтобы выяснить темпы их изменения с

изменением времени или координаты, выявить критические ве

личины аргументов, при которых функции принимают экстре

мальные значения, определить положения критических точек и

точек перегиба на соответствующих графиках функций. Ради

краткости формулы для частных производных от каждой фун

кции здесь не приводятся, но в следующей главе некоторые из

таких формул для плоско-радиального потока выведены.

Заметим, что во все общие для всех одномерных потоков

формулы (4.9), (4.18), (4.27) величина а входит как параметр; во

все формулы входит коэффициент пьезопроводности пласта к —

основная характеристика темпов перераспределения величин в

нестационарных потоках. Как и следовало ожидать,

Ар, и Vg

прямо пропорциональны постоянному дебиту Qc стока.

Помимо перечисленных величин а , ^ , QCf в общую форму

лу (4.9) для понижения давления Ар явно входят коэффициент

проницаемости пласта к, коэффициент вязкости жидкости jll и

величина Аа, зависящая от геометрии потока (см.равенства (3.19)—

(3.21). Эти величины должны были явно входить в формулу для

понижения давления, так как оно является динамической характе

ристикой потока и существенно зависит от того, какие сопротив

ления приходится жидкости преодолевать при ее движении в

пласте. Коэффициенты проницаемости и вязкости к и ц, конечно,

оказывают влияние и на величины Qg и Vg, но неявно —через

коэффициент пьезопроводности к.

Анализ раздельного влияния времени t и координаты % начнем

с величины понижения давления Ар ( ^ , t) . Будем учитывать

частные значения специальных функций, определенные в § 2 и 3

Приложения.

Из всех формул (4.13)—(4.15) следует, что

т.к. в начальный момент поле давлений было невозмущенным —

движения жидкости в пласте не было.

Судя по формулам (4.13) и (4.14), видим, что в условиях

прямолинейно-параллельного и плоско-радиального потоков при

любом значении ^

т.е. с течением времени давление неограниченно снижается во всем

поле. Однако, судя по формуле (4.15), в условиях сферического ра

диального потока

Ар — 0 при t = О, % Ф О, (4.31)

Ар —> оо при t —> оо 9

(4.32)

(4.33)

т.е. с течением времени понижение давления в каждой точке поля

увеличивается, асимптотически приближаясь к некоторой конечной

величине, обратно пропорциональной расстоянию 5 точки от стока.

Из формул (4.14) и (4.15) следует, что в условиях плоско-ра-

диального и сферического радиального потоков

Это естественно, так как обеспечить получение конечной

величины дебита линейного или точечного стока в пространстве

можно, теоретически, только при бесконечном понижении давления

в таком стоке.

Из формулы (4.13) с учетом соотношения (П.35) следует, что

в условиях прямолинейно-параллельного потока, когда жидкость

притекает к плоскому стоку в пространстве, будет справедливо

следующее равенство:

Судя по формуле (4.35), понижение давления Ар в любой точке

плоского стока изменяется с течением времени по параболическому

закону — соответствующим графиком служит парабола с вершиной

в начале координат.

Если продифференцировать по времени равенства (4.13)—(4.15),

то можно обнаружить*, что при t = 0, 5^0 оказываются равными

нулю первая и последующие производные от понижения давления.

Это означает, что все кривые линии, соответствующие графикам

зависимости понижения давления от времени в любой точке поля,

за исключением стока (т.е. при 5*0)» касаются оси времени в

начале координат (см. рис. 4.1—4.3).

то можно определить абсциссы точек перегиба графиков зависи-

Заметим, что при подстановке значения t = 0 в выражения соответствующих

производных получаются неопределенности. Начиная стандартным способом исполь

зовать правило Лопиталя для раскрытия таких неопределенностей, сталкиваемся с

осложнениями и даже с «реальным бессилием» этого правила, прокомментирован

ного с особой тщательностью в книге акад.Н. Н. Лузина [411] в специальном заме

чании в § 149. Поэтому при раскрытии таких неопределенностей удобно

использовать соотношения типа (3.10).

Др = оо при £, = 0, t * о .

(4.34)

(4.35)

Если приравнять нулю вторые производные по времени— ^ ,

д2Лр

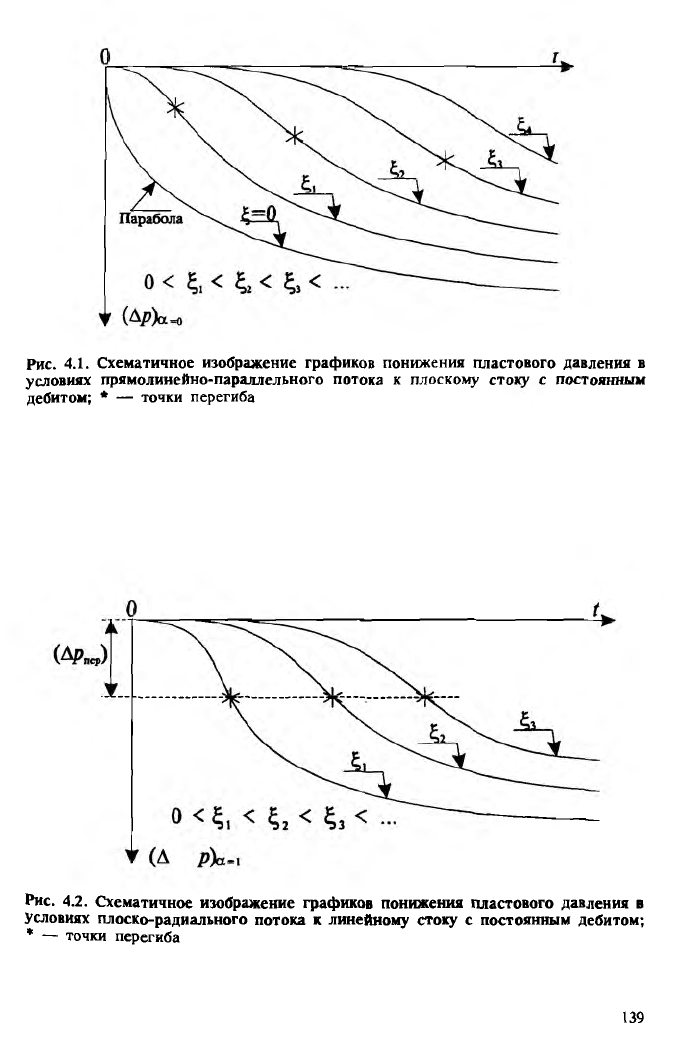
Рис. 4.1. Схематичное изображение графиков понижения пластового давления в

условиях прямолинейно-параллельного потока к плоскому стоку с постоянным

дебитом; * — точки перегиба

Рис. 4.2. Схематичное изображение графиков понижения пластового давления в

Условиях плоско-радиального потока к линейному стоку с постоянным дебитом;

* — точки перегиба

мости Др от t Для случаев а = 0,а=1 и а = 2, т.е. в условиях

прямолинейно-параллельного, плоско-радиального и сферического

радиального потоков, абсциссы f пер точек перегиба определяются

соответственно равенствами:

( t пер )а = 0 —

( ^ пер )а = 1

(4.36а)

2 к ’

1 ^ (4.366)

4 к ’

( t пер )а = 2 —

= 1 ^ (4.37)

6 к

Если подставить значения абсцисс точек перегиба в равенства

(4.14) и (4.15), то получим соответствующие ординаты точек

перегиба:

( ^ - . ^ i e r f c V F . O ^ , <4'38»

С-386*

(Ad ) ^ ^ ^ erfc — - 0 0339 ^ ^ (4-39)

( Ар пер )а = 2- erfc 2 _ 0,0339 .

На основании формулы (4.386) ординаты всех точек перегиба

одинаковы для всех кривых, соответствующих различным значе

ниям 5- Судя же по формуле (4.39), ординаты точек перегиба

графиков зависимости Ар от t обратно пропорциональны величине 5*

Все выявленные свойства графиков зависимости понижения

давления Ар от времени t для трех простейших одномерных потоков

отражены схематично на рис. 4.1, 4.2, 4.3. На рис. 4.2 все точки

перегиба, отмеченные крестиками, лежат на прямой, параллельной

оси абсцисс. На рис. 4.3 пунктиром отмечены асимптоты.

Судя по всем графикам на рис. 4.1—4.3, практически заметное

понижение давления в любой точке пласта, удаленной от стока,

обнаруживается не сразу (хотя, теоретически, давление начинает

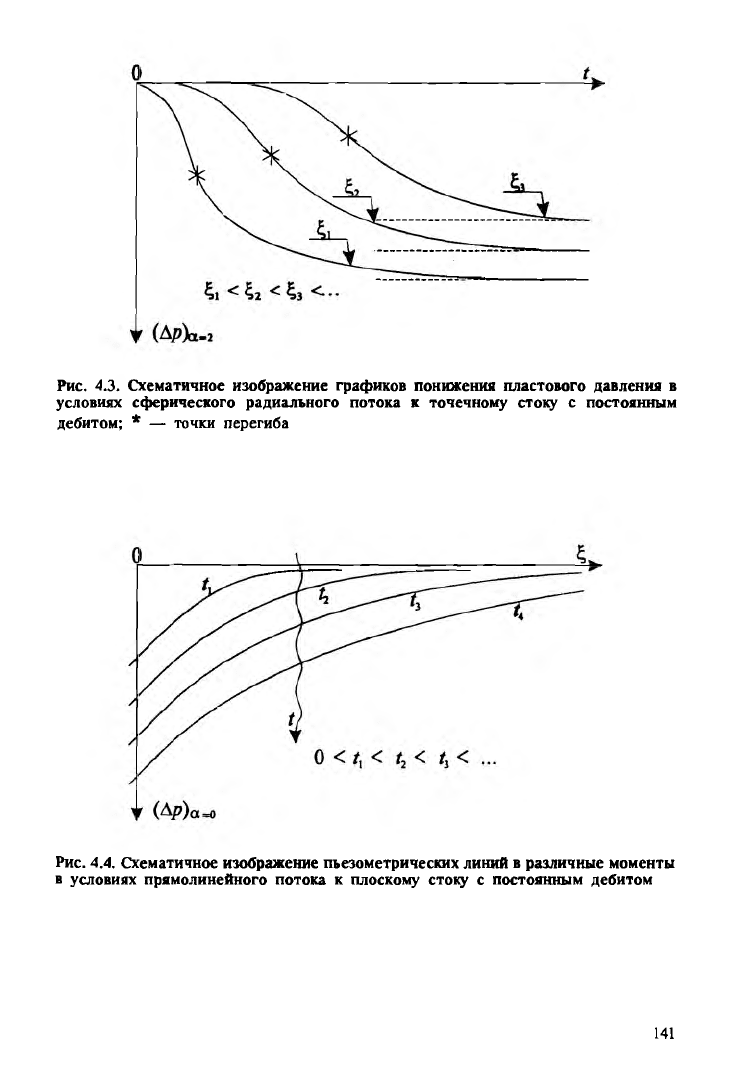
Рис. 4.3. Схематичное изображение графиков понижения пластового давления в

условиях сферического радиального потока к точечному стоку с постоянным

дебитом; * — точки перегиба

Рис. 4.4. Схематичное изображение пьезометрических линий в различные моменты

в условиях прямолинейного потока к плоскому стоку с постоянным дебитом