Сборник заданий для выпускного экзамена по математике на уровне общего базового образования под редакцией Адамовича

Подождите немного. Документ загружается.

200

Раздел V

201

5-й уровень

285*. а) Известно, что каждая сторона одного тре уголь ника

больше любой стороны другого тре уголь ника. Следует

ли из этого, что площадь первого тре уголь ника больше

площади второго тре уголь ника?

б) Внутри тре уголь ника АВС найдите такую точку Х,

что S

ABX

= S

XAC

= S

XBC

286**. а) Найдите длину отрезка, делящего трапецию

ABCD с основаниями AD = а, BC = b (a  b) на две

равновеликие трапеции, заключенного между боко-

выми сторонами трапеции и параллельного ее основа-

ниям.

б) Проведите прямую через одну из вершин произволь-

ного выпуклого че ты рех уголь ника, которая делит его

на

две равновеликие части.

287. а) Существует ли равнобедренный тре уголь ник, вер-

шины которого на координатной плоскости находятся в

точках с целочисленными координатами?

б) Существует ли прямоугольный тре уголь ник, верши-

ны которого на координатной плоскости находятся в

точках с целочисленными координатами?

288**. а) Докажите, что тре уголь ник, у которого две бис-

сектрисы

равны, является равнобедренным.

б) Докажите, что в че ты рех уголь нике, вписанном в

окружность, произведение длин диагоналей равно сум-

ме произведений длин противоположных сторон.

289*. Установите, может ли быть разверткой пирамиды:

а) правильный тре уголь ник;

б) правильный че ты рех уголь ник.

290*. Внутри данного тре уголь ника найдите точку, сум-

ма расстояний от которой до

его вершин наименьшая,

если известно, что:

а) тре уголь ник равносторонний;

б) тре уголь ник равнобедренный прямоугольный.

291*. Дан отрезок а. С помощью циркуля и линейки по-

строй те отрезок, удовлетворяющий условию:

а)

;

aax

б)

−

292. а) Докажите, что если в тре уголь нике две медианы

равны, то он равнобедренный.

б) Установите, верно ли утверждение: если тре уголь-

ник равнобедренный, то две его медианы равны.

293**. а) Из всех тре уголь ников с данным углом α при

вершине и данной суммой a + b его боковых сторон

найдите тре

уголь ник с наименьшим основанием.

б) Из всех тре уголь ников с данным углом α при верши-

не и данным противолежащим ему основанием а най-

дите тре уголь ник с наибольшим периметром.

294*. а) В трапеции ABCD (AD и BC — основания) точка K

лежит на стороне CD, причем CK  KD = 1  2, AK

пересе-

кает BD в точке O. Докажите, что если: BC  AD = 1  2,

то ВО = ОD.

б) В трапеции ABCD (AD  BC) точка M лежит на сторо-

не CD, причем CM  MD = 2  3, AB = AD, BC  AD = 1  3.

Докажите, что BD ⊥ AM

295*. а) В тре уголь нике АВС точка D лежит на сто-

роне АС, DC = a, AC = b, BC =

.ab

Докажите, что

∠ ВАС = ∠ DВC.

б) В трапеции ABCD (AD  BC) AD = a, BC = b, AC =

.ab

Докажите, что ∠ ВАС = ∠ ADC.

296**. а) Высота AK, биссектриса BL и медиана CM тре-

уголь ника ABC пересекаются в одной точке О, причем

АО = ОВ. Докажите, что тре уголь ник АВС — равно-

сторонний.

б) В тре уголь нике АВС все углы острые, высота СН и

медиана BK равны, кроме

того, ∠ KBC = ∠ HCB. Дока-

жите, что тре уголь ник АВС — равносторонний.

202

Раздел V

297**. а) В равнобедренном тре уголь нике длина основа-

ния равна

см, а длины медиан, проведенных к

боковым сторонам, равны 3 см. Докажите, что эти ме-

дианы перпендикулярны.

б) Докажите, что квадрат медианы, проведенной к ги-

потенузе прямоугольного тре уголь ника, в 5 раз мень-

ше суммы квадратов двух других медиан.

Раздел VI

ТЕКСТОВЫЕ ЗАДАЧИ

1-й уровень

1. а) В двузначном числе сумма цифр равна 10. Число

единиц на 6 больше числа десятков. Выберите систему

уравнений, решив которую можно найти данное чис-

ло:

А:

10,

⎧

⎨

−=

⎩

Б:

10,

⎧

⎨

−=

⎩

В:

10 10,

⎧

⎨

−=

⎩

(x — число десятков, y — число единиц данного числа).

б) В двузначном числе сумма цифр равна 13. Число де-

сятков на 3 больше числа единиц. Выберите систему

уравнений, решив которую можно найти данное число:

А:

13,

⎧

⎨

−=

⎩

Б:

13,

⎧

⎨

−=

⎩

В:

10 13,

⎧

⎨

−=

⎩

(x — число десятков, y — число единиц данного числа).

2*. а) Сумма трех последовательных нечетных чисел рав-

на 45. Выберите уравнение, с помощью которого мож-

но найти эти числа (буквой n обозначено натуральное

число):

А: n + (n + 2) + (n + 4) = 45

Б: (n + 1) + (n + 3) + (n + 5) =

В: (2n − 1) + (2n + 1) + (2n + 3) = 45

б) Разность квадратов двух последовательных нату-

ральных чисел равна 21. Выберите уравнение, с помо-

щью которого можно найти эти числа (буквой n обо-

значено натуральное число):

А: (n + 1)

− n

= 21

Б: n

− (n − 1)

= 21

В: (2n + 1)

− (2n − 1)

= 21

3*. а) В двузначном числе цифра десятков в два раза боль-

ше цифры единиц. Если цифры числа переставить, то

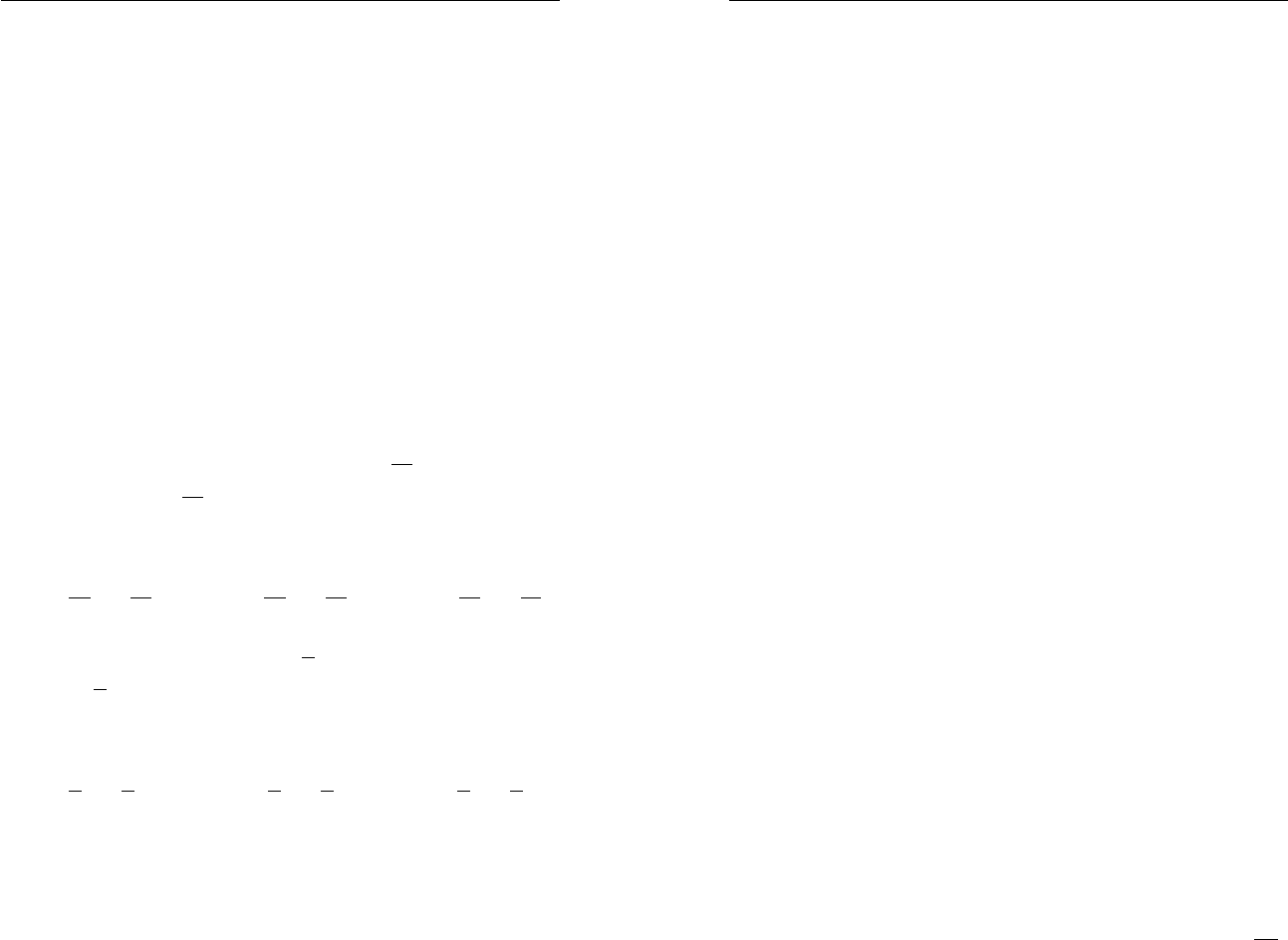
204

Раздел VI

205

1-й уровень

полученное число будет меньше данного на 36. Вы-

берите уравнение, с помощью которого можно найти

двузначное число, зная, что х — цифра единиц:

А: (10  2х + х) − (10х + 2х)

= 36

Б: (10  2х + х) + 36 = 10х + 2х

В: 10х + 2х = 36 − (10  2х + х)

б) В двузначном числе цифра единиц в три раза мень-

ше цифры десятков. Если цифры числа переставить,

то полученное число будет меньше данного на 36. Вы-

берите уравнение, с помощью которого

можно найти

двузначное число, зная, что х — цифра единиц:

А: (10х + 3х) = (10  3х + х) + 36

Б: (10  3х + х) − 36 = 10х + 3х

В: 10х + 3х = 36 − (10  3х + х)

4. а) Одно число больше другого на 16,

большего чис-

ла составляют

меньшего. Укажите систему уравне-

ний, с использованием которой можно найти эти числа:

А:

32 16

16,xy

−=

⎧

⎪

⎨

⎪

⎩

Б:

32 16

16,xy

−=

⎧

⎪

⎨

⎪

⎩

В:

32 16

16,xy

⎧

⎪

⎨

⎪

⎩

б) Сумма двух чисел 76, а

большего числа состав-

ляют

меньшего. Укажите систему уравнений, с ис-

пользованием которой можно найти эти числа:

А:

76,xy

⎧

⎪

⎨

⎪

⎩

Б:

76,xy

−=

⎧

⎪

⎨

⎪

⎩

В:

76,xy

⎧

⎪

⎨

⎪

⎩

5. а) Разность двух чисел равна 7, а их произведение рав-

но 54. Укажите систему уравнений, с использованием

которой можно найти эти числа:

А:

⎧

⎨

⎩

Б:

−=

⎧

⎨

⎩

В:

54,

⎧

⎨

⎩

б) Сумма двух чисел равна 21, а их произведение рав-

но 108. Укажите систему уравнений, с использованием

которой можно найти эти числа:

А:

21,

108

⎧

⎨

⎩

Б:

21,

108

−=

⎧

⎨

⎩

В:

108,

⎧

⎨

⎩

6. а) Сумма трех последовательных натуральных чи-

сел равна 423. Укажите уравнение, с помощью кото-

рого можно решить задачу (n — любое натуральное

число):

А: n + (n + 1) + (n + 2) = 423

Б: (n + 2) + (4n + 4) + n = 423

В: (n + 3) + (n + 5) + (n + 7) = 423

б) Сумма

трех последовательных натуральных чисел

равна 366. Укажите уравнение, с помощью которого

можно решить задачу (n — любое натуральное число):

А: n + (n + 1) + (n + 2) = 366

Б: (n + 2) + (4n + 4) + n = 366

В: (n + 3) + (n + 5) + (n + 7) = 366

7. а) Произведение двух последовательных четных

на-

туральных чисел равно 840. Выберите уравнение, с

помощью которого можно найти эти числа (буквой n

обозначено натуральное число):

А: 2n 2 (n + 1) = 840

Б: 2n (2n + 1) = 840

В: n (n + 1) = 840

б) Произведение двух последовательных нечетных на-

туральных чисел равно 675. Выберите уравнение, с

помощью которого можно найти эти

числа (буквой n

обозначено натуральное число):

А: (2n − 1)  (2n + 1) = 675

Б: 2n  (2n + 1) = 675

В: (n − 1) (n + 1) = 675

8. а) Скорость движения лодки по течению реки 15,3

км

Укажите правильное выражение для решения задачи

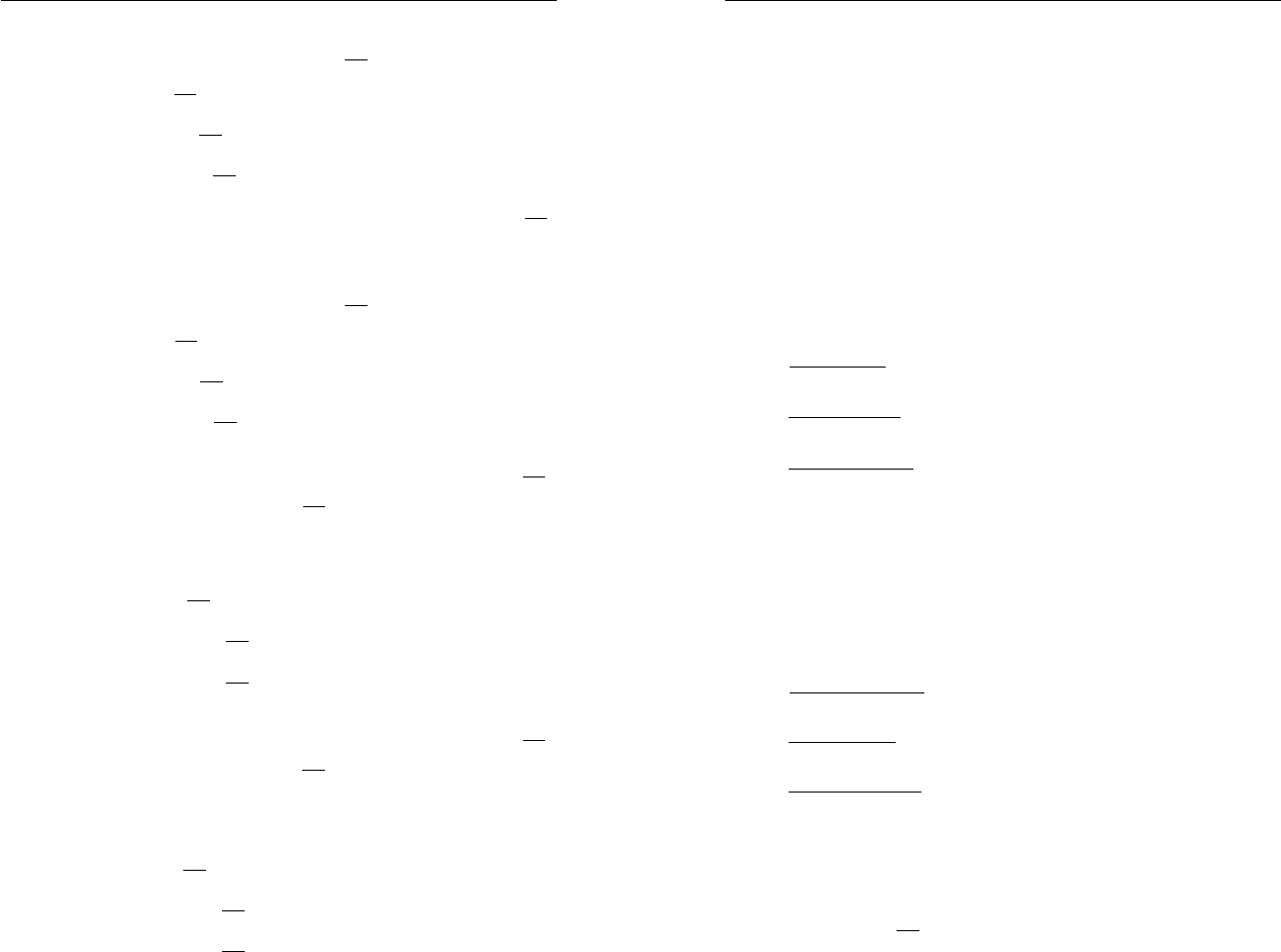
206

Раздел VI

207

1-й уровень

и найдите скорость движения лодки против течения,

если скорость течения реки 4,5

км

А: (15,3 − 4,5)

км

Б: (15,3 − 4,5  2)

км

В: ((15,3 + 4,5)  2)

км

б) Скорость движения катера по течению реки 40,2

км

Выберите правильное выражение для решения задачи

и найдите скорость движения катера против течения,

если скорость течения реки 4,2

км

А: (40,2 − 4,2)

км

Б: (40,2 − 4,2  2)

км

В: ((40,2 + 4,2)  2)

км

9. а) Скорость движения катера по течению реки 38,6

км

а против течения — 33,6

км

Выберите правильное

выражение для решения задачи и найдите скорость

течения реки:

А: (38,6 − 33,6)

км

Б: ((38,6 + 33,6)  2)

км

В: ((38,6 − 33,6)  2)

км

б) Скорость движения лодки по течению реки 16,8

км

а против течения — 11,8

км

Выберите правильное

выражение для решения задачи и найдите скорость

течения реки:

А: (16,8 − 11,8)

км

Б: ((16,8 − 11,8)  2)

км

В: ((16,8 + 11,8)  2)

км

10. Пройденный пешеходом путь s, его скорость v и время

движения t связаны соотношением s = vt. Найдите ско-

рость пешехода, если:

а) за 4 ч он прошел 24 км;

б) за 7 ч он прошел 35 км;

11*. а) Расстояние между двумя городами, равное 720 км,

скорый поезд проходит за 9 ч, а пассажирский — за

12 ч.

Когда пассажирский поезд прошел 0,1 пути, сле-

дом вышел скорый поезд. Выберите правильное вы-

ражение для решения задачи и укажите, через какое

время скорый поезд догонит пассажирский:

А:

720 0,1

720 (12 9)−



Б:

720 0,1

720:9 720:12−



В:

720 0,1

720 12 720 9+





б) Расстояние между двумя городами, равное 960 км,

скорый поезд проходит за 12 ч, а пассажирский — за

16 ч. Когда пассажирский поезд прошел 0,1 пути, сле-

дом вышел скорый поезд. Выберите правильное вы-

ражение для решения задачи и укажите, через какое

время скорый поезд догонит пассажирский:

А:

−

960 0,1

960 12 960 16





Б:

−

960 0,1

960 (16 12)





В:

960 0,1

960 12 960 16+





12. Используя формулу пути равномерного движения

s = vt, найдите:

а) время движения теплохода, прошедшего 270 км со

скоростью 45

км

;

б) скорость поезда, прошедшего 480 км за 4 ч.

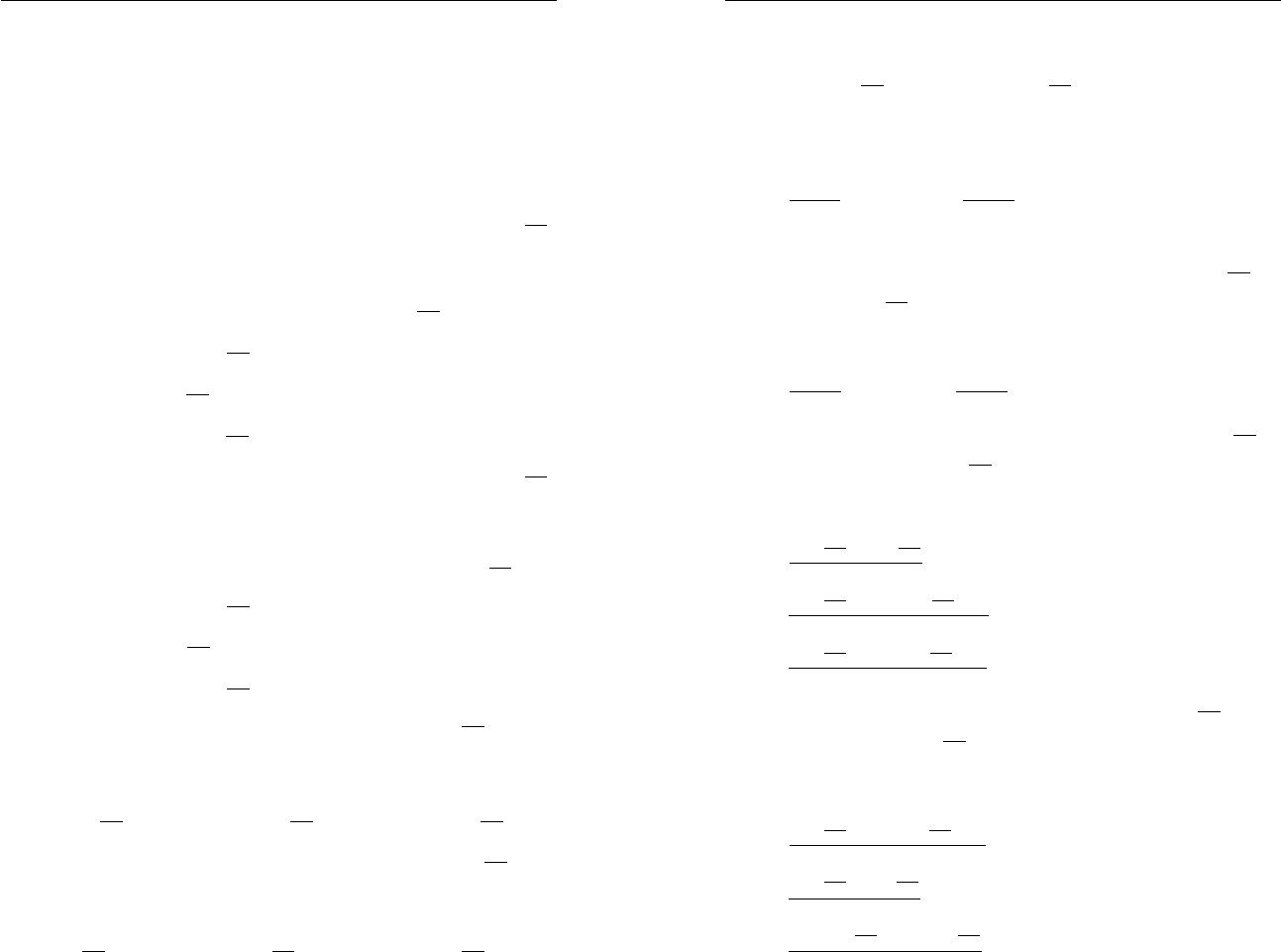
208

Раздел VI

209

1-й уровень

13. а) Выберите из чисел 1, 2, 3 то число, которое следу-

ет написать вместо многоточия: «Преодолевая за один

час 4 км, туристы за четверть часа проходят … км».

б) Выберите из чисел 12, 14, 16 то число, которое сле-

дует написать вместо многоточия: «Проплывая на бай-

дарках за четверть часа 4 км, туристы преодолевают за

час … км».

14. а) Собственная

скорость движения катера 32,8

км

Выберите правильное выражение для решения задачи

и укажите скорость течения реки, если при движении

по течению скорость катера равна 34,2

км

А: ((34,2 − 32,8)  2)

км

Б: (34,2 − 32,8)

км

В: ((34,2 + 32,8)  2)

км

б) Собственная скорость движения теплохода 53,2

км

Выберите правильное выражение для решения задачи

и укажите скорость течения реки, если при движении

против течения скорость теплохода равна 50,5

км

А: ((50,5 + 53,2)  2)

км

Б: (53,2 − 50,5)

км

В: ((53,2 − 50,5)  2)

км

15. а) Человек идет с постоянной скоростью 4,5

км

Какой

путь он пройдет за х ч? Выберите правильное выраже-

ние для решения задачи:

А: 4,5

км

 х ч Б: 4,5

км

 х ч В: 4,5

км

+ х ч

б) Велосипедист ехал полчаса со скоростью v

км

Ка-

кой путь он проехал? Выберите правильное выражение

для решения задачи:

А: v

км

 0,5 ч Б: v

км

 0,5 ч В: v

км

+ 0,5 ч

16. а) Из двух населенных пунктов выехали одновременно

навстречу друг другу два мотоциклиста: один со ско-

ростью v

км

а другой — v

км

Найдите расстояние

между пунктами, если известно, что мотоциклисты

встретились через 2,5 ч. Выберите правильное выра-

жение для решения задачи:

А:

2,5

vv+

км Б:

2,5

vv+

км В:

2,5( )vv+

км

б) Из двух городов выехали одновременно навстречу

друг другу два автобуса: один со скоростью v

км

другой — v

км

Найдите расстояние между городами,

если известно, что автобусы встретились через 3,5 ч.

Выберите правильное выражение для решения за дачи:

А:

3,5

vv+

км Б:

3,5

км В:

(( ) 3,5)vv+ 

км

17*. а) Моторная лодка шла 3 ч со скоростью 17,9

км

5 ч со скоростью 18,7

км

Определите ее среднюю ско-

рость. Выберите правильное выражение для решения

задачи:

А:

км км

17,9 18,7

чч

2 ч

Б:

км км

17,9 3 ч 18,7 5 ч

чч

3 ч 5 ч



В:

км км

17,9 3 ч 18,7 5 ч

чч

2 ч

+

б) Велосипедист ехал 4 ч со скоростью 12,3

км

и 2 ч

со скоростью 11,7

км

Определите его среднюю ско-

рость. Выберите правильное выражение для решения

задачи:

А:

км км

12,3 4 ч 11,7 2 ч

чч

4 ч 2 ч



Б:

км км

12,3 11,7

чч

2 ч

В:

км км

4ч 12,3 2ч 11,7

чч

4 ч 2 ч

−



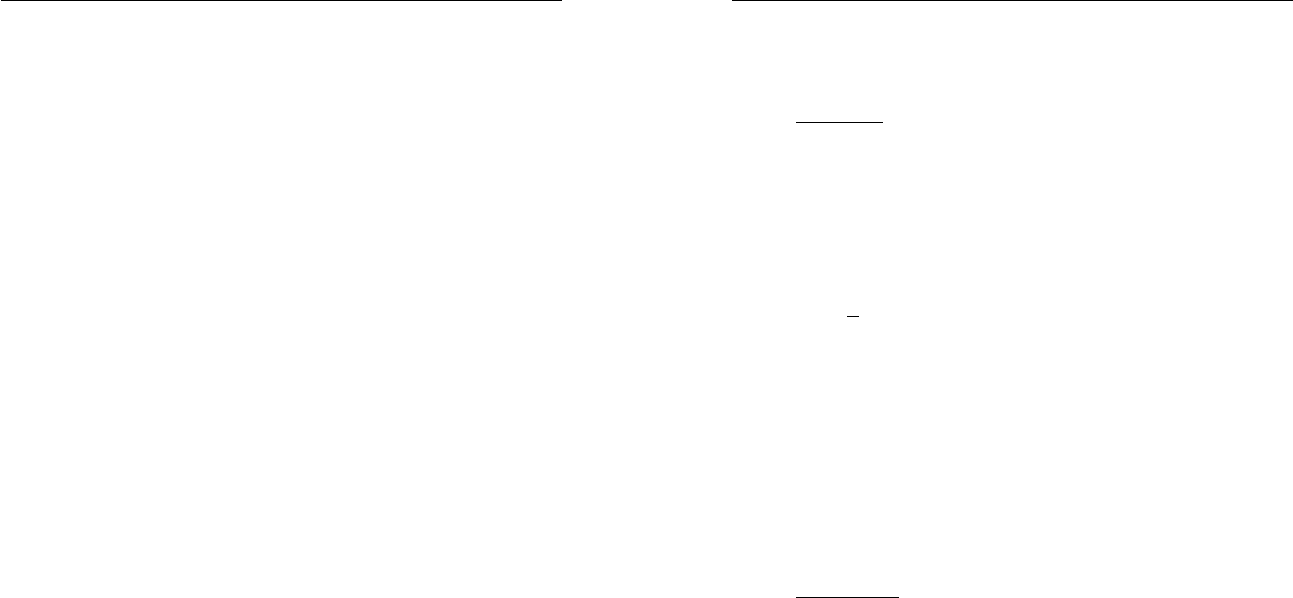
210

Раздел VI

211

1-й уровень

18. а) За контрольную работу по математике 15 % учени-

ков получили отметку «10» баллов. Если «10» баллов

получили 6 учеников, то сколько человек писали конт-

рольную работу? Выберите правильное ра венст во для

решения задачи:

А: 6  0,85 = 51 (уч.)

Б: 6  15 = 90 (уч.)

В: 6  0,15 = 40 (уч.)

б) В олимпиаде по математике приняли участие 120

учащихся восьмых

и девятых классов. Если восьми-

классники составили 55 % всех учащихся, то сколь-

ко девятиклассников приняло участие в олимпиаде?

Выберите правильное ра венст во для решения за-

дачи:

А: 120  0,55 = 66 (уч.)

Б: 120  0,45 = 54 (уч.)

В: 120 − 55 = 65 (уч.)

19. а) Выберите из чисел 30, 108, 150 то, которое следу-

ет записать вместо многоточия: «В магазин

привезли

180 кг яблок. За день продали 60 % привезенных яб-

лок, что составило … кг».

б) Выберите из чисел 10, 16, 24 то, которое следует

записать вместо многоточия: «В классе 40 учеников.

В спортивных секциях занимается 40 % учеников, что

составляет … человек».

20. а) От Минска до Бреста 360 км. Мотоциклист проехал

35 % этого расстояния и сделал остановку. Сколько

километров составил

путь мотоциклиста до остановки?

Выберите правильное ра венст во для решения задачи:

А: 360  3 = 120 (км)

Б: 360  0,35 = 126 (км)

В: 360  0,65 = 234 (км)

б) На стадионе 540 мест. На футбольный матч было

продано 55 % всех билетов. Сколько билетов было

продано? Выберите правильное ра венст во для реше-

ния задачи:

А: 540  0,55 = 297 (бил.)

540 100%

55%

981,82 (бил.)=



В: 540 (1 − 0,55) = 243 (бил.)

21. а) От Минска до Бреста 360 км. Мотоциклист проехал

35 % этого пути и сделал остановку. Сколько километ-

ров осталось проехать мотоциклисту? Выберите пра-

вильное ра венст во для решения задачи:

А: 360 

= 240 (км)

Б: 360  0,35 = 126 (км)

В: 360  0,65 = 234 (км)

б) На стадионе 540 мест. На футбольный матч было

продано 55 % всех билетов. Сколько мест осталось

незаполненными? Выберите правильное ра венст во для

решения задачи:

А: 540  0,55 = 297 (мест)

Б: 540  0,45 = 243 (места)

В:

540 100%

100% 55 %

1200 (мест)

−



22. а) В библиотеке 12 % всех книг — словари. Сколько

всего книг в библиотеке, если словарей 900? Выберите

правильное ра венст во для решения задачи:

А: 900  0,12 = 7500 (кн.)

Б: (900  0,12) − 900 = 6600 (кн.)

В: 900  12 = 10 800 (кн.)

б) В парке 8 % всех деревьев — клены. Сколько всего

деревьев в парке, если кленов 60? Выберите правиль-

ное ра

венст во для решения задачи:

А: (60  0,08) − 60 = 690 (д.)

Б: 60  8 = 480 (д.)

В: 60  0,08 = 750 (д.)

212

Раздел VI

213

1-й уровень

23*. а) В классе а учащихся. Из них отличников — b, что

составляет р % общего числа учащихся класса. Выра-

зите зависимость между a, b и p. Выберите правильное

ра венст во для решения задачи:

А:

p =

Б:

100

p = 

В:

100

p = 

б) Зарплата рабочего m p. в месяц, премия — a p.,

что составляет р % зарплаты. Выразите зависимость

между а, m и p. Выберите правильное ра венст во для

решения задачи:

А:

p =

Б:

100%

p = 

В:

100%

p =



24*. а) При выпечке хлеба припек составляет 40 % массы

муки. Сколько можно получить хлеба из 250 кг муки?

Выберите правильное выражение для решения задачи

и ответьте на поставленный вопрос:

А: 250 + 250  0,4

Б: 250 − 250  0,4

В: 250 + 250  0,4

б) Грибы при сушке теряют 90 % своей массы. Сколь-

ко нужно взять свежих грибов, чтобы получить

кг

сухих? Выберите правильное выражение для решения

задачи и ответьте на поставленный вопрос:

А:

90,1

Б:

990,9+ 

В:

9 : 10 100%

25*. а) В трех классах школы 90 учеников. В первом клас-

се учеников на 10 % больше, чем во втором, а в тре-

тьем — на 6 человек меньше, чем в первом. Выбери-

те уравнение, соответствующее условию задачи, если

х — число учеников во втором классе:

А: (х + 10) + х + (х + 10 − 6) = 90

Б: (

х + 0,1х) + х + (х + 0,1х − 6) = 90

В: (х + 10х) + х + (х − 6) = 90

б) В двух классах 63 ученика. Во втором классе число

учеников составляет

числа учеников первого клас-

са. Выберите уравнение, соответствующее условию за-

дачи, если х — число учеников в первом классе:

А:

(63 ) 63xx+−=

Б:

63 63x−=

В:

63xx+=

26**. а) Вещь стоила 25 000 р. После снижения цены она

стала стоить 20 000 р. Укажите нера венст во, при по-

мощи которого можно ответить на вопрос: верно ли что

цена снизилась не более чем на 20 %?

А:

20000 100%

25000

100% 20%−





Б:

20000 100%

25000

100% 20 %−





В:

20000 100%

25000

100% 20 %−





б) Рабочий по плану должен был изготовить 120 дета-

лей, а он изготовил 138 деталей. Укажите нера венст-

во, при помощи которого можно ответить на вопрос:

верно ли, что рабочий перевыполнил план не более чем

на 16 %?

А:

138 100%

120

100% 16 %−





Б:

138 100%

120

100% 16 %−





В:

138 100%

120

100% 16 %−





27. а) В двух бригадах 56 рабочих. В первой — в три раза

больше, чем во второй. Сколько рабочих во второй

бригаде? Выберите уравнение, соответствующее усло-

вию задачи, и решите его (х — число рабочих во вто-

рой бригаде):

А: 3х + х = 56 Б: (3 + х) + х = 56 В:

3х =

б) На двух улицах 117 домов. На первой — в два раза

меньше, чем на второй. Сколько домов на первой ули-

це? Выберите уравнение, соответствующее условию

214

Раздел VI

215

1-й уровень

задачи, и решите его (х — число домов на первой

улице):

А: 2х − х = 117 Б: 2х + х = 117 В:

117

х +=

28. а) Сыну 20 лет. Его возраст относится к возрасту отца

как 4  9. Сколько лет отцу? Выберите правильный от-

вет:

А: 40 лет Б: 45 лет В: 50 лет

б) Брату 18 лет. Его возраст относится к возрасту сес-

тры как 3  4. Сколько лет сестре?

А: 24 года Б: 16 лет В: 12 лет

29. а) Точка М делит отрезок АВ

, равный 48 см, на части

в соотношении 3  5. Найдите длину каждой части. Вы-

берите правильный ответ:

А: 15 см и 33 см

Б: 20 см и 28 см

В: 18 см и 30 см

б) Точка А делит отрезок MN, равный 63 см, на части

в соотношении 4  5. Найдите длину каждой части. Вы-

берите правильный ответ:

А: 28 см и

35 см

Б: 30 см и 33 см

В: 27 см и 36 см

30*. а) Мастер изготовил сплав золота и серебра в соот-

ношении 5  8 соответственно, причем золота он взял

40 г. Найдите массу сплава. Выберите правильное

выражение для решения задачи и найдите его зна-

чение:

А: 40  5  (5 + 8)

Б: 40  5  8

В: 40 + 40  5

 8

б) Сплав содержит медь и никель в соотношении 8  3

соответственно, причем никель составляет 180 г. Най-

дите массу сплава. Выберите правильное выражение

для решения задачи и найдите его значение:

А: 180  3  (8 + 3)

Б: 180  3  8

В: 180  3 + 180

31*. а) В растворе уксуса соотношение уксусной кислоты и

воды равно 2  11

соответственно. Сколько надо взять

уксусной кислоты, чтобы получить 780 г раствора?

Выберите правильное выражение для решения задачи

и найдите его значение:

А: 780  (2 + 11)  2

Б: 780  11  2

В: 780  (11 + 2)  11

б) В сиропе соотношение сахара и воды равно 2  21

соответственно. Сколько надо взять сахара, чтобы по-

лучить 920 г сиропа? Выберите

правильное выражение

для решения задачи и найдите его значение:

А: 920  (2 + 21)  2

Б: 920  21  2

В: 920  (21 + 2)  21

32*. а) Кусок сплава массой 36 кг содержит медь и цинк

в соотношении 5  7 соответственно. Сколько цинка в

данном сплаве? Выберите правильное выражение для

решения задачи и найдите его значение:

А: 36 

(5 + 7)  5

Б: 36  (5 + 7)

В: 36  (5 + 7)  7

б) Кусок сплава весом 45 кг содержит медь и цинк в

соотношении 4  5 соответственно. Сколько меди в дан-

ном сплаве? Выберите правильное выражение для ре-

шения задачи и найдите его значение:

А: 45  (5 + 4)  5

Б: 45  (5 + 4)

В: 45  (5 + 4)  4

33*. а) Некоторый сплав состоит из двух металлов, входящих

в него в соотношении 3  4 соответственно. Извест но, что

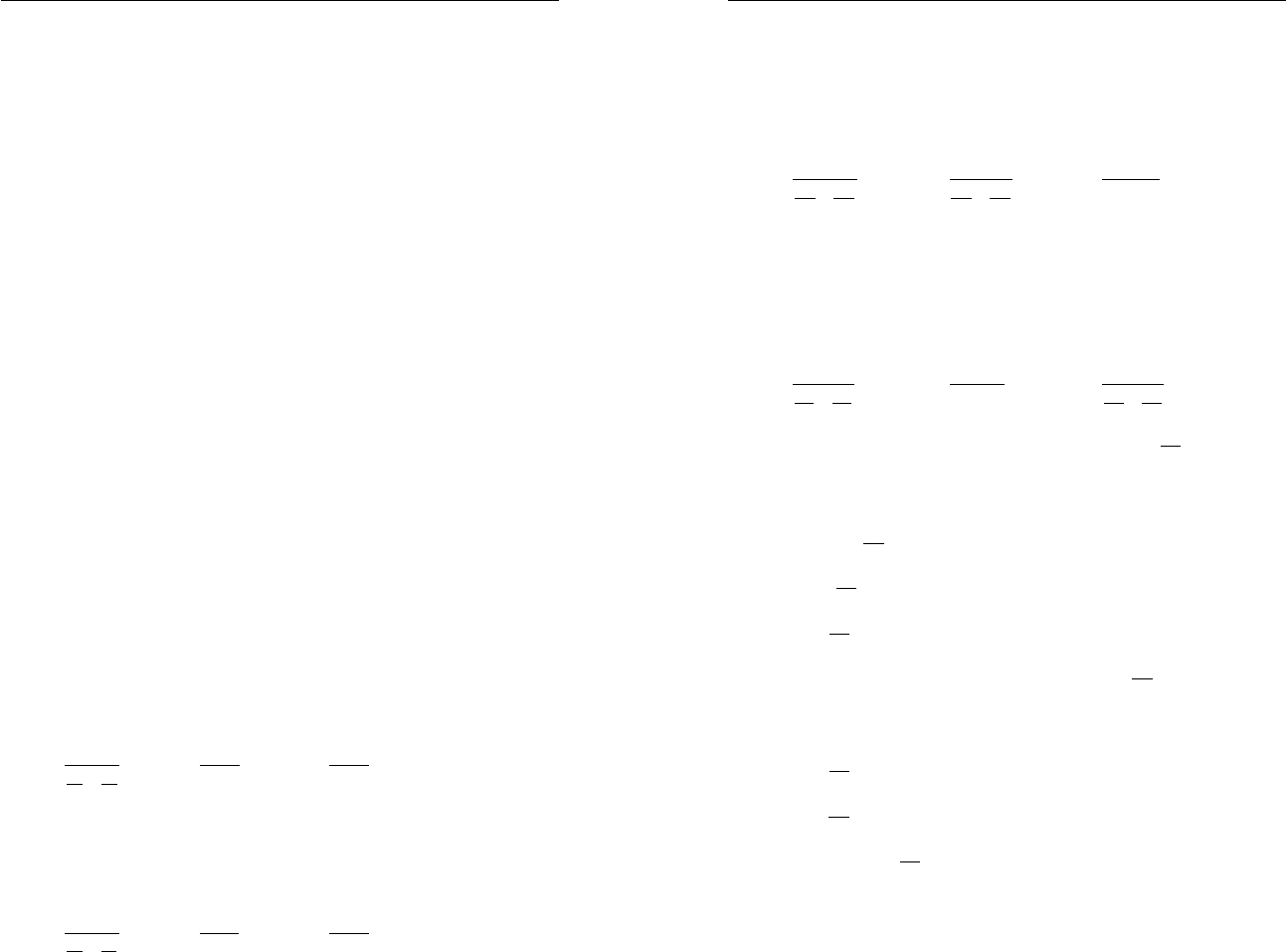
216

Раздел VI

217

1-й уровень

в сплаве содержится первого металла 120 г. Найдите

массу второго металла. Выберите правильное выраже-

ние для решения задачи и найдите его значение:

А: 120  (3 + 4)

Б: 120  3  (3 + 4)

В: 120  3  4

б) Некоторый сплав состоит из двух металлов, входящих

в него в соотношении 5  4 соответственно. Известно,

что в сплаве содержится первого металла 200 г. Найди-

те массу второго металла. Выберите правильное выра-

жение для решения задачи и найдите его значение:

А: 200  (5 +

Б: 200  5  4

В: 200  4  5

34*. Используя основное свойство пропорции, решите за-

дачу:

а) Три ученика пропололи грядку за 4 ч. За сколько ча-

сов выполнят эту работу два ученика?

б) Четыре каменщика могут выполнить работу за

15 дней. За сколько дней выполнят эту работу три ка-

менщика?

35*. а) Одна труба

заполняет бассейн за 6 ч, а вторая —

за 9 ч. За какое время заполнится бассейн, если будут

работать две трубы одновременно? Выберите правиль-

ное выражение для решения задачи и найдите его зна-

чение:

А:

Б:

В:

69+

б) Один насос заполняет бак за 2 ч, а второй — за 3 ч.

За какое время заполнится бак, если будут работать

два насоса одновременно? Выберите правильное выра-

жение для решения задачи и найдите его значение:

А:

Б:

В:

23+

36*. а) Два каменщика вместе сложили стену за 20 дней,

один из них мог бы выполнить эту работу за 36 дней.

За сколько дней может выполнить эту работу второй?

Выберите правильное выражение для решения задачи

и найдите его значение:

А:

20 36

Б:

20 36

−

В:

36 20−

б) Одна машинистка может перепечатать рукопись

за 15 ч, а две, работая вместе, — за 10 ч. За сколько

часов выполнит эту работу вторая машинистка? Вы-

берите правильное выражение для решения задачи и

найдите его значение:

А:

10 15

Б:

15 10−

В:

10 15

−

37. а) Ширина прямоугольника составляет

его пери-

метра. Чему равен периметр прямоугольника, если его

ширина равна 42 см? Выберите правильное решение:

А:

42 2 42 93+=

(см)

Б:

42 2 2 42 102+= 



(см)

В:

42 196=

(см)

б) Длина прямоугольника составляет

его перимет-

ра. Чему равен периметр прямоугольника, если его

длина равна 60 см? Выберите правильное решение:

А:

60 25=

(см)

Б:

60 144=

(см)

В:

260 60 145+=

(см)

38. а) Выберите из чисел 10; 15; 20 то, которое следует за-

писать вместо многоточия: «Расстояние между двумя

пунктами на карте равно 1,5 см. Если масштаб карты

218

Раздел VI

219

1-й уровень

1  1 000 000, то расстояние между этими пунктами на

местности равно ... км».

б) Выберите из чисел 8,2; 82; 102 то, которое следует

записать вместо многоточия: «Расстояние между дву-

мя пунктами на карте равно 8,2 см. Если масштаб кар-

ты 1  100 000, то расстояние между этими пунктами

на местности равно ... км».

39. а) Площадь прямоугольной ледовой площадки для хок

кея с шайбой 1830 м

. Найдите длину площадки, если

ширина на 31 м меньше длины. Выберите уравнение

и решите его относительно а, если а — длина пло-

щадки:

А: а (а − 31) = 1830

Б: а (а + 31) = 1830

В: а

= 1830 − 31

б) Площадь прямоугольной спортивной площадки для

игры с мячом 6175 м

. Найдите ширину площадки,

если длина на 30 м больше ширины. Выберите урав-

нение и решите его относительно b, если b — ширина

площадки:

А: b (b − 30) = 6175

Б: b

= 6175 − 30

В: b (b + 30) = 6175

40*. а) Ширина прямоугольника вдвое меньше его длины.

Если ширину увеличить на 3 см, а длину — на 2 см, то

площадь его увеличится на 78 см

. Выберите уравне-

ние, с помощью которого можно найти длину и ширину

прямоугольника, если х см — его ширина:

А: (х + 2) (2х + 3) − х  2х = 78

Б: (х + 3) (2х + 2) − 2х  х = 78

В: (х + 3) (2х + 2) + 78 = 2х  х

б) Длина прямоугольника на 12 дм больше его

ши-

рины. Если длину увеличить на 3 дм, а ширину — на

2 дм, то площадь его увеличится на 80 дм

. Выберите

уравнение, с помощью которого можно найти длину и

ширину прямоугольника, если х дм — его ширина:

А: (х + 3) (х + 14) − (х + 12)х = 80

Б: (х + 2) (х + 15) + 80 = х (х + 12)

В: (х + 2) (х + 15) − х(х + 12) = 80

41*. а) На сколько сантиметров нужно увеличить каждую

сторону квадрата

, равную 5 см, чтобы площадь квад-

рата увеличилась не меньше чем на 5 см

? Выберите

нера венст во, с помощью которого можно решить за-

дачу:

А: (5 + х)

− 5

 5

Б: х

− (х + 5)

 5

В: (х + 5)

− 5

5

б) На сколько сантиметров нужно уменьшить каж-

дую сторону квадрата, равную 14 см, чтобы площадь

квадрата уменьшилась не более чем на 4 см

? Укажи-

те нера венст во, с помощью которого можно решить за-

дачу:

А: х

− (14 − х)

 4

Б: 14

− (14 − х)

 4

В: (14 − х)

− х

 4

42*. а) Периметр прямоугольника равен 82 см. Если его

длину увеличить на 5 см, а ширину — на 4 см, то пло-

щадь прямоугольника увеличится на 200 см

. Укажи-

те систему уравнений, решая которую можно найти

стороны прямоугольника, если а см — его длина, а

b см — ширина:

А:

82,

( 5)( 4) 200

ab ab

⎧

⎨

++−=

⎩

Б:

2( ) 82,

( 5)( 4) 200

ab ab

⎧

⎨

++−=

⎩

В:

2( ) 82,

( 5)( 4) 200

ab ab

⎧

⎨

+++=

⎩