Сборник заданий для выпускного экзамена по математике на уровне общего базового образования под редакцией Адамовича

Подождите немного. Документ загружается.

180

Раздел V

181

4-й уровень

175. Найдите биссектрису прямоугольного тре уголь ника,

проведенную из вершины прямого угла, если катеты

тре уголь ника равны:

а) 3 см и 6 см; б) 4 см и 8 см.

176*. а) Биссектриса прямого угла прямоугольного тре-

уголь ника делит его гипотенузу на отрезки длиной

5 см и 8 см. Найдите длины отрезков гипотенузы, на

которые ее делит высота тре

уголь ника, проведенная из

вершины прямого угла.

б) Высота прямоугольного тре уголь ника делит гипоте-

нузу на отрезки 6 см и 9 см. Найдите длины отрезков

гипотенузы, на которые ее делит биссектриса прямого

угла этого тре уголь ника.

177. Найдите синус большего угла между диагоналями

прямоугольника, стороны которого равны:

а) 4 и 5; б) 5 и 7.

178. С помощью

циркуля и линейки без делений по строй те

равнобедренный тре уголь ник:

а) по основанию и высоте, проведенной к боковой сто-

роне;

б) по основанию и углу при вершине.

179*. а) От участка земли, имеющего форму трапеции,

нужно отделить тре уголь ный участок так, чтобы его

площадь была равна площади оставшейся части. Как

это

можно сделать?

б) Через вершину ромба проведите две прямые, деля-

щие ромб на три равновеликие части.

180. а) Высота равнобедренного тре уголь ника, проведен-

ная к основанию, равна

43.

Найдите другую высоту

тре уголь ника, если известно, что один из его углов ра-

вен 120°.

б) В тре уголь нике АВС АВ = 1 дм, ∠ А = 45°, ∠ В = 30°.

Найдите высоту тре уголь ника, проведенную к сторо-

не АВ.

181. а) Длина гипотенузы прямоугольного тре уголь ника

равна 10 см. Найдите длины

его катетов, если извест-

но, что больший из них равен среднему арифметичес-

кому длин меньшего катета и гипотенузы.

б) Длина меньшего катета прямоугольного тре уголь-

ника равна 3 дм. Найдите длины второго катета и

гипотенузы, если известно, что больший катет равен

среднему арифметическому длин меньшего катета и

гипотенузы.

182**. а) С помощью

циркуля и линейки без делений по-

строй те ромб с острым углом 60°, если дан отрезок,

равный сумме длин его большей диагонали и стороны.

б) С помощью циркуля и линейки без делений по строй-

те ромб с углом 120°, если дан отрезок, равный разно-

сти его большей диагонали и стороны.

183**. а)

С помощью циркуля и линейки без делений по-

строй те па рал ле ло грамм, если даны три точки: М и

K — середины двух смежных сторон па рал ле ло грамма,

О — точка пересечения его диагоналей.

б) С помощью циркуля и линейки без делений по строй-

те ромб АВСD, если даны три точки: А, О —

точка пе-

ресечения его диагоналей, М — произвольная точка на

стороне АВ.

184*. а) Боковая сторона равнобедренного тре уголь ника

равна а, а основание равно b. Найдите радиус окруж-

ности, описанной около этого тре уголь ника.

б) Найдите радиус окружности, описанной около рав-

нобедренного тре уголь ника, если известны его боко-

вая сторона а и

высота h, проведенная к основанию.

185**. а) Докажите, что если центры описанной и вписан-

ной окружностей совпадают, то тре уголь ник является

равносторонним.

б) Докажите, что если в тре уголь нике одна из сторон

точкой касания вписанной окружности делится попо-

лам, то тре уголь ник — равнобедренный.

182

Раздел V

183

4-й уровень

186*. а) Докажите, что если две стороны и медиана, вы-

ходящие из одной вершины, одного тре уголь ника со-

ответственно пропорциональны двум сторонам и меди-

ане, выходящим из одной вершины, другого тре уголь-

ника, то такие тре уголь ники подобны.

б) Докажите, что если две стороны и биссектриса, вы-

ходящие из одной вершины, одного

тре уголь ника соот-

ветственно пропорциональны двум сторонам и биссек-

трисе, выходящим из одной вершины, другого тре уголь-

ника, то такие тре уголь ники подобны.

187*. а) По одну сторону от железной дороги расположены

два населенных пункта. В каком месте надо построить

у дороги остановку, чтобы сумма расстояний от нее до

этих пунктов

была наименьшей?

б) Два населенных пункта разделены каналом. Где

надо возвести мост через канал, чтобы путь из одного

пункта в другой был кратчайшим?

188**. а) Пусть М и М

— точки пересечения меди-

ан тре уголь ников АВС и А

. Докажите, что

1111

.MM AA BB СС=++

JJJJJG JJJJG JJJJG JJJG



б) Пусть М и М

— точки пересечения диагоналей

па рал ле ло граммов АВСD и А

. Докажите, что

11111

.MM AA BB СС DD=+++

JJJJJG JJJJG JJJJG JJJG JJJJG



189*. а) Проведены две взаимно перпендикулярные пря-

мые, пересекающие противоположные стороны пра-

вильного че ты рех уголь ника. Докажите, что отрезки

этих прямых, заключенные между противоположными

сторонами, равны.

б) Через центр правильного тре уголь ника проведены

две прямые, пересекающие его стороны и образующие

угол 60°. Докажите, что отрезки этих прямых, заклю-

ченные между сторонами,

равны.

190. а) Один из углов прямоугольного тре уголь ника равен

30°. Длина меньшего катета равна 1 дм. Найдите дли-

ну биссектрисы этого тре уголь ника, проведенной из

вершины прямого угла.

б) Один из углов прямоугольного тре уголь ника равен

60°. Длина большего катета равна 2 см. Найдите длину

медианы этого тре уголь ника, проведенной из

вершины

его меньшего угла.

191*. а) Докажите, что если высота тре уголь ника делит его

на два тре уголь ника с равными периметрами, то тре-

уголь ник — равнобедренный.

б) Докажите, что два тре уголь ника с равными перимет-

рами и двумя соответственно равными углами равны.

192**. Установите, верно ли, что длина любого отрезка,

расположенного внутри

че ты рех уголь ника, не превос-

ходит длины:

а) наибольшей стороны че ты рех уголь ника;

б) наибольшей диагонали че ты рех уголь ника.

193**. а) С помощью циркуля и линейки без делений по-

строй те тре уголь ник данного периметра, подобный

данному тре уголь нику.

б) С помощью циркуля и линейки без делений по строй-

те тре уголь

ник по данным двум его углам и радиусу

описанной около него окружности.

194*. Длины катетов прямоугольного тре уголь ника равны

8 см и 15 см. Найдите расстояние от центра окружнос-

ти, вписанной в этот тре уголь ник, до вершины:

а) его наименьшего угла;

б) его большего острого угла.

195**. Найдите радиус окружности, вписанной в прямо-

угольный тре уголь ник, биссектриса прямого угла ко-

торого делит гипотенузу на отрезки:

а) 7 дм и 24 дм;

б) 8 дм и 25 дм.

196**. В окружность вписан правильный шестиугольник.

Постройте с использованием одной лишь линейки от-

резок, равный:

184

Раздел V

185

4-й уровень

а) 25 % радиуса этой окружности;

б) 20 % радиуса этой окружности.

197*. Установите, можно ли построить прямоугольник:

а) со сторонами 1 см, 3 см и углом 45° между его диа-

гоналями;

б) со сторонами 2 см, 3 см и углом 45° между его диа-

гоналями.

198**. а) Установите, найдется ли тре уголь ник, у которо-

го каждая из высот меньше

1 см, а площадь больше

1 см

б) Установите, верно ли, что тре уголь ник равнобедрен-

ный, если центр вписанной в него окружности одина-

ково удален от середин двух его сторон.

199**. Известны координаты вершин тре уголь ника ОАВ:

О(0; 0), А(2; 0), В(0; 5). В этом тре уголь нике проведена

высота ОК. Запишите уравнение окружности, описан-

ной около тре уголь ника:

а) ОАК; б

) ОВК.

200**. а) В тре уголь нике АВС угол С прямой, СН — высо-

та, Р — середина отрезка СН, М — середина отрезка

ВН. Докажите, что отрезок АР перпендикулярен отрез-

ку СМ.

б) В квадрате АВСD точка М — середина стороны ВС,

точка К делит диагональ ВD в отношении 3  1, считая

от вершины В

. Докажите, что отрезок АК перпендику-

лярен отрезку КМ.

201**. а) Около окружности описана равнобедренная

трапеция с периметром, равным Р, и острым углом α.

Найдите площадь трапеции.

б) Около окружности описан ромб с острым углом,

равным α. Найдите площадь ромба, если его большая

диагональ равна d.

202*. а) Даны две параллельные прямые и

точка, лежащая

между ними. С помощью циркуля и линейки без деле-

ний по строй те окружность, касающуюся данных пря-

мых и проходящую через данную точку.

б) С помощью циркуля и линейки без делений по строй-

те окружность, касающуюся сторон данного угла и

проходящую через данную внутри угла точку.

203**. Два угла тре

уголь ника равны 45° и 60°, а его пло-

щадь равна S. Найдите длину окружности:

а) описанной около этого тре уголь ника;

б) вписанной в этот тре уголь ник.

204**. В тре уголь нике АВС ∠ А = 45°, ∠ В = 60°. Около

этого тре уголь ника описана окружность с центром О.

Найдите:

а)

;OA OB

JJJG JJJG



б)

.OA OC

JJJG JJJG



205**. Отрезок АВ равен 2 дм. Какую фигуру образуют

все точки М, удовлетворяющие равенству:

а) МА

+ МВ

= 5; б) МА

− МВ

= 2?

206. а) Катеты прямоугольного тре уголь ника относятся

как 1  2. С помощью циркуля и линейки без делений

по строй те этот тре уголь ник, если известна длина его

высоты, проведенной к гипотенузе.

б) С помощью циркуля и линейки без делений по строй-

те ромб по данным острому углу и диагонали, выходя-

щей из

вершины этого угла.

207. С помощью циркуля и линейки без делений по строй те

правильный 12-угольник:

а) описанный около данной окружности;

б) вписанный в данную окружность.

208*. Докажите, что:

а) медианы тре уголь ника пересекаются в одной точке;

б) биссектрисы тре уголь ника пересекаются в одной

точке.

209*. а) Внутри тре уголь ника найдите такую точку,

чтобы

отрезки, соединяющие ее с вершинами тре уголь ника,

делили тре уголь ник на три равновеликие части.

186

Раздел V

187

4-й уровень

б) Докажите, что сумма расстояний от произвольной

точки, взятой внутри равнобедренного тре уголь ника,

до его сторон постоянна.

210*. Для тре уголь ника со сторонами

46;

найдите радиус:

а) описанной окружности;

б) вписанной окружности.

211**. а) Стороны тре уголь ника относятся как 2  3  4.

Медиана, проведенная к меньшей стороне, равна

42.

Найдите периметр тре уголь ника.

б) Стороны тре уголь ника относятся как 2  3  4, а его

площадь равна

315.

Найдите периметр тре уголь ника.

212**. С помощью циркуля и линейки без делений по строй-

те правильный тре уголь ник так, чтобы:

а) его вершины лежали на трех данных параллельных

прямых;

б) две его вершины лежали на двух пересекающихся

прямых, а третья находилась в точке, не принадлежа-

щей этим прямым.

213. С помощью циркуля

и линейки без делений по строй те

равносторонний тре уголь ник по данному радиусу:

а) описанной около него окружности;

б) вписанной в него окружности.

214. Разделите с использованием циркуля и линейки:

а) прямой угол на три равных угла;

б) развернутый угол на три равных угла.

215**. С помощью циркуля и линейки без делений

по строй-

те равносторонний тре уголь ник по данной:

а) разности между его стороной и высотой;

б) сумме его стороны и высоты.

216*. а) Гипотенуза прямоугольного тре уголь ника равна 5,

а высота, проведенная к ней, равна 2. Найдите радиус

окружности, вписанной в этот тре уголь ник.

б) Гипотенуза равнобедренного прямоугольного тре-

уголь ника равна 9. Найдите радиус

окружности, впи-

санной в этот тре уголь ник.

217. Найдите площадь поверхности куба, сумма длин всех

ребер которого равна:

а)

см; б)

см.

218*. а) Основанием прямой призмы является прямоуголь-

ный тре уголь ник с катетами 9 см и 12 см. Высота приз-

мы равна

см. Найдите площадь боковой поверх-

ности призмы.

б) Основанием прямой призмы является прямоуголь-

ный тре уголь ник с катетами 24 см и 10 см. Высота

призмы равна

см. Найдите площадь боковой по-

верхности призмы.

219. Разделите на две равновеликие части построенную

вами трапецию ломаной, состоящей из двух звеньев,

концы которой находятся в вершинах трапеции, если

известно, что трапеция:

а) равнобедренная; б) прямоугольная.

220**. а) Разделите построенную вами прямоугольную

трапецию на два равновеликих многоугольника лучом,

исходящим из одной ее

вершины.

б) Разделите построенную вами равнобедренную тра-

пецию на два равновеликих многоугольника лучом,

исходящим из одной ее вершины.

221*. С помощью циркуля и линейки без делений по строй-

те квадрат, равновеликий:

а) па рал ле ло грамму со сторонами а и b и острым уг-

лом, равным 30°;

б) ромбу со стороной а и

острым углом, равным 60°.

222. Найдите периметр тре уголь ника АВС, если:

а) АВ = 6, АС = 10, sin A =

;

б) АВ = 5, АС = 9, sin A =

188

Раздел V

189

4-й уровень

223*. а) Тре уголь ник с основанием а и высотой h, прове-

денной к нему, вписан в квадрат так, что две его вер-

шины лежат на основании, а две другие — на боковых

сторонах тре уголь ника. Найдите сторону квадрата.

б) В тре уголь ник АВС вписан ромб ADEF так, что угол

А у них

общий, точка Е лежит на стороне ВС, точка

D — на стороне AB, точка F — на стороне AC. Найди-

те сторону ромба, если АВ = с, АС = b.

224*. а) В сегмент круга, дуга которого содержит 120°,

вписан квадрат так, что две его вершины лежат на дуге

сегмента, а две — на

хорде. Найдите площадь круга,

если сторона квадрата равна

19 2.−

б) В сектор с центральным углом 60° вписана окруж-

ность, которая касается дуги сектора и радиусов. Най-

дите радиус этой окружности, при котором площадь

круга, ограниченного ею, равна π.

225**. Докажите, что:

а) сумма квадратов расстояний от данной точки окруж-

ности до концов любого из ее диаметров постоянна;

б) если середина

данного отрезка является центром

окружности, то сумма квадратов расстояний от про-

извольной точки этой окружности до концов отрезка

постоянна.

226*. Найдите площадь:

а) правильного десятиугольника, если известны ради-

усы его описанной и вписанной окружностей;

б) правильного пятиугольника, если известны радиусы

его описанной и вписанной окружностей.

227*. а) Высота равнобедренной трапеции равна 3 см

, а ее

площадь равна S. Найдите диагональ трапеции.

б) Диагональ равнобедренной трапеции равна 5 см, а

ее площадь равна S. Найдите высоту трапеции.

228*. а) Из всех че ты рех уголь ников с данными равными

диагоналями найдите че ты рех уголь ник наибольшей

площади.

б) Из всех че ты рех уголь ников, вписанных в данную

окружность, найдите че

ты рех уголь ник наибольшей

площади.

229**. Докажите, что в подобных тре уголь никах:

а) биссектрисы, проведенные из равных углов, отно-

сятся как сходственные стороны;

б) медианы, проведенные к сходственным сторонам,

относятся как эти стороны.

230**. а) Около окружности, радиус которой равен 2 см,

описана равнобедренная трапеция. Найдите периметр

этой трапеции, если ее площадь равна 20

см

б) Разность длин оснований трапеции равна 14 см, одна

боковая сторона равна 13 см, а другая равна 15 см.

Найдите площадь этой трапеции, если известно, что в

нее можно вписать окружность.

231**. а) На сторонах АС и ВС тре уголь ника АВС взяты

точки K и M так, что CK  KA = 2  3, CM

 MB = 4  3.

Найдите отношение OK  OB, где О — точка пересече-

ния BK и AM.

б) Точка N лежит на стороне ВС тре уголь ника АВС,

точка М лежит на продолжении стороны АС за точку А,

AM = AC, BN  NC = 3  4. Найдите отношение OA  OB,

где O — точка пересечения AB и MN.

232**. а) Площадь тре уголь ника АВС равна S. ∠ ВАС = α,

АС = b. Найдите ВС.

б) Площадь тре уголь ника АВС равна S. ∠ АВС = β,

АС = b. Найдите АВ.

233**. Установите, существует ли тре уголь ник с высота-

ми, равными:

а) 3 см

, 4 см, 5 см;

б) 2 см, 3 см, 4 см.

190

Раздел V

191

5-й уровень

234*. а) Существует ли правильный многоугольник, сто-

рона которого равна 3 см, а радиус вписанной окруж-

ности равен 2 см?

б) Существует ли правильный многоугольник, сторона

которого равна 6 см, а радиус описанной окружности

равен 5 см?

235. Докажите, что в любом прямоугольном тре уголь нике:

а) сумма полупериметра и радиуса вписанной в этот

тре уголь ник

окружности равна сумме его катетов;

б) сумма диаметров описанной и вписанной в этот тре-

уголь ник окружностей равна сумме его катетов.

236*. а) Можно ли построить па рал ле ло грамм со сторона-

ми 1 см, 3 см и углом 45° между диагоналями?

б) В па рал ле ло грамме ABCD

2.AC AB=

Докажите,

что угол между диагоналями па рал ле ло грамма равен

углу между его сторонами.

237**. а) Докажите, что если отрезки, соединяющие се-

редины противолежащих сторон че ты рех уголь ника,

равны, то его диагонали перпендикулярны.

б) Докажите, что если отрезки, соединяющие середи-

ны противолежащих сторон че ты рех уголь ника, пер-

пендикулярны, то его диагонали равны

238. Найдите радиус окружности и координаты ее центра,

если уравнение окружности имеет вид:

а) x

+ y

+ 6x − 8y + 5 = 0;

б) x

+ y

− 10x + 4y − 3 = 0.

239. а) В окружности перпендикулярно диаметру AB про-

ведена хорда CD. Точка их пересечения делит диаметр

на отрезки 18 см и 32 см. Найдите длину хорды.

б) Точка P удалена от центра окружности радиусом

11 см на расстояние 7 см. Через эту точку проведена

хорда длиной 18 см. Найдите

длины отрезков, на кото-

рые хорда делится точкой P.

240. а) Из одной точки окружности проведены две хорды

длинами 9 см и 17 см. Найдите радиус окружности,

если расстояние между серединами данных хорд равно

5 см.

б) Из одной точки окружности проведены две хорды

длинами 3 см и 8 см. Найдите радиус окружности, если

угол между

хордами равен 60°.

241. а) Из внешней точки A проведены к окружности секу-

щие, которые пересекают окружность соответственно

в точках B, C и D, E. Известно отношение их внешних

частей:

Найдите отношение

ABE

ADC



б) Из внешней точки A проведены к окружности каса-

тельная AB и секущая AD, которая пересекает окруж-

ность в точке С. Известно, что

ABC

ABD



Найдите

отношение

242. а) Стороны угла ACB, равного 60°, касаются двух

окружностей с центрами O

и O

, касающихся одна

другой, причем CO

= 12 см. Найдите радиус меньшей

окружности с центром O

б) Стороны угла CED, равного 60°, касаются двух

окружностей с центрами O

и O

, касающихся одна

другой, причем EO

= 21 см. Найдите радиус меньшей

окружности с центром O

243*. а) AB — диаметр окружности, равный 10 см, AC —

хорда. Из точки B проведены перпендикуляр к хорде,

равный 6 см, и касательная, которая пересекает про-

должение хорды в точке D. Найдите отрезок BD.

б) Из точки A, взятой вне окружности, проведены ка-

сательная AB (B — точка касания) и секущая, которая

пересекает окружность в

точках D и C. Во сколько раз

отрезок DC длиннее отрезка AB, если AB в три раза

короче AC?

192

Раздел V

193

5-й уровень

244. а) Точка внутри угла, равного 60°, удалена от его сто-

рон на 5 см и 2 см. Найдите расстояние от этой точки

до вершины угла.

б) Точка внутри угла, равного 30°, удалена от его вер-

шины на

см, а от одной из сторон — на 2 см.

Найдите расстояние от этой точки до другой стороны

угла.

245. а) В окружность радиусом 6 см вписан тре уголь ник,

две стороны которого равны 9 см и 4 см. Найдите вы-

соту тре уголь ника, опущенную на третью сторону.

б) Около тре уголь ника ABC описана окружность ра-

диусом

8 см. Найдите сторону AB, если известно, что

сторона BC равна 14 см, а высота, опущенная на сто-

рону AC, равна 5,25 см.

246. а) Около окружности радиусом 6 см описан прямо-

угольный тре уголь ник, гипотенуза которого равна

39 см. Вычислите периметр этого тре уголь ника.

б) В прямоугольном тре уголь нике точка касания впи-

санной окружности

делит гипотенузу на отрезки 5 см и

12 см. Найдите катеты тре уголь ника.

247*. а) Около окружности описан че ты рех уголь ник,

две смежные стороны которого равны 5 см и 12 см и

образуют угол 90°. Найдите две другие стороны че ты-

рех уголь ника, если они образуют угол 60°.

б) Около окружности описан че ты рех уголь ник,

две

смежные стороны которого равны 2 дм и 3 дм и обра-

зуют угол 60°. Найдите две другие стороны че ты рех-

уголь ника, если они образуют угол 120°.

248*. а) Около окружности описан че ты рех уголь ник ABCD,

у которого AB = 18 см, BC = 8 см, диагональ AC = 20 см

и ∠ ACD = 90°.

Найдите площадь че ты рех уголь ника.

б) Около окружности описан че ты рех уголь ник ABCD,

у которого ∠ B = 90°, диагональ AC = CD = 15 см и

AD = 18 см. Найдите площадь че ты рех уголь ника.

249. а) В прямоугольном тре уголь нике ABC (∠ C = 90°)

BC = 8 см, AB = 10 см

, CD — высота. Найдите отноше-

ние площади тре уголь ника BDC к площади тре уголь-

ника ADC.

б) В прямоугольном тре уголь нике MKP (∠ K = 90°)

MK = 6 см, MP = 10 см, KD — высота. Найдите отноше-

ние площади тре уголь ника MKD к площади тре уголь-

ника KDP.

250. а) Длины катетов прямоугольного тре

уголь ника рав-

ны 5 см и 12 см. Найдите расстояние между центрами

описанной и вписанной окружностей.

б) Длины катетов прямоугольного тре уголь ника рав-

ны 15 см и 20 см. Найдите расстояние между центрами

описанной и вписанной окружностей.

251. а) В равнобедренном тре уголь нике к боковой стороне

длиной 4 см проведена медиана, равная 3 см. Найдите

периметр тре

уголь ника.

б) В равнобедренном тре уголь нике к боковой стороне

длиной 10 см проведена медиана, равная 9 см. Найдите

площадь тре уголь ника.

252. а) В равнобедренном тре уголь нике ABC (AB = BC = a)

точка M делит сторону BA так, что

а точ-

ка K находится на стороне BC так, что ∠ BMK = 30°,

∠ MKB = 45°. Найдите отношение стороны BC к отрез-

ку BK.

б) Дан правильный тре уголь ник ABC со стороной a.

Точка K делит сторону AC так, что

а точка M

делит сторону AB так, что

Найдите длину от-

резка KM.

253. а) Найдите биссектрису прямоугольного тре уголь-

ника с катетами 3 см и 6 см, проведенную из вершины

прямого угла.

194

Раздел V

195

5-й уровень

б) Гипотенуза прямоугольного тре уголь ника равна

см, а катет — 5 см. Найдите его биссектрису,

проведенную из вершины прямого угла.

254. а) Длина катета прямоугольного тре уголь ника рав-

на 18 см. Точка, которая принадлежит данному кате-

ту, удалена от гипотенузы и от другого катета на 8 см.

Найдите периметр тре уголь ника.

б) Длина катета прямоугольного тре уголь ника равна

28 см. Точка,

которая лежит на гипотенузе, удалена от

каждого из катетов на 12 см. Найдите периметр тре-

уголь ника.

255. а) В прямоугольный тре уголь ник вписана окруж-

ность. Точка касания делит гипотенузу в отношении

2  3. Найдите стороны тре уголь ника, если центр впи-

санной окружности удален от вершины прямого угла

на расстояние

см.

б) В тре уголь ник вписана окружность радиусом 3 см.

Вычислите длины сторон тре уголь ника, если одна из

них разделена точкой касания на отрезки длинами 4 см

и 3 см.

256**. а) Длины катетов прямоугольного тре уголь ника

равны 8 дм и 15 дм. Найдите расстояние от вершины

прямого угла до центра вписанной окружности.

б) Найдите отношение

большего катета прямоугольно-

го тре уголь ника к меньшему, если радиус вписанной

окружности равен полуразности катетов.

257. Длины сторон тре уголь ника равны 4 см, 5 см и 6 см.

а) Вычислите длины его наибольшей медианы и наи-

меньшей биссектрисы.

б) Вычислите длины его наименьшей медианы и наи-

большей биссектрисы.

258. а) Периметр тре уголь ника равен 30

см. Найдите угол,

противолежащий стороне, равной 14 см, если биссект-

риса тре уголь ника делит ее в отношении 3  5.

б) Найдите угол тре уголь ника, если биссектриса, про-

веденная из вершины этого угла, делит противолежа-

щую сторону на отрезки 21 см и 35 см, а разность двух

других сторон равна 16 см.

259. а) ME и PC —

высоты тре уголь ника MKP. MP =

см, KE =

см, CE =

см. Найдите длину

отрезка MK.

б)

AM и CK — высоты тре уголь ника ABC. AC =

12 3

см,

BK =

см, BC =

см. Найдите длину отрезка KM.

260*. а) Из вершины тре уголь ника проведены биссектриса

и диаметр описанной окружности. Выразите угол меж-

ду ними через углы тре уголь ника.

б) Из вершины тре уголь ника проведены высота и диа-

метр описанной окружности. Выразите угол между

ними через углы тре уголь ника.

261*. а) В тре уголь нике

ABC угол A равен 32°. Окружность

с центром в точке B проходит через точку A, пересекает

сторону AC в точке M, а сторону BC — в точке N. Най-

дите угол ANM.

б) Длины сторон AB, BC и CA тре уголь ника ABC равны

соответственно 2 см, 4 см и 3 см. Окружность, которая

проходит через

точки B и C, пересекает прямую AC в

точке M, а прямую AB — в точке N. Найдите MN и AN,

если AM = 1 см, CM = 4 см.

262. а) Найдите площадь равнобедренной трапеции, сред-

няя линия которой равна 5 см, а диагонали взаимно

перпендикулярны.

б) Площадь равнобедренной трапеции, диагонали ко-

торой взаимно

перпендикулярны, равна 100 см

. Най-

дите высоту.

263. а) Длина средней линии трапеции равна 12,5 см, а

разность оснований равна 13 см. Найдите площадь

трапеции, если длины ее боковых сторон равны 15 см

и 14 см.

196

Раздел V

197

5-й уровень

б) Сумма длин оснований прямоугольной трапеции

равна 25 дм, а их разность равна 13 дм. Найдите пло-

щадь трапеции, если разность ее боковых сторон рав-

на 1 дм.

264. а) Найдите площадь равнобедренной трапеции с

основаниями длинами 13 см и 5 см, если известно,

что ее диагонали перпендикулярны боковым сторо-

нам.

б) В равнобедренной трапеции диагонали

перпендику-

лярны боковым сторонам. Найдите ее площадь, если

известно, что высота делит большее основание на от-

резки длинами 1 см и 9 см.

265. а) В равнобедренную трапецию, боковая сторона

ко торой равна 17 см, вписана окружность диаметром

15 см. Найдите основания трапеции.

б) Равнобедренная трапеция с боковой стороной 8 см

и углом при основании 60°

описана около круга. Най-

дите основания трапеции.

266. а) В трапеции диагонали длинами 6 см и 8 см взаимно

перпендикулярны. Найдите длину средней линии тра-

пеции.

б) Найдите длину меньшего основания трапеции, если

ее высота равна 12 см, длины боковых сторон рав-

ны 13 см и 15 см, а длина большего основания равна

20 см.

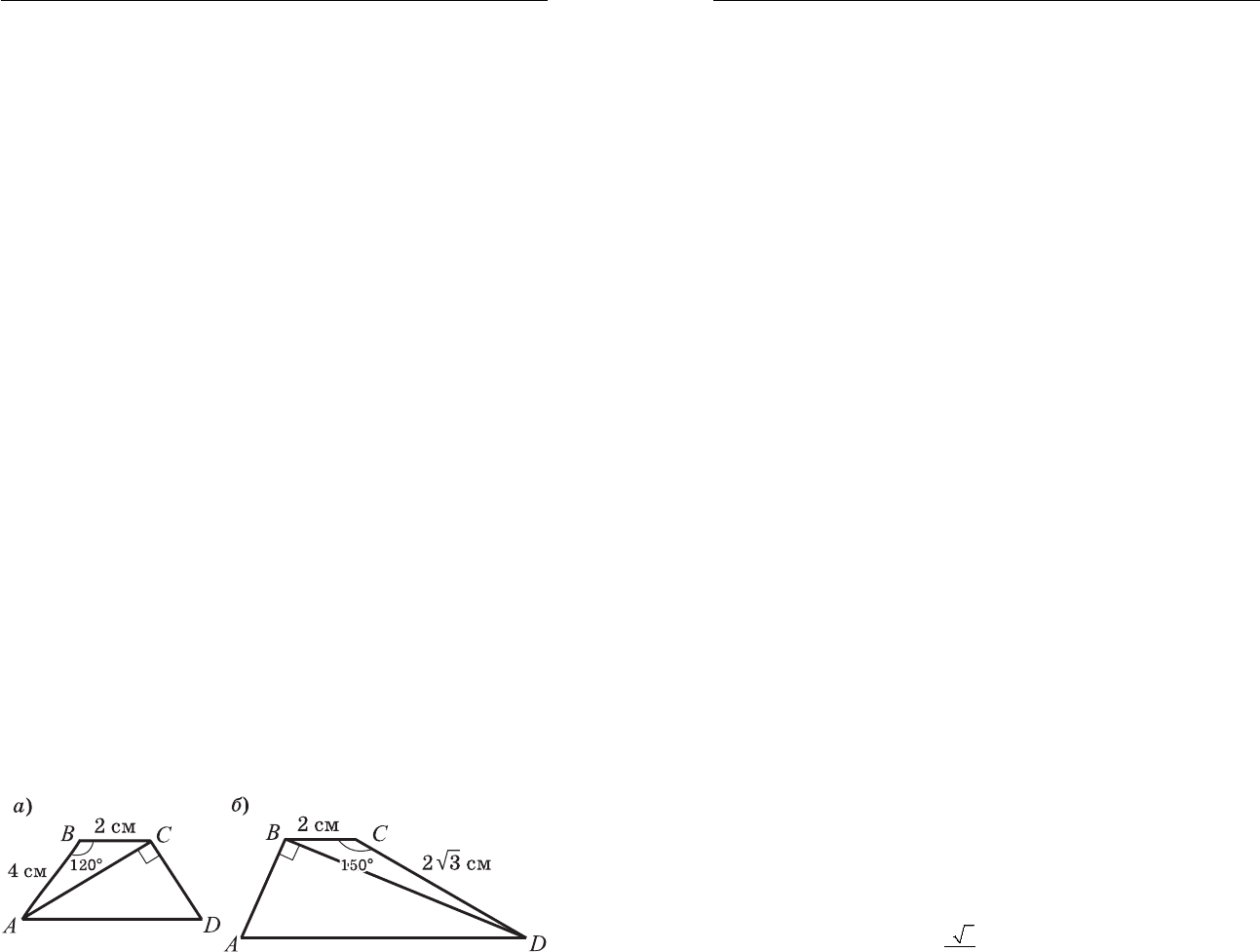
267. ABCD —

трапеция. Пользуясь рисунком, найдите ос-

нование AD.

268**. а) Центр окружности, вписанной в прямоугольную

трапецию, удален от концов ее боковой стороны на

3 см и 9 см. Найдите стороны трапеции.

б) Центр окружности, вписанной в прямоугольную тра-

пецию, удален от концов ее боковой стороны на 8 см и

4 см. Найдите среднюю линию трапеции.

269. а) С помощью циркуля и линейки без

делений по строй-

те тре уголь ник по двум углам и медиане, проведенной

из вершины одного из них.

б) С помощью циркуля и линейки без делений по строй-

те тре уголь ник по двум углам и биссектрисе, проведен-

ной из вершины третьего угла.

270. а) С помощью циркуля и линейки без делений по строй-

те тре уголь ник по стороне и медианам, проведенным к

двум другим сторонам.

б) С помощью циркуля и линейки без делений по строй-

те тре уголь ник по двум сторонам и высоте, проведен-

ной к одной из них.

271. С помощью циркуля и линейки без делений по строй те

прямоугольный тре уголь ник:

а) по проекциям

катетов на гипотенузу;

б) по гипотенузе и высоте, проведенной из вершины

прямого угла.

272. а) С помощью циркуля и линейки без делений по-

строй те тре уголь ник по углу, отношению сторон, кото-

рые заключают этот угол, и биссектрисе, проведенной

из вершины этого угла.

б) С помощью циркуля и линейки без делений

по строй-

те тре уголь ник по отношению трех сторон и медиане,

проведенной к меньшей из них.

273. а) Дан отрезок c. С помощью циркуля и линейки по-

строй те отрезок

x =

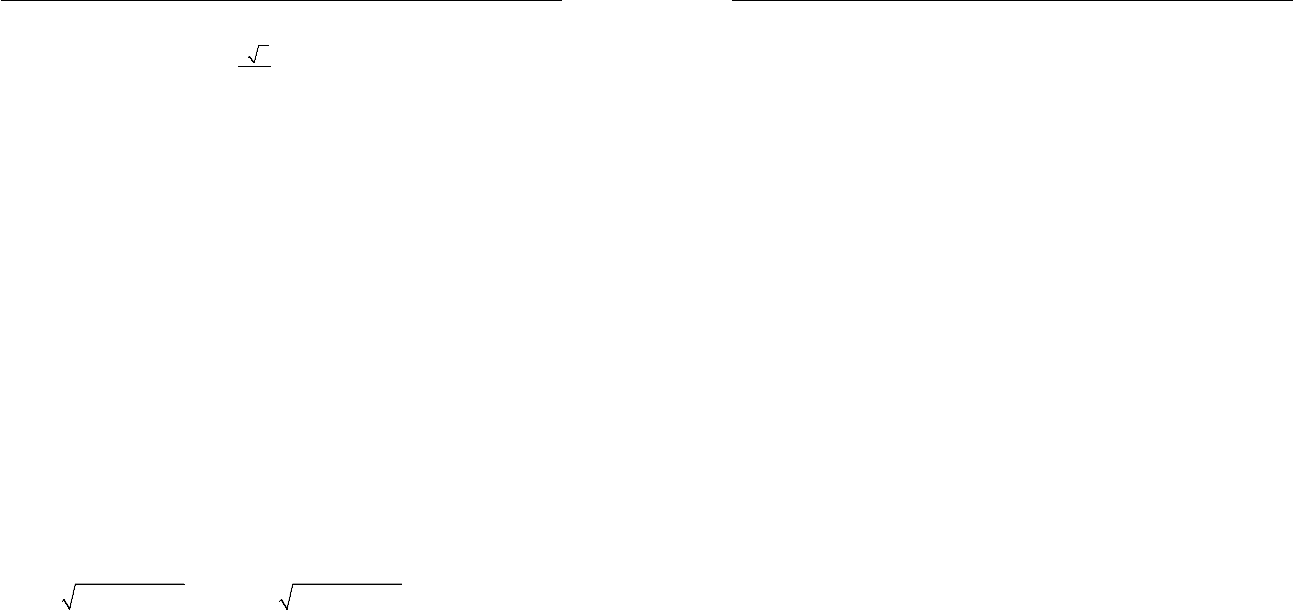
198

Раздел V

199

5-й уровень

б) Дан отрезок b. С помощью циркуля и линейки по-

строй те отрезок

x =

274*. а) С помощью циркуля и линейки по строй те тре-

уголь ник по двум сторонам и медиане, проведенной к

третьей стороне.

б) С помощью циркуля и линейки по строй те тре уголь-

ник по серединам его сторон.

275*. а) С помощью циркуля и линейки по строй те квадрат

по сумме диагонали и стороны.

б) С

помощью циркуля и линейки по строй те прямо-

угольный тре уголь ник по острому углу и разности ка-

тетов.

276*. а) С помощью циркуля и линейки по строй те квадрат,

равновеликий трапеции с основаниями a и b и высотой h.

б) С помощью циркуля и линейки по строй те квадрат,

равновеликий па рал ле ло грамму со

сторонами a и b и

острым углом 30°.

277**. Даны отрезки a и b. С помощью циркуля и линейки

по строй те отрезок, равный:

а)

;aabb−+

б)

.aabb++

278**. а) Даны точки C(−3; −1), D(4; y), A(−1; 4), B(2; −1).

При каком значении y векторы

JJJG

перпенди-

кулярны?

б) Даны точки A(−3; −2), B(1; 4), M(−5; 3), N(2; y). При

каком значении y векторы

JJJJG

JJJG

перпендикулярны?

279**. а) ABCD — па рал ле ло грамм,

,AB a=

JJJG

.AD b=

JJJG

Вы-

разите через векторы

вектор

,KM

JJJG

если K — се-

редина AD, M делит BD в отношении 1  3, считая от

точки B.

б) ABCD — па рал ле ло грамм,

,CB a=

JJJG

.CD b=

JJJG

Вырази-

те через векторы

вектор

,EF

JJJG

если E — середи-

на AB, F делит BD в отношении 1  3, считая от точки D.

280**. а) При каком значении a векторы

JJJG

колли-

неарны, если A(2; −1), B(−4; 3), C(5; −1), D(1; a)?

б) При каком значении b векторы

JJJG

коллине-

арны, если M(−3; 2), P(−1; −2), K(2; 1), D(5; b)?

281*. а) Прямая, проходящая через середины противопо-

ложных сторон ВС и AD че ты рех уголь ника ABCD, об-

разует равные углы с прямыми АВ и CD. Докажите, что

стороны АВ и CD че ты рех уголь ника ABCD равны.

б) В че ты

рех уголь нике ABCD, не имеющем параллель-

ных сторон, противоположные стороны АВ и CD рав-

ны. Докажите, что прямая, проходящая через середи-

ны диагоналей че ты рех уголь ника, пересекает равные

стороны под равными углами.

282*. а) Углы А и В тре уголь ника АВС равны соответ-

ственно 30° и 50°, ВС = а, АС

= b, AB = c. Докажите, что

стороны а, b и с такого тре уголь ника удовлетворяют

равенству ab = c

− b

б) Установите вид тре уголь ника, в котором а +

+ h

= b + h

, где а, b — стороны тре уголь ника, h

— проведенные к этим сторонам высоты тре уголь-

ника.

283*. а) В выпуклом че ты рех уголь нике ABCD длина от-

резка, соединяющего середины сторон АВ и CD, равна

1 дм. Известно также, что прямые ВС и AD перпенди-

кулярны. Найдите длину отрезка, соединяющего сере-

дины диагоналей АС и BD.

б) В тре уголь нике АВС

с углом А, равным 120°, прове-

дены биссектрисы АА

, ВВ

, СС

. Найдите угол А

тре-

уголь ника А

284*. а) Докажите, что точка пересечения диагоналей тра-

пеции и середин ее оснований лежит на одной прямой.

б) Докажите, что середины оснований трапеции и точ-

ка пересечения прямых, содержащих ее боковые сто-

роны, лежат на одной прямой.