Salby M.L. Fundamentals of Atmospheric Physics
Подождите немного. Документ загружается.


360
11
Atmospheric Equations of Motion
where the geopotential q~ is given by (6.7). Then with (11.49), the horizontal
momentum equations become
Ov__k _ (
Ot b ('0 " VI~h)P -'[-
f-'["U
tana ~b) k x
Vh
- -Vpdp - Dh,
(11.52)
where
D h
denotes the horizontal component of drag. Simple substitution trans-
forms the hydrostatic equation into
= -a. (11.53)
ap
The continuity equation follows from its expression in terms of specific
volume, which holds irrespective of coordinate system. In isobaric coordinates,
(10.31) becomes
dolp
dt
= ap(V.
V)p,
(11.54.1)
where
Cgp
refers to the incremental material volume
dVp
and
Then (11.6) implies
According to (11.9),
(V-l~)p
~- V p . l~ h -Jr-
dro
op
(11.54.2)
ap = J(x, Xp )a.
(11.55)
ap
J(x,x~) =
= pg,
(11.56)
SO
It follows that
Olp --" pa " g
=g.
(11.57)
dap
dt
=0, (11.58)
which asserts that the volume of a material element is conserved in isobaric
coordinates. Then (11.54) implies
69(.0
-~ =0. (11.59)
VP" llh -~
Op
Requiring the three-dimensional divergence to vanish, the continuity equation
in isobaric coordinates has the same form as that for incompressible motion
(11.30).

11.5
Thermodynamic Coordinates 361
The thermodynamic equation can be developed from the first law for an
individual air parcel (2.22), which implies
dT dp
Cp--~
-- a-~--7 -- qnet"
(11.60)
With (11.49), this becomes
aT
+ (vh.VT)p
a~o
_ _ qne______tt ,
(11.61.1)
at
Cp Cp
in which expansion work is proportional to the motion across isobaric surfaces.
As before, the thermodynamic equation assumes a more compact form when
expressed in terms of potential temperature:
80 0
dt + (vh " VO)p -
~{r (11.61.2)
the derivation of which is left as an exercise.
Collectively, the equations of motion in isobaric coordinates are then given
by
dv____Eh_(
tan (h)
dt f- f + U~a k x v h - -Vp~- D h,
(11.62.1)
d~
- -a, (11.62.2)
ap
(V 9 tl)p --0,
(11.62.3)
with
dO 0
--
cpTqnet,
(11.62.4)
dt
d 8 d
at = at + Vh " Vp + to~.
(11.62.5)
ap
The lower boundary condition requires air to maintain the surface elevation
Zs,
SO
d~ dz s
dt = g dt
(11.63)
at p =
ps(X, y, t).
Simplifications introduced by transforming the equations into this coordi-
nate system include the following:
1. The pressure gradient force has been linearized through elimination
of p.
2. The continuity equation has reduced to a statement of three-
dimensional nondivergence. In addition to being linear, it is now
"diagnostic" (i.e., it involves no time derivatives).

362
11
Atmospheric Equations of Motion
These simplifications are not acquired without a price. Coordinate surfaces
p = const are now time dependent, so their positions evolve with the circula-
tion. Further, isobaric surfaces need not coincide with the ground. The lower
boundary condition (11.63) must then be prescribed on different values of the
vertical coordinate p = ps(X, y, t), which complicates its application.
Complications in the lower boundary condition can be averted by introduc-
ing the modified pressure coordinate
P
tr - ~, (11.64)
Ps
which preserves a constant value at the ground. Although they pass the com-
plication into the governing equations, or coordinates are advantageous from a
computational standpoint and are used in general circulation models (GCMs)
(see, e.g., Haltiner and Williams, 1980).
11.5.2 Log-Pressure Coordinates
Combining some of the virtues of height and pressure is the modified vertical
coordinate
z* - -H In (~00) , (11.65.1)
with
H- RT~ (11.65.2)
treated as constant. At this level of approximation, the basic pressure and
density associated with static conditions are described by
z*
po(z*)- po(O)e ",
z*
po(z*)- po(O)e ..
(11.66)
Log-pressure height, which is formally constant on isobaric surfaces, is based
on the stratification under static conditions (e.g., global-mean properties), so
it only approximates geopotential height, However, discrepancies between z*
and z are typically small and the two are identical under isothermal conditions.
In terms of z*, the hydrostatic equation becomes
d~ RT
= . (11.67)
3z* H
The vertical velocity in log-pressure coordinates is given by
dz*
dt
H dp
p dt
H
= ---to. (11.68)
P

11.5
Thermodynamic Coordinates
363
Then the Lagrangian derivative translates into
d d d
dt = dt + vh "
Vz*
+ w*~,Oz,
(11.69)
where Vz, reflects the horizontal gradient evaluated on an isobaric surface.
Likewise, vertical divergence in pressure coordinates becomes
@
ogW * W*
3z* H
1 0
= Po Oz* (poW*),
(11.70)
which transforms the continuity equation into
1 d
Vz,.
Vh + ~ (PoW*) -- O.
(11.71)
PO dz*
The thermodynamic equation is transformed in similar fashion, which is left
as an exercise.
With the foregoing expressions, the equations of motion in log-pressure
coordinates become
dVh(
tan 4~)
d----t -+- f + u a k x Vh --
-Vz,~-
Dh,
(11.72.1)
d~ RT
= (11.72.2)
Oz* H '
Vz,
1 3
Vh + --~ (PoW*) -- O,
(11.72.3)
Po dz*
-~ + v h . Vz, ~ + N*2w * -
o~Z, ~Onet,
(11.72.4)
where
d
dt
d d
m + Vh.
Vz * + w*~, (11.72.5)
dt 3z*
and
(11.72.6)
represents the static stability in log-pressure coordinates. In the troposphere,
N *: varies with height only weakly, so it can be treated as constant to first
order. The lower boundary condition, in which geometric vertical velocity is
specified (11.63), becomes
3~ RT dz s
Ot + vh "
Vz*~
+ --~w* - g dt "
(11.73)

364
11 Atmospheric Equations of Motion
At the level of approximation inherent to log-pressure coordinates, this can be
* * accounted
evaluated at the constant elevation
z* - z s ,
but with variations of
z s
for in the right-hand side of (11.73).
The equations in log-pressure coordinates have several advantages. Vari-
ables are analogous to those in physical coordinates, so they are easily inter-
preted. Yet, the pressure gradient force, hydrostatic equation, and continuity
equation retain nearly the same simplified forms as in isobaric coordinates. In
addition, mathematical complications surrounding comparatively small varia-
tions of temperature are ignored.
11.5.3 Isentropic Coordinates
The nearly adiabatic nature of air motion simplifies the governing equations
when 0 is treated as the vertical coordinate. Isentropic surfaces are then coor-
dinate surfaces, to which air motion is nearly tangential (Fig. 2.9). Hence, we
consider a transformation from the standard spherical coordinates x = (x, y, z)
to the modified coordinates
Xo = (x, y, 0).
For it to serve as a vertical coordi-
nate, potential temperature must vary monotonically with altitude. Hydrostatic
stability requires
dOl,~z
> 0, so we are ensured of a single-valued relationship
between potential temperature and height as long as the stratification remains
stable. As is true for isobaric coordinates, using isentropic surfaces as coordi-
nate surfaces leads to a coordinate system that is nonorthogonal.
Consider the scalar variable
q, = ~[x, y, O(x, y, z, t), t].
(11.74)
Proceeding as in the development of (11.43) and (11.44) transforms vertical
and horizontal derivatives into
~qJ ~q, ~0
= (11.75.1)
~z dO dz'
a~
Vzr = Vo@ + --~VzO,
(11.75.2)
where 0 is held fixed unless otherwise noted and
()
a i + j (11.75.3)
V o "- ~x yOt ~Y x Ot
represents the horizontal gradient evaluated on an isentropic surface. Then
the Lagrangian derivative becomes
dO aqJ
d---t = dt + (v. VO) 0
~ dO ~0
= ~--7 + Vh" Vo~ +
dt o~--0'
(11.76)

11.5 Thermodynamic Coordinates
365
in which we identify
dO
o~
o = dt
(11.77)
as the vertical velocity in potential temperature coordinates. Positive upward,
oo o represents the Lagrangian derivative of vertical position in this coordinate
system.
Taking q/= z(x, y, O, t) in (11.75), which for fixed 0 represents the height
of an isentropic surface, leads to the identities
O0 (OZ) -1
7zz- ~ ' (11.78.1)
0z
Voz = ---VzO. (11.78.2)
O0
Then substituting (11.78.2) transforms (11.75.2) into
a~
VzqJ - Voq, -~-~z Vo z. (11.79)
Taking 0 - P and incorporating (11.79) transforms the pressure gradient
force in the horizontal momentum equations into
1
lop
_1 VzP _ __ Vop + _ Voz
p p p~z
1
= --Vop - gVez. (11.80)
P
Poisson's relationship for potential temperature (2.31) implies the identity
In 0 - In T - K(ln p -- In
P0)-
By applying the horizontal gradient evaluated on an isentropic surface, we
obtain
RT
cpVoT --
~Vop
P
1
= -Vop.
(11.81)
P
Then the pressure gradient force (11.80) reduces to
1
__Vzp - -cpVoT - gVoz
P
= -Vo*, (11.82)
where the Montgomery streamfunction
xlt - c p T -Jr- g z
= cpT-k-~
(11.83)

366
11
Atmospheric Equations of Motion
plays a role in isentropic coordinates analogous to the one played by geopo-
tential in isobaric coordinates. With (11.82) and (11.76), the horizontal mo-
mentum equations become
d V_~h _
(tan~b)
at F- (v.
Vl3h) 0 +
f + u a k x V h -- --VOatt --D h.
(11.84)
To transform the hydrostatic equation, we consider (11.75.1) with qJ = p,
which gives
az ap
-pg-~ - -~.
(11.85)
Poisson's relationship implies
1
m
0
Then substituting into (11.85) obtains
or
l aT Kap
T 30 p 30
aT az cpT
o
o~0 --
Cp
(11.86)
for the hydrostatic equation in isentropic coordinates.
The continuity equation follows from its expression in terms of specific
volume. In isentropic coordinates, this becomes
dao
dt = a~ v)~
(11.87.1)
where
a o
refers to the incremental material volume
dV o
and
dto 0
(V.
v)o = Vo. v h + .
(11.87.2)
aO
According to (11.6),
where
a o - J(x, xo)a ,
(11.88)
aO
J(x, xo)-
By incorporating (11.85) with (11.78.1), we obtain
(0,t-1
ao -- Pa " g -~
(o )1
= g -~ .
(11.89)
(11.90)

11.5 Thermodynamic Coordinates
367
Then (11.87) yields
or
d 1 (0,)-1
for the continuity equation in isentropic coordinates. Note that (11.91) is
identical to the continuity equation in physical coordinates (11.25) if
(ap/dO)
is identified with density. The thermodynamic equation has the same form as
earlier.
Collectively, the equations of motion in isentropic coordinates are then
given by
dV__hh_(
tan 4~)
dt ~- f + U~a k x v h - -Vo~- Dh,
(11.92.1)
dO - Cp ,
(11.92.2)
dt ~ + ~ (V'v)~ (11.92.3)
0
o)0 - c~0net , (11.92.4)
with
d d
dt - dt + vh "
V~ + w~ (11.92.5)
The lower boundary condition becomes (Problem 11.22)
d* d (OO*) dz s
dt dt \ O0 / - g dt "
(11.93)
These equations simplify the description of vertical motion, which is re-
lated directly to the rate at which heat is absorbed by an air parcel (11.92.4).
Under adiabatic conditions, there is no motion across coordinate surfaces, so
w 0 and vertical advection vanish. Under diabatic conditions, the system is still
advantageous because it relates vertical motion (which is difficult to measure
due to its smallness) to quantities that are more reliably determined. An-
other advantage of isentropic coordinates is enhanced resolution in regions
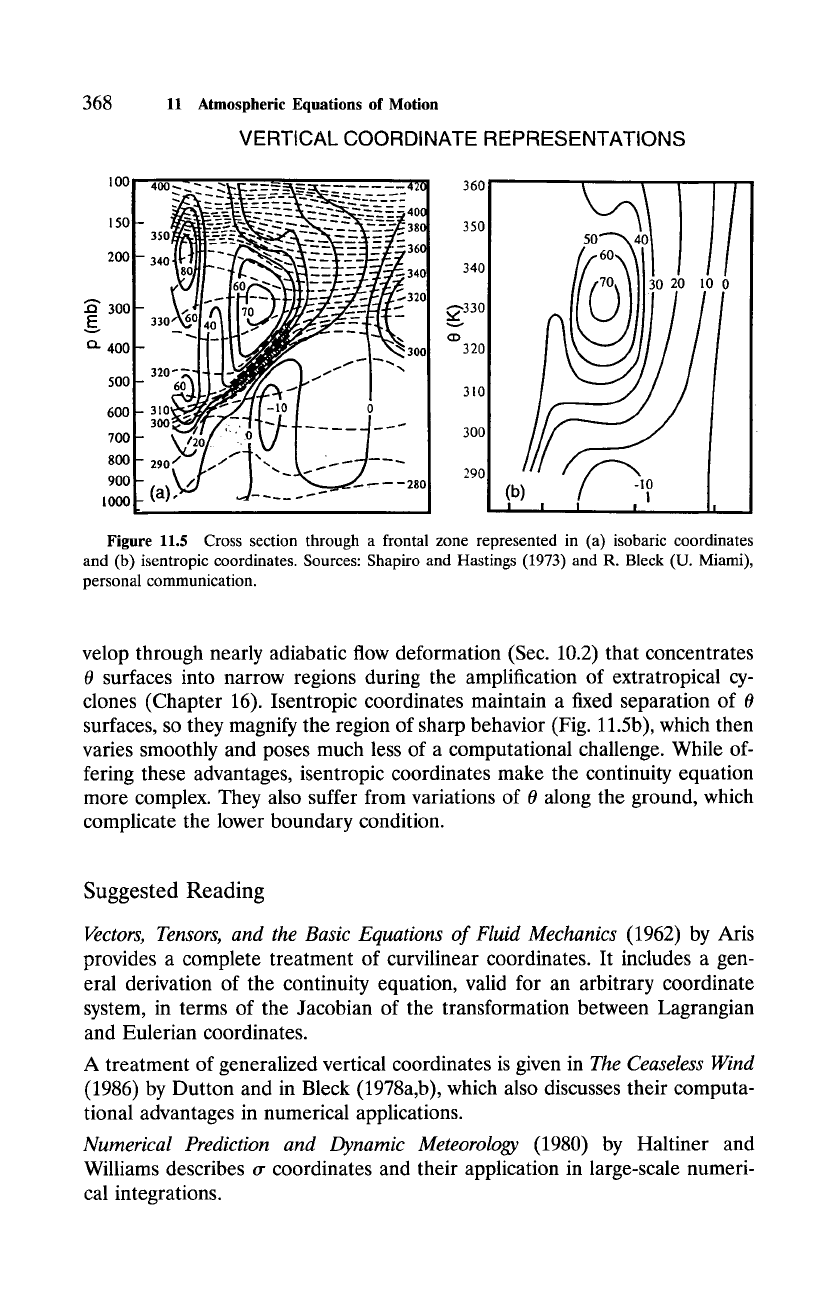
of strong temperature gradient, such as those typical of frontal zones. Fig-
ure 11.5 shows a frontal surface represented in terms of isobaric and isentropic
coordinates. In the isobaric representation (Fig. l l.5a), motion and potential
temperature vary sharply across the frontal zone, which then requires a fine
computational mesh to be properly represented. These sharp gradients de-
368
11 Atmospheric Equations of Motion
VERTICAL COORDINATE REPRESENTATIONS
100
150
200
~" 300
E
o. 400
500
600
700
800 ~
900
1000
350
- 340
330
320
- 310
300
290
(a)
/
~. :.- --
_
34(
-- -"
-"-_2 -- ~.32c
30(
~280
401 I ]1 [
~'3301
II 0
11130 20 10 0 |
.
Figure 11.5 Cross section through a frontal zone represented in (a) isobaric coordinates
and (b) isentropic coordinates. Sources: Shapiro and Hastings (1973) and R. Bleck (U. Miami),
personal communication.
velop through nearly adiabatic flow deformation (Sec. 10.2) that concentrates
0 surfaces into narrow regions during the amplification of extratropical cy-
clones (Chapter 16). Isentropic coordinates maintain a fixed separation of 0
surfaces, so they magnify the region of sharp behavior (Fig. l l.5b), which then
varies smoothly and poses much less of a computational challenge. While of-
fering these advantages, isentropic coordinates make the continuity equation
more complex. They also suffer from variations of 0 along the ground, which
complicate the lower boundary condition.
Suggested Reading
Vectors, Tensors, and the Basic Equations of Fluid Mechanics
(1962) by Aris
provides a complete treatment of curvilinear coordinates. It includes a gen-
eral derivation of the continuity equation, valid for an arbitrary coordinate
system, in terms of the Jacobian of the transformation between Lagrangian
and Eulerian coordinates.
A treatment of generalized vertical coordinates is given in
The Ceaseless Wind
(1986) by Dutton and in Bleck (1978a,b), which also discusses their computa-
tional advantages in numerical applications.
Numerical Prediction and Dynamic Meteorology
(1980) by Haltiner and
Williams describes ~r coordinates and their application in large-scale numeri-
cal integrations.

Problems
369
Problems
11.1.
11.2.
11.3.
11.4.
11.5.
11.6.
11.7.
11.8.
11.9.
11.10.
11.11.
11.12.
11.13.
Demonstrate that the Jacobian satisfies the reciprocal property (11.4).
Show that the Jacobian reduces to the product of the metric scale
factors (11.7) if the curvilinear coordinate system is orthogonal.
Express spherical coordinates in terms of the rectangular Cartesian
coordinates (11.13).
Show that metric scale factors for spherical coordinates are given by
(11.14).
(a) Express the spherical coordinate vectors in terms of the Cartesian
coordinate vectors (11.20). (b) Show that the spherical coordinate vec-
tors have spatial derivatives
3i 3i 3i
= sin ~bj - cos ~bk = 0 = 0
oj oj oj
= -sin ~bi = -k = 0
ok Ok Ok
= cos ~bi =j -- = O.
Oh 0~, 3z
(Hint."
Obtain reciprocal identities for el, e2, and e 3 in terms of
i, j,
and
k.) (c) Evaluate the Lagrangian derivatives of the spherical coordinate
vectors to obtain (11.21).
Derive the angular momentum principle implied by the vector equa-
tions of motion in full spherical geometry.
Show that the equations of motion in an inertial reference frame are
expressed by (11.27).
(Hint:
See Problem 10.11.)
Show that the approximate system (11.28) has the angular momentum
principle (11.29).
(a) Derive the approximate expression (11.35) for the specific buoyancy
force. (b) Discuss the validity of this approximation.
Perform a dimensional analysis to demonstrate that, for scales represen-
tative of the midlatitude stratospheric circulation (e.g., the polar-night
jet disturbed by planetary waves; refer to Fig. 1.10), metric and Cori-
olis terms proportional to cos ~b appearing in the equations of motion
are negligible.
The equations of motion are expressed conveniently in terms of the
Exner function 7r = Cp(p/po) K
as the vertical coordinate, where P0 =
1000 mb. Transform the equations from isobaric coordinates to Exner
coordinates.
In isobaric coordinates, derive the thermodynamic equation in terms of
potential temperature (11.61.2).
Show that isochoric surfaces are material if the motion is steady and v
is everywhere orthogonal to V p.
