Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.

1000

900

000

700

600

500

400

300

200

100

.2 .4

1.0

1.2 1.4

1.6

1.8

2.0

(L)

1000

900

800

700

600

500

400

300

200

100

150 200 250

300

350

400

(K)

100

150 200 250

300

350

400

(K)

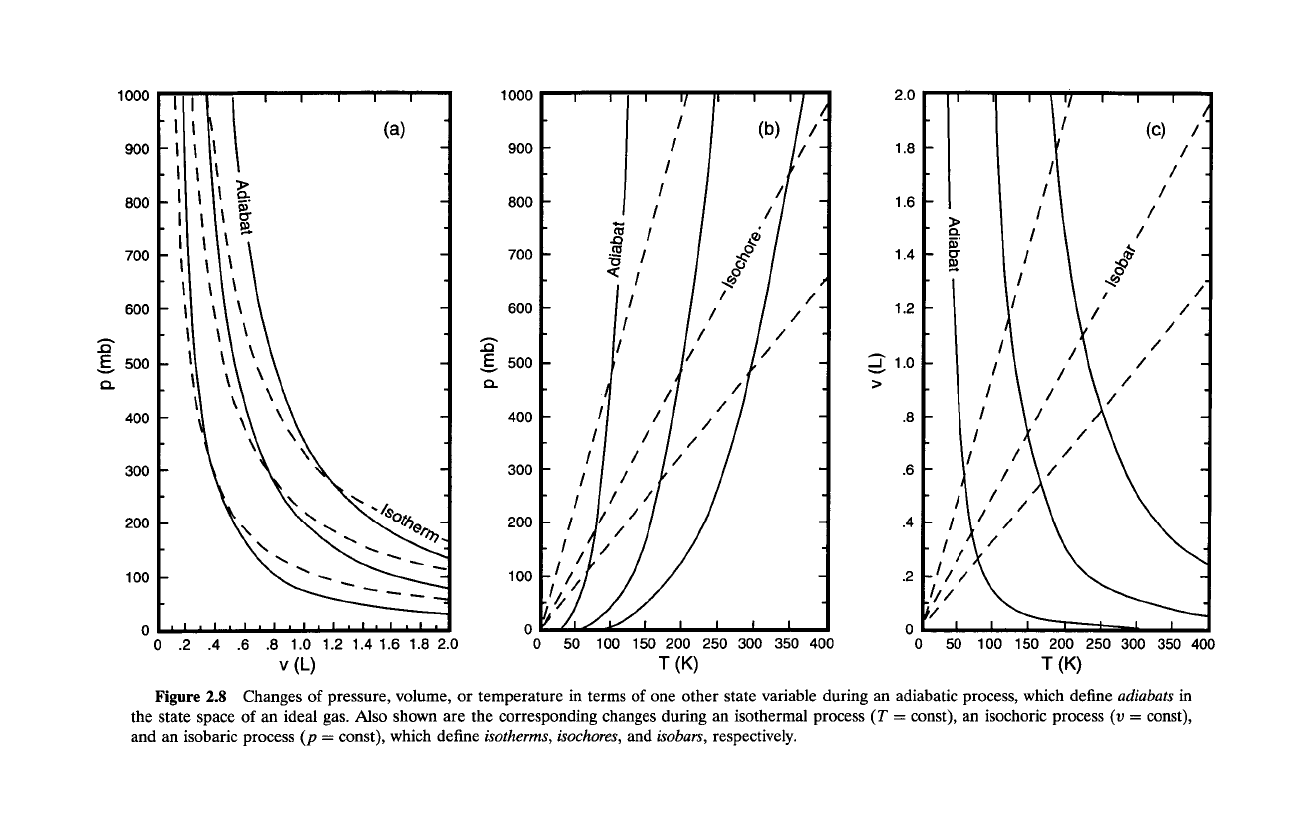
Figure

2.8

Changes

pressure, volume,

temperature in terms

one other state variable during an adiabatic process, which define

adiabats

the state space

ideal gas.

Also

shown are the corresponding changes during an isothermal process

const), an isochoric process

const),

and an isobaric process

const), which define

isotherms, isochores,

and

isobars,

respectively.

2.4 Adiabatic Processes 71

and isochoric processes describe a family of

isochores

(v = const), which are

superposed in Fig. 2.8. Just as each of the foregoing paths is characterized by

invariance of a certain state variable, so too are adiabats.

2.4.1 Potential Temperature

Poisson's relation between pressure and temperature motivates the introduc-

tion of a new state variable that is preserved during an adiabatic process. The

potential temperature 0

is defined as that temperature assumed by the system

when compressed or expanded adiabatically to a reference pressure of P0 =

1000 mb. According to (2.30.2), an adiabatic process from the state (p, T) to

the reference state (P0, 0) satisfies

Opo~= rp-~.

Hence, the potential temperature is described by

~= P . (2.31)

A function of pressure and temperature, 0 is a state variable. According to

(2.31) and Poisson's relation (2.30.2), 0 is invariant along an adiabatic path in

state space.

Adiabatic behavior of individual air parcels is a good approximation for

many atmospheric applications. Above the boundary layer and outside of

clouds, the timescale of heat transfer is of order two weeks and thus long

compared to the characteristic timescale of displacements, which influence an

air parcel through changes of pressure and expansion work. For instance, ver-

tical displacements of air and accompanying changes of pressure and volume

occur in cumulus convection on a timescale of minutes to hours. Even in mo-

tions of large horizontal dimension (e.g., in sloping convection associated with

synoptic disturbances), air displacements occur on a characteristic timescale

of order one day. Thus, over a fairly wide range of motions, the timescale for

an air parcel to adjust to changes of pressure and to perform expansion work

is short compared to the characteristic timescale of heat transfer.

Under these circumstances, the potential temperature of individual air

parcels is approximately conserved. An air parcel descending to greater pres-

sure experiences an increase of temperature according to (2.30.2) due to com-

pression work performed on it, but in such proportion to its increase of pres-

sure as to preserve the parcel's potential temperature through (2.31). Similar

considerations apply to an air parcel that is ascending. It follows that, un-

der adiabatic conditions, 0 is a conserved quantity and therefore behaves as

a tracer of air motion. On timescales for which individual parcels can be re-

garded as adiabatic, particular values of 0 track the movement of those bodies

of air. Conversely, a collection of air parcels that has a particular value of 0

Thermodynamics of Gases

Adiabatic

O 7 ~ ...................

Diabatic

._ "

0=01

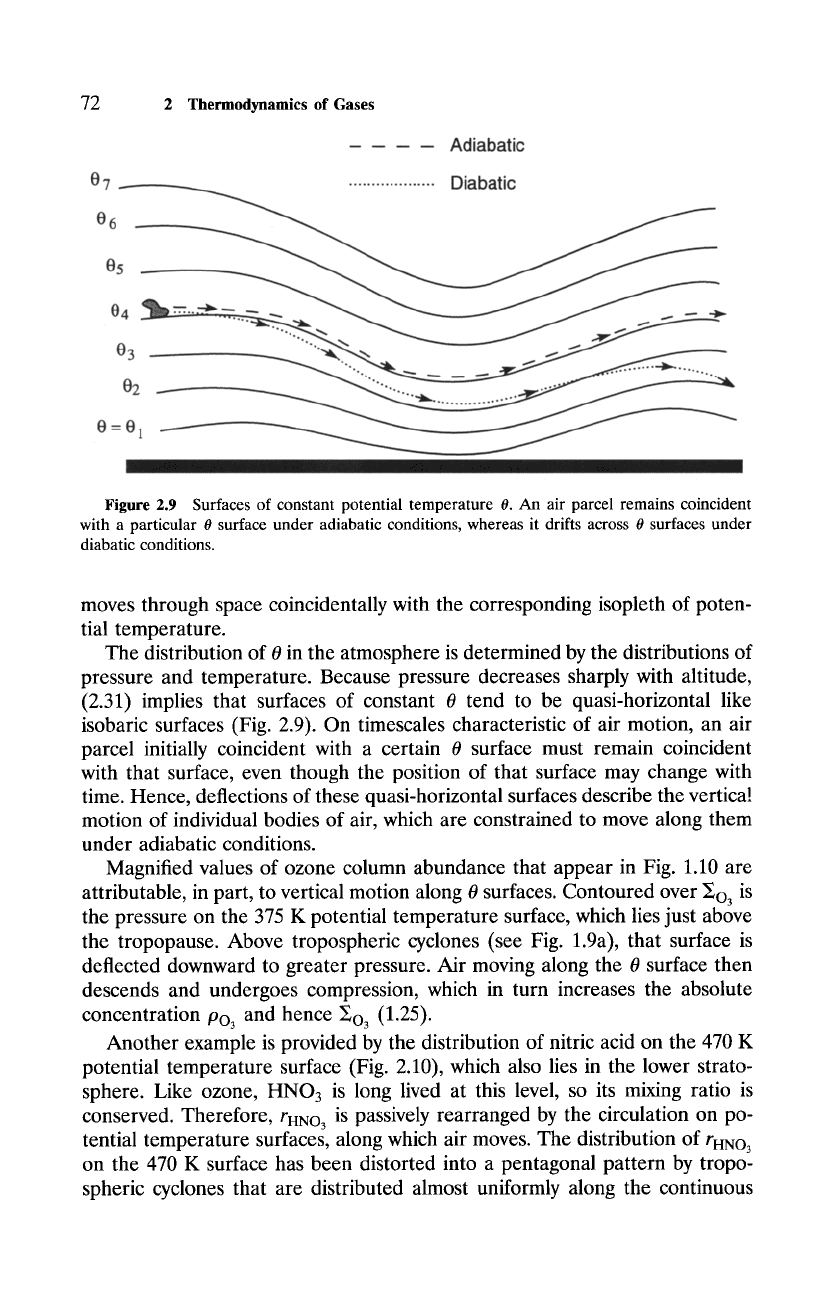
Figure

2.9 Surfaces of constant potential temperature 0. An air parcel remains coincident

with a particular 0 surface under adiabatic conditions, whereas it drifts across 0 surfaces under

diabatic conditions.

moves through space coincidentally with the corresponding isopleth of poten-

tial temperature.

The distribution of 0 in the atmosphere is determined by the distributions of

pressure and temperature. Because pressure decreases sharply with altitude,

(2.31) implies that surfaces of constant 0 tend to be quasi-horizontal like

isobaric surfaces (Fig. 2.9). On timescales characteristic of air motion, an air

parcel initially coincident with a certain 0 surface must remain coincident

with that surface, even though the position of that surface may change with

time. Hence, deflections of these quasi-horizontal surfaces describe the vertical

motion of individual bodies of air, which are constrained to move along them

under adiabatic conditions.

Magnified values of ozone column abundance that appear in Fig. 1.10 are

attributable, in part, to vertical motion along 0 surfaces. Contoured over Eo3 is

the pressure on the 375 K potential temperature surface, which lies just above

the tropopause. Above tropospheric cyclones (see Fig. 1.9a), that surface is

deflected downward to greater pressure. Air moving along the 0 surface then

descends and undergoes compression, which in turn increases the absolute

concentration Po3 and hence Eo3 (1.25).

Another example is provided by the distribution of nitric acid on the 470 K

potential temperature surface (Fig. 2.10), which also lies in the lower strato-

sphere. Like ozone, HNO3 is long lived at this level, so its mixing ratio is

conserved. Therefore, rHNO3 is passively rearranged by the circulation on po-

tential temperature surfaces, along which air moves. The distribution of rHNO3

on the 470 K surface has been distorted into a pentagonal pattern by tropo-

spheric cyclones that are distributed almost uniformly along the continuous

.... :3.8

:~iiiiiiiiil

~iiiiiiiiii~

............

ij{iiiiiii~ii

>;. 1

!ii!ii!

2.4

.... 4

180

2.4

Adiabatic Processes

, .g

1.7 0

Figure 2.10 Distribution of nitric acid mixing ratio

rHNO3

(ppbv) on the 0 = 470 K potential

temperature surface over the Southern Hemisphere on January 3, 1979, as observed by Nimbus-7

LIMS. Adapted from Miles and Grose (1986).

storm track of the Southern Hemisphere (see Fig. 1.25a). In fact, the pattern

of rHNO3 suggests that air is being overturned horizontally by those synoptic

disturbances.

2.4.2 Thermodynamic Behavior Accompanying Vertical Motion

According to (2.30.2), the temperature of an air parcel moving vertically

changes due to expansion work, but in such proportion to its pressure as to

preserve its potential temperature. An expression for the rate that a parcel's

temperature T' changes with its altitude z' under adiabatic conditions follows

from (2.25.2) in combination with hydrostatic equilibrium (1.16). With the gas

law, the change with altitude of environmental pressure p is described by

dlnp- H' (2.32)

where H is given by (1.17.2). Since the parcel's pressure p' adjusts automati-

cally to the environmental pressure to preserve mechanical equilibrium, (2.32)

also describes how the parcel's pressure changes with altitude. Then, for the

2 Thermodynamics of Gases

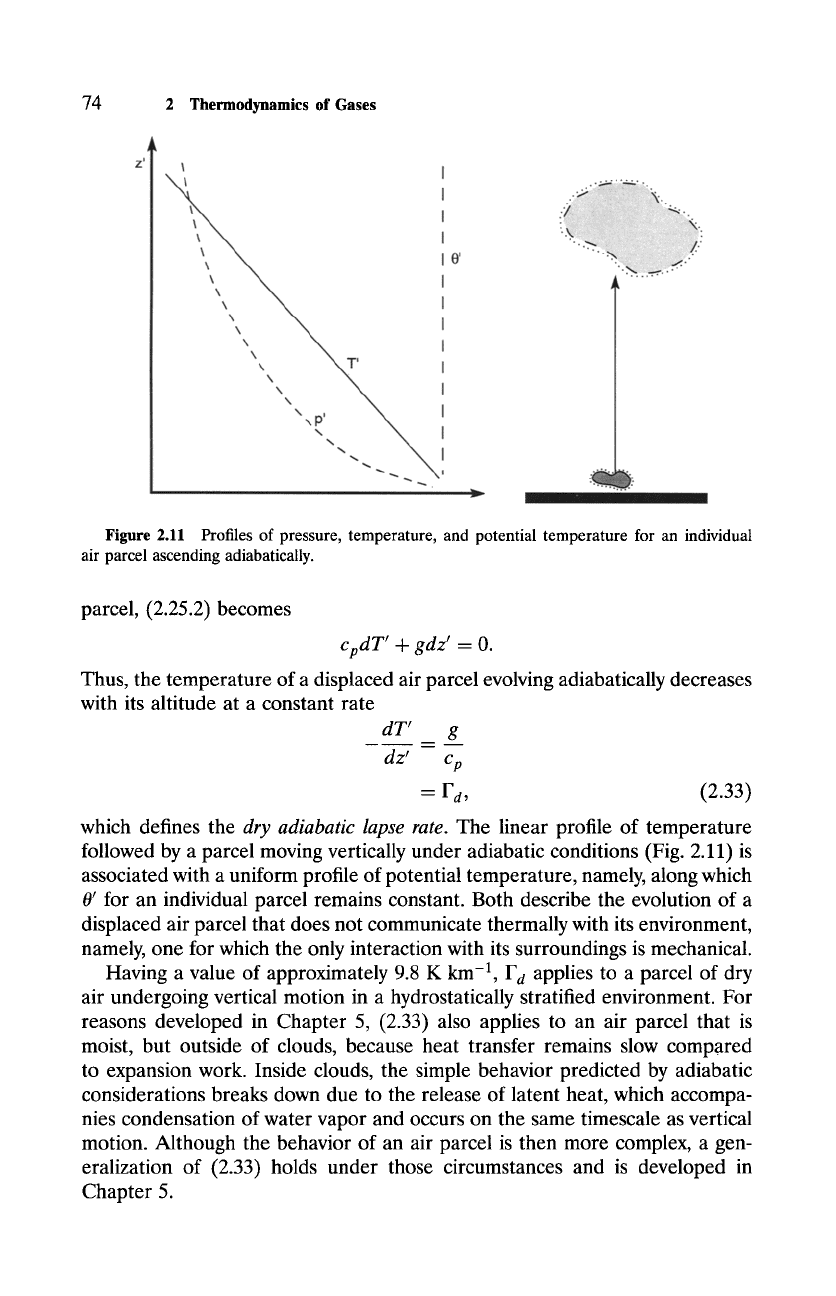
Figure 2.11 Profiles of pressure, temperature, and potential temperature for an individual

air parcel ascending adiabatically.

parcel, (2.25.2) becomes

cpdT' + gdz' = O.

Thus, the temperature of a displaced air parcel evolving adiabatically decreases

with its altitude at a constant rate

dT' g

dz ~ Cp

= F d, (2.33)

which defines the

dry adiabatic lapse rate. The linear profile of temperature

followed by a parcel moving vertically under adiabatic conditions (Fig. 2.11) is

associated with a uniform profile of potential temperature, namely, along which

0' for an individual parcel remains constant. Both describe the evolution of a

displaced air parcel that does not communicate thermally with its environment,

namely, one for which the only interaction with its surroundings is mechanical.

Having a value of approximately 9.8 K

km -1,

IF" d applies to a parcel of dry

air undergoing vertical motion in a hydrostatically stratified environment. For

reasons developed in Chapter 5, (2.33) also applies to an air parcel that is

moist, but outside of clouds, because heat transfer remains slow compared

to expansion work. Inside clouds, the simple behavior predicted by adiabatic

considerations breaks down due to the release of latent heat, which accompa-

nies condensation of water vapor and occurs on the same timescale as vertical

motion. Although the behavior of an air parcel is then more complex, a gen-

eralization of (2.33) holds under those circumstances and is developed in

Chapter 5.

2.5 Diabatic Processes

Whereas for many purposes the behavior of an air parcel can be regarded

as adiabatic, that condition is violated in certain locations and over long

timescales. Near the surface, thermal conduction and turbulent mixing be-

come important on timescales of order one day. A similar conclusion holds

inside clouds, where the release of latent heat operates on the same timescale

as vertical motion. Over timescales longer than a week, radiative transfer be-

comes important.

Under diabatic conditions, the system interacts with its environment ther-

mally as well as mechanically. The potential temperature of an air parcel is

then no longer conserved. Instead, 0 changes in proportion to heat transferred

into the system, where 0 and other unprimed variables are hereafter under-

stood to refer to an individual air parcel. Taking the logarithm of (2.31) gives

a differential relation among the variables 0, p, and T

dln 0 - dln T -- -Kdln p.

(2.34)

Likewise, dividing the first law (2.22.2) by T and incorporating the gas law

leads to a similar relation

d In T - Kd In p = ~. (2.35)

cpT

Combining (2.34) and (2.35) then yields

d In 0

cpT"

(2.36)

Thus, the increase of potential temperature is a direct measure of the heat

transferred into the system. For this reason, an air parcel will drift across

potential temperature surfaces in proportion to the net heat exchanged with

its environment (Fig. 2.9). Equation (2.36) can be regarded as an alternate

and more compact expression of the first law, one in which expansion work

has been absorbed into the state variable 0. In this light, 0 for a compressible

fluid like air is analogous to T for an incompressible fluid like water. Each

increases in direct proportion to the heat absorbed by the system.

2.5.1 Polytropic Processes

Most of the energy exchanged between the earth's surface and the atmosphere

and between one atmospheric layer and another is accomplished through ra-

diative transfer (refer to Fig. 1.27). In fact, radiative transfer is the primary

diabatic influence outside of the boundary layer and clouds. It is sometimes

convenient to model radiative transfer as a polytropic process

3q = cdT, (2.37)

Thermodynamics of Gases

wherein the heat transferred into the system is proportional to the system's

change of temperature. The constant of proportionality c is the

polytropic spe-

cific heat capacity. Newtonian cooling,

in which heat transfer is proportional to

the departure from an equilibrium temperature, can be regarded as a poly-

tropic process. For deep temperature anomalies, as is characteristic of plan-

etary waves, Newtonian cooling is a useful approximation to IR cooling to

space.

For a polytropic process, the two expressions of the first law (2.22) reduce

(c v - c)dT + pdv

= 0,

(2.38.1)

(Cp - c)dT - vdp

= 0. (2.38.2)

Equations (2.38) resemble the first law for an adiabatic process, but with

modified specific heats. Consequently, previous formulas valid for an adiabatic

process hold for a polytropic process with the transformation

Cp --> (Cp - C),

(2.39)

Then (2.39) may be used in (2.31) to define a

polytropic potential temperature

0, which is conserved during a polytropic process (Problem 2.9). Analogous to

potential temperature, O is the temperature assumed by an air parcel if com-

pressed polytropically to 1000 mb, and it characterizes a family of polytropes

in state space.

In terms of potential temperature, the first law becomes

dln O = (~p)dln T.

(2.40)

If c is positive, the effective specific heats

(Cp- c)

and (c o -c) are reduced

from their adiabatic values. Therefore, a given change of pressure or volume

in (2.38) leads to a greater change of temperature. For an increase of temper-

ature, the additional warming implies heat absorption from the environment

and an increase of 0 by (2.40). This would be the situation for an air parcel

that is cooler than its surroundings. For a decrease of temperature, the ad-

ditional cooling implies heat rejection to the environment and a decrease of

0, as would occur for an air parcel that is warmer than its environment. The

reverse behavior follows if c is negative.

Suggested Reading

A thorough discussion of thermodynamic properties of gases is given in

Atmo-

spheric Thermodynamics

(1981) by Iribarne and Godson.

Statistical Thermodynamics

(1973) by Lee, Sears, and Turcotte provides a clear

treatment of specific heats and other gas properties from the perspective of

statistical mechanics.

Problems 77

Problems

2.1.

2.2.

2.3.

2.4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10.

2.11.

A plume of heated air leaves the cooling tower of a power plant at 1000

mb with a temperature of 30~ If the air may be treated as dry, to

what level will the plume ascend if the ambient temperature varies with

altitude as: (a)

T(z)

= 20- 8z(C) and (b)

T(z)

= 20 + z(C), with z in

kilometers.

Suppose that the air in Problem 2.1 contains moisture, but its effect is

negligible beneath a cumulus cloud, which forms overhead between 900

and 700 mb. (a) What is the potential temperature inside the plume at

950 mb? (b) How is the potential temperature inside the plume at 800 mb

related to that at 950 mb? (c) How is the buoyancy of air at 800 mb relat-

ed to that if the air were perfectly dry?

One mole of water is vaporized at 100~ and 1 atm of pressure (1.013 x

105 Pa), with an observed increase in volume of 3.02 x 10 -2 m 3. (a) How

much work is performed by the water? (b) How much work would be

performed if the water behaved as an ideal gas and accomplished the

same change of volume isobarically? (c) The enthalpy of vaporization

for water is 4.06 x 10

J mol -~. What heat input is necessary to accom-

plish the above change of state? Why does the heat input differ from the

work performed?

Demonstrate (a) that h =

h(T)

and (b) relation (2.19).

Demonstrate that 0 is conserved during an adiabatic process.

A large helium-filled balloon carries an instrumented payload from sea

level into the stratosphere. If the balloon ascends rapidly enough for

heat transfer across its surface to be negligible, what relative increase in

volume must be accommodated for the balloon to reach 10 mb?

(Note:

The balloon exerts negligible surface tension~it serves merely to contain

the helium.)

Derive (2.27) for an ideal gas.

Describe physical circumstances under which polytropic heat transfer

would be a useful approximation to actual heat transfer.

Use transformation (2.29) to define a

polytropic potential temperature O,

which is conserved during a polytropic process. How is 0 related to 0?

Through sloping convection, dry air initially at 20~ ascends from sea

level to 700 mb. Calculate (a) its initial and final specific volumes, (b) its

final temperature, (c) the specific work performed, and (d) changes in

its specific energy and enthalpy.

A commercial aircraft is en route to New York City from Miami, where

the surface pressure was 1013 mb and its altimeter was adjusted at

takeoff to indicate 0 ft above sea level. If the surface pressure at New

Thermodynamics of Gases

2.12.

2.13.

2.14.

2.15.

2.16.

York is 990 mb and the temperature is -3~ estimate the altimeter

reading when the aircraft lands if no subsequent adjustments are made.

Commercial aircraft normally cruise near 200 mb, where T = -60~

(a) Calculate the temperature of air if compressed adiabatically to the

cabin pressure of 800 mb. (b) How much specific heat must then be

added/removed to maintain a cabin temperature of 25~

A system comprised of pure water is maintained at 0~ and 6.1 mb,

at which the specific volumes of ice, water, and vapor are

= 1.09 x

10 -3 m3kg -1,

v w

-- 1.00 x 10 -3 m 3 kg -1,

v v

= 206 m 3 kg -1. (a) How

much work is performed by the water substance if 1 kg of ice melts?

(b) How much work is performed by the water substance if 1 kg of

water evaporates? (c) Contrast the values in (a) and (b) in light of the

heat transfers required to accomplish the preceding transformations of

phase:

afusion-

0.334

• 10 6 J

and

Qvaporization ~-2.50 x 10 6 J.

Surface winds blow down a mountain range during a

Chinook,

which is

an Indian term for "snow eater." If the temperature at 14,000 ft along

the continental divide is -10~ and if the sky is cloud-free leeward

of the divide, what is the surface temperature at Denver, which lies at

approximately 5000 ft?

A scuba diver releases a bubble at 30~ at a depth of 32 ft, where the

absolute pressure is 2 atm. Presume that the bubble remains intact, is

large enough for heat transfer across its surface to be negligible, and

condensational heating in its interior can be ignored. Beginning from

hydrostatic equilibrium and the first law, (a) derive an expression for

the bubble's temperature as a function of its elevation z above its initial

elevation and (b) determine the bubble's temperature upon reaching

the surface under the foregoing conditions. (c) How would these results

be modified under fully realistic conditions?

(Note:

Normal respiration

processes only about 30% of the oxygen available, so the bubble can be

treated as air.)

An air parcel descends from 10 to 100 mb. (a) How much specific work

is performed on the parcel if its change of state is accomplished adiabat-

ically? (b) If its change of state is accomplished isothermally at 220 K?

the change of state? (d) What is the parcel's change of potential temper-

ature under the same conditions?

Chapter 3

The Second Law and Its Implications

The first law of thermodynamics describes how the state of a system changes

in response to work it performs and heat absorbed by it. The second law of

thermodynamics deals with the direction of thermodynamic processes and the

efficiency with which they occur. Since these characteristics control how a

system evolves out of a given state, the second law also underlies the stability

of thermodynamic equilibrium.

3.1 Natural and Reversible Processes

A process for which the system can be restored to its initial state, without

leaving a net influence on the system or on its environment, is said to be

reversible.

A reversible process is actually an idealization: one that is devoid of

friction and for which changes of state occur slowly enough for the system to

remain in thermodynamic equilibrium. By contrast, a

naturalprocess

is one that

proceeds freely, for example, a spontaneous process which can be stimulated

by a small perturbation to the system. Because the system is then out of

thermodynamic equilibrium with its surroundings, a natural process cannot be

reversed entirely, that is, without leaving a net influence on either the system

or its environment. Thus, a natural process is inherently "irreversible,"

Irreversibility is introduced by any process that drives the system out of

thermodynamic equilibrium, as occurs during rapid changes of state. Perform-

ing work across a finite pressure difference, wherein the system is out of

mechanical equilibrium, and transferring heat across a finite temperature dif-

ference, wherein the system is out of thermal equilibrium, are both irreversible.

A process involving friction (e.g., turbulent mixing, which is accompanied by

frictional dissipation) is also irreversible, as are transformations of phase when

different phases are not at equilibrium with one another (e.g., in states away

from saturation).

An example of irreversible work follows from a gas that is acted on by a

piston and is maintained at a constant temperature through contact with a

heat reservoir (Fig. 3.1). Suppose the gas is expanded isothermally at temper-

ature T~2 from state 1 to state 2 and subsequently restored to state 1 through