Саградов В.А, Ионцев А.А. Введение в демографию

Подождите немного. Документ загружается.

473

жизни людей, которые родились в t–3 году. Таким образом, прогнозируе-

мая численность населения состоит из людей, которые 1 января года

t на-

ходились в возрасте

х полных лет и объединялись отрезком AB. Эта чис-

ленность населения (обозначим ее, соответственно,

m,x,t

) и послужит нам

базой для прогноза.

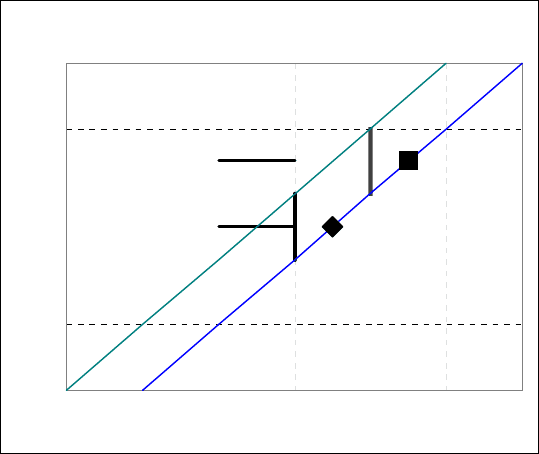
Календарное время

Возраст

t-3

t-2

t-1 t

t+1 t+2

x+1

x+2

x+3

x-1

x-2

Рис. 20.2 Метод передвижки на сетке Лексиса

Очевидно, прогнозируемая численность населения P

m,x+1,t+1

отличается

от базовой численности населения

m,x,t

, поскольку некоторая ее часть

не доживет до 1 января

t+1 года. Строго говоря, прогнозируемая и базовая

численности населения связаны следующим уравнением:

)1(

,2/1,,,1,1, txmtxmtxm

qPP

+++

−

, (20.8)

где

m,x+1/2,t

— вероятность того, живой мужчина, достигший точного воз-

раста

х+1/2 лет в середине года t, не доживет до середины года t+1

(на сетке Лексиса линия жизни такого мужчины прервется на отрезке, ог-

раниченном точками

Y и Z).

Выражение (

txm

,2/1,

− ) используется в уравнении (20.8), так как

средний возраст в совокупности людей, которым в предыдущий день рож-

дения исполнилось

х полных лет (то есть в базовой численности населе-

ния), составляет

х+1/2 года.

474

Поскольку точка Z принадлежит 1

t году, данными за который мы

не располагаем на момент построения прогноза, постольку выражение

txm

,2/1,

− мы заменяем на приблизительно равное:

)/(

,,,1,,,1,1, txmtxmtxmtxm

LLPP

+++

≈

, (20.9)

где

m,x+1,t

, L

m,x,t

— соответственно, числа живущих в возрастах х+1 и х лет,

рассчитанные для мужского населения в году

t (на сетке Лексиса этим чис-

лам соответствуют отрезки

GH и EF).

Соотношение

)/(

,,,1, txmtxm

получило название коэффициента пе-

редвижки

, а процедура, применяющая данное соотношение, — метода

передвижки возрастов

Для прогноза численности мужского населения в возрасте 0 лет в году

1+t (

1,0

+tm

) используется следующая формула:

)1(

,0,2/1,1,0, tmtmtm

qNP

−

, (20.10)

где

m,t

— число мальчиков, родившихся в период от середины года t

до середины года

1+t

,0,2/1

— вероятность того, что мальчик, родив-

шийся между серединой года

t и серединой года 1

t , не доживет

до середины года

1+t .

Выражение

)1(

,0,2/1 tm

q−

используется в уравнении (20.10), так как

средний возраст людей, которым в середине года

t было меньше 1 года,

составляет 1/2 года. Аналогично уравнению (20.9), мы можем заменить

правую часть уравнения (20.10) на приблизительно равную:

)/(

,0,,0,,1,0, tmtmtmtm

lLNP =

, (20.11)

где

m,0,t

— число живущих в возрасте 0 лет, рассчитанное для мужского

населения в году

t; l

m,0,t

– корень таблицы смертности, рассчитанной для

мужского населения в году t.

Чтобы рассчитать величину

m,t

, необходимы данные об общих числах

родившихся в годы

t и t+1:

(

)

)(

1,,,,,,

2/12/1

∑

++−

+−

δ=

txftxtxftx

mtm

PfPf

(20.12)

где

t–1/2

и N

t+1/2

— числа родившихся в календарные годы t и t+1 (символы

t–1/2 и t+1/2 обозначают, что учитываемые рождения произошли, соответ-

ственно, до середины года

t и после середины года t+1);

— доля маль-

чиков в общем числе родившихся;

x,t–1/2

и f

x,t+1/2

— возрастные коэффици-

енты рождаемости в календарные годы

t и t+1; P

f,x,t

и P

f,x,t+1

— численности

женского населения в возрасте

х в годы t и t+1, соответственно.

475

Исходя из того, что возрастные коэффициенты рождаемости за один

календарный год изменяются мало, уравнение (20.12) можно записать сле-

дующим образом:

∑

+δ≈ 2/)(

1,,,,,, txftxftxmtm

PPfN . (20.13)

Если учесть влияние миграции, то прогнозируемые численности насе-

ления составят:

m,x+1,t+1

≈ P

m,x,t

m,x+1,t

/ L

m,x,t

) + MIGR

m,x+1,t+1

(20.14)

m,0,t+1

≈ N

m,t

m,0,t

/ l

m,0,t

) + MIGR

m,0,t+1

(20.15)

где

MIGR

m,x+1,t+1

, MIGR

m,0,t+1

— сальдо миграции мужского населения, пе-

режившего середину

t+1 года в возрасте х+1 и 0 лет, соответственно,

за период с середины года

t до середины года t+1.

Для прогноза на срок больший, чем один год, вычисления

по формулам (20.14) и (20.15) могут быть итеративно повторены необхо-

димое число раз. На практике, однако, значительно чаще используется дру-

гой способ — с применением более широких возрастных групп. При этом

все возрастные группы (кроме наиболее старшей) должны быть одинаковой

«ширины», а срок прогнозирования за одну итерацию должен быть равен

«ширине» возрастных групп:

m,x+n,t+n

m,x,t

(

m,x+n,t

/ /

m,x,t

) +

MIGR

m,x+n,t+n

, (20.16)

m,0,t+n

m,t

(

m,0,t

) +

MIGR

m,0,t+n

, (20.17)

= n

∑

x,t

(

f,x,t

f,x,t+n

) / 2. (20.18)

где

n — ширина используемых возрастных групп и срок прогнозирования

за одну итерацию;

m,x+n,t

m,x,t

— числа живущих в возрастах х и

х+n лет;

m,x,t

— численность мужского населения в возрасте от х

до

х+n лет в середине года t;

MIGR

m,x+n,t+n

— сальдо миграции мужского

населения, пережившего середину года

t+n в возрасте от х до х+n лет,

за период с середины года

t до середины года t+n;

— число родившихся

за период с середины года

t до середины года t+n;

x,t

— возрастной коэф-

фициент рождаемости в группе от

х до x+n лет за период с середины года t

до середины года t+n.

Смысл уравнений (20.16)–(20.18) состоит в том, что при отсутствии

внешней миграции разность между численностью населения в возрасте

476

лет и старше в году t и численностью населения в возрасте х+n лет и стар-

ше в году

t+n равна числу смертей, произошедших за период с года t

до года

t+n среди лиц, которым в году t исполнилось х и более лет. Чтобы

определить общее число смертей за указанный период, необходимо допол-

нительно учесть смертность детей, родившихся за период с

t до t+n года.

Прогноз на срок, продолжительность которого отличается от величи-

ны кратной «ширине» используемых возрастных групп (например, на срок

12 лет при 5-летних возрастных группах), может быть получен интерполя-

цией прогнозов на стандартные сроки (в указанном случае — на сроки 10 и

15 лет). Такая интерполяция может быть произведена с помощью какой-

либо из математических моделей (линейного, геометрического или экспо-

ненциального роста). Другой способ (при наличии численности населения

и коэффициентов дожития по одногодичным возрастным интервалам) со-

стоит в нескольких итерациях прогноза сроком в 1 год.

Основное преимущество метода компонент (когортно-компонентного

метода) заключается в возможности прогнозирования возрастно-половой

структуры населения (для прогноза численности женского населения при-

меняются уравнения, аналогичные уравнениям (20.8) – (20.18), используе-

мым для прогноза численности мужского населения). Перспективные

оценки возрастно-половой структуры населения служат основой

для функциональных прогнозов населения.

Вставка 20.4. При прогнозе возрастно-половой структуры населения с учетом из-

менения его образовательного уровня применяется расширенный когортно-

компонентный метод. Для реализации данного метода необходимы исходные дан-

ные о возрастно-половой и образовательной структурах населения, а также предпо-

ложения о будущих уровнях рождаемости, смертности и миграции населения. Рас-

ширенный когортно-компонентный метод предполагает отсутствие

дифференциации смертности по уровню образования (United Nations, 1985). По-

строенный таким методом прогноз состоит из двух частей:

• население в возрасте 30 лет и старше по 5-летним возрастным группам, полу и

уровню образования;

• население в возрасте до 30 лет по однолетним возрастным группам и полу

На методе компонент основывается и такой метод прогнозирования

числа и структуры домохозяйств как «

метод коэффициентов глав домохо-

зяйств

» (United Nations, 1989). В соответствии с этим методом, число домо-

хозяйств, возглавляемых лицом, которое принадлежит к возрастной группе a

и полу

s, в году t+n (n, как правило, кратно 5 годам) составляет

ntas

+,,

ntasntasntas

HRPH

+++

⋅

,,,,,,

(20.19)

477

где P

s,a,t+n

— прогнозируемая методом компонент численность населения,

принадлежащего к полу

s и возрастной группе a в году t+n; HR

s,a,t+n

— ко-

эффициент глав домохозяйств, равный отношению числа глав домохо-

зяйств, принадлежащих к полу s и возрастной группе a, к общей численно-

сти населения данного пола и возраста.

Предположения относительно будущих изменений коэффициентов

глав домохозяйств строятся методом экстраполяции, исходя из анализа

имеющихся данных, или

ad hoc, учитывая тенденции изменения типов

брачного поведения (в первую очередь — среднего возраста вступления

в первый брак), величины семейных доходов, темпов жилищного строи-

тельства и т.д.

Полученные данные о числе домохозяйств

ntas

+,,

могут суммиро-

ваться по полу главы домохозяйства и его возрасту, в том числе

для прогноза среднего размера семьи

AHS

∑∑

ntsa

AHS

(20.20)

Результаты прогноза численности, структуры и среднего размера до-

мохозяйств также имеют важное значение для разработки функциональных

прогнозов.

20.5. КАУЗАЛЬНЫЙ МЕТОД

В современной демографии используется еще один метод построения про-

гнозной модели, непосредственно примыкающий к математическому мето-

ду и получивший название

каузального метода. Он предназначен для про-

гноза отдельных показателей воспроизводства населения (рождаемости,

смертности и др.) как результата изменения их социально-экономических

детерминант. Прогнозные модели, основанные на данном методе, описы-

ваются эконометрическими уравнениями и применяются в качестве со-

ставных частей сложных динамических моделей, а также для уточнения

моделей, основанных на методе компонент. Целесообразность такого уточ-

нения вызвана тем, что метод компонент предполагает неизменность па-

раметров модели (чисел доживающих и возрастных коэффициентов рож-

даемости) или их изменение

вне модели, а средне- и долгосрочные

прогнозы предполагают существенное изменение условий жизни.

Ввиду различного назначения прогнозов, специфики применяемых

концептуальных подходов и ограничений, накладываемых наличием стати-

стических данных, в прогнозных моделях, основанных на каузальном ме-

478

тоде, используются различные комбинации социально-экономических де-

терминант.

Рассмотрим наиболее известные прогнозные модели, основанные

на каузальном методе.

В модели «

Мир-3» (Meadows et al., 1972), предназначенной для отра-

жения взаимосвязанных изменений численности населения, объема произ-

водства, состояния окружающей среды и запаса природных ресурсов, вы-

делен демографический блок, в котором население разделено

на 4 возрастные группы: 0–14 лет (

); 15–44 лет (P

); 45–64 лет (P

); 65 лет

и старше (

). Динамика численности этих групп описывается дифферен-

циальными уравнениями, построенными на основе метода компонент и

переменной (

N), изменение которой прогнозируется с помощью каузально-

го метода:

15/

11,1

PQPN

−−=

30/15/

22,21

PQPP

−−= ,

20/30/

33,32

PQPP

−−= ,

4,43

20/

QPP

−=

где N — общее число рождений; Q

e,i

— вероятность умереть в i-том возрас-

тном интервале.

В свою очередь число рождений (

B) зависит от численности жен-

щин в репродуктивном возрасте (половина численности населения

в возрасте 15–44 лет —

) и величины суммарного коэффициента рож-

даемости:

TFR = Min {MTF;

⋅

(1 – FCE) + DTFFCE

⋅

} (20.21)

где

TFR — суммарный коэффициент рождаемости; MTF — физиологиче-

ский максимум суммарной рождаемости;

FCE — эффективность контроля

над рождаемостью;

DTF — желаемый уровень суммарной рождаемости.

Таким образом, если

DTF превышает MTF, то TFR равен MTF. Если

DTF ниже MTF, то TFR равен их среднему взвешенному, где весами слу-

жит

FCE. При этом, если FCE=1, то суммарный коэффициент рождаемости

равен

DTF, а если FCE=0, то — MTF.

479

Вставка 20.5. Три перечисленных фактора суммарного коэффициента рождаемости

также имеют свои детерминанты:

MTF = ηN

(20.22)

DTF = δN

(20.23)

FCE = M

Ω

(20.24)

где η — константа физиологического максимума суммарной рождаемости, равная

12; N

e —

компонент физиологического максимума суммарной рождаемости, нели-

нейная зависимость которого от ожидаемой продолжительности жизни e

описыва-

ется выпуклой вверх возрастающей кривой (при e

=20 лет — N

=0,4; при e

=40

лет — N

=0,8; при e

=60 лет — N

=1,0 при e

=80 лет — N

=1,1 (см. Егоров и др.

1980, с. 49)); δ — константа «нормального» желаемого уровня суммарной рождае-

мости, равная 4; N

— «социальная норма размера семьи», нелинейная зависимость

которой от среднедушевого уровня промышленного производства 20-тилетней дав-

ности I описывается выпуклой вниз убывающей кривой (при I=200 долл. США

в ценах 1968 г. — N

=1,0; при I=400 долл. — N

=0,9; при I=600 долл. — N

=0,8

(см. Егоров и др., 1980, С. 49)); N

— «реакция средней семьи на социальную норму

размера семьи», нелинейная зависимость которой от темпов изменения обеспечен-

ности промышленной продукцией W за предшествующие 3 года описывается воз-

растающей ломаной линией (при W=(-2%) — N

=0,5; при W=0% — N

=0,7;

при W=2% — N

=1,0 (см. Егоров и др. 1980, С. 50)); M

— «коэффициент, учиты-

вающий младенческую смертность», нелинейная зависимость которого от ожидае-

мой продолжительности жизни 20-тилетней давности e

0,20

описывается выпуклой

вниз убывающей кривой (при e

0,20

=20 — M

=1,625; при e

0,20

=40 — M

=1,3;

при e

0,20

=60 — M

=1,1; при e

0,20

=80 — M

=1,0 (см. Егоров и др., 1980, С. 48)); M

Ω

—

показатель эффективности услуг планирования семьи, нелинейная зависимость

которого от произведенных 20 лет назад инвестиций в производство средств кон-

трацепции в расчете на душу населения Ω

описывается выпуклой вверх возрас-

тающей кривой (при Ω

=0,5 долл. — M

Ω

=0,85; при Ω

=1,0 долл. — M

Ω

=0,9;

при Ω

=2,0 долл. — M

Ω

=0,98; при Ω

=3,0 долл. — M

Ω

=1,0 (см. Егоров и др., 1980,

С. 51)).

Вероятности умереть в i-том возрастном интервале (Q

e,i

) находятся

в нелинейной зависимости от ожидаемой продолжительности жизни при рождении

). Так, Q

e,1

приблизительно составляет 0,058 при e

=20; 0,037 — при e

=30;

0,026 — при e

=40; 0,016 — при e

=50; 0,009 — при e

=70; 0,008 — при e

=80.

e,2

приблизительно составляет 0,03 при e

=20; 0,015 — при e

=30; 0,006 —

при e

=50; 0,001 — при e

=70 и e

=80. Q

e,3

приблизительно составляет 0,058

при e

=20; 0,037 — при e

=30; 0,026 — при e

=40; 0,013 — при e

=50; 0,004 —

при e

=70; 0,001 — при e

=80. Q

e,4

приблизительно составляет 0,123 — при e

=20;

0,069 — при e

=50; 0,04 — при e

=80 (см. Егоров и др., 1980, С. 49).

В свою очередь, ожидаемая продолжительность жизни при рождении

рассчитывается по формуле:

LMPLMCLMHSLMFee

⋅

,00

, (20.25)

480

где e

0,b

— базовая величина ожидаемой продолжительности жизни, равная

28 годам;

LMF — коэффициент влияния уровня питания; LMHS — коэффи-

циент «эффективного» (с 20-летним лагом) влияния медицинского обслу-

живания;

LMC — коэффициент влияния городского образа жизни; LMP —

коэффициент влияния загрязнения окружающей среды.

Вставка 20.6. LMF нелинейно зависит от уровня питания F, определяемого как

отношение среднедушевого производства продовольствия к величине прожиточно-

го минимума в зерновом эквиваленте, равной 230 кг /чел·год (при F=1 —

LMF≈0,635; при F=2 — LMF≈1,205; при F=3 — LMF ≈1,295; при F=4 —

LMF≈1,365; при F=5 — LMF ≈1,409 (см. Егоров и др., 1980, С. 51)). LMHS нелиней-

но зависит от HS — уровня расходов на здравоохранение в расчете на душу населе-

ния (при HS=20 долл. — LMHS≈1,38; при HS=60 долл. — LMHS≈1,82; при

HS=80 долл. — LMHS≈1,93; при HS=100 долл. — LMHS≈2 (см. Егоров и др., 1980,

С. 51)); LMC=1– IU ⋅ , где U — коэффициент влияния урбанизации, нелинейно за-

висящий от численности населения P (при P=4 млрд. чел. — U=0,4;

при P=6 млрд. чел. — U=0,525; при P=8 млрд. чел. — U=0,6; при P=12 млрд. чел. —

U=0,725 (см. Егоров и др., 1980, С. 51)), а I — коэффициент влияния индустриализа-

ции, нелинейно зависящий от промышленного производства на душу населения Y (при

Y=0 — I≈0,5; при Y=200 долл. — I≈0,025; при Y=400 долл. — I≈–0,1; при Y=600 — I≈–

0,063; при Y=800 — I≈–0,013; при Y=1200 — I≈0,1; при Y=1600 — I≈0,2 (см. Егоров и

др., 1980, С. 51)); LMP нелинейно зависит от Z — отношения фактического уровня

загрязнения к уровню загрязнения 1970 г. (при Z=0 — LMP=1; при Z=20 — LMP≈0,96;

при Z=30 — LMP≈0,94; при Z=50 — LMP≈0,85; при Z=80 — LMP≈0,55; при Z=90 —

LMP≈0,4; при Z=100 — LMP≈0,2 (см. Егоров и др., 1980, С. 50)).

Очевидно, что вычисления, основанные на модели «Мир-3», отлича-

ются значительной трудоемкостью. Эта модель не может быть использова-

на на уровне отдельной страны и, тем более, ее региона. Наконец, тот факт,

что между социально-экономическими и демографическими показателями

существуют как прямые, так и обратные нелинейные (к тому же, зачастую,

с временным лагом) связи, существенно усложняет интерпретацию резуль-

татов вычислений.

Более простые прогнозные модели, основанные на каузальном методе,

использованы в моделях семейства

Bachue, разработанных по инициативе

Международной Организации Труда в рамках основанной ею Всемирной

Программы Занятости в конце 1970-х — начале 1980-х гг.

В модели

Bachue-Phulippines (Rodgers et al., 1978), брутто-

коэффициент воспроизводства населения (

GRR) рассчитывается на основе

регрессионного уравнения, параметры которого получены на основе анали-

за данных по 47 развивающимся странам:

GRR

= b

– 0,0064R

t-1

+ 0,0106I

t-1

– 0,0446e

0,t-1

+ 0,0059L

t-1

(20.26)

481

где b

— константа, характеризующая городское или сельское население;

t-1

— доля занятых среди женщин в возрасте 15–44 лет в предшествующий

период;

t-1

— доля неграмотных среди взрослого населения

в предшествующий период;

0,t-1

— ожидаемая продолжительность жизни

при рождении в предшествующий период;

t-1

— доля занятых в аграрном

секторе в предшествующий период.

Ожидаемая продолжительность жизни при рождении в модели

Bachue-Phulippines вычисляется по формуле:

= 87,2 – 3389/Y + 76880/Y

– 36,47G, (20.27)

где

Y — ВВП на душу населения в долларах США; G — коэффициент Джини.

В модели

Bachue–International (Moreland, 1984), построенной

на основе данных по 25 странам и представляющей собой генерализацию

моделей данного семейства, то есть сохраняющей базовые параметры

взаимосвязей, описанных в частных моделях, специальный коэффициент

рождаемости (

FR) и ожидаемая продолжительность жизни (e

) вычисляют-

ся по формулам:

ln(

FR) = 5,1 + 0,12ln(I) – 0,21ln(R) +

+ 0,43ln(

) – 0,25ln(Y) – 0,24ln(LOW40), (20.28)

= 69,9 – 1500/Y – 0,2I + 0,27LOW40 + 0,00008DRS, (20.29)

где

I — доля неграмотных среди взрослого населения; R — доля занятых

среди женщин в возрасте 15–44 лет;

Y — ВВП на душу населения;

LOW40 — доля доходов, приходящаяся на 40 наименее богатых процентов

населения;

DRS — численность врачей на душу населения.

Каузальная модель Д. Уилера, построенная на основе эконометриче-

ского анализа социально-экономической и демографической динамики

в развивающихся странах (Wheeler, 1984), была предназначена именно

для прогноза, причем прогноза изменений величины показателей воспроиз-

водства населения. Так, изменение специального коэффициента рождаемо-

сти (∆

FR) в 1960–1977 гг. оценивается по формуле, рассчитанной на основе

данных по 62 странам:

∆

FR = 187,338∆w + 9,63614∆cdr – 0,247∆(cdr)

–

– 15,4159∆

y – 1,3122plan, (20.30)

где

∆w — изменение доли женщин в возрасте 25–34 лет в численности

женщин в возрастной группе 15–49 лет;

∆cdr — изменение общего коэф-

фициента смертности;

∆y — процентное изменение величины ВВП на душу

населения;

plan — специальный индекс планирования семьи Молди-

на-Берельсона

(см. Mauldin and Berelson, 1978).

482

Изменение общего коэффициента смертности в 1960–1977 гг. опреде-

ляется уравнением, полученным на основе анализа данных по 64 странам:

∆

cdr = 6,6523 – 1,06705cdr

t-1

+ 0,0193 (cdr

t-1

)

+ 0,000024956

med

t-1

+19,3986∆p

0-14

+ 19,8577∆p

50+

(20.31)

где

med — численность населения, приходящегося на 1 врача; p

0-14

— про-

цент населения в возрасте 0–14 лет;

50+ —

процент населения в возрасте

50 лет и старше;

t-1 — исходный момент времени.

К сожалению, модель Д. Уилера включает ряд редко используемых

(индекс

Молдина-Берельсона) и недостаточно надежных (общий коэффи-

циент смертности) показателей, что существенно снижается ее практиче-

скую значимость, во всяком случае — применительно к экономически раз-

витым странам и странам, возрастная структура которых подвержена

периодическим колебаниям.

Существенный интерес представляют каузальные модели семейства

ESCAP (разработанные в рамках деятельности Экономической и Социаль-

ной Комиссии ООН для Азии и Тихого океана) для Индонезии, Южной

Кореи, Малайзии, Филиппин и Таиланда. Среди них наибольшего внима-

ния заслуживают модели рождаемости, построенные на основе данных

по Таиланду и Филиппинам, тогда как остальные модели рождаемости, а

также смертности страдают определенными статистическими погрешно-

стями (см. Bilsborrow, 1989).

Модель рождаемости для Таиланда базируется на сопоставлении дан-

ных по его 72 провинциям за 1980 г. и оценивает приближение к некоему

пороговому значению, округленно соответствующему уровню простого

воспроизводства населения:

log (

TFR – 2,0) = 2,08 – 0,19SED + 0,1005Y – 0,0016Y

(20.32)

где

TFR — суммарный коэффициент рождаемости; SED — доля населения

со средним и выше образованием;

Y — ВВП на душу населения.

Модель рождаемости для Филиппин базируется на анализе связанных

изменений социально-демографических переменных за 1957–1977 гг.:

log

GMFR = 8,03 – 0,0011Yp – 0,0045IMR – 0,006RPF, (20.33)

где

GMFR — коэффициент брачной рождаемости; Yp — среднедушевой

личный доход;

IMR — коэффициент младенческой смертности; RPF — от-

носительная цена продуктов питания.

В целом каузальные модели представляют собой попытки количест-

венного описания процесса демографического перехода. Несмотря на ис-

пользование различных комбинаций экзогенных переменных, они относят-

ся к четырем основным группам: