Ревинская О.Г., Кравченко Н.С. Изучение моделей физических процессов и явлений на компьютере
Подождите немного. Документ загружается.


ɆɨɞO-01 ɇɨɪɦɚɥɶɧɚɹ ɞɢɫɩɟɪɫɢɹ ɫɜɟɬɚ
421
22222
0
22
00
4)(
sin2cos)(
ZZZ
ZZZZZ
b
tbt
m
Ee
r
G
G
ɢɥɢ
22222
0
0
4)(
)cos(
ZZZ
IZ
b
tE
m
e
r
G
G
,
ɝɞɟ
22
0
2
arctg
ZZ
Z
I
b
.
ɉɨɫɬɨɹɧɧɚɹ ɜɟɥɢɱɢɧɚ I – ɪɚɡɧɨɫɬɶ ɮɚɡ ɦɟɠɞɭ ɜɵɧɭɠɞɟɧɧɵɦɢ ɤɨ-
ɥɟɛɚɧɢɹɦɢ ɨɩɬɢɱɟɫɤɨɝɨ ɷɥɟɤɬɪɨɧɚ ɜ ɚɬɨɦɟ ɢ ɤɨɥɟɛɚɧɢɹɦɢ ɜɟɤɬɨɪɚ ɧɚ-
ɩɪɹɠɟɧɧɨɫɬɢ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ ɷɥɟɤɬɪɨɦɚɝɧɢɬɧɨɣ ɜɨɥɧɵ, ɜɵɡɜɚɧɧɚɹ
ɡɚɬɭɯɚɧɢɟɦ (ɩɨɝɥɨɳɟɧɢɟɦ ɫɜɟɬɚ ɜɟɳɟɫɬɜɨɦ).
ȿɫɥɢ ɫɪɟɞɚ (ɜɟɳɟɫɬɜɨ) ɫɥɚɛɨ ɩɨɝɥɨɳɚɟɬ ɢɡɥɭɱɟɧɢɟ, ɪɚɡɧɨɫɬɶ ɮɚɡ
ɦɟɠɞɭ ɜɵɧɭɠɞɟɧɧɵɦɢ ɤɨɥɟɛɚɧɢɹɦɢ ɨɩɬɢɱɟɫɤɨɝɨ ɷɥɟɤɬɪɨɧɚ ɢ ɩɨɥɟɦ
ɦɨɠɧɨ ɫɱɢɬɚɬɶ ɪɚɜɧɨɣ ɧɭɥɸ (I | 0), ɬɨɝɞɚ
22222
0
22222
0
0
4)(4)(
cos
ZZZ
ZZZ
Z
b
E
m
e
b
tE
m
e
r
G
G
G
ɤɨɥɟɛɚɧɢɹ ɨɩɬɢɱɟɫɤɨɝɨ ɷɥɟɤɬɪɨɧɚ ɨɩɪɟɞɟɥɹɸɬɫɹ ɤɨɥɟɛɚɧɢɹɦɢ ɷɥɟɤɬɪɢ-
ɱɟɫɤɨɝɨ ɩɨɥɹ ɷɥɟɤɬɪɨɦɚɝɧɢɬɧɨɣ ɜɨɥɧɵ, ɩɪɨɯɨɞɹɳɟɣ ɱɟɪɟɡ ɜɟɳɟɫɬɜɨ. ȼ
ɪɟɡɭɥɶɬɚɬɟ ɞɢɩɨɥɶɧɵɣ ɦɨɦɟɧɬ ɚɬɨɦɚ (ɦɨɥɟɤɭɥɵ) ɬɚɤɠɟ ɨɩɪɟɞɟɥɹɟɬɫɹ
ɤɨɥɟɛɚɧɢɹɦɢ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ
22222
0
2
4)( ZZZ
b
E
m
e
rep
G
G
G
ɢɥɢ ɜ ɫɤɚɥɹɪɧɨɣ ɮɨɪɦɟ
22222
0
2
4)( ZZZ
b
E
m
e
p .
Ɍɨɝɞɚ, ɭɱɢɬɵɜɚɹ ɩɨɥɭɱɟɧɧɨɟ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɞɢɩɨɥɶɧɨɝɨ ɦɨɦɟɧɬɚ,
ɩɨɥɭɱɢɦ ɡɚɜɢɫɢɦɨɫɬɶ ɩɨɤɚɡɚɬɟɥɹ ɩɪɟɥɨɦɥɟɧɢɹ ɜɟɳɟɫɬɜɚ (ɫɪɟɞɵ) ɨɬ ɱɚɫ-
ɬɨɬɵ ɫɜɟɬɚ:
E
pN
n
H
0
2
1
22222
0
2
0
2
4)(
1
1
ZZZ
H
b
m
eN
n
.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɩɨɤɚɡɚɬɟɥɶ ɩɪɟɥɨɦɥɟɧɢɹ ɜɟɳɟɫɬɜɚ n ɡɚɜɢɫɢɬ ɨɬ
ɱɚɫɬɨɬɵ ɫɜɟɬɚ Z, ɬɨ ɟɫɬɶ ɮɚɡɨɜɚɹ ɫɤɨɪɨɫɬɶ ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɹ ɫɜɟɬɚ ɪɚɡɧɨɣ
ɱɚɫɬɨɬɵ (ɞɥɢɧɵ ɜɨɥɧɵ) ɜ ɨɞɧɨɣ ɢ ɬɨɣ ɠɟ ɫɪɟɞɟ ɛɭɞɟɬ ɪɚɡɥɢɱɧɚ.

Ɉɩɬɢɤɚ
422
Ƚɪɚɮɢɤ ɩɨɥɭɱɟɧɧɨɣ ɚɧɚɥɢɬɢ-
ɱɟɫɤɨɣ ɡɚɜɢɫɢɦɨɫɬɢ ɩɨɤɚɡɚɬɟɥɹ
ɩɪɟɥɨɦɥɟɧɢɹ n ɨɬ ɱɚɫɬɨɬɵ ɫɜɟɬɚ Z
ɢɡɨɛɪɚɠɟɧ ɧɚ ɪɢɫ. 2. ɍɱɢɬɵɜɚɹ
ɫɜɹɡɶ ɞɥɢɧɵ ɜɨɥɧɵ ɫɜɟɬɚ ɫ ɱɚɫɬɨ-
ɬɨɣ
Z
S
O
c
2
, ɦɨɠɧɨ ɡɚɦɟɬɢɬɶ, ɱɬɨ
ɧɚ ɪɢɫɭɧɤɚɯ 1 ɢ 2 ɢɡɨɛɪɚɠɟɧɵ ɚɧɚ-
ɥɨɝɢɱɧɵɟ ɡɚɜɢɫɢɦɨɫɬɢ. ɉɪɢɱɟɦ
ɚɧɨɦɚɥɶɧɚɹ ɞɢɫɩɟɪɫɢɹ ɧɚɛɥɸɞɚɟɬɫɹ
ɜɛɥɢɡɢ Z
0
– ɱɚɫɬɨɬɵ ɫɨɛɫɬɜɟɧɧɵɯ
ɤɨɥɟɛɚɧɢɣ. ɑɚɫɬɨɬɚ ɫɨɛɫɬɜɟɧɧɵɯ
ɤɨɥɟɛɚɧɢɣ ɚɬɨɦɚ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɱɚɫɬɨɬɟ ɩɨɝɥɨɳɟɧɢɹ ɜɟɳɟɫɬɜɚ. ɋɥɟɞɨɜɚ-
ɬɟɥɶɧɨ, ɟɫɥɢ ɚɬɨɦ (ɦɨɥɟɤɭɥɚ) ɜɟɳɟɫɬɜɚ ɢɦɟɟɬ ɧɟɫɤɨɥɶɤɨ ɨɩɬɢɱɟɫɤɢɯ
ɷɥɟɤɬɪɨɧɨɜ ɫ ɪɚɡɥɢɱɧɵɦɢ ɫɨɛɫɬɜɟɧɧɵɦɢ ɱɚɫɬɨɬɚɦɢ, ɬɨ ɩɨɤɚɡɚɬɟɥɶ ɩɪɟ-
ɥɨɦɥɟɧɢɹ ɬɚɤɨɝɨ ɜɟɳɟɫɬɜɚ ɛɭɞɟɬ ɢɦɟɬɶ ɧɟɫɤɨɥɶɤɨ ɨɛɥɚɫɬɟɣ ɚɧɨɦɚɥɶɧɨɣ
ɞɢɫɩɟɪɫɢɢ ɜɛɥɢɡɢ ɤɚɠɞɨɣ ɱɚɫɬɨɬɵ ɩɨɝɥɨɳɟɧɢɹ.
1.2. Ⱦɢɫɩɟɪɫɢɹ ɫɜɟɬɚ ɜ ɨɩɬɢɱɟɫɤɨɦ ɞɢɚɩɚɡɨɧɟ
ȼ ɨɩɬɢɱɟɫɤɨɦ ɞɢɚɩɚɡɨɧɟ (380–740 ɧɦ) ɨɩɬɢɱɟɫɤɢ ɩɪɨɡɪɚɱɧɵɟ
ɫɬɟɤɥɚ ɧɟ ɩɨɝɥɨɳɚɸɬ ɫɜɟɬ (ɧɟ ɢɦɟɸɬ ɩɨɥɨɫ ɩɨɝɥɨɳɟɧɢɹ). ɉɨɷɬɨɦɭ ɬɟɨ-
ɪɟɬɢɱɟɫɤɭɸ ɡɚɜɢɫɢɦɨɫɬɶ ɩɨɤɚɡɚɬɟɥɹ ɩɪɟɥɨɦɥɟɧɢɹ n ɨɬ ɱɚɫɬɨɬɵ ɫɜɟɬɚ Z,
ɩɨɥɭɱɟɧɧɭɸ ɪɚɧɟɟ, ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ, ɫɱɢɬɚɹ ɤɨɷɮɮɢɰɢɟɧɬ ɡɚɬɭɯɚɧɢɹ
b = 0, ɜ ɜɢɞɟ
22222
0
2
0
2
4)(
1
1
ZZZ
H
b
m
eN
n
22
0
2
0
1
1
ZZ
H
m
eN
.
Ⱦɥɹ ɛɨɥɶɲɢɧɫɬɜɚ ɨɩɬɢɱɟɫɤɢ ɩɪɨɡɪɚɱɧɵɯ ɫɬɟɤɨɥ ɱɚɫɬɨɬɚ ɫɨɛɫɬɜɟɧ-
ɧɵɯ ɤɨɥɟɛɚɧɢɣ ɨɩɬɢɱɟɫɤɨɝɨ ɷɥɟɤɬɪɨɧɚ Z
0
ɦɧɨɝɨ ɛɨɥɶɲɟ ɱɚɫɬɨɬɵ ɫɜɟɬɚ Z
ɜ ɨɩɬɢɱɟɫɤɨɦ ɞɢɚɩɚɡɨɧɟ (Z
0
>> Z). Ɍɨɝɞɚ ɨɬɧɨɲɟɧɢɟ Z/Z
0
ɦɨɠɧɨ ɫɱɢ-
ɬɚɬɶ ɦɚɥɵɦ
2
0
2
00
2
2
1
1
1
¸
¸
¹
·
¨
¨
©
§
Z
Z
ZH
m
Ne
n
n
Z
Z
0
Ɋɢɫ. 2

ɆɨɞO-01 ɇɨɪɦɚɥɶɧɚɹ ɞɢɫɩɟɪɫɢɹ ɫɜɟɬɚ
423
Ɋɚɫɤɥɚɞɵɜɚɹ ɞɪɨɛɶ
2
0
1
1
¸
¸
¹
·
¨
¨
©
§
Z
Z
ɜ ɪɹɞ ɩɨ ɜɟɥɢɱɢɧɟ Z/Z
0
, ɩɨɥɭɱɢɦ
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
Z
Z
¸
¸
¹
·
¨
¨
©
§
Z
Z
ZH
...11
4
0
2
0
2
00
2
2
m
Ne
n
ɢɥɢ
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
Z
Z
¸
¸
¹
·
¨
¨
©
§
Z
Z
ZH
...11
4
0
2
0
2
00
2
m
Ne
n
ɂɫɩɨɥɶɡɭɹ ɫɬɚɧɞɚɪɬɧɨɟ ɪɚɡɥɨɠɟɧɢɟ ɜ ɪɹɞ
2
11
x
x |
(ɟɫɥɢ x –
ɦɚɥɨ), ɩɨɥɭɱɢɦ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɩɨɤɚɡɚɬɟɥɹ ɩɪɟɥɨɦɥɟɧɢɹ ɜ ɜɢɞɟ
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
Z
Z
¸
¸
¹
·
¨
¨
©
§
Z
Z
ZH
¸
¸
¹
·
¨
¨
©
§
ZH
...
2
21
2
1
4
0
2
0
2
00
2
2/1
2
00
2
m
Ne
m
Ne
n
ɍɱɢɬɵɜɚɹ, ɱɬɨ
O
S
Z
c2
, ɡɚɩɢɲɟɦ ɡɚɜɢɫɢɦɨɫɬɶ ɩɨɤɚɡɚɬɟɥɹ ɩɪɟ-
ɥɨɦɥɟɧɢɹ n ɨɬ ɞɥɢɧɵ ɜɨɥɧɵ ɫɜɟɬɚ O
¸
¸
¹
·
¨
¨
©
§
¸
¹
·
¨
©
§
O
O
¸
¹
·
¨
©
§
O
O
HS
O
¸
¸
¹
·
¨
¨
©
§
HS
O
...
2
2
4
1
2
1
4
0
2
0
2
0
2
2
0
2
2/1
2
0
2
2
0
2
mc
Ne
mc
Ne
n
ɂɡ ɩɨɥɭɱɟɧɧɨɝɨ ɜɵɪɚɠɟɧɢɹ ɜɢɞɧɨ, ɱɬɨ ɤɨɷɮɮɢɰɢɟɧɬɵ ɩɪɢ ɪɚɡ-
ɥɢɱɧɵɯ ɫɬɟɩɟɧɹɯ O
–2
, O
–4
… ɡɚɜɢɫɹɬ ɬɨɥɶɤɨ ɨɬ ɯɚɪɚɤɬɟɪɢɫɬɢɤ ɫɚɦɨɝɨ ɜɟ-
ɳɟɫɬɜɚ ɢ ɞɥɹ ɞɚɧɧɨɝɨ ɤɨɧɤɪɟɬɧɨɝɨ ɜɟɳɟɫɬɜɚ ɹɜɥɹɸɬɫɹ ɤɨɧɫɬɚɧɬɚɦɢ. ɉɨ-
ɷɬɨɦɭ ɡɚɜɢɫɢɦɨɫɬɶ ɩɨɤɚɡɚɬɟɥɹ ɩɪɟɥɨɦɥɟɧɢɹ ɨɬ ɞɥɢɧɵ ɜɨɥɧɵ ɦɨɠɧɨ
ɩɪɟɞɫɬɚɜɢɬɶ ɜ ɜɢɞɟ
...
42
O
O
CB
An
ɝɞɟ ɤɨɧɫɬɚɧɬɵ A, B, C (ɜ ɪɚɦɤɚɯ ɤɥɚɫɫɢɱɟɫɤɨɣ ɷɥɟɤɬɪɨɧɧɨɣ ɬɟɨɪɢɢ) ɜɵ-
ɪɚɠɚɸɬɫɹ ɱɟɪɟɡ ɬɚɤɢɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɜɟɳɟɫɬɜɚ ɤɚɤ ɤɨɧɰɟɧɬɪɚɰɢɹ ɚɬɨ-
ɦɨɜ N ɢ ɫɨɛɫɬɜɟɧɧɚɹ ɞɥɢɧɚ ɜɨɥɧɵ ɨɩɬɢɱɟɫɤɨɝɨ ɷɥɟɤɬɪɨɧɚ O
0
. Ʉɨɧɫɬɚɧɬɵ
A, B, C ɪɚɡɥɢɱɧɵ ɞɥɹ ɪɚɡɧɵɯ ɜɟɳɟɫɬɜ ɢ ɦɨɝɭɬ ɛɵɬɶ ɪɚɫɫɱɢɬɚɧɵ ɧɚ ɨɫɧɨ-
ɜɟ ɷɤɫɩɟɪɢɦɟɧɬɚɥɶɧɨ ɩɨɥɭɱɟɧɧɨɣ ɡɚɜɢɫɢɦɨɫɬɢ n = n(O).
ɉɨɥɭɱɟɧɧɚɹ ɡɚɜɢɫɢɦɨɫɬɶ ɤɨɷɮɮɢɰɢɟɧɬɚ ɩɪɟɥɨɦɥɟɧɢɹ ɨɬ ɞɥɢɧɵ
ɜɨɥɧɵ ɨɩɢɫɵɜɚɟɬ ɧɨɪɦɚɥɶɧɭɸ ɞɢɫɩɟɪɫɢɸ ɫɜɟɬɚ ɢ ɢɡɜɟɫɬɧɚ ɤɚɤ ɮɨɪɦɭɥɚ
Ʉɨɲɢ. Ⱦɥɹ ɛɨɥɶɲɢɧɫɬɜɚ ɨɩɬɢɱɟɫɤɢ ɩɪɨɡɪɚɱɧɵɯ ɜɟɳɟɫɬɜ ɜ ɮɨɪɦɭɥɟ Ʉɨ-

Ɉɩɬɢɤɚ
424
ɲɢ ɞɥɹ ɩɨɥɭɱɟɧɢɹ ɯɨɪɨɲɟɝɨ ɫɨɝɥɚɫɢɹ ɬɟɨɪɢɢ ɫ ɷɤɫɩɟɪɢɦɟɧɬɨɦ ɦɨɠɧɨ
ɨɝɪɚɧɢɱɢɬɶɫɹ ɩɟɪɜɵɦɢ ɞɜɭɦɹ ɱɥɟɧɚɦɢ
2
O
|
B
An
.
ȿɫɥɢ ɷɤɫɩɟɪɢɦɟɧɬɚɥɶɧɨ ɨɩɪɟɞɟɥɢɬɶ ɩɨɤɚɡɚɬɟɥɶ ɩɪɟɥɨɦɥɟɧɢɹ ɞɥɹ
ɪɚɡɥɢɱɧɵɯ ɞɥɢɧ ɜɨɥɧ n = n(O), ɬɨ ɱɢɫɥɨɜɵɟ ɡɧɚɱɟɧɢɹ ɤɨɧɫɬɚɧɬ A ɢ B
ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɩɨ ɦɟɬɨɞɭ ɧɚɢɦɟɧɶɲɢɯ ɤɜɚɞɪɚɬɨɜ, ɥɢɛɨ ɢɡ ɝɪɚɮɢɤɚ
ɞɚɧɧɨɣ ɡɚɜɢɫɢɦɨɫɬɢ.
1.3. ɋɜɨɣɫɬɜɚ ɨɩɬɢɱɟɫɤɢɯ ɫɬɟɤɨɥ
Ɉɩɬɢɱɟɫɤɢ ɩɪɨɡɪɚɱɧɵɟ ɜɟɳɟɫɬɜɚ, ɢɫɩɨɥɶɡɭɟɦɵɟ ɜ ɬɟɯɧɢɤɟ, ɧɚɡɵ-
ɜɚɸɬ ɨɩɬɢɱɟɫɤɢɦɢ ɫɬɟɤɥɚɦɢ. Ɉɩɬɢɱɟɫɤɢɟ ɫɬɟɤɥɚ ɛɵɜɚɸɬ ɩɪɢɪɨɞɧɨɝɨ ɢ
ɢɫɤɭɫɫɬɜɟɧɧɨɝɨ ɩɪɨɢɫɯɨɠɞɟɧɢɹ. Ɉɧɢ ɨɛɥɚɞɚɸɬ ɪɚɡɥɢɱɧɵɦɢ ɩɨɤɚɡɚɬɟ-
ɥɹɦɢ ɩɪɟɥɨɦɥɟɧɢɹ ɢ ɪɚɡɥɢɱɧɵɦɢ ɞɢɫɩɟɪɫɢɹɦɢ. Ⱦɥɹ ɨɛɴɟɤɬɢɜɧɨɫɬɢ
ɫɪɚɜɧɟɧɢɹ ɪɚɡɥɢɱɧɵɯ ɨɩɬɢɱɟɫɤɢɯ ɫɬɟɤɨɥ ɜ ɮɢɡɢɱɟɫɤɢɯ ɢ ɬɟɯɧɢɱɟɫɤɢɯ
ɫɩɪɚɜɨɱɧɢɤɚɯ ɩɪɢɜɨɞɹɬ ɫɜɟɞɟɧɢɹ ɨ ɢɯ ɩɨɤɚɡɚɬɟɥɹɯ ɩɪɟɥɨɦɥɟɧɢɹ ɞɥɹ ɨɞ-
ɧɢɯ ɢ ɬɟɯ ɠɟ ɞɥɢɧ ɜɨɥɧ
: ɞɥɹ ɠɟɥɬɨɣ ɥɢɧɢɢ ɝɟɥɢɹ (587,6 ɧɦ), ɤɪɚɫɧɨɣ ɢ
ɝɨɥɭɛɨɣ ɥɢɧɢɣ ɜɨɞɨɪɨɞɚ (656,3 ɧɦ ɢ 486,1 ɧɦ). Ʌɢɧɢɢ ɢɡɥɭɱɟɧɢɹ ɚɬɨɦɨɜ
ɨɛɨɡɧɚɱɚɸɬ ɩɪɨɩɢɫɧɵɦɢ ɢ ɫɬɪɨɱɧɵɦɢ ɛɭɤɜɚɦɢ ɥɚɬɢɧɫɤɨɝɨ ɚɥɮɚɜɢɬɚ. ȼ
ɱɚɫɬɧɨɫɬɢ, ɠɟɥɬɚɹ ɥɢɧɢɹ ɝɟɥɢɹ ɨɛɨɡɧɚɱɚɟɬɫɹ d, ɤɪɚɫɧɚɹ ɥɢɧɢɹ ɜɨɞɨɪɨɞɚ
– C, ɚ ɝɨɥɭɛɚɹ ɥɢɧɢɹ ɜɨɞɨɪɨɞɚ – F. ȼ ɬɚɛɥɢɰɚɯ ɩɨɤɚɡɚɬɟɥɢ ɩɪɟɥɨɦɥɟɧɢɹ
ɨɩɬɢɱɟɫɤɢɯ ɫɬɟɤɨɥ ɞɥɹ ɞɥɢɧ ɜɨɥɧ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɥɢɧɢɣ
ɨɛɨɡɧɚɱɚɸɬ
ɤɚɤ n
d
, n
C
ɢ n
F
. ȼ ɬɚɛɥɢɰɚɯ ɨɛɵɱɧɨ ɩɪɢɜɨɞɢɬɫɹ ɫɪɟɞɧɟɟ ɡɧɚɱɟɧɢɟ ɩɨɤɚɡɚ-
ɬɟɥɹ ɩɪɟɥɨɦɥɟɧɢɹ, ɤɨɬɨɪɨɟ ɪɚɫɫɱɢɬɵɜɚɟɬɫɹ ɦɟɠɞɭ ɩɨɤɚɡɚɬɟɥɹɦɢ ɩɪɟ-
ɥɨɦɥɟɧɢɹ n
C
ɢ n
F
ɥɢɧɢɣ ɜɨɞɨɪɨɞɚ
)(
2
1
FC
nnn .
Ⱦɥɹ ɩɪɚɤɬɢɱɟɫɤɨɝɨ ɫɪɚɜɧɟɧɢɹ ɞɢɫɩɟɪɫɢɨɧɧɵɯ ɫɜɨɣɫɬɜ ɨɩɬɢɱɟɫɤɢɯ
ɦɚɬɟɪɢɚɥɨɜ ɜɜɨɞɹɬ ɤɨɷɮɮɢɰɢɟɧɬ ɞɢɫɩɟɪɫɢɢ V (ɢɥɢ ɱɢɫɥɨ Ⱥɛɛɟ), ɤɨɬɨ-
ɪɵɣ ɪɚɫɫɱɢɬɵɜɚɸɬ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ
CF
d
nn
n
V
1
.
ɑɟɦ ɛɨɥɶɲɟ ɱɢɫɥɨ Ⱥɛɛɟ V, ɬɟɦ ɦɟɞɥɟɧɧɟɟ ɦɟɧɹɟɬɫɹ ɤɨɷɮɮɢɰɢɟɧɬ
ɩɪɟɥɨɦɥɟɧɢɹ ɜ ɨɩɬɢɱɟɫɤɨɦ ɞɢɚɩɚɡɨɧɟ ɞɥɢɧ ɜɨɥɧ (ɪɚɡɧɢɰɚ n
F
– n
C
ɦɟɧɶ-
ɲɟ ɤɨɷɮɮɢɰɢɟɧɬ ɞɢɫɩɟɪɫɢɢ V ɛɨɥɶɲɟ).

ɆɨɞO-01 ɇɨɪɦɚɥɶɧɚɹ ɞɢɫɩɟɪɫɢɹ ɫɜɟɬɚ
425
2. Ɋɚɛɨɱɢɟ ɮɨɪɦɭɥɵ
2.1. Ɉɩɪɟɞɟɥɟɧɢɟ ɤɨɷɮɮɢɰɢɟɧɬɚ ɩɪɟɥɨɦɥɟɧɢɹ
ɩɨ ɯɨɞɭ ɥɭɱɟɣ ɜ ɬɪɟɭɝɨɥɶɧɨɣ ɩɪɢɡɦɟ
ɋɨɝɥɚɫɧɨ ɡɚɤɨɧɚɦ ɝɟɨɦɟɬɪɢɱɟɫɤɨɣ ɨɩɬɢɤɢ ɩɪɢ ɩɪɨɯɨɠɞɟɧɢɢ ɥɭɱɚ
ɫɜɟɬɚ ɧɟɤɨɬɨɪɨɣ ɞɥɢɧɵ ɜɨɥɧɵ ɱɟɪɟɡ ɝɪɚɧɢɰɭ ɪɚɡɞɟɥɚ ɞɜɭɯ ɫɪɟɞ, ɢɦɟɸ-
ɳɢɯ ɪɚɡɧɵɣ ɩɨɤɚɡɚɬɟɥɶ ɩɪɟɥɨɦɥɟɧɢɹ, ɧɚɩɪɚɜɥɟɧɢɟ ɟɝɨ ɞɜɢɠɟɧɢɹ ɦɟɧɹ-
ɟɬɫɹ. ɉɭɫɬɶ ɥɭɱ ɫɜɟɬɚ ɩɚɞɚɟɬ ɧɚ ɝɪɚɧɢɰɭ ɦɟɠɞɭ ɜɚɤɭɭɦɨɦ (n
0
= 1) ɢ ɨɩ-
ɬɢɱɟɫɤɢ ɩɪɨɡɪɚɱɧɨɣ ɫɪɟɞɨɣ (n > 1) ɩɨɞ ɭɝɥɨɦ D ɤ ɧɨɪɦɚɥɢ (ɭɝɨɥ ɩɚɞɟ-
ɧɢɹ). Ɍɨɝɞɚ ɜ ɫɪɟɞɟ ɥɭɱ ɫɜɟɬɚ ɛɭɞɟɬ ɞɜɢɝɚɬɶɫɹ ɩɨɞ ɭɝɥɨɦ E ɤ ɧɨɪɦɚɥɢ
(ɭɝɨɥ ɩɪɟɥɨɦɥɟɧɢɹ), ɤɨɬɨɪɵɣ ɨɩɪɟɞɟɥɹɟɬɫɹ ɫɨɝɥɚɫɧɨ ɡɚɤɨɧɭ ɩɪɟɥɨɦɥɟ-
ɧɢɹ
n
n
n
E
D
0
sin
sin
.
ɗɤɫɩɟɪɢɦɟɧɬɚɥɶɧɨɟ ɨɩɪɟɞɟɥɟɧɢɟ ɩɨɤɚɡɚɬɟɥɹ ɩɪɟɥɨɦɥɟɧɢɹ ɞɥɹ
ɫɜɟɬɚ ɮɢɤɫɢɪɨɜɚɧɧɨɣ ɞɥɢɧɵ ɜɨɥɧɵ ɜɵɩɨɥɧɹɟɬɫɹ, ɤɚɤ ɩɪɚɜɢɥɨ, ɧɚ ɨɫɧɨɜɟ
ɷɬɨɝɨ ɡɚɤɨɧɚ. ɇɚ ɩɪɚɤɬɢɤɟ ɢɫɩɨɥɶɡɭɸɬ ɧɟɛɨɥɶɲɨɝɨ ɪɚɡɦɟɪɚ ɬɪɟɭɝɨɥɶɧɭɸ
ɩɪɢɡɦɭ, ɩɪɨɯɨɞɹ ɱɟɪɟɡ ɤɨɬɨɪɭɸ ɥɭɱ ɫɜɟɬɚ ɩɪɟɥɨɦɥɹɟɬɫɹ ɞɜɚɠɞɵ (ɪɢɫ. 3)
ɩɪɢ ɩɟɪɟɯɨɞɟ ɢɡ ɜɚɤɭɭɦɚ ɜ ɫɪɟɞɭ ɫ ɩɨɤɚɡɚɬɟɥɟɦ ɩɪɟɥɨɦɥɟɧɢɹ n, ɢ ɨɛɪɚɬ-
ɧɨ.
ɉɪɢ ɩɪɨɯɨɠɞɟɧɢɢ ɱɟɪɟɡ ɩɪɢɡɦɭ ɢɡɦɟɧɟɧɢɟ ɧɚɩɪɚɜɥɟɧɢɹ
ɥɭɱɚ ɫɜɟ-
ɬɚ ɡɚɜɢɫɢɬ ɨɬ ɭɝɥɚ ɦɟɠɞɭ ɞɜɭɦɹ ɝɪɚɧɢɰɚɦɢ ɪɚɡɞɟɥɚ ɫɪɟɞ (ɝɪɚɧɹɦɢ ɩɪɢɡ-
ɦɵ). ɍɝɨɥ G ɦɟɠɞɭ ɝɪɚɧɹɦɢ ɩɪɢɡɦɵ, ɱɟɪɟɡ ɤɨɬɨɪɵɟ ɫɜɟɬ ɜɯɨɞɢɬ ɢ ɜɵɯɨ-
ɞɢɬ ɢɡ ɩɪɢɡɦɵ, ɧɚɡɵɜɚɟɬɫɹ
ɩɪɟɥɨɦɥɹɸɳɢɦ ɭɝɥɨɦ ɩɪɢɡɦɵ. ɇɚɩɪɚɜɥɟɧɢɟ
ɬɪɟɬɶɟɣ ɝɪɚɧɢ ɩɪɢɡɦɵ (ɬɪɟɬɶɟɣ ɝɪɚɧɢɰɵ ɪɚɡɞɟɥɚ ɫɪɟɞ) ɧɚ ɯɨɞ ɥɭɱɚ ɧɟ
ɜɥɢɹɟɬ. Ⱦɥɹ ɩɪɨɫɬɨɬɵ
ɛɭɞɟɦ ɫɱɢɬɚɬɶ ɩɪɢɡɦɭ
ɪɚɜɧɨɛɟɞɪɟɧɧɨɣ, ɱɟɪɟɡ
ɨɫɧɨɜɚɧɢɟ ɤɨɬɨɪɨɣ
ɫɜɟɬ ɧɟ ɩɪɨɯɨɞɢɬ.
Ɋɚɫɫɦɨɬɪɢɦ
ɩɪɨɯɨɠɞɟɧɢɟ ɥɭɱɟɣ
ɱɟɪɟɡ ɪɚɜɧɨɛɟɞɪɟɧɧɭɸ
ɩɪɢɡɦɭ (ɪɢɫ. 3). ɉɭɫɬɶ
ɥɭɱ ɫɜɟɬɚ ɩɚɞɚɟɬ ɧɚ
ɥɟɜɭɸ ɝɪɚɧɶ ɩɪɢɡɦɵ
ɩɨɞ ɭɝɥɨɦ D
1
ɤ ɧɨɪɦɚ-
D
1
D
2
E
1
E
2
G
G
M
Ɋɢɫ. 3

Ɉɩɬɢɤɚ
426
ɥɢ. ɋɨɝɥɚɫɧɨ ɡɚɤɨɧɭ ɩɪɟɥɨɦɥɟɧɢɹ ɥɭɱ ɜɧɭɬɪɢ ɩɪɢɡɦɵ ɛɭɞɟɬ ɞɜɢɝɚɬɶɫɹ
ɩɨɞ ɭɝɥɨɦ E
1
ɤ ɧɨɪɦɚɥɢ ɥɟɜɨɣ ɝɪɚɧɢ ɢ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɩɨɞ ɭɝɥɨɦ E
2
ɤ
ɧɨɪɦɚɥɢ ɩɪɚɜɨɣ ɝɪɚɧɢ. ɉɨɫɥɟ ɩɪɟɥɨɦɥɟɧɢɹ ɧɚ ɩɪɚɜɨɣ ɝɪɚɧɢ ɥɭɱ ɜɵɣɞɟɬ
ɢɡ ɩɪɢɡɦɵ ɩɨɞ ɭɝɥɨɦ D
2
ɤ ɧɨɪɦɚɥɢ ɩɪɚɜɨɣ ɝɪɚɧɢ. Ⱦɚɧɧɚɹ ɤɚɪɬɢɧɚ ɯɨɞɚ
ɥɭɱɟɣ ɹɜɥɹɟɬɫɹ ɨɛɪɚɬɢɦɨɣ: ɟɫɥɢ ɥɭɱ ɧɚɩɪɚɜɢɬɶ ɩɨɞ ɭɝɥɨɦ D
2
ɤ ɩɪɚɜɨɣ
ɝɪɚɧɢ, ɬɨ ɜ ɪɟɡɭɥɶɬɚɬɟ ɩɪɟɥɨɦɥɟɧɢɹ ɜ ɩɪɢɡɦɟ ɥɭɱ ɜɵɣɞɟɬ ɩɨɞ ɭɝɥɨɦ D
1
ɤ
ɥɟɜɨɣ ɝɪɚɧɢ. ɉɪɢɱɟɦ ɫɨɝɥɚɫɧɨ ɡɚɤɨɧɵ ɩɪɟɥɨɦɥɟɧɢɹ ɫɜɟɬɚ
n
E
D
1
1
sin
sin
ɢ
n
E
D
2
2
sin
sin
.
ɇɚ ɩɪɚɤɬɢɤɟ ɢɫɩɨɥɶɡɭɸɬ ɩɪɢɡɦɵ ɧɟɛɨɥɶɲɨɝɨ ɪɚɡɦɟɪɚ, ɩɨɷɬɨɦɭ
ɭɝɥɵ E
1
ɢ E
2
(ɜɧɭɬɪɢ ɩɪɢɡɦɵ) ɩɥɨɯɨ ɩɨɞɞɚɸɬɫɹ ɢɡɦɟɪɟɧɢɹɦ. Ⱦɥɹ ɷɤɫɩɟ-
ɪɢɦɟɧɬɚɥɶɧɨɝɨ ɨɩɪɟɞɟɥɟɧɢɹ ɩɨɤɚɡɚɬɟɥɹ ɩɪɟɥɨɦɥɟɧɢɹ ɧɟɨɛɯɨɞɢɦɨ ɜɵɪɚ-
ɡɢɬɶ n ɱɟɪɟɡ ɜɧɟɲɧɢɟ ɭɝɥɵ D
1
ɢ D
2
. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɫ ɭɱɟɬɨɦ ɬɪɢɝɨɧɨ-
ɦɟɬɪɢɢ ɜ ɜɵɪɚɠɟɧɢɹɯ ɡɚɤɨɧɚ ɩɪɟɥɨɦɥɟɧɢɹ ɧɭɠɧɨ ɢɫɤɥɸɱɢɬɶ ɭɝɥɵ E
1
ɢ
E
2
.
ɂɡ ɬɪɟɭɝɨɥɶɧɢɤɚ, ɨɛɪɚɡɨɜɚɧɧɨɝɨ ɥɭɱɨɦ ɫɜɟɬɚ ɢ ɧɨɪɦɚɥɹɦɢ ɤ ɩɪɚ-
ɜɨɣ ɢ ɥɟɜɨɣ ɝɪɚɧɹɦ, ɜɢɞɧɨ, ɱɬɨ
E
1
+ E
2
= G.
Ɍɨɝɞɚ, ɧɚɩɪɢɦɟɪ, E
2
= G – E
1
.
ɂɡ ɡɚɤɨɧɨɜ ɩɪɟɥɨɦɥɟɧɢɹ ɫɜɟɬɚ ɧɚ ɩɪɚɜɨɣ ɢ ɥɟɜɨɣ ɝɪɚɧɹɯ ɩɪɢɡɦɵ
2
2
1
1
sin
sin
sin
sin
E
D
E
D
n
ɫɥɟɞɭɟɬ
1
2
1
2
sin
sin
sin
sin
E
E
D
D
.
ɂɡ ɬɪɢɝɨɧɨɦɟɬɪɢɢ
1112
sincoscossin)sin(sin EGEG EG E . Ɍɨɝɞɚ
GEG
E
EGEG
E
E
D
D
cosctgsin
sin
sincoscossin
sin
sin
sin
sin
1
1
11
1
2
1
2
.
ɂɡ ɩɨɥɭɱɟɧɧɨɣ ɮɨɪɦɭɥɵ ɜɵɪɚɡɢɦ
1
ctgE :
GD
GDD
E
sinsin
cossinsin
ctg
1
12
1
.
ɍɱɢɬɵɜɚɹ ɬɪɢɝɨɧɨɦɟɬɪɢɱɟɫɤɢɟ ɬɨɠɞɟɫɬɜɚ
1sincos
1
2
1
2
EE
1
2
1
2
ctg1
sin
1
E
E
ɢ ɩɨɥɭɱɟɧɧɭɸ ɡɚɜɢɫɢɦɨɫɬɶ ɦɟɠɞɭ ɭɝɥɚɦɢ
GD
GDD
E
2
1
2
2
12
1
2
sinsin
)cossin(sin
1
sin
1

ɆɨɞO-01 ɇɨɪɦɚɥɶɧɚɹ ɞɢɫɩɟɪɫɢɹ ɫɜɟɬɚ
427
GD
GDDDD
2
1
2
212
2
1
2
sinsin
cossinsin2sinsin
,
ɡɚɩɢɲɟɦ ɡɚɤɨɧ ɩɪɟɥɨɦɥɟɧɢɹ ɫɜɟɬɚ ɧɚ ɥɟɜɨɣ ɝɪɚɧɢ ɩɪɢɡɦɵ
1
1
sin
sin
E
D
n ɜ
ɜɢɞɟ
1
2
1
2
2
sin
sin
E
D
n
ɢ ɩɨɞɫɬɚɜɢɦ ɩɨɥɭɱɟɧɧɨɟ ɜɵɪɚɠɟɧɢɟ ɞɥɹ
1
2
sin
1
E
G
GDDDD
2
212
2
1
2
2
sin
cossinsin2sinsin
n
.
ɉɨɥɭɱɟɧɧɨɟ ɜɵɪɚɠɟɧɢɟ ɩɨɡɜɨɥɹɟɬ ɪɚɫɫɱɢɬɚɬɶ ɩɨɤɚɡɚɬɟɥɶ ɩɪɟɥɨɦ-
ɥɟɧɢɹ
n, ɢɡɦɟɪɢɜ ɭɝɥɚ D
1
ɢ D
2
(ɭɝɥɵ ɩɨɞ ɤɨɬɨɪɵɦɢ ɥɭɱ ɩɚɞɟɬ ɧɚ ɩɪɢɡɦɭ ɢ
ɜɵɯɨɞɢɬ ɢɡ ɧɟɟ).
ɉɪɢ ɫɢɦɦɟɬɪɢɱɧɨɦ ɯɨɞɟ ɥɭɱɟɣ (D
1
= D
2
) ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɩɨɤɚɡɚɬɟ-
ɥɹ ɩɪɟɥɨɦɥɟɧɢɹ ɫɭɳɟɫɬɜɟɧɧɨ ɭɩɪɨɳɚɟɬɫɹ. Ɉɞɧɚɤɨ ɧɚ ɩɪɚɤɬɢɤɟ ɬɪɭɞɧɨ
ɞɨɛɢɬɶɫɹ ɚɛɫɨɥɸɬɧɨ ɫɢɦɦɟɬɪɢɱɧɨɝɨ ɯɨɞɚ ɥɭɱɟɣ.
2.2. Ɂɚɜɢɫɢɦɨɫɬɶ ɭɝɥɚ ɨɬɤɥɨɧɟɧɢɹ
M
ɥɭɱɚ
ɨɬ ɩɪɟɥɨɦɥɹɸɳɟɝɨ ɭɝɥɚ ɩɪɢɡɦɵ
ɉɨɥɭɱɟɧɧɨɟ ɜɵɲɟ ɜɵɪɚɠɟɧɢɟ ɫɜɹɡɵɜɚɟɬ ɭɝɥɵ D
1
ɢ D
2
, ɩɨɞ ɤɨɬɨ-
ɪɵɦɢ ɥɭɱ ɫɜɟɬɚ ɩɚɞɚɟɬ ɧɚ ɩɪɢɡɦɭ ɢ ɜɵɯɨɞɢɬ ɢɡ ɧɟɟ, ɫ ɤɨɷɮɮɢɰɢɟɧɬɨɦ
ɩɪɟɥɨɦɥɟɧɢɹ
n ɢ ɩɪɟɥɨɦɥɹɸɳɢɦ ɭɝɥɨɦ G ɩɪɢɡɦɵ:
G
GDDDD
2
212
2
1
2
2
sin
cossinsin2sinsin
n
ɢɥɢ
G GDDDD
22
212
2
1
2
sincossinsin2sinsin n
.
ɑɬɨɛɵ ɧɚ ɨɫɧɨɜɟ ɷɬɨɣ ɡɚɜɢɫɢɦɨɫɬɢ ɩɪɨɚɧɚɥɢɡɢɪɨɜɚɬɶ, ɤɚɤ ɭɝɨɥ D
2
ɡɚɜɢɫɢɬ ɨɬ ɩɪɟɥɨɦɥɹɸɳɟɝɨ ɭɝɥɚ ɩɪɢɡɦɵ G, ɩɪɟɨɛɪɚɡɭɟɦ ɩɨɥɭɱɟɧɧɭɸ
ɮɨɪɦɭɥɭ ɢ ɜɵɪɚɡɢɦ sin D
2
ɜ ɜɢɞɟ
GDDG D cossinsinsinsin
11
2
2
n
.
ɂɡ ɮɢɡɢɱɟɫɤɨɝɨ ɫɦɵɫɥɚ ɩɨɤɚɡɚɬɟɥɹ ɩɪɟɥɨɦɥɟɧɢɹ
n ɫɥɟɞɭɟɬ, ɱɬɨ
ɞɥɹ ɜɫɟɯ ɫɪɟɞ (ɤɪɨɦɟ ɜɚɤɭɭɦɚ)
n > 1.
ȼɵɪɚɠɟɧɢɟ ɜ ɩɪɚɜɨɣ ɱɚɫɬɢ ɩɨ ɦɨɞɭɥɸ ɞɨɥɠɧɨ ɛɵɬɶ ɧɟ ɛɨɥɶɲɟ
ɟɞɢɧɢɰɵ (ɬ.ɤ.
1sin
2
dD ), ɬɨɝɞɚ ɥɭɱ ɩɪɨɣɞɟɬ ɱɟɪɟɡ ɩɪɢɡɦɭ. ȿɫɥɢ ɜɟɥɢ-
ɱɢɧɚ
GDDG cossinsinsin
11
2
n ɩɨ ɦɨɞɭɥɸ ɛɨɥɶɲɟ ɟɞɢɧɢɰɵ, ɬɨ ɥɭɱ
ɧɟ ɦɨɠɟɬ ɜɵɣɬɢ ɢɡ ɩɪɢɡɦɵ. ɗɬɨ ɹɜɥɟɧɢɟ ɧɚɡɵɜɚɟɬɫɹ
ɩɨɥɧɵɦ ɜɧɭɬɪɟɧ-

Ɉɩɬɢɤɚ
428
ɧɢɦ ɨɬɪɚɠɟɧɢɟɦ (ɩɪɟɥɨɦɥɟɧɢɟ ɫɜɟɬɚ ɧɚ ɩɪɚɜɨɣ ɝɪɚɧɢ ɩɪɢɡɦɵ ɧɟ ɧɚ-
ɛɥɸɞɚɟɬɫɹ).
ȼ ɭɫɥɨɜɢɹɯ, ɤɨɝɞɚ ɩɨɥɧɨɟ ɜɧɭɬɪɟɧɧɟɟ ɨɬɪɚɠɟɧɢɟ ɇȿ ɧɚɛɥɸɞɚɟɬɫɹ,
ɩɪɨɚɧɚɥɢɡɢɪɭɟɦ ɤɚɤ ɭɝɨɥ D
1
, ɩɨɞ ɤɨɬɨɪɵɦ ɥɭɱ ɜɵɯɨɞɢɬ ɱɟɪɟɡ ɩɪɚɜɭɸ
ɝɪɚɧɶ ɩɪɢɡɦɵ, ɡɚɜɢɫɢɬ ɨɬ ɩɪɟɥɨɦɥɹɸɳɟɝɨ ɭɝɥɚ ɩɪɢɡɦɵ G ɩɪɢ ɩɨɫɬɨɹɧ-
ɧɨɦ ɭɝɥɟ D
1
ɩɚɞɟɧɢɹ ɫɜɟɬɚ ɧɚ ɥɟɜɭɸ ɝɪɚɧɶ ɩɪɢɡɦɵ. Ⱦɥɹ ɭɩɪɨɳɟɧɢɹ ɚɧɚ-
ɥɢɡɚ ɩɪɟɞɩɨɥɨɠɢɦ, ɱɬɨ ɜɫɟ ɭɝɥɵ (D
1
, D
2
, G) ɦɚɥɵ. Ɍɨɝɞɚ ɦɨɠɧɨ ɫɱɢɬɚɬɶ,
ɱɬɨ
11
sin D|D ,
22
sin D|D , G|Gsin , cos G | 1.
ȼ ɷɬɨɦ ɫɥɭɱɚɟ
11
2
2
DDG|D n .
ɑɟɦ ɛɨɥɶɲɟ ɩɪɟɥɨɦɥɹɸɳɢɣ ɭɝɨɥ G ɩɪɢɡɦɵ, ɬɟɦ ɛɨɥɶɲɟ ɭɝɨɥ D
2
,
ɩɨɞ ɤɨɬɨɪɵɦ ɥɭɱ ɜɵɯɨɞɢɬ ɢɡ ɩɪɚɜɨɣ ɝɪɚɧɢ ɩɪɢɡɦɵ (ɩɪɢ D
1
= const). ɗɬɚ
ɡɚɜɢɫɢɦɨɫɬɶ ɫɩɪɚɜɟɞɥɢɜɚ ɬɚɤɠɟ ɢ ɞɥɹ ɛɨɥɶɲɢɯ ɭɝɥɨɜ.
ȼɜɟɞɟɦ ɭɝɨɥ M ɦɟɠɞɭ ɩɚɞɚɸɳɢɦ ɥɭɱɨɦ ɢ ɥɭɱɨɦ, ɜɵɲɟɞɲɢɦ ɢɡ
ɩɪɢɡɦɵ, ɤɨɬɨɪɵɣ ɧɚɡɵɜɚɸɬ ɭɝɥɨɦ ɨɬɤɥɨɧɟɧɢɹ ɫɜɟɬɚ ɩɪɢ ɩɪɨɯɨɠɞɟɧɢɢ
ɱɟɪɟɡ ɩɪɢɡɦɭ. ɂɡ ɝɟɨɦɟɬɪɢɢ ɧɟɬɪɭɞɧɨ ɩɨɤɚɡɚɬɶ, ɱɬɨ M = D
1
+ D
2
– G
(ɪɢɫ. 3). Ɉɬɫɸɞɚ D
2
= M + G – D
1
. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɞɥɹ ɦɚɥɵɯ ɭɝɥɨɜ
1
1
2
DG|M n .
Ɍɨ ɟɫɬɶ ɱɟɦ ɛɨɥɶɲɟ ɩɪɟɥɨɦɥɹɸɳɢɣ ɭɝɨɥ ɩɪɢɡɦɵ G, ɬɟɦ ɫɢɥɶɧɟɟ
ɥɭɱ ɫɜɟɬɚ ɨɬɤɥɨɧɹɟɬɫɹ ɨɬ ɩɟɪɜɨɧɚɱɚɥɶɧɨɝɨ ɧɚɩɪɚɜɥɟɧɢɹ ɩɪɢ ɩɪɨɯɨɠɞɟ-
ɧɢɢ ɱɟɪɟɡ ɩɪɢɡɦɭ (ɩɪɢ ɨɞɧɨɦ ɢ ɬɨɦ ɠɟ ɭɝɥɟ ɩɚɞɟɧɢɹ D
1
).
ɉɨɷɬɨɦɭ, ɟɫɥɢ ɯɨɬɹɬ ɞɨɛɢɬɶɫɹ ɛ
ɨɥɶɲɟɝɨ ɨɬɤɥɨɧɟɧɢɹ ɥɭɱɚ ɨɬ ɩɟɪ-
ɜɨɧɚɱɚɥɶɧɨɝɨ ɧɚɩɪɚɜɥɟɧɢɹ, ɞɥɹ ɷɤɫɩɟɪɢɦɟɧɬɚ ɩɨɞɛɢɪɚɸɬ ɩɪɢɡɦɵ ɫ
ɛ
ɨɥɶɲɢɦ ɭɝɥɨɦ ɩɪɟɥɨɦɥɟɧɢɹ.
2.3. Ɂɚɜɢɫɢɦɨɫɬɶ ɭɝɥɚ
M
ɨɬɤɥɨɧɟɧɢɹ ɥɭɱɚ ɨɬ ɪɚɡɧɢɰɵ
ɦɟɠɞɭ ɩɚɞɚɸɳɢɦ ɢ ɜɵɲɟɞɲɢɦ ɥɭɱɚɦɢ
Ⱦɥɹ ɞɚɥɶɧɟɣɲɟɝɨ ɚɧɚɥɢɡɚ ɜɜɟɞɟɦ ɭɝɨɥ ' = D
1
– D
2
, ɤɨɬɨɪɵɣ ɩɨɤɚ-
ɡɵɜɚɟɬ ɧɚɫɤɨɥɶɤɨ ɨɬɤɥɨɧɟɧɢɟ ɨɬ ɧɨɪɦɚɥɢ ɩɚɞɚɸɳɟɝɨ ɥɭɱɚ ɛɨɥɶɲɟ, ɱɟɦ
ɭ ɜɵɲɟɞɲɟɝɨ. ɇɚɩɪɢɦɟɪ, ɞɥɹ ɫɢɦɦɟɬɪɢɱɧɨɝɨ ɯɨɞɚ ɥɭɱɟɣ D
1
= D
2
ɭɝɨɥ
' = 0. Ɍɨɝɞɚ ɢɡ ɞɜɭɯ ɭɪɚɜɧɟɧɢɣ M = D
1
+ D
2
– G ɢ ' = D
1
– D
2
ɜɵɪɚɡɢɦ ɭɝ-
ɥɵ D
1
ɢ D
2
)(
2
1
1
'GM D
ɢ
)(
2
1
2
'GM D
.
Ɍɨɝɞɚ ɩɨɫɥɟ ɬɪɢɝɨɧɨɦɟɬɪɢɱɟɫɤɢɯ ɩɪɟɨɛɪɚɡɨɜɚɧɢɣ ɩɨɥɭɱɟɧɧɨɟ ɪɚ-
ɧɟɟ ɜɵɪɚɠɟɧɢɟ

ɆɨɞO-01 ɇɨɪɦɚɥɶɧɚɹ ɞɢɫɩɟɪɫɢɹ ɫɜɟɬɚ
429
G GDDDD
22
212
2
1
2
sincossinsin2sinsin n
ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɜ ɜɢɞɟ
G G'GMG'
22
sincoscos)cos()cos(cos1 n .
ȼɵɪɚɡɢɜ cos(M + G), ɩɨɥɭɱɢɦ
G'
G'G
GM
coscos
coscossin1
)cos(
22
n
.
Ⱦɥɹ ɭɩɪɨɳɟɧɢɹ ɚɧɚɥɢɡɚ ɨɩɹɬɶ ɠɟ ɪɚɫɫɦɨɬɪɢɦ ɫɥɭɱɚɣ ɦɚɥɵɯ ɭɝ-
ɥɨɜ. Ɍɨɝɞɚ
2
)(
1)cos(
2
GM
|GM
,
2
1cos
2
'
|'
,
2
1cos
2
G
|G
, G|Gsin .
ɉɨɞɫɬɚɜɢɜ ɢ ɩɪɢɜɟɞɹ ɩɨɞɨɛɧɵɟ, ɩɨɥɭɱɢɦ
22
22
22
4
4
)(
G'
'
G|GM
n
ɢɥɢ
¸
¸
¹
·
¨
¨
©
§
G'
'
G|M 1
4
4
22
22
n
.
(ɞɥɹ ɦɚɥɵɯ ɭɝɥɨɜ ɨɱɟɜɢɞɧɨ, ɱɬɨ
04
22
!G'
, ɚ
04
22
z'n
)
Ⱦɥɹ ɮɢɤɫɢɪɨɜɚɧɧɨɣ ɩɪɢɡɦɵ (G = const) ɭɝɨɥ ɨɬɤɥɨɧɟɧɢɹ M ɥɭɱɚ ɨɬ
ɩɟɪɜɨɧɚɱɚɥɶɧɨɝɨ ɧɚɩɪɚɜɥɟɧɢɹ ɡɚɜɢɫɢɬ ɨɬ ɪɚɡɧɢɰɵ ' ɦɟɠɞɭ ɩɚɞɚɸɳɢɦ ɢ
ɜɵɲɟɞɲɢɦ ɥɭɱɚɦɢ ɧɟɥɢɧɟɣɧɨ. ɂɫɫɥɟɞɭɟɦ ɷɬɭ ɡɚɜɢɫɢɦɨɫɬɶ ɧɚ ɷɤɫɬɪɟ-
ɦɭɦ. Ⱦɥɹ ɷɬɨɝɨ ɜɵɱɢɫɥɢɦ ɩɪɨɢɡɜɨɞɧɭɸ
2/3222/122
22
)4()4(
)44(
G''
GG'
'
M
n
n
d
d
.
ȼɟɥɢɱɢɧɚ
0)1(4
22
!Gn ɜɫɟɝɞɚ. ɉɨɷɬɨɦɭ ɩɪɨɢɡɜɨɞɧɚɹ ɞɥɹ ɨɬ-
ɪɢɰɚɬɟɥɶɧɵɯ ɭɝɥɨɜ ' ɦɟɧɶɲɟ ɧɭɥɹ, ɞɥɹ ɩɨɥɨɠɢɬɟɥɶɧɵɯ – ɛɨɥɶɲɟ ɧɭɥɹ,
ɚ ɩɪɢ ' = 0 – ɨɛɪɚɳɚɟɬɫɹ ɜ ɧɨɥɶ. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɩɪɢ ' = 0 ɭɝɨɥ M ɨɬ-
ɤɥɨɧɟɧɢɹ ɥɭɱɚ ɨɬ ɩɟɪɜɨɧɚɱɚɥɶɧɨɝɨ ɧɚɩɪɚɜɥɟɧɢɹ ɢɦɟɟɬ ɦɢɧɢɦɭɦ.
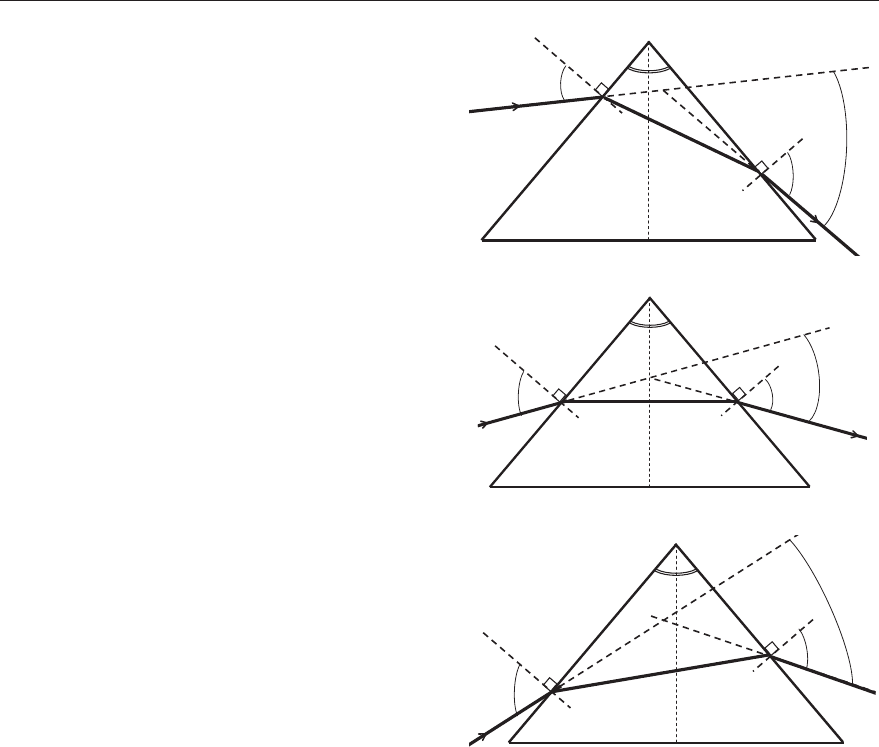
ɉɪɢ ɫɢɦɦɟɬɪɢɱɧɨɦ ɯɨɞɟ ɥɭɱɟɣ (' = 0) ɭɝɨɥ ɨɬɤɥɨɧɟɧɢɹ M ɨɤɚ-
ɡɵɜɚɟɬɫɹ ɦɢɧɢɦɚɥɶɧɵɦ ɞɥɹ ɮɢɤɫɢɪɨɜɚɧɧɨɣ ɞɥɢɧɵ ɜɨɥɧɵ
. ɗɬɚ ɡɚɜɢ-
ɫɢɦɨɫɬɶ ɫɩɪɚɜɟɞɥɢɜɚ ɬɚɤɠɟ ɢ ɞɥɹ ɛɨɥɶɲɢɯ ɭɝɥɨɜ (ɪɢɫ. 4).
Ɇɢɧɢɦɚɥɶɧɵɣ ɭɝɨɥ M ɨɬɤɥɨɧɟɧɢɹ ɥɭɱɚ ɨɬ ɩɟɪɜɨɧɚɱɚɥɶɧɨɝɨ ɧɚ-
ɩɪɚɜɥɟɧɢɹ, ɧɚɛɥɸɞɚɸɳɢɣɫɹ ɩɪɢ ɫɢɦɦɟɬɪɢɱɧɨɦ ɯɨɞɟ ɥɭɱɟɣ ɱɟɪɟɡ ɩɪɢɡ-
ɦɭ (ɪɢɫ. 4ɛ), ɧɚɡɵɜɚɟɬɫɹ ɭɝɥɨɦ ɧɚɢɦɟɧɶɲɟɝɨ ɨɬɤɥɨɧɟɧɢɹ.
Ɉɩɬɢɤɚ
430
2.4. ȼɵɛɨɪ ɨɩɬɢɦɚɥɶɧɵɯ
ɭɫɥɨɜɢɣ ɷɤɫɩɟɪɢɦɟɧɬɚ
Ɋɚɡɧɢɰɚ ɦɟɠɞɭ ɭɝɥɚɦɢ ɧɚɢ-
ɦɟɧɶɲɟɝɨ ɨɬɤɥɨɧɟɧɢɹ ɥɭɱɚ ɨɬ ɩɟɪ-
ɜɨɧɚɱɚɥɶɧɨɝɨ ɧɚɩɪɚɜɥɟɧɢɹ ɞɥɹ ɫɜɟ-
ɬɚ ɜ ɨɩɬɢɱɟɫɤɨɦ ɞɢɚɩɚɡɨɧɟ ɫɨɫɬɚɜ-
ɥɹɟɬ 2–3 ɝɪɚɞɭɫɚ, ɚ ɩɨɤɚɡɚɬɟɥɶ ɩɪɟ-
ɥɨɦɥɟɧɢɹ ɨɬɥɢɱɚɟɬɫɹ ɜ ɬɪɟɬɶɟɦ ɡɧɚ-
ɤɟ ɩɨɫɥɟ ɡɚɩɹɬɨɣ. ɉɨɷɬɨɦɭ ɞɢɫɩɟɪ-
ɫɢɹ ɨɬɧɨɫɢɬɫɹ ɤ ɞɨɫɬɚɬɨɱɧɨ ɬɨɧɤɢɦ
ɷɮɮɟɤɬɚɦ ɢ ɦɨɠɟɬ ɛɵɬɶ ɞɨɫɬɨɜɟɪɧɨ
ɢɡɦɟɪɟɧɚ ɩɪɢɛɨɪɨɦ, ɢɦɟɸɳɢɦ ɞɨɫ-
ɬɚɬɨɱɧɭɸ ɬɨɱɧɨɫɬɶ, ɢ ɩɪɢ
ɞɨɫɬɚ-
ɬɨɱɧɨɣ ɬɳɚɬɟɥɶɧɨɫɬɢ ɜɵɩɨɥɧɟɧɢɹ
ɷɤɫɩɟɪɢɦɟɧɬɚ.
ɉɪɢ ɜɵɩɨɥɧɟɧɢɢ ɢɡɦɟɪɟɧɢɣ
ɧɚ ɥɸɛɨɦ ɩɪɢɛɨɪɟ ɫɥɟɞɭɟɬ ɩɨɦɧɢɬɶ,
ɱɬɨ ɨɬɧɨɫɢɬɟɥɶɧɚɹ ɩɨɝɪɟɲɧɨɫɬɶ ɢɡ-
ɦɟɪɟɧɢɣ ɭɦɟɧɶɲɚɟɬɫɹ ɫ ɭɜɟɥɢɱɟɧɢ-
ɟɦ ɚɛɫɨɥɸɬɧɨɝɨ ɡɧɚɱɟɧɢɹ ɢɡɦɟɪɹɟ-
ɦɨɣ ɜɟɥɢɱɢɧɵ.
ɉɪɢ ɢɫɩɨɥɶɡɨɜɚɧɢɢ ɬɪɟɭɝɨɥɶ-
ɧɨɣ ɩɪɢɡɦɵ ɞɥɹ ɪɚɫɱɟɬɚ ɩɨɤɚɡɚɬɟɥɹ
ɩɪɟɥɨɦɥɟɧɢɹ n ɫɜɟɬɚ ɮɢɤɫɢɪɨɜɚɧ-
ɧɨɣ ɞɥɢɧɵ ɜɨɥɧɵ (ɤɚɤ ɛɵɥɨ ɩɨɤɚɡɚɧɨ ɜɵɲɟ) ɧɟɨɛɯɨɞɢɦɨ ɢɡɦɟɪɢɬɶ ɭɝɥɵ
D
1
ɢ D
2
ɨɬɤɥɨɧɟɧɢɹ ɩɚɞɚɸɳɟɝɨ ɢ ɜɵɲɟɞɲɟɝɨ ɥɭɱɟɣ ɨɬ ɧɨɪɦɚɥɟɣ, ɩɪɨɜɟ-
ɞɟɧɧɵɯ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɤ ɥɟɜɨɣ ɢ ɩɪɚɜɨɣ ɝɪɚɧɹɦ ɩɪɢɡɦɵ. ɋɥɟɞɨɜɚɬɟɥɶ-
ɧɨ, ɞɥɹ ɩɨɜɵɲɟɧɢɹ ɬɨɱɧɨɫɬɢ ɢɡɦɟɪɟɧɢɹ ɩɨɤɚɡɚɬɟɥɹ ɩɪɟɥɨɦɥɟɧɢɹ ɧɟɨɛ-
ɯɨɞɢɦɨ ɩɨɞɨɛɪɚɬɶ ɬɚɤɨɣ ɯɨɞ ɥɭɱɟɣ ɱɟɪɟɡ ɩɪɢɡɦɭ, ɱɬɨɛɵ ɭɝɥɵ D
1
ɢ D
2
ɛɵɥɢ ɩɨ ɜɨɡɦɨɠɧɨɫɬɢ ɤɚɤ ɦɨɠɧɨ ɛɨɥɶɲɟ. ɍɝɨɥ D
1
ɩɚɞɚɸɳɟɝɨ ɥɭɱɚ
ɨɛɵɱɧɨ ɦɨɠɧɨ ɪɟɝɭɥɢɪɨɜɚɬɶ ɡɚ ɫɱɟɬ ɩɨɥɨɠɟɧɢɹ ɢɫɬɨɱɧɢɤɚ ɫɜɟɬɚ. Ⱦɥɹ
ɭɜɟɥɢɱɟɧɢɹ ɭɝɥɚ D
2
ɜɵɲɟɞɲɟɝɨ ɥɭɱɚ ɦɨɠɧɨ ɢɫɩɨɥɶɡɨɜɚɬɶ ɩɪɢɡɦɵ ɫ
ɛɨɥɶɲɢɦ ɩɪɟɥɨɦɥɹɸɳɢɦ ɭɝɥɨɦ, ɩɪɢ ɤɨɬɨɪɨɦ ɩɨɥɧɨɟ ɜɧɭɬɪɟɧɧɟɟ ɨɬɪɚ-
ɠɟɧɢɟ, ɨɞɧɚɤɨ, ɧɟ ɧɚɛɥɸɞɚɟɬɫɹ.
ɋɥɟɞɭɟɬ ɨɬɦɟɬɢɬɶ, ɱɬɨ ɭɝɥɵ D
1
ɢ D
2
ɧɟɭɞɨɛɧɵ ɞɥɹ ɩɪɚɤɬɢɱɟɫɤɨɝɨ
ɢɡɦɟɪɟɧɢɹ, ɬɚɤ ɤɚɤ ɨɬɫɱɢɬɵɜɚɸɬɫɹ ɨɬ ɪɚɡɧɵɯ ɝɪɚɧɟɣ ɩɪɢɡɦɵ. Ⱦɥɹ ɩɪɚɤ-
D
1
D
2
G
M
ɚ) D
1
< D
2
, M > M
min
D
1
D
2
G
M
ɛ) D
1
= D
2
, M = M
min
D
1
D
2
G
M
ɜ) D
1
> D
2
, M > M
min
Ɋɢɫ. 4
