Ревинская О.Г., Кравченко Н.С. Изучение моделей физических процессов и явлений на компьютере

Подождите немного. Документ загружается.

161

ɅȺȻɈɊȺɌɈɊɇȺə ɊȺȻɈɌȺ ʋ ɆɨɞɌ-03

ɉɈ ɂɁɍɑȿɇɂɘ ɆɈȾȿɅȿɃ ɎɂɁɂɑȿɋɄɂɏ

ɉɊɈɐȿɋɋɈȼ ɂ əȼɅȿɇɂɃ ɇȺ ɄɈɆɉɖɘɌȿɊȿ

Ⱦɜɢɠɟɧɢɟ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ

ɐɟɥɶ ɪɚɛɨɬɵ: ɢɡɭɱɟɧɢɟ ɞɜɢɠɟɧɢɹ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ. Ɉɩɪɟɞɟ-

ɥɟɧɢɟ ɩɨɫɬɨɹɧɧɨɣ Ȼɨɥɶɰɦɚɧɚ, ɤɨɷɮɮɢɰɢɟɧɬɚ ɞɢɮɮɭɡɢɢ ɢ ɞɥɢɧɵ ɫɜɨ-

ɛɨɞɧɨɝɨ ɩɪɨɛɟɝɚ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ.

1. Ɍɟɨɪɟɬɢɱɟɫɤɨɟ ɫɨɞɟɪɠɚɧɢɟ

ɉɨɞ ɛɪɨɭɧɨɜɫɤɢɦ ɞɜɢɠɟɧɢɟɦ ɩɨɧɢɦɚɸɬ ɯɚɨɬɢɱɟɫɤɨɟ ɞɜɢɠɟɧɢɟ

ɦɢɤɪɨɫɤɨɩɢɱɟɫɤɢɯ ɱɚɫɬɢɰ, ɜɡɜɟɲɟɧɧɵɯ ɜ ɠɢɞɤɨɫɬɢ ɢɥɢ ɝɚɡɟ, ɩɪɨɢɫɯɨ-

ɞɹɳɟɟ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɭɞɚɪɨɜ ɦɨɥɟɤɭɥ ɨɤɪɭɠɚɸɳɟɣ ɫɪɟɞɵ. ɗɬɨ ɹɜɥɟɧɢɟ

ɜɩɟɪɜɵɟ ɢɫɫɥɟɞɨɜɚɧɨ ɚɧɝɥɢɣɫɤɢɦ ɭɱɟɧɵɦ Ɋɨɛɟɪɬɨɦ Ȼɪɨɭɧɨɦ, ɤɨɬɨɪɵɣ ɜ

1827 ɝ. ɧɚɛɥɸɞɚɥ ɜ ɦɢɤɪɨɫɤɨɩ ɞɜɢɠɟɧɢɟ ɰɜɟɬɨɱɧɨɣ ɩɵɥɶɰɵ, ɜɡɜɟɲɟɧ-

ɧɨɣ ɜ ɜɨɞɟ. ɉɨɥɧɚɹ ɬɟɨɪɢɹ ɛɪɨɭɧɨɜɫɤɨɝɨ ɞɜɢɠɟɧɢɹ ɛɵɥɚ ɞɚɧɚ ɜ 1905–

06 ɝɝ

. Ⱥ. ɗɣɧɲɬɟɣɧɨɦ ɢ ɩɨɥɶɫɤɢɦ ɮɢɡɢɤɨɦ Ɇ. ɋɦɨɥɭɯɨɜɫɤɢɦ.

ɉɪɢɱɢɧɚ ɛɪɨɭɧɨɜɫɤɨɝɨ ɞɜɢɠɟɧɢɹ – ɬɟɩɥɨɜɨɟ ɞɜɢɠɟɧɢɟ ɦɨɥɟɤɭɥ

ɫɪɟɞɵ. ɋɬɨɥɤɧɨɜɟɧɢɹ ɦɨɥɟɤɭɥ ɫɪɟɞɵ ɫ ɱɚɫɬɢɰɟɣ ɧɨɫɹɬ ɫɥɭɱɚɣɧɵɣ ɯɚ-

ɪɚɤɬɟɪ, ɩɨɷɬɨɦɭ ɭɞɚɪɵ ɫ ɪɚɡɧɵɯ ɫɬɨɪɨɧ ɨɤɚɡɵɜɚɸɬɫɹ ɧɟ ɫɤɨɦɩɟɧɫɢɪɨ-

ɜɚɧɧɵɦɢ. ɍɞɚɪɵ ɦɨɥɟɤɭɥ ɫɪɟɞɵ ɩɪɢɜɨɞɹɬ ɱɚɫɬɢɰɭ ɜ ɛɟɫɩɨɪɹɞɨɱɧɨɟ

ɞɜɢɠɟɧɢɟ: ɫɤɨɪɨɫɬɶ ɟɟ ɯɚɨɬɢɱɟɫɤɢ ɦɟɧɹɟɬɫɹ ɩɨ ɜɟɥɢɱɢɧɟ ɢ ɧɚɩɪɚɜɥɟ-

ɧɢɸ. Ȼɪɨɭɧɨɜɫɤɨɟ

ɞɜɢɠɟɧɢɟ – ɧɚɢɛɨɥɟɟ ɧɚɝɥɹɞɧɨɟ ɷɤɫɩɟɪɢɦɟɧɬɚɥɶɧɨɟ

ɩɨɞɬɜɟɪɠɞɟɧɢɟ ɩɪɟɞɫɬɚɜɥɟɧɢɣ ɦɨɥɟɤɭɥɹɪɧɨ-ɤɢɧɟɬɢɱɟɫɤɨɣ ɬɟɨɪɢɢ ɨ

ɯɚɨɬɢɱɟɫɤɨɦ ɬɟɩɥɨɜɨɦ ɞɜɢɠɟɧɢɢ ɚɬɨɦɨɜ ɢ ɦɨɥɟɤɭɥ.

ɑɟɦ ɛɨɥɶɲɟ ɪɚɡɦɟɪ ɱɚɫɬɢɰɵ, ɬɟɦ ɛɨɥɶɲɟɟ ɱɢɫɥɨ ɦɨɥɟɤɭɥ ɨɤɪɭ-

ɠɚɸɳɟɣ ɫɪɟɞɵ ɦɨɝɭɬ ɫɬɨɥɤɧɭɬɶɫɹ ɫ ɧɟɣ ɢ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɬɟɦ ɦɟɧɶɲɟɟ

ɤɨɥɢɱɟɫɬɜɨ ɭɞɚɪɨɜ ɨɫɬɚɧɟɬɫɹ ɧɟ ɫɤɨɦɩɟɧɫɢɪɨɜɚɧɧɵɦ. ɉɨɷɬɨɦɭ ɛɨɥɶɲɚɹ

ɱɚɫɬɢɰɚ ɧɟ ɩɪɢɞɟɬ ɜ ɞɜɢɠɟɧɢɟ. ȿɫɥɢ ɱɚɫɬɢɰɚ ɢɦɟɟɬ ɧɟɛɨɥɶɲɢɟ

ɪɚɡɦɟɪɵ

(a 1 ɦɤɦ = 10

–4

ɫɦ =10

–6

ɦ), ɱɢɫɥɨ ɫɬɨɥɤɧɨɜɟɧɢɣ ɛɭɞɟɬ ɧɟɜɟɥɢɤɨ, ɫɥɟɞɨɜɚ-

ɬɟɥɶɧɨ, ɛɨɥɶɲɟɟ ɤɨɥɢɱɟɫɬɜɨ ɭɞɚɪɨɜ ɨɫɬɚɧɟɬɫɹ ɧɟ ɫɤɨɦɩɟɧɫɢɪɨɜɚɧɧɵɦ, ɢ

ɱɚɫɬɢɰɚ ɩɪɢɞɟɬ ɜ ɞɜɢɠɟɧɢɟ. Ɍɚɤɭɸ ɱɚɫɬɢɰɭ ɧɚɡɵɜɚɸɬ ɛɪɨɭɧɨɜɫɤɨɣ.

ɏɨɬɹ ɛɪɨɭɧɨɜɫɤɚɹ ɱɚɫɬɢɰɚ ɞɜɢɠɟɬɫɹ ɜ ɪɟɡɭɥɶɬɚɬɟ ɯɚɨɬɢɱɟɫɤɢɯ

ɫɬɨɥɤɧɨɜɟɧɢɣ ɫ ɦɨɥɟɤɭɥɚɦɢ ɫɪɟɞɵ ɢ ɧɟɜɨɡɦɨɠɧɨ ɬɨɱɧɨ ɨɩɪɟɞɟɥɢɬɶ ɟɟ

ɬɪɚɟɤɬɨɪɢɸ, ɫɬɚɬɢɫɬɢɱɟɫɤɢɟ ɦɟɬɨɞɵ ɩɨɡɜɨɥɹɸɬ ɨɩɪɟɞɟɥɢɬɶ ɫɪɟɞɧɢɣ

ɤɜɚɞɪɚɬ ɨɬɤɥɨɧɟɧɢɹ ɱɚɫɬɢɰɵ ɨɬ ɧɚɱɚɥɶɧɨɝɨ ɩɨɥɨɠɟɧɢɹ ɤɚɤ

ɮɭɧɤɰɢɸ

ɜɪɟɦɟɧɢ.

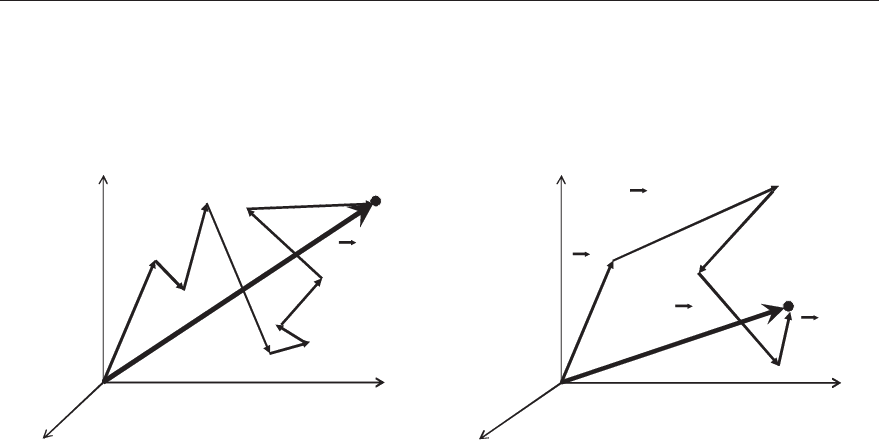
Ɋɚɫɫɦɨɬɪɢɦ ɫɦɟɳɟɧɢɟ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɨɬɧɨɫɢɬɟɥɶɧɨ ɬɨɱɤɢ

Ɉ, ɜɵɛɪɚɧɧɨɣ ɡɚ ɧɚɱɚɥɨ ɨɬɫɱɟɬɚ. ɉɨɥɨɠɟɧɢɟ ɱɚɫɬɢɰɵ ɛɭɞɟɦ ɮɢɤɫɢɪɨ-

Ɏɢɡɢɤɚ ɠɢɞɤɨɫɬɟɣ ɢ ɝɚɡɨɜ

162

ɜɚɬɶ ɱɟɪɟɡ ɪɚɜɧɵɟ ɢɧɬɟɪɜɚɥɵ ɜɪɟɦɟɧɢ

t' . ɏɨɬɹ ɡɚ ɜɪɟɦɹ t' ɱɚɫɬɢɰɚ

ɞɜɢɠɟɬɫɹ ɩɨ ɫɥɨɠɧɨɣ ɥɨɦɚɧɨɣ ɬɪɚɟɤɬɨɪɢɢ, ɧɟɫɤɨɥɶɤɨ ɪɚɡ ɦɟɧɹɹ ɧɚɩɪɚɜ-

ɥɟɧɢɟ ɫɤɨɪɨɫɬɢ, ɟɟ ɫɦɟɳɟɧɢɟ ɢɡ ɬɨɱɤɢ Ɉ ɡɚ ɜɪɟɦɹ

t' ɨɩɢɫɵɜɚɟɬɫɹ ɪɚɞɢ-

ɭɫ-ɜɟɤɬɨɪɨɦ

(ɪɢɫ. 1).

Ɋɢɫ. 1

Ɋɢɫ. 2

ɉɭɫɬɶ ɡɚ ɩɪɨɦɟɠɭɬɨɤ ɜɪɟɦɟɧɢ

tnt '

ɫ ɢɧɬɟɪɜɚɥɨɦ

ɡɚɮɢɤɫɢ-

ɪɨɜɚɧɨ

n ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɵɯ ɫɦɟɳɟɧɢɣ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ, ɨɩɢɫɵ-

ɜɚɟɦɵɯ ɪɚɞɢɭɫ-ɜɟɤɬɨɪɚɦɢ

, …

ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ (ɪɢɫ 2). Ɋɟɡɭɥɶɬɢ-

ɪɭɸɳɟɟ ɫɦɟɳɟɧɢɟ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɡɚ ɩɪɨɦɟɠɭɬɨɤ ɜɪɟɦɟɧɢ

ɨɩɢ-

ɫɵɜɚɟɬɫɹ ɪɚɞɢɭɫ-ɜɟɤɬɨɪɨɦ



rrrrr

...

Ʉɜɚɞɪɚɬ ɪɚɞɢɭɫ-ɜɟɤɬɨɪɚ

r ɢ ɛɭɞɟɬ ɨɩɢɫɵɜɚɬɶ ɤɜɚɞɪɚɬ ɨɬɤɥɨɧɟɧɢɹ

ɱɚɫɬɢɰɵ ɨɬ ɧɚɱɚɥɶɧɨɝɨ ɩɨɥɨɠɟɧɢɹ

¦¦¦¦

  

rrrrrrrr

)()()(

ɉɪɨɜɟɞɹ ɪɹɞ ɧɟɡɚɜɢɫɢɦɵɯ ɷɤɫɩɟɪɢɦɟɧɬɨɜ, ɩɨɥɭɱɢɦ ɪɚɡɥɢɱɧɵɟ

ɡɧɚɱɟɧɢɹ ɤɜɚɞɪɚɬɚ ɫɦɟɳɟɧɢɹ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɡɚ ɜɪɟɦɹ

. ɇɚɣɞɟɦ

ɫɪɟɞɧɟɟ ɡɧɚɱɟɧɢɟ ɤɜɚɞɪɚɬɚ ɫɦɟɳɟɧɢɹ

¦¦

!!! 

rrrr

)(

ȼɫɟ ɫɦɟɳɟɧɢɹ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɡɚ ɨɞɢɧɚɤɨɜɵɟ ɢɧɬɟɪɜɚɥɵ

ɜɪɟɦɟɧɢ

ɪɚɜɧɨɜɟɪɨɹɬɧɵ. ɉɨɷɬɨɦɭ ɜɫɟ ɫɪɟɞɧɢɟ ɫɦɟɳɟɧɢɹ ɱɚɫɬɢɰɵ

!

r ɡɚ ɜɪɟɦɹ

ɨɞɢɧɚɤɨɜɵ

ɆɨɞɌ-03 Ⱦɜɢɠɟɧɢɟ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ

163

const...

! ! ! !

rrrr .

Ɉɛɨɡɧɚɱɢɦ ɤɨɧɫɬɚɧɬɭ

!

const

ɱɟɪɟɡ

. Ɍɨɝɞɚ

!

, ɚ

nCr

!

ɋɪɟɞɧɟɟ ɡɧɚɱɟɧɢɟ ɫɤɚɥɹɪɧɨɝɨ ɩɪɨɢɡɜɟɞɟɧɢɹ ɧɟɨɞɢɧɚɤɨɜɵɯ ɜɟɤɬɨ-

ɪɨɜ ɫɦɟɳɟɧɢɹ

! )(

ɨɛɪɚɳɚɟɬɫɹ ɜ ɧɨɥɶ ɢɡ-ɡɚ ɪɚɜɧɨɩɪɚɜɢɹ ɜɫɟɯ ɧɚ-

ɩɪɚɜɥɟɧɢɣ ɫɦɟɳɟɧɢɹ

rrrrrrrr

jiijjiijjiji

!!! M!!! M!  00coscos)(

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɫɪɟɞɧɢɣ ɤɜɚɞɪɚɬ ɫɦɟɳɟɧɢɹ ɱɚɫɬɢɰɵ ɡɚ ɜɪɟɦɹ

r !  ,

ɝɞɟ

– ɱɢɫɥɨ ɢɡɦɟɪɟɧɢɣ ɡɚ ɜɪɟɦɹ ɞɜɢɠɟɧɢɹ ɱɚɫɬɢɰɵ

, ɚ

–

ɩɪɨɦɟɠɭɬɨɤ ɜɪɟɦɟɧɢ ɦɟɠɞɭ ɢɡɦɟɪɟɧɢɹɦɢ. Ɍɨɝɞɚ

! 

, ɝɞɟ

ɂɥɢ

D! 

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜɟɥɢɱɢɧɚ ɫɪɟɞɧɟɝɨ ɤɜɚɞɪɚɬɚ ɫɦɟɳɟɧɢɹ ɛɪɨɭɧɨɜ-

ɫɤɨɣ ɱɚɫɬɢɰɵ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɚ ɜɪɟɦɟɧɢ ɧɚɛɥɸɞɟɧɢɹ

Ⱦɥɹ ɬɨɝɨ ɱɬɨɛɵ ɨɩɪɟɞɟɥɢɬɶ ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨɫɬɢ

D ,

ɪɚɫɫɦɨɬɪɢɦ ɫɢɥɵ, ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɱɚɫɬɢɰɭ.

ɑɚɫɬɢɰɚ ɧɚɯɨɞɢɬɫɹ ɜɨ ɜɡɜɟɲɟɧɧɨɦ ɫɨɫɬɨɹɧɢɢ ɜ ɧɟɤɨɬɨɪɨɣ ɜɹɡɤɨɣ

ɫɪɟɞɟ, ɩɨɷɬɨɦɭ ɛɭɞɟɦ ɫɱɢɬɚɬɶ, ɱɬɨ ɥɸɛɵɟ ɫɦɟɳɟɧɢɹ ɱɚɫɬɢɰɵ ɜ ɧɚɩɪɚɜ-

ɥɟɧɢɢ OZ (ɜ ɧɚɩɪɚɜɥɟɧɢɢ ɫɢɥɵ ɬɹɠɟɫɬɢ) ɧɟɜɨɡɦɨɠɧɵ. Ɍɨɝɞɚ ɞɜɢɠɟɧɢɟ

ɩɪɨɢɫɯɨɞɢɬ ɜ ɩɥɨɫɤɨɫɬɢ XOY. ɋɨ ɫɬɨɪɨɧɵ ɫɪɟɞɵ ɧɚ ɱɚɫɬɢɰɭ ɞɟɣɫɬɜɭɸɬ

ɫɢɥɚ ɜɹɡɤɨɝɨ ɬɪɟɧɢɹ (ɫɢɥɚ ɋɬɨɤɫɚ) ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɚɹ ɫɤɨɪɨɫɬɢ

ɫɨɩɪ

 (ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨɫɬɢ b ɡɚɜɢɫɢɬ ɨɬ ɪɚɡɦɟɪɨɜ ɢ

ɮɨɪɦɵ ɱɚɫɬɢɰɵ, ɚ ɬɚɤɠɟ ɨɬ ɫɜɨɣɫɬɜ ɜɹɡɤɨɣ ɫɪɟɞɵ). Ʉɪɨɦɟ ɬɨɝɨ, ɞɟɣɫɬɜɭ-

ɟɬ ɪɟɡɭɥɶɬɢɪɭɸɳɚɹ ɫɢɥɚ

ɭɞɚɪɨɜ ɦɨɥɟɤɭɥ ɨ ɱɚɫɬɢɰɭ ɫ ɪɚɡɧɵɯ ɫɬɨɪɨɧ.

ɗɬɚ ɫɢɥɚ (ɫɢɥɚ Ʌɚɧɠɟɜɟɧɚ) ɧɨɫɢɬ ɫɥɭɱɚɣɧɵɣ ɯɚɪɚɤɬɟɪ. ɍɪɚɜɧɟɧɢɟ ɞɜɢ-

ɠɟɧɢɹ ɱɚɫɬɢɰɵ ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɜ ɜɢɞɟ:

am  .

Ɋɚɫɫɦɨɬɪɢɦ ɩɪɨɟɤɰɢɸ ɷɬɨɝɨ ɭɪɚɜɧɟɧɢɹ ɧɚ ɨɫɶ OX

xbFxm



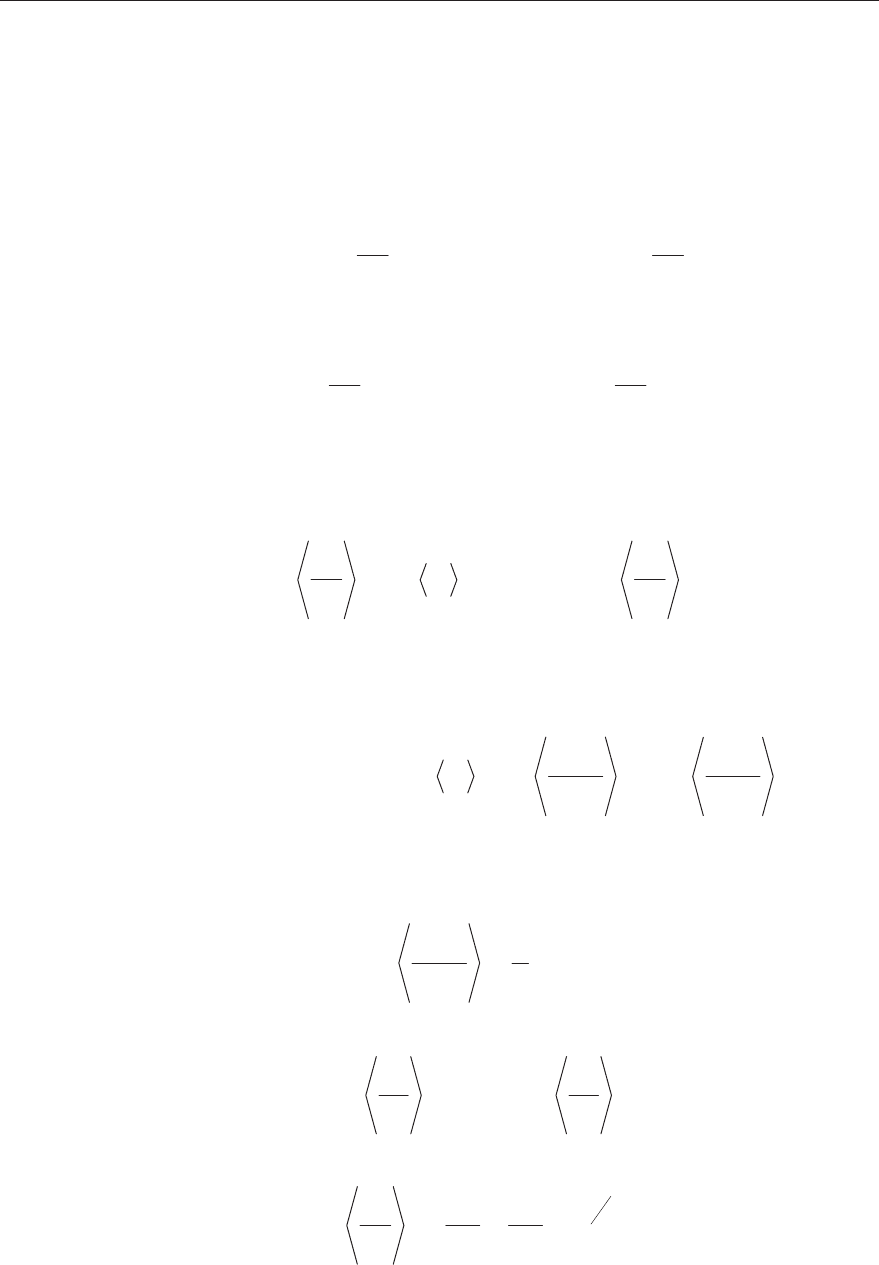
Ɏɢɡɢɤɚ ɠɢɞɤɨɫɬɟɣ ɢ ɝɚɡɨɜ

164

ɉɪɟɠɞɟ ɱɟɦ ɩɨɥɭɱɢɬɶ ɭɪɚɜɧɟɧɢɟ ɞɥɹ ɫɪɟɞɧɢɯ ɜɟɥɢɱɢɧ, ɜɵɩɨɥɧɢɦ

ɪɹɞ ɜɫɩɨɦɨɝɚɬɟɥɶɧɵɯ ɩɪɟɨɛɪɚɡɨɜɚɧɢɣ. ɍɦɧɨɠɢɦ ɨɛɟ ɱɚɫɬɢ ɷɬɨɝɨ ɭɪɚɜ-

ɧɟɧɢɹ ɧɚ

xbxxFxmx





ɉɪɢɧɢɦɚɹ ɜɨ ɜɧɢɦɚɧɢɟ, ɱɬɨ







;



ɩɨɥɭɱɟɧɧɨɟ ɭɪɚɜɧɟɧɢɟ ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɜ ɜɢɞɟ





bxFxm

ɍɫɪɟɞɧɢɦ ɩɨɥɭɱɟɧɧɨɟ ɭɪɚɜɧɟɧɢɟ ɩɨ ɜɫɟɦ ɧɚɛɥɸɞɟɧɢɹɦ, ɭɱɢɬɵ-

ɜɚɹ, ɱɬɨ ɫɪɟɞɧɟɟ ɡɧɚɱɟɧɢɟ ɩɪɨɢɡɜɨɞɧɨɣ ɪɚɜɧɨ ɩɪɨɢɡɜɨɞɧɨɣ ɫɪɟɞɧɟɝɨ

ɡɧɚɱɟɧɢɹ. Ɍɨɝɞɚ

! 



bxFxm

Ʉɨɨɪɞɢɧɚɬɚ

x ɱɚɫɬɢɰɵ ɢ ɫɨɨɬɜɟɬɫɬɜɭɸɳɚɹ ɩɪɨɟɤɰɢɹ ɫɢɥɵ Ʌɚɧ-

ɠɟɜɟɧɟ

F ɹɜɥɹɸɬɫɹ ɫɥɭɱɚɣɧɵɦɢ ɢ ɧɟ ɡɚɜɢɫɹɳɢɦɢ ɞɪɭɝ ɨɬ ɞɪɭɝɚ ɜɟɥɢ-

ɱɢɧɚɦɢ. ɉɨɷɬɨɦɭ

0!  xF

Ɂɧɚɹ, ɱɬɨ

x v

, ɩɨɥɭɱɢɦ

, ɝɞɟ

– ɫɪɟɞ-

ɧɹɹ ɷɧɟɪɝɢɹ, ɩɪɢɯɨɞɹɳɚɹɫɹ ɧɚ ɨɞɧɭ ɫɬɟɩɟɧɶ ɫɜɨɛɨɞɵ. ɑɚɫɬɢɰɚ ɢ ɫɪɟɞɚ

ɧɚɯɨɞɹɬɫɹ ɜ ɫɨɫɬɨɹɧɢɢ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɨɝɨ ɪɚɜɧɨɜɟɫɢɹ, ɩɨɷɬɨɦɭ ɢɡ ɡɚ-

ɤɨɧɚ ɨ ɪɚɜɧɨɦɟɪɧɨɦ ɪɚɫɩɪɟɞɟɥɟɧɢɢ ɷɧɟɪɝɢɢ ɩɨ ɫɬɟɩɟɧɹɦ ɫɜɨɛɨɞɵ

Ɍɨɝɞɚ ɭɪɚɜɧɟɧɢɟ ɧɚ ɫɪɟɞɧɢɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɞɜɢɠɟɧɢɹ ɩɪɢɦɟɬ ɜɢɞ

 

bkT

Ɋɟɲɟɧɢɟ ɞɚɧɧɨɝɨ ɭɪɚɜɧɟɧɢɹ ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɜ ɜɢɞɟ

kTx





ɆɨɞɌ-03 Ⱦɜɢɠɟɧɢɟ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ

165

Ⱦɥɹ ɦɚɤɪɨɫɤɨɩɢɱɟɫɤɢɯ ɱɚɫɬɢɰ ɡɧɚɱɟɧɢɟ ɤɨɧɫɬɚɧɬɵ

ɬɚɤɨɜɨ, ɱɬɨ

ɜɥɢɹɧɢɟ ɷɤɫɩɨɧɟɧɬɵ ɜ ɩɨɥɭɱɟɧɧɨɦ ɪɟɲɟɧɢɢ ɫɤɚɡɵɜɚɟɬɫɹ ɬɨɥɶɤɨ ɩɪɢ

ɞɥɢɬɟɥɶɧɨɫɬɢ ɧɚɛɥɸɞɟɧɢɹ t ɩɨɪɹɞɤɚ ɜɪɟɦɟɧɢ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ ɱɚɫɬɢɰɵ ɫ

ɦɨɥɟɤɭɥɨɣ ɫɪɟɞɵ (~ 10

–12

ɫ). Ⱦɥɹ ɛɨɥɶɲɢɯ ɢɧɬɟɪɜɚɥɨɜ ɜɪɟɦɟɧɢ ɧɚɛɥɸ-

ɞɟɧɢɹ t ɜɬɨɪɵɦ ɫɥɚɝɚɟɦɵɦ ɦɨɠɧɨ ɩɪɟɧɟɛɪɟɱɶ. Ɍɨɝɞɚ ɫɤɨɪɨɫɬɶ ɢɡɦɟɧɟ-

ɧɢɹ ɫɪɟɞɧɟɝɨ ɤɜɚɞɪɚɬɚ X-ɫɦɟɳɟɧɢɹ



ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɜɪɟɦɟɧɢ

kTx

ɉɨɫɬɨɹɧɧɚɹ ɜɟɥɢɱɢɧɚ

ɯɚɪɚɤɬɟɪɢɡɭɟɬ ɤɨɥɢɱɟɫɬɜɨ ɱɚɫɬɢɰ

ɞɚɧɧɨɝɨ ɜɢɞɚ, ɩɪɨɯɨɞɹɳɢɯ ɱɟɪɟɡ ɟɞɢɧɢɱɧɭɸ ɩɥɨɳɚɞɤɭ ɜ ɟɞɢɧɢɰɭ ɜɪɟ-

ɦɟɧɢ ɢ ɧɚɡɵɜɚɟɬɫɹ ɤɨɷɮɮɢɰɢɟɧɬɨɦ ɞɢɮɮɭɡɢɢ. Ʉɨɷɮɮɢɰɢɟɧɬ ɞɢɮɮɭ-

ɡɢɢ ɡɚɜɢɫɢɬ ɨɬ ɬɟɦɩɟɪɚɬɭɪɵ ɢ ɫɜɨɣɫɬɜ ɠɢɞɤɨɫɬɢ, ɚ ɬɚɤɠɟ ɨɬ ɪɚɡɦɟɪɨɜ ɢ

ɮɨɪɦɵ ɞɜɢɠɭɳɢɯɫɹ ɱɚɫɬɢɰ.

Ɍɨɝɞɚ ɞɢɮɮɟɪɟɧɰɢɚɥɶɧɨɟ ɭɪɚɜɧɟɧɢɟ ɧɚ ɫɪɟɞɧɢɣ ɤɜɚɞɪɚɬ X-

ɫɦɟɳɟɧɢɹ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɩɪɢɦɟɬ ɜɢɞ

 .

ɉɪɨɢɧɬɟɝɪɢɪɨɜɚɜ ɞɚɧɧɨɟ ɭɪɚɜɧɟɧɢɟ, ɩɨɥɭɱɢɦ ɢɫɤɨɦɭɸ ɡɚɜɢɫɢ-

ɦɨɫɬɶ ɜ ɜɢɞɟ

!  .

ɉɨɥɭɱɟɧɧɨɟ ɭɪɚɜɧɟɧɢɟ ɧɚɡɵɜɚɸɬ ɮɨɪɦɭɥɨɣ ɗɣɧɲɬɟɣɧɚ-

ɋɦɨɥɭɯɨɜɫɤɨɝɨ. Ɉɧɚ ɩɨɡɜɨɥɢɥɚ ɀ. ɉɟɪɪɟɧɭ ɷɤɫɩɟɪɢɦɟɧɬɚɥɶɧɨ ɨɩɪɟɞɟ-

ɥɢɬɶ ɩɨɫɬɨɹɧɧɭɸ Ȼɨɥɶɰɦɚɧɚ ɢ ɱɢɫɥɨ Ⱥɜɨɝɚɞɪɨ.

ɋɨɜɪɟɦɟɧɧɵɟ ɦɟɬɨɞɵ ɢɡɦɟɪɟɧɢɣ ɩɨɡɜɨɥɢɥɢ ɩɨɥɭɱɢɬɶ ɫɥɟɞɭɸɳɟɟ

ɡɧɚɱɟɧɢɟ ɩɨɫɬɨɹɧɧɨɣ Ȼɨɥɶɰɦɚɧɚ

k = 1,380 662 4410

–23

Ⱦɠ/Ʉ = 1,380 662 4410

–16

ɝɫɦ

/(ɫ

Ʉ).

ɉɪɢ ɞɜɢɠɟɧɢɢ ɜ ɩɥɨɫɤɨɫɬɢ XOY ɤɜɚɞɪɚɬ ɨɬɤɥɨɧɟɧɢɹ ɱɚɫɬɢɰɵ ɨɬ

ɧɚɱɚɥɶɧɨɝɨ ɩɨɥɨɠɟɧɢɹ ɜɵɪɚɠɚɟɬɫɹ ɱɟɪɟɡ ɤɨɨɪɞɢɧɚɬɵ ɱɚɫɬɢɰɵ

222

yxr  . ɋɪɟɞɧɟɟ ɡɧɚɱɟɧɢɟ ɤɜɚɞɪɚɬɚ ɨɬɤɥɨɧɟɧɢɹ ɱɚɫɬɢɰɵ, ɫɨɨɬɜɟɬ-

ɫɬɜɟɧɧɨ, ɜɵɪɚɠɚɟɬɫɹ ɱɟɪɟɡ ɫɪɟɞɧɢɟ ɤɜɚɞɪɚɬɵ X- ɢ Y-ɤɨɨɪɞɢɧɚɬ

!! !

222

yxr

. ȼɫɟ ɧɚɩɪɚɜɥɟɧɢɹ ɞɜɢɠɟɧɢɹ ɱɚɫɬɢɰɵ ɪɚɜɧɨ-

ɩɪɚɜɧɵ, ɩɨɷɬɨɦɭ

! !

yx ɢ ! !

2 xr .

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɫɪɟɞɧɢɣ ɤɜɚɞɪɚɬ ɫɦɟɳɟɧɢɹ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ

ɜ ɩɥɨɫɤɨɫɬɢ XOY ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɚ ɜɪɟɦɟɧɢ

Ɏɢɡɢɤɚ ɠɢɞɤɨɫɬɟɣ ɢ ɝɚɡɨɜ

166

Dtr 4

!

ɫ ɤɨɷɮɮɢɰɢɟɧɬɨɦ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨɫɬɢ

D4 D .

Ʉɨɷɮɮɢɰɢɟɧɬ ɞɢɮɮɭɡɢɢ

ɡɚɜɢɫɢɬ ɨɬ ɤɨɷɮɮɢɰɢɟɧɬɚ ɫɨɩɪɨ-

ɬɢɜɥɟɧɢɹ ɫɪɟɞɵ b. ɋɨɝɥɚɫɧɨ ɮɨɪɦɭɥɟ ɋɬɨɤɫɚ ɞɥɹ ɱɚɫɬɢɰɵ ɲɚɪɨɨɛɪɚɡɧɨɣ

ɮɨɪɦɵ ɤɨɷɮɮɢɰɢɟɧɬ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɫɪɟɞɵ ɡɚɜɢɫɢɬ ɨɬ ɞɢɚɦɟɬɪɚ d ɱɚɫ-

ɬɢɰɵ ɢ ɤɨɷɮɮɢɰɢɟɧɬɚ ɜɹɡɤɨɫɬɢ ɫɪɟɞɵ

b SK

Ɍɨɝɞɚ ɤɨɷɮɮɢɰɢɟɧɬ ɞɢɮɮɭɡɢɢ

ȼɵɱɢɫɥɢɜ ɢɡ ɷɤɫɩɟɪɢɦɟɧɬɚ ɫɪɟɞɧɢɣ ɤɜɚɞɪɚɬ ɫɦɟɳɟɧɢɹ ɛɪɨ-

ɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɡɚ ɮɢɤɫɢɪɨɜɚɧɧɨɟ ɜɪɟɦɹ, ɦɨɠɧɨ ɪɚɫɫɱɢɬɚɬɶ ɤɨ-

ɷɮɮɢɰɢɟɧɬ ɞɢɮɮɭɡɢɢ, ɚ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɢ ɩɨɫɬɨɹɧɧɭɸ Ȼɨɥɶɰɦɚɧɚ.

ɋ ɞɪɭɝɨɣ ɫɬɨɪɨɧɵ ɤɨɷɮɮɢɰɢɟɧɬ ɞɢɮɮɭɡɢɢ ɡɚɜɢɫɢɬ ɨɬ ɫɪɟɞɧɟɣ

ɞɥɢɧɵ ɫɜɨɛɨɞɧɨɝɨ ɩɪɨɛɟɝɚ

!O ɢ ɫɪɟɞɧɟɣ ɫɤɨɪɨɫɬɢ ! v ɱɚɫɬɢɰɵ.

Ⱦɥɹ ɞɜɭɦɟɪɧɨɝɨ ɞɜɢɠɟɧɢɹ ɤɨɷɮɮɢɰɢɟɧɬ ɞɢɮɮɭɡɢɢ ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ

!!O v

D .

Ʉɚɤ ɛɵɥɨ ɩɨɤɚɡɚɧɨ ɪɚɧɟɟ, ɜ ɭɫɥɨɜɢɹɯ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɨɝɨ ɪɚɜɧɨ-

ɜɟɫɢɹ ɫɨɝɥɚɫɧɨ ɡɚɤɨɧɭ ɨ ɪɚɜɧɨɪɚɫɩɪɟɞɟɥɟɧɢɢ ɷɧɟɪɝɢɢ ɩɨ ɫɬɟɩɟɧɹɦ ɫɜɨ-

ɛɨɞɵ

kTmmm

222

!! ! vvv (ɩɪɢ ɞɜɢɠɟɧɢɢ ɜ ɩɥɨɫɤɨ-

ɫɬɢ). Ɍɨɝɞɚ ɫɪɟɞɧɹɹ ɫɤɨɪɨɫɬɶ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɪɚɜɧɚ

!  v .

ɋɪɟɞɧɟɣ ɞɥɢɧɨɣ ɫɜɨɛɨɞɧɨɝɨ ɩɪɨɛɟɝɚ

!O ɱɚɫɬɢɰɵ ɧɚɡɵɜɚɸɬ

ɪɚɫɫɬɨɹɧɢɟ, ɤɨɬɨɪɨɟ ɱɚɫɬɢɰɵ ɩɪɨɯɨɞɢɬ ɛɟɡ ɫɬɨɥɤɧɨɜɟɧɢɣ ɫ ɞɪɭɝɢɦɢ ɱɚɫ-

ɬɢɰɚɦɢ.

ɇɚɩɪɢɦɟɪ, ɩɪɢ ɬɟɦɩɟɪɚɬɭɪɟ 25qɋ ɢ ɧɨɪɦɚɥɶɧɨɦ ɞɚɜɥɟɧɢɢ ɫɪɟɞɧɹɹ

ɫɤɨɪɨɫɬɶ ɦɨɥɟɤɭɥ ɜɨɞɵ ɪɚɜɧɚ 5,247 ɫɦ/ɫ. ɗɤɫɩɟɪɢɦɟɧɬɚɥɶɧɨ ɭɫɬɚɧɨɜɥɟ-

ɧɨ, ɱɬɨ ɤɨɷɮɮɢɰɢɟɧɬ ɞɢɮɮɭɡɢɢ ɜɨɞɵ ɜ ɫɨɫɬɨɹɧɢɢ ɩɚɪɚ ɪɚɜɟɧ

0,277 ɫɦ

/ɫ, ɚ ɤɨɷɮɮɢɰɢɟɧɬ ɞɢɮɮɭɡɢɢ ɜɨɞɵ ɜ ɫɨɫɬɨɹɧɢɢ ɠɢɞɤɨɫɬɢ ɪɚɜɟɧ

1,07610

–5

ɫɦ

/ɫ. Ɍɨɝɞɚ ɫɪɟɞɧɹɹ ɞɥɢɧɚ ɫɜɨɛɨɞɧɨɝɨ ɩɪɨɛɟɝɚ ɦɨɥɟɤɭɥ ɜɨɞɵ

ɜ ɩɚɪɨɨɛɪɚɡɧɨɦ ɫɨɫɬɨɹɧɢɢ ɨɰɟɧɢɜɚɟɬɫɹ ɤɚɤ 0,158 ɫɦ, ɚ ɫɪɟɞɧɹɹ ɞɥɢɧɚ

ɫɜɨɛɨɞɧɨɝɨ ɩɪɨɛɟɝɚ ɦɨɥɟɤɭɥ ɜɨɞɵ ɜ ɠɢɞɤɨɦ ɫɨɫɬɨɹɧɢɢ – ɤɚɤ

6,1510

–6

ɫɦ. Ⱦɢɚɦɟɬɪ ɦɨɥɟɤɭɥɵ ɜɨɞɵ ɪɚɜɟɧ 3,510

–8

ɫɦ. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ,

ɆɨɞɌ-03 Ⱦɜɢɠɟɧɢɟ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ

167

ɫɪɟɞɧɹɹ ɞɥɢɧɚ ɫɜɨɛɨɞɧɨɝɨ ɩɪɨɛɟɝɚ ɦɨɥɟɤɭɥɵ ɜɨɞɵ ɜ ɠɢɞɤɨɫɬɢ ɜ

1,7610

ɪɚɡɚ ɛɨɥɶɲɟ ɟɟ ɞɢɚɦɟɬɪɚ, ɚ ɜ ɝɚɡɟ – ɜ 4,5310

ɪɚɡɚ.

Ɇɚɫɫɚ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɦɧɨɝɨ ɛɨɥɶɲɟ ɦɚɫɫɵ ɦɨɥɟɤɭɥɵ ɠɢɞ-

ɤɨɫɬɢ ɢɥɢ ɝɚɡɚ. ɉɨɷɬɨɦɭ ɫɪɟɞɧɹɹ ɫɤɨɪɨɫɬɶ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɦɧɨɝɨ

ɦɟɧɶɲɟ ɫɪɟɞɧɟɣ ɫɤɨɪɨɫɬɢ ɦɨɥɟɤɭɥ ɫɪɟɞɵ, ɜ ɤɨɬɨɪɨɣ ɨɧɚ ɧɚɯɨɞɢɬɫɹ.

ɉɨɫɤɨɥɶɤɭ ɩɥɨɳɚɞɶ ɩɨɜɟɪɯɧɨɫɬɢ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɞɨɜɨɥɶɧɨ

ɡɧɚɱɢɬɟɥɶɧɚɹ, ɟɟ ɫɬɨɥɤɧɨɜɟɧɢɹ ɫ ɦɨɥɟɤɭɥɚɦɢ ɨɤɪɭɠɚɸɳɟɣ ɫɪɟɞɵ ɜɟɫɶɦɚ

ɱɚɫɬɵ, ɬɨ ɫɥɟɞɭɟɬ ɨɠɢɞɚɬɶ, ɱɬɨ ɫɪɟɞɧɹɹ ɞɥɢɧɚ ɫɜɨɛɨɞɧɨɝɨ ɩɪɨɛɟɝɚ

ɬɚɤɨɣ

ɱɚɫɬɢɰɵ ɛɭɞɟɬ ɧɟ ɜɟɥɢɤɚ.

Ɂɧɚɹ ɩɨɫɬɨɹɧɧɭɸ Ȼɨɥɶɰɦɚɧɚ, ɬɟɦɩɟɪɚɬɭɪɭ ɫɪɟɞɵ, ɩɥɨɬɧɨɫɬɶ ɢ

ɞɢɚɦɟɬɪ ɱɚɫɬɢɰɵ, ɦɨɠɧɨ ɨɰɟɧɢɬɶ ɫɪɟɞɧɸɸ ɫɤɨɪɨɫɬɶ ɢ ɫɪɟɞɧɸɸ ɞɥɢɧɭ

ɫɜɨɛɨɞɧɨɝɨ ɩɪɨɛɟɝɚ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ.

2. Ɇɨɞɟɥɶ ɷɤɫɩɟɪɢɦɟɧɬɚɥɶɧɨɣ ɭɫɬɚɧɨɜɤɢ

ȼ ɞɚɧɧɨɣ ɪɚɛɨɬɟ ɫ ɩɨɦɨɳɶɸ ɫɪɟɞɫɬɜ ɤɨɦɩɶɸɬɟɪɧɨɣ ɝɪɚɮɢɤɢ ɦɨ-

ɞɟɥɢɪɭɟɬɫɹ ɩɪɨɰɟɫɫ ɞɜɢɠɟɧɢɹ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɜ ɜɹɡɤɨɣ ɫɪɟɞɟ. Ɉɬ

ɜɹɡɤɨɫɬɢ ɢ ɬɟɦɩɟɪɚɬɭɪɵ ɫɪɟɞɵ ɡɚɜɢɫɢɬ, ɤɚɤ ɢɧɬɟɧɫɢɜɧɨ ɛɭɞɟɬ ɞɜɢɝɚɬɶɫɹ

ɱɚɫɬɢɰɚ ɢ ɧɚ ɤɚɤɨɟ ɪɚɫɫɬɨɹɧɢɟ ɨɧɚ ɫɦɟɫɬɢɬɫɹ ɡɚ ɜɪɟɦɹ ɷɤɫɩɟɪɢɦɟɧɬɚ.

Ɍɟɦɩɟɪɚɬɭɪɚ ɫɪɟɞɵ ɦɨɠɟɬ ɢɡɦɟɧɹɬɶɫɹ ɜ ɢɧɬɟɪɜɚɥɟ ɨɬ ɬɨɱɤɢ ɡɚɬɜɟɪɞɟɜɚ-

ɧɢɹ ɞɨ ɬɨɱɤɢ ɤɢɩɟɧɢɹ. Ⱦɥɢɬɟɥɶɧɨɫɬɶ

ɷɤɫɩɟɪɢɦɟɧɬɚ ɦɨɠɧɨ ɪɟɝɭɥɢɪɨɜɚɬɶ

ɫ ɲɚɝɨɦ 5 ɫ. ȼ ɷɤɫɩɟɪɢɦɟɧɬɟ ɦɨɝɭɬ ɭɱɚɫɬɜɨɜɚɬɶ ɫɮɟɪɢɱɟɫɤɢɟ ɱɚɫɬɢɰɵ

ɪɚɡɥɢɱɧɨɝɨ ɞɢɚɦɟɬɪɚ (ɨɬ 0,5 ɞɨ 2,5 ɦɤɦ). X ɢ Y ɤɨɨɪɞɢɧɚɬɵ ɱɚɫɬɢɰɵ

ɦɨɠɧɨ ɢɡɦɟɪɹɬɶ ɫ ɬɨɱɧɨɫɬɶɸ 0,2 ɦɤɦ. ɉɪɢ ɡɚɞɚɧɧɵɯ ɭɫɥɨɜɢɹɯ ɩɨɝɪɟɲ-

ɧɨɫɬɶ ɨɩɪɟɞɟɥɟɧɢɹ ɩɨɫɬɨɹɧɧɨɣ Ȼɨɥɶɰɦɚɧɚ ɧɟ ɩɪɟɜɵɲɚɟɬ 1%.

Ɋɚɛɨɬɚ ɜɵɩɨɥɧɹɟɬɫɹ ɧɚ IBM-ɫɨɜɦɟɫɬɢɦɨɦ ɩɟɪɫɨɧɚɥɶɧɨɦ ɤɨɦɩɶɸ-

ɬɟɪɟ ɜ ɜɢɞɟ ɫɚɦɨɫɬɨɹɬɟɥɶɧɨɝɨ Windows-ɩɪɢɥɨɠɟɧɢɹ. Ⱦɥɹ ɭɞɨɛɫɬɜɚ ɜɵ-

ɩɨɥɧɟɧɢɹ

ɪɚɛɨɬɵ ɜ ɩɪɨɝɪɚɦɦɟ ɩɪɟɞɭɫɦɨɬɪɟɧɵ ɬɪɢ ɪɚɡɞɟɥɚ: ɤɪɚɬɤɨɟ ɨɩɢ-

ɫɚɧɢɟ ɪɚɛɨɬɵ; ɩɨɪɹɞɨɤ ɜɵɩɨɥɧɟɧɢɹ ɪɚɛɨɬɵ ɢ ɷɤɫɩɟɪɢɦɟɧɬ. ɉɟɪɟɤɥɸɱɟ-

ɧɢɟ ɦɟɠɞɭ ɪɚɡɞɟɥɚɦɢ ɨɫɭɳɟɫɬɜɥɹɟɬɫɹ ɫ ɩɨɦɨɳɶɸ ɤɧɨɩɨɤ «ɏɨɞ ɪɚɛɨɬɵ»

ɢ «ɗɤɫɩɟɪɢɦɟɧɬ». ɇɚɠɚɬɢɟ ɷɬɢɯ ɤɧɨɩɨɤ ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɤɨɧɬɟɤɫɬɚ ɪɚ-

ɛɨɬɵ ɩɪɨɝɪɚɦɦɵ ɩɪɢɜɨɞɢɬ ɥɢɛɨ ɤ ɜɵɡɨɜɭ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɪɚɡɞɟɥɨɜ,

ɥɢɛɨ ɤ ɜɨɡɜɪɚɳɟɧɢɸ ɜ ɪɚɡɞɟɥ ɨɩɢɫɚɧɢɹ.

Ɏɢɡɢɤɚ ɠɢɞɤɨɫɬɟɣ ɢ ɝɚɡɨɜ

168

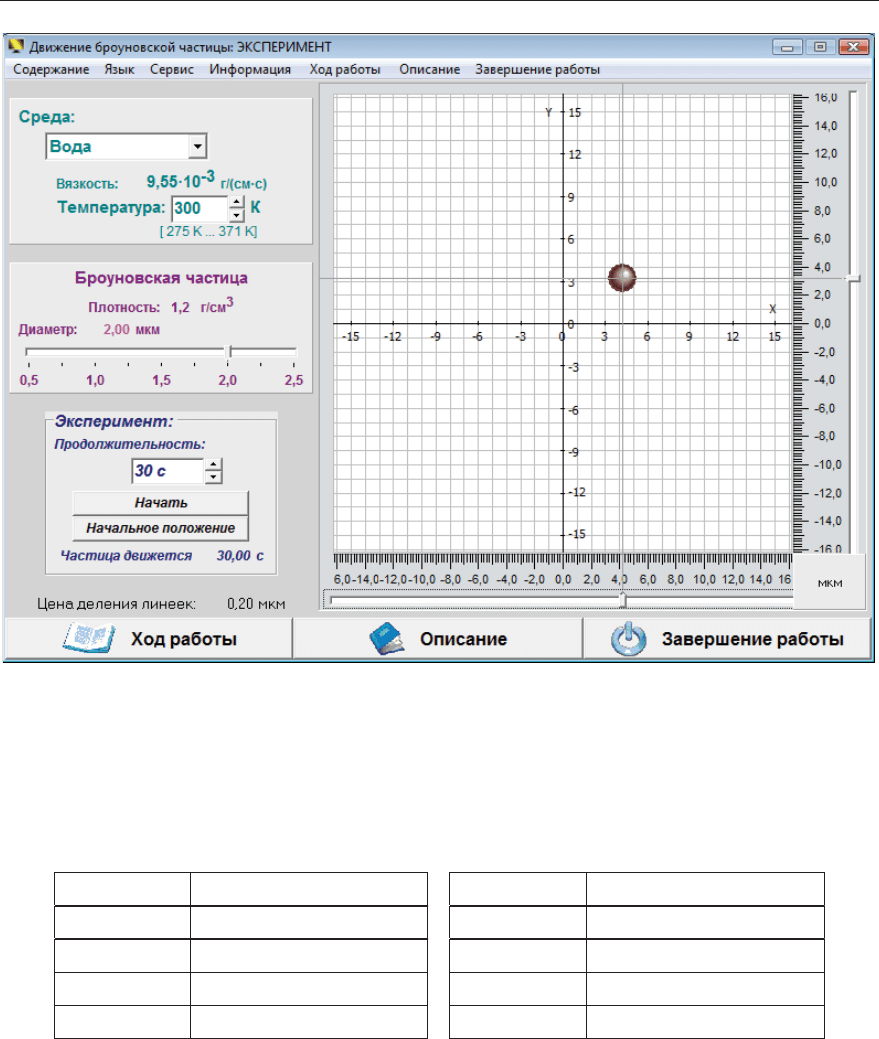
Ɋɚɡɞɟɥ ɩɪɨɝɪɚɦɦɵ «ɗɤɫɩɟɪɢɦɟɧɬ» ɫɨɞɟɪɠɢɬ ɪɚɫɤɪɵɜɚɸɳɢɣɫɹ

ɫɩɢɫɨɤ ɞɥɹ ɜɵɛɨɪɚ ɫɪɟɞɵ, ɫɱɟɬɱɢɤɢ ɞɥɹ ɢɡɦɟɧɟɧɢɹ ɬɟɦɩɟɪɚɬɭɪɵ ɫɪɟɞɵ ɢ

ɞɥɢɬɟɥɶɧɨɫɬɢ ɷɤɫɩɟɪɢɦɟɧɬɚ, ɩɨɥɡɭɧɨɤ ɩɪɨɤɪɭɬɤɢ ɞɥɹ ɜɵɛɨɪɚ ɞɢɚɦɟɬɪɚ

ɱɚɫɬɢɰɵ, ɚ ɬɚɤɠɟ ɜɫɩɨɦɨɝɚɬɟɥɶɧɵɟ ɤɧɨɩɤɢ, ɩɨɡɜɨɥɹɸɳɢɟ ɭɩɪɚɜɥɹɬɶ

ɷɤɫɩɟɪɢɦɟɧɬɨɦ.

ȼɚɪɢɚɧɬɵ ɜɵɩɨɥɧɟɧɢɹ ɪɚɛɨɬɵ

ȼɚɪɢɚɧɬ ɋɪɟɞɚ ȼɚɪɢɚɧɬ ɋɪɟɞɚ

1. Ⱥɧɢɥɢɧ 5. ȼɨɞɚ

2. Ȼɭɬɢɥɨɜɵɣ ɫɩɢɪɬ 6. Ȼɟɧɡɨɥ

3. ɉɪɨɩɚɧɨɥ 7. Ɇɟɬɚɧɨɥ

4. ɗɬɢɥɨɜɵɣ ɫɩɢɪɬ 8. Ⱥɰɟɬɨɧ

3. ɉɨɪɹɞɨɤ ɜɵɩɨɥɧɟɧɢɹ ɪɚɛɨɬɵ

3.1. Ʉɪɚɬɤɨɟ ɨɩɢɫɚɧɢɟ ɯɨɞɚ ɪɚɛɨɬɵ

1. ȼɵɛɟɪɢɬɟ ɫɪɟɞɭ (ɩɨ ɭɤɚɡɚɧɢɸ ɩɪɟɩɨɞɚɜɚɬɟɥɹ).

ɆɨɞɌ-03 Ⱦɜɢɠɟɧɢɟ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ

169

ɋɟɪɢɹ ɷɤɫɩɟɪɢɦɟɧɬɨɜ ʋ 1. ɑɚɫɬɢɰɚ ɛɨɥɶɲɨɝɨ ɞɢɚɦɟɬɪɚ ɩɪɢ

ɜɵɫɨɤɨɣ ɬɟɦɩɟɪɚɬɭɪɟ.

2. Ɂɚɞɚɣɬɟ ɬɟɦɩɟɪɚɬɭɪɭ ɫɪɟɞɵ.

3. Ɂɚɞɚɣɬɟ ɞɢɚɦɟɬɪ ɱɚɫɬɢɰɵ.

4. Ɂɚɞɚɣɬɟ ɞɥɢɬɟɥɶɧɨɫɬɶ ɷɤɫɩɟɪɢɦɟɧɬɚ ɪɚɜɧɨɣ 15 ɫ.

5. ȼɵɩɨɥɧɢɬɟ ɷɤɫɩɟɪɢɦɟɧɬ.

6. ɂɡɦɟɪɶɬɟ X- ɢ Y-ɤɨɨɪɞɢɧɚɬɵ ɱɚɫɬɢɰɵ.

7. ɉɨɜɬɨɪɢɬɟ ɷɤɫɩɟɪɢɦɟɧɬ 12–15 ɪɚɡ, ɧɚɱɢɧɚɹ ɫ ɩɭɧɤɬɚ 5.

8. Ⱦɥɹ ɤɚɠɞɨɝɨ ɷɤɫɩɟɪɢɦɟɧɬɚ ɜɵɱɢɫɥɢɬɟ ɤɜɚɞɪɚɬ ɫɦɟɳɟɧɢɹ ɛɪɨ-

ɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ.

9. ȼɵɱɢɫɥɢɬɟ ɫɪɟɞɧɢɣ ɤɜɚɞɪɚɬ ɫɦɟɳɟɧɢɹ.

10.

ȼɵɱɢɫɥɢɬɟ ɤɨɷɮɮɢɰɢɟɧɬ ɞɢɮɮɭɡɢɢ ɢ ɩɨɫɬɨɹɧɧɭɸ Ȼɨɥɶɰɦɚɧɚ.

11. ɉɨɜɬɨɪɢɬɟ ɷɤɫɩɟɪɢɦɟɧɬ ɞɥɹ ɞɥɢɬɟɥɶɧɨɫɬɢ ɷɤɫɩɟɪɢɦɟɧɬɚ 30 ɢ

45 ɫ, ɧɚɱɢɧɚɹ ɫ ɩɭɧɤɬɚ 5.

12. ȼɵɱɢɫɥɢɬɟ ɫɪɟɞɧɟɟ ɡɧɚɱɟɧɢɟ ɤɨɷɮɮɢɰɢɟɧɬɚ ɞɢɮɮɭɡɢɢ ɢ ɩɨ-

ɫɬɨɹɧɧɨɣ Ȼɨɥɶɰɦɚɧɚ.

13. ȼɵɱɢɫɥɢɬɟ ɫɪɟɞɧɸɸ ɫɤɨɪɨɫɬɶ ɢ ɞɥɢɧɭ ɫɜɨɛɨɞɧɨɝɨ ɩɪɨɛɟɝɚ.

ɋɟɪɢɹ ɷɤɫɩɟɪɢɦɟɧɬɨɜ ʋ 2. ɑɚɫɬɢɰɚ ɛɨɥɶɲɨɝɨ ɞɢɚɦɟɬɪɚ ɩɪɢ

ɧɢɡɤɨɣ ɬɟɦɩɟɪɚɬɭɪɟ.

14. Ɂɚɞɚɣɬɟ ɬɟɦɩɟɪɚɬɭɪɭ ɫɪɟɞɵ.

15. Ɂɚɞɚɣɬɟ ɞɢɚɦɟɬɪ ɱɚɫɬɢɰɵ.

16.

ɉɨɜɬɨɪɢɬɟ ɷɤɫɩɟɪɢɦɟɧɬɵ ɫ ɩɭɧɤɬɚ 4 ɩɨ ɩɭɧɤɬ 13.

ɋɟɪɢɹ ɷɤɫɩɟɪɢɦɟɧɬɨɜ ʋ 3. ɑɚɫɬɢɰɚ ɦɚɥɨɝɨ ɞɢɚɦɟɬɪɚ ɩɪɢ ɧɢɡ-

ɤɨɣ ɬɟɦɩɟɪɚɬɭɪɟ.

17. Ɂɚɞɚɣɬɟ ɬɟɦɩɟɪɚɬɭɪɭ ɫɪɟɞɵ.

18. Ɂɚɞɚɣɬɟ ɞɢɚɦɟɬɪ ɱɚɫɬɢɰɵ.

19. ɉɨɜɬɨɪɢɬɟ ɷɤɫɩɟɪɢɦɟɧɬɵ ɫ ɩɭɧɤɬɚ 4 ɩɨ ɩɭɧɤɬ 13.

20. ɉɨɫɬɪɨɣɬɟ ɝɪɚɮɢɤɢ ɡɚɜɢɫɢɦɨɫɬɢ ɫɪɟɞɧɟɝɨ ɤɜɚɞɪɚɬɚ ɫɦɟɳɟɧɢɹ

ɱɚɫɬɢɰɵ ɨɬ ɜɪɟɦɟɧɢ ɧɚɛɥɸɞɟɧɢɹ.

21. ȼɵɱɢɫɥɢɬɟ ɫɪɟɞɧɟɟ ɡɧɚɱɟɧɢɟ ɩɨɫɬɨɹɧɧɨɣ Ȼɨɥɶɰɦɚɧɚ.

22. ɋɞɟɥɚɣɬɟ ɜɵɜɨɞɵ.

23. ɋɞɟɥɚɣɬɟ ɢ

ɨɛɨɫɧɭɣɬɟ ɩɪɨɝɧɨɡ: ɤɚɤ ɛɭɞɟɬ ɞɜɢɝɚɬɶɫɹ ɱɚɫɬɢɰɚ

ɦɚɥɨɝɨ ɞɢɚɦɟɬɪɚ ɩɪɢ ɜɵɫɨɤɨɣ ɬɟɦɩɟɪɚɬɭɪɟ.

3.2. ɉɨɞɪɨɛɧɨɟ ɨɩɢɫɚɧɢɟ ɯɨɞɚ ɪɚɛɨɬɵ

ɉɪɢ ɜɵɩɨɥɧɟɧɢɢ ɪɚɛɨɬɵ ɪɟɤɨɦɟɧɞɭɟɬɫɹ ɫɥɟɞɭɸɳɚɹ ɩɨɫɥɟɞɨɜɚ-

ɬɟɥɶɧɨɫɬɶ ɞɟɣɫɬɜɢɣ:

Ɏɢɡɢɤɚ ɠɢɞɤɨɫɬɟɣ ɢ ɝɚɡɨɜ

170

1. Ɋɚɫɤɪɵɜɚɸɳɢɣɫɹ ɫɩɢɫɨɤ «ɋɪɟɞɚ» ɫɨɞɟɪɠɢɬ ɧɚɛɨɪ ɠɢɞɤɨɫɬɟɣ, ɨɛɥɚɞɚɸ-

ɳɢɯ ɪɚɡɥɢɱɧɵɦɢ ɜɹɡɤɨɫɬɹɦɢ: ɚɧɢɥɢɧ, ɛɭɬɢɥɨɜɵɣ ɫɩɢɪɬ, ɩɪɨɩɚɧɨɥ, ɷɬɢɥɨɜɵɣ ɫɩɢɪɬ,

ɜɨɞɚ, ɛɟɧɡɨɥ, ɦɟɧɬɨɥ, ɚɰɟɬɨɧ. ȼɵɛɟɪɢɬɟ ɠɢɞɤɨɫɬɶ, ɜ ɤɨɬɨɪɨɣ ɛɭɞɟɬ ɩɪɨɯɨɞɢɬɶ ɷɤɫ-

ɩɟɪɢɦɟɧɬ (ɩɨ ɭɤɚɡɚɧɢɸ ɩɪɟɩɨɞɚɜɚɬɟɥɹ). Ⱦɥɹ ɜɵɛɪɚɧɧɨɣ ɫɪɟɞɵ ɩɨɞ ɫɩɢɫɤɨɦ ɚɜɬɨɦɚ-

ɬɢɱɟɫɤɢ ɭɤɚɡɵɜɚɟɬɫɹ ɟɟ ɜɹɡɤɨɫɬɶ.

ɋɟɪɢɹ ɷɤɫɩɟɪɢɦɟɧɬɨɜ ʋ 1. ɑɚɫɬɢɰɚ ɛɨɥɶɲɨɝɨ ɞɢɚɦɟɬɪɚ ɩɪɢ ɜɵɫɨɤɨɣ

ɬɟɦɩɟɪɚɬɭɪɟ.

ȼ ɞɚɧɧɨɣ ɫɟɪɢɢ ɷɤɫɩɟɪɢɦɟɧɬɨɜ ɧɟɨɛɯɨɞɢɦɨ ɢɡɭɱɢɬɶ ɡɚɜɢɫɢɦɨɫɬɶ ɫɪɟɞɧɟɝɨ

ɫɦɟɳɟɧɢɹ ɱɚɫɬɢɰɵ ɨɬ ɜɪɟɦɟɧɢ ɧɚɛɥɸɞɟɧɢɹ ɞɥɹ ɱɚɫɬɢɰɵ ɛɨɥɶɲɨɝɨ ɞɢɚɦɟɬɪɚ ɩɪɢ ɜɵ-

ɫɨɤɨɣ ɬɟɦɩɟɪɚɬɭɪɟ.

2. Ɍɟɦɩɟɪɚɬɭɪɭ ɫɪɟɞɵ ɦɨɠɧɨ ɢɡɦɟɧɹɬɶ ɜ ɩɪɟɞɟɥɚɯ ɨɬ ɬɨɱɤɢ ɡɚɬɜɟɪɞɟɜɚɧɢɹ ɞɨ

ɬɨɱɤɢ ɤɢɩɟɧɢɹ (ɭ ɤɚɠɞɨɣ ɠɢɞɤɨɫɬɢ ɫɜɨɣ ɞɢɚɩɚɡɨɧ ɬɟɦɩɟɪɚɬɭɪ, ɩɪɢ ɤɨɬɨɪɨɦ ɞɚɧɧɨɟ

ɜɟɳɟɫɬɜɨ ɧɚɯɨɞɢɬɫɹ ɜ ɠɢɞɤɨɦ ɫɨɫɬɨɹɧɢɢ). ɋ ɩɨɦɨɳɶɸ

ɫɱɟɬɱɢɤɚ «Ɍɟɦɩɟɪɚɬɭɪɚ»

ɜɵɛɟɪɢɬɟ ɜɵɫɨɤɭɸ ɬɟɦɩɟɪɚɬɭɪɭ ɫɪɟɞɵ, ɧɨ ɨɬɥɢɱɚɸɳɭɸɫɹ ɨɬ ɦɚɤɫɢɦɚɥɶɧɨɣ (ɬɨɱɤɢ

ɤɢɩɟɧɢɹ). ɂɧɬɟɪɜɚɥ ɞɨɫɬɭɩɧɵɯ ɬɟɦɩɟɪɚɬɭɪ ɭɤɚɡɚɧ ɩɨɞ ɫɱɟɬɱɢɤɨɦ.

3. Ⱦɢɚɦɟɬɪ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɦɨɠɧɨ ɢɡɦɟɧɹɬɶ ɜ ɩɪɟɞɟɥɚɯ ɨɬ 0,5 ɞɨ

2,5 ɦɤɦ. ɋ ɩɨɦɨɳɶɸ ɛɟɝɭɧɤɚ ɩɪɨɤɪɭɬɤɢ «Ⱦɢɚɦɟɬɪ» ɜɵɛɟɪɢɬɟ ɱɚɫɬɢɰɭ ɛɨɥɶɲɨɝɨ

ɞɢɚɦɟɬɪɚ (ɛɨɥɶɲɟ 1,5 ɦɤɦ). Ɍɨɱɧɨɟ ɡɧɚɱɟɧɢɟ ɜɵɛɪɚɧɧɨɝɨ ɞɢɚɦɟɬɪɚ ɭɤɚɡɵɜɚɟɬɫɹ ɧɚɞ

ɛɟɝɭɧɤɨɦ ɩɪɨɤɪɭɬɤɢ.

4. Ⱦɥɢɬɟɥɶɧɨɫɬɶ ɷɤɫɩɟɪɢɦɟɧɬɚ ɦɨɠɧɨ ɢɡɦɟɧɹɬɶ ɫ ɢɧɬɟɪɜɚɥɨɦ 5 ɫ. ɑɟɦ ɛɨɥɶɲɟ

ɞɥɢɬɟɥɶɧɨɫɬɶ ɷɤɫɩɟɪɢɦɟɧɬɚ, ɬɟɦ ɦɟɧɶɲɟ ɩɨɝɪɟɲɧɨɫɬɶ ɩɨɥɭɱɟɧɧɵɯ ɫ ɟɝɨ ɩɨɦɨɳɶɸ

ɪɟɡɭɥɶɬɚɬɨɜ. ɋ ɩɨɦɨɳɶɸ ɫɱɟɬɱɢɤɚ «ɉɪɨɞɨɥɠɢɬɟɥɶɧɨɫɬɶ» ɧɚ ɩɚɧɟɥɢ ɭɩɪɚɜɥɟɧɢɹ

ɷɤɫɩɟɪɢɦɟɧɬɨɦ «ɗɤɫɩɟɪɢɦɟɧɬ» ɜɵɛɟɪɢɬɟ ɞɥɢɬɟɥɶɧɨɫɬɶ ɷɤɫɩɟɪɢɦɟɧɬɚ ɪɚɜɧɨɣ 15 ɫ.

5. ɇɚɠɦɢɬɟ ɤɧɨɩɤɭ «ɇɚɱɚɬɶ ɷɤɫɩɟɪɢɦɟɧɬ» – ɱɚɫɬɢɰɚ ɧɚɱɧɟɬ ɞɜɢɝɚɬɶɫɹ ɜ ɡɚ-

ɞɚɧɧɵɯ ɭɫɥɨɜɢɹɯ. ȼɨ ɜɪɟɦɹ ɷɤɫɩɟɪɢɦɟɧɬɚ ɧɚ ɩɚɧɟɥɢ ɭɩɪɚɜɥɟɧɢɹ ɷɤɫɩɟɪɢɦɟɧɬɨɦ

ɨɬɨɛɪɚɠɚɟɬɫɹ ɜɪɟɦɹ, ɩɪɨɲɟɞɲɟɟ ɨɬ ɧɚɱɚɥɚ ɷɤɫɩɟɪɢɦɟɧɬɚ. ɗɤɫɩɟɪɢɦɟɧɬ ɡɚɜɟɪɲɢɬɫɹ

ɩɨ ɢɫɬɟɱɟɧɢɢ ɡɚɞɚɧɧɨɝɨ ɜɪɟɦɟɧɢ.

6. ɉɨ ɨɛɟɢɦ ɫɬɨɪɨɧɚɦ ɨɬ ɨɛɥɚɫɬɢ ɷɤɫɩɟɪɢɦɟɧɬɚ, ɜɧɭɬɪɢ ɤɨɬɨɪɨɣ ɞɜɢɠɟɬɫɹ

ɱɚɫɬɢɰɚ, ɪɚɫɩɨɥɨɠɟɧɵ ɢɡɦɟɪɢɬɟɥɶɧɵɟ ɥɢɧɟɣɤɢ. Ʉɚɠɞɚɹ ɢɡ ɥɢɧɟɟɤ ɫɧɚɛɠɟɧɚ ɛɟɝɭɧ-

ɤɨɦ ɩɪɨɤɪɭɬɤɢ ɢ ɢɡɦɟɪɢɬɟɥɶɧɨɣ ɥɢɧɢɟɣ ɞɥɹ ɢɡɦɟɪɟɧɢɹ ɤɨɨɪɞɢɧɚɬ ɱɚɫɬɢɰɵ. ɋ ɩɨ-

ɦɨɳɶɸ ɛɟɝɭɧɤɨɜ ɩɪɨɤɪɭɬɤɢ ɫɨɜɦɟɫɬɢɬɟ ɨɛɟ ɢɡɦɟɪɢɬɟɥɶɧɵɟ

ɥɢɧɢɢ (ɜɟɪɬɢɤɚɥɶɧɭɸ ɢ

ɝɨɪɢɡɨɧɬɚɥɶɧɭɸ) ɫ ɰɟɧɬɪɨɦ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ. ɉɨ ɥɢɧɟɣɤɚɦ ɨɩɪɟɞɟɥɢɬɟ X ɢ Y

ɤɨɨɪɞɢɧɚɬɵ ɱɚɫɬɢɰɵ. Ɉɛɪɚɬɢɬɟ ɜɧɢɦɚɧɢɟ, ɱɬɨ ɰɟɧɚ ɞɟɥɟɧɢɹ ɥɢɧɟɟɤ ɪɚɜɧɚ 0,2 ɦɤɦ.

ɊȿɁɍɅɖɌȺɌɕ ɂɁɆȿɊȿɇɂɃ ɁȺɉɂɒɂɌȿ ȼ ɌȺȻɅɂɐɍ.

7. Ⱦɜɢɠɟɧɢɟ ɱɚɫɬɢɰɵ ɧɨɫɢɬ ɯɚɨɬɢɱɟɫɤɢɣ ɯɚɪɚɤɬɟɪ. ɉɨɷɬɨɦɭ, ɧɚɱɚɜ ɞɜɢɝɚɬɶɫɹ

ɢɡ ɧɚɱɚɥɚ ɤɨɨɪɞɢɧɚɬ, ɱɚɫɬɢɰɚ ɦɨɠɟɬ ɫ ɪɚɜɧɨɣ ɜɟɪɨɹɬɧɨɫɬɶɸ ɞɜɢɝɚɬɶɫɹ ɜ ɥɸɛɨɦ ɧɚ-

ɩɪɚɜɥɟɧɢɢ. Ⱦɥɹ ɩɨɥɭɱɟɧɢɹ

ɧɚɢɛɨɥɟɟ ɞɨɫɬɨɜɟɪɧɵɯ ɪɟɡɭɥɶɬɚɬɨɜ ɩɪɢ ɢɡɭɱɟɧɢɢ ɫɥɭ-

ɱɚɣɧɵɯ ɩɪɨɰɟɫɫɨɜ ɧɟɨɛɯɨɞɢɦɨ ɩɪɨɜɨɞɢɬɶ ɤɚɤ ɦɨɠɧɨ ɛɨɥɶɲɟɟ ɤɨɥɢɱɟɫɬɜɨ ɷɤɫɩɟɪɢ-

ɦɟɧɬɨɜ. ɉɨɜɬɨɪɢɬɟ ɷɤɫɩɟɪɢɦɟɧɬ 12-15 ɪɚɡ, ɧɚɱɢɧɚɹ ɫ ɩɭɧɤɬɚ 5, ɪɟɡɭɥɶɬɚɬɵ ɢɡɦɟɪɟ-

ɧɢɣ ɡɚɩɢɲɢɬɟ ɜ ɬɚɛɥɢɰɭ.

8. Ȼɪɨɭɧɨɜɫɤɚɹ ɱɚɫɬɢɰɚ ɜ ɤɚɠɞɨɦ ɨɩɵɬɟ ɧɚɱɢɧɚɟɬ ɞɜɢɠɟɧɢɟ ɢɡ ɧɚɱɚɥɚ ɤɨɨɪ-

ɞɢɧɚɬ. ɉɨɷɬɨɦɭ ɤɜɚɞɪɚɬ ɫɦɟɳɟɧɢɹ ɱɚɫɬɢɰɵ ɪɚɜɟɧ r

= x

+ y

9. ɑɬɨɛɵ ɜɵɱɢɫɥɢɬɶ ɫɪɟɞɧɢɣ ɤɜɚɞɪɚɬ ɫɦɟɳɟɧɢɹ <r

>, ɧɟɨɛɯɨɞɢɦɨ ɫɥɨɠɢɬɶ

ɜɫɟ ɩɨɥɭɱɟɧɧɵɟ ɡɧɚɱɟɧɢɹ ɤɜɚɞɪɚɬɨɜ ɫɦɟɳɟɧɢɹ ɢ ɪɚɡɞɟɥɢɬɶ ɷɬɭ ɫɭɦɦɭ ɧɚ ɤɨɥɢɱɟɫɬɜɨ

ɩɪɨɜɟɞɟɧɧɵɯ ɷɤɫɩɟɪɢɦɟɧɬɨɜ (ɫɪɟɞɧɟɟ ɚɪɢɮɦɟɬɢɱɟɫɤɨɟ).