Поклонский Н.А. и др. Полупроводники: основные понятия

Подождите немного. Документ загружается.

ние интерференции электронных волн при рассеянии на упоря-

доченно расположенных атомах). Прыжковая электропровод-

ность доминирует в области температур и степеней неупорядо-

ченности кристалла, когда время “оседлой” жизни носителя за-

ряда в локализованном состоянии (на дефекте) гораздо больше

времени “пролета” между дефектами. Иногда выделяю т еще один

механизм электропроводности — скачковый (jumping) — в амор-

фных материалах, когда уровень Ферми расположен вблизи од-

ного из краев подвижности (для электронов или дырок), где со-

сто яния в значительной мере уже делокализованы, но отсутствует

фазовая когерентность при переходе электрона (дырки) от атома

к атому.

# Механизм электропереноса в молекулярных кристаллах мо-

жет быть когерентным (зонным) и

или некогерентным (прыж-

ковым), в зависимости от взаимодействия электрона проводи-

мости с фононами (решеткой, в каждом узле которой находится

молекула). Если время перехода электрона от узла к узлу решет-

ки τ

меньше периода ее акустиче ских (межмолекулярных) ко-

лебаний τ

и периода оптических (внутримолекулярных) коле-

баний τ

, то движение электрона будет зонным. При этом движе-

ние электрона является столь быстрым, что колебательное дви-

жение атомов можно рассматривать как стационарное, являю-

щееся лишь возмущением поступательного движения электро-

на, который можно рассматривать как волну, успевающую до

рассеяния миновать несколько узлов решетки. Если τ

< τ

то за период внутримолекулярного колебания электрон движет-

ся в окре стности одного узла решетки, поэтому ионные остовы,

ближайшие к этому узлу, успевают сместиться в новое положе-

ние, что ведет к образованию “полярона”, движение которого по

узлам решетки будет прыжковым. В зависимости от соотноше-

ния между шириной зоны проводимости (зоной свободного дви-

жения) E

≈ h

и энергией по ляризации U

возникают поляро-

ны большого радиуса, в которых область локализации электрона

в поляронной потенциальной яме охватыв ает мног о узлов решет-

ки (при E

>> |U

|), или поляроны малого радиуса, в которых эта

область охватывает один узел (при E

<< |U

|).

# Если пространство движения элек тронов проводимости и про-

странство локализации равного им числа ионизированных до-

норов не совпадают, то образуется двойной э лектрический слой

(например, в полупроводниковых гетероструктурах).

# Под “порогом подвижности” понимается значение энергии,

при котором локализованные состояния электронов в конденси-

рованной системе сменяются делокализованными. Если энергия

электрона меньше порога подвижности (уровня протекания в

классическом приближении), то электрон может двигаться толь-

ко в ограниченной области пространства (занимаемого системой).

# Амбиполярная диффузия — совместный диффузионный пе-

ренос противоположно заряженных частиц в направлении у мень-

шения (падения) их концентрации.

# Холла эффект — возникновение электрического E

∝ [J

×B]

поля в немагнитном образце с дрейфовым электронным ток ом

плотностью J

, помещенном во внешнее магнитное поле B —

есть результат действия силы Лоренца на поток электронов. В

случае доминирования в образце дырочного тока плотностью J

поле Холла E

∝ [B×J

]. Так называемый спонтанный эффект

Холла наблюдается в образце с намагниченностью M и плотно-

стью тока J: электрическое поле E

∝ [J× M] частью имеет ло-

ренцево происхождение, но в основном связано со спецификой

электронной системы в магнитоупорядоченных материалах. В

частности, в материале, где за намагниченность и электропро-

водность ответственны разные группы частиц, холлово поле E

возникает из-за асимметрии магнитного взаимодействия дрей-

фового потока обладающих спином носителей заряда и ориен-

тированных магнитных моментов ионных остовов.

# Эффект Дембера (или кристалл-фотоэффект) — возникно-

вение электрического поля в однородном неравномерно ос вещен-

ном полупроводнике (при межзонной генерации светом носите-

лей заряда поле Д ембера компенсирует сумму диффузионных

токов электронов и дырок).

# Фото м агнитоэлектрический эффект (Кикоина–Носк ова) —

возникновение электрическог о поля в помещенном в магнитное поле

неравномерно освещенном изотермическом полупроводнике —

проявление действия силы Лоренца на диффузионный поток но-

сителей заряда от освещенной поверхности в глубь образца.

# Зеебека эффект — возникновение электродвижущей силы

(ЭДС) в материале при наличии в нем градиента температуры;

электрическая цепь, состоящая из двух разнородных проводни-

ков, контакты между которыми имеют разную температуру, на-

зывается термопарой. Наблюдая отклонение магнитной стрел-

ки вблизи термопары, Зеебек сделал вывод, что материалы на-

магничиваются благодаря наличию градиента температ уры. Этой

гипотезой он х отел объяснить намагничение Земли как следствие

разности температур между полюсами и экватором.

# Термомагнитный эффект (Риги–Ледюка) — возникновение

в проводнике с градиентом температуры ∇T, помещенном в маг-

нитное поле B, вторичной разности температур, пропорциональ-

ной векторному произведению [B×∇T], — обусловлен искрив-

лением траекторий носителей заряда магнитным полем.

# Пельтье эффект — выделение или поглощение теплоты при

протекании носителей заряда через контакт (спай) двух различ-

ных материалов (теплота пропорциональна плотности электри-

ческого ток а J). Коэффициент Пельтье равен средней энергии,

переносимой одним зарядом при изотермическом установившем-

ся процессе на контакте. Пельтье рассмат ривал результаты сво-

их измерений как доказательство того, что якобы закон Джоуля–

Ленца (выделение теплоты пропорционально J

) справедлив

лишь для электрических токов большой плотности.

# Эффект Томсона — выделение или поглощение тепла, обус-

ловленное взаимодействием потока носителей заряда с градиен-

том температуры в однородно м образце; выделение (поглоще-

ние) теплоты в термоэлектрическом поле.

# Сверхпро во димость материало в в рамках существующих мо-

делей связывается с объединением (в импульсном и

или коорди-

натно м пространствах) делокализованных электронов в пары; на

постоянном токе когерентное коллективное движение пар про-

исходит без диссипации энергии.

# Изотопический эффект в сверхпроводниках электриче-

ства — зависимость температуры перехода металла в сверхпро-

водящее состояние от изотопической массы его атомов.

# Критический ток — значение электрического тока, при кото-

ром происходит разрушение сверхпроводящего состояния.

# В массивном сверхпроводящем кольце с ток ом магнитное

поле, создаваемое током, как раз достаточно для поддержания

тока, который его создает.

# Про межуточное состо яние сверхпроводящего образца — со-

стояние с чередующимися областями нормальной и сверхпрово-

дящей фазы.

# Эффектом Мейснера– Окс енфельда называют свойство

сверхпроводника выталкивать из своей толщи магнитное поле

независимо от того, в каких условиях оно было включено — до

или после перехода в сверхпроводящее состояние. Но в идеаль-

ном проводнике электричества магнитное поле, включенное при

температуре T > T

, т. е. выше температуры T

перехода в состоя-

ние с нулевым сопротивлением, не выталкивалось бы при T < T

(Это следует из уравнений Максвелла). Существование эффекта

Мейснера – Оксенфельда побуждает считать идеальный диамаг-

нетизм и отсутствие электрического сопротивления основны-

ми свойствами сверхпроводящего состояния.

# Теория БКШ (предложена Бардиным, Купером, Шриффе-

ром) — теория св ерхпроводимо сти мета ллов, использующая

представление о межэлектронном притяжении за счет электрон-

фононных взаимодействий.

# Объяснить сверхпроводимость удалось лишь за пределами од-

ноэлектронного приближения, учитывая взаимодействие дело-

кализованных электронов между собой. Средняя кинетическая

энергия (3

5 от энергии Ферми) электронов в металле отнюдь не

велика по сравнению со средней энергией их кулоновского взаи-

модействия. Например, в металлическом серебре концентрация

электронов проводимо сти n ≈ 6⋅10

см

−3

и энергия Ферми

= h

(3π

≈ 5.6 эВ, а e

4πε

≈ 5.6 эВ, где масса элек-

трона считалась равной м ассе э лектрона в вакууме, а относитель-

ная диэлектрическая проницаемость ионных остовов металла —

единице. Таким образом, электроны проводимости в металле об-

разуют “жидкость”.

# Куперовская электронная пара — квазичастица, описываю-

щая связанное состояние двух электронов с противоположно на-

правленными спинами и квазиимпульсами вблизи поверхности

Ферми, обусловленное притяжением электронов через деформи-

руемую ими кристаллическую решетку ионных остовов метал-

ла. В конденсированной системе электроны могут притягивать-

ся (формально это следует даже из обобщенного закона Кулона

4πεr, где ε = ε

— диэлектрическая проницаемость, могу-

щая быть отрицательной). Так как квазиимпульсы электронов в

паре равны по величине и направлены противоположно, то теп-

ловая скорость движения пары как целого равна нулю, а длина

волны — бесконечности. Разрушение сверхпроводящих куперов-

ских пар магнитным полем связано с двумя эффектами: пара-

магнитным и орбитальным. Парамагнитное критическое поле

соответствует “разворачиванию” спинов противоположной ори-

ентации, образующих куперовскую пару в магнитном поле. По-

скольку импульсы элек тронов в куперовской паре противополож-

ны, то в магнитном поле на эти электроны действуют противо-

положно направленные силы Лоренца. В результате само дви-

жение электронов с импульс ами p и −p в магнитном поле приво-

дит к разрушению куперовской пары. Этот механизм подавле-

ния сверхпров одимости называют орбитальным эффектом. Раз-

мер к уперовских пар для сверхпров одников I рода (10

−5

…10

−4

см)

сильно превосходит межат омное (и межэлектронное) расстояние

(10

−8

… 10

−7

см). Поэтому об индивидуальных парах трудно (а

по сути и нельзя говорить); образуется некоторое единое “коге-

рентное” состояние.

# Щель в спектре возбуждения сверхпроводника — область

энергий вблизи поверхности Ферми, в которой отсутствуют эле-

ментарные возбуждения.

# Квазичастицу можно трактовать как элемент беспорядка в си-

стеме с высоким уровнем упорядоченности (корреляции между

состояниями объектов, образующих систему).

# Длина когерентности — расстояние, на котором существен-

но коррелировано движение электронов в сверхпроводнике. Ха-

рактерный размер (длину ког ерентности) куперовской пары мож-

но оценить, исходя из квантово-механического принципа неопре-

деленности. Так, в сверхпроводимости при T ≤ T

, где T

— тем-

пература перехода металла в сверхпроводящее состояние, глав-

ную роль могут играть только электроны с энергиями ≈ k

, от-

считанными от уровня Ферми E

, а эти электроны имеют диапа-

зон значений (квази)импульса, равный δp ≈ k

, где v

= (dE

dp)

— фермиевская скорость. Тогда характерная длина

когерентности δx ≥ h

δp ≈ hv

# Джозефсона эффект стационарный — существование конеч-

ного туннельного сверхпроводящего ток а при нулевой разности

потенциалов между двумя сверхпроводниками, разделенными

несверхпроводящей прослойкой (толщиной несколько наномет-

ров). Если между сверхпроводниками поддерживать постоян-

ную разность потенциалов U, то сверхпроводящая составляю-

щая по лного тока будет осциллировать с круг ов ой частот ой 2eU

# В кристаллическом диэлектрике (изоляторе) имеется энерге-

тическая щель (запрещенная зона) между заполненной электро-

нами v-зоной и пустой c-зоной. Можно было бы ожидать, что

она будет играть такую же роль, как и энергетическая щель над

“замороженным” распределением электронов в сверхпроводни-

ке, т. е. не будет давать электронам возможности покидать рас-

пределение с равным нулю полным импульсом. Почему же изо-

лятор не является сверхпроводником? Из-за того, что в изоля-

торе скорости электронов с наивысшей энергией (наверх у v-зоны)

равны нулю, а в сверхпроводнике — нет, так как щель на повер-

хности Ферми формируется в результате взаимодействия (через

виртуальные фононы) между электронами проводимости с не-

нулевыми скорост ями , и, вследствие этого, электроны могут сме-

щаться относительно решетки ионных остовов. Так как дисси-

пативные потери при движении электронов сверхпроводника

могут происходить лишь порциями, бо

льшими ширины энерге-

тической щели в окрестности поверхности Ферми, потери при

малой скорости дрейфа электронов отсутствуют. Фактически это

и есть сверхпроводящий ток — электрический ток без потерь.

# Андреевское отражение — отражение электронов проводи-

мости и дырок в металле, находящемся в нормальном состоя-

нии, от границы со сверхпроводником. При андреевском отра-

жении электрон с импульсом, большим фермиевского, подхва-

тывает электрон с антипараллельным импульсом, меньшим фер-

миевского, и образует куперовскую пару. В нормальном металле

остается дырка с импульсом, противоположным импульсу под-

хваченного электрона.

# Сверхтекучесть — состояние квантовой жидкости, при кото-

ром она протекает через узкие щели и капилляры без трения.

Жидкий гелий

He становится сверхтекучим ниже температуры

= 2.17 К при давлении его насыщенных паров 38.8

мм

рт.

ст.

(при этом кипение жидко сти внезапно прекращается). Появле-

ние сверхтекучести в жидкости, состоящей из атомов с целым

спином (бозонов), например ат омов

He, связано с переходом при

T < T

значительного числа атомов в состояние с нулевым им-

пульсом (конденсация Бозе–Эйнштейна). Состояние жидкого ге-

лия при T > T

обозначают He

I, при T < T

— He

II. Чтобы испа-

рить один литр He

I, надо примерно в 10

раз меньше тепла, чем

для испарения одного литра воды. He

I в 600 раз более легко сжи-

маемая жидкость, чем H

O. При использовании He

II в качестве

охлаждающего вещества (хладоагента) важную роль играет тон-

кая (около 0.3 нм) пленка сверхтекучего гелия, которая непре-

рывно поднимается вверх по стенкам сосуда, достигает зоны вы-

соких температур и испаряется, увеличивая таким образом по-

тери гелия и ухудшая существующий в криогенной системе ох-

лаждения вакуум. He

II состоит как бы из двух компонент: нор-

мальной и сверхтекучей. Наряду с обычными звуковыми волна-

ми — колебаниями плотности — в He

II возможно распростра-

нение волн температуры, связанное с колебаниями концентра-

ций сверхтекучей и нормальной компонент при сохранении пол-

ной плотности. Эти волны называются вторым звуком.

# Электрический ток в невырожденном полупроводнике куби-

ческой симметрии в отсутствие внешнего магнитного поля

Стационарный ток в изотермических условиях. “Движущие

силы” и потоки (дрейфовая и диффузионная компоненты плотнос-

ти тока) в кристалле с объемными концентрациями делокализован-

ных электронов n и дырок (электронных вакансий) p, дрейфовыми

скоростями v

и v

, подвижностями µ

и µ

, коэффициентами диф-

фузии D

и D

Полная плотность тока электронов J

= J

+ J

и дырок J

= J

+ J

. В равновесии J

+ J

= 0 и D

n /

= D

= k

e, где

T — тепловая энергия.

В переменном во времени электриче ском поле плотность тока

J = J

+ J

+ ε∂E

∂t,

где ε = ε

— диэлектриче ская проницаемость кристаллической

решетки, t — время, E — напряженность электрического поля.

Уравнения непрерывности

∂n

∂t = G

− R

+ ∂(J

∂x; ∂p

∂t = G

− R

− ∂(J

∂x,

где G

, G

; R

, R

— темпы генерации и рекомбинации; если реком-

бинация электронов и дырок происходит в соотношении 1:1 (от-

сутствует захват носителей заряда ловушками, например, то чечны-

ми атомными дефектами решетки), то R

= R

Электро-

статический

потенци ал

Концентрация

электронов,

дырок

Координата x

(x)

= −

dx; dp

p(x)

n(x)

Электрон с зарядом −e

Дырка с зарядом +e

= epv

= epµ

E = σ

= −

Электрон

Дырка

= −env

= enµ

E = σ

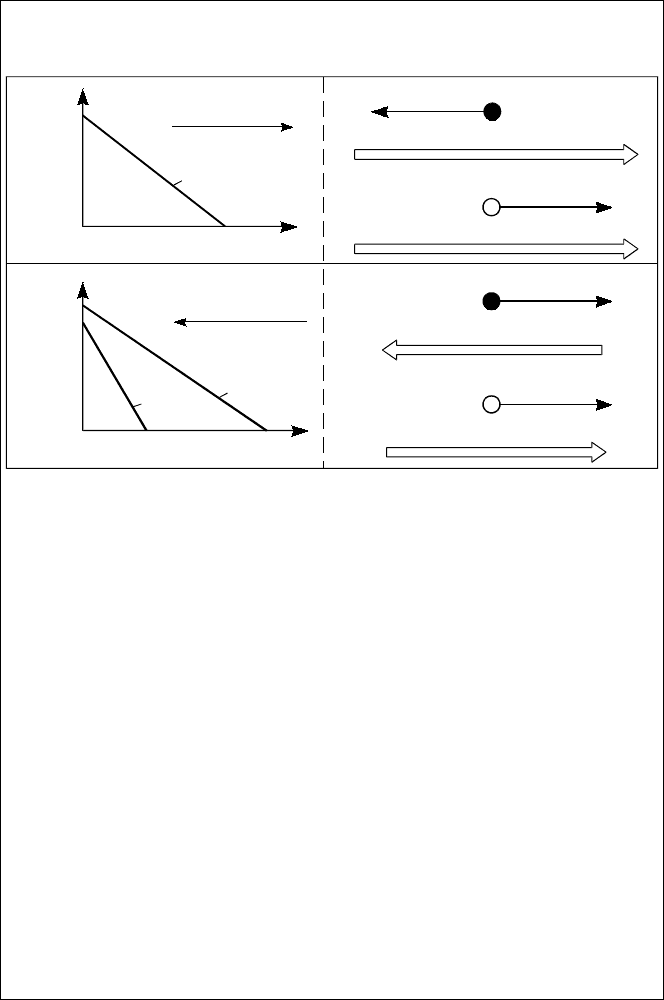
# Зависимость электросопротивления ковалентных и металли-

ческих кристаллов с неподвижными точечными дефектами ре-

шетки от температуры

а) Изменение электросопротивления ρ (в логарифмическом мас-

штабе) ковалентного кристалла с электрически активными дефек-

тами (кривая 1) и без них (2) при нагревании; предполагается, что

энергетические уровни и местоположения дефектов в решетке от

температуры Т не зависят, а их концентрация мала.

б) Изменение электросопротивления нормального (1) и сверх-

проводящего (2) металлов при охлаждении; Т

— температура пе-

рехода в сверхпроводящее состояние. В легированном магнитны-

ми примесями нормальном металле (3) при температуре Кондо Т

достигается минимум ρ(Т); крив ая 4 отражает “замораживание” ло-

кализованных магнитных моментов в как ой-то одной ориентации.

ln ρ

Прыжки электронов (электронных

вакансий) между дефектами

б)

Рост частоты электрон-

фононных столкновений

при нагревании металла

Рассеяние носителей заряда

при полной ионизации дефектов

а)

Переходы электронов из v-зоны в c-зону; энергия

термической активации равна половине ширины

запрещенной зоны (щели)

Переходы электронов (дырок) с энерге-

тических уровней дефектов в c(v)-зону

100

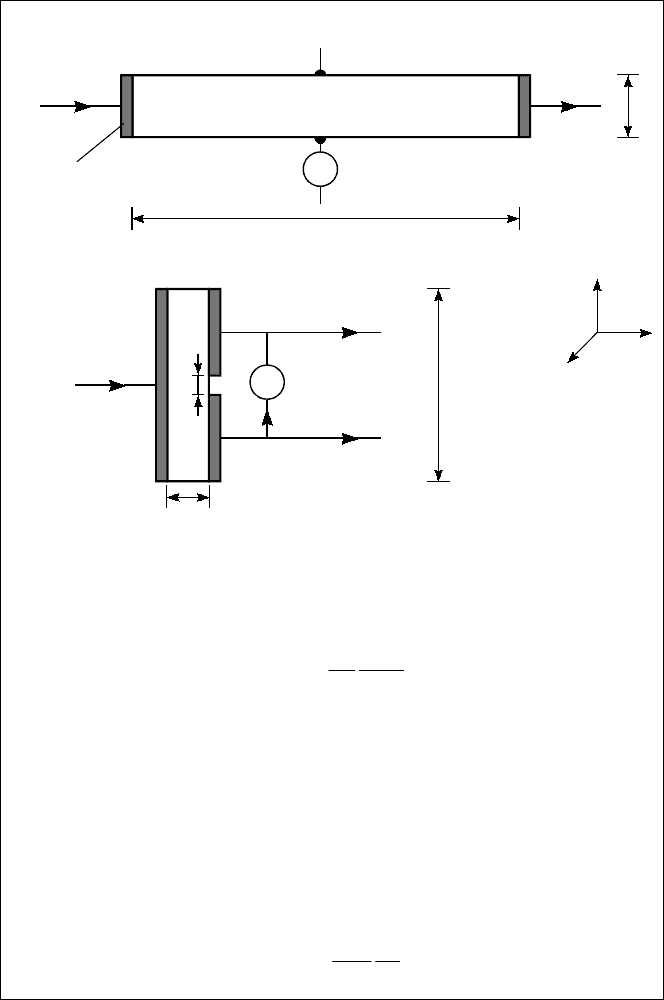
# Классический эффект Холла

а) При измерении ЭДС Холла U

вольтметром V в длинном прямо-

угольном образце (L

>> L

) с разностью потенциалов U

между то-

ковыми электро дами определяем произведение холловской по движ-

ности носителей заряда µ

на магнитную индукцию B

в виде:

=µ

Холловская подвижность µ

= r

⋅µ, где r

— холл-фактор, µ —

дрейфовая подвижность носителей заряда. В сильных магнитных

полях (µB >> 1) и для вырожденных полупроводников r

= 1. Для

полупроводника n-типа |U

| = |R

, где |R

| = r

en — посто-

янная Холла, n — концент рация электронов проводимости, J

= enµE

= enµU

— плотность тока.

б) При измерении тока Холла I

амперметром A в разрыве токо-

вого электрода (δ << L

) в коротком образце (L

<< L

) с дрейфовым

током I

= I

+ I

определяем:

=µ

Кристаллический полупроводник

Холловский контакт

Омический контакт

(токовый электрод)

⊗ B

а)

б)

⊗ B