Плоткин Б.К., Делюкин Л.А. Экономико-математические методы и модели в логистике

Подождите немного. Документ загружается.

МИНИСТЕРСТВО ОБРАЗОВ АНИЯ И НАУКИ РОССИЙСКОЙ ФЕ-

ДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВ АНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ЭКОНОМИКИ И ФИНАНСОВ»

КАФЕДРА КОММЕРЦИИ И ЛОГИСТИКИ

Б.К. ПЛОТКИН

Л.А. ДЕЛЮКИН

ЭКОНОМИКО-

МАТЕМАТИЧЕСКИЕ МЕТОДЫ

И МОДЕЛИ В ЛОГИСТИКЕ

УЧЕБНОЕ ПОСОБИЕ

ИЗДАТЕЛЬСТВО

САНКТ-ПЕТЕРБУРГСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕ-

ТА

ЭКОНОМИКИ И ФИНАНСОВ

2010

ББК 65.40

П 39

Плоткин Б.К., Делюкин Л.А.

Экономико-математические методы и модели в логистике: Учебное

пособие. – СПб.: Изд-во СПбГУЭФ, 2010. – 96 с.

В учебном пособии представлен широкий круг экономико-

математических методов и моделей логистики. Приведены основные понятия о

методах и моделях, используемых в логистике, даётся классификация экономи-

ко-математических моделей логистических процессов и операций. Особое вни-

мание уделено моделям управление запасами, а также моделям логистических

систем массового обслуживания. Излагаются основные положения оптимиза-

ции по Парето.

Рекомендовано студентам, аспирантам и соискателям факультета ком-

мерции и маркетинга, изучающим дисциплины логистического цикла.

Рецензенты: д-р экон. наук, проф. С.Г. Плещиц

канд. экон. наук, проф. В.И. Ченцов

ВВЕДЕНИЕ

Логистика как наука и практическая деятельность стала неотъемле-

мой частью и инструментом современной экономики. По своей сущности

логистика носит универсальный характер, ибо все субъекты интегриро-

ванного рынка занимаются логистикой и используют логистические мето-

ды управления производством и торговлей.

В общем виде логистика определяется как управление потоками в

экономике. Отсюда возникает необходимость логистизации производст-

венно-коммерческой деятельности. Под логистизацией понимается пред-

ставление экономических процессов в виде постоянно циркулирующих

потоков – материальных (товарных), финансовых, информационных, ко-

торые в той или иной форме образуют логистические системы.

Универсальность логистики выражается ещё и в том, что логистиче-

ская система есть субъект интегрированного рынка, который порождает

или через который проходят экономические потоки. Из этого следует, что

любое предприятие – будь то производственное, сферы обслуживания или

торговое – представляет собой логистическую систему.

В таком случае логистика составляет инструментарий управления

производственно-коммерческой деятельностью, в котором используются

специальные концепции логистики и экономико-математические методы.

Применение математики в экономике является одним из важнейших на-

правлений в развитии экономической теории и коммерческой деятельно-

сти, в том числе и логистики. Как в теории, так и в практике логистика

достигла такого уровня, когда применение математических методов стало

не только возможным, но и необходимым.

В настоящем пособии в основном рассматриваются модели и методы

коммерческой логистики, т. е. коммерческие аспекты логистики. Будучи

прикладной экономической наукой нового научно-практического направ-

ления, логистика базируется на положениях экономической теории, кото-

рые в большинстве случаев представлены в математической форме, а по-

этому равным образом должна быть математизированы. Необходимость

применения математики в логистике обусловлена еще и тем, что одним из

принципов логистики является усиление расчетного начала в организации

процессов товародвижения (от древнегреч. logiste – искусство счета). Тем

самым логистика отражает количественную сторону потоковых экономи-

ческих процессов.

Арсенал математических методов в логистике включает широкий

круг разделов математики, а именно:

1. Классический математический анализ.

2. Теория вероятностей.

3. Математическая статистика.

4. Теория массового обслуживания.

5. Математическое (линейное программирование).

6. Теория надежности.

7. Теория игр.

8. Гармонический анализ.

Целью преподавания дисциплины является изучение теоретических

положений и практических вопросов применения экономико-

математических методов и построения математических моделей при орга-

низации и управлении логистическими процессами товародвижения и

производственно-коммерческой деятельности.

Для достижения поставленной цели студенты в результате изучения

дисциплины должны знать теоретические положения построения эконо-

мико-математических моделей, отражающих логистические процессы и

операции с использованием различных методов. Так, в частности, студен-

ты должны отработать практические навыки в применении математиче-

ских методов в моделировании и решении задач по логистике, т. е уметь:

1. Строить математические модели логистики с помощью методов

классического математического анализа.

2. Выводить формулу Уилсона для расчета оптимального размера пар-

тии поставки и других параметров процесса поставок.

3. Представлять процессы логистики в виде элементарных функций с

последующим исследование их на экстремум.

4. Строить графики, иллюстрирующие зависимости и взаимосвязи в

логистике.

5. Выявлять стохастические величины и оценивать вид распределения

вероятностей.

6. Определять тесноту связи между величинами статистических про-

цессов.

7. Строить уравнения регрессии, описывающие логистические процессы.

8. Интерпретировать функционирование объектов в логистике как сис-

тем массового обслуживания.

9. Вычислять параметры систем массового обслуживания в логистиче-

ских процессах.

10. Строить уравнения регрессии, описывающие логистические процессы.

11. Применять компьютерные технологии для решения логистических

задач с помощью математических методов.

Глава 1. ОСНОВНЫЕ ПОНЯТИЯ

ОБ ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДАХ

И МОДЕЛЯХ В ЛОГИСТИКЕ

Логистические потоковые процессы в форме системы товародвиже-

ния на практике образуют следующие блоки:

1) закупки (снабжение);

2) сбыт (продажи);

3) перемещение (транспортировка);

4) складирование (запасы).

Каждое предприятие в силу универсальности логистики – в той или

иной мере выполняет указанные блоки в своей производительно-

коммерческой деятельности. Вследствие чего эти блоки увязываются в

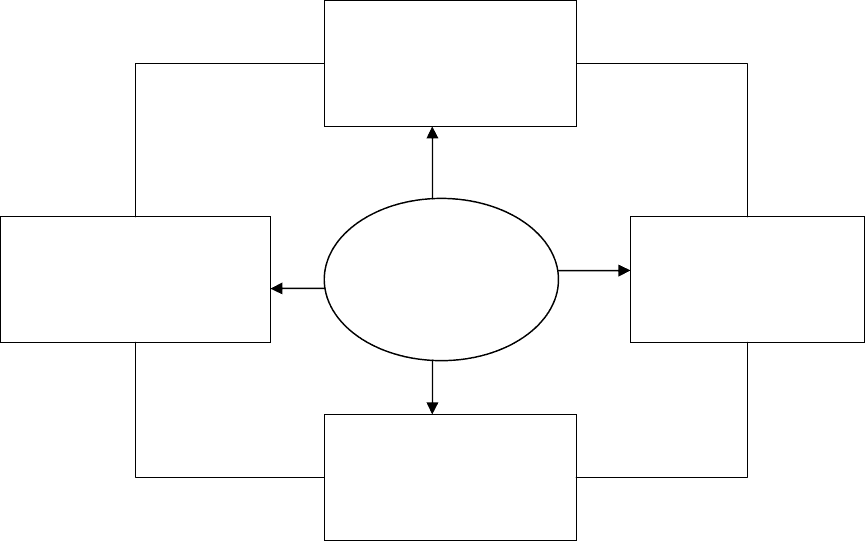
единую систему с помощью управления (рис. 1.1).

Рис. 1.1. Логистический функциональный блок

Как следует из рис. 1.1, управление есть тот инструмент, который

обеспечивает системность логистических процессов и их результатив-

ность, а вместе с этим – результативность производственно-коммерческой

деятельности. Результативность в логистике выражается количественно, а

поэтому управление включает математические методы.

Таким образом, при рассмотрении математических методов и моде-

лей в логистике исходным положением являются теория и практика

Перемещение

(транспортировка)

Складирование

(запасы)

Сбыт

(продажи)

Управление

Закупки

(снабжение)

управления. При этом следует иметь в виду, что в числе величин, которы-

ми оперирует математика в логистике, важное место занимают стоимост-

ные, т. е. экономические, параметры. Именно поэтому в логистике речь

идет об экономико-математических методах и моделях. Так, в частности, в

указанных моделях – в зависимости от моделируемых ситуаций – исполь-

зуются следующие стоимостные параметры:

1) стоимость выполнения заказа (поставки);

2) стоимость содержания единицы запаса за определенный период;

3) постоянные (условно-постоянные) расходы;

4) стоимость перевозки единицы груза;

5) убытки от отказа в обслуживании;

6) убытки от простоя транспортных или иных технических средств;

7) потери от дефицитов товаров.

Перечисленные параметры конкретизируются в зависимости от мо-

делируемых ситуаций.

Кроме того, в ряде моделей, прежде всего динамических, присутст-

вуют временные параметры (интервалы поставок, время хранения запаса,

время транспортировки и т. п.), которые в свою очередь также определяют

стоимостные характеристики логистичеких процессов.

Логистика предусматривает управление движением материальных и

финансовых потоков в цепях поставок. Управление есть комплекс управ-

ляющих воздействий на потоковые процессы, т. е. на логистические про-

цессы и операции (см. рис. 1.1).

В логистике требуется обеспечить прохождение материального по-

тока от начальной до конечной точки его траектории с наименьшими за-

тратами живого и овеществленного труда. Однако для принятия управ-

ленческого решения требуется модель управляемого процесса. Таким об-

разом, модель представляет собой отображение управляемого процесса

или отображение процесса или объекта в целях управления или изучения.

Любое отображение – есть модель.

Модели бывают абстрактные и физические. Физические модели

строятся с помощью физических тел, например в виде макетов. Для по-

строения абстрактных моделей требуется язык, так в частности словесные

описания процесса или объекта будут его моделью. Такие модели назы-

ваются вербальными. Вербальные модели недостаточно точно

отображают моделируемый объект, что обусловлено объективными

свой-

ствами обычного живого языка.

Качество модели характеризуется ее адекватностью, т. е. степенью

приближения к реальному процессу или объекту. Максимальной адекват-

ностью обладают математические модели, т. е. модели, построенные с по-

мощью математического языка. В данном случае математический язык

объективно является точным и лаконичным.

Математические модели отображают процесс или объект с помощью

математической символики, что дает основание говорить о математиче-

ской орфографии. Такие модели, как правило, имеют иллюстративный ха-

рактер.

В современных условиях логистические процессы могут быть также

выражены с помощью массива цифр при использовании компьютерных

технологий. Цифровые компьютерные модели также входят в разряд ма-

тематических моделей, поскольку отражают количественную сторону

логистических процессов. Классификация моделей представлена на

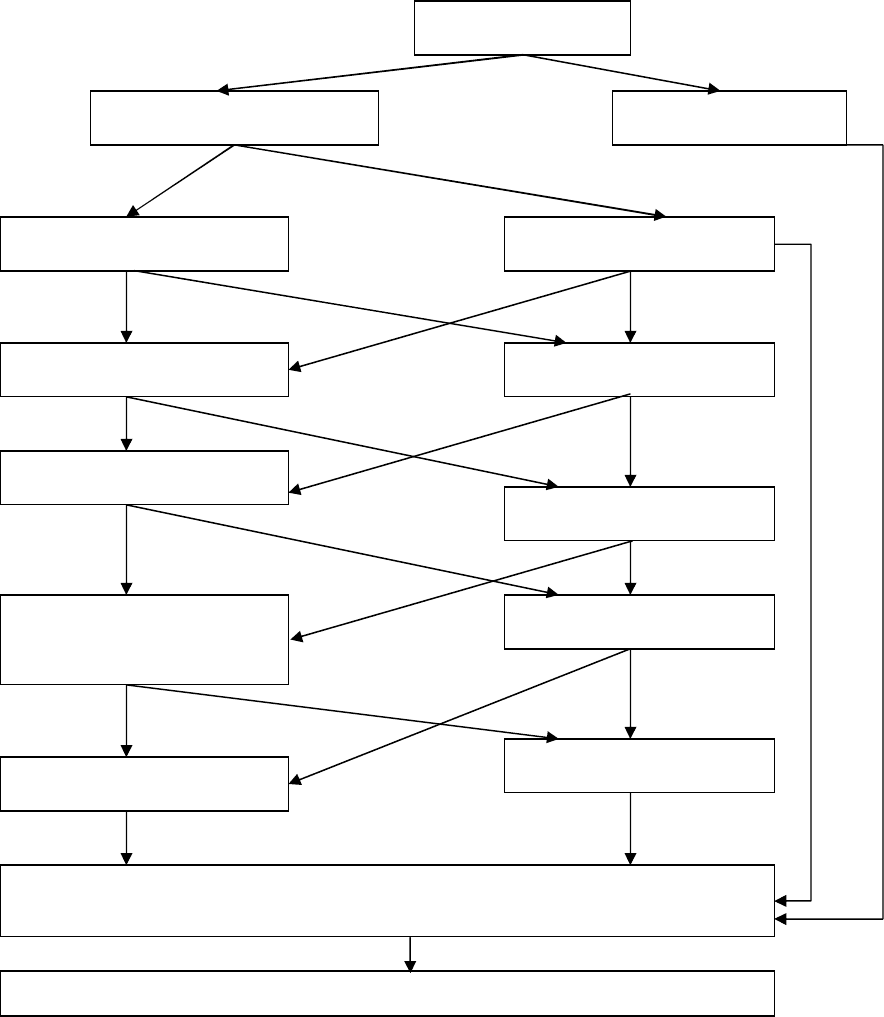
рис. 1.2.

Рис. 1.2. Классификация экономико-математических моделей

в логистике

Модели

Расчетные

(оптимизационные)

Однофакторные

Детерминированные

Аналитические

Математические

Потоков

Вербальные

Числовые

Стохастические

Многофакторные

Иллюстрированные

Запасов

Производственно-коммерческая деятельность

Товародвижение

В приведенной классификации следует обратить внимание на группу

расчетных моделей, которые по своей сущности являются оптимизацион-

ными. Данное утверждение обосновывается тем, что модели указанной

группы имеют целью получения наилучшего, т. е. оптимального результата.

Математическая модель предопределяет и методы решения. Любая

модель в той или иной форме содержит целевую функцию и ограничения.

Поэтому модель может интерпретироваться как задача, в которой даны

исходные данные и требуется определить значение искомых величин. На-

хождение этих величин и определяет метод решения задачи для построен-

ной модели. Методы могут интерпретироваться как модели, доведенные

до численного результата. В логистике в ряде случаев методы и модели

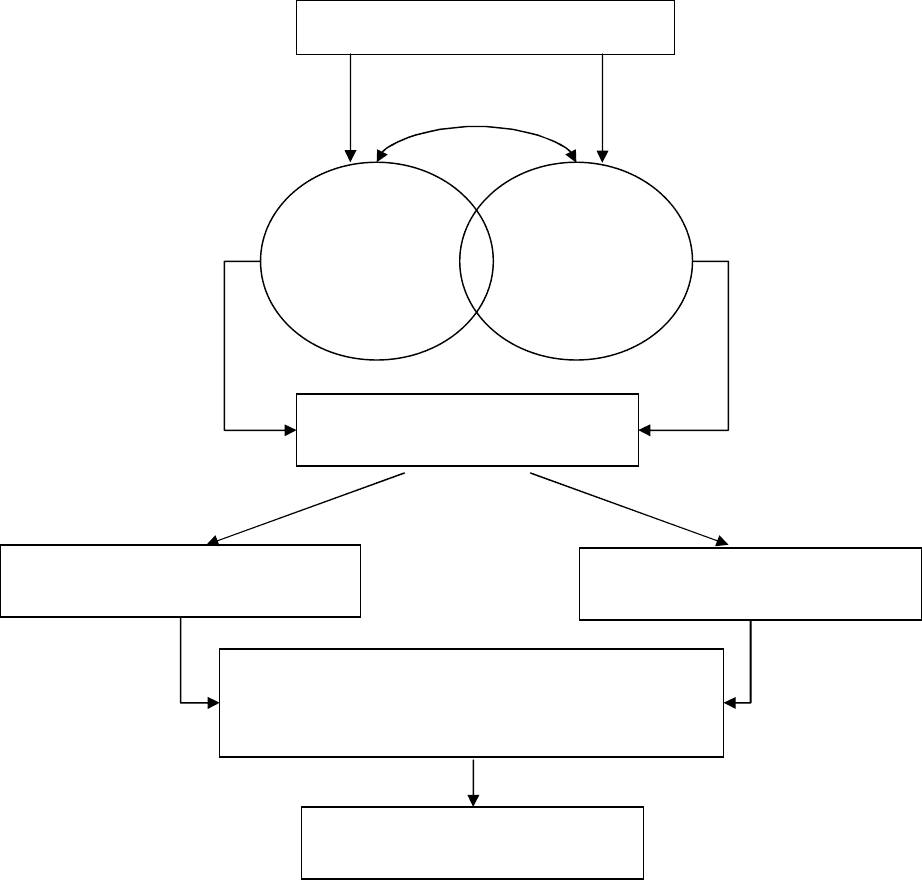
могут совпадать (рис. 1.3).

Рис. 1.3. Взаимосвязь методов и моделей

Математика

Методы

Модели

Логистика

Производство

Коммерция

Производственно-коммерческая

деятельность

Эффект

Процесс построения модели именуется как процесс моделирования

или просто моделирование той или иной логистической операции.

Таким образом, имеет место следующая последовательность:

1) наличие ситуации в том или ином логистическом процессе;

2) характеристика этой ситуации;

3) выявление проблемы – выявление той проблемы, которую ставит

данная ситуация;

4) характеристика проблемы;

5) определение цели для разрешения данной проблемы;

6) постановка задачи (в данном случае задача ставится в обычном

арифметическом смысле по схеме: «дано – найти»);

7) построение модели (изначально модель отображает ситуацию, но

для построения конкретной модели необходима задача, поэтому исполь-

зуют и такое выражение «модель – задачи»);

8) исследование модели и выявление метода;

9) разработка алгоритма – «правила – решения» задачи согласно мо-

дели;

10) процесс решения – осуществляется с помощью разработанного

алгоритма;

11) принятие решения;

12) выполнение решения (полученное управленческое решение пре-

образовывается в управляющие воздействия, которые и доводятся до

управляемого процесса логистической системы);

13) результат;

14) анализ результата.

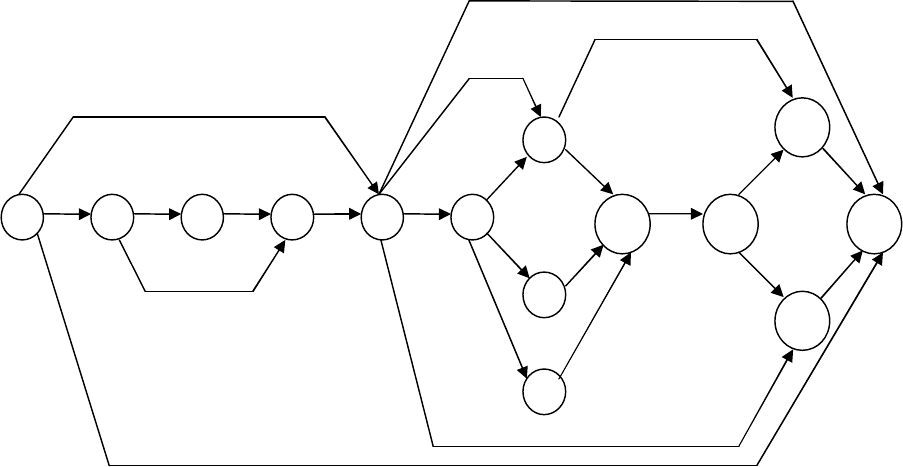
Рис. 1.4. Сетевой график моделирования ситуации в логистике

11 10

С помощью результатов анализа определяются степень адекватности

модели и эффективность методов ее решения, на основании этого анализа

в модель и в метод вносятся определенные коррективы. Представленная

последовательность действий может быть изображена в виде сетевого

графика (рис 1.4).

Как показывает график на (рис. 1.4), процесс моделирования логи-

стичеких ситуаций является сложным, поскольку ряд действий выполня-

ется параллельно, некоторые действия непосредственно и опосредованно

связаны между собой. Так, в частности, при анализе результата внедрения

управленческого решения (событие 14) учитывается исходная ситуация

(событие 1) и поставленная цель решения проблемы (событие 5). При всей

сложности моделирования прослеживаются этапы: «ситуация – модель –

метод – результат». Из этого следует, что модель является первичной по

отношению к методу.

В ситуациях, связанных с логистической деятельностью, присутст-

вуют экономические, а точнее, коммерческие составляющие. Так, в част-

ности, многие модели предусматривают минимизацию затрат на те или

иные логистические процессы или операции. Однако к настоящему вре-

мени логистика под влиянием практики и накопленной научной информа-

ции подразделилась на отдельные, относительно самостоятельные логи-

стические научные дисциплины – функциональные и отраслевые (пред-

метные). C точки зрения применения экономико-математических методов

и моделей логистика включает следующие логистические научные дисци-

плины:

1. Коммерческая логистика, в том числе логистика закупочная (снабже-

ния) и распределительная (сбытовая).

2. Производственная (внутрипроизводственная) логистика.

3. Транспортная логистика.

4. Складская логистика.

Перечисленные логистики являются наиболее распространенными, но

при этом функционируют такие логистики, как услуг, недвижимости и др.

Основные логистические дисциплины как объекты экономико-

математических методов и моделей представлены в табл. 1.1.

Сведения, приведенные в табл. 1.1, показывают, с одной стороны,

соотношение понятий методов и моделей, а с другой стороны, охват

разделами математики совокупности основных логистических научных

дисциплин. В этом смысле метод есть инструмент для построения модели.

Так, например, с помощью методов классического математического

анализа строится ряд моделей формирования и управления запасами, в

частности, модель (формула) Уилсона для определения оптимального

размера партий поставок.