Плоткин Б.К., Делюкин Л.А. Экономико-математические методы и модели в логистике
Подождите немного. Документ загружается.


41
5) вид экспоненциального закона:
х
еу
041,0
041,0
.
Таблица 3.3
Расчет средней реализации и среднеквадратического отклонения
№ х
i
i
xх
2
)(
i
xx
1 2,7 21,4 457,96
2 3,5 20,6 424,36
3 3,8 20,3 412,09
4 7,5 16,6 275,56
5 9,4 14,7 216,09
6 10,0 14,1 198,81
7 12,4 11,7 136,89
8 13,4 10,7 114,49
9 14,5 9,6 92,16
10 14,5 9,6 92,16
11 16,5 7,6 57,76
12 18,3 5,8 33,64
13 18,5 5,6 31,36
14 19,5 4,6 21,16
15 22,1 2,0 4,00
16 24,5 -0,4 0,16
17 24,8 -0,7 0,49
18 25,5 -1,4 1,96
19 27,0 -2,9 8,41
20 27,4 -3,3 10,89
21 27,4 -3,3 10,89
22 29,5 -5,4 29,16
23 32,1 -8,0 64,00
24 34,5 -10,4 108,16
25 35,0 -10,9 118,81
26 41,2 -17,1 292,41
27 42,0 -17,9 320,41
28 48,3 -24,2 585,64
29 54,0 -29,9 894,01
30 64,5 -40,4 1632,16
Итого:
30 724,3 0 6646,05
Далее следует установить интервалы значений и вычислить факти-
ческие частоты двумя способами:
а) через нормальное распределение (табл. 3.4, рис. 3.4)
Таблица 3.4
№
п/п
Интервал 0-10 10-20 20-30 30-40
40-50
50-60
Свыше
60
Итого
1
Количество
случаев
6 8 8 3 3 1 1 30
2 Частоты 0,2 0,27 0,27 0,1 0,1 0,03 0,03 1

42
Рис. 3.4. Нормальный закон распределения вероятностей
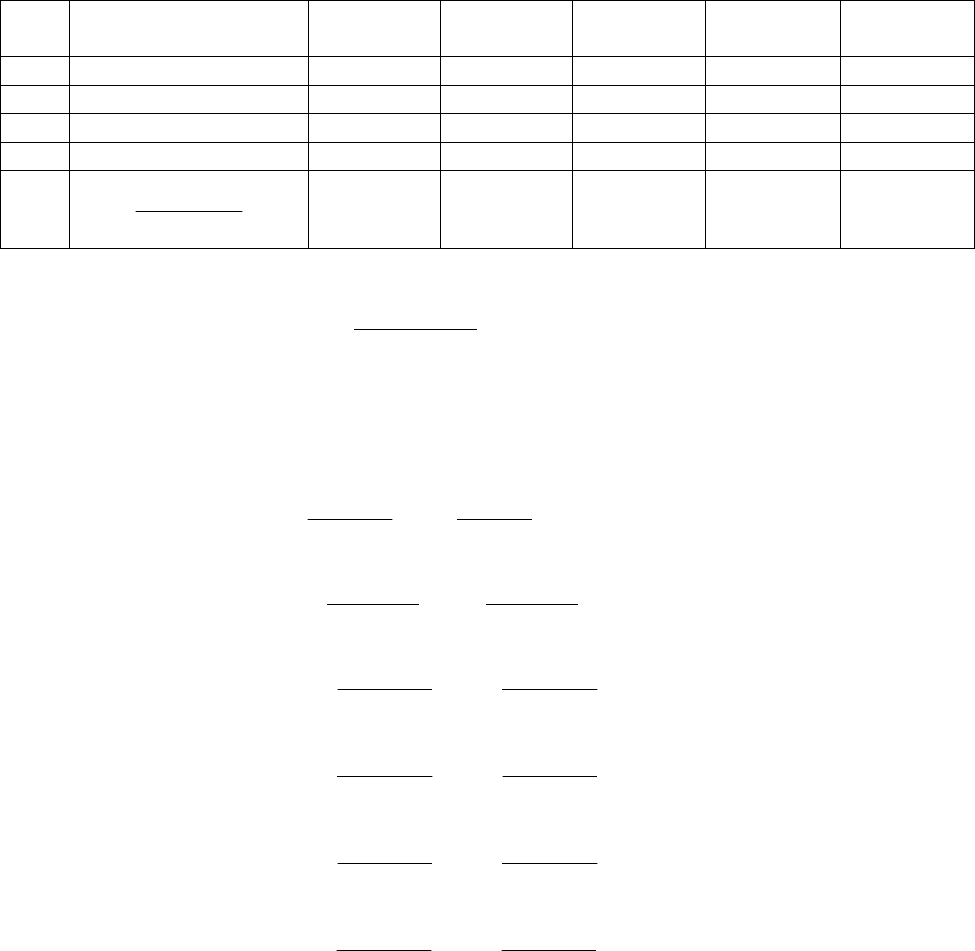
б) через экспоненциальное распределение (табл. 3.5, рис. 3.5)
Таблица 3.5
№ Интервал 0-20 20-40 40-60 Свыше 60 Итого
1 Количество случаев 14 11 4 1 30
2 Частоты 0,47 0,37 0,13 0,03 1
х
еу
041.0
041,0
Рис. 3.5. Экспоненциальный закон распределения вероятностей
8,29
)1.24(
2
0268,0
х
еу

43
На основании полученного выражения для экспоненциального зако-
на определяются его теоретические значения (табл. 3.6)
Таблица 3.6
Построение теоретического распределения
реализации продукции по экспоненциальному закону
№ Показатели 0 20 40 60
1 -0,041х 0 -0,82 -1,64 -2,46
2 е
-0,041х
1 0,44 0,194 0,0085
3 0,041·е
-0,041х
0,041 0,018 0,008 0,003
4
1
ii
xх
eе
0,023 0,01 0,005 0,038
5
Частота теоретиче-
ская
0,61 0,26 0,13 1
Примечание: для определения теоретических частот (строка 5) зна-
чение суммы 0,038 (строка 4) принимается за единицу.
Вероятности по гипотезе нормального закона для каждого интервала
определяются с помощью функции Лапласа:
.
2
)(
0
dtехФ
х
t
Вероятность в интервале [a; b]:
dxedxxfbxаР
b
a
mx
2
)(
2
2
1
)()(
.
Введем обозначения:
2
mx
t
,
2
ma
,
2
mb
.
Тогда:
)]()([)(
ФФbxaP
.
Функция Лапласа табулирована и при вычислении вероятностей
конкретных значений интервалов используются ее табличные значения.
Для того чтобы проверить, насколько соответствует теоретическое
распределение фактическому, необходимо использовать критерий согла-
сия. Рассчитаем значение χ
2
для экспоненциального и нормального рас-
пределений. Значение χ
2
, которое будет меньше, говорит о более высоком
уровне соответствия данного теоретического распределения фактическо-
му (табл. 3.7).
44
Таблица 3.7
Расчеты экспоненциального распределения
№
п/п
Величины 0-20 20-40 40-60 Свыше 60 Итого
1 n
ф
47 37 13 3 100
2 n
т
61 26 13 - 100
3 (n
ф
- n
т
) -14 11 0 3 0
4 (n
ф
- n
т
)
2
196 121 0 9 3
5
т
тф
n
nn
2
)(
3,21 4,65 0 - 7,86
86,765,421,3
)(
2
2
т
тф
n
nn
Х
.
Расчеты для нормального распределения:
а) рассчитываются вероятности для каждого из интервалов (с помощью
табличных значений функции Лапласа):
12
,0)617,1()95,0(
9,14
1,240
9,14
1,2410
)100(
ФФФФxP
,
20,0)95,0()275,0(
9,14
4,2110
9,14
1,2420
)2010(
ФФФФxP
;
41,0)275,0()395,0(
9,14
1,2420
9,14
1,2430
)3020(
ФФФФxР
;
19,0)395,0()067,1(
9,14
1,2430
9,14
1,2440
)4030(
ФФФФxР
;
08,0)067,1()738,1(
9,14
1,2440
9,14
1,2450
)5040(
ФФФФxР
;
02,0)738,1()4,2(
9,14
1,2450
9,14
1,2460
)6050(
ФФФФxР
.
б) рассчитываются n
т
для каждого интервала:
1) 0,12 · 30 = 3,6;
2) 0,20 · 30 = 6,0;
3) 0,41 · 30 = 12,3;
4) 0,19 · 30 = 5,7;
5) 0,08 · 30 = 2,4;
6) 0,02 · 30 = 0,6.

45
в) рассчитываются значения
т
тф
п
пп
2
)(
для каждого интервала:
1)
6,1
6,3
)6,36(
2
,
2)
47,0
0,6
)0,68(
2
,
3)
5,1
3,12
)3,128(
2
,
4)
28,1
7,5
)7,53(
2
,
5)
15,0
4,2
)4,23(
2
,
6)
26,0
4,2
)6,01(
2
.
Отсюда значение χ
2
:
46,526,015,028,15,167,06,1
)(
2
2
т
тф
n
nn
Х
.
При вычислении значения χ
2
в качестве фактических частот (п
ф
)
принято количество случаев (табл. 3.4, строка 1).
Производится сравнение полученных результатов:
1) Х
2
= 7,86 – при экспоненциальном распределении;
2) Х
2
= 5,46 – при нормальном распределении;
5,46 < 7,86 – следовательно, теоретическое нормальное распределе-
ние в большей степени соответствует фактическому, чем экспоненциаль-
ное.
В общем случае ряд логистических процессов, а именно: продажи, от-
грузка продукции с оптово-торговых предприятий, движение запасов, ока-
зание услуг при поставках продукции, расходование материальных ресур-
сов и т.п. описывается нормальным законом распределения вероятностей.
Отличительным признаком такого распределения является наличие выра-
женной симметрии случайных величин относительно их среднего значе-
ния. Для указанных процессов нормальный закон применим для всей про-
дукции, определенных ассортиментных групп или отдельных наименова-
ний товаров.
При АВС – анализе структуры логистических процессов, получае-
мые характеристики в стоимостном или натуральном выражениях подчи-
нены экспоненциальному распределению.

46
Тот факт, что реализация продукции соответствует нормальному за-
кону, имеет важное значение для логистики, поскольку позволяет опреде-
лять величину товарного запаса, для чего рекомендуется следующая фор-
мула:
3 GV
,
где
V
– необходимая величина товарного запаса на определенный период;
G
– средняя реализация в единицу времени (день, неделя, месяц);
– среднеквадратическое отклонение.
Для рассматриваемого примера товарный запас равен:
V = 24,1 + 3·14,9 = 68,8 тыс. руб.
Данная модель показывает, что любое требование покупателя на то
или иное количество товара должно быть удовлетворено с вероятностью
близкой к 1. В этой модели используется правило «трех сигм»: в нормаль-
ном законе 3σ соответствует вероятности 0,99.
В современных условиях компьютерные технологии позволяют от-
слеживать в текущем режиме времени среднюю реализацию и средне-
квадратические отклонения и, соответственно, корректировать величину
товарного запаса.
Предоставленная модель определения товарного запаса может быть
использована как для розничной, так и для оптовой торговли.
Упражнения для самоконтроля:
1. Дано:
Сведения о реализации продукции (табл. 3.8).
Таблица 3.8
Объемы
реализации,
млн руб.
До 1 1-2 2-3 3-4 4-5 5-6
Свыше
6
Количество
случаев
2 4 6 10 8 3 2
Определить:
а) вычислить параметры закона распределения вероятностей;
б) построить график закона распределения вероятностей.
2. Дано:
- время погрузки одной автомашины, час-мин:
2-40, 1-25, 1-10, 1-45, 0-30, 0-35, 0-35, 0-40, 0-40, 1-45, 1-20, 0-56, 0-50, 0-
45, 0-40, 0-40, 4-10, 3-10, 3-15, 3-25.
Сгруппировать ряд времени погрузки автомашин, вычислить пара-
метры Закона распределения вероятностей, построить график.
47
3. Дано:
- база снабжает 10 магазинов, вероятность поступления заявки от одного
магазина – 0,4.
Определить:
- наивероятнейшее число заявок;
- вероятность поступления наивероятнейшего числа заявок;
- вероятность поступления заявок от 5 магазинов.
4. Дано:
- время работы базы с 8
00
до 20
00
ежедневно;
- ежедневное поступление заявок – 36 автомашин.
Определить вероятности поступления на базу в течение одного часа 0,
1, 2, 3, 4, 5, 6 автомашин.
5. Дано:
- среднее число заявок, поступающих в систему в течение одного часа – 5.
Вычислить распределение вероятностей поступления в систему в те-
чение одного часа от 0 до 10 заявок, построить график.
Глава 4. МЕТОДЫ И МОДЕЛИ МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ В ЛОГИСТИКЕ
Методы математической статистики позволяют выявлять характер
действия факторов – причин на следствия. Эти методы дают возможность
по одним величинам вычислять другие, недоступные или малодоступные.
Методы математической статистики позволяют предвидеть течение
и развитие логистических процессов. При помощи методов математиче-
ской статистики решаются такие вопросы, как построение кривых распре-
деления вероятностей и оценка степени согласия фактических характери-
стик с теоретическими, позволяют определять эмпирические зависимости,
оценивать тесноту связи между изучаемыми величинами.
В логистике наиболее часто применяется корреляционно-
регрессионный анализ, с помощью которого выявляются качественные и
количественные влияния различных факторов на показатели логистиче-
ской деятельности.
Этот анализ позволяет измерять тесноту связи между величинами и
строить теоретические зависимости влияния одной величины на другую,
т. е. уравнения регрессии. Вычисленное уравнение товарооборота на из-
держки есть не что иное, как уравнение регрессии.
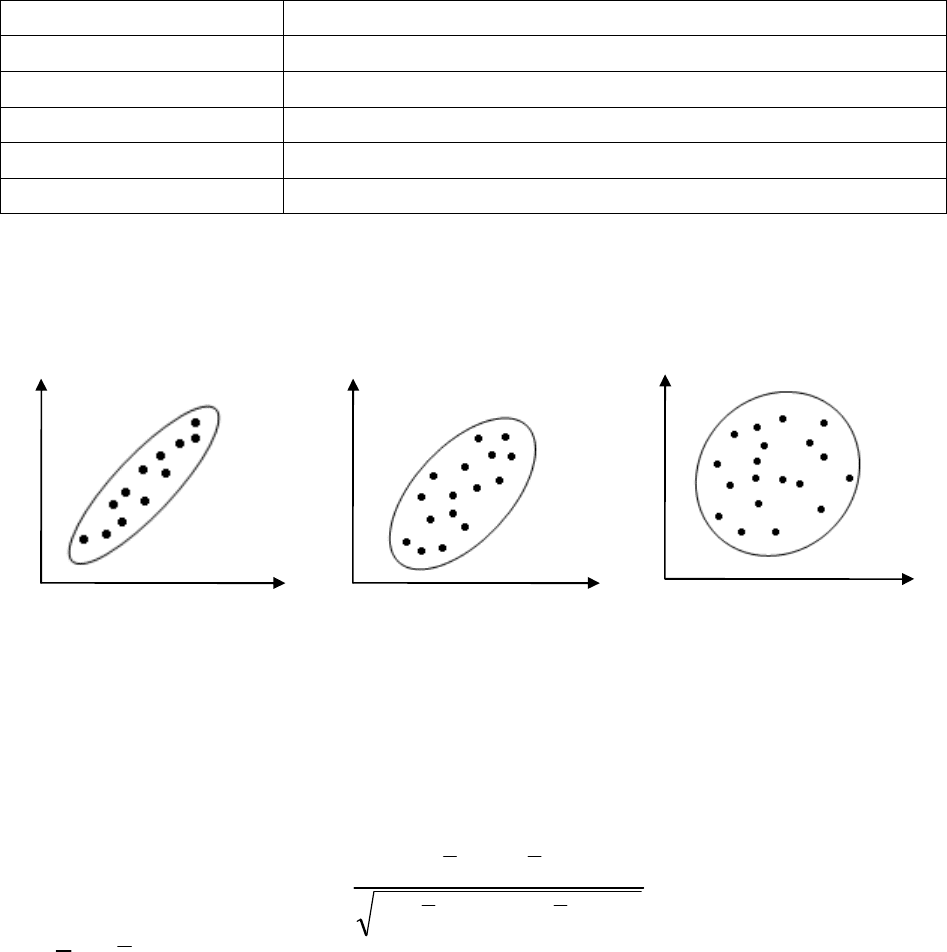
Теснота связи при линейной зависимости измеряется коэффициен-
том корреляции r, а теснота связи при нелинейной зависимости измеряет-
ся корреляционным отношением h. Для нужд логистики целесообразно
48
использовать линейные зависимости и тесноту связи измерять с помощью
коэффициента корреляции. В данном случае подразумевается линеариза-
ция зависимостей.
Коэффициент корреляции изменяется от 0 до 1, 0<r<1
Чем ближе значение показателей тесноты связей к единице, тем
сильнее влияние одной величины на другую, а стремление к нулю указы-
вает на ослабление тесноты связи.
Применительно к логистике используется шкала тесноты связи
(табл. 4.1)
Таблица 4.1
Шкала тесноты связи
Значения
r, h
Характеристика степени тесноты связи
0,9 – 1 Очень сильная зависимость
0,75 – 0,9 Сильная зависимость
0,5 – 0,75 Средняя по тесноте зависимость
0,3 – 0,5 Слабая зависимость
Менее 0,3 Очень слабая зависимость
Представленная шкала измерения тесноты связи иллюстрируется
графиком (рис. 4.1).
Рис. 4.1. Графики, иллюстрирующие тесноту связи
между зависимыми случайными величинами
Коэффициент корреляции определяется по следующей формуле:
22
)()(
))((
ii
ii
yyxx
yyxx
r
,
где
х
и
у
– средние значения исследуемых величин.
Расчет коэффициента корреляции предлагается вести в табличной
форме (табл. 4.2).
у
у
у
х
х х
175,0
r
75,05,0
r
5,00
r
а) сильная
зависимость
б) средняя
зависимость
в) слабая
зависи
мость
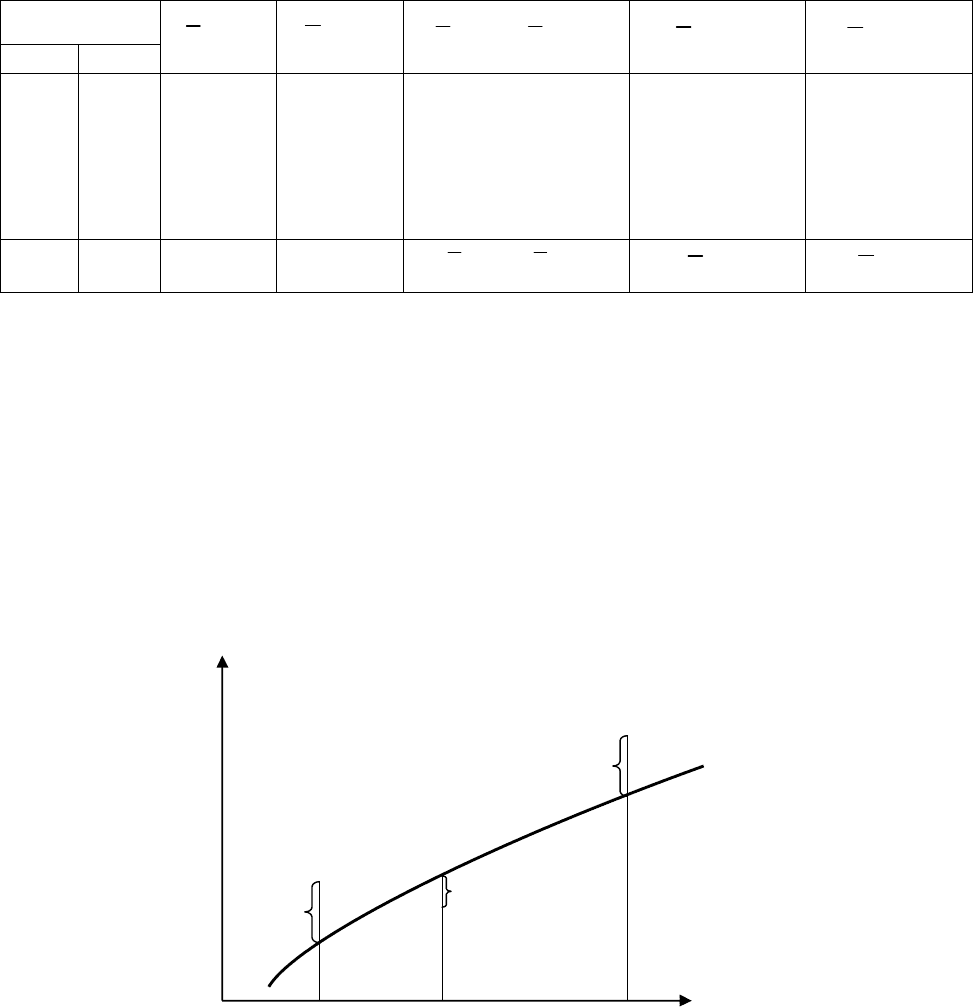
49
Таблица 4.2
Расчет коэффициента корреляции
Исх. данные
i
хх
i
yy
))((
ii
yyхх
2
)(
i
хх
2
)(
i
yy
Х У
х
1
х
2
…
х
i
…
х
n
у
1
у
2
…
у
i
…
у
n
...
…
...
…
...
…
...
…
...
…
Σх
i
Σу
i
0 0
))((
ii
yyхх
2
)(
i
хх
2
)(
i
yy
Другой составляющей корреляционно-регрессионного анализа явля-
ется определение уравнения, связывающего исследуемые величины, т. е.
установление вида уравнения регрессии. С этой целью в математической
статистике используется метод «наименьших квадратов». Согласно этому
методу, сумма квадратов отклонений фактических данных от теоретиче-
ских значений соответствующих величин, полученных по уравнению рег-
рессии, должна быть наименьшей.
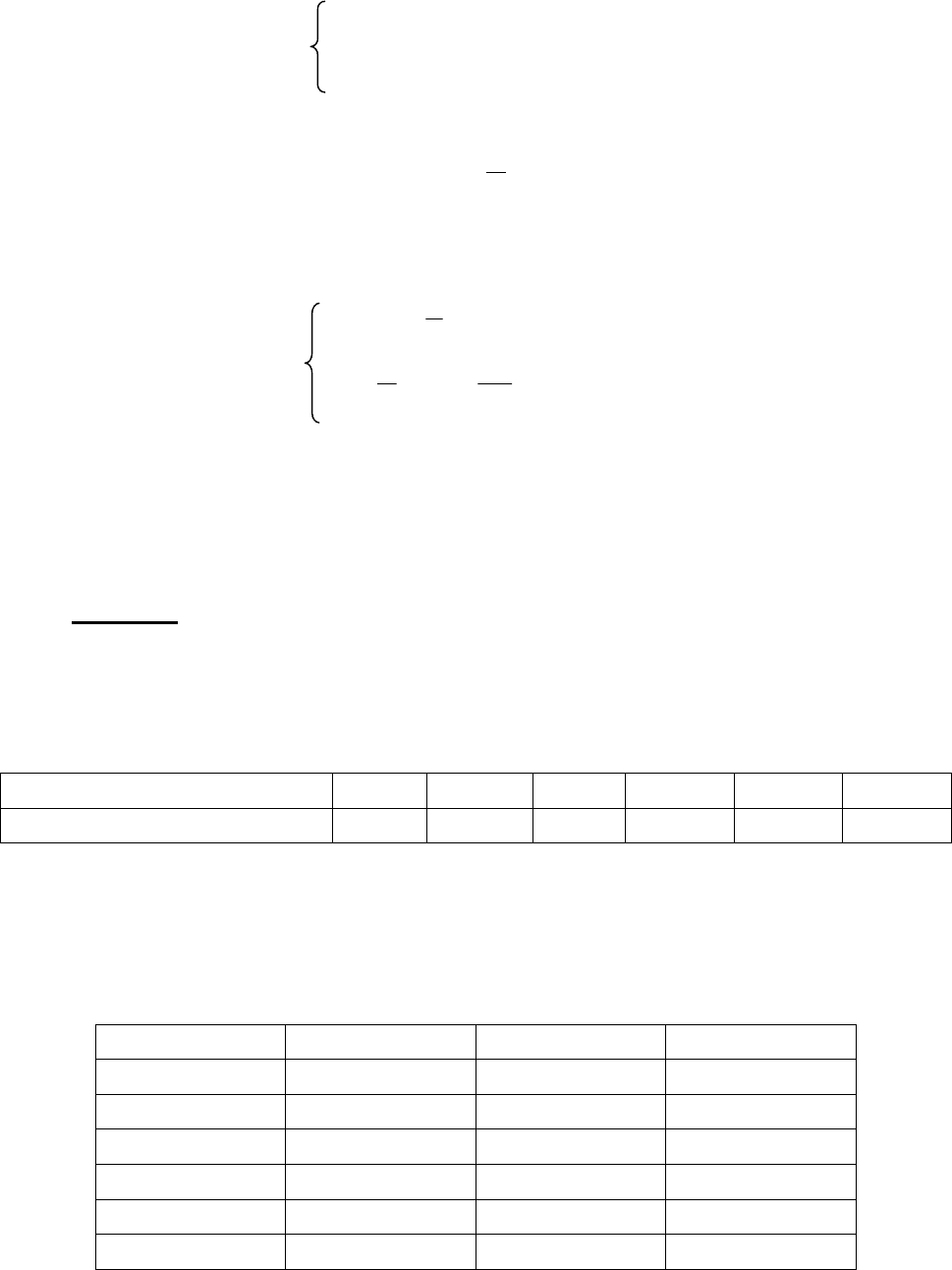
Сущность метода «наименьших квадратов» иллюстрируется графи-
ком (рис. 4.2).
Рис. 4.2. График метода «наименьших квадратов»
На графике фактическое значение величины обозначено
i
y
, а теоре-
тическое значение, полученное из уравнения регрессии -
i
y
~
. Отсюда раз-
ность отклонений
)
~
(
ii
yy
. Уравнение регрессии должно удовле-
творять условию:
min)
~
(
22
ii
yy
.
у
х
у
1
у
2
у
i
Δ
1
Δ
2
Δ
i
1
~
у
2
~
у
i
у
~
50
Для использования метода «наименьших квадратов» решаются сис-
темы нормальных уравнений.
Для линейной зависимости у = а
0
+ ах система нормальных уравне-
ний имеет вид:
yxana
10
xyxaxa
2
10
,
Для обратной зависимости
b
x
a
y
решается следующая система
уравнений:
yn
x
n
anb
2
x
n
a
x
n
b
,
При вычислении параметров уравнения регрессии исходными дан-
ными являются попарно упорядоченные фактические значения исследуе-
мых величин х и у. В нормальных уравнениях неизвестными являются па-
раметры а
о
и а
1
.
Пример: Имеются данные о товарообороте торгового предприятия
за определенный период в млн руб. и соответствующих издержках обра-
щения (табл. 4.3).
Таблица 4.3
Товарооборот, млн руб. х 1 3 5 8 12
Издержки, %% У 10 5 7 3 1
Подготовка данных для составления системы нормальных уравнений
ведется в табличной форме (табл. 4.4).
Таблица 4.4
Х
у
х
2
х
у
1 10 1 10
3 5 9 15
5 7 25 35
8 3 64 24
12 1 144 12
29
26
243
96
