Плоткин Б.К., Делюкин Л.А. Экономико-математические методы и модели в логистике

Подождите немного. Документ загружается.

Пример 5.3: В магазине обслуживание покупателей осуществляют

два продавца. Магазин работает с 10 ч. до 19 ч. с часовым обеденным пе-

рерывом. В среднем за день магазин посещают 120 человек, среднее вре-

мя обслуживания одного покупателя 5 минут. Необходимо определить ха-

рактеристики обслуживания.

Решение:

Поток заявок – простейший, его плотность

25,0

480

120





20,0





225,1  n





По формулам (1) и (2) рассчитываются вероятности состояния сис-

темы (магазина), результаты расчета приведены в табл. 5.5.

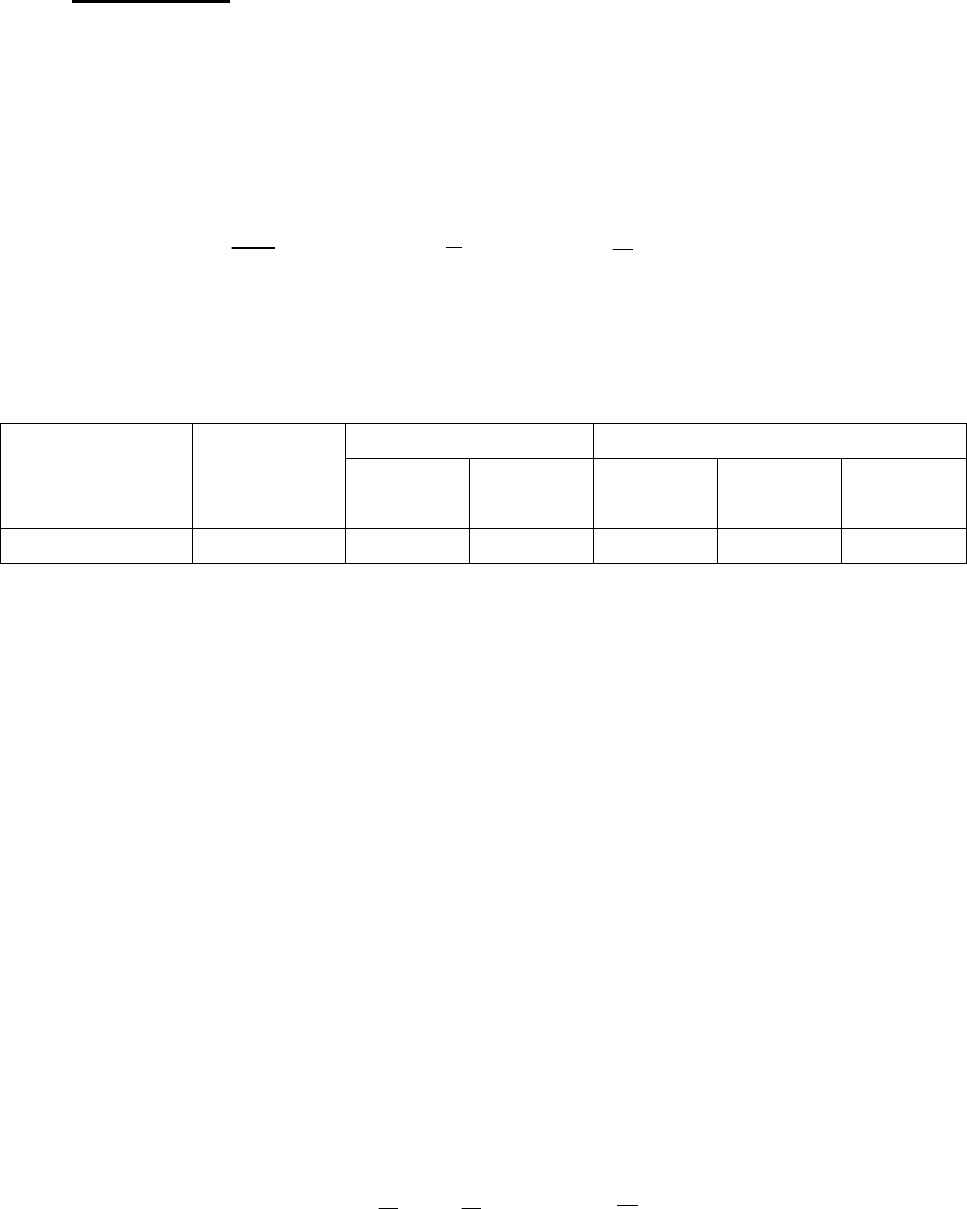
Таблица 5.5

Состояния

системы

Продавцы

свободны,

к = 0

Продавцы заняты

Наличие очереди, чел.

к = 1 к = 2 S=1 S=2 S=3

Вероятности

0,233 0,293 0,182 0,114 0,073 0,044

На основании полученных данных определяется вероятность нали-

чия очереди:

Р = 1 – (Р

+ Р

) или Р = 1 – (0,233 + 0,293 + 0,182) = 0,292.

Пор формуле (3) определяется средняя длина очереди:

S = 0,7 чел.

Таким образом, в рассматриваемом примере вероятность образова-

ния очереди сравнительно высока, однако если покупатель и застает оче-

редь, то в среднем не более одного человека.

Методы теории массового обслуживания применяются в некоторых

задачах управления запасами. С точки зрения теории массового обслужи-

вания запас – это «очередь» товаров, ожидающих «обслуживание», т. е.

спрос со стороны потребителей. Если товары поступают на склад и уходят

со склада по пуассоновскому закону с плотностями соответственно λ и μ,

то вероятность наличия на складе n единиц товара - Р

, а вероятность от-

сутствия товара – P

определяются соответственно следующими форму-

лами:





































Р ,





1

Затраты на содержание аппаратов обслуживания, так же как и вели-

чина убытков от отказов в обслуживании, определяются методом прямой

калькуляции для данной системы обслуживания или для данной логисти-

ческой системы.

Упражнения для самоконтроля:

1. Продовольственный магазин самообслуживания имеет два расчетно-

кассовых узла, в которые в течение одного часа приходят в среднем 30

покупателей, время обслуживания – 2 минуты.

Определить:

- вероятность образования очереди покупателей в расчетно-кассовые

узлы;

- вероятность застать расчетно-кассовые узлы свободными.

2. На базу в течение 12 часов приходят под погрузку товаров 24 автома-

шины. Обслуживание автомашин осуществляется с 4 погрузочных площа-

док, время погрузки – 30 мин. Содержание одной погрузочной площадки –

25 тыс. руб./год, убытки от отказов в обслуживании автомашины – 5 тыс.

руб. в сутки.

Определить:

- вероятности занятости 0, 1, 2, 3 и 4 погрузочных площадок;

- количество погрузочных площадок при детерминированном по-

токе автомашин;

- оптимальное количество погрузочных площадок при стохастиче-

ском потоке автомашин

3. Имеется склад с годовым грузооборотом 182,5 тыс. тонн, период про-

хождения груза – 365 суток. Средний срок хранения – 5 суток. Груз по-

ступает партиями в 250 тонн и в этом количестве хранится в соответст-

вующих секциях, нагрузка на склад – 1 т/м

. Эксплуатационные расходы

по содержанию складской площади – 10 руб./м

– год; убытки от отказа

склада в приемке груза на хранение – 200 руб./сут.

Определить оптимальную величину складской площади при стохас-

тическом потоке грузов, поступающих на склад.

Глава 6. МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

В ЛОГИСТИКЕ

В логистике имеется ряд ситуаций, которые описываются моделями

линейного программирования. Эти ситуации формулируются в виде задач.

К таким задачам в логистике относятся:

 транспортная задача;

 задача на раскрой материалов;

 задача размещения баз снабжения;

 задача по оптимизации ассортиментной загрузки производства.

6.1. Транспортная задача

Наиболее распространенной является транспортная задача линейно-

го программирования. Эта задача формируется следующим образом:

товары, сосредоточенные в m пунктах отправления в количествах а

, …, а

необходимо доставить в каждый из n пунктов назначения в ко-

личествах b

, b

, …, b

. Стоимость перевозки товара из i пункта отправле-

ния в j пункт назначения равна с

. Следует определить оптимальный план

развозки, т. е. найти х

для этого оптимального плана.

В общем виде модель линейного программирования состоит из це-

левой функции и ограничений (условий). Для транспортной задачи целе-

вая функция имеет следующий вид:

min

1 1





 

XCL

Целевая функция предусматривает минимизацию перевозки всех то-

варов из пункта i в пункт j.

Ограничения:

bx 



1

ax 



1

0

Ограничения показывают, что все имеющиеся товары, сосредото-

ченные во всех i-х пунктах отправления, должны быть полностью достав-

лены в требуемых количествах в пункты потребления j.

Сущность транспортной задачи иллюстрируется следующим приме-

ром (числа условные):

Имеются следующие количества товаров, находящихся в трех пунк-

тах отправления: а

= 6, а

= 8, а

= 10, потребность в этих товарах в сле-

дующих четырех пунктах назначения b

= 4, b

= 6, b

= 8, b

= 6.

Стоимость перевозок из пункта i в пункт j единицы товара представ-

лена в табл. 6.1.

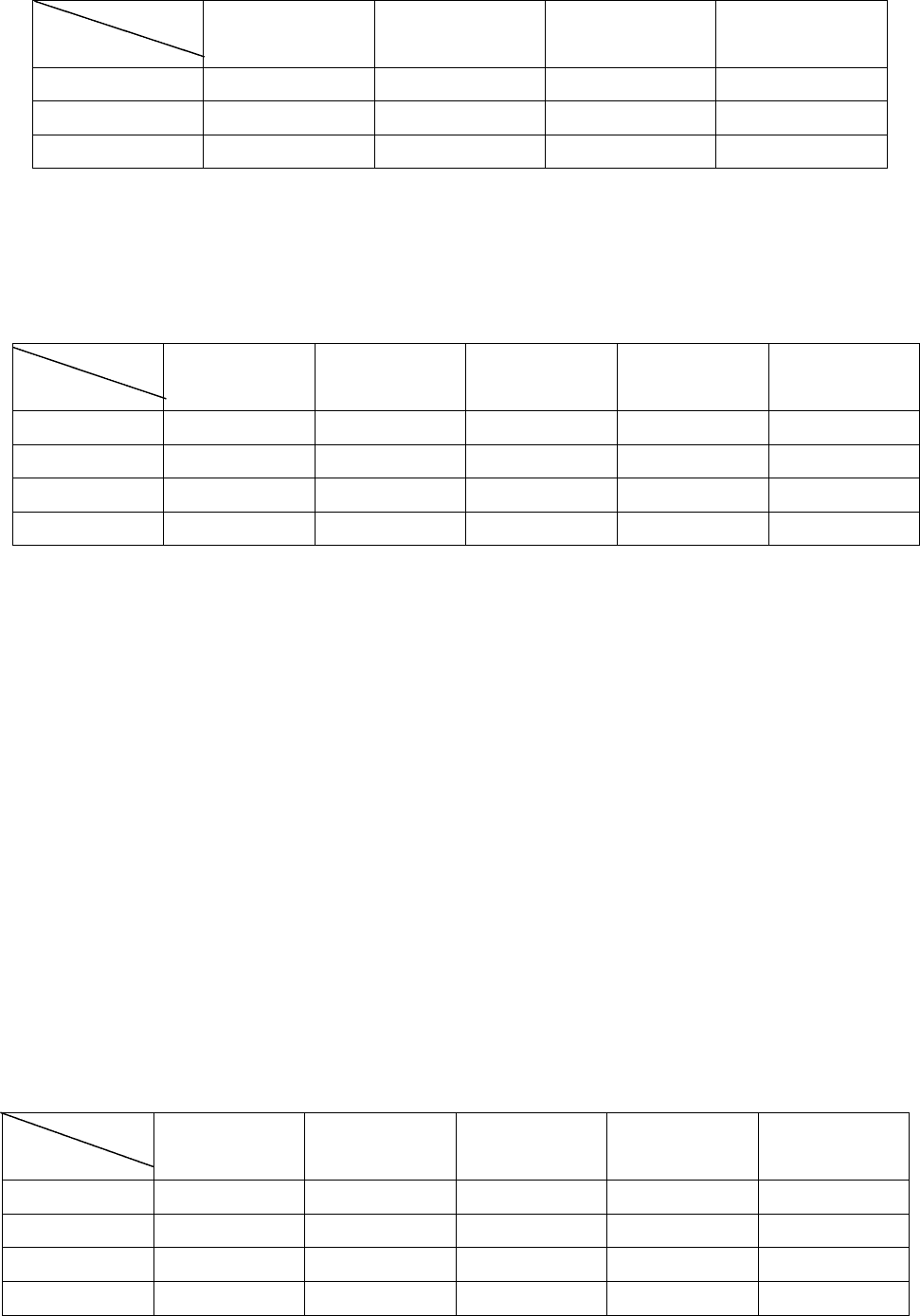
Таблица 6.1

1 2 3 4

4 2 3 4

4 3 2 1

1 2 2 1

Для решения транспортной задачи предварительно составляется ис-

ходный план перевозки по правилу «Северо-западного угла» (табл. 6.2).

Таблица 6.2.

1 2 3 4 Итого

4 2 6

4 4 8

4 6 10

Итого

4 6 8 6 24

Далее определяется стоимость перевозки по исходному плану:

4 · 4 = 16;

2 · 2 = 4;

4 · 3 = 12;

4 · 2 = 8;

6 · 1 = 6.

Итого: 54.

Исходный план с помощью специальных алгоритмов улучшается до

оптимального, т. е. когда стоимость перевозки будет минимальна. С этой

целью используются такие алгоритмы, как симплекс-метод, метод потен-

циалов и др.

Используя указанные алгоритмы, получаем оптимальный план раз-

возки продукции (табл. 6.3).

Таблица 6.3

1 2 3 4 Итого

6 6

2 6 8

4 6 10

Итого

4 6 8 6 24

Определяется стоимость перевозки по оптимальному плану:

4 · 1 = 4;

6 · 2 = 12;

2 · 2 = 4;

6 · 1 = 6;

6 · 2 = 12.

Итого: 38.

Алгоритмы решения задач линейного программирования предусмат-

ривают перебор возможных вариантов, ориентируясь на целевую функ-

цию и ограничения. Стоимость перевозки по оптимальному варианту – 38

стоимостных единиц, экономия составила 16 стоимостных единиц или

29,6%.

В реальных условиях транспортная задача линейного программиро-

вания применяется в сетевой торговле при развозке товаров с распредели-

тельных центров каждому магазину сети, в соответствии с потребностями

каждого магазина.

В условиях рыночной экономики, когда действует рынок транспорт-

ных услуг, грузоотправители выбирают себе подходящего перевозчика со-

гласно своим критериям оптимальности по Парето и независимо друг от

друга. Однако за определенный период времени (например, за год) сум-

марный объем транспортной работы для совокупности грузоотправителей

и грузополучателей установится на оптимальном уровне согласно модели

транспортной задачи линейного программирования

6.2. Раскройная задача линейного программирования

При раскрое материалов образуется два вида отходов:

1) концевые отходы, обусловленные некратностью исходного материала

и нарезаемых заготовок;

2) отходы, обусловленные требованиями комплектности.

Целевая функция:

min







xCL

Целевая функция предусматривает минимум отходов, при соблюде-

нии требований комплектности, отсюда

Ограничения:

axК







где виды заготовок по размерам:

1, 2, …. j … n – варианты раскроя материала;

1, 2, …. i … m – виды заготовок;

– количество заготовок в комплекте;

– количество заготовок i вида в варианте раскроя j;

– концевые отходы в варианте раскроя j.

Требуется определить х

, количество исходного материала (прутков,

листов), раскраиваемых по каждому варианту, которое удовлетворяет тре-

бованию комплектности и обеспечивает минимум отходов.

Для решения задачи предварительно составляется таблица возмож-

ных вариантов раскроя, абстрагируясь на этом этапе от требований ком-

плектности.

Пример: Требуется изготовить 100 комплектов заготовок длиной

1,5 м; 2,1 м; 2,9 м. Из прутков металлопроката длиной 7,4 м.

Простейший способ раскроя – изготовления из каждого прутка по

комплекту: 7,4 = 1,5 + 2,1 + 2,9 + 0,9, где 0,9 – концевые отходы.

Для решения данной задачи методом линейного программирования

предварительно составляется таблица возможных вариантов раскроя

(табл. 6.4).

Таблица 6.4.

Заготовки

Варианты раскроя Количество

заготовок в

комплекте

1 2 3 4 5 6

1,5 3 1 2 - 3 1 100

2,1 - - 2 2 1 1 100

2,9 1 2 - 1 - 1 100

Отходы,

0 0,1 0,2 0,3 0,8 0,9

Целевая функция: L = 0х

+ 0,1х

+ 0,2х

… = min

Ограничения:

3х

+ 1х

+ 2х

+ 0х

+ 3х

+ 1х

= 100

0х

+ 0х

+ 2х

+ 1х

= 100

1х

+ 2х

+ 0х

+ 1х

+ 0х

+ 1х

= 100

Для решения раскройной задачи используются либо общие методы

(общие алгоритмы), либо специальные алгоритмы решения раскройной

задачи. В настоящее время непосредственно решение задач линейного

программирования осуществляется с помощью компьютерных техноло-

гий. В результате решения данной задачи получаем:

= 30, х

= 10, х

= 50.

Полученный результат означает, что по первому варианту следует

раскроить 30 исходных прутков, по второму – 10, по четвертому – 50.

Итого для данного раскроя требуется 90 исходных прутков.

Согласно полученным результатам имеем:

Заготовки х

Итого

1,5 90 10 - 100

2,1 - - 100 100

2,9 30 20 50 100

Отходы, м 0 1 15 16

Таким образом, алгоритм решения задачи предусматривает перебор

возможных вариантов раскроя, ориентируясь на целевую функцию и тре-

бования комплектности.

При простом раскрое необходимо иметь 100 исходных прутков при

этом отходы составят 90 метров, т. е. 13,8%. При оптимальном раскрое

потребуется 90 исходных прутков, а отходы составят 16 метров, т. е. 2,5%.

В некоторых случаях, например при массовом производстве ком-

плектность задается в виде соотношения по каждому виду заготовок. На-

пример, в данной задаче имеет место отношение 1 : 1 : 1.

6.3. Размещение баз оптово-торговых предприятий

Рассматриваемая модель предусматривает минимизацию суммарных

затрат на доставку продукции от проектируемых баз снабжения до суще-

ствующих предприятий-потребителей и затрат на эксплуатацию указан-

ных баз.

Целевая функция:

min)(

11 1





 

iij

xfxCL

Ограничения:

bx 



1

xx 



1

где 1, 2, …. i … m – возможные пункты размещения баз;

1, 2, …. j … n – существующие пункты расположения потребителей;

– стоимость перевозки единицы продукции от i-й базы до j-го потре-

бителя;

– годовой объем потребления j-го потребителя;

– объем поставок с i-ой базы j-му потребителю;

f(х) – затраты на эксплуатацию базы как функция от мощности базы х

Упражнения для самоконтроля:

1. Дано:

- ресурсы поставщиков, ед.: 120

110

Итого: 300 ед.

- потребности потребителей, ед.: 50

100

Итого: 300 ед.

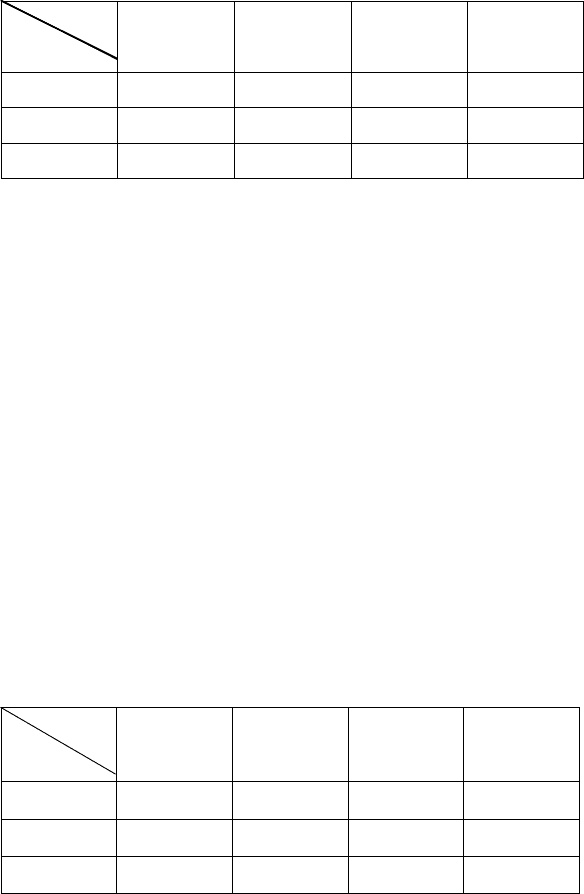
- стоимость перевозки единицы груза из пункта i в пункт j (С

1 2 3 4

2 2 4 6

1 2 4 5

4 6 7 10

Определить оптимальный план перевозки грузов.

2. Дано:

- ресурсы поставщиков, ед.: 300

300

400

Итого: 1000 ед.

- потребности потребителей, ед.: 50

150

500

300

Итого: 1000 ед.

- стоимость перевозки единицы груза из пункта i в пункт j (С

1 2 3 4

8 6 4 4

5 4 8 6

2 4 4 8

Определить оптимальный план перевозки грузов.

3. Дано:

- ресурсы поставщиков, ед.: 1200

800

2000

Итого: 4000 ед.

- потребности потребителей, ед.: 320

280

600

1300

1000

500

Итого: 4000 ед.

- стоимость перевозки единицы груза из пункта i в пункт j (С

1 2 3 4 5 6

4 12 10 3 6 8

6 8 12 12 4 10

4 2 2 8 14 16

Определить оптимальный план перевозки грузов.

4. Дано:

- ресурсы поставщиков, ед.: 1300

700

1000

Итого: 3000 ед.

- потребности потребителей, ед.: 300

400

800

500

300

700

Итого: 3000 ед.

- стоимость перевозки единицы груза из пункта i в пункт j (С

1 2 3 4 5 6

2 4 4 6 8 10

4 5 5 6 4 4

6 6 6 10 10 12

Определить оптимальный план перевозки грузов.

В следующих упражнениях (5-8) требуется выполнить раскрой ис-

ходного материала на заготовки (по длинам) в указанном количестве –

комплектности.

5. Дано:

- длина исходного материала: 4,5 м;

- заготовки и комплектность: 0,8 м – 200 шт., 1,2 м – 200 шт., 1,8 м – 300 шт.,

Определить оптимальный план раскроя исходного материала.

6. Дано:

- длина исходного материала: 3,4 м;

- заготовки и комплектность: 0,8 м – 200 шт.,

1,5 м – 200 шт.,

1,8 м – 300 шт.,

Определить оптимальный план раскроя исходного материала.

7. Дано:

- длина исходного материала: 130 см;

- заготовки и комплектность: 40 см – 400 шт.,

50 см – 200 шт.,

70 см – 100 шт.,

Определить оптимальный план раскроя исходного материала.

8. Дано:

- длина исходного материала: 130 см;

- заготовки и комплектность: 40 см – 100 шт.,

50 см – 200 шт.,

70 см – 300 шт.,

Определить оптимальный план раскроя исходного материала.

Глава 7. МЕТОДЫ И МОДЕЛИ ТЕОРИИ НАДЕЖНОСТИ

В ЛОГИСТИКЕ

Важное место в номенклатуре материальных ресурсов занимают за-

пасные части, а также материалы для ремонтно-эксплуатационных нужд.

Значение запасных частей в обеспечении ритмичной и эффективной рабо-

ты оборудования всех отраслей хозяйства общеизвестно. Отсюда следует,

насколько важна и ответственна работа по определению необходимого

количества запасных частей.

Наличие необходимого комплекта запасных частей – существенный

фактор надежности. В общем виде необходимое количество запасных час-

тей определяется надежностью оборудования.