Плоткин Б.К., Делюкин Л.А. Экономико-математические методы и модели в логистике
Подождите немного. Документ загружается.

31
Определить:
а) оптимальный размер партии поставки;
б) общие затраты содержания запаса и выполнения поставки
в) сравнить исходные данные упражнений 1 и 2.
3. Дано:
– потребность предприятия в продукции – 1000 т/год;
– издержки хранения запаса – 400 руб./т – год;
– стоимость выполнения поставок – 700 руб.
Определить:
а) оптимальный размер партии поставки;
б) количество поставок в год;
в) интервалы между поставками;
г) общие затраты содержания запаса и выполнения поставок.
4. Дано:
– потребность предприятия в продукции – 600 т/год;
– издержки содержания запаса – 15 руб./т – год;
– условно-постоянные расходы – 45 руб.
Определить:
а) оптимальный размер партии поставки;
б) общие затраты содержания запаса и выполнения поставок;
в) составить таблицу, показывающую влияние величины партий поставок
на общие издержки, т. е. С = f(V), при размерах партий поставок в т: 20,
40, 60, 80, 100, 120.
г) составить таблицу, показывающую влияние стоимости запаса на опти-
мальный размер партии поставки, при следующих издержках хранения,
руб./т-год: 5, 10, 15, 20, 25, 30.
5. Дано:
– годовая потребность предприятия – 1800 т;
– среднесуточное потребление материала – 9 т/сутки;
– среднесуточный расход материала – 5 т/сутки
– издержки содержания запаса – 12 руб./т – год;
– условно-постоянные расходы – 12 руб.
Определить:
– оптимальный размер партии поставки.
6. Дано:
– годовая потребность предприятия – 1800 т;
– издержки содержания запаса – 12 руб./т – год;
– потери от дефицита – 44 руб./т – год;
– условно-постоянные расходы – 12 руб.

32
Определить:
а) оптимальный размер партии поставки;
б) величину начального запаса;
в) максимальный дефицит
г) длительность дефицитной ситуации.
7. Дано:
– коэффициент прямых затрат;
– значение величины конечного потребления (табл. 2.5).
Таблица 2.5
Коэффициент прямых затрат и конечное потребление
Отрасли
производства
Отрасли-потребители
Конечное
потребление
1 2 3
1 а
11
= 0,3 а
12
= 0,1 а
13
= 0,2 13,0
2 а
21
= 0,7 а
22
= 0,4 а
23
= 0,1 17,7
3 а
31
= 0,6 а
32
= 0,3 а
31
= 0,3 19,7
Определить:
межотраслевой баланс для трех отраслей.
33
Глава 3. МЕТОДЫ И МОДЕЛИ ТЕОРИИ ВЕРОЯТНОСТЕЙ
В ЛОГИСТИКЕ
Случайные отклонения сопутствуют любому закономерному про-
цессу, а тем более логистическим процессам в рыночной экономике.
Практика ставит такие задачи, в которых различные факторы играют су-
щественную роль в рассматриваемых процессах, однако число этих фак-
торов столь велико, что проследить причинно-следственные связи между
ними не всегда представляется возможным. Элементы неопределенности,
сложности, многопричинности присущи случайным явлениям и процес-
сам в логистике, а поэтому требуются специальные методы для их иссле-
дования, изучения и управления. Такие методы и разрабатывает теория
вероятностей. Таким образом, теория вероятностей в логистике рассмат-
ривает случайные величины, обусловленные логистическими процессами
и операциями.
Так, в частности, в логистике имеют место следующие стохастиче-
ские случайные величины:
1. Спрос (платежеспособность).
2. Объем реализации (объем продаж).
3. Длительность (период реализации).
4. Выручка от реализации продукции.
5. Издержки:
- общие;
- логистические;
- транзакционные.
6. Время погрузки-выгрузки транспортных средств.
7. Время доставки (перемещения продукции).
8. Уровень использования грузоподъемности и грузовместимости
транспортных средств.
9. Время обслуживания покупателей (потребителей).
10. Товарооборот торгового предприятия.
11. Оборот оптово-торговой базы.
12. Поток потребителей (поток заявок на обслуживание).
13. Время занятости средств обслуживания.
14. Движение товарного запаса.
15. Объем партии отгрузки реализуемой продукции.
16. Распределение продукции по группам АВС.
17. Процесс поставки – надежность поставок и другие.
Если изучаемое явление представляется в виде полной группы собы-
тий, которые несовместимы и равновозможны, то вероятность данного

34
события равна отношению числа m благоприятствующих этому событию
случаев к общему числу n возможных случаев, т. е. вероятность равна:
.
n
m
p
На практике рассматривается статистическая вероятность, в резуль-
тате накопленных статистических данных о благоприятствующих событи-
ях m и общего числа событий n.
Так, например, в логистике используется такая величина, как надеж-
ность снабжения. Надежность снабжения в большинстве случаев величина
случайная и определяется за определенный период времени как отноше-
ние числа поставок, выполненных согласно договору поставки, к общему
числу поставок.
Допустим, за рассматриваемый период было выполнено поставщи-
ком 24 поставки, из них 18 поставок соответствуют параметрам, преду-
смотренным договором поставки. Отсюда надежность равняется:
.75,0
24
18
p
Поставка соответствующей надежности определяется следующими
параметрами: количество, качество, сроки поставок.
Случайные величины характеризуются законом распределения или
плотностью распределения вероятностей.
х х
1
х
2
… х
n
р р
1
р
2
… р
n
x
1,
x
2,
… x
n
– конкретные значения, принимаемые данной величиной;
p
1,
p
2,
… p
n
– вероятности указанных значений, при этом:
.1
1
n
i
i
P
В логистике наиболее распространенными являются следующие за-
коны распределения вероятностей: нормальное, экспоненциальное, бино-
минальное, Пуассона.
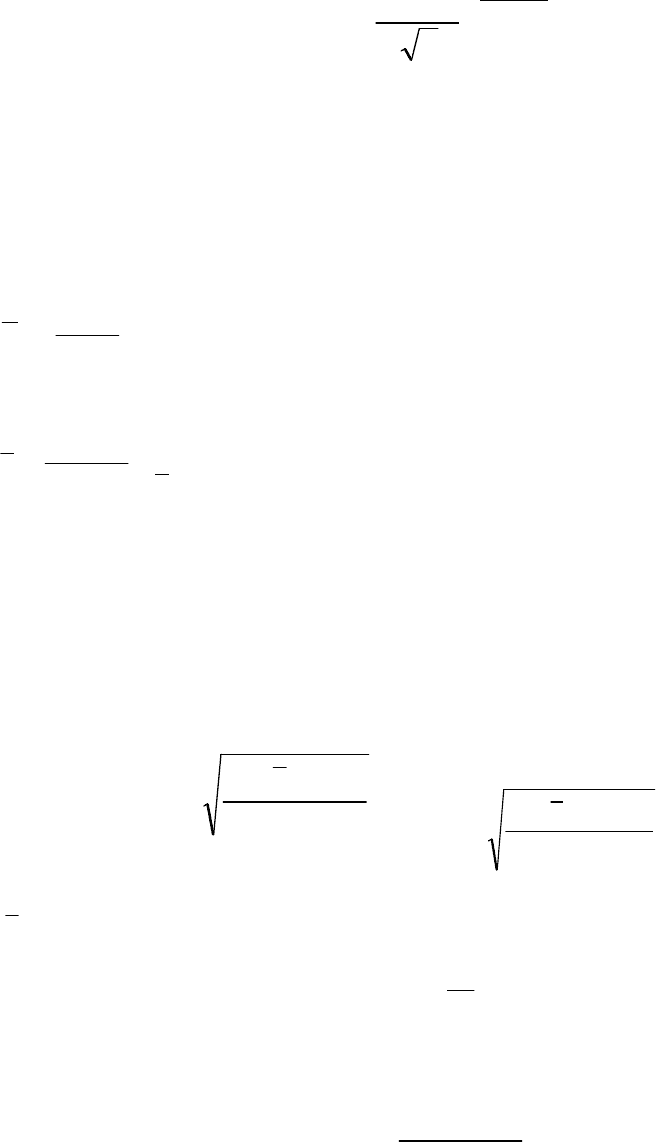
35
3.1. Нормальный закон распределения вероятностей
Плотность нормального распределения имеет следующий вид:
2
2
2
)(
2
1
ax
ey
,
где а – центр распределения вероятностей или математическое ожидание
данной случайной величины, т. е. а = М (х);
σ- среднеквадратичное отклонение данной случайной величины.
На практике исчисляются соответствующие статистические оценки.
Так, оценкой для математического ожидания будет средняя величина
а) простая:
n
х
х
или
б) средневзвешенная
n
nх
х
ii
,
a
x
, при
n
,
где n – количество данных в рассматриваемом статистическом массиве.
Математическое ожидание есть то теоретическое значение данной
случайной величины, к которому стремится средняя величина при неогра-
ниченном увеличении количества данных.
Среднеквадратичное отклонение:
n
хх
i
2
)(
или
.
)(
2
i
ii
n
nхх
В логистике то или иное значение величины оценивается значени-
ем
x
x
, при этом вычисляется коэффициент вариации.
.
x
k
При достаточно больших количествах данных σ определяется по
следующей формуле:
,
3
minmax
xx
при n>30, где
minmax
xx
– размах значений

36
На рис. 3.1. представлен график нормального закона распределения
вероятностей.
Рис. 3.1. Нормальный закон распределения вероятностей
3.2. Экспоненциальный закон распределения вероятностей
Плотность экспоненциального закона распределения вероятностей
имеет следующий вид:
t
еу
,
где е – основание натурального логарифма, е= 2,72…
Экспоненциальный закон описывает временные параметры случай-
ных логистических процессов. Под экспоненциальный закон подпадают
следующие случайные величины:
1) время обслуживания покупателей;
2) время погрузки-выгрузки транспортных средств;
3) время, затрачиваемое на выполнение прочих логистических опе-
раций
4) интервал между заявками, приходящими на обслуживание.
Особенностью экспоненциального закона является то, что он опре-
деляется одним параметром λ. При этом
,
1
Т
где
Т
– среднее значение исследуемого временного параметра.
х
у
а
37
Для величин, подчиняющихся экспоненциальному закону, матема-
тическое ожидание М и среднеквадратичное значение равны между собой.
,
1
М
.
1
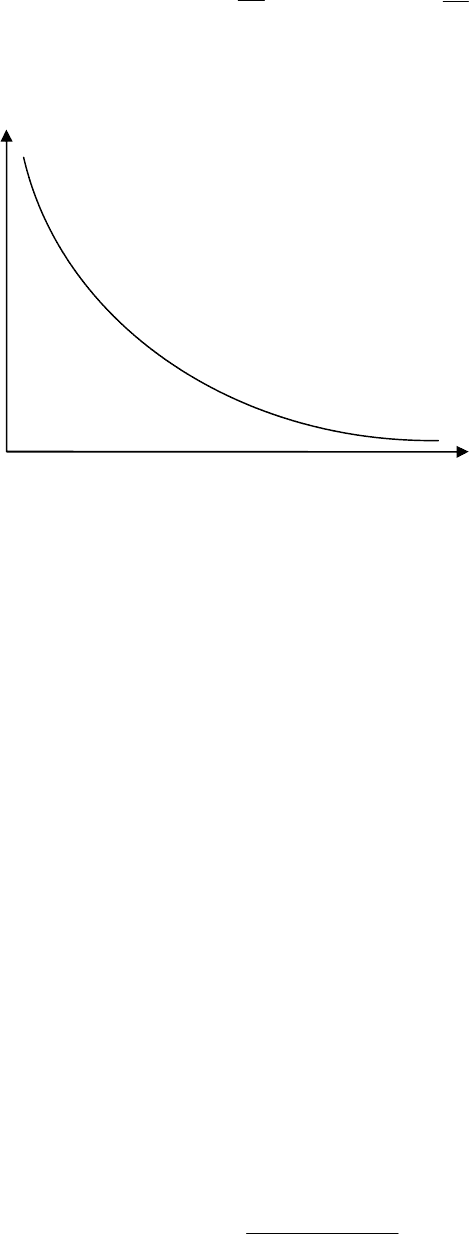
На рис. 3.2 представлен график экспоненциального закона.
Рис. 3.2. Экспоненциальный закон распределения вероятностей
Экспоненциальный закон описывает распределение номенклатуры
продукции в зависимости от частоты её использования в производствен-
но-коммерческой деятельности на группы А, В и С.
3.3. Биноминальный закон распределения вероятностей
Биноминальный закон распределения вероятностей выражается
формулой:
mnmm
nmn
qpCP
,
.
Указанный закон определяет вероятности наступления m событий из
общего числа событий n, где p – вероятность наступления одного события
из данной группы событий;
q – вероятность ненаступления указанного события, q = 1- р.
Величина
m
n
С
– количество сочетаний из n по m, определяется по
формуле:
,
)!(!
!
mnm
n
С
m
n
где n! = 1·2·3·…·n (n – факториал).
у
х
38
Для вычисления числа сочетаний используется равенство:
.
mn
n
m
n
CС
При биноминальном распределении наивероятнейшее число собы-
тий равно:
.pnN
Пример: База снабжает 10 потребителей. Вероятность поступления
заявки от одного потребителя р = 0,8 (q = 0,2), тогда наивероятнейшее
число заявок равно: n p = 10 · 0,8 = 8 заявок. Определить вероятности по-
ступления заявок 0, 1, 2…10.
Решение:
Определяется вероятность поступления наивероятнейшего количе-
ства заявок:
288
108,10
2,08,0 CP
.
Вычисления:
,45
2
109
876543212
10987654321
!8!2
!10
2
10
8
10
СС
0,8
8
= 0,17,
0,2
2
= 0,04, отсюда вероятность при m=8
Р
10,8
= 45·0,7·0,004 = 0,306.
Аналогичным способом вычисляются остальные вероятности. Ре-
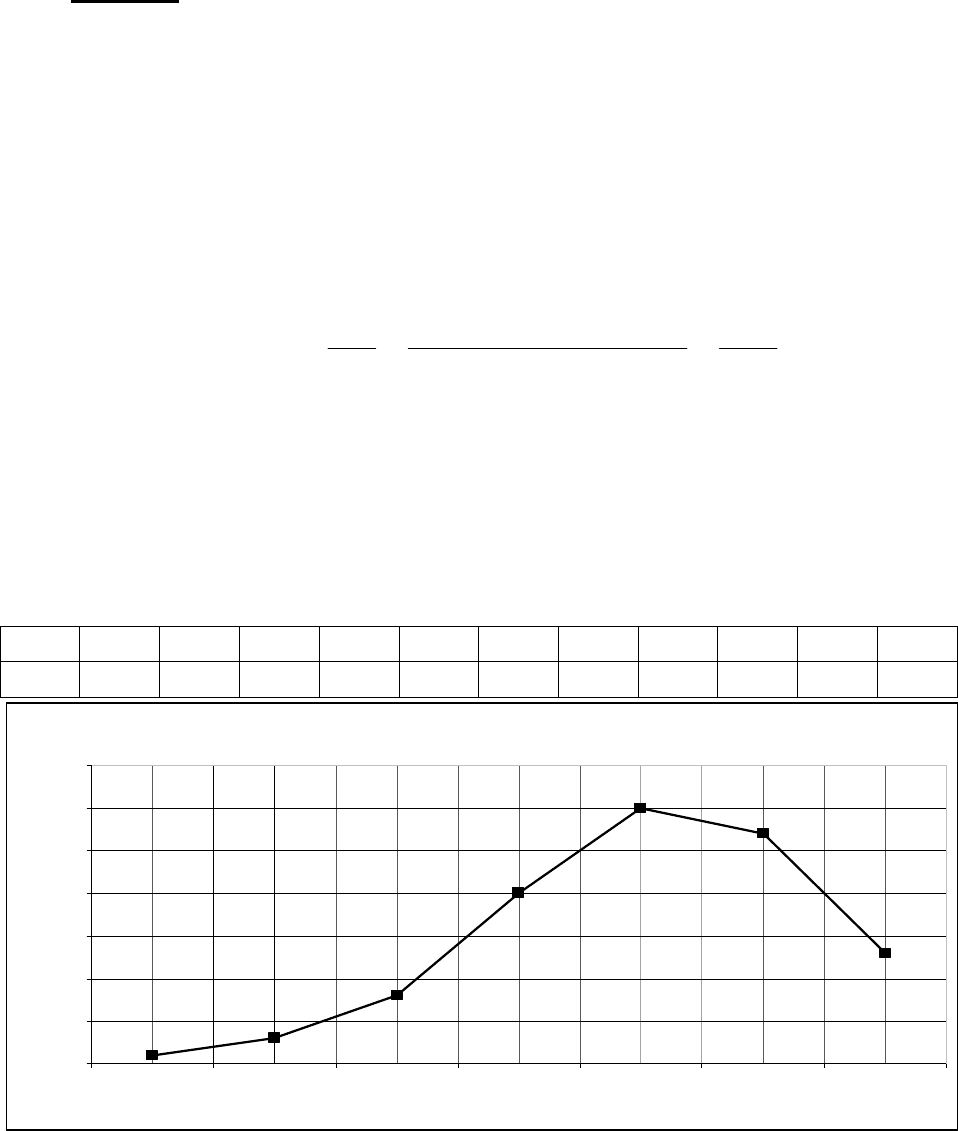
зультаты приведены в табл. 3.1 и на рис. 3.3.
Таблица 3.1
m 0 1 2 3 4 5 6 7 8 9 10
P
10,m
0 0 0 0 0,01 0,03 0,08 0,20 0,30 0,27 0,13
P10,m
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
4 5 6 7 8 9 10
m
P
Рис. 3.3. График распределения вероятностей Р
10,m

39
3.4. Распределение Пуассона
Вероятность того, что в течение времени t произойдет ровно m собы-
тий, определяется по формуле:
.
!
)(
)(
t
m
m
e
m
t
tP
Распределение Пуассона показывает вероятность наступления опре-
деленного числа событий за данный промежуток времени. В логистике с
помощью формулы Пуассона определяется вероятность поступления ав-
томашин на базу, например, в течение одного часа. Из этого следует, что
формула Пуассона моделирует случайный процесс поступления заявок на
то или иное обслуживание, именно поэтому формула Пуассона является
одной из основных в теории массового обслуживания.
3.5. Сравнение законов распределения вероятностей: критерии согласия
В теории вероятностей разработаны методы, позволяющие оцени-
вать степень соответствия фактических распределения вероятностей их
теоретическим значениям. С этой целью используется так называемые
критерии согласия, наиболее известным из которых является критерий χ
2
(«критерий хи-квадрат»). Указанный критерий позволяет сравнивать меж-
ду собой эмпирические законы распределения, полученные по одним и
тем же исходным фактическим данным.
Чем меньше значение χ
2
, тем лучше данный эмпирический закон со-
гласуется с теоретическим. Для сравнения эмпирических законов распре-
деления вероятностей вычисляются значения χ
2
по следующей формуле:
,
)(
2
2
Т
ТФ
п
пп
X
где п
ф
и п
т
– соответственно фактические и теоретические значения частот
исследуемых законов распределения.
Величина χ
2
также является случайной, а поэтому подчиняется сво-
ему закону распределения. Методический подход к сравнению эмпириче-
ских законов распределения иллюстрируется примером.
Следует установить, какой закон распределения вероятностей – нор-
мальный или экспоненциальный – лучше отражает распределение данной
величины, т.е. осуществляется проверка гипотез. В качестве исследуемой
величины прият объем реализации (продаж) определенного товара. Ис-
ходные данные о реализации товара представлены в табл. 3.2.
40
Таблица 3.2
Сведения о реализации товара (исходные данные)
дата
Реализация
(тыс. руб.)
Дата
Реализация
(тыс. руб.)
1 3,5 16 27
2 3,8 17 29,5
3 2,7 18 22,1
4 14,5 19 48,3
5 18,3 20 64,5
6 13,4 21 18,5
7 7,5 22 19,5
8 24,8 23 27,4
9 16,5 24 35
10 12,4 25 42
11 34,5 26 54
12 41,2 27 32,1
13 27,4 28 14,5
14 24,5 29 9,4
15 25,5 30 10
Задача формулируется следующим образом: построить распределение
вероятностей величины спроса на данный товар, если в результате прове-
денного исследования получены результаты о реализации, в тыс. руб. в день.
Для построения нормального и экспоненциального законов распре-
деления вероятностей вычисляются среднее значение реализации товара в
день
х
, среднеквадратическое отклонение σ, а также параметр экспонен-
циального закона λ. Для расчета указанных величин ряд фактических дан-
ных упорядочивается от х
min
до х
max
. Необходимые вычисления представ-
лены в табл. 3.3.
По итогам табл. 3.3 получаем:
1) среднее значение реализации
1,24
30
3,724
n
х
х
i
;
2) среднеквадратическое отклонение:
9,14
30
05,6646
(
n
хх
i
;
3) параметр экспоненциального распределения:
041,0
1,24
1
;
4) вид нормального закона:
8,29
)1,24(
9,142
)1,24(
2
)(
22
2
0268,0
14,329,14
1
2
1
хх
ха
еееу
;
