Питолин В.М., Попова Т.В., Беляков П.Ю., Кобзистый С.Ю. Теоретические основы электротехники: элементы теории с примерами решения задач. Учебное пособие

Подождите немного. Документ загружается.

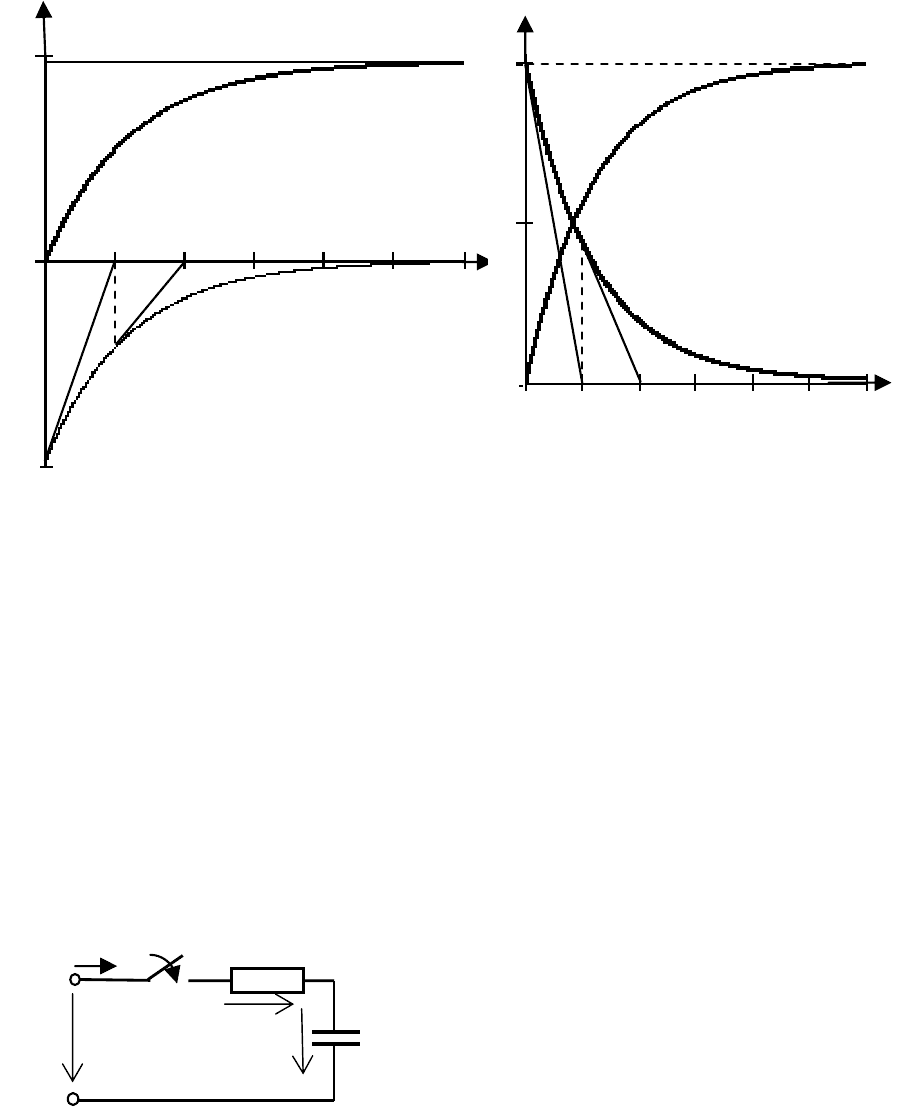
170

ная времени численно равна длине любой подкасательной (рис.

6.2). Для графического определения τ проводится касательная

к кривой свободной составляющей любой электрической ве-

личины в любой точке, и на оси времени находится под-

касательная.

Рис. 6.2 Рис. 6.3

Переходный процесс можно считать практически завер-

шенным через промежуток времени t = 4÷5τ, а теоретически он

длится бесконечно долго, так как экспонента свободной со-

ставляющей никогда не пересечет ось времени.

6.1.4 Переходные процессы в цепи с последовательным

соединением резистора и конденсатора

Рассмотрим переходный процесс при включении цепи R,

C на постоянное напряжение (рис.

6.4). После замыкания ключа в це-

пи возникает ток и конденсатор за-

ряжается до величины напряжения

источника U, после чего ток стано-

вится равным нулю. Это физиче-

(

)

(

)

(

)

Рис. 6.4

i(t)=i

св

(t)+i

пр

(t)

пр

(

)

св

(t)

2τ

3τ 4τ

пп

=5τ

(

)

(t)

2τ

3τ 4τ

(t)

пп

=5τ

171

ское понимание переходного процесса. Опишем теперь этот

процесс математически.

В соответствии со вторым законом Кирхгофа составим

уравнение электрического состояния для рассматриваемой це-

пи относительно напряжения конденсатора:

U)t(u

)t(du

RC)t(u)t(Ri

=+=+ .

Решение этого дифференциального уравнения находится

как сумма свободной и принужденной составляющих:

(t) = u

cсв

+ u

cпр

= Вe

+ U.

Характеристическое уравнение для этой схемы:

pRC + 1 = 0, корень этого уравнения p = –1/RC.

Постоянная времени переходного процесса

==τ

Постоянную интегрирования В найдем, рассмотрев иско-

мую функцию в момент времени t = 0. Так как схема до ком-

мутации была отключена от источника питания, то есть кон-

денсатор не был заряжен, то согласно второму закону комму-

тации начальное значение напряжения на емкости:

(0+) = u

(0–) = 0.

Так как u

(0+)=B + U =0, то В = u

(0+) – U = –U.

Искомая переходная функция имеет вид:

).e1(U)e1(UeUU)t(u

−−−

−=−=⋅−=

Ток в цепи:

−

RC/t

)UeU(d

)t(du

C)t(i.

Напряжение на резистивном элементе с сопротивлением

.UeUe)e

(R)t(iR)t(u

/tRC/tRC/t

τ−−−

===⋅=

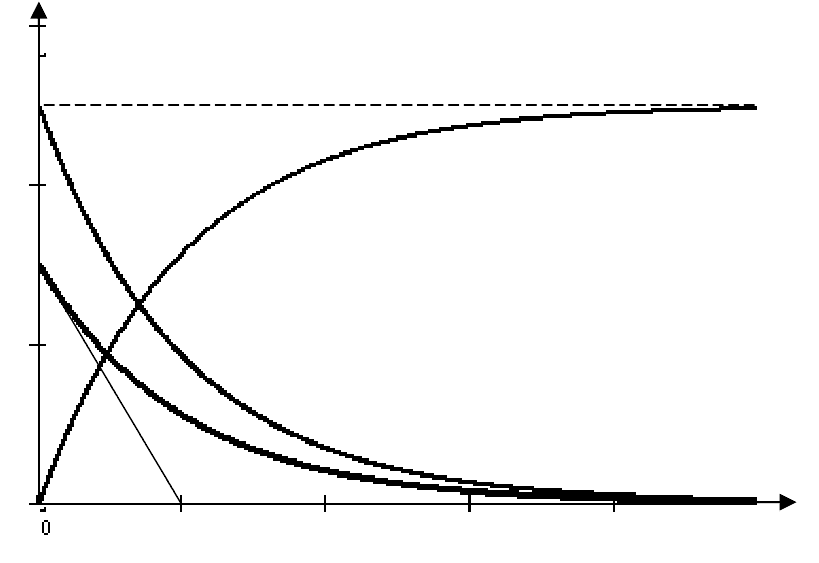
Графики

переходных функций тока и напряжений пред-

172

i, u

τ t

пп

=5τ

i(t)

(t)

ставлены на рис. 6.5.

Рис. 6. 5

6.1.5 Алгоритм расчета переходных процессов

классическим методом

Переходные функции тока и напряжения имеют вид:

i(t) = i

св

(t) + i

пр

, u(t) = u

св

(t) + u

пр

При расчете переходных процессов классическим мето-

дом удобно использовать следующий алгоритм.

1 Показать положительные направления токов и напря-

жений на элементах рассматриваемой цепи. В дальнейшем вы-

бранные направления должны оставаться неизменными.

2 Определить независимые начальные значения, исполь-

зуя законы коммутации i

(0+) = i

(0–) и u

(0+) = u

(0–). Для

этого необходимо рассчитать ток индуктивной катушки i

(0–)

и напряжение на конденсаторе u

(0-) в цепи до коммутации.

3 Рассчитать принужденную составляющую искомой ве-

личины. Для этого необходимо определить

установившиеся

173

значения токов и напряжений в послекоммутационном режи-

ме. Необходимо помнить, что в цепях постоянного тока в уста-

новившемся режиме индуктивная катушка представляет собой

проводник с сопротивлением равным нулю, а конденсатор –

разомкнутый участок цепи.

4 Составить характеристическое уравнение и найти его

корни. Для этого необходимо определить входное сопротивле-

ние Z(p) относительно любых разомкнутых зажимов пассивной

части схемы после коммутации, в которой все источники элек-

трической энергии исключены, а реактивные индуктивные и

емкостные сопротивления заменены на операторные сопротив-

ления Lp и 1/Cp. Полученное выражение приравнивается к ну-

лю и находятся его корни.

5 Рассчитать свободную составляющую

св

(t)=

∑

eA или u

св

(t) =

∑

eB , то есть опреде-

лить постоянные интегрирования А

и В

. Для этого необхо-

димо рассмотреть искомую функцию в момент времени t = 0

и, используя известные значения независимых и зависимых

начальных условий, определить постоянные интегрирования.

6 Построить график временной зависимости искомой

функции на промежутке времени t = 0 ÷ 5τ.

При расчете переходных процессов классическим мето-

дом необходимо иметь в виду, что проще всего вести расчет

тех переходных функций, начальные значения которых опре-

деляются законами коммутации, то есть тока индуктивной ка-

тушки i

(t) и напряжения конденсатора u

(t). Остальные пере-

ходные функции удобно находить с помощью законов Ома и

Кирхгофа, записанных в дифференциальной форме.

6.2 Примеры решения задач

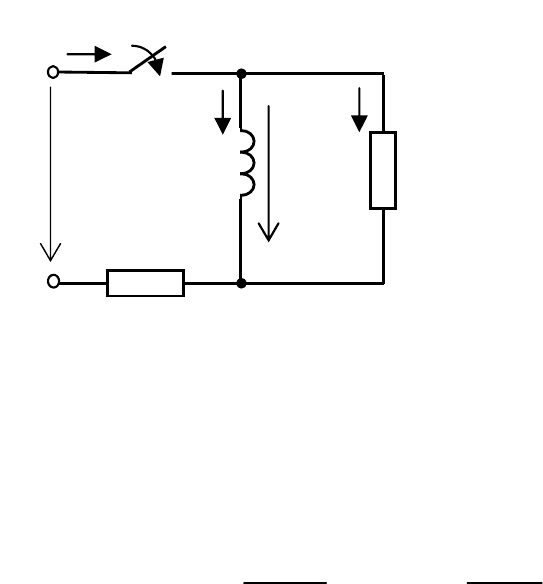
6.2.1 В электрической цепи, схема которой показана на

рис. 6.6, происходит коммутация. Найти зависимость токов

174

ветвей и напряжения индуктивной катушки от времени при пе-

реходном процессе.

Исходные данные U = 50 B, R

= R

= 100 Ом, L = 0,5 Гн.

Расчет переходных

процессов в цепи будем выполнять

согласно алгоритму, приведен-

ному выше.

Покажем положительные

направления токов и напряжений

на элементах электрической цепи.

Электрическая цепь содер-

жит индуктивную катушку, на-

чальное значение тока которой оп-

ределяется по первому закону коммутации. Поэтому определе-

ние переходных функций начнем с нахождения тока индуктив-

ной катушки i

(t). Остальные переходные функции найдем, ис-

пользуя законы Ома и Кирхгофа для мгновенных значений:

)t(di

L)t(u

)t(u

)t(i =

, )t(i)t(i)t(i

2L1

До замыкания ключа электрическая цепь была отключена

от источника напряжения, и токи во всех ветвях отсутствовали.

То есть в докоммутационной цепи ток индуктивной катушки

) = 0.

Согласно первому закону коммутации ток индуктивной

катушки в момент коммутации не может измениться скачком и

в первый момент остается равным докоммутационному значе-

нию i

) = i

) = 0.

Искомая переходная функция тока представляет собой

сумму свободной и принужденной составляющей:

(t) = i

Lсв

(t) + i

Lпр

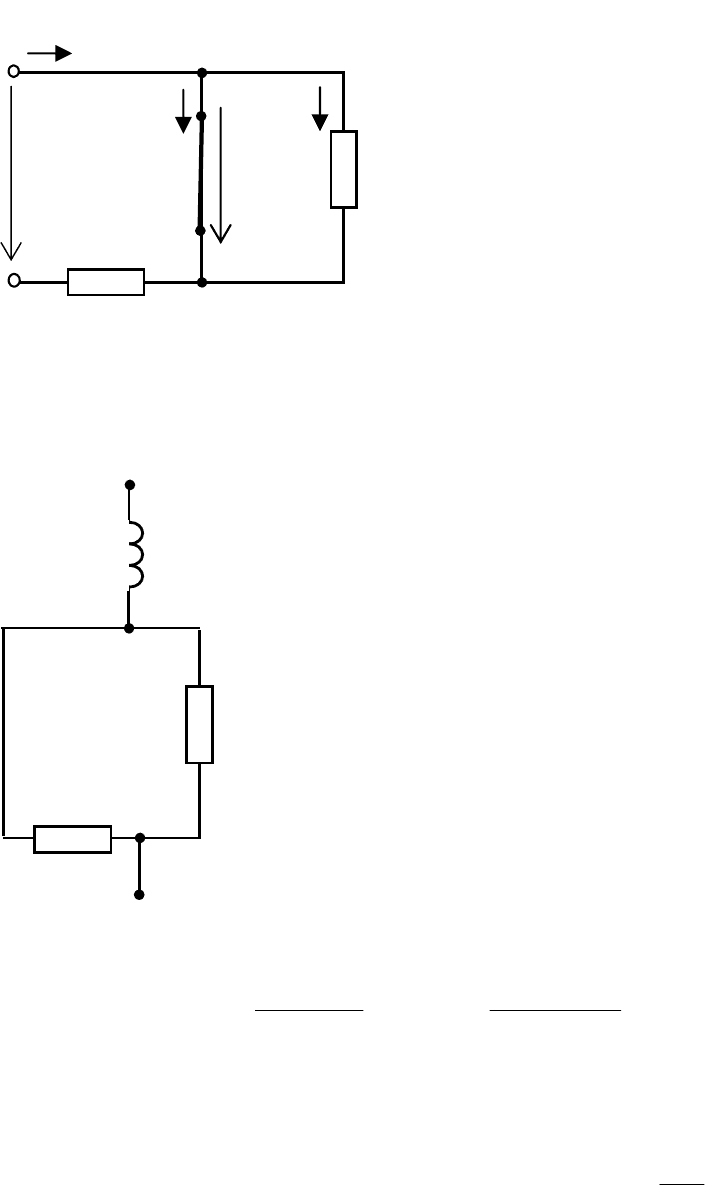
Найдем принужденное значение тока катушки. Для этого

рассчитаем величину тока в установившемся режиме в цепи

после коммутации (рис. 6.7). В цепи постоянного тока в уста-

новившемся режиме идеальная индуктивная катушка пред-

(

)

(t)

Рис. 6.6

(t) i

(

)

175

ставляет собой участок цепи с сопротивлением равным нулю,

напряжение на зажимах которого так же равно нулю u

Lпр

= 0.

Так как катушка и резистор R

со-

единены параллельно, то есть на-

пряжения на их зажимах одинако-

вы и равны нулю, то и принужден-

ное значение тока второй ветви

2пр

= 0.

Принужденный ток катушки:

Lпр

= i

1пр

=U/R

=50/100=0,5 А.

Для определения свободной

составляющей необходимо соста-

вить характеристическое уравне-

ние и найти его корни.

Составим характеристическое уравне-

ние путем определения входного сопротив-

ления Z(p) пассивной части цепи после

коммутации (рис. 6.8). В рассматриваемой

цепи источник напряжения заменяется ко-

роткозамкнутым участком, а индуктивная

катушка операторным сопротивлением Lp.

Наиболее целесообразно размыкать цепь на

участке, который содержит реактивный эле-

мент. В нашем случае находим входное со-

противление относительно разомкнутых за-

жимов ветви, содержащей индуктивную ка-

тушку:

50p5,0

100100

p5,0

Lp)p(Z

⋅

+= .

Приравняв полученное выражение нулю, получим харак-

теристическое уравнение:

050p5,0 =+ , которое имеет один корень c/1100

5,0

p −=−= .

1п

Lпр

Рис. 6.7

Lпр

2п

Рис. 6.8

176

Свободную составляющую тока катушки запишем

t100pt

AeАеi

−

== . Для нахождения постоянной интегрирова-

ния А рассмотрим искомую функцию тока

(t) = i

Lсв

(t) + i

Lпр

= 5,0Ae

t100

−

в момент времени t = 0

)=А+0,5.

Так как согласно закону коммутации i

) = 0, то полу-

чим уравнение А + 0,5 = 0, откуда найдем значение постоянной

интегрирования А = –0,5 (А).

Переходная функция тока катушки i

(t) = –0,5е

-100t

+0,5

(А).

Напряжение индуктивной катушки:

).B(e25e)5,0)(100(5,0

)5,0e5,0(d

5,0

)t(di

L)t(u

t100t100

t100

−−

−

=−−=

+−

Ток второй ветви:

t100

e25,0

100

e25

)t(u

)t(i

−

===

(А).

Входной ток:

)t(i)t(i)t(i

2L1

= (–0,5е

-100t

+ 0,5) + 0,25е

-100t

= –0,25e

-100t

+ 0,5 (A).

Временные зависимости токов и напряжения индуктив-

ной катушки показаны на рис. 6.9, 6.10, 6.11. График переход-

ного процесса строится на промежутке времени t = 5τ, так как

за это время свободная составляющая переходной функции

практически становится равной нулю и переходный процесс

завершается. Постоянная времени τ = 1/|р| = 1/100 = 0,01 с.

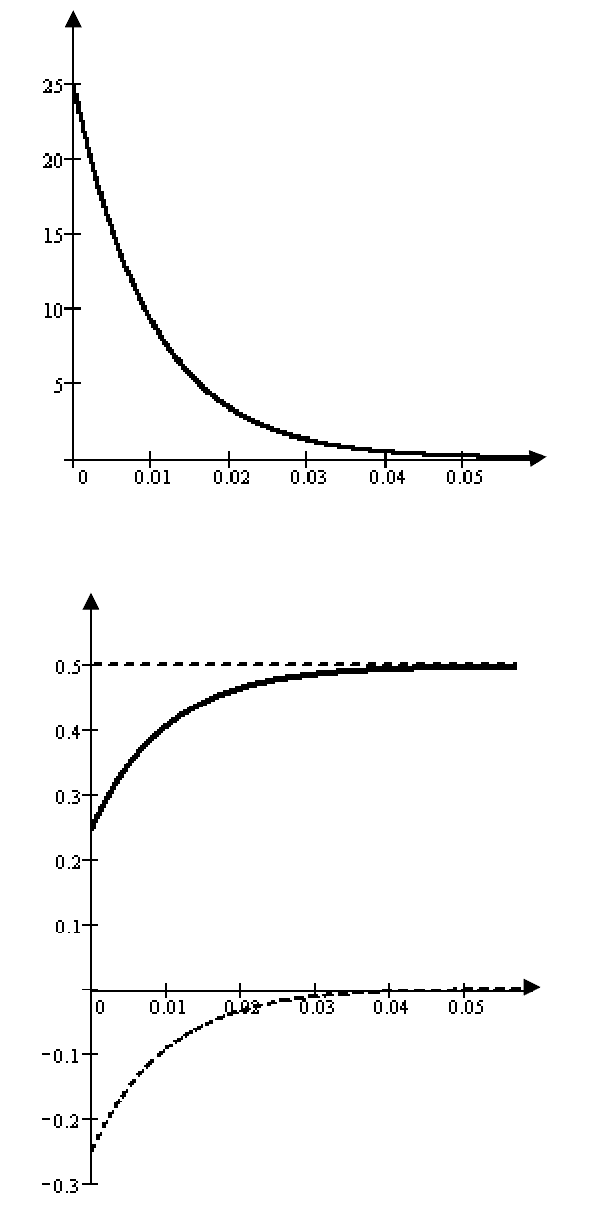
177

i(t)= i

пр

(t)+ i

св

(t)

i(t), A

св

(t)

пр

(t)

Рис. 6.10

(t), B

(t)

t, c

Рис. 6.9

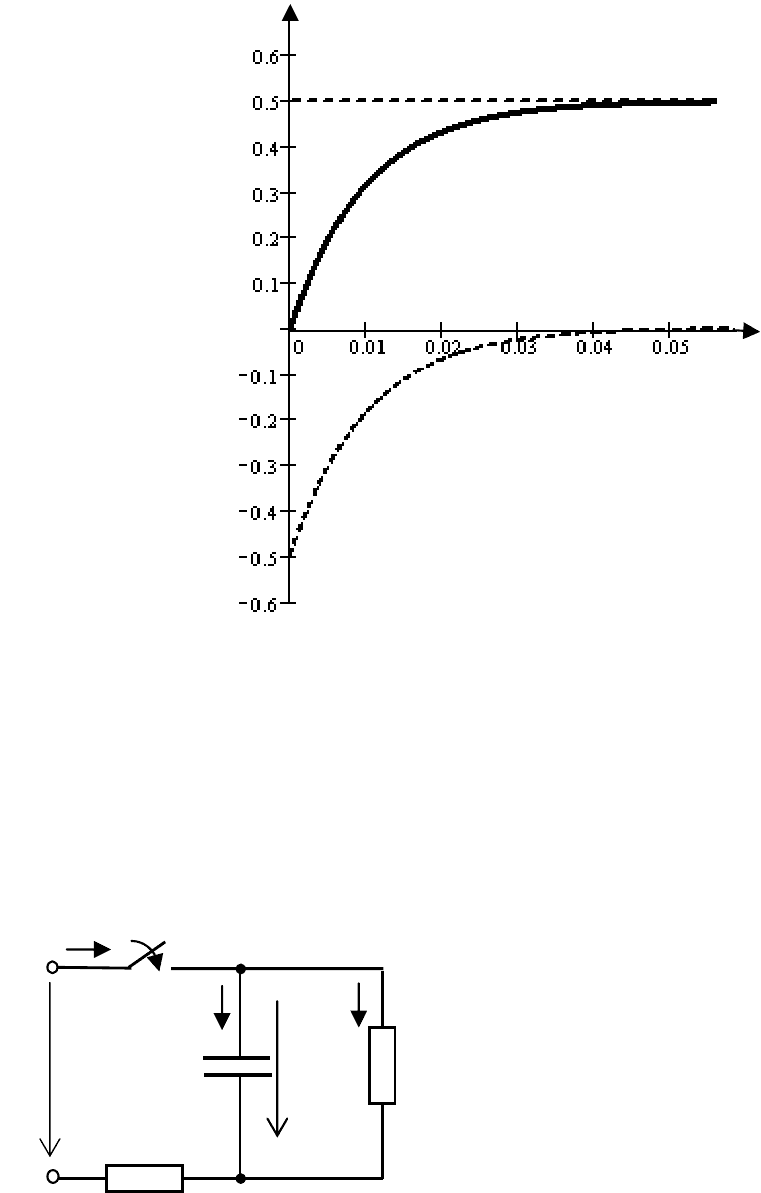
178

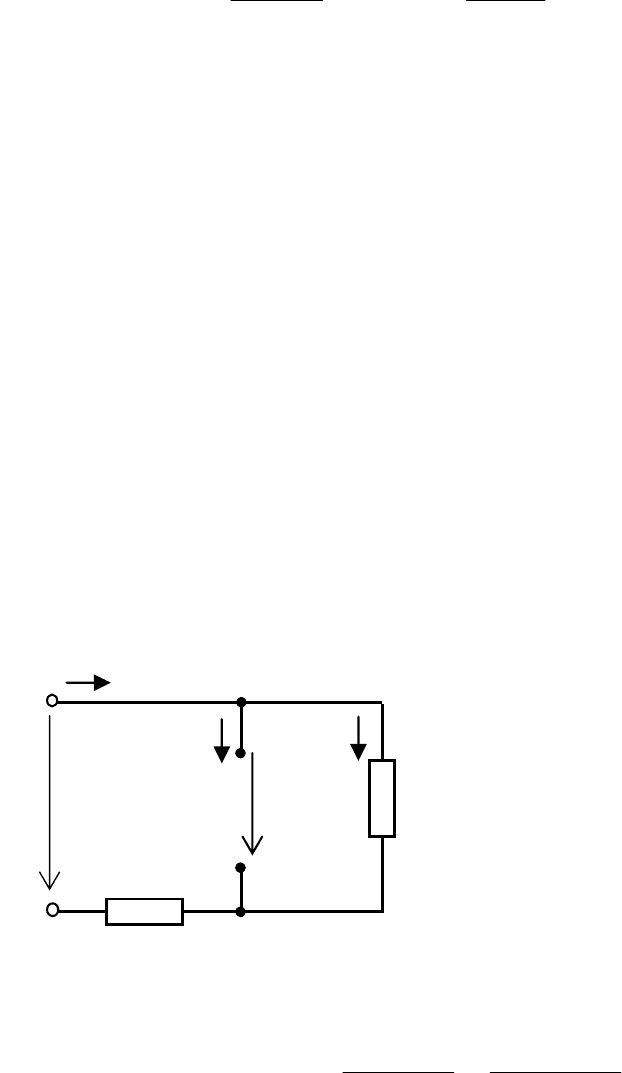
6.2.2 В электрической цепи, схема которой показана на

рис. 3.12, происходит коммутация. Найти зависимость от вре-

мени токов ветвей и напряжения конденсатора при переходном

процессе.

Исходные данные: U = 100 B, R

= R

= 100 Ом, С = 10

мкФ.

На схеме указаны положи-

тельные направления токов и на-

пряжений на всех элементах элек-

трической цепи.

Электрическая цепь содержит

конденсатор, начальное значение

напряжения на котором определя-

ется по второму закону коммута-

ции. Поэтому определение пере-

ходных функций начнем с нахож-

(

)

t, c

пр

св

(t)

(t)= i

пр

(t)+ i

св

(t)

Рис. 6.11

(

)

(t)

Рис. 6.12

(t) i

(

)

179

дения напряжения конденсатора u

(t). Остальные переходные

функции найдем, используя законы Ома и Кирхгофа для мгно-

венных значений:

)t(du

C)t(i

)t(u

)t(i = ,

)t(i)t(i)t(i

2C1

До замыкания ключа электрическая цепь была отключена

от источника напряжения, токи во всех ветвях отсутствовали и

конденсатор не был заряжен. То есть в докоммутационной це-

пи напряжение конденсатора u

) = 0.

Согласно второму закону коммутации напряжение кон-

денсатора в момент коммутации не может измениться скачком

и в первый момент остается равным докоммутационному зна-

чению u

)=u

)=0.

Искомая переходная функция напряжения конденсатора

представляет собой сумму свободной и принужденной состав-

ляющей:

(t) = u

Cсв

(t) + u

Cпр

Для определения принужденной составляющей рассчита-

ем установившееся значение напряжения конденсатора в схеме

после коммутации (рис. 6.13). При

составлении схемы для расчета

принужденных значений необхо-

димо помнить, что в установив-

шемся режиме в цепи постоянного

тока конденсатор представляет со-

бой разомкнутый участок цепи.

В ветви с конденсатором ток

не протекает i

Спр

= 0, входной ток

равен току второй ветви и опреде-

ляется по закону Ома:

1пр

= i

2пр

= A5,0

100100

100

Напряжение конденсатора равно напряжению второй

ветви, которая соединена с ним параллельно:

1п

Cп

Рис. 6.13

Спр

2п