Питолин В.М., Попова Т.В., Беляков П.Ю., Кобзистый С.Ю. Теоретические основы электротехники: элементы теории с примерами решения задач. Учебное пособие
Подождите немного. Документ загружается.

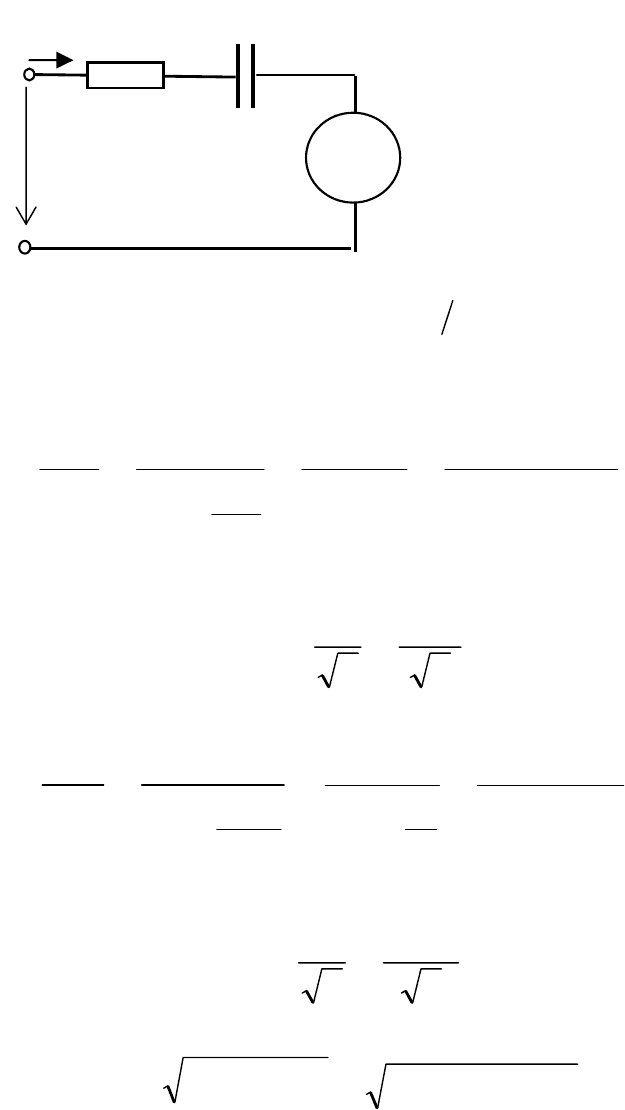
120
4.2.2 Определить показания амперметра в цепи, схема
которой представлена на рис.
4.11, рассчитать активную
мощность всей цепи, записать
выражение мгновенного
значения тока цепи и
построить графики временных
зависимостей входного тока
i(t) и напряжения u(t), если:
=
ω
C1
11 Ом; R = 10 Ом;
а подведенное напряжение: u(t) = 310sin(ωt) + 176sin(3ωt).
Ток основной гармоники:
.Ae9,20
e87,14
310
11j10
310
C
1
jR
U
Z
U
I
73,47j
73,47j
)1(
m
)1(
)1(
m
)1(
m
o
o
&&
&
==
−
=
ω
−
==
−
Действующее значение тока первой гармоники:
.A8,14
2
9,20
2
I
I
)1(
m
)1(
===
Ток третьей гармоники:
=
ω
−
==
C3
1
jR
U
Z
U
I
)3(
m
)3(
)3(
m
)3(
m
&&
&
.Ae52,16
e65,10
176
3
11
j10
176
20j
20j
o
o
==
−
−
Действующее значение тока третьей гармоники:
.A72,11
2
52,16
2
I
I
)3(
m
)3(
===
Показания амперметра:
A9,1872,118,14III
22
2
)3(
2
)1(
=+=+=
.
Выражение для мгновенного значения тока:
.A),20t3sin(1,5)73,47tsin(9,20
)t3sin(I)tsin(Iii)t(i
3
)3(
m1
)1(
m
)3()1(
oo
+ω++ω=
=ψ+ω+ψ+ω=+=
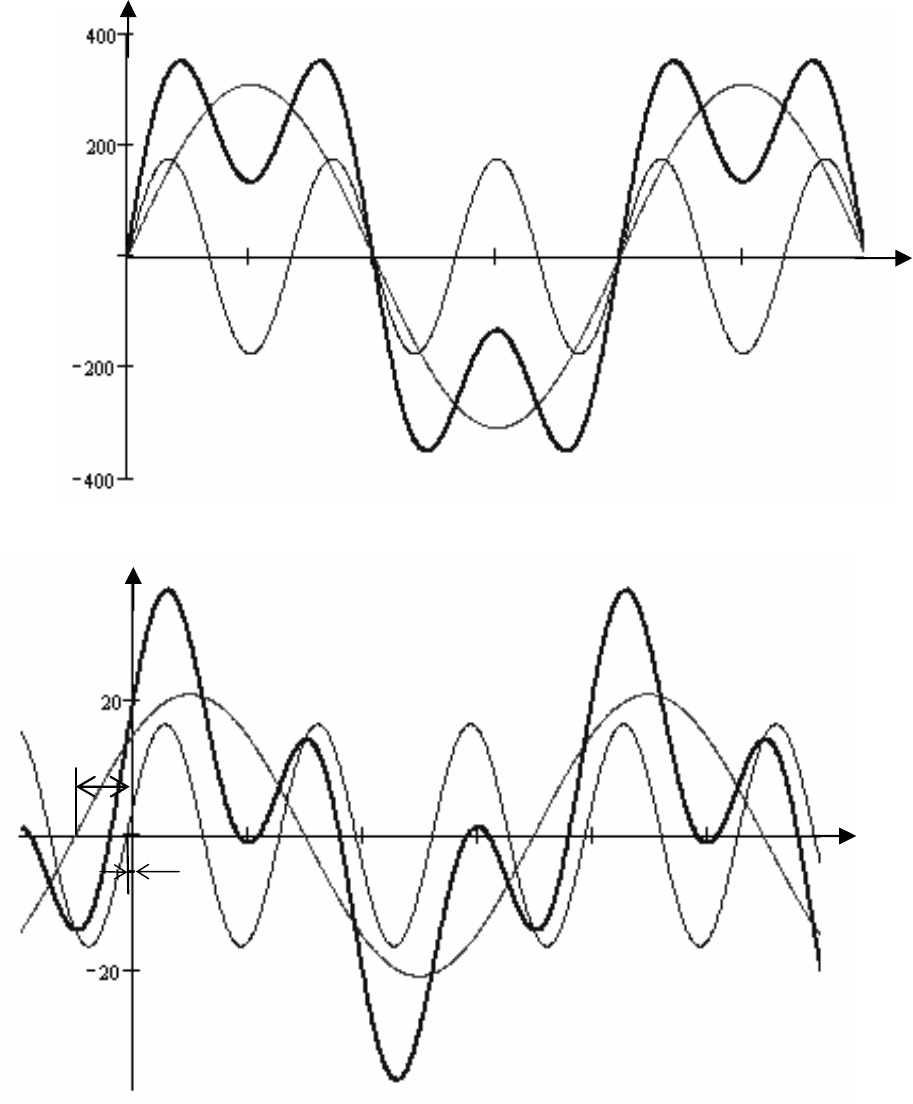
На рис. 4.12 и 4.13 представлены графики временных за-
R
i
(
t
)
С
u (t)
Рис. 4.11
А
121
висимостей входного напряжения и тока, а также составляю-
щих их гармоник.
ωt
u
(1)
u, B
u
(3)
u= u
(1)
+ u
(3)
2π
π
Рис. 4. 12
ωt
i
(1)
i
,
A
i
(3)
i = i
(1)
+ i
(3)
ψ
i1
2π
π
ψ
i3
Рис. 4.13
122
Активная мощность цепи:
.Вт35709,1810RIRIRI
cosIUcosIUPPP
22
2
)3(
2
)1(
3
)3()3(
1
)1()1()3()1(
=⋅==+=
=ϕ+ϕ=+=
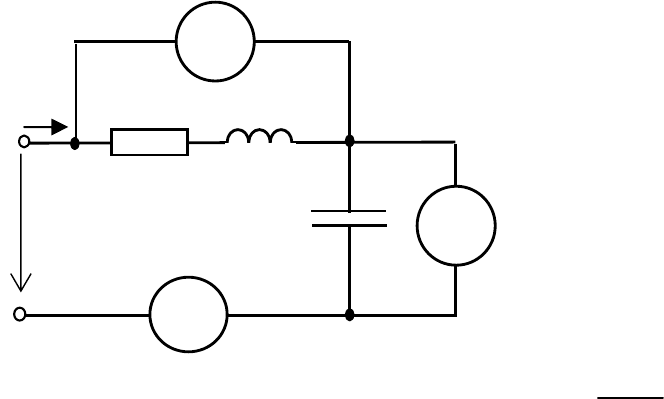
4.2.3 Определить показания приборов электромагнитной
системы в цепи, схе-
ма которой показана
на рис. 4.14, записать
выражение мгновен-
ного значения тока и
построить временные
зависимости напря-
жения u(t) и тока i(t),
если:
R = 50 Ом, ωL = 10
Ом,
=
ωC
1
90 Ом.
На вход цепи подано несинусоидальное напряжение, за-
данное в виде ряда Фурье:
u(t) = 100 + 310sin(ωt + 30°) + 106sin(3ωt – 30°).
Рассчитаем токи и напряжения нулевой гармоники.
Постоянная составляющая тока I
(0)
в цепи отсутствует,
так как сопротивление конденсатора на постоянном токе равно
бесконечности Х
С
= ∞, то есть конденсатор представляет собой
разомкнутый участок цепи. Напряжение постоянной состав-
ляющей U
(0)
приложено к месту разрыва цепи, то есть к кон-
денсатору:
B100UUU
)0(
2
)0()0(
C
=== .
Постоянные составляющие напряжений на остальных
участках цепи равны нулю.
Рассчитаем токи и напряжения
первой гармоники.
Комплексное сопротивление первой гармоники:
R
i
(
t
)
L
u (t)
Рис. 4.14
А
V
1
С
V
2
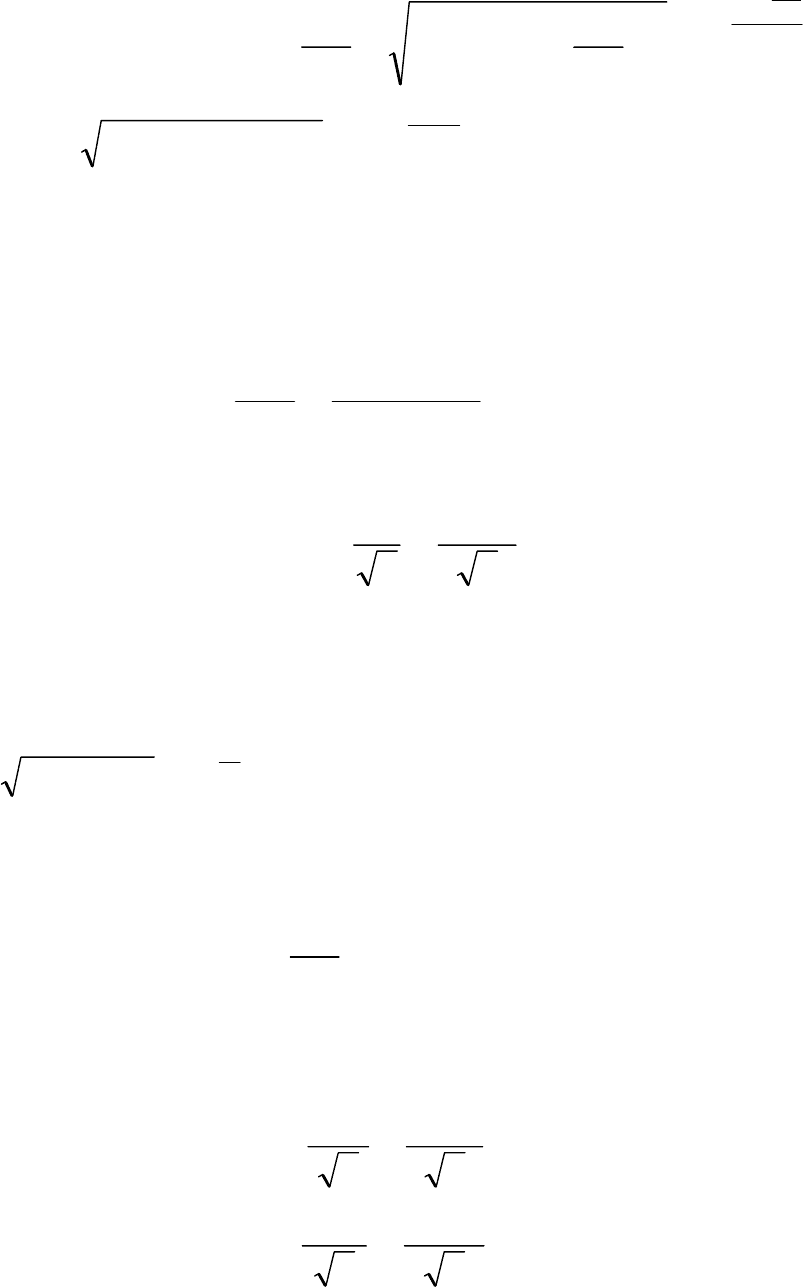
123
.Омe34,94e)9010(50
e)
C
1
L(R
C
1
jLjRZ
58j
50
9010
jarctg
22
R
C
1
L
jarctg
22)1(
o
−
−
ω
−ω
⋅=⋅−+=
=⋅
ω
−ω+=
ω
−ω+=
Комплексная амплитуда входного напряжения первой
гармоники:
Be310U
30j)1(
m
o
&
=
.
Ток основной гармоники:
.Ae286,3
e34,94
e310
Z
U
I
88j
58j
30j
)1(
)1(
m
)1(
m
o
o
o
&
&
===
−
Действующее значение тока первой гармоники:
.A33,2
2
286,3
2
I
I
)1(
m
)1(
===
Комплексная амплитуда напряжения первой гармоники
на зажимах индуктивной катушки:
.Be6,167e286,3e51e286,3e1050
e286,3)10j50(I)LjR(U
3,99j88j3,11j88j
50
10
jarctg
22
88j)1(
m
)1(
m1
oooo
o
&&
=⋅=⋅+=
=⋅+=⋅ω+=
Комплексная амплитуда напряжения первой гармоники
на конденсаторе:
.Be7,295e286,3e90
e286,3)90j(I)
C
1
j(U
2j88j90j
88j)1(
m
)1(
m2
ooo
o
&&
−−
=⋅=
=⋅−=⋅
ω
−=
Действующие значения напряжений первой гармоники:
,B9,118
2
6,167
2
U
U
)1(
m1
)1(
1
===
.B7,209
2
7,295
2
U
U
)1(
m2
)1(
2
===
Выполним расчет тока и напряжений
третьей гармони-
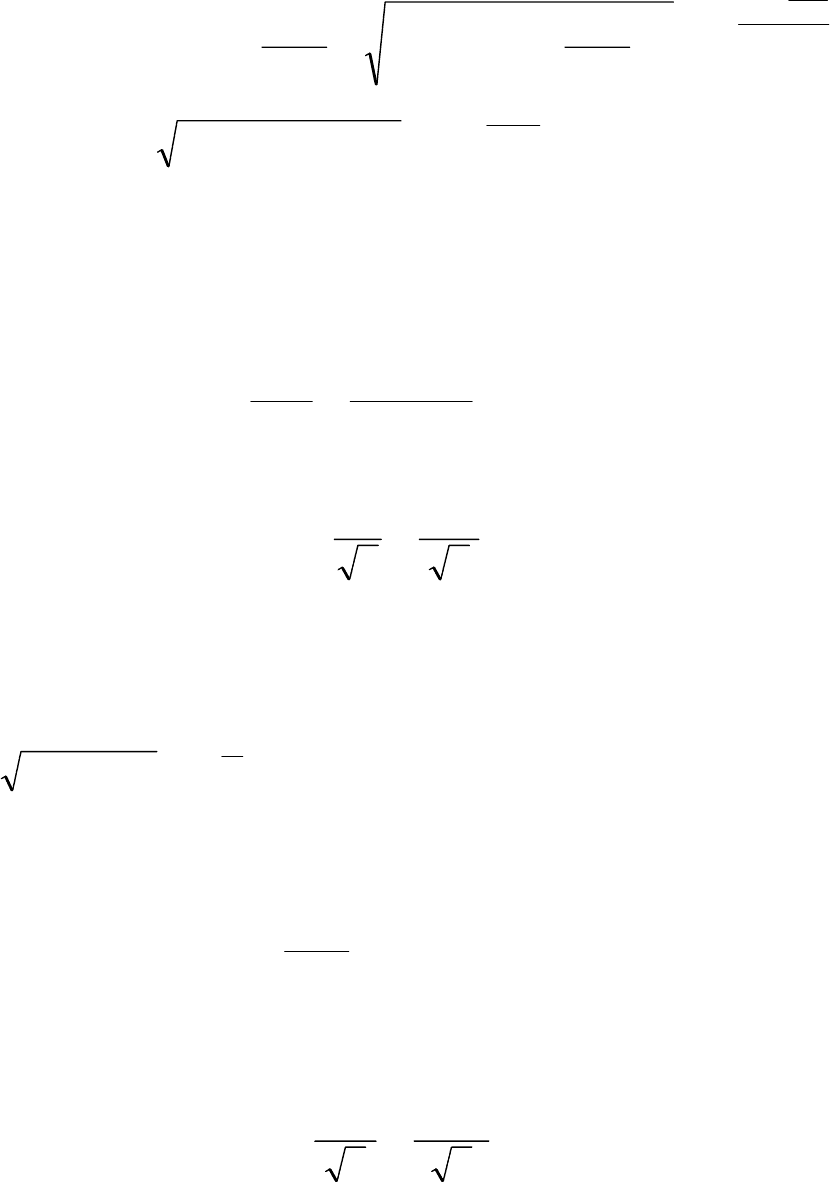
124
ки.
Комплексное сопротивление третьей гармоники:
.Омe50e)3030(50
e)
C3
1
L3(R
C3
1
jL3jRZ
0j
50
3030
jarctg
22
R
C3
1
L3
jarctg
22)3(
o
⋅=⋅−+=
=⋅
ω
−ω+=
ω
−ω+=
−
ω
−ω
Комплексная амплитуда входного напряжения третьей
гармоники:
Be106U
30j)3(
m
o
&
−
= .
Ток третьей гармоники:
.Ae12,2
e50
e106
Z
U
I
30j
0j
30j
)3(
)3(
m
)3(
m
o
o
o
&
&
−
−
===
Действующее значение тока третьей гармоники:
.A5,1
2
12,2
2
I
I
)3(
m
)3(
===
Комплексная амплитуда напряжения третьей гармоники
на зажимах индуктивной катушки:
.Be6,123e12,2e3,58e12,2e3050
e12,2)30j50(I)L3jR(U
1j30j31j30j
50
30
jarctg
22
30j)3(
m
)3(
m1
oooo
o
&&
=⋅=⋅+=
=⋅+=⋅ω+=
−−
−
Комплексная амплитуда напряжения третьей гармоники
на конденсаторе:
.Be6,63e12,2e30
e12,2)30j(I)
C3
1
j(U
120j30j90j
30j)3(
m
)3(
m2
ooo
o
&&
−−−
−
=⋅=
=⋅−=⋅
ω
−=
Действующие значения напряжений третьей гармоники:
,B7,87
2
6,123
2
U
U
)3(
m1
)3(
1
===
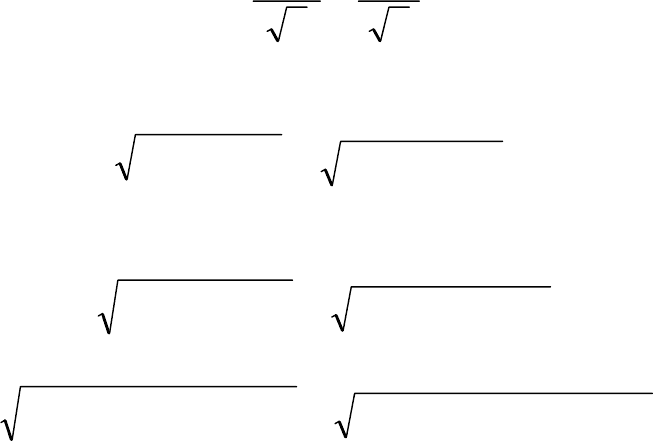
125
.B8,57
2
6,63
2
U
U
)3(
m2
)3(
2
===
Амперметр измеряет действующее значение входного то-
ка:
.A77,25,133,2III
22
2
)3(
2
)1(
=+=+=
Показания первого и второго вольтметров, также
измеряющих действующие значения напряжений:
,B7,1477,879,118UUU
22
2
)3(
1
2
)1(
11V
=+=+=
.B4,2398,577,209100UUUU
222
2
)3(
2
2
)1(
2
2
)0(
22V
=++=++=
Выражение для мгновенного значения тока можно
записать в виде:
.A),30t3sin(12,2)88tsin(286,3
)t3sin(I)tsin(Iii)t(i
3
)3(
m1
)1(
m
)3()1(
oo
−ω++ω=
=ψ+ω+ψ+ω=+=
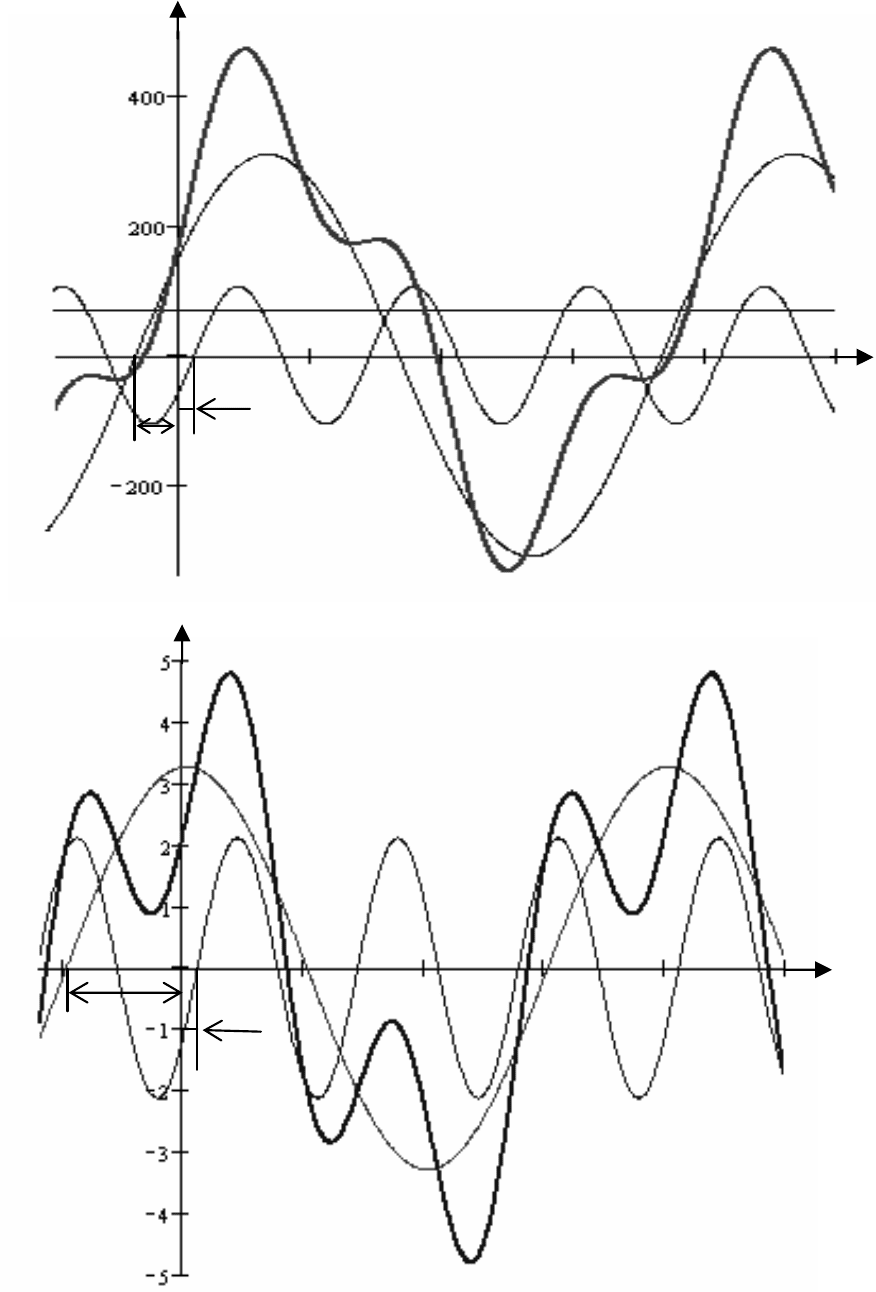
На рис. 4.15 и 4.16 представлены графики временных за-
висимостей входного напряжения и тока, а также составляю-
щих их гармоник.
При вычерчивании кривых отдельных гармоник учитыва-
ем тот факт, что период гармоники обратно пропорционален ее
номеру. То есть период третьей гармоники в три раза меньше
периода первой гармоники. А так как по оси абсцисс отклады-
ваем величину ωt, то при построении графиков третьей гармо-
ники напряжения и тока их начальные фазы необходимо раз-
делить на номер гармоники.
126
i
(1)
(t)
i
(3)
(t)
i
(
t
)
=i
(1)
(
t
)
+i
(3)
(
t
)
ωt
i(ωt), A
Ψ
i1
Ψ
i3
π
2π
Рис. 4.16
u
(0)
u
(1)
(t)
u
(3)
(t)
u(t)=u
(0)
+u
(1)
+u
(3)
ωt
π
2π
ψ
u1
ψ
u3
u
(1)
,B
Рис. 4. 15
127
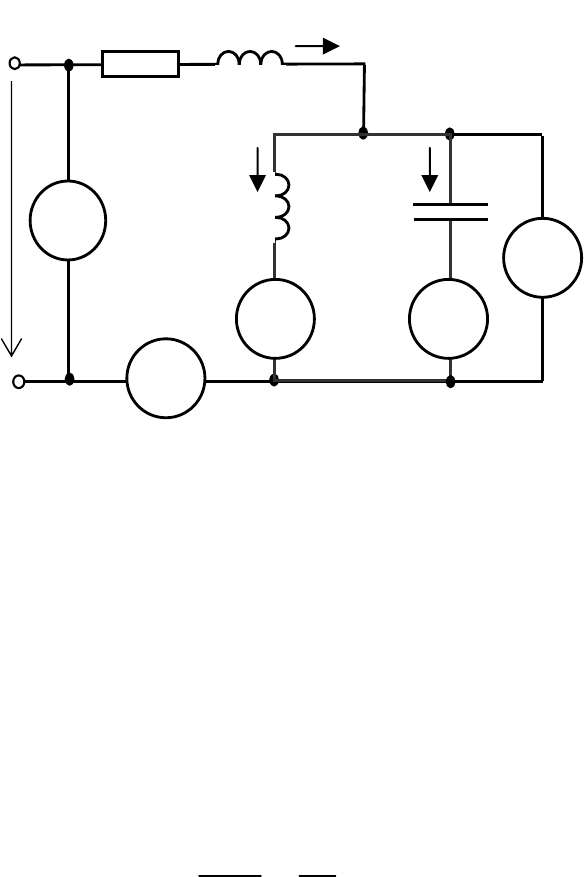
4.2.4 На вход электрической цепи, схема которой
приведена на рис. 4.17, подано несинусоидельное напряжение,
аналитически заданное в виде разложения в ряд Фурье:
t3sin85,2)30tsin(07,75)t(u ω++ω+=
o
.
Определить показания приботов электромагнитной
системы и мощность, потребляемую цепью.
Параметры элементов цепи: R = 50 Ом, L = 0,00625 Гн, L
1
= 0,05 Гн, С = 2·10
-5
Ф, ω = 1000 рад/с.
Токи в цепи рассчитываем методом наложения. Расчет
для каждой из гармоник будем выполнять в комплексной
форме.
Определим
постоянную составляющую токов в каждой
из ветвей. Так как в цепи постоянного тока конденсатор
представляет собой разомкнутый участок цепи, а идеальная
катушка короткозамкнутый участок, то нулевая гармоника
тока второй ветви отсутствует, а входной ток равен току
первой ветви и определяется:
.A1,0
50
5
R
U
II
)0(
)0(
1
)0(
====
Постоянная составляющая напряжения на зажимах
параллельных ветвей равна нулю.
R
L
u (t)
Рис.4.17
V
1
С
L
1
V
2
i
1
(
t
)
i
2
(
t
)
A
1
A
2
A
i
(
t
)

128
Выполним расчет для
первой гармоники.
Сопротивления реактивных элементов для первой
гармоники:
;Ом25,60062,01000LX
)1(
L
=⋅=ω=
;Ом5005,01000LX
1
)1(
1L
=⋅=ω=
.Ом50
21000
10
C
1
X
5
)1(
C
=
⋅
=
ω
=
Реактивные опротивления параллельных ветвей равны, то
есть в цепи наблюдается резонанс токов и комплексное
сопротивление параллельных ветвей:
.
0
)50j(50j
50j50j
)50j(50j
jXjX
)jX(jX
Z
)1(
C
)1(
1L
)1(
C
)1(
1L
)1(
12
∞=
−⋅
=
−
−⋅
=
−
−⋅
=
Тогда первая гармоника входного тока равна нулю
.0I
)1(
m
=
&
Все входное напряжение первой гармоники приложено к
параллельному контуру: .e07,7UU
30j)1(
m
)1(
2m
o
&&
==
Можно определить комплексные амплитуды токов
параллельных ветвей:
,Ae14,0
e50
e07,7
50j
e07,7
jX
U
I
60j
90j
30j30j
)1(
1L
)1(
m
)1(
1m
o
o
oo
&
&
−
====
.Ae14,0
e50
e07,7
50j
e07,7
jX
U
I
120j
90j
30j30j
)1(
C
)1(
m
)1(
2m
o
o
oo
&
&
==
−
==
−
Действующие значения напряжения и токов
параллельных ветвей:
,B5
41,1
07,7
2
U
U
)1(
2m
)1(
2
===
.A1,0
41,1
14,0
2
I
II
)1(
m
)1(
2
)1(
1
====
Рассчитаем токи и напряжения для третьей гармоники.
С увеличением намера гармоники индуктивные

129
сопротивления увеличиваются, а емкостные уменьшаются:
;Ом75,1800625,010003L3X3X
)1(
L
)3(
L
=⋅⋅=ω==
;Ом15005,010003L3X3X
1
)1(
1L
)3(
1L
=⋅⋅=ω==
.Ом66,16
210003
10
C3
1
3
X
X
5)1(
C
)3(
C
=
⋅⋅
=
ω
==
Комплексное сопротивление параллельных ветвей для
третьей гармоники:
.Ом75,18j
34,133j
2500
66,16j150j
)66,16j(150j
jXjX
)jX(jX
Z
)3(
C
)3(
1L
)3(
C
)3(
1L
)3(
12
−==
−
−⋅
=
−
−⋅
=
Входное сопротивление для третьей гармоники:
.Ом5075,18j75,18j50ZjXRZ
)3(
12
)3(
L
(3)
=−+=++=
Входной ток:
.A057,0
50
82,2
Z
U
I
)3(
)3(
m
)3(
m
===
&
&
Его действующее значение;
.A04,04,1/057,02/II
)3(
m
)3(
===
Напряжение на параллельных ветвях:
.Be069,1057,0e75,18IZU
90j90j)3(
m
)3(
12
)3(
2m
oo
&&
−−
=⋅==
Третья гармоника токов параллельных ветвей:
,Ae0071,0
e150
e069,1
150j
e069,1
jX
U
I
180j
90j
90j90j
)3(
1L
)3(
m
)3(
1m
o
o
oo
&
&
−
−−
====
.Ae0642,0
e66,16
e069,1
66,16j
e069,1
jX
U
I
0j
90j
90j90j
)3(
C
)3(
m
)3(
2m
o
o
oo
&
&
==
−
==
−
−−
Действующие значения напряжения и токов парал-
лельных ветвей:
,A005,0
41,1
0071,0
2
I
I
)3(
1m
)3(
1
===
,A045,0
41,1
0642,0
2
I
I
)3(
2m
)3(
2
===
