Питолин В.М., Попова Т.В., Беляков П.Ю., Кобзистый С.Ю. Теоретические основы электротехники: элементы теории с примерами решения задач. Учебное пособие
Подождите немного. Документ загружается.

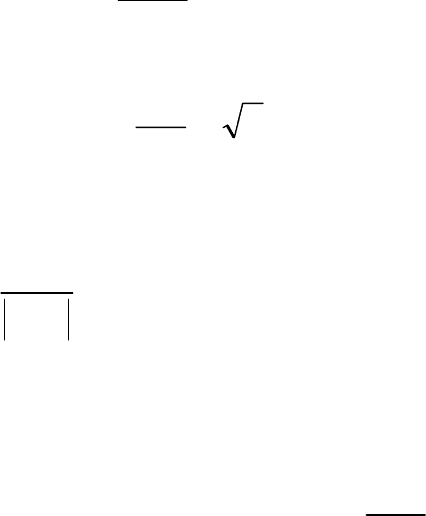
110
ного значения несинусоидального напряжения или тока к дей-
ствующему значению:
U
U
K
max
a
=
.
Коэффициент амплитуды для синусоидальной функции:
.2
U
U
K
m
a
==
Коэффициент
формы равен отношению действующего
значения несинусоидальной функции к его среднему по моду-
лю значению:
СР
Ф
U
U
K =
.
Для синусоидальной функции К
Ф
= 1,11.
Коэффициент
искажения определяется, как отношение
действующего значения первой гармоники к действующему
значению несинусоидальной функции:
U
U
K
)1(
И
=
.
Для синусоидальной функции коэффициент искажения
К
И
= 1.
В промышленных сетях кривые напряжения отличаются
от идеальной синусоиды. Поэтому в электроэнергетике вводят
понятие о
практически синусоидальной кривой. По стандарту
коэффициент искажения напряжения сети равен 0,995, поэтому
анализ систем электроснабжения проводят в предположении
синусоидальности напряжения.
4.1.5 Измерение несинусоидальных периодических
напряжений и токов
При измерении несинусоидальных токов и напряжений
измерительными приборами различных систем можно полу-
чить неодинаковые результаты.
Приборы электромагнитной, электродинамической, элек-
тростатической и тепловой систем реагируют на действующее
значение измеряемой величины. Магнитоэлектрические при-
111
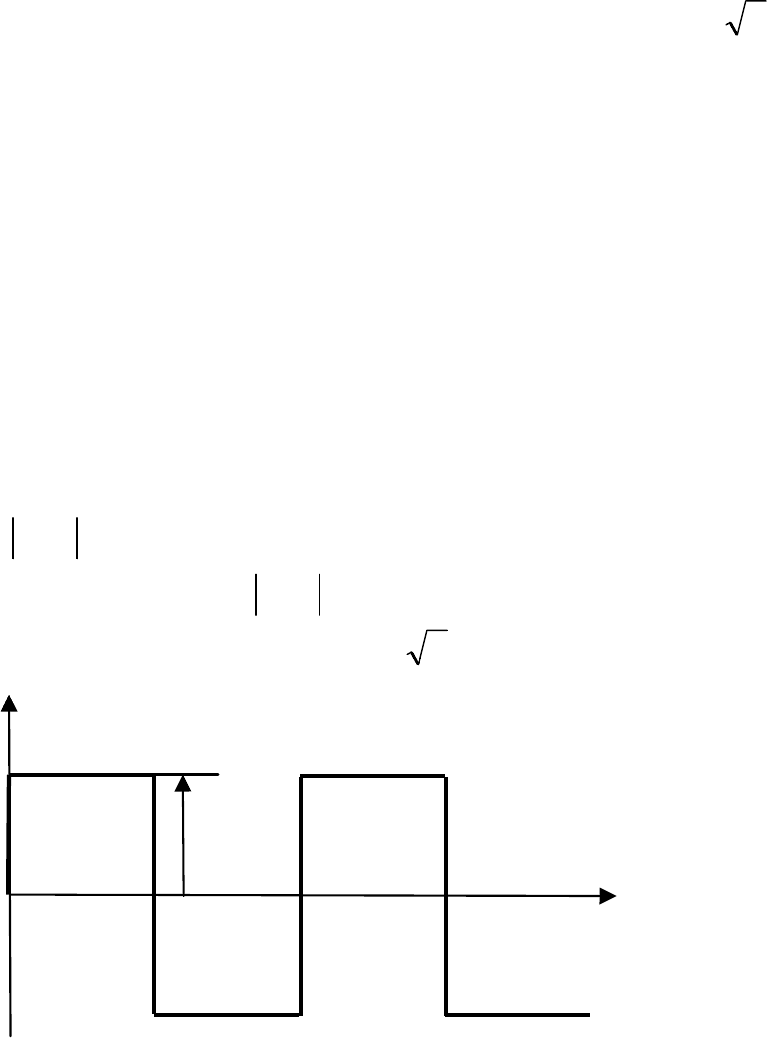
боры без выпрямителя реагируют на постоянную составляю-
щую, с выпрямителем – на среднее по модулю значение. Ам-
плитудные электронные вольтметры реагируют на амплитуд-
ное значение измеряемой величины. Так как обычно нас инте-
ресуют действующие значения напряжений и токов, то шкалы
этих приборов градуируют на напряжение U = 1,11U
СР
в при-
борах выпрямительной системы, и на напряжение U = U
max
/
2
в амплитудном электронном вольтметре, то есть эти приборы
предназначены для измерения синусоидальных величин, а при
использовании их для измерения несинусоидальных величин
необходимо избавиться от проведенной градуировки.
В качестве примера определим показания вольтметров
выпрямительной, электромагнитной и тепловой систем, а так-
же амплитудного электронного вольтметра, подключаемых к
источнику несинусоидального напряжения с максимальным
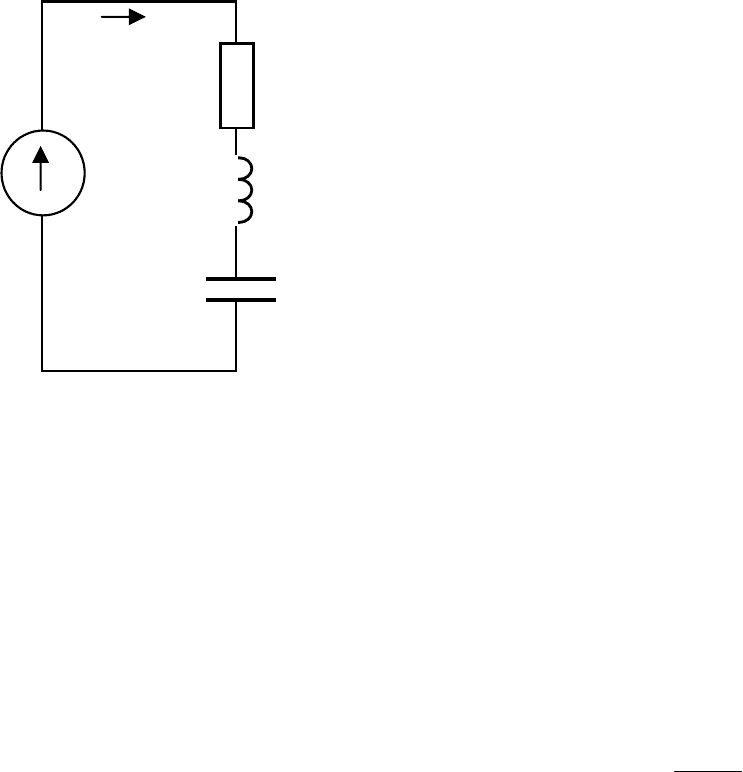
значением 100 В, форма которого показана на рис. 4.3.
Действующее значение измеряемого напряжения равно
100 В. Следовательно, вольтметры электромагнитной и тепло-
вой систем покажут 100 В. Среднее по модулю значение на-
пряжения
СР
U
=100 В, поэтому вольтметр выпрямительной
системы покажет
.B111U11,1U
СР
=⋅=
Амплитудный элек-
тронный вольтметр покажет U = U
max
/ 2 = 70,7 В.
Рис. 4.3
π
2π
3π
10
-
100
ω
t
U
m
u
(
t
),
B
112
4.1.6 Расчет электрических цепей с
несинусоидальными токами и напряжениями
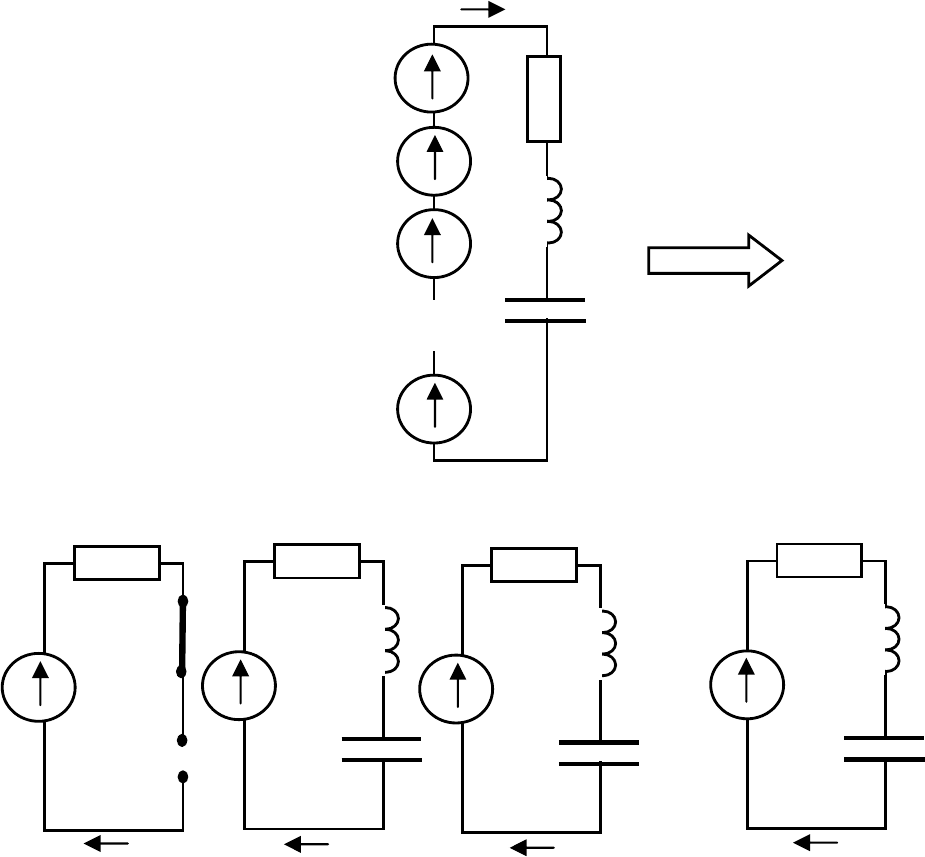
Если в линейной электрической цепи действует несину-
соидальный периодический источник ЭДС (рис. 4.4), то расчет
токов и напряжений в такой цепи выполняется следующим об-
разом.
Заданную несинусоидальную ЭДС представляют в виде
разложения в ряд Фурье:
)k()2()1()0(
e...eee)t(e ++++= и на
эквивалентной схеме замещения (рис. 4.5, а) представляют в
виде последовательного соединения нескольких синусоидаль-
ных источников ЭДС различной частоты.
Расчет линейной цепи с несинусои-
дальными ЭДС и токами выполняется
методом наложения и сводится к опре-
делению токов и напряжений в не-
скольких частичных схемах (рис. 4.5,
б, в, г). То есть расчет сводится к ре-
шению k задач с синусоидальными
ЭДС и токами, где k – число синусои-
дальных составляющих ряда Фурье, и
одной задачи с постоянными ЭДС и
токами, при условии наличия нулевой
гармоники в аналитическом разложе-
нии несинусоидальных величин в ряд Фурье. В пределах одной
гармоники расчеты можно выполнять в комплексной форме,
так как все напряжения и токи в частичной схеме изменяются
во времени по синусоидальному закону.
При расчете гармонических составляющих необходимо
иметь в виду, что сопротивления индуктивных и емкостных
элементов зависят от частоты, то есть от порядкового номера
гармоники:
Ck
1
XиLkX
)K(
C
)K(
L
ω
=ω= .
R
i
(
t
)
L
e (t)
Рис. 4.4
C
113
Активное сопротивление при достаточно низких частотах
и малых сечениях проводов можно считать независящим от
номера гармоники.
В частичной схеме (рис. 4.5, б), являющейся схемой за-
мещения по постоянной составляющей (ω = 0) сопротивление
индуктивного элемента ωL равно нулю, поэтому постоянная
составляющая напряжения u
L
(0)
также равна нулю. Сопротив-
ление емкостного элемента 1/(ωС) равно бесконечности, то
Рис. 4.5
R
I
(0)
Е
(0)
R
İ
m
(1)
Ė
m
(1)
R
İ
m
(2)
Ė
m
(2)
R
İ
m
(k)
Ė
m
(
k
)
jωL
1/(jωC)
j
2ωL
1/(j2ωC)
j
kωL
1/(jkωC)
+
+
+…+
R
i(t)=i
(0)
+ i
(1)
+ i
(2)
+…+ i
(k)
L
е
(0)
=Е
(0)
C
…
е
(1)
(t)= )tsin(E
1E
)1(
m
ψ+ω
е
(2)
(t)= )t2sin(E
2E
)2(
m
ψ+ω
е
(k)
(t)= )tksin(E
Ek
)k(
m
ψ+ω
а)
б)
в)
г)
д)

114
есть он представляет собой разомкнутый участок цепи. Поэто-
му постоянная составляющая тока ветви, содержащей конден-
сатор, i
C
(0)
отсутствует.
В цепи (рис. 4.5, в) действует ЭДС первой гармоники
е
(1)
(t)=
)tsin(E
1E
)1(
m
ψ+ω
. Запишем комплексную амплитуду
этой ЭДС:
1E
j
)1(
m
)1(
m
eEE
ψ
=
&
.
Комплексное сопротивление цепи:
1
j
)1(
R
)C/(1L
jarctg
22)1(
eze)
C
1
L(R
C
1
jLjRZ
ϕ
ω−ω
=
ω
−ω+=
ω
−ω+= .
Комплексная амплитуда тока:
1I11E
1
1E
j
)1(
m
jj
)1(
)1(
m
j
)1(
j
)1(
m
)1(
)1(
m
)1(
m
eIe
z
E
ez
eE
Z
E
I
ψϕ−ψ
ϕ
ψ
====
&
&
.
Тогда мгновенное значение тока первой гармоники:
)tsin(I)t(i
1i
)1(
m
)1(
ψ+ω= .
ЭДС второй гармоники (рис. 1.5, г):
е
(2)
(t)= )t2sin(E
2E
)2(
m
ψ+ω .
Комплексная амплитуда ЭДС второй гармоники:
2E
j
)2(
m
)2(
m
eEE
ψ
=
&
.
Комплексное сопротивление цепи второй гармоники:
2
j
)2(
R
)C2/(1L2
jarctg
22
)2(
eze)
C2
1
L2(R
C2
1
jL2jRZ
ϕ
ω−ω
=
ω
−ω+=
=
ω
−ω+=
.
Комплексная амплитуда тока второй гармоники:
2I22E
2
2E
j
)2(
m
jj
)2(
)2(
m
j
)2(
j
)2(
m
)2(
)2(
m
)2(
m
eIe
z
E
ez
eE
Z
E
I
ψϕ−ψ
ϕ
ψ
====
&
&
.
Тогда мгновенное значение тока второй гармоники:
)t2sin(I)t(i
2i
)2(
m
)2(
ψ+ω=
.
Аналогичные расчеты выполняются и для остальных
гармоник.
Для k-той гармоники (рис. 4.5, д):

115
е
(k)
(t)=
)tksin(E
Ek
)k(
m
ψ+ω
.
Комплексная амплитуда ЭДС k-той гармоники:
Ek
j
)k(
m
)k(
m
eEE
ψ
=
&
.
Комплексное сопротивление цепи:
k
j
)k(
R
)Ck/(1Lk
jarctg
22
)k(
eze)
Ck
1
Lk(R
Ck
1
jLjkRZ
ϕ
ω−ω
=
ω
−ω+=
=
ω
−ω+=
.
Комплексная амплитуда тока:
IkkEk
k
Ek
j
)k(
m
jj
)k(
)k(
m
j
)k(
j
)k(
m
)k(
)k(
m
)k(
m
eIe
z
E
ez
eE
Z
E
I
ψϕ−ψ
ϕ
ψ
====
&
&
.
Мгновенное значение тока k-той гармоники:
)tksin(I)t(i
ik
)k(
m
)k(
ψ+ω= .
Мгновенное значение несинусоидального тока цепи оп-
ределяется как алгебраическая сумма токов всех гармоник:
i(t) = i
(0)
(t) + i
(1)
(t) + i
(2)
(t) +…+ i
(k)
(t) =
=)tsin(I0
1i
)1(
m
ψ+ω+ )t2sin(I
2i
)2(
m
ψ+ω+ )tksin(I...
ik
)k(
m
ψ+ω++ .
Аналогичным образом выполняется расчет несинусои-
дальных напряжений на отдельных участках электрической
цепи.
Для построения графика временной зависимости несину-
соидальной функции строят в одних осях координат графики
синусоидальных составляющих всех гармоник. При вычерчи-
вании кривых отдельных гармоник необходимо учитывать тот
факт, что период гармоники обратно пропорционален ее номе-
ру. А так как по оси абсцисс откладывают величину ωt, то при
построении графика k-той гармоники несинусоидальной функ-
ции ее начальная фаза делится на номер гармоники.
Таким образом, расчет токов и напряжений в линейных
цепях при воздействии несинусоидальной ЭДС выполняется в
следующем порядке.
1. Заданные несинусоидальные ЭДС представляют в виде
116
разложения в ряд Фурье.
2. Проводят расчет методом наложения, то есть рассчи-
тывают токи и напряжения в цепи для каждой составляющей
ряда в отдельности.
3. Записывают мгновенные значения токов и напряжений,
алгебраически суммируя мгновенные значения всех гармони-
ческих составляющих.
4.1.7 Резонансные явления в цепи несинусоидального тока
Резонансным режимом работы электрической цепи, со-
держащей индуктивные и емкостные элементы, называют та-
кой режим, при котором ток и напряжение на входе цепи сов-
падают по фазе.
При несинусоидальных напряжениях и токах резонанс-
ные режимы (резонанс токов или резонанс напряжений) могут
возникать не только на первой гармонике, но и на высших гар-
мониках. Условие возникновения резонансного режима в иде-
альных последовательных или параллельных LC контурах на
любой гармонике одинаково:
Ck
1
Lk
ω
=ω , где k – номер гармоники.
Из этого условия следует, что резонансный режим работы
электрической цепи при несинусоидальных ЭДС и токах мо-
жет быть достигнут изменением любой из трех величин при
постоянстве двух оставшихся.
Резонансы напряжений и токов для от-
дельных гармоник используют в так называе-
мых резонансных фильтрах для выделения
сигналов требуемых частот, а также для по-
давления нежелательных частот.
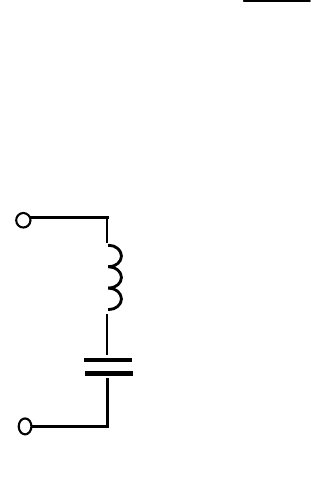
При последовательном соединении эле-
ментов L и C (рис. 4.6) в цепи возможен резо-
нанс напряжений. Если для какой-либо гар-
L
С
Рис. 4.6
117
моники выполняется условие
)k(
C
)k(
L
XX = , то напряжение k-той
гармоники на этом участке равно нулю, так как равны реак-
тивные напряжения
)k(
C
)k(
L
UU = . И в выходном сигнале напря-
жение k-той гармоники будет отсутствовать.
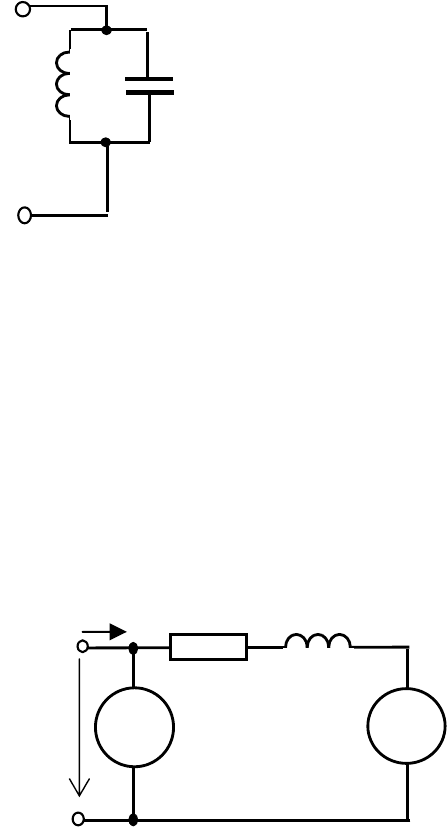
При параллельном соединении элемен-
тов L и C (рис. 4.7) в цепи возможен резонанс
токов. И если для какой-либо гармоники вы-
полняется условие
)k(
C
)k(
L
bb = , для k-той гар-
моники проводимость равна нулю и ток на
входе контура отсутствует, так как равны ре-
активные токи параллельных ветвей
)k(
C
)k(
L
II = .
Контур представляет собой разомкнутый участок цепи и мож-
но выделить напряжение k-той гармоники, так как оно прило-
жено к месту разрыва.
4.2 Примеры решения задач
4.2.1 Определить показания приборов электромагнитной
системы в цепи, схема кото-
рой показана на рис. 4.8, за-
писать выражение мгновен-
ного значения тока и постро-
ить временные зависимости
напряжения u(t) и тока i(t),
если:
ωL=11 Ом, R= 10 Ом.
На вход цепи подано
несинусоидальное напряжение, представленное в виде ряда
Фурье:
.B),14,73t3sin(176)tsin(310)t(u
o
+ω+ω=
Расчет гармонических составляющих тока и напряжения
проведем методом комплексных амплитуд.
Ток основной гармоники:
R
i
(
t
)
L
u (t)
Рис. 4.8
А
V
L
С
Рис. 4.7
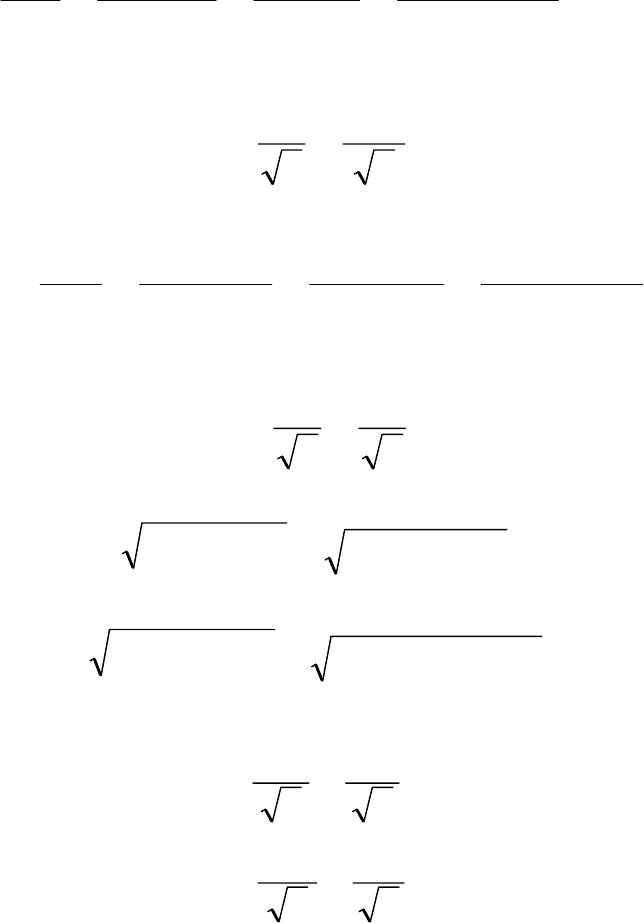
118
.Ae9,20
e87,14
310
11j10
310
LjR
U
Z
U
I
73,47j
73,47j
)1(
m
)1(
)1(
m
)1(
m
o
o
&&
&
−
==
+
=
ω+
==
Действующее значение тока первой гармоники:
.A8,14
2
9,20
2
I
I
)1(
m
)1(
===
Ток третьей гармоники:
.A1,5
e48,34
e176
33j10
e176
L3jR
U
Z
U
I
14,73j
14,73j14,73j
)3(
m
)3(
)3(
m
)3(
m
==
+
=
ω+
==
o
oo
&&
&
Действующее значение тока третьей гармоники:
.A6,3
2
1,5
2
I
I
)3(
m
)3(
===
Определим показания амперметра:
A2,156,38,14III
22
2
)3(
2
)1(
=+=+=
.
Показания вольтметра
B1,2525,1242,219UUU
22
2
)3(
2
)1(
=+=+=
,
где действующие значения напряжений гармоник:
;B2,219
2
310
2
U
U
)1(
)1(
m
===
.B5,124
2
176
2
U
U
)3(
)3(
m
===
Запишем выражение для мгновенного значения тока:
.A),t3sin(1,5)73,47tsin(9,20
)t3sin(I)tsin(I)t(i)t(i)t(i
3
)3(
m1
)1(
m
)3()1(
ω+−ω=
=ψ+ω+ψ+ω=+=
o
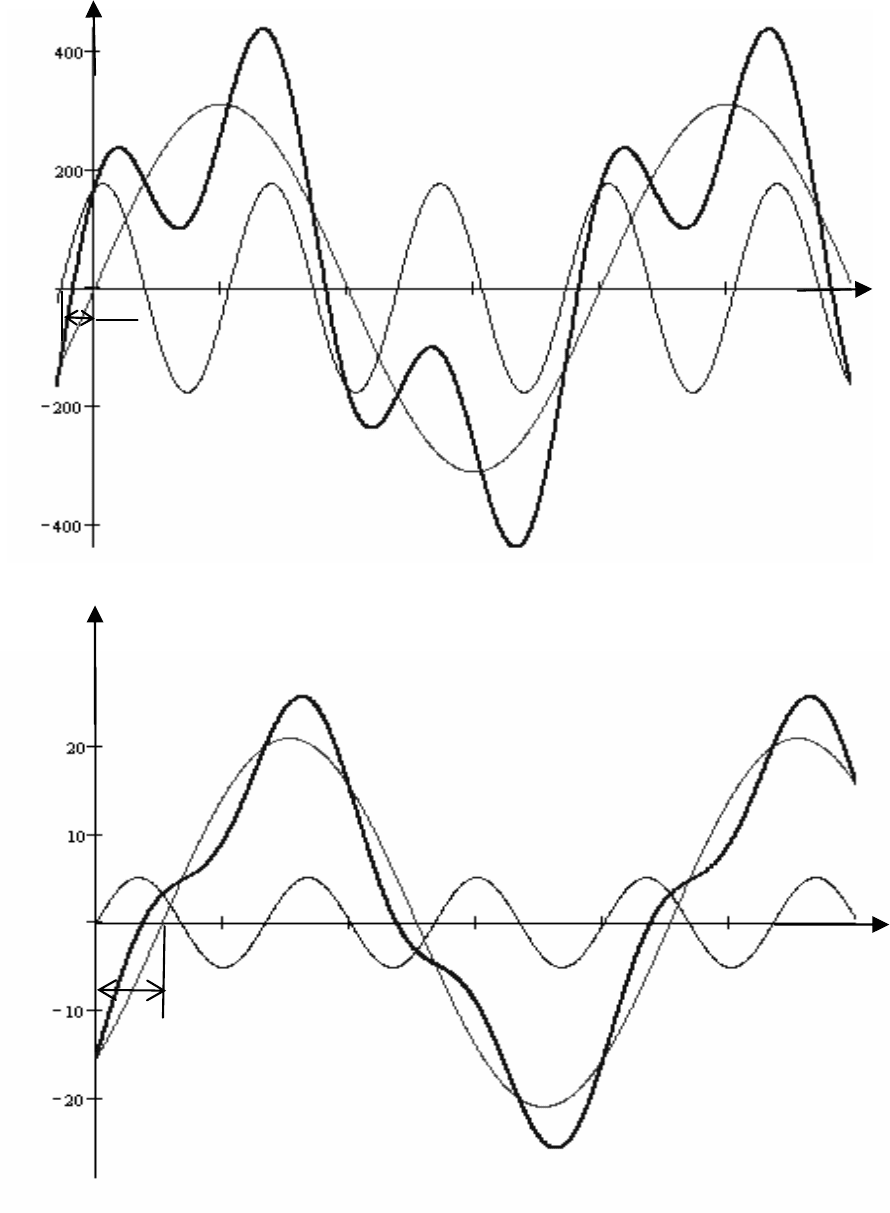
На рис. 4.9 и 4.10 представлены графики временных за-
висимостей входного напряжения и тока, а также составляю-
щих их гармоник. При вычерчивании кривых отдельных гар-
моник учитываем тот факт, что период гармоники обратно
пропорционален ее номеру. Так как по оси абсцисс откладыва-
ем величину ωt, то при построении графика третьей гармоники
119
напряжения ее начальная фаза (73,14°) разделена на номер гар-
моники (
°=° 38,243/73,14 ).
ωt
i
(1)
i
(3)
i = i
(1)
+ i
(3)
i, A
ψ
1
2π
π
Рис. 4.10
u(t) = u
(1)
+ u
(3)
u
(1)
u
(3)
ωt
u, B
ψ
u3
2π
π
Рис. 4.9
