Питолин В.М., Попова Т.В., Беляков П.Ю., Кобзистый С.Ю. Теоретические основы электротехники: элементы теории с примерами решения задач. Учебное пособие
Подождите немного. Документ загружается.


100
Рис. 3.10
При симметричной нагрузке расчет токов и напряжений
для схемы с нулевым проводом и без нулевого провода вы-
полняется одинаково, так как в трехпроводной схеме напряже-
ние смещения нейтрали равно нулю
00
U
′
&
= 0 и, следовательно,
фазные напряжения приемников равны фазным напряжениям
генератора, а в четырехпроводной схеме ток нулевого провода
отсутствует I
0
= 0.
Фазные напряжения генератора U
фг
= U
Л
/
3
= 220/
3
=
127 В.
Фазные напряжения генератора в комплексной форме за-
писи:
B.127eUeU
, B127eUeU B,e 127UeU
j120j120
C
j120-j120-
B
j0j0
À
oo
oo
&
&&
==
====
°°
Фазные напряжения приемников равны соответствую-
щим фазным напряжениям генератора:
B.127eUU , B127eUU B,e 127UU
j120
Cc
j120-
Bb
j0
Aa
oo
&&&&&&
======
°
Фазные токи приемников определим по закону Ома:
.Ae27,1
100
e127
Z
U
I
,Ae27,1
100
e127
Z
U
I,Ae27,1
100
e127
Z
U
I
120j
120j
c
c
c
120j
120j
b
b
b
0j
0j
a
a
a
o
o
o
o
o
o
&
&
&
&
&
&
===
======
−
−
101
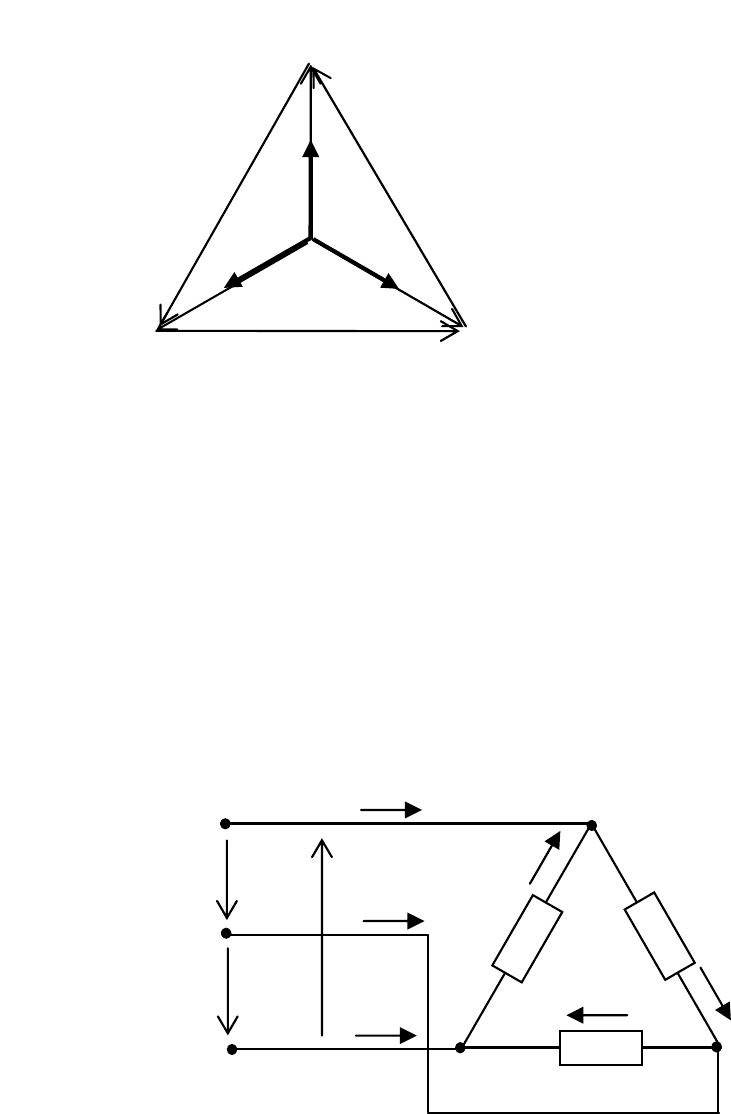
Построим
векторную диа-
грамму токов и
напряжений для
режима симмет-
ричной нагрузки
(рис. 3.11).
Рис. 3.11
3.2.2 Определить линейные и фазные токи и напряжения
в трехфазной нагрузке, соединенной по схеме треугольник
(рис. 3.12), питающейся от источника с линейным напряжени-
ем U
Л
= 220В, сопротивления фаз нагрузки одинаковы и равны
Z
аb
= Z
bc
= Z
ca
= Z
Ф
= R = 100 Ом.
Построить векторную диаграмму рассчитанных токов и
напряжений.
Рис. 3.12
Фазные напряжения приемников, при соединении фаз на-
грузки треугольником, равны линейным напряжениям генера-
тора, поэтому фазные токи легко определяются по закону Ома:
İ
А
İ
B
İ
C
Z
ab
Z
b
c
Z
ca
AB
U
&
BC
U
&
CA
U
&
A
B
C
a
b
c
İ
ab
İ
bc
İ
ca
bB
UU
&&
=
BC
U
&
c
I
&
b
I
&
a
I
&
CA
U
&
AB
U
&
cC
UU
&&
=
aA
UU
&&
=

102
,Ae2,2
100
e220
Z
U
I
30j
30j
ab
ab
ab
o
o
&
&
===
,Ae2,2
100
e220
Z
U
I
90j
90j
bc
bc
bc
o
o
&
&
−
−
===
.Ae2,2
100
e220
Z
U
I
150j
150j
ca
ca
ca
o
o
&
&
===
Как видно по расчетам, все токи получились одинаковые
по модулю и сдвинуты друг относительно друга по фазе на
120°.
Линейные токи определяем по уравнениям, составлен-
ным с помощью первого закона Кирхгофа:
.Ae8,3e2,2e2,2I-II
A,8e,3e2,2e2,2I-II
,Ae8,3e2,2e2,2I-II
120j90j150j
bccaC
j120-30j90j
abbcB
0j150j30j
caabA
ooo
ooo
ooo
&&&
&&&
&&&
=−==
=−==
=−==
−
−
Линейные токи при симметричной нагрузке также полу-
чаются одинаковыми по модулю и сдвинутыми друг относи-
тельно друга по фазе на 120°. Это хорошо видно на векторной
диаграмме токов и напряжений (рис. 3.13).
Рис. 3.13
Линейные и фазные токи приемника при симметричной
ca
I
&
−
bc
I
&
−
ab
I
&
−
ca
I
&
bc
I
&
ab
I
&
C
I
&
B
I
&
BC
U
&
A
I
&
CA
U
&
AB
U
&
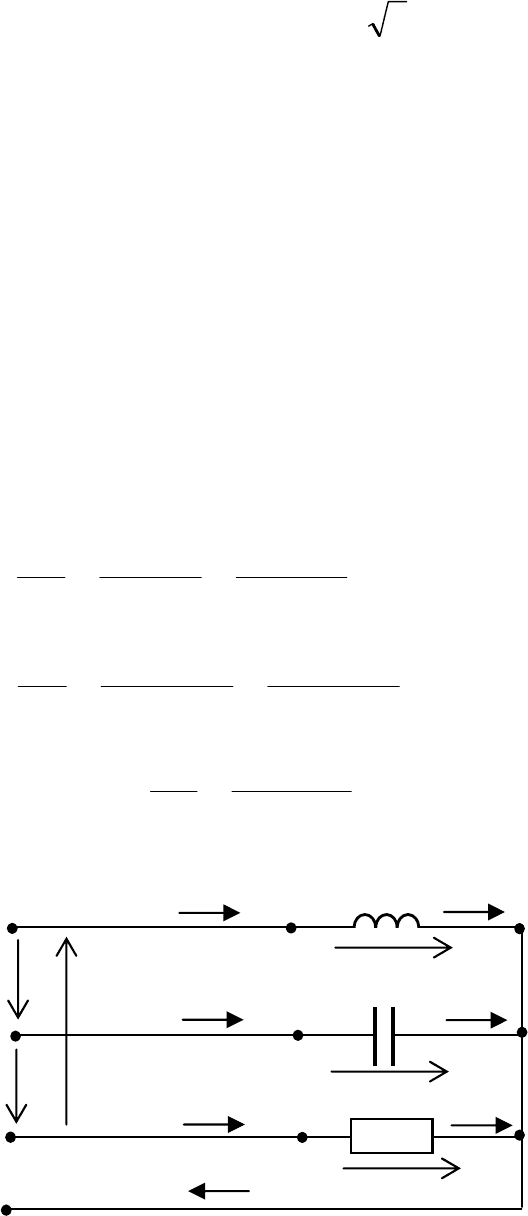
103
нагрузке связаны соотношением: I
Л
=
3
I
Ф
.
3.2.3 Определить линейные и фазные токи и напряжения
в трехфазной нагрузке, соединенной по схеме звезда с нулевым
проводом (рис. 3.14). Питание осуществляется от источника с
линейным напряжением U
Л
= 220В, сопротивления фаз нагруз-
ки: Z
а
= jX
L
=j100 Ом, Z
b
= –jX
c
= –j100 Ом, Z
c
= R = 100 Ом. По-
строить векторную диаграмму токов и напряжений.
В схеме с нулевым проводом фазные напряжения прием-
ника равны соответствующим фазным напряжениям генерато-
ра:
B.127eUU , B127eUU B,e 127UU
j120
Cc
j120-
Bb
j0
Aa
oo
&&&&&&
======
°
Фазные токи приемников определим по закону Ома:
,Ae27,1
e100
e127
100j
e127
Z
U
I
,Ae27,1
e100
e127
100j
e127
Z
U
I
30j
90j
120j120j
b
b
b
90j
90j
0j0j
a
a
a
o
o
oo
o
o
oo
&
&
&
&
−
−
−−
−
==
−
==
====
.Ae27,1
100
e127
Z
U
I
120j
120j
c
c
c
o
o
&
&
===
Рис. 3.14
a
U
&
b
U
&
c
U
&
İ
А
İ
B
İ
C
Z
a
Z
c
AB
U
&
BC
U
&
CA
U
&
A
B
C
0
a
b
İ
0
İ
a
İ
b
İ
c
0'
с
Z
b

104
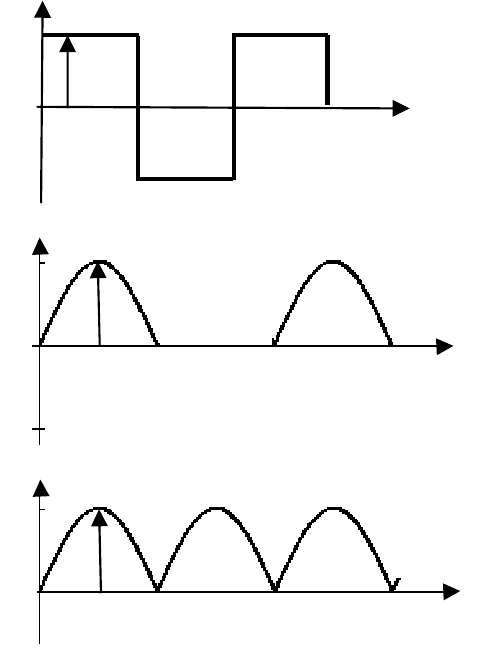
Рис. 3.15
Ток в нулевом проводе определяется с помощью первого
закона Кирхгофа:
A.0,929e805,0j465,0j1,10,635-635,0j1,127,1j
e27,1e27,1e27,1III I
j60-
j120-j30-j90
cba0
o
ooo
&&&&
=−=+−+−=
=++=++=
Построим векторную диаграмму токов и напряжений
(рис. 3.15).
3.2.4 По данным задачи 3.2.3. рассчитать значение актив-
ного сопротивления резистора R, включенного в фазу
с нагруз-
ки, при котором ток нулевого провода будет равен нулю.
Как видно по векторной диаграмме (рис. 3.15), ток нуле-
вого провода будет отсутствовать в том случае, если дейст-
вующее значение тока фазы
с будет равно сумме токов фаз a и
b. Сумма фазных токов:
A.e2,2905,1j1,1635,0j1,127,1j
e27,1e27,1II
j60-
-j30-j90
ba
o
oo
&&
=−=−+−=
=+=+
Действующее значение тока фазы
с:
2,2I
c
=
А.
Сопротивление резистора определим по закону Ома:
7,57
2,2
127
I
U
R
c
c
=== Ом.
bB
UU
&&
=
0
I
&
BC
U
&
c
I
&
b
I
&
a
I
&
CA
U
&
cC
UU
&&
=
aA
UU
&&
=
a
I
&
b
I
&
AB
U
&
105
4 ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ
РЕЖИМЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
4.1 Основы теории
4.1.1 Способы представления периодических
несинусоидальных электрических величин
Первым способом является представление периодических
несинусоидальных электрических величин графиками зависи-
мости их мгновенных значений от времени.
На рис. 4.1, а представлен график выходного напряжения
диодного ограничителя, на рис. 4.1, б и в изображены графики
напряжения на нагрузочном сопротивлении однополупериод-
ного и двухполупериодного выпрямителей.
а)
б)
в)
Вторым способом представления периодических несину-
U
ωt
u
u
u
U
U
ωt
ωt
Рис 41
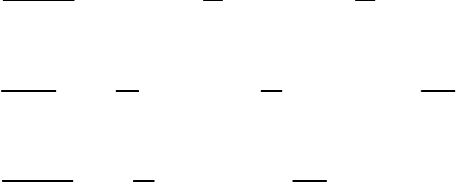
106
соидальных величин является аналитическое разложение пе-
риодических функций в ряд Фурье.
Как известно, любая периодическая функция f(ωt), удов-
летворяющая условиям Дирихле, то есть имеющая на всяком
конечном интервале конечное число разрывов первого рода и
конечное число максимумов и минимумов, может быть разло-
жена в тригонометрический ряд Фурье:
,)tksin(AA)tksin(A
...)t2sin(A)tsin(AA)t(f
1k
k
)k(
m
)0(
k
)k(
m
2
)2(
m1
)1(
m
)0(
∑
∞
=
ψ+ω+=ψ+ω+
+ψ+ω+ψ+ω+=ω
где А
(0)
называют постоянной составляющей или нулевой гар-
моникой
, второй член разложения )tsin(A
1
)1(
m
ψ+ω – основной
синусоидой или
первой гармоникой, период Т которой равен
периоду данной несинусоидальной функции, а все остальные
члены разложения вида )tksin(A
k
)k(
m
ψ+ω при k > 1 носят на-
звание
высших гармоник. Гармонические составляющие для
краткости часто называют
гармониками.
Для несинусоидальных функций токов и напряжений,
наиболее часто встречающихся в электротехнике, разложение
в ряд Фурье можно найти в справочниках по математике и
электротехнике.
В качестве примера приведем разложение в ряд Фурье
функций u(ωt), показанных на рис. 4.1, а, б, в:
......)t5sin
5
1
t3sin
3
1
t(sin
U4
)t(u
m
+ω+ω+ω
π
=ω
(рис. 4.1, а);
...)t4cos
15
2
t2cos
3
2
tcos
2
1(
U
)t(u
m
+ω−ω+ω
π
+
π
=ω
(рис.4.1, б);
......)t4cos
15
2
t2cos
3
2
1(
U2
)t(u
m
+ω−ω+
π
=ω (рис. 4.1, в).
Как видно из приведенных выражений, несинусоидаль-
ные напряжения имеют различный состав гармоник в ряде Фу-
рье. В приведенных выражениях начальные фазы гармоник
107
равны нулю. Однако довольно часто начальные фазы имеют
ненулевые значения.
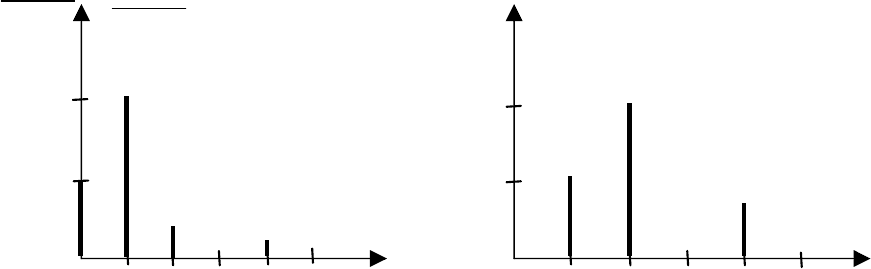
Амплитуды и начальные фазы гармоник определяют
спектральный состав несинусоидальной кривой. Спектры ам-
плитуд и начальных фаз представлены на рис. 4.2.
На диаграмме амплитудно-частотного спектра (рис. 4.2,
а) отложены относительные значения постоянной
составляющей и амплитуд остальных гармоник ряда. Значения
амплитуд берутся положительными, а их отрицательный знак
учи-тывается фазой.
Как правило, амплитуда гармонических составляющих
резко уменьшается с ростом номера гармоники, поэтому при
анализе электрических цепей несинусоидального тока
ограничиваются учетом только нескольких первых членов
ряда.
Рис. 4.2
4.1.2 Действующее и среднее значения несинусоидальных
электрических величин
Пусть несинусоидальное напряжение выражается рядом:
).tksin(U
...)t2sin(U)tsin(UU)t(u
k
)k(
m
2
)2(
m1
)1(
m
)0(
ψ+ω+
++ψ+ω+ψ+ω+=ω
ψ
u
1,0
0,5
m)1(
0
U
U
m)1(
m
U
U
ω
2ω 3ω
4ω 5ω
ω
2ω
3ω
4ω
5ω
kω kω
π
π/2
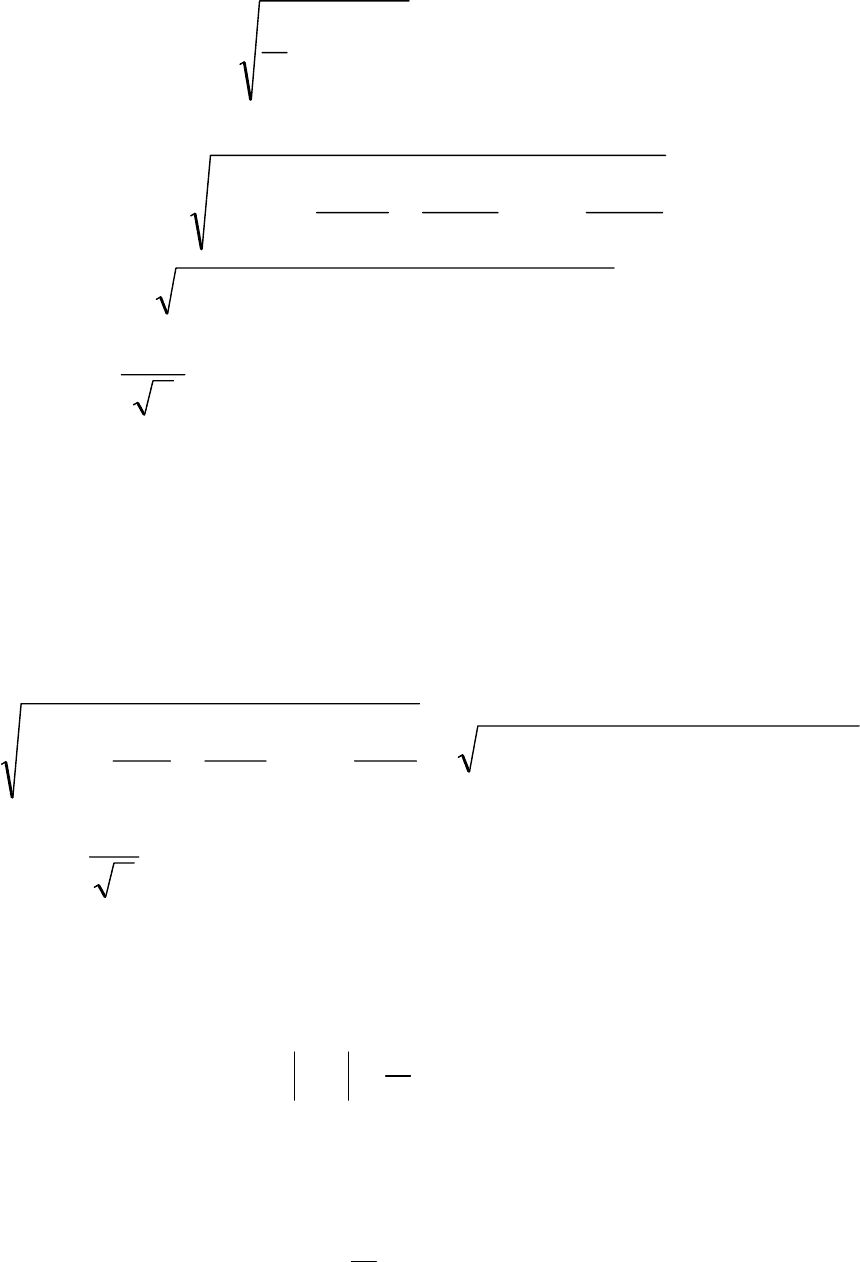
108
Действующее значение напряжения определяется
выражением:
.dt)t(u
T
1
U
T
0
2
∫
=
После интегрирования оно будет иметь вид:
,U...UUU
2
U
...
2
U
2
U
UU
2
)k(
2
)2(
2
)1(
2
)0(
2
)k(
m
2
)2(
m
2
)1(
m
2
)0(
++++=
=++++=
где
−=
2
U
U
)k(
m
)k(
действующее значение напряжения k-той
гармоники.
Таким образом, действующее значение несинусоидально-
го напряжения равно квадратному корню из суммы квадратов
постоянной составляющей и действующих значений напряже-
ний всех гармонических составляющих.
Аналогичное выражение можно записать для определе-
ния действующего значения несинусоидального тока:
,I...III
2
I
...
2
I
2
I
II
2
)k(
2
)2(
2
)1(
2
)0(
2
)k(
m
2
)2(
m
2
)1(
m
2
)0(
++++=++++=
где
−=
2
I
I
)k(
m
)k(
действующее значение тока k-той гармоники.
В ряде случаев (в частности при электрических
измерениях) рассматривается среднее по модулю значение
несинусоидальной функции:
∫
=
T
0
ср
dt)t(u
T
1
U
.
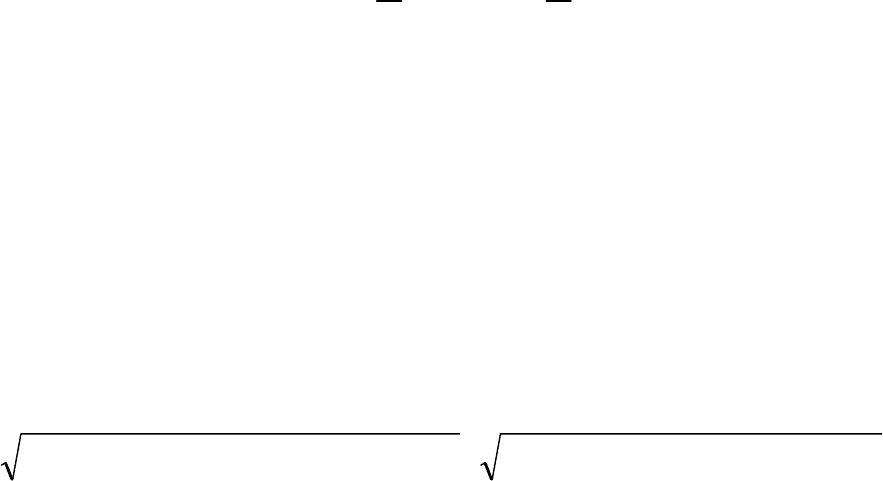
Среднее арифметическое значение несинусоидальной
функции равно её постоянной составляющей:
)0(
T
0
ср
Udt)t(u
T
1
U ==
∫
.
109
4.1.3 Активная, реактивная и полная мощности
Активная мощность определяется как среднее значение
мгновенной мощности:
∫∫
==
T
0
T
0
dt)t(i)t(u
T
1
dt)t(p
T
1
P
.
После подстановки мгновенных значений тока и напря-
жения получаем выражение:
.cosIU.....cosIUcosIUIUP
k
)k()k(
2
)2()2(
1
)1()1()0()0(
ϕ++ϕ+ϕ+=
Активная мощность электрической цепи при несинусои-
дальных напряжении и токе равна сумме активных мощностей
от постоянной и каждой из гармонических составляющих.
Произведение действующих значений напряжения и тока
представляет собой полную мощность:
.I...IIIU...UUU
UIS
2
)k(
2
)2(
2
)1(
2
)0(
2
)k(
2
)2(
2
)1(
2
)0(
++++⋅++++=
=
=
Реактивная мощность:
∑∑
∞
=
∞
=
=ϕ=
1k
)k(
1k
k
)k()k(
.QsinIUQ
Для цепей с несинусоидальными токами и напряжения-
ми:
222
QPS +≠ .
4.1.4 Коэффициенты, характеризующие форму
несинусоидальных кривых
Несинусоидальность кривых тока и напряжения в ряде
случаев оценивается с помощью коэффициентов амплитуды,
формы и искажения. Сопоставление этих коэффициентов с та-
кими же коэффициентами для синусоидальной кривой показы-
вает, насколько данная функция отличается от синусоидаль-
ной.
Коэффициент
амплитуды равен отношению максималь-
