Овчаров Л.А. и др. Математические модели информационых процессов и управления
Подождите немного. Документ загружается.

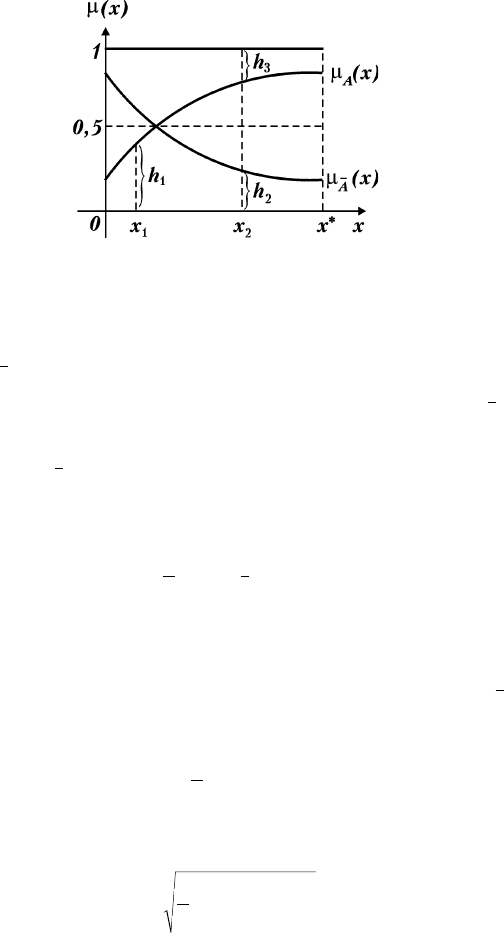
228
íÂÓÂÏÛ ı ÓÓ¯Ó ËÎβÒÚËÛÂÚ ËÒ. 5.6, ËÁ ÍÓÚÓÓ„Ó ‚ˉÌÓ,
˜ÚÓ ‰Îfl
µ
Ä
x() ,≤ 0 5 (̇ÔËÏ , ‚ ÚӘ͠ı
1
) Á̇˜ÂÌËÂ
hxıı
ÄA A
A
111
==−
∩∗
µµµ( ) ( ) ( ), Ú‡Í Í‡Í
µ
A
ı
∗
=() .
1
0
ÑÎfl ÒÎÛ˜‡fl
µ
A
ı() ,> 0 5 (‚ ÚӘ͠ı
2
) Á̇˜ÂÌËÂ
hx
ÄA22
=
∩
µ ()
‚ ÒËÎÛ ÚÓ„Ó, ˜ÚÓ
µ
A
ı
∗
=()
2
1 Ë Ú‡Í Í‡Í, ÔÓ ÓÔ‰ÂÎÂÌ˲,
µµ
AA
ıı() (),
22
1= − ÚÓ h
2
= h
3
Ë
h ıı
Ä
Ä222
= − =
∗
µµ() ()
= −1
2
µ
Ä
ı( ), ˜ÚÓ ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ ÛÚ‚ÂʉÂÌ˲ ÚÂÓÂÏ˚.
ë Î Â ‰ Ò Ú ‚ Ë Â ËÁ ÚÂÓ ÂÏ˚ 6.
ν µ() ( ).Ax
n
AA
i
n
i
=
∩
=
∑
2
1
(5.14)
ùÚ‡ ÙÓÏÛ· ÔÓÎÛ˜‡ÂÚÒfl ËÁ ÛÚ‚ÂʉÂÌËfl ÚÂÓÂÏ˚ 6 ÒÛÏÏË-
Ó‚‡ÌËÂÏ ÔÓ i = 1, 2,..., n, ΂˚ı Ë Ô‡‚˚ı ˜‡ÒÚÂÈ ÒÓÓÚ‚ÂÚÒÚ-
‚Û˛˘Ëı ‡‚ÂÌÒÚ‚.
ç˜ÂÚÍÓ ÏÌÓÊÂÒÚ‚Ó Ò ÙÛÌ͈ËÂÈ ÔË̇‰ÎÂÊÌÓÒÚË
2
µ
ÄÄ
ı
∩
()
ËÌÓ„‰‡ ̇Á˚‚‡˛Ú ‚ÂÍÚÓÌ˚Ï Ë̉Ë͇ÚÓÓÏ Ì˜ÂÚÍÓÒÚË Ì.Ï. Ä.
é·ÓÁ̇˜ËÏ Â„Ó ç(Ä). íÓ„‰‡
ν µ() ( ).
()
Ax
n
A
i
n
i
=
=
∑
2
1
ç
(5.15)
Ä̇Îӄ˘̇fl ÙÓÏÛ· ÏÓÊÂÚ ·˚Ú¸ ÔÓÎÛ˜Â̇ ‰Îfl Í‚‡‰‡Ú˘-
ÌÓ„Ó Ë̉ÂÍÒ‡ ̘ÂÚÍÓÒÚË:
η µ() ( ().
()
Ax
n
A
i
n
i
=
=
∑
1
1
2
ç
(5.16)
á‡ÏÂÚËÏ, ˜ÚÓ ‚ ÙÓÏÛÎ˚, ÔÓÎÛ˜ÂÌÌ˚ ‰Îfl ÎËÌÂÈÌÓ„Ó Ë Í‚‡-
êàë. 5.6
229
‰‡Ú˘ÌÓ„Ó Ë̉ÂÍÒÓ‚ ̘ÂÚÍÓÒÚË, ÒËÏÏÂÚ˘ÌÓ ‚ıÓ‰flÚ Ì.Ï. Ä Ë
Ä . ùÚÓ „Ó‚ÓËÚ Ó ÚÓÏ, ˜ÚÓ Ë̉ÂÍÒ˚ ̘ÂÚÍÓÒÚË ÏÌÓÊÂÒÚ‚‡ Ë Â„Ó
‰ÓÔÓÎÌÂÌËfl ÒÓ‚Ô‡‰‡˛Ú. ÑÓ͇ÊÂÏ ˝ÚÓ.
í Â Ó Â Ï ‡ 7.
νν() ()AA= ;
ηη() ()AA= .
Ñ Ó Í ‡ Á ‡ Ú Â Î ¸ Ò Ú ‚ Ó: ÇÓÒÔÓθÁÛÂÏÒfl ÙÓÏÛÎÓÈ (5.14):
ν µµν() () () ();Ax xÄ
nn
AÄ
i
n
iAÄ
i
n
i
22
11
∩
=
∩
=
∑∑
==
‡Ì‡Îӄ˘ÌÓ
η µµη( ) ( ( )) ( ( )) ( ).Ax xÄ
nn
AÄ
i
n
iAÄ
i
n
i
===
∩
=
∩
=
∑∑
22
11
1
2
1
2
íÂÓÂχ ‰Ó͇Á‡Ì‡.
åÌÓÊÂÒÚ‚Ó – ÒÚÂÔÂ̸ ̘ÂÚÍÓ„Ó ÏÌÓÊÂÒÚ‚‡. èÓ ‡Ì‡ÎÓ„ËË Ò
ÓÔ‰ÂÎÂÌËÂÏ ÚÂÓËË ÏÌÓÊÂÒÚ‚ ÏÌÓÊÂÒÚ‚ÓÏ-ÒÚÂÔÂ̸˛ ̘ÂÚ-
ÍÓ„Ó ÏÌÓÊÂÒÚ‚‡ Ä ·Û‰ÂÏ Ì‡Á˚‚‡Ú¸ ÏÌÓÊÂÒÚ‚Ó Â„Ó ÔÓ‰ÏÌÓÊÂÒÚ‚.
é·ÓÁ̇˜‡Ú¸ ÏÌÓÊÂÒÚ‚Ó-ÒÚÂÔÂ̸ Ä ·Û‰ÂÏ ê(Ä). í‡ÍËÏ Ó·‡ÁÓÏ,
ê(Ä) = {Ç/Ç ⊆ Ä}.
èÛÒÚ¸ ÛÌË‚Â҇θÌÓ ÏÌÓÊÂÒÚ‚Ó U ÒÓÒÚÓËÚ ËÁ n ˝ÎÂÏÂÌÚÓ‚.
è‰ÔÓÎÓÊËÏ ‚̇˜‡Î n = 2, Ú‡Í ˜ÚÓ U = {ı
1
, ı
2
}. èÛÒÚ¸ Ó·-
·ÒÚ¸
Á̇˜ÂÌËÈ
ÙÛÌ͈ËË
ÔË̇‰ÎÂÊÌÓÒÚË
–
ÏÌÓÊÂÒÚ‚Ó
å
– ÒÓ-
ÒÚÓËÚ ËÁ m ˝ÎÂÏÂÌÚÓ‚ Ë m = 2. í.Â. å {0, 1} – ‰‚Ûı˝ÎÂÏÂÌÚ-
ÌÓ ÏÌÓÊÂÒÚ‚Ó, Ë Ï˚ ÔÓÔ‡‰‡ÂÏ ‚ ӷ·ÒÚ¸ Ó·˚˜Ì˚ı ÏÌÓÊÂÒÚ‚.
ç‡È‰ÂÏ ÏÌÓÊÂÒÚ‚Ó-ÒÚÂÔÂ̸ ê(U) Ë ËÁÓ·‡ÁËÏ Â„Ó Ì‡ „‡ÙË-
ÍÂ, „‰Â ÔÓ ÓÒË ‡·ÒˆËÒÒ ÓÚÎÓÊËÏ
µ
Ä
ı
()
1
, ‡ ÔÓ ÓÒË Ó‰ËÌ‡Ú –
µ
Ä
ı
()
2
‰Îfl ÔÓ‰ÏÌÓÊÂÒÚ‚ Ä ÏÌÓÊÂÒÚ‚‡ U. é·ÓÁ̇˜ËÏ Í‡Ê‰ÓÂ
ÔÓ‰ÏÌÓÊÂÒÚ‚Ó Ä ⊆ U ͇Í
Ä
ii
1 2
, „‰Â
ixix
AA1122
==µµ(), () . íÓ„-
‰‡ ÔÓ‰ÏÌÓÊÂÒÚ‚‡
Ä
ii
1 2
ÏÌÓÊÂÒÚ‚‡ U ÏÓÊÌÓ Ô‰ÒÚ‡‚ËÚ¸ ÒΉÛ-
˛˘ËÏ Ó·‡ÁÓÏ:
Ax x
00 1 2
=
{}
(; ; ; 0), ( 0)
Ax x
011 2
=
{}
(; ; ; 0), ( 1)
Ax x
10 1 2
=
{}
(; ; ; 1), ( 0)
Ax x
11 1 2
=
{}
(; ; . 1), ( 1)
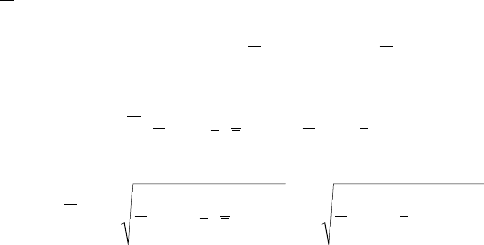
ç‡ ÔÎÓÒÍÓÒÚË
µµ
AA
xx() ()
1 2
× ÏÌÓÊÂÒÚ‚Ó P(U) ËÁÓ·‡ÁËÚÒfl
‚ ‚ˉ ˜ÂÚ˚Âı ÚÓ˜ÂÍ ( ËÒ. 5.7):
PU AAAA() ,,, .=
{}
00 0110 11
230
è‰ÔÓÎÓÊËÏ ÚÂÔ¸, ˜ÚÓ ÏÌÓÊÂÒÚ‚Ó å ÒÓÒÚÓËÚ ËÁ ÚÂı
˝ÎÂÏÂÌÚÓ‚, ÔÛÒÚ¸, ̇ÔËÏÂ, å = {0; 0,5; 1}. íÓ„‰‡ ÔÓ‰ÏÌÓÊÂ-
ÒÚ‚‡ÏË U ·Û‰ÛÚ:
Ax x
00 1 2
=
{}
(; ; ; 0), ( 0)
Axx
00 5 1 2,
(; ; ;=
{}
0), ( 0,5)
Ax x
011 2
=
{}
(; ; ; 0), ( 1)
Ax x
050 1 2,
(; ; ;=
{}
0,5), ( 0)
.......................................
Ú.Â.
PU A A A A Ä() , , , , .
,,,
=
{}
00 00 5 0 1 050 11
...,
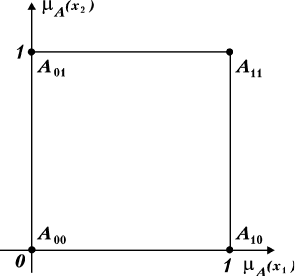
ùÚÓ ÏÌÓÊÂÒÚ‚Ó ËÁÓ·‡ÊÂÌÓ Ì‡ ËÒ. 5.8, ËÁ ÍÓÚÓÓ„Ó ‚ˉÌÓ,
˜ÚÓ ÍÓ΢ÂÒÚ‚Ó ˝ÎÂÏÂÌÚÓ‚ ÏÌÓÊÂÒÚ‚‡ P(U) ‡‚ÌÓ ‚ ˝ÚÓÏ ÒÎÛ-
˜‡Â 9. éÔ‰ÂÎËÏ, ˜ÂÏÛ ‡‚̇ ÏÓ˘ÌÓÒÚ¸ P(U) ‚ ·ÓΠӷ˘ÂÏ
ÒÎÛ˜‡Â.
í Â Ó Â Ï ‡ 8. Ç ÒÎÛ˜‡Â, ÍÓ„‰‡ ÍÓ΢ÂÒÚ‚Ó ˝ÎÂÏÂÌÚÓ‚ ÛÌË‚Â-
҇θÌÓ„Ó ÏÌÓÊÂÒÚ‚‡ U ‡‚ÌÓ n, ‡ ÍÓ΢ÂÒÚ‚Ó ˝ÎÂÏÂÌÚÓ‚ å
‡‚ÌÓ m, ÏÌÓÊÂÒÚ‚Ó-ÒÚÂÔÂ̸ P(U) ÒÓÒÚÓËÚ ËÁ m
n
˝ ÎÂÏÂÌÚÓ‚.
Ñ Ó Í ‡ Á ‡ Ú Â Î ¸ Ò Ú ‚ Ó : ã˛·Ó Ì˜ÂÚÍÓ ÔÓ‰ÏÌÓÊÂÒÚ‚Ó ÏÌÓÊÂ-
ÒÚ‚‡ U ‚ ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò Ó·ÓÁ̇˜ÂÌËÂÏ, ÔËÌflÚ˚Ï ‚˚¯Â, ÏÓÊÌÓ
Ô‰ÒÚ‡‚ËÚ¸ Ú‡Í:
Axixixi
ii i
n
nn
1 2
11 22
), ( ), (
...,
( ; ; ... ; ) ,=
{}
„‰Â i
j
– Á̇˜ÂÌËfl ËÁ ÏÌÓÊÂÒÚ‚‡ å. í‡ÍËÏ Ó·‡ÁÓÏ, ͇ʉÓÏÛ
ÔÓ‰ÏÌÓÊÂÒÚ‚Û Ä ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ ‚ÂÍÚÓ-ÙÛÌ͈Ëfl
êàë. 5.7
231
ξ
Än
ii i= (, , ),
1 2
...,
ÒÓÒÚÓfl˘‡fl ËÁ Á̇˜ÂÌËÈ ÙÛÌ͈ËË ÔË̇‰ÎÂÊÌÓÒÚË ÒÓÓÚ‚ÂÚÒÚ-
‚Û˛˘Ëı ˝ ÎÂÏÂÌÚÓ‚. ÅÂÁ Ó„‡Ì˘ÂÌËfl Ó·˘ÌÓÒÚË ·Û‰ÂÏ Ò˜ËÚ‡Ú¸
Á̇˜ÂÌËflÏË ÙÛÌ͈ËË
µ
A
x
()
, Ú.Â. ˝ÎÂÏÂÌÚ‡ÏË ÏÌÓÊÂÒÚ‚‡ å,
˜ËÒ· 1, 2,..., m.
燘ÌÂÏ ÔÓ‰Ò˜ÂÚ ‡Á΢Ì˚ı ‚ÂÍÚÓ-ÙÛÌ͈ËÈ, Ú‡ÍËÏ Ó·‡ÁÓÏ
ÔÓ‰Ò˜ËÚ˚‚‡fl ÍÓ΢ÂÒÚ‚Ó ‡Á΢Ì˚ı ÔÓ‰ÏÌÓÊÂÒÚ‚.
ç‡ Ô‚ÓÏ ÏÂÒÚ ‚ÂÍÚÓ-ÙÛÌ͈ËË
ξ
Ä
, ÒÓÓÚ‚ÂÚÒÚ‚Û˛˘ÂÈ
ÔÓËÁ‚ÓθÌÓÏÛ ÔÓ‰ÏÌÓÊÂÒÚ‚Û Ä, ÏÓÊÂÚ ·˚Ú¸ m ‡Á΢-
Ì˚ı Á̇˜ÂÌËÈ ˝ÎÂÏÂÌÚ‡ i
1
: 1, 2,..., m. ÑÎfl Í‡Ê‰Ó„Ó ËÁ ˝ÚËı
Á̇˜ÂÌËÈ Ì‡ ‚ÚÓÓÏ ÏÂÒÚ ÏÓÊÂÚ ·˚Ú¸ m ‚ÓÁÏÓÊÌ˚ı Á̇-
˜ÂÌËÈ ˝ÎÂÏÂÌÚ‡ i
2
, Ë Ú‡Í ‰‡ÎÂÂ. ÑÎfl Í‡Ê‰Ó„Ó ËÁ m ‚ÓÁÏÓÊÌ˚ı
Á̇˜ÂÌËÈ ˝ÎÂÏÂÌÚ‡ i
n–1
‚ÓÁÏÓÊÌÓ m ‡Á΢Ì˚ı Á̇˜ÂÌËÈ ˝ÎÂ-
ÏÂÌÚ‡ i
n
.
í‡ÍËÏ Ó·‡ÁÓÏ, ÍÓ΢ÂÒÚ‚Ó ‚Ò‚ÓÁÏÓÊÌ˚ı ÔÓ‰ÏÌÓÊÂÒÚ‚ ·Û-
‰ÂÚ
mm m
n
n
m⋅⋅ ⋅= ...
1244344
.
íÂÓÂχ ‰Ó͇Á‡Ì‡.
ùÚ‡ ÚÂÓÂχ fl‚ÎflÂÚÒfl Ó·Ó·˘ÂÌËÂÏ ÚÂÓÂÏ˚ Ó ÍÓ΢ÂÒÚ‚Â
˝ÎÂÏÂÌÚÓ‚ ÏÌÓÊÂÒÚ‚‡-ÒÚÂÔÂÌË ÍÓ̘ÌÓ„Ó ÏÌÓÊÂÒÚ‚‡, ‰Ó͇Á‡ÌÌÓÈ
‚ Í·ÒÒ˘ÂÒÍÓÈ ÚÂÓËË ÏÌÓÊÂÒÚ‚.
àÁ ÚÂÓÂÏ˚ 8 ÒΉÛÂÚ, ˜ÚÓ ÏÌÓÊÂÒÚ‚Ó ÔÓ‰ÏÌÓÊÂÒÚ‚ P(U)
ÍÓ̘ÌÓ Î˯¸ ‚ ÒÎÛ˜‡Â, ÍÓ„‰‡ n Ë m ÍÓ̘Ì˚.
êàë. 5.8

232
åÌÓÊÂÒÚ‚Ó α-ÛÓ‚Ìfl. é·Ó·˘ÂÌËÂÏ ÔÓÌflÚËfl Ó·˚˜ÌÓ„Ó ÏÌÓ-
ÊÂÒÚ‚‡, ·ÎËÊ‡È¯Â„Ó Í Ì˜ÂÚÍÓÏÛ, fl‚ÎflÂÚÒfl ÔÓÌflÚË ÏÌÓÊÂÒÚ‚‡
α-ÛÓ‚Ìfl. îÛÌ͈Ëfl ÔË̇‰ÎÂÊÌÓÒÚË ˝ÚÓ„Ó ÏÌÓÊÂÒÚ‚‡ ÓÔ‰Â-
ÎflÂÚÒfl ÔË Ò‡‚ÌÂÌËË ÙÛÌ͈ËË ÔË̇‰ÎÂÊÌÓÒÚË Ì˜ÂÚÍÓ„Ó
ÏÌÓÊÂÒÚ‚‡ ÌÂ Ò ÍÓÌÒÚ‡ÌÚÓÈ 0,5 ‡ Ò ÔÓËÁ‚ÓθÌ˚Ï ˜ËÒÎÓÏ
0 ≤ α ≤ 1.
åÌÓÊÂÒÚ‚ÓÏ
α
-ÛÓ‚Ìfl ̘ÂÚÍÓ„Ó ÏÌÓÊÂÒÚ‚‡ Ä Ì‡Á˚‚‡ÂÚÒfl
Ó·˚˜ÌÓ ÏÌÓÊÂÒÚ‚Ó Ä
α
, Ú‡ÍÓÂ, ˜ÚÓ
µ
µ α
µ α
α
A
x
ı
ı
()
() ,
() .
=
<
≥
0
1
ÔË
ÔË
Ä
Ä
(5.17)
ÇˉÌÓ, ˜ÚÓ ÔË α = 0,5 ˝ÚÓ ÓÔ‰ÂÎÂÌË ÒÓ‚Ô‡‰‡ÂÚ Ò ÓÔ‰ÂÎÂ-
ÌËÂÏ Ó·˚˜ÌÓ„Ó ÏÌÓÊÂÒÚ‚‡, ·ÎËÊ‡È¯Â„Ó Í Ä.
è Ë Ï Â 3. èÛÒÚ¸
U x xxx=
{}
1 234
,,,;
Ax x x x=
{}
(;;;;.
1 234
0,5), ( 0,8), ( 0,9), ( 0,4)
Ç˚˜ËÒÎËÏ ‰Îfl Ì.Ï. Ä ÏÌÓÊÂÒÚ‚‡ α-ÛÓ‚Ìfl, ̇ÔËÏÂ, ‰Îfl
α = 0,7 Ë α = 0,4.
Axx
07 1 3,
,=
{}
;
A xxxx U
04 1 234,
,,,=
{}
= . ➤
á ‡ Ï Â ˜ ‡ Ì Ë Â: ÖÒÎË α
1
≥ α
2
, ÚÓ
ÄÄ
αα
2 1
⊆
. ÑÓ͇Á‡ÚÂθÒÚ‚Ó
ÒΉÛÂÚ ËÁ ÓÔ‰ÂÎÂÌËfl ÏÌÓÊÂÒÚ‚‡ Ä
α
. àÁ ÔËχ 3 ‚ˉÌÓ,
˜ÚÓ, ÔÓÒÍÓθÍÛ 0,7 > 0,4, ÚÓ
ÄÄ
07 04,,
⊆
.
ë ÔÓÏÓ˘¸˛ ÔÓÌflÚËfl ÏÌÓÊÂÒÚ‚‡ ÛÓ‚Ìfl α ÏÓÊÂÚ ·˚Ú¸ Á‡‰‡ÌÓ
‡ÁÎÓÊÂÌˠ̘ÂÚÍÓ„Ó ÏÌÓÊÂÒÚ‚‡ Ä. ëÙÓÏÛÎËÛÂÏ ˝ÚÓÚ Â-
ÁÛÎ¸Ú‡Ú ‚ ‚ˉ ÚÂÓÂÏ˚.
í Â Ó Â Ï ‡ 9. (íÂÓÂχ Ó ‰ÂÍÓÏÔÓÁˈËË.) èÛÒÚ¸
U =
=
{}
xx x
n1 2
,, . ..., é·ÓÁ̇˜ËÏ α
i
– Á̇˜ÂÌË ÙÛÌ͈ËË ÔË̇‰-
ÎÂÊÌÓÒÚË Ì.Ï. Ä ‰Îfl ˝ÎÂÏÂÌÚ‡ ı
i
:
α µ
iAi
xi n==(), , . 2,..., 1
íÓ„‰‡ ‚ÂÍÚÓ-ÙÛÌÍˆË˛ ÔË̇‰ÎÂÊÌÓÒÚË Ì˜ÂÚÍÓ„Ó ÏÌÓÊÂÒÚ‚‡ Ä
ÏÓÊÌÓ ‡ÁÎÓÊËÚ¸ ̇ ÔÓËÁ‚‰ÂÌË ‚ÂÍÚÓ-ÙÛÌ͈ËÈ ÔË̇‰-
ÎÂÊÌÓÒÚË ÏÌÓÊÂÒÚ‚
Ä
i
α
, „‰Â 0 < α
i
≤ 1, i = 1, 2,..., n, ÒÎÂ‰Û˛-
˘ËÏ Ó·‡ÁÓÏ:
ξαξαξαξ
αα α
ÄÄÄnÄ
n
= max( ; ; ).
1
1
2
2
...; (5.18)
233
Ñ Ó Í ‡ Á ‡ Ú Â Î ¸ Ò Ú ‚ Ó : èÓ͇ÊÂÏ ‚˚ÔÓÎÌÂÌË ‡‚ÂÌÒÚ‚‡ (5.18),
̇ÔËÏÂ, ‰Îfl Ô‚ÓÈ ÍÓÓ‰Ë̇Ú˚ ‚ÂÍÚÓ‡
ξ
Ä
. èÓ ÓÔ‰ÂÎÂ-
Ì˲,
ξαα α
Än
= (, , ).
1 2
..., 肇fl ÍÓÓ‰Ë̇ڇ ‡‚̇ α
1
. éÔÂ-
‰ÂÎËÏ, ˜ÂÏÛ ‡‚̇ Ô‚‡fl ÍÓÓ‰Ë̇ڇ ‚ÂÍÚÓ-ÙÛÌ͈ËË
ξ
α
Ä
Í
ÏÌÓÊÂÒÚ‚‡ ÛÓ‚Ìfl α
Í
.
ÖÒÎË α
Í
> α
1
, ÚÓ
ξ
α
Ä
Í
ËÏÂÂÚ ÔÂ‚Û˛ ÍÓÓ‰Ë̇ÚÛ, ‡‚ÌÛ˛ 0,
Í‡Í ÒΉÛÂÚ ËÁ ÓÔ‰ÂÎÂÌËfl (5.17) ÏÌÓÊÂÒÚ‚‡ Ä
α
. ÖÒÎË α
Í
≤
≤ α
1
, ÚÓ Ô‚‡fl ÍÓÓ‰Ë̇ڇ ‚ÂÍÚÓ‡
ξ
α
Ä
Í
‡‚̇ 1. çÓ Ú‡Í Í‡Í
ÔË ‚ÂÍÚÓ‡ı
ξ
α
Ä
Í
, ‰Îfl ÍÓÚÓ˚ı α
Í
≤ α
1
, ‚ Ô˂‰ÂÌÌÓÏ ‡Á-
ÎÓÊÂÌËË ËϲÚÒfl ÏÌÓÊËÚÂÎË α
Í
, ÚÓ Ï‡ÍÒËχθÌÓ Á̇˜ÂÌËÂ
Ô‚ÓÈ ÍÓÓ‰Ë̇Ú˚ ‡‚ÌÓ α
1
.
è Ë Ï Â 4. чÌÓ Ì.Ï.
Ax x x=
{}
(; ; ; .
1 23
0,5), ( 0,8), ( 0,2)
á‡Ô˯ÂÏ ‡ÁÎÓÊÂÌË ‚ÂÍÚÓ-ÙÛÌ͈ËË
ξ
Ä
ÔÓ ‚ÂÍÚÓ‡Ï
ξ
α
Ä
i
,
i = 1, 2, 3.
àÏÂÂÏ
ξξξξ
ÄÄÄÄ
==max( , ; ; )
,,,
05
05 08 02
0,8 0,2
= max(0,5(1; 1; 0); 0,8(0; 1; 0); 0,2(1; 1; 1)) =
= (0,5; 0,8; 0,2) = ( µµµ
AA A
xxx( ), ( ), ( )).
1 23
艷„‡ÂÚÒfl Ò‡ÏÓÒÚÓflÚÂθÌÓ Ì‡ÈÚË
ξ
Ä
Ì.Ï.
Ax=
{
(;
1
0,1),
( 0,2), ( 0,5)xx
25
;;
}
Ò ÔÓÏÓ˘¸˛ ‡ÁÎÓÊÂÌËfl ÔÓ ‚ÂÍÚÓ -
ÙÛÌ͈ËflÏ ÏÌÓÊÂÒÚ‚ ÛÓ‚Ìfl α: α = 0,1; 0,2;...; 0,5. ➤
éÔ‰ÂÎÂÌË ÏÌÓÊÂÒÚ‚‡ α-ÛÓ‚Ìfl ‡ÒÔÓÒÚ‡ÌflÂÚÒfl Ë Ì‡
ÒÎÛ˜‡È, ÍÓ„‰‡ ÛÌË‚Â҇θÌÓ ÏÌÓÊÂÒÚ‚Ó U – Ò˜ÂÚÌÓ ËÎË ËÏÂÂÏ
˜ËÒÎÓ ˝ÎÂÏÂÌÚÓ‚ ÍÓÌÚËÌÛÛÏ. èÛÒÚ¸, ̇ÔËÏÂ, U – ÏÌÓÊÂÒÚ‚Ó
‚¢ÂÒÚ‚ÂÌÌ˚ı ˜ËÒÂÎ (–∞, ∞), Ä – ̘ÂÚÍÓ ÔÓ‰ÏÌÓÊÂÒÚ‚Ó U,
Óڇʇ˛˘Â ÒÓÓÚÌÓ¯ÂÌË ı ≈ ‡ (ı ÔË·ÎËÁËÚÂθÌÓ ‡‚ÌÓ ‡),
„‰Â ‡ – ‚¢ÂÒÚ‚ÂÌÌÓ ˜ËÒÎÓ.
ç˜ÂÚÍÓ ÏÌÓÊÂÒÚ‚Ó Ä ÏÓÊÂÚ ·˚Ú¸ ÓÔ‰ÂÎÂÌÓ, ̇ÔËÏÂ,
Ú‡Í:
Ax ııU ı
xa
= ∈
−
−
(, , . ()) ()=2
ÄÄ
µµ
2

234
é˜Â‚ˉÌÓ, ̇˷Óθ¯Â Á̇˜ÂÌË ÙÛÌ͈Ëfl ÔË̇‰ÎÂÊÌÓÒÚË
ËÏÂÂÚ ÔË ı = ‡.
ç‡È‰ÂÏ ÏÌÓÊÂÒÚ‚Ó ÛÓ‚Ìfl α = 0,5. çÂÚÛ‰ÌÓ Û·Â‰ËÚ¸Òfl, ˜ÚÓ
µ
A
x
ı
axa
axa
xa
xa
0,5
()
()=
1, ‰Îfl
Ë ‰Îfl
‰Îfl
Ë ‰Îfl
≤≤+
−≤ <
>+
> −
2
2
02
2
,
,
.
Ç Í·ÒÒ˘ÂÒÍÓÈ ÚÂÓËË ÏÌÓÊÂÒÚ‚ ÏÓ˘ÌÓÒÚ¸ ÏÌÓÊÂÒÚ‚‡ ÓÔ-
‰ÂÎflÂÚÒfl Í‡Í ˜ËÒÎÓ ÒÓÒÚ‡‚Îfl˛˘Ëı ˝ÎÂÏÂÌÚÓ‚. é˜Â‚ˉÌÓ ‚
ÚÂÓËË ÏÌÓÊÂÒÚ‚ ÔÓÌflÚË ÏÓ˘ÌÓÒÚË ‚ ÚÂÓËË Ì˜ÂÚÍËı ÏÌÓ-
ÊÂÒÚ‚ ÒÚ‡ÌÓ‚ËÚÒfl ‚ÂҸχ ÚÛχÌÌ˚Ï. ÑÂÈÒÚ‚ËÚÂθÌÓ, ͇ÍÓ‚Ó ÍÓ-
΢ÂÒÚ‚Ó ˝ÎÂÏÂÌÚÓ‚ ÏÌÓÊÂÒÚ‚‡ ‚ ÒÎÛ˜‡Â, ÍÓ„‰‡ Ò‡ÏÓ ÔÓÌflÚËÂ
ÔË̇‰ÎÂÊÌÓÒÚË ˝ÎÂÏÂÌÚ‡ ÏÌÓÊÂÒÚ‚Û fl‚ÎflÂÚÒfl “‡ÁÏ˚Ú˚Ï”?
àÏÂÂÚÒfl ÌÂÒÍÓθÍÓ ÒÔÓÒÓ·Ó‚ ËÁÏÂÂÌËfl ÏÓ˘ÌÓÒÚË Ì.Ï., ÓÒ-
ÌÓ‚‡ÌÌ˚ı ̇ ÒÛÏÏËÓ‚‡ÌËË Ì‡‚Ì˚ı “‚ÂÒÓ‚” ˝ÎÂÏÂÌÚÓ‚, ÔÓ-
ÔÓˆËÓ̇θÌ˚ı Ëı ÙÛÌ͈ËflÏ ÔË̇‰ÎÂÊÌÓÒÚË. é·ÓÁ̇˜ËÏ
N(A) ÏÓ˘ÌÓÒÚ¸ Ì.Ï. Ä.
é‰ËÌ ËÁ ÒÔÓÒÓ·Ó‚ ËÁÏÂÂÌËfl N(A) ÒÓÒÚÓËÚ ‚ ‚˚˜ËÒÎÂÌËË
ÒÛÏÏ˚ ‚Á‚¯ÂÌÌ˚ı ÏÓ˘ÌÓÒÚÂÈ ÏÌÓÊÂÒÚ‚ ÛÓ‚Ìfl α ‰Îfl ‰‡ÌÌÓ„Ó
Ì.Ï. Ä.
èÛÒÚ¸
ÛÌË‚Â҇θÌÓÂ
ÏÌÓÊÂÒÚ‚Ó
U = {x
1
, x
2
,..., x
n
}, A ⊆ U –
̘ÂÚÍÓ ÔÓ‰ÏÌÓÊÂÒÚ‚Ó. ëӄ·ÒÌÓ ÚÂÓÂÏÂ Ó ‰ÂÍÓÏÔÓÁˈËË
ξαξ
α
AiA
i
i
n
=
=
∑
1
, „‰Â
A
i
α
– ÏÌÓÊÂÒÚ‚Ó ÛÓ‚Ìfl α
i
. íÓ„‰‡ ̘ÂÚ͇fl
ÏÓ˘ÌÓÒÚ¸ ÓÔ‰ÂÎflÂÚÒfl ÒÎÂ‰Û˛˘ËÏ Ó·‡ÁÓÏ.
NA
i
i
i
n
NA
()
()
=
=
∑
α
α
1
, (5.19)
„‰Â
NA
i
()
α
– ÏÓ˘ÌÓÒÚ¸ ÏÌÓÊÂÒÚ‚‡ ÛÓ‚Ìfl α
i
;
A
i
α
– Ó·˚˜ÌÓÂ
ÏÌÓÊÂÒÚ‚Ó.
è Ë Ï Â 5. èÛÒÚ¸
U = {x
1
, x
2
,..., x
n
},
Ax x x=
{}
(;;;.
1 23
0,5), ( 0,2), ( 0,8)
éÔ‰ÂÎËÏ N(A). åÌÓÊÂÒÚ‚Ó Ä ‡ÒÍ·‰˚‚‡ÂÚÒfl ÔÓ ÏÌÓÊÂÒÚ-
‚‡Ï ÛÓ‚Ìfl 0,2; 0,5; 0,8:
Axxx
02 1 23,
;=
{}
, ,

235
Axx
05 1 3,
;=
{}
,
Ax
08 3,
.=
{}
íÓ„‰‡ ̘ÂÚ͇fl ÏÓ˘ÌÓÒÚ¸ Ä ‡‚̇
NA
NA NA NA
() , .
,
()
,
()
,
()
,,,
=++≈
02 05 08
02 05 08
112 ➤
5.3. çÖóÖíäàÖ éíçéòÖçàü.
ëÇéâëíÇÄ çÖóÖíäàï éíçéòÖçàâ
ç˜ÂÚÍËÏ ·Ë̇Ì˚Ï ÓÚÌÓ¯ÂÌËÂÏ ρ (ÒÓ͇˘ÂÌÌÓ Ì.·.Ó.)
̇ÁÓ‚ÂÏ ÏÌÓÊÂÒÚ‚Ó ÛÔÓfl‰Ó˜ÂÌÌ˚ı Ô‡ (ı, Û), „‰Â ı ∈ ï,
Û
∈ Y
Ò ÙÛÌ͈ËÂÈ ÔË̇‰ÎÂÊÌÓÒÚË
µ
ρ
(, ).xy
èÓ ‡Ì‡ÎÓ„ËË Ò ‚˚·ÓÓÏ Ó·Î‡ÒÚË Á̇˜ÂÌËÈ ‰Îfl ÙÛÌ͈ËË
ÔË̇‰ÎÂÊÌÓÒÚË Ì˜ÂÚÍÓ„Ó ÏÌÓÊÂÒÚ‚‡, ‚ ͇˜ÂÒڂ ӷ·ÒÚË Á̇-
˜ÂÌËÈ ‰Îfl
µ
ρ
(, )xy ‚˚·Ë‡ÂÚÒfl Á‡ÏÍÌÛÚ˚È ËÌÚ‚‡Î [0, 1].
Ç ˝ÚÓÏ ÒÎÛ˜‡Â, ÂÒÎË
µ
ρ
(, )xy = 0, ÚÓ „Ó‚ÓflÚ, ˜ÚÓ ÏÂÊ‰Û ı Ë
Û Ì.·.Ó. ρ Ì ‚˚ÔÓÎÌflÂÚÒfl, ËÎË ıÛ.
ÖÒÎË
µ
ρ
(, )xy = 1, ÚÓ „Ó‚ÓflÚ, ˜ÚÓ ÏÂÊ‰Û ı Ë Û ‚˚ÔÓÎÌflÂÚ-
Òfl ÓÚÌÓ¯ÂÌË ρ, ËÎË ˜ÚÓ ıρÛ. ÖÒÎË Ê 0 < µ
ρ
(x, y) < 1, ÚÓ
„Ó‚ÓflÚ, ˜ÚÓ ıρÛ ‚˚ÔÓÎÌflÂÚÒfl Ò ÙÛÌ͈ËÂÈ ÔË̇‰ÎÂÊÌÓÒÚË
µ
ρ
(x, y).
èËÏÂ˚ ̘ÂÚÍËı ÓÚÌÓ¯ÂÌËÈ.
è Ë Ï Â 1. Ç Í·ÒÒ˘ÂÒÍÓÈ Ï‡ÚÂχÚËÍ ‚ÒÚ˜‡ÂÚÒfl ÌÂχÎÓ
ÔËÏ ӂ ̘ÂÚÍËı ÔÓÌflÚËÈ, ÓÚÌÓ¯ÂÌËÈ. ÇÓÚ Ó‰ÌÓ ËÁ ÌËı:
ı ≈ Û. ä‡Í ˝ÚÓ ÔÓÌËχڸ? í‡ÍÓ ÒÓÓÚÌÓ¯ÂÌË ÏÂÊ‰Û ı Ë Û
ÏÓÊÌÓ ‚˚‡ÁËÚ¸ ‚ Ú ÏË̇ı ̘ÂÚÍËı ·Ë̇ Ì˚ı ÓÚÌÓ¯ÂÌËÈ,
̇ÔËÏÂ, Ú‡Í:
ρ µµ
ρρ
==
+ −
(, ), (, ) (, ) .
()
xy xy xy
xy
1
1
2
ÇˉÌÓ, ˜ÚÓ ˜ÂÏ ÏÂ̸¯Â ‡·ÒÓβÚ̇fl ‚Â΢Ë̇ ‡ÁÌÓÒÚË ı – Û,
ÚÂÏ ·ÎËÊ Á̇˜ÂÌËÂ
µ
ρ
(, )xy Í 1 Ë ÚÂÏ “‚ ·Óθ¯ÂÈ ÒÚÂÔÂÌË”
ÒÔ‡‚‰ÎË‚‡ Á‡ÔËÒ¸ ı ≈ Û. ùÚÓ Òӄ·ÒÛÂÚÒfl Ò ËÌÚÛËÚË‚Ì˚Ï ÔÓ-
ÌflÚËÂÏ Ú‡ÍÓ„Ó ÒÓÓÚÌÓ¯ÂÌËfl ÏÂÊ‰Û ı Ë Û.

236
è Ë Ï Â 2. Ç˚‡ÁËÏ, ËÒÔÓθÁÛfl ̘ÂÚÍÓ ·Ë̇ÌÓ ÓÚÌÓ-
¯ÂÌËÂ, χÚÂχÚ˘ÂÒÍÓ ÒÓÓÚÌÓ¯ÂÌË “ı „Ó‡Á‰Ó ·Óθ¯Â Û”,
Ó·ÓÁ̇˜‡ÂÏÓ ı >> Û. éÔËÒ‡Ú¸ Â„Ó ÏÓÊÌÓ, ̇ÔËÏÂ, ̘ÂÚÍËÏ
·Ë̇Ì˚Ï ÓÚÌÓ¯ÂÌËÂÏ
ρ µµ
ρρ
==
≤
+
−
(, ), (, ) (, )
,
,.xy xy xy
xy
xy
xy
>
0
1
1
1
ì ˝ÚÓ„Ó ÓÚÌÓ¯ÂÌËfl ÙÛÌ͈Ëfl ÔË̇‰ÎÂÊÌÓÒÚË ‰Îfl x > y Á‡‚Ë-
ÒËÚ ÓÚ ‚Â΢ËÌ˚ ı – Û. óÂÏ ˝Ú‡ ‚Â΢Ë̇ ·Óθ¯Â, ÚÂÏ ·ÎËÊÂ
Á̇˜ÂÌËÂ
µ
ρ
(, )xy Í 1. ùÚÓ ÓڇʇÂÚ ı‡ ‡ÍÚ ÓÔËÒ˚‚‡ÂÏÓÈ
Á‡‚ËÒËÏÓÒÚË. ➤
ÑÎfl ̘ÂÚÍÓ„Ó ÓÚÌÓ¯ÂÌËfl ÔÓ ‡Ì‡ÎÓ„ËË Ò Ì˜ÂÚÍËÏ ÏÌÓÊÂÒÚ-
‚ÓÏ ÏÓÊÂÚ ·˚Ú¸ ÓÔ‰ÂÎÂÌÓ ÏÌÓÊÂÒÚ‚Ó ÛÓ‚Ìfl α ‰‡ÌÌÓ„Ó
Ì.·.Ó. ρ:
Axyxy
A
αρ
ρ
µ α
()
(, ) (, ) ,= ≥
{}
(5.20)
Ë̇˜Â „Ó‚Ófl
A
xy
xy
A
αρ
ρ
ρ
µ α
µ α
()
,(,) ,
,(,) .
=
<
≥
0
1
çÓÒËÚÂÎÂÏ Ì˜ÂÚÍÓ„Ó ·Ë̇ÌÓ„Ó ÓÚÌÓ¯ÂÌËfl ρ ̇Á˚‚‡ÂÚ-
Òfl Ó·˚˜ÌÓ ÏÌÓÊÂÒÚ‚Ó S
(ρ)
ÛÔÓfl‰Ó˜ÂÌÌ˚ı Ô‡ (ı, Û), ‰Îfl
ÍÓÚÓ˚ı ÙÛÌ͈Ëfl ÔË̇‰ÎÂÊÌÓÒÚË ÔÓÎÓÊËÚÂθ̇:
S
()ρ
=
=>
{}
(, ) (, ) .xy xy µ
ρ
0 á‡ÏÂÚËÏ, ˜ÚÓ ÌÓÒËÚÂθ ̘ÂÚÍÓ„Ó ·Ë̇-
ÌÓ„Ó ÓÚÌÓ¯ÂÌËfl fl‚ÎflÂÚÒfl Ô‰ÂθÌ˚Ï ÒÎÛ˜‡ÂÏ ÏÌÓÊÂÒÚ‚‡ ÛÓ‚-
Ìfl α ÔË α → 0.
èÓÂ͈Ëfl ̘ÂÚÍÓ„Ó ·Ë̇ÌÓ„Ó ÓÚÌÓ¯ÂÌËfl. è‚ÓÈ ÔÓÂÍ-
ˆËÂÈ Ì.·.Ó. ρ ·Û‰ÂÏ Ì‡Á˚‚‡Ú¸ ÙÛÌÍˆË˛
µµ
ρρ
()
( ) max ( , ).
1
x
y
xy= (5.21)
ÇÚÓÓÈ ÔÓÂ͈ËÂÈ Ì.·.Ó. ρ ·Û‰ÂÏ Ì‡Á˚‚‡Ú¸ ÙÛÌÍˆË˛
µµ
ρρ
()
( ) max ( , ).
2
x
x
xy= (5.22)
237
ÇÚÓ‡fl ÔÓÂ͈Ëfl Ô‚ÓÈ ÔÓÂ͈ËË ‡‚̇ Ô‚ÓÈ ÔÓÂ͈ËË
‚ÚÓÓÈ ÔÓÂ͈ËË, ÔÓÒÍÓθÍÛ Ï‡ÍÒËÏÛÏ ÔÓ ı Ë ÔÓ Û Ë˘ÂÚÒfl ÌÂ-
Á‡‚ËÒËÏÓ. èÓÎÛ˜ÂÌ̇fl ‚Â΢Ë̇ ̇Á˚‚‡ÂÚÒfl „ÎÓ·‡Î¸ÌÓÈ ÔÓÂÍ-
ˆËÂÈ Ì˜ÂÚÍÓ„Ó ·Ë̇ÌÓ„Ó ÓÚÌÓ¯ÂÌËfl Ë Ó·ÓÁ̇˜‡ÂÚÒfl
h
xy
xy
xy
xy( ) max(max ( , )) max(max ( , )).ρ µµ
ρρ
== (5.23)
ÖÒÎË h(ρ) = 1, ÚÓ „Ó‚ÓflÚ, ˜ÚÓ ÓÚÌÓ¯ÂÌË ρ ÌÓχθÌÓ, ÂÒÎË
h(ρ) < 1, ÚÓ ÓÚÌÓ¯ÂÌË ÒÛ·ÌÓχθÌÓ.
è Ë Ï Â 3. èÛÒÚ¸ Ì.·.Ó. Ô‰ÒÚ‡‚ÎÂÌÓ ÙÛÌ͈ËÂÈ ÔË̇‰-
ÎÂÊÌÓÒÚË
hxy
xy
()
(, ) ,
ρ
=
+ −
1
1
‡ ӷ·ÒÚË ÓÔ‰ÂÎÂÌËfl ˝ÎÂÏÂÌÚÓ‚ ı Ë Û – ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ ÏÌÓ-
ÊÂÒÚ‚‡ÏË
X = {1, 2, 3} Ë Y = {3, 4, 5} .
íÓ„‰‡ Ô‚‡fl ÔÓÂ͈Ëfl ·Û‰ÂÚ ‡‚̇
µµ
ρρ
()
( ) max ( , )
2
x
y
xy==
=
+ −
1
1 3x
,
‚ÚÓ‡fl ÔÓÂ͈Ëfl
µµ
ρρ
()
( ) max ( , )
2
1
1 3
y
x
xy
y
==
+ −
Ë „ÎÓ·‡Î¸Ì‡fl ÔÓÂ͈Ëfl
h
x
y
y
y( ) max ( ) max ( )
() ( )
ρ µµ
ρρ
===
1 2
==
+ −
max .
x
x
1
1 3
1
ùÚÓÚ ÂÁÛÎ¸Ú‡Ú Ì‡„Îfl‰ÌÓ Ô‰ÒÚ‡‚ÎflÂÚÒfl Ú‡·ÎˈÂÈ Á̇˜ÂÌËÈ
ÙÛÌ͈ËË ÔË̇‰ÎÂÊÌÓÒÚË (Ú‡·Î. 5.2) ‰Îfl ‡Á΢Ì˚ı Ô‡ ˝ÎÂ-
ÏÂÌÚÓ‚ (ı, Û).
퇷Îˈ‡ 5.2
ı 345
1-fl ÔÓÂ͈Ëfl
µ
ρ
()
()
1
ı
11/3 1/4 1/5 1/3
2 1/2 1/3 1/4 1/2
3 11/2 1/3 1
ÉÎÓ·‡Î¸Ì‡fl
2-fl ÔÓÂ͈Ëfl 11/2 1/3 1 ÔÓÂ͈Ëfl
µ
ρ
()
()
2
y
h(ρ)
