Овчаров Л.А. и др. Математические модели информационых процессов и управления
Подождите немного. Документ загружается.

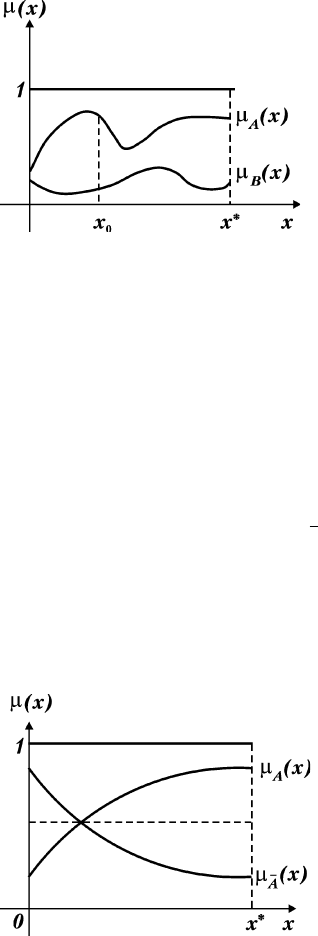
218
ÔflÏÓÈ
µ()ı = 1. èË ˝ÚÓÏ Ò‡Ï‡ Ôflχfl
µ()ı = 1 Ô‰ÒÚ‡‚ÎflÂÚ,
Ә‚ˉÌÓ, ÙÛÌÍˆË˛ ÔË̇‰ÎÂÊÌÓÒÚË ÛÌË‚Â҇θÌÓ„Ó ÏÌÓÊÂÒÚ-
‚‡ U (ËÒ. 5.2).
ÖÒÎË ‰‚‡ ̘ÂÚÍËı ÏÌÓÊÂÒÚ‚‡ ‡‚Ì˚, ÚÓ Ú‡ÍË „‡Ù˘ÂÒÍËÂ
ËÁÓ·‡ÊÂÌËfl ‰Îfl ÌËı ‰ÓÎÊÌ˚ ÒÓ‚Ô‡‰‡Ú¸. ã˛·Ó ÔÓ‰ÏÌÓÊÂÒÚ‚Ó
̘ÂÚÍÓ„Ó ÏÌÓÊÂÒÚ‚‡ B ⊆ A ËÁÓ·‡ÁËÚÒfl, Ә‚ˉÌÓ, ÍË‚ÓÈ,
‡ÒÔÓÎÓÊÂÌÌÓÈ ‚ÌÛÚË Ó·Î‡ÒÚË, Ә˜ÂÌÌÓÈ ÙÛÌ͈ËÂÈ
µ
Ä
ı(),
Ú‡Í Í‡Í
µµ
BA
ıı() ()≤ ‚ ͇ʉÓÈ ÚӘ͠ı ∈ [0, x
∗
].
Ç ÒÓÓÚ‚ÂÚÒÚ‚ËË Ò ÓÔ‰ÂÎÂÌËÂÏ Ì˜ÂÚÍÓ„Ó ‰ÓÔÓÎÌÂÌËfl, ı‡-
‡ÍÚÂËÒÚ˘ÂÒ͇fl ÙÛÌ͈Ëfl ÔË̇‰ÎÂÊÌÓÒÚË
µ
A
ı( ) ·Û‰ÂÚ ÁÂ-
͇θÌ˚Ï ÓÚÓ·‡ÊÂÌËÂÏ ÙÛÌ͈ËË
µ
Ä
ı( ) ÓÚÌÓÒËÚÂθÌÓ ÔflÏÓÈ
µ() ,ı = 05 (ËÒ. 5.3).
ÑÎfl ÙÛÌ͈ËÈ ÔË̇‰ÎÂÊÌÓÒÚË Ó·˙‰ËÌÂÌËfl Ë ÔÂÂÒ˜ÂÌËfl
̘ÂÚÍËı ÏÌÓÊÂÒÚ‚ ÌÂÓ·ıÓ‰ËÏÓ ‚ ͇ʉÓÈ ÚӘ͠‚ÁflÚ¸ ̇˷Óθ-
¯Â ËÎË Ì‡ËÏÂ̸¯Â Á̇˜ÂÌË ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ. ùÚÓ ÔË‚Ó‰ËÚ Í
êàë. 5.2
êàë. 5.3

219
„‡Ù˘ÂÒÍÓÏÛ Ô‰ÒÚ‡‚ÎÂÌ˲ (ËÒ. 5.4 Ë ËÒ. 5.5). èÓÒÚÓËÚ¸
‰Ë‡„‡ÏÏ˚ ‰Îfl ÓÔ‡ˆËÈ ÓÚÌÓÒËÚÂθÌÓ„Ó ‰ÓÔÓÎÌÂÌËfl Ë ÒËÏÏÂ-
Ú˘ÂÒÍÓÈ ‡ÁÌÓÒÚË, ËÒıÓ‰fl ËÁ Ëı ÓÔ‰ÂÎÂÌËÈ, Ô‰·„‡ÂÚÒfl
Ò‡ÏÓÒÚÓflÚÂθÌÓ Ë ÂÁÛÎ¸Ú‡Ú ÔÓ͇Á‡Ú¸ ÔÂÔÓ‰‡‚‡ÚÂβ.
èÂʉ ˜ÂÏ ÔÂÂÈÚË Í ‰‡Î¸ÌÂȯÂÏÛ ËÁÛ˜ÂÌ˲ ÚÂÓËË ÌÂ-
˜ÂÚÍËı ÏÌÓÊÂÒÚ‚, ҉·ÂÏ ÌÂÍÓÚÓ˚ ‚˚‚Ó‰˚ Ë ‚˚fl‚ËÏ Ò‚flÁ¸
ÏÂÊ‰Û ‡Î„·ÓÈ Ì˜ÂÚÍËı ÏÌÓÊÂÒÚ‚ Ë ‡Î„· ÓÈ Ó·˚˜Ì˚ı ÏÌÓ-
ÊÂÒÚ‚.
Ç ˚ ‚ Ó ‰ 1. ÖÒÎË Ó·Î‡ÒÚ¸ Á̇˜ÂÌËÈ ÙÛÌ͈ËË ÔË̇‰ÎÂÊÌÓÒ-
ÚË – ‰‚Ûı˝ÎÂÏÂÌÚÌÓ ÏÌÓÊÂÒÚ‚Ó M = {0, 1}, ÚÓ Ì.Ï. Ä ÂÒÚ¸
Ó·˚˜ÌÓ ÏÌÓÊÂÒÚ‚Ó. íÓ„‰‡ ‚ ÓÔ‰ÂÎÂÌËË Ì.Ï., Á‡ÔËÒ‡ÌÌÓÏ ‚
‚ˉ (5.5), ‚ÚÓ˚ÏË ÍÓÓ‰Ë̇ڇÏË ‚ ÛÔÓfl‰Ó˜ÂÌÌ˚ı Ô‡‡ı
(5.4) ·Û‰ÛÚ ÌÛÎË Ë Â‰ËÌˈ˚, ‚ Á‡‚ËÒËÏÓÒÚË ÓÚ ÚÓ„Ó, fl‚ÎflÂÚÒfl
ÎË ı ˝ÎÂÏÂÌÚÓÏ Ä. Ç ˜‡ÒÚÌÓÒÚË, Ò‡ÏÓ ÛÌË‚Â҇θÌÓ ÏÌÓÊÂÒÚ‚Ó
U Ô‰ÒÚ‡‚Îfl ÂÚÒfl ÛÔÓfl‰Ó˜ÂÌÌÓÈ Ô‡ÓÈ, Ëϲ˘ÂÈ Ô ‚Û˛ ÍÓ-
Ó‰Ë̇ÚÛ ı Ë ÔÓÒÚÓflÌÌÛ˛ ‚ÚÓÛ˛ ÍÓÓ‰Ë̇ÚÛ
µ
Ä
ı()= 1.
êàë. 5.4
êàë. 5.5
220
Ç ˚ ‚ Ó ‰ 2. éÔ‰ÂÎÂÌËfl ÓÔ‡ˆËÈ Ë ÓÚÌÓ¯ÂÌËÈ Ì‡‰ ̘ÂÚ-
ÍËÏË ÏÌÓÊÂÒÚ‚‡ÏË ‚ ÒÎÛ˜‡Â, ÍÓ„‰‡ ӷ·ÒÚ¸ Á̇˜ÂÌËÈ ÙÛÌ͈ËË
ÔË̇‰ÎÂÊÌÓÒÚË M – ‰‚Ûı˝ÎÂÏÂÌÚÌÓ ÏÌÓÊÂÒÚ‚Ó, ÔÂÂıÓ‰flÚ ‚
ÓÔ‰ÂÎÂÌËfl ÓÔ‡ˆËÈ Ë ÓÚÌÓ¯ÂÌËÈ Ì‡‰ Ó·˚˜Ì˚ÏË ÏÌÓÊÂÒÚ‚‡-
ÏË ÚÂÓËË ÏÌÓÊÂÒÚ‚.
èÓ‚ÂËÏ ˝ÚÓ, ̇ÔËÏÂ, ‰Îfl ÓÚÌÓ¯ÂÌËfl ‚Íβ˜ÂÌËfl. èÛÒÚ¸
Ä, B – ÔÓ‰ÏÌÓÊÂÒÚ‚‡ U Ë B ⊆ A. èÛÒÚ¸ M = {0, 1}. èÓ͇ÊÂÏ,
˜ÚÓ ‚ ˝ÚÓÏ ÒÎÛ˜‡Â ÓÔ‰ÂÎÂÌˠ̘ÂÚÍÓ„Ó ÓÚÌÓ¯ÂÌËfl ‚Íβ˜ÂÌËfl
ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ ‡Ì‡Îӄ˘ÌÓÏÛ ÓÔ‰ÂÎÂÌ˲ ÓÚÌÓ¯ÂÌËfl ‚Íβ˜Â-
ÌËfl ‚ Ó·˚˜ÌÓÈ ÚÂÓËË ÏÌÓÊÂÒÚ‚.
ÑÂÈÒÚ‚ËÚÂθÌÓ, ‰Îfl Ì.Ï. Ä Ë B ‚˚ÔÓÎÌÂÌË ÓÚÌÓ¯ÂÌËfl
B ⊆ Ä ÓÁ̇˜‡ÂÚ, ˜ÚÓ ‰Îfl ‚ÒÂı ˝ ÎÂÏÂÌÚÓ‚ ı ∈ U
µµ
ÄB
ıı() ()≥ .
çÓ ÂÒÎË M
= {0, 1}, ÚÓ ÙÛÌ͈ËË
µ
Ä
ı() Ë
µ
B
ı( ) ÏÓ„ÛÚ ÔËÌË-
χڸ Î˯¸ Á̇˜ÂÌËfl 0 Ë 1. ÇÓÁ¸ÏÂÏ ÔÓËÁ‚ÓθÌ˚È ˝ÎÂÏÂÌÚ
ı ∈ U. ÖÒÎË
µ
B
ı() = 1, ÚÓ ‰ÓÎÊÌÓ ·˚Ú¸
µ
Ä
ı() = 1, ˜ÚÓ·˚ ‚˚-
ÔÓÎÌflÎÓÒ¸ ̇‚ÂÌÒÚ‚Ó
µµ
ÄB
ıı() ()≥ . ùÚÓ ÓÁ̇˜‡ÂÚ, ˜ÚÓ ËÁ
ÚÓ„Ó, ˜ÚÓ ı ∈ B, ÒΉÛÂÚ ı ∈ Ä. Ä ÔÓÒΉÌ ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ ÓÔ-
‰ÂÎÂÌ˲ ÓÚÌÓ¯ÂÌËfl ‚Íβ˜ÂÌËfl Ó·˚˜ÌÓÈ ÚÂÓËË ÏÌÓÊÂÒÚ‚.
èÓ‚ÂËÏ ÚÂÔ¸ ‚˚‚Ó‰ 2 ‰Îfl ͇ÍÓÈ-ÌË·Û‰¸ ÓÔ‡ˆËË, ̇-
ÔËÏÂ, ‰Îfl Ó·˙ ‰ËÌÂÌËfl.
èÛÒÚ¸ ë = Ä ∪ B – Ó·˙‰ËÌÂÌË ‰‚Ûı ̘ÂÚÍËı ÏÌÓÊÂÒÚ‚ Ä
Ë B. èÛÒÚ¸ M = {0, 1}. èÓ ÓÔ‰ÂÎÂÌ˲, ÓÔ‡ˆËË Ì˜ÂÚÍÓ„Ó
Ó·˙‰ËÌÂÌËfl
µµµ
ëAB
ııı( ) max( ( ), ( ))= ‰Îfl β·Ó„Ó ı ∈ U. çÓ
Ú‡Í Í‡Í ÙÛÌ͈ËË
µ
Ä
ı(),
µ
B
ı( ) ÏÓ„ÛÚ ÔËÌËχڸ Î˯¸ Á̇˜Â-
ÌËfl 0 Ë 1, ÚÓ Ë Û ÙÛÌ͈ËË
µ
C
ı( ) Ì ÏÓÊÂÚ ·˚Ú¸ ‰Û„Ëı Á̇˜Â-
ÌËÈ, ‡
µ
C
ı()= 1 ÚÓθÍÓ ‚ ÒÎÛ˜‡Â, ÍÓ„‰‡ ıÓÚfl ·˚ Ó‰ÌÓ ËÁ Á̇˜Â-
ÌËÈ
µ
Ä
ı(),
µ
B
ı() ‡‚ÌÓ 1. ùÚÓ Á̇˜ËÚ, ˜ÚÓ ˝ÎÂÏÂÌÚ ı ÔË̇‰-
ÎÂÊËÚ Ó·˙‰ËÌÂÌ˲ ÚÓθÍÓ ÚÓ„‰‡, ÍÓ„‰‡ ÓÌ ÔË̇‰ÎÂÊËÚ, ÔÓ
͇ÈÌÂÈ ÏÂÂ, Ó‰ÌÓÏÛ ËÁ ÏÌÓÊÂÒÚ‚. èÓÎÛ˜ÂÌÌÓ ÛÚ‚ÂʉÂÌËÂ
ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ ÓÔ‰ÂÎÂÌ˲ ÓÔ‡ˆËË Ó·˙‰ËÌÂÌËfl, ‰‡ÌÌÓÏÛ ‚
Í·ÒÒ˘ÂÒÍÓÈ ÚÂÓËË ÏÌÓÊÂÒÚ‚.
å‡ Ì˜ÂÚÍÓÒÚË. å˚ ÔËÒÚÛÔ‡ÂÏ Í ËÁÛ˜ÂÌ˲ ÔÓÌflÚËÈ, ÍÓ-
ÚÓ˚ ÔÓÁ‚ÓÎflÚ Ì‡Ï ‚ ‰‡Î¸ÌÂȯÂÏ ÔÓÁ̇ÍÓÏËÚ¸Òfl Ò ÓÒÌÓ‚ÌÓÈ
ı‡‡ÍÚÂËÒÚËÍÓÈ Ì˜ÂÚÍÓ„Ó ÏÌÓÊÂÒÚ‚‡ – ÏÂÓÈ Ì˜ÂÚÍÓÒÚË.
èÓÒÍÓθÍÛ Â˜¸ ÔÓȉÂÚ Ó· ËÁÏÂÂÌËË ‚Â΢ËÌ, ÌÂÓ·ıÓ‰ËÏÓ
‚ÒÔÓÏÌËÚ¸, ˜ÚÓ Ú‡ÍӠχ. ÖÒÎË Ï˚ ıÓÚËÏ ‚‚ÂÒÚË ÏÂÛ (ËÎË
ÙÛÌÍˆË˛ ‡ÒÒÚÓflÌËfl) d(x, y) ̇ ÏÌÓÊÂÒÚ‚Â R, „‰Â x, y ∈ R,
ÚÓ ‰Îfl Ì ‰ÓÎÊÌ˚ ‚˚ÔÓÎÌflÚ¸Òfl ÒÎÂ‰Û˛˘Ë ˜ÂÚ˚ ÛÒÎÓ‚Ëfl:
‡) d(x, y) ≥ 0 (ÌÂÓÚˈ‡ÚÂθÌÓÒÚ¸);
·) d(x, y) = d(x, y) (ÒËÏÏÂÚ˘ÌÓÒÚ¸);
221
‚) d(x, y) = 0 ÚÓ„‰‡ Ë ÚÓθÍÓ ÚÓ„‰‡, ÍÓ„‰‡ x = y;
„) d(x, z) ≤ d(x, y) + d(y, z) (Ú ‡ÌÁËÚË‚ÌÓÒÚ¸) ‰Îfl β·˚ı
˝ÎÂÏÂÌÚÓ‚ x, y, z ∈ R.
åÓÊÌÓ ÔÓ‚ÂËÚ¸, ˜ÚÓ ‚Ò ËÁ‚ÂÒÚÌ˚ ÙÛÌ͈ËË ‡ÒÒÚÓflÌËfl
(̇ÔËÏÂ, ‡ÒÒÚÓflÌË ւÍÎˉ‡) Û‰Ó‚ÎÂÚ‚Ó fl˛Ú ˝ÚËÏ
ÛÒÎÓ‚ËflÏ.
èÂʉ ˜ÂÏ ‚‚ÂÒÚË ÙÛÌÍˆË˛ ‡ÒÒÚÓflÌËfl ÏÂÊ‰Û Ì˜ÂÚÍËÏ
ÏÌÓÊÂÒÚ‚‡ÏË, ‰Ó͇ÊÂÏ ÎÂÏÏÛ:
ã Â Ï Ï ‡. ÑÎfl β·˚ı ‚¢ÂÒÚ‚ÂÌÌ˚ı ˜ËÒÂÎ a, b, c ÒÔ‡‚‰ÎË-
‚Ó Ì‡‚ÂÌÒÚ‚Ó:
ac ab bc−≤−+ − .
Ñ Ó Í ‡ Á ‡ Ú Â Î ¸ Ò Ú ‚ Ó:
é·ÓÁ̇˜ËÏ q = b – c. í‡ÍÓ ˜ËÒÎÓ ‚Ò„‰‡ ̇ȉÂÚÒfl, Ú‡Í Í‡Í
‰Îfl β·˚ı ‰‚Ûı ‚¢ÂÒÚ‚ÂÌÌ˚ı ˜ËÒÂÎ ÒÛ˘ÂÒÚ‚ÛÂÚ Ëı ‡ÁÌÓÒÚ¸.
燂ÂÌÒÚ‚Ó ÔÂÂÔ˯ÂÚÒfl ‚ ‚ˉÂ:
abq ab q− + ≤ + − + .
é·ÓÁ̇˜ËÏ = ‡ – ‚. èÓÎÛ˜ËÏ Ì‡‚ÂÌÒÚ‚Ó:
pq p q+ ≤ + .
í‡Í Í‡Í Ó·Â ˜‡ÒÚË ˝ÚÓ„Ó Ì‡‚ÂÌÒÚ‚‡ ÌÂÓÚˈ‡ÚÂθÌ˚ , ÚÓ ÏÓÊ-
ÌÓ ‚ÓÁ‚ÂÒÚË Ëı ‚ Í‚‡‰‡Ú. èË ˝ÚÓÏ ·Û‰ÂÏ ÓÚ·‡Ò˚‚‡Ú¸ Á̇Í
ÏÓ‰ÛÎfl Ú‡Ï, „‰Â ˝ÚÓ ‚ÓÁÏÓÊÌÓ:
ppqqp pqq
222 2
22++≤ ++.
èÓÒΠÔ˂‰ÂÌËfl ÔÓ‰Ó·Ì˚ı ˜ÎÂÌÓ‚ ÔÓÎÛ˜ËÏ Ó˜Â‚Ë‰ÌӠ̇-
‚ÂÌÒÚ‚Ó
pq p q≤⋅, ˜ÚÓ Ë Ú·ӂ‡ÎÓÒ¸ ‰Ó͇Á‡Ú¸.
ê‡ÒÒÚÓflÌË ï˝ÏÏËÌ„‡ ÏÂÊ‰Û Ì˜ÂÚÍËÏË ÏÌÓÊÂÒÚ‚‡ÏË.
èÛÒÚ¸ U – ÛÌË‚Â҇θÌÓ ÏÌÓÊÂÒÚ‚Ó, ÒÓÒÚÓfl˘Â ËÁ ˝ÎÂÏÂÌÚÓ‚
x
1
, x
2
,..., x
n
; A Ë B – ̘ÂÚÍË ÔÓ‰ÏÌÓÊÂÒÚ‚‡ U. ê‡ÒÒÚÓflÌËÂÏ
ï˝ÏÏËÌ„‡ ÏÂÊ‰Û ÏÌÓÊÂÒÚ‚‡ÏË Ä Ë B ̇Á˚ ‚‡ÂÚÒfl ‚Â΢Ë̇
dA B x x
Ai Bi
i
n
(, () (). )= µµ−
∑
=1
(5.6)
óÚÓ·˚ ˝ÚÓ ÓÔ‰ÂÎÂÌË ·˚ÎÓ ÍÓÂÍÚÌ˚Ï, ÌÂÓ·ıÓ‰ËÏÓ ÔÓ-
‚ÂËÚ¸ ‰Îfl ‡ÒÒÚÓflÌËfl
dA B(, ) ‚˚ÔÓÎÌÂÌË ˜ÂÚ˚Âı Ò‚ÓÈÒÚ‚
ÏÂ˚. Ç˚ÔÓÎÌÂÌË ÛÒÎÓ‚ËÈ ‡, ·, ‚ Ә‚ˉÌÓ Ë ÒΉÛÂÚ ËÁ Ò‚ÓÈ-
ÒÚ‚‡ ÙÛÌ͈ËË ÏÓ‰ÛÎfl.
èÓ͇ÊÂÏ ‚˚ÔÓÎÌÂÌË ҂ÓÈÒÚ‚‡ Ú‡ÌÁËÚË‚ÌÓÒÚË, Ú.Â. ‰Ó͇-

222
ÊÂÏ, ˜ÚÓ ‰Îfl ÔÓËÁ‚ÓθÌ˚ı Ì.Ï. Ä, Ç ë d(A, C) ≤ d(A, B) +
+ d(B, C). èÓ ÓÔ‰ÂÎÂÌ˲ ‡ÒÒÚÓflÌËfl ï˝ÏÏËÌ„‡ ˝ÚÓ
ÓÁ̇˜‡ÂÚ:
µµ µµ µµ
Ai ëi
i
n
Ai Bi
i
n
Bi ëi
i
n
xx xx xx() () () () () ().−≤ −+ −
===
∑∑∑
111
èÓ ÎÂÏÏ ‰Îfl
µµµ
Ai Bi ëi
xxx(), (), () ‚˚ÔÓÎÌflÂÚÒfl ̇‚ÂÌÒÚ‚Ó:
µ µ µµ µµ
Ai ëi Ai Bi Bi Ci
x x xx xx() () () () () (),−≤−+ −
„‰Â x
i
– ÔÓËÁ‚ÓθÌ˚È ˝ÎÂÏÂÌÚ ÏÌÓÊÂÒÚ‚‡ U.
ëÛÏÏËÓ‚‡ÌËÂÏ n ̇‚ÂÌÒÚ‚ ‰Îfl i = 1, 2,..., n ÔÓÎÛ˜ËÏ ‰Ó-
͇Á˚‚‡ÂÏÓ ÛÚ‚ÂʉÂÌËÂ.
éÚÌÓÒËÚÂθÌ˚Ï ‡ÒÒÚÓflÌËÂÏ ï˝ÏÏËÌ„‡ ̇Á˚‚‡ÂÚÒfl ‚ÂÎË-
˜Ë̇
δ(A, B) = d(A, B)/n. (5.7)
é˜Â‚ˉÌÓ, ‰Îfl δ(A, B) Ú‡ÍÊ ‚˚ÔÓÎÌflÂÚÒfl ˜ÂÚ˚ ҂ÓÈÒÚ‚‡
‡ÒÒÚÓflÌËfl.
á ‡ Ï Â ˜ ‡ Ì Ë Â: ‚ ÒÎÛ˜‡Â, ÍÓ„‰‡ Ä Ë B – Ó·˚˜Ì˚ ÏÌÓÊÂÒÚ‚‡,
‚‚‰ÂÌÌ˚ ‡ÒÒÚÓflÌËfl ÒÓ‚Ô‡‰‡˛Ú Ò ÒÓÓÚ‚ÂÚÒÚ‚Û˛˘ËÏË Ï‡ÏË
Ó·˚˜ÌÓÈ ÚÂÓËË ÏÌÓÊÂÒÚ‚.
ì Ú ‚ Â Ê ‰ Â Ì Ë Â 1. ç‡ËÏÂ̸¯Â Á̇˜ÂÌË ÓÚÌÓÒËÚÂθÌÓ„Ó
‡ÒÒÚÓflÌËfl ï˝ÏÏËÌ„‡ ‡‚ÌÓ ÌÛβ, ̇˷Óθ¯Â Á̇˜ÂÌË ‡‚ÌÓ
‰ËÌˈÂ, Ú.Â. 0 ≤ δ(A, B) ≤ 1.
ÑÂÈÒÚ‚ËÚÂθÌÓ, ÔÓÒÍÓθÍÛ δ(A, B) fl‚ÎflÂÚÒfl ÒÛÏÏÓÈ ÌÂÓÚË-
ˆ‡ÚÂθÌ˚ı Ò·„‡ÂÏ˚ı, ÚÓ δ(A, B) Ì ÏÓÊÂÚ ·˚Ú¸ ÏÂ̸¯Â ÌÛÎfl.
á̇˜ÂÌË δ(A, B) = 0 ‰ÓÒÚË„‡ÂÚÒfl, ÍÓ„‰‡ ‚Ò Ò·„‡ÂÏ˚Â
µµ
Ai Bi
xx() ()− = 0, ÚÓ ÂÒÚ¸ ÍÓ„‰‡
µµ
Ai Bi
xx() ()− ‰Îfl i = 1, 2,
..., n. Ä ˝ÚÓ ÓÁ̇˜‡ÂÚ, ˜ÚÓ Ä = B.
å‡ÍÒËÏÛÏ ‚Â΢ËÌ˚ δ(A, B) ÔÓÎÛ˜‡ÂÚÒfl, ÍÓ„‰‡ ‚Ò Ò·„‡Â-
Ï˚ ӉÌÓ‚ÂÏÂÌÌÓ ‰ÓÒÚË„‡˛Ú Ò‚ÓÂ„Ó Ï‡ÍÒËχθÌÓ„Ó Á̇˜ÂÌËfl .
çÂÚÛ‰ÌÓ ‚ˉÂÚ¸, ˜ÚÓ
max ( ) ( ) ,µµ
Ai Bi
xx− = 1 Ë ˝ÚÓ Á̇˜ÂÌËÂ
‰ÓÒÚË„‡ÂÚÒfl, ÍÓ„‰‡ Ӊ̇ ËÁ ÙÛÌ͈ËÈ ÔË̇‰ÎÂÊÌÓÒÚË ‡‚̇ 0,
‡ ‰Û„‡fl – 1, Ú.Â. ÍÓ„‰‡ Ä, B – Ó·˚˜Ì˚ ÏÌÓÊÂÒÚ‚‡, Ô˘ÂÏ
Ä = B.
àÌÓ„‰‡ ‚ ͇˜ÂÒÚ‚Â ÏÂ˚ ·ÎËÁÓÒÚË Ì˜ÂÚÍËı ÏÌÓÊÂÒÚ‚ ËÒ-
ÔÓθÁÛÂÚÒfl Ö‚ÍÎË‰Ó‚Ó ‡ÒÒÚÓflÌËÂ.
EA B x x
Ai Bi
i
n
( , ) ( ( ) ( ( )) . = −
=
∑
µµ
2
1
(5.8)
óËÚ‡ÚÂβ Ô‰ÓÒÚ‡‚ÎflÂÚÒfl ‚ÓÁÏÓÊÌÓÒÚ¸ Ò‡ÏÓÒÚÓflÚÂθÌÓ

223
۷‰ËÚ¸Òfl ‚ ÚÓÏ, ˜ÚÓ ˝Ú‡ ‚Â΢Ë̇ Û‰Ó‚ÎÂÚ‚ÓflÂÚ ˜ÂÚ˚ÂÏ
Ò‚ÓÈÒÚ‚‡Ï ‡ÒÒÚÓflÌËfl. ÑÎfl ‰Ó͇Á‡ÚÂθÒÚ‚‡ Ò‚ÓÈÒÚ‚‡ Ú‡ÌÁË-
ÚË‚ÌÓÒÚË Ô‰·„‡ÂÚÒfl ÒÙÓÏÛÎËÓ‚‡Ú¸ Ë ‰Ó͇Á‡Ú¸ ÌÂÓ·ıÓ‰Ë-
ÏÛ˛ ÎÂÏÏÛ.
éÚÌÓÒËÚÂθÌ˚Ï ‡ÒÒÚÓflÌËÂÏ Ö‚ÍÎˉ‡ ̇Á˚‚‡ÂÚÒfl ‚ÂÎË-
˜Ë̇
eA B
EA B
n
(, ) .
(,
)
= (5.9)
åÓÊÌÓ ÔÓ‚ÂËÚ¸, ˜ÚÓ ˝Ú‡ χ Û‰Ó‚ÎÂÚ‚ÓflÂÚ ÛÒÎÓ‚ËflÏ
‡ – „ ÙÛÌ͈ËË ‡ÒÒÚÓflÌËfl.
艷„‡ÂÚÒfl Ò‡ÏÓÒÚÓflÚÂθÌÓ ÔÓ‚ÂËÚ¸ ‚˚ÔÓÎÌÂÌË ‰Îfl
ÓÚÌÓÒËÚÂθÌÓ„Ó ‡ÒÒÚÓflÌËfl Ö‚ÍÎˉ‡ (5.9) ÛÚ‚ÂʉÂÌËfl, ‡Ì‡ÎÓ-
„˘ÌÓ„Ó ÛÚ‚ÂʉÂÌ˲ 1, Ú.Â.
0 1≤≤ÂA B(, ) .
êÂÁÛÎ¸Ú‡Ú ÔÓ͇Á‡Ú¸ ÔÂÔÓ‰‡‚‡ÚÂβ.
ǂ‰ÂÌÌ˚ ÙÛÌ͈ËË ‡ÒÒÚÓflÌËfl ‰Îfl Ì.Ï. ‡ÒÔÓÒÚ‡Ìfl˛ÚÒfl
̇ ÒÎÛ˜‡È, ÍÓ„‰‡ ˜ËÒÎÓ ˝ÎÂÏÂÌÚÓ‚ ÏÌÓÊÂÒÚ‚‡ U – ·ÂÒÍÓ̘ÌÓÂ.
Ç ˝ÚÓÏ ÒÎÛ˜‡Â ÍÓ̘Ì˚ ÒÛÏÏ˚ ‚ ÓÔ‰ÂÎÂÌÌ˚ı ÙÛÌ͈Ëflı ‡Ò-
ÒÚÓflÌËfl Á‡ÏÂÌfl˛ÚÒfl ̇ ÒÛÏÏ˚ Ò ·ÂÒÍÓ̘Ì˚Ï Ô‰ÂÎÓÏ, ÔË
ÛÒÎÓ‚ËË, ˜ÚÓ ÓÌË ÒıÓ‰flÚÒfl, ËÎË Ì‡ ËÌÚ„‡Î˚, ‚ Á‡‚ËÒËÏÓÒÚË
ÓÚ ÚÓ„Ó, fl‚ÎflÂÚÒfl ÎË ÏÌÓÊÂÒÚ‚Ó U Ò˜ÂÚÌ˚Ï ËÎË ËÏÂÂÚ ˜ËÒÎÓ
˝ÎÂÏÂÌÚÓ‚ ÍÓÌÚËÌÛÛÏ (ÒÏ. „·‚Û 1).
í‡Í, ̇ÔËÏÂ, ‡ÒÒÚÓflÌË ï˝ÏÏËÌ„‡ ‰Îfl ÛÌË‚Â҇θÌÓ„Ó
ÏÌÓÊÂÒÚ‚‡, ÒÓ‚Ô‡‰‡˛˘Â„Ó Ò ÏÌÓÊÂÒÚ‚ÓÏ ‰ÂÈÒÚ‚ËÚÂθÌ˚ı ˜ËÒÂÎ,
ÓÔ‰ÂÎflÂÚÒfl Ú‡Í:
DA B x xdx
AB
(, ) () () = −
−∞
∞
∫
µµ (5.10)
‚ ÒÎÛ˜‡Â, ÂÒÎË ˝ÚÓÚ ËÌÚ„‡Î ÒıÓ‰ËÚÒfl. èË ˝ÚÓÏ ‡ÒÒÚÓflÌËÂ
Ö‚ÍÎˉ‡
EA B x x dx
AB
(, ) ( () ()) = −
−∞
∞
∫
µµ
2
(5.11)
‚ ÒÎÛ˜‡Â ÒıÓ‰ËÏÓÒÚË ËÌÚ„‡Î‡ ÔÓ‰ Á̇ÍÓÏ ÍÓÌfl .
åÌÓÊÂÒÚ‚ÓÏ, ·ÎËʇȯËÏ Í Ì˜ÂÚÍÓÏÛ, ̇ÁÓ‚ÂÏ Ó·˚˜ÌÓÂ
ÏÌÓÊÂÒÚ‚Ó, ‡ÒÒÚÓflÌË ÓÚ ÍÓÚÓÓ„Ó ‰Ó ‰‡ÌÌÓ„Ó Ì˜ÂÚÍÓ„Ó ÏÌÓ-
ÊÂÒÚ‚‡ ÏËÌËχθÌÓ ‚ ÒÏ˚ÒΠ͇ÍÓÈ-ÌË·Û‰¸ ËÁ ‚‚‰ÂÌÌ˚ı ÏÂ.
é·ÓÁ̇˜ËÏ Ä
∗
– ÏÌÓÊÂÒÚ‚Ó, ·ÎËʇȯÂÂ Í Ì˜ÂÚÍÓÏÛ ÏÌÓÊÂÒÚ-
‚Û Ä.

224
ä‡Í ÒΉÛÂÚ ËÁ ÓÔ‰ÂÎÂÌËfl ‚‚‰ÂÌÌ˚ı ÙÛÌ͈ËÈ ‡ÒÒÚÓfl-
ÌËfl, ‰Îfl ÚÓ„Ó, ˜ÚÓ·˚ ÛÔÓÏflÌÛÚÓ ‡ÒÒÚÓflÌË ÓÚ Ì.Ï. Ä ‰Ó Ä
∗
·˚ÎÓ Ì‡ËÏÂ̸¯ËÏ, ÌÂÓ·ıÓ‰ËÏÓ, ˜ÚÓ·˚ ‚ ͇ʉÓÈ ÚӘ͠ı ÛÌË-
‚Â҇θÌÓ„Ó ÏÌÓÊÂÒÚ‚‡ U ‚Â΢Ë̇
µµ
A
Ä
xx() ()−
∗
·˚· ̇Ë-
ÏÂ̸¯ÂÈ ‰Îfl ‚ÒÂı Ó·˚˜Ì˚ı ÏÌÓÊÂÒÚ‚ Ä
∗
⊆ U. ÑÎfl ˝ÚÓ„Ó ÌÂÓ·-
ıÓ‰ËÏÓ, ˜ÚÓ·˚ Á̇˜ÂÌËÂ
µ
Ä
x
∗
() ·˚ÎÓ ‡‚ÌÓ 0 ËÎË 1, ‚ Á‡‚ËÒË-
ÏÓÒÚË ÓÚ ÚÓ„Ó, Í Í‡ÍÓÏÛ Á̇˜ÂÌ˲ “·ÎËÊ” ‚Â΢Ë̇
µ
Ä
x
∗
() –
Í 0 ËÎË Í 1. íÓ ÂÒÚ¸ ‰Îfl Í‡Ê‰Ó„Ó ˝ÎÂÏÂÌÚ‡ ı ∈ U Á̇˜ÂÌËÂ
ÙÛÌ͈ËË ÔË̇‰ÎÂÊÌÓÒÚË Ó·˚˜ÌÓ„Ó ÏÌÓÊÂÒÚ‚‡ Ä
∗
ÌÂÓ·ıÓ‰ËÏÓ
‚˚·Ë‡Ú¸ Ú‡Í:
µ
µ
µ
µ
Ä
Ä
Ä
Ä
x
x
x
x
∗
=
<
>
<
()
,(),;
,(),;
() ,.
005
1 05
005
ÂÒÎË
ÂÒÎË
ËÎË 1, ÂÒÎË
ÑÓ„Ó‚ÓËÏÒfl ‚ ÒÎÛ˜‡Â
µ
Ä
x
()
= 0,5 ·‡Ú¸ Á̇˜ÂÌË 0.
è Ë Ï Â 2. èÛÒÚ¸
U xxxx=
{}
1 234
,,, ;
Axxxx=
{}
(; ;,;,;.
1 234
0,7), ( 0,2) ( 0,5) ( 1)
íÓ„‰‡
Axxxx
∗
=
{}
(; ;, ;, ; .
1 234
1), ( 0) ( 0) ( 1)
íÓ ÂÒÚ¸ ‚ Ó·ÓÁ̇˜ÂÌËflı, ÔËÌflÚ˚ı ‚ Ó·˚˜ÌÓÈ ÚÂÓËË ÏÌÓ-
ÊÂÒÚ‚,
Axx
∗
=
{}
(; .
1 4
) Ç˚˜ËÒÎËÏ ‡ÒÒÚÓflÌË ÓÚ Ì.Ï. Ä ‰Ó Ä
∗
:
dA A(, ) , , , ;
∗
=+++=03 02 05 0 1
δ(, ) , ;AA
∗
= 025
EA A(, ) , , ,
∗
=+++009 004 025 0 . 0,62
eA A(, ) , .
∗
= 031 ➤
艷„‡ÂÚÒfl Ò‡ÏÓÒÚÓflÚÂθÌÓ ÔÓ‚Â ËÚ¸, ˜ÚÓ, ‚Áfl‚ β·Ó ‰Û-
„Ó ӷ˚˜ÌÓ ÏÌÓÊÂÒÚ‚Ó
BA
∗∗
≠ , ÔÓÎÛ˜ËÏ ‡ÒÒÚÓflÌË ÓÚ Ì.Ï. Ä
‰Ó
B
∗
·Óθ¯ÂÂ, ˜ÂÏ ÓÚ Ì.Ï. Ä ‰Ó
A
∗
. í‡ÍËÏ Ó·‡ÁÓÏ,
A
∗
–
·ÎËʇȯÂÂ Í Ì.Ï. Ä Ó·˚˜ÌÓ ÏÌÓÊÂÒÚ‚Ó.
ì Ú ‚ Â Ê ‰ Â Ì Ë Â 2.
‡) åËÌËχθÌÓ Á̇˜ÂÌË ÓÚÌÓÒËÚÂθÌÓ„Ó ‡ÒÒÚÓflÌËfl ï˝Ï-
ÏËÌ„‡ (ËÎË Ö‚ÍÎˉ‡) ÏÂÊ‰Û Ì˜ÂÚÍËÏ ÏÌÓÊÂÒÚ‚ÓÏ Ä Ë ÏÌÓÊÂ-

225
ÒÚ‚ÓÏ
A
∗
, ·ÎËʇȯËÏ Í ÌÂÏÛ, ‰ÓÒÚË„‡ÂÚÒfl ‚ ÒÎÛ˜‡Â, ÍÓ„‰‡ Ä –
Ó·˚˜ÌÓ ÏÌÓÊÂÒÚ‚Ó Ë
ÄA=
∗
.
·) å‡ÍÒËχθÌÓ Á̇˜ÂÌË ÓÚÌÓÒËÚÂθÌÓ„Ó ‡ÒÒÚÓflÌËfl ï˝Ï-
ÏËÌ„‡ (ËÎË Ö‚ÍÎˉ‡) ‡‚ÌÓ 0,5. ùÚÓ Á̇˜ÂÌË ‰ÓÒÚË„‡ÂÚÒfl, ÍÓ„-
‰‡ ̘ÂÚÍÓ ÏÌÓÊÂÒÚ‚Ó Ä Ú‡ÍÓ‚Ó, ˜ÚÓ Â„Ó ÙÛÌ͈Ëfl ÔË̇‰ÎÂÊ-
ÌÓÒÚË ÔÓÒÚÓflÌ̇ Ë ‡‚̇
µ
Ä
ı
()
,= 05 ‰Îfl ‚ÒÂı ı ∈ U.
ÑÓ͇ÊÂÏ ÔÛÌÍÚ ‡). ÑÎfl ÔÓËÁ‚ÓθÌÓ„Ó ˝ÎÂÏÂÌÚ‡ ı ∈ U ËÏÂ-
ÂÏ:
min ( ) ( )µµ
Ä
Ä
ıı− =
∗
0, Ú‡Í Í‡Í Ó·Â ÙÛÌ͈ËË ÔË̇‰ÎÂÊÌÓ-
ÒÚË
µ
Ä
ı() Ë
µ
Ä
ı
∗
( ) – ÌÂÓÚˈ‡ÚÂθÌ˚ Ë Ì Ô‚˚¯‡˛Ú Á̇˜Â-
ÌË 1. éÚÒ˛‰‡
µµ
Ä
Ä
ıı() ()=
∗
, ‡ ˝ÚÓ Á̇˜ËÚ Ä = Ä
∗
.
ÑÓ͇ÊÂÏ ÔÛÌÍÚ ·).
max () () ,µµ
Ä
Ä
ıı==
∗
05 ‰Îfl ÔÓËÁ‚Óθ-
ÌÓ„Ó ı ∈ U. ÑÂÈÒÚ‚ËÚÂθÌÓ, ÂÒÎË
µ
Ä
ı() ,< 0 5, ÚÓ
µ
Ä
ı
∗
=() 0
(ÔÓ ÓÔ‰ÂÎÂÌ˲). Ç ˝ÚÓÏ ÒÎÛ˜‡Â
µµ
Ä
Ä
ıı() () ,− <
∗
0 5. ÖÒÎË
µ
Ä
ı() ,> 0 5, ÚÓ
µ
Ä
ı
∗
=() 1 (ÔÓ ÓÔ‰ÂÎÂÌ˲) Ë Á̇˜ËÚ
µµ
Ä
Ä
ıı() () ,− <
∗
0 5. ÖÒÎË
µ
Ä
ı() ,= 0 5, ÚÓ
µµ
Ä
Ä
ıı() ()− =
∗
= 05, . å‡ÍÒËχθÌÓ Á̇˜ÂÌË ‡ÒÒÚÓflÌËfl ·Û‰ÂÚ ‰ÓÒÚË„ÌÛÚÓ,
ÂÒÎË ‚Ó ‚ÒÂı ÚӘ͇ı ı ÛÌË‚Â҇θÌÓ„Ó ÏÌÓÊÂÒÚ‚‡ ÔÓÎÛ˜ÂÌÌÓÂ
‡‚ÂÌÒÚ‚Ó ·Û‰ÂÚ ‚˚ÔÓÎÌflÚ¸Òfl, Ú.Â. ÂÒÎË
µ
Ä
ı() ,= 05 ‰Îfl ‚ÒÂı
ı ∈ U. Ç ˝ÚÓÏ ÒÎÛ˜‡Â
δ(, ) , ,; (, ) (,) ,.AA eAA
n
n
i
n
i
n
∗
=
∗
=
== = =
∑∑
11
05 05 05 05
1
2
1
óÚÓ Ë Ú·ӂ‡ÎÓÒ¸ ‰Ó͇Á‡Ú¸.
í Â Ó Â Ï ‡ 1. åÌÓÊÂÒÚ‚Ó, ·ÎËʇȯÂÂ Í Ó·˙‰ËÌÂÌ˲ ‰‚Ûı
̘ÂÚÍËı ÏÌÓÊÂÒÚ‚ Ä Ë Ç, ÒÓ‚Ô‡‰‡ÂÚ Ò Ó·˙‰ËÌÂÌËÂÏ ÏÌÓÊÂÒÚ-
‚‡, ·ÎËÊ‡È¯Â„Ó Í Ä, Ò ÏÌÓÊÂÒÚ‚ÓÏ, ·ÎËʇȯËÏ Í Ç:
(Ä ∪ Ç)
∗
= Ä ∪ Ç
∗
. (5.12)
Ñ Ó Í ‡ Á ‡ Ú Â Î ¸ Ò Ú ‚ Ó: ÇÓÁ¸ÏÂÏ ÔÓËÁ‚ÓθÌ˚È ˝ÎÂÏÂÌÚ ı ËÁ
ÛÌË‚Â҇θÌÓ„Ó ÏÌÓÊÂÒÚ‚‡ U. ê‡ÒÒÏÓÚËÏ ‰‚‡ ÒÎÛ˜‡fl:
‡) Á̇˜ÂÌËfl ÙÛÌ͈ËÈ ÔË̇‰ÎÂÊÌÓÒÚË Ì.Ï. Ä Ë Ç Ú‡ÍÓ‚˚,
˜ÚÓ
µ
A
x() ,≤ 05 Ë
µ
Ç
x() ,≤ 05,
Ë ‡Î¸ÚÂ̇ÚË‚Ì˚È ÒÎÛ˜‡È:
·) ıÓÚfl ·˚ Ó‰ÌÓ ËÁ Á̇˜ÂÌËÈ ÙÛÌ͈ËÈ ÔË̇‰ÎÂÊÌÓÒÚË
·Óθ¯Â 0,5.

226
ÑÎfl ÒÎÛ˜‡fl ‡ ËÏÂÂÏ:
µµ
ÄÇ
xx
∗∗
==() () 0.
µµµ
ÄÇ A B
xxx
∪
= ≤( ) max( ( ), ( )) , 05.
îÛÌ͈Ëfl ÔË̇‰ÎÂÊÌÓÒÚË Î‚ÓÈ ˜‡ÒÚË ‡‚ÂÌÒÚ‚‡ (5.12) ‚
˝ÚÓÏ ÒÎÛ˜‡Â ‡‚̇
µ
ÄÇ
x
∪
∗
=() 0.
îÛÌ͈Ëfl ÔË̇‰ÎÂÊÌÓÒÚË Ô‡‚ÓÈ ˜‡ÒÚË ÛÚ‚ÂʉÂÌËfl ÔË
˝ÚÓÏ ÓÔ‰ÂÎflÂÚÒfl Ú‡Í:
µµµ
ÄÇ A B
xxx
∗
∪
∗∗∗
==( ) max( ( ), ( )) 0.
àÚ‡Í, ‰Îfl ÒÎÛ˜‡fl ‡ ÛÚ‚ÂʉÂÌË ‰Ó͇Á‡ÌÓ.
ê‡ÒÒÏÓÚËÏ ÒÎÛ˜‡È ·. ÅÂÁ Ó„‡Ì˘ÂÌËfl Ó·˘ÌÓÒÚË ·Û‰ÂÏ Ò˜Ë-
Ú‡Ú¸
µ
Ä
x() ,> 0 5, Ú‡Í Í‡Í ÏÌÓÊÂÒÚ‚‡ Ä Ë Ç, ‚ ÒËÎÛ ÍÓÏÏÛÚ‡ÚË‚-
ÌÓÒÚË ÓÔ‡ˆËÈ Ó·˙‰ËÌÂÌËfl, ‚ıÓ‰flÚ ‚ ÛÚ‚ÂʉÂÌË ÚÂÓÂÏ˚
ÒËÏÏÂÚ˘ÌÓ. Ç ˝ÚÓÏ ÒÎÛ˜‡Â
µ
Ä
x
∗
=() 1 Ë
µµµ
ÄÇ
AB
xxx
∪
=>( ) max( ( ), ( )) , . 05
îÛÌ͈Ëfl ÔË̇‰ÎÂÊÌÓÒÚË Î‚ÓÈ ˜‡ÒÚË (5.12) ‚ ˝ÚÓÏ ÒÎÛ˜‡Â
‡‚̇
µ
()
()
ÄÇ
x
∪
∗
= 1.
èË ˝ÚÓÏ ÙÛÌ͈Ëfl Ô Ë̇‰ÎÂÊÌÓÒÚË Ô ‡‚ÓÈ ˜‡ÒÚË (5.12)
ÓÔ‰ÂÎflÂÚÒfl Ú‡Í:
µµ
ÄÇ B
xx
∗
∪
∗∗
==( ) max( , ( )) .11
ょfl ˜‡ÒÚ¸ ‡‚̇ Ô‡‚ÓÈ ˜‡ÒÚË, ˜ÚÓ Ë Ú·ӂ‡ÎÓÒ¸ ‰Ó͇-
Á‡Ú¸.
Ç Í‡˜ÂÒÚ‚Â ÛÔ‡ÊÌÂÌËÈ ˜ËÚ‡ÚÂβ Ô‰·„‡ÂÚÒfl ‰Ó͇Á‡Ú¸
ÒÎÂ‰Û˛˘Ë ÚÂÓÂÏ˚:
í Â Ó Â Ï ‡ 2.
() .AB A B∩ = ∩
∗∗∗
í Â Ó Â Ï ‡ 3.
() .AA
∗∗
=
í Â Ó Â Ï ‡ 4.
() .AB A B− = −
∗∗∗
í Â Ó Â Ï ‡ 5.
() .AB A B+=+
∗∗∗
à Ì ‰ Â Í Ò Ì Â ˜ Â Ú Í Ó Ò Ú Ë.
å˚ ‚˚flÒÌËÎË, ˜ÚÓ Ë ÓÚÌÓÒËÚÂθÌÓ ‡ÒÒÚÓflÌË ï˝ÏÏËÌ„‡
(5.7) Ë ÓÚÌÓÒËÚÂθÌÓ ‡ÒÒÚÓflÌË ւÍÎˉ‡ (5.9) ÏÂÊ‰Û Ì˜ÂÚ-
ÍËÏ ÏÌÓÊÂÒÚ‚ÓÏ Ë ·ÎËʇȯËÏ Í ÌÂÏÛ Ó·˚˜Ì˚Ï ÏÂÌfl˛ÚÒfl ‚
ÒÎÂ‰Û˛˘Ëı ԉ·ı:
005≤≤
∗
δ(, ) ,AÄ ;
005≤≤
∗
ÂA Ä(, ) , .

227
ÖÒÎË ÛÏÌÓÊËÏ ÓÚÌÓÒËÚÂθÌÓ ‡ÒÒÚÓflÌË ï˝ÏÏËÌ„‡ Ë Ö‚ÍÎˉ‡
̇ 2, ÚÓ ÔÓÎÛ˜ËÏ ‚Â΢ËÌÛ, ̇Á˚‚‡ÂÏÛ˛ Ë̉ÂÍÒÓÏ Ì˜ÂÚÍÓÒÚË
̘ÂÚÍÓ„Ó ÏÌÓÊÂÒÚ‚‡ Ä, ÍÓÌÍ ÂÚÌÂÂ
νδ() (, )AAÄ=
∗
2 – ÎËÌÂÈÌ˚È Ë̉ÂÍÒ Ì˜ÂÚÍÓÒÚË;
η() (, )AÂAÄ=
∗
2 – Í‚‡‰‡ÚÌ˚È Ë̉ÂÍÒ Ì˜ÂÚÍÓÒÚË.
åÌÓÊËÚÂθ 2 ÔÓfl‚ËÎÒfl ‚ Ò‚flÁË Ò ÌÓÏËÓ‚‡ÌËÂÏ, Ú.Â. ‰Îfl ÚÓ„Ó,
˜ÚÓ·˚ ÔÓÎÛ˜ËÚ¸
0 1≤≤ν()A
;
0 1≤≤η()A
.
àÁ ÛÚ‚ÂʉÂÌËfl 2 ÒΉÛÂÚ, ˜ÚÓ ÂÒÎË Ä – Ó·˚˜ÌÓ ÏÌÓÊÂÒÚ‚Ó,
ÚÓ Ä = Ä
∗
Ë ν(Ä) = 0 (ÏÓÊÌÓ ÔÓ‚ÂËÚ¸, ˜ÚÓ Ô Ë ˝ÚÓÏ Ë
η(Ä)
=
= 0. ùÚÓ Á̇˜ËÚ, ˜ÚÓ Ì‡ËÏÂ̸¯ËÏ Ë̉ÂÍÒÓÏ Ì˜ÂÚÍÓÒÚË Ó·Î‡‰‡-
ÂÚ Ó·˚˜ÌÓ ÏÌÓÊÂÒÚ‚Ó. à ˝ÚÓ ÂÒÚÂÒÚ‚ÂÌÌÓ, Ú‡Í Í‡Í ‰Îfl Ú‡ÍÓ„Ó
ÏÌÓÊÂÒÚ‚‡ ÔË̇‰ÎÂÊÌÓÒÚ¸ Í ÌÂÏÛ ˝ÎÂÏÂÌÚÓ‚ ÓÔ‰ÂÎÂ̇
“˜ÂÚÍÓ” Ë ‚ ˝ÚÓÏ ÏÌÓÊÂÒÚ‚Â ÌË͇ÍÓÈ “̘ÂÚÍÓÒÚË” ÌÂÚ. Ç ÒÎÛ-
˜‡Â, ÂÒÎË ÙÛÌ͈Ëfl ÔË̇‰ÎÂÊÌÓÒÚË ÏÌÓÊÂÒÚ‚‡ ËÏÂÂÚ ÔÓÒÚÓflÌ-
ÌÓ Á̇˜ÂÌËÂ
µ
Ä
x
()
,=
05
‰Îfl ‚ÒÂı ı ∈ U, Ë̉ÂÍÒ Ì˜ÂÚÍÓÒÚË
(ÎËÌÂÈÌ˚È Ë Í‚‡‰‡Ú˘Ì˚È) ËÏÂÂÚ Ï‡ÍÒËχθÌÓ Á̇˜ÂÌËÂ,
‡‚ÌÓ 1. ÑÂÈÒÚ‚ËÚÂθÌÓ, ‚ ˝ÚÓÏ ÒÎÛ˜‡Â ‰Îfl β·Ó„Ó ˝ÎÂÏÂÌÚ‡
ı ∈ U “ÌÂÓÔ‰ÂÎÂÌÌÓÒÚ¸” Â„Ó ÔË̇‰ÎÂÊÌÓÒÚË ÏÌÓÊÂÒÚ‚Û Ä
χÍÒËχθ̇, Ú‡Í Í‡Í ÔË ˝ÚÓÏ Ó‰Ë̇ÍÓ‚‡ ‚ÓÁÏÓÊÌÓÒÚ¸ ‰Îfl ı
ÔË̇‰ÎÂʇڸ Ì.Ï. Ä (‡ÒÒÚÓflÌË ÓÚ µ = 1) Ë Ì ÔË̇‰ÎÂ-
ʇڸ Ä (‡ÒÒÚÓflÌË ÓÚ µ = 0).
í‡ÍËÏ Ó·‡ÁÓÏ, Ë̉ÂÍÒ˚ ̘ÂÚÍÓÒÚË ı‡‡ÍÚÂËÁÛ˛Ú ÒÚÂÔÂ̸
ÓÚ‰‡ÎÂÌÌÓÒÚË Ì˜ÂÚÍËı ÏÌÓÊÂÒÚ‚ ÓÚ Ó·˚˜Ì˚ı ÏÌÓÊÂÒÚ‚.
í Â Ó Â Ï ‡ 6. ÑÎfl ‚ÒÂı ˝ÎÂÏÂÌÚÓ‚ ı ∈ U Ë ‰Îfl Ì.Ï. Ä ⊆ U
‚˚ÔÓÎÌflÂÚÒfl ÒÓÓÚÌÓ¯ÂÌËÂ
µµ η
Ä
Ä
ÄÄ
xx ı() () ().− =
∗∩
(5.13)
Ñ Ó Í ‡ Á ‡ Ú Â Î ¸ Ò Ú ‚ Ó: ÇÓÁ¸ÏÂÏ ÔÓËÁ‚ÓθÌ˚È ˝ÎÂÏÂÌÚ ı ∈ U.
ê‡ÒÒÏÓÚËÏ ÒÎÛ˜‡È
µ
Ä
x() ,.≤ 0 5 íÓ„‰‡
µ
Ä
x
∗
=( ) 0 Ë Î‚‡fl ˜‡ÒÚ¸
ÛÚ‚ÂʉÂÌËfl (5.13) ‡‚̇
µ
Ä
x(). 臂‡fl ˜‡ÒÚ¸ (5.13) ÔË ˝ÚÓÏ
µµµµ
ÄÄ Ä A A
xxıı
∩
= − =( ) min( ( ), ( )) ( ),1
Ú‡Í Í‡Í ‚ ˝ÚÓÏ ÒÎÛ˜‡Â
1 05− >µ
A
ı()) ,.
ê‡ÒÒÏÓÚËÏ ‡Î¸ÚÂ̇ÚË‚Ì˚È ÒÎÛ˜‡È:
µ
A
ı() ,.> 05 èË ˝ ÚÓÏ
µ
A
ı
∗
=() 1. ょfl ˜‡ÒÚ¸ ‡‚̇
1 −η
A
ı(). 臂‡fl ˜‡ÒÚ¸ ÂÒÚ¸
min( ( ), ( ) ( ),µµ µ
ÄA A
x ıı 11− = − ˜ÚÓ ÒÓ‚Ô‡‰‡ÂÚ ÒÓ Á̇˜ÂÌËÂÏ
΂ÓÈ ˜‡ÒÚË. íÂÓÂχ ‰Ó͇Á‡Ì‡.
