Оганесов О.А., Кайль В.А., Рябикова И.М., Кузенева Н.Н. Курс лекций по начертательной геометрии. Часть 1
Подождите немного. Документ загружается.

61
Задана призматическая поверхностьПРИМЕР 7.1.
{l(l,a)(l a, l l)} a[A,B,D,E]
M N N
N
F
, (рис. 7.5). 1. Построить проекции произ-
вольной точки . 2. Построить проекцию точки по
известной проекции . 3. Определить, принадлежит ли поверхнос-
ти заданная точка .
Ô
Ô
Произвольную точку строят с
помощью произвольной образую
щей :
M
l
-
Ô
i i
Ô
1
2
i
a
a
D
D
F
2
1
F
l
1
i
2
3
1
E
2
E
1
A
2
A
1
M
2
M
1
B
1
B
2
N
N
l
i
2
3
1
1
1
l
1
l
1
1
1
l
1
2
1
1
1
1
2
2
l
2
l
2
2
2
2
2
l
2
2
2
Проекцию точки находят
с использованием образующей ,
проходящей через точку :
N N
l
N
1.
2
=
1
l
1
2.
2
2
l
3.
5.
N
l
2 2
4.
.
2 2
2l N
1
l
1
1
.
1
a
1
.
a
.
2
l
2
l
2
l
.
2
1
1
1
1
1 1
1
Для определения принадлежности
точки поверхности делается попытка
построить образующую , проходящую
через точку :
F
l
F
2
Ô
Рис. 7.5
1.
1
=
1
l
1
2.
1
2
l
3.
5.
1
1
M l
2
6.
M
2
4
.
2
2
1
i
l a
1
i
l
1
1
.
1
i
a
1
.
a
.
2
i
l
2
l
2
i
l
.
i
l
i
.
.
1. 3
=
l
2. 3
1
l 3. 4.
.
2
3
l Fl . a . a .
l l l
2
2
2
2
2 2 2 2 2
2
1 1
2
11 1
Вывод: .F l F l F
1 1
2
2
Ô
7.1.3. Коническая и пирамидальная поверхности
Формула конической поверхности имеет вид:
. Если кривая линия, то формула определяет
коническую поверхность, если ломаная линия, то пирамидаль
ную (в обоих случаях и не лежат в одной плоскости), если пря-
мая линия, то плоскость. Точку называют вершиной поверхности.
{l(a,S)(l a, l S)} a
a
a S a
S
-
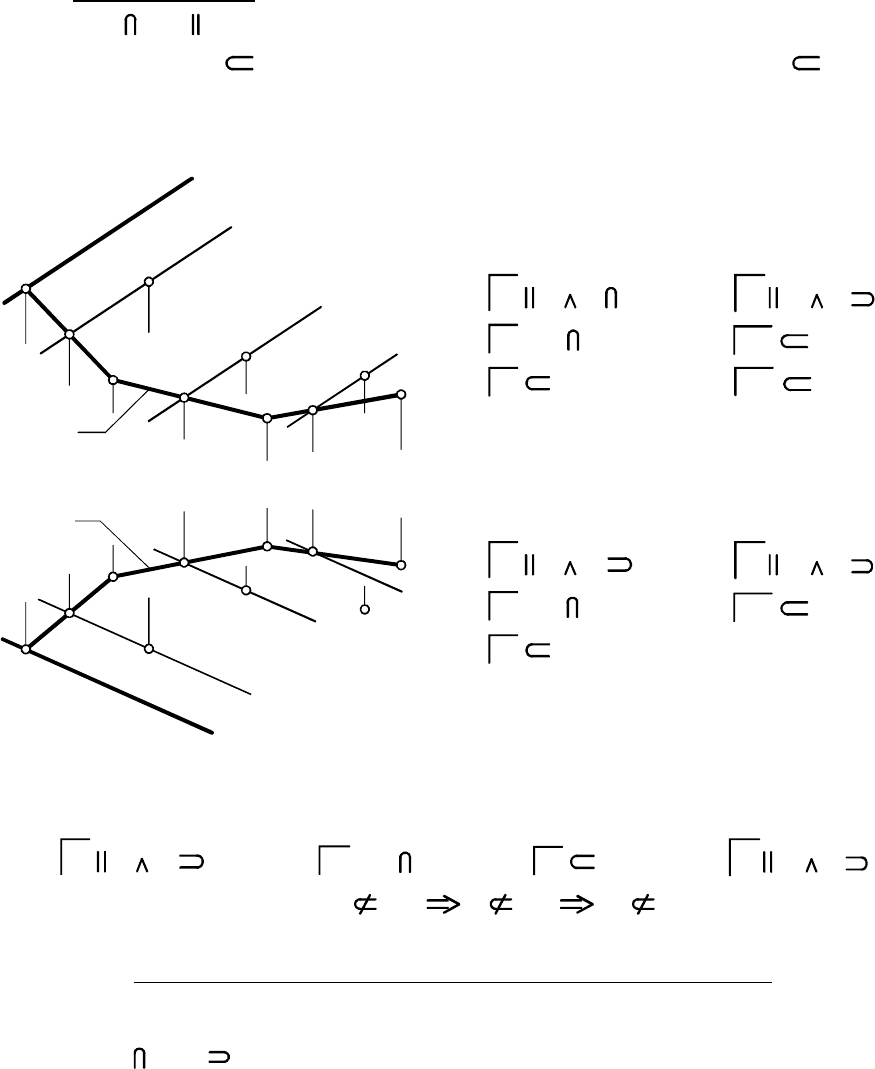
На рис. 7.6 приведен элементарный чертеж конической поверх-
ности, на рис. 7.8 - пирамидальной поверхности (направляющая -
треугольник ), на рис. 7.7 - основной чертеж отсека конической
поверхности, а на рис. 7.9 - отсека пирамидальной поверхности.
a
ABDA
Ô
i i
62
Рис. 7.6
a
2
a
S
2
S
1
1
Рис. 7.8
D
D
A
2
A
1
B
1
B
2
1
2
На элементарных чертежах поверхностей заданы элементы их
определителей. Контурными линиями отсека конической поверхнос
ти (рис. 7.7) являются: линия обреза кривая , вершина , образую
щие и , а также образующие и - линии касания поверхнос-
ти проецирующими лучами, перпендикулярными и соответ
ственно. Контурные линии отсека пирамидальной поверхности -
линия обреза ломаная , точка и ребра поверхности , и .
Коническая и пирамидальная поверхности в общем случае
имеют две полости, простирающиеся в бесконечность от вершины
в обе стороны. На рис. 7.7 и 7.9 показано только по одной “нижней”
полости поверхностей.
-
-
-
a S
l l l l
a S AS BS DS
S
2 31 4
Ï
12
Ï
a
2
a
S
2
S
1
1
l
3
4
2
a
2
a
S
2
S
1
1
2
l
1
2
l
2
2
l
2
l
1
1
l
1
Рис. 7.7
l
2
Рис. 7.9
a
2
a
S
2
S
1
1
D
D
A
2
A
1
B
1
B
2
1
2
2
1
1
1
M
2
M
1
i
l
i
1
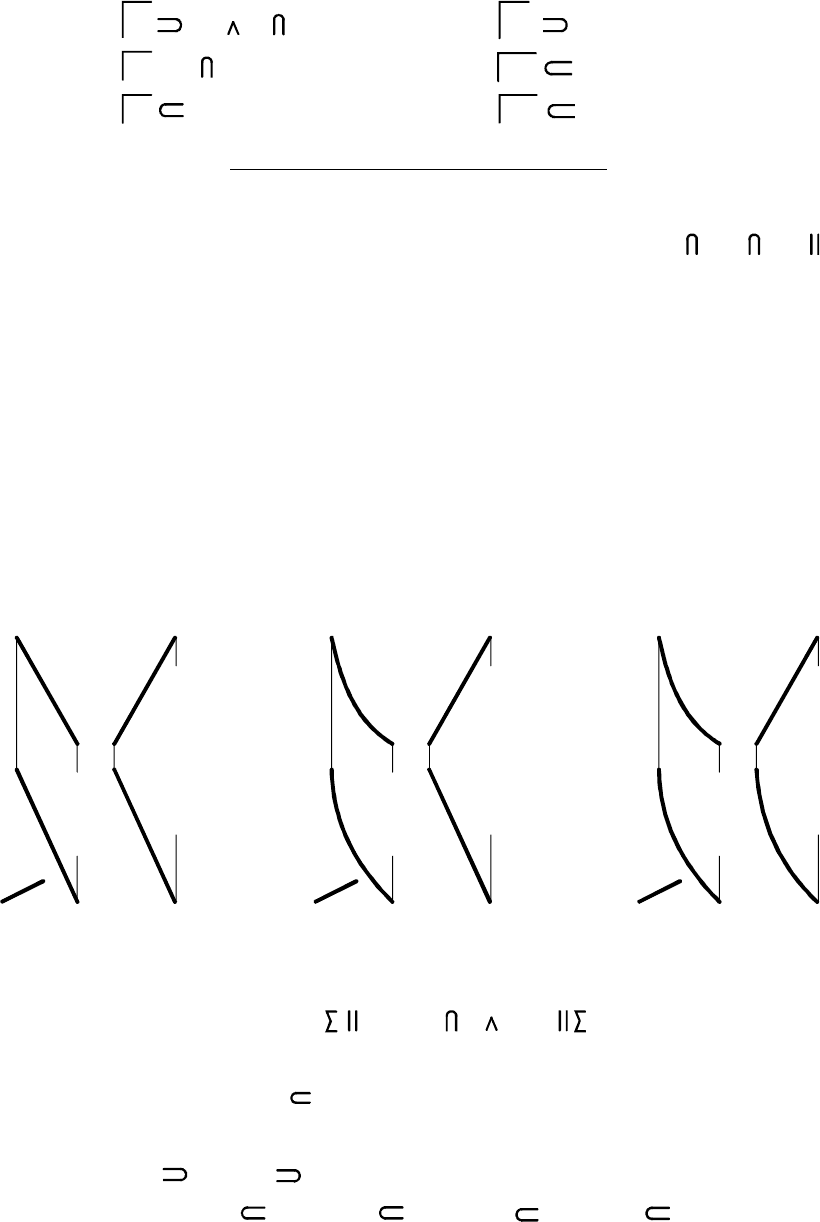
63
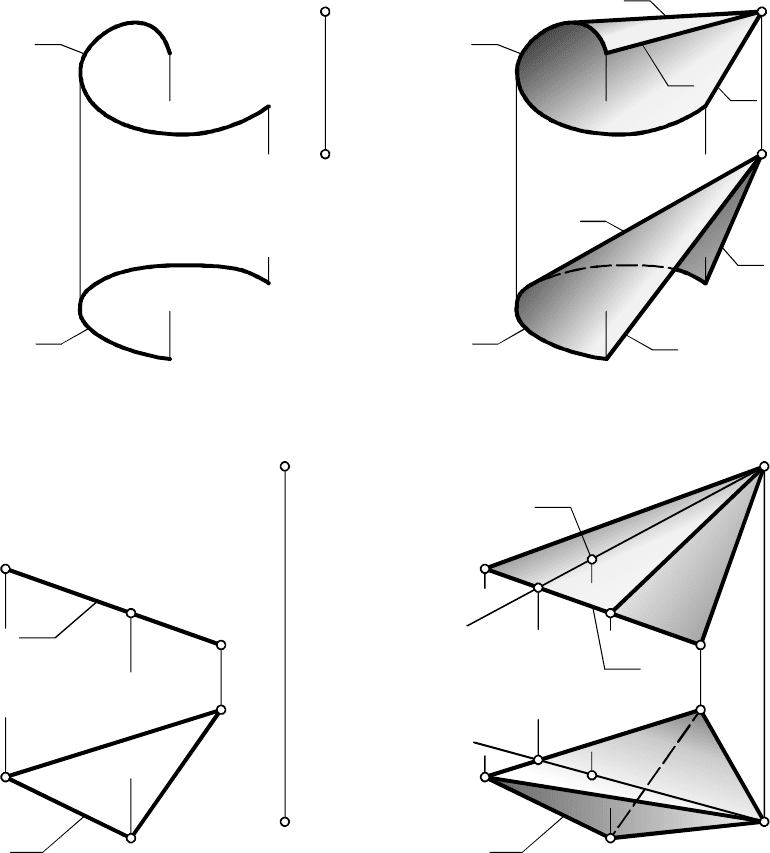
На рис. 7.9 задана произвольная точка пирамидальной
поверхности, для чего строилась её произвольная образующая :
M
l
i
1.
1
=
1
S
1
2.
1
2
l
3.
5.
1
1
M l
2
6.
M
2
4.
2
2
1
i
l a
1
i
l
1
1
.
1
i
a
1
.
a
.
2
i
l
.
i
l
i
.
.
S
2
,
7.1.4. Поверхности Каталана
Поверхности Каталана - это линейчатые поверхности с двумя на
правляющими и плоскостью параллелизма: .
-
{t(b,d, )(t b, t d, t )}
Все образующие этих поверхностей пересекают обе направляющие
и параллельны плоскости параллелизма.
В зависимости от формы направляющих образуются различ-
ные поверхности: если направляющие скрещивающиеся прямые, то
поверхность называется гиперболический параболоид (косая
плоскость); если одна направляющая кривая линия, а вторая прямая,
то поверхность называется коноид; если обе направляющие кривые
линие, то поверхность называют цилиндроидом. Элементарные
чертежи гиперболического параболоида, коноида и цилиндроида
показаны соответственно на рис. 7.10 - 7.12.
Ô
i
à Ã
i i
d
1
Ã
1
Ã
1
Ã
1
b
2
b
1
d
2
d
1
b
2
b
1
d
2
d
1
b
2
b
1
d
2
Рис. 7.10 Рис. 7.11 Рис. 7.12
На рис. 7.13 приведен основной чертеж отсека гиперболичес-
кого параболоида , границами которо-
го являются линии , и образующие и , проходящие соответ-
ственно через точки , . Для получения чертежа сначала строят
достаточно плотный дискретный каркас образующих , включая
образующие и . В результате определяют отрезки линий
обреза отсека: , , , , и получают
возможность провести проекцию параболы как огибающую
{t(a, b, )(t a b; t )}
a b t t
A B a
t
t A t B
[A,B] a [D,E] b [A,D] t [B,E] t
p p
Ô
2
Ï
i i
1
2
1
1
2
i
2
2
64
проекций образую-
щих . Парабола -
линия касания поверх-
-
-
t
t p
ности гиперболичес
к ого п арабол о ид а
проецирующими луча-
ми, перпендикуляр
ными .
2
Ï
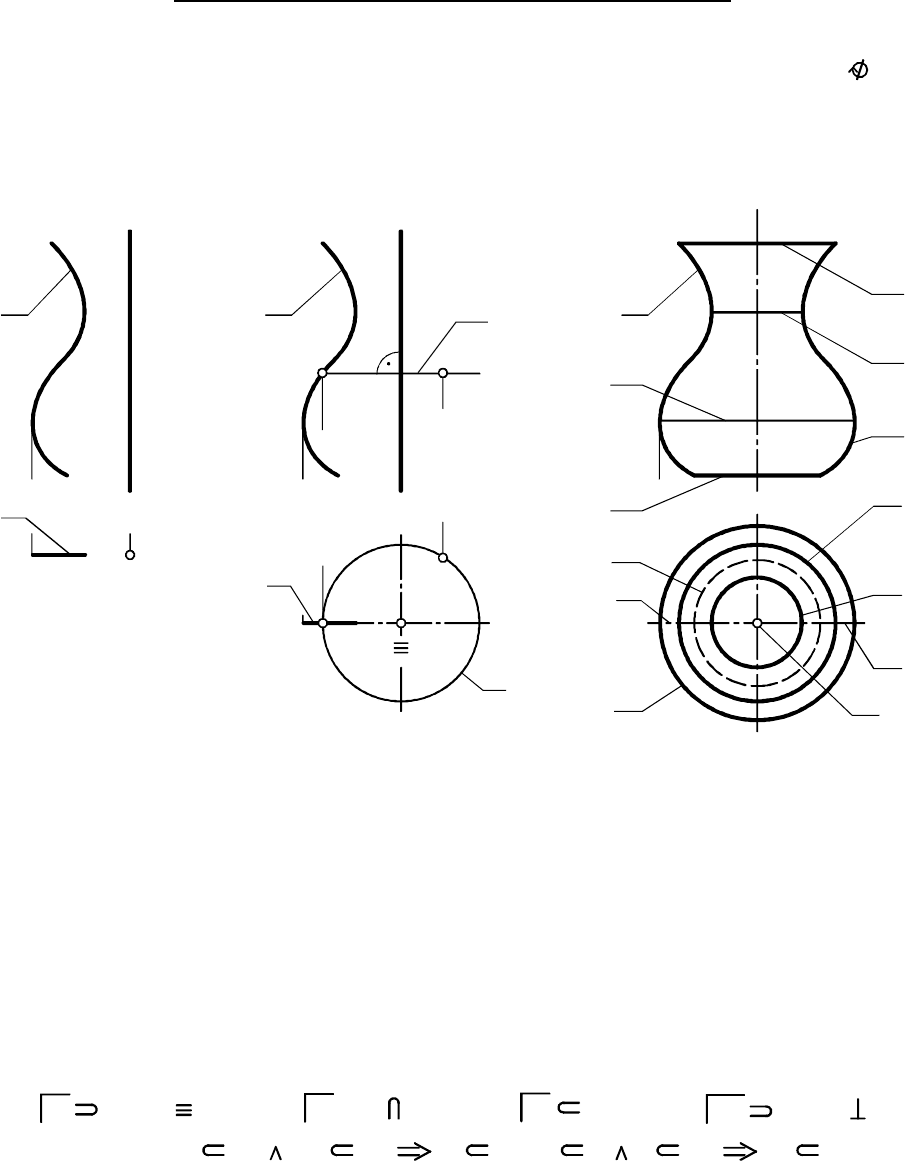
7.2. Поверхности вращения
7.2.1. Образование поверхностей вращения
(рис. 7.14).
При вращении линии вокруг точки
образующей вращаются вокруг оси по
окружностям, называемым параллелями.
Так, при вращении точки образуется
параллель . Плоскости параллелей пер-
пендикулярны оси вращения. Поэтому на
ПП, перпендикулярную оси, параллели
проецируются в окружности, а на другую
ПП - в отрезки прямых В этой связи точку
на поверхности вращения в общем
случае строят с помощью окружности
(параллели) согласно ПА (рис. 7.14):
{a(a,j)(a =a j)}
a j
a j
K a
m
M
m
.
Поверхность вращения образуется при вращении вокруг не-
подвижной оси какой-то образующей линии :j a
Ô
Ô
i
i
i
i
.
.
m
M
Ô
m
i
i
.
.
Параллель наименьшего радиуса называют горлом, а наи
большего - экватором ( ). Параллель - граница или линия обреза
отсека. Плоская кривая, расположенная в плоскости, проходящей
через ось вращения, называется меридианом поверхности (кривая ,
m
m m
a
-
1
2 3
2
i
D
2
A
2
A
1
E
1
E
2
B
2
B
1
D
1
b
a
t
ð
i
1
1
t
i
2
1
a
2
t
1
1
t
1
2
1
t
1
t
2
2
2
2
Рис. 7.13
Рис. 7.14
j
m
m
m
m
k
k
a
M
1
1
2
3
K
i
i
i
b
2
65
контурные кривые и ).k k Меридиан, лежащий в плоскости,
параллельной ПП, называют главным. При задании поверхности
вращения элементарным чертежом удобно, чтобы её образующая
являлась главным меридианом.
1
7.2.2. Поверхность вращения общего вида
Поверхность вращения общего вида образуется при вращении во-
круг оси произвольной кривой . Формула поверхности: .k {k(k,j)(k =k j)}
i
Ô
На рис. 7.15 задан элементарный чертеж поверхности вращения
общего вида, а на рис. 7.17 - основной чертеж отсека этой поверх-
ности с границами и . На основном чертеже главные мериди-m m
1
2
k
k
j
1
2
j
1
2
M
q
1
C
2
2
2
k
k
j
1
2
j
1
2
1
1
M
1
1
q
q
1
m
4
k
k
j
1
2
j
1
2
m
m
1
1
1
1
2
3
k
1
1
m
1
m
2
2
4
m
2
m
3
2
m
1
2
k
1
2
Рис. 7.15
Рис. 7.16 Рис. 7.17
аны и являются линиями касания поверхности проецирующими
лучами, перпендикулярными , а горло и экватор - пер-
пендикулярными (проекции и обычно не показывают, так
как относительно и не являются контурными линиями).
На рис. 7.16 решается ОПЗ: определяют, принадлежит ли рас-
сматриваемой поверхности точка ( , ). Для этого делается
попытка построить параллель поверхности, на которой может
располагаться точка :
k k
m m
m m
m m
M M M
q
M
1
2
Ï
3
4
Ï
1
3
2
4
2
2
Ï
3
4
1 2
q
C
,
11
M
q
1
j
1
1. . 1
1
q
1
2.
=
k
1
.
3.
1
2
k
2
. 4. ,
2 2 2
q 1
2
q j
.
Вывод: ; .M q M q M q M q q M
1 21 2
Ô Ô
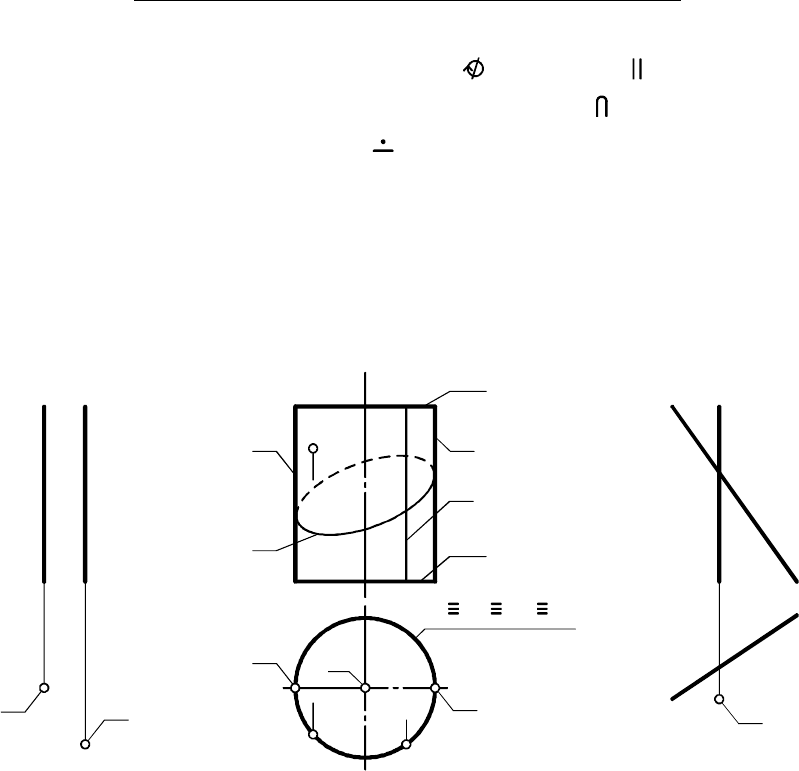
66
Линейчатая поверхность вращения образуется при враще-
нии вокруг оси прямой : . Если , то образуется
цилиндрическая поверхность вращения, если - коническая по-
верхность вращения, если - однополостный гиперболоид
вращения.
j l {l(l,j)(l =l j)} l j
l j
l j
На рис. 7.18 приведен элементарный чертеж цилиндрической
поверхности вращения, на рис. 7.19 - основной чертеж отсека этой
поверхности, ограниченного окружностями и ( и - линии ка
сания поверхности проецирующими лучами, перпендикулярными ).
m m l l -
7.2.3. Линейчатые поверхности вращения
Ô
i
1 2 1 2
2
Ï
M
2
M
1
Ô
1
k
2
k
1
Рис. 7.18
l
2
l
1
j
2
j
1
Рис. 7.19 Рис. 7.20
j
2
j
1
l
1
l
2
l
2
l
1
l
2
m
2
2
l
2
m
2
1
j
2
1
m
1
1
m
1
2
l
1
1
l
1
2
j
1
Чертежи конической поверхности вращения и примеры
решения ОПЗ - см. разделы 6.3.1 и 6.3.2, рис. 6.5 и 6.7.
Однополостный гиперболоид вращения можно получить также
вращением гиперболы вокруг её мнимой оси. Эта поверхность
широко используется в инженерной практике: телевизионная башня
известного ученого и инженера Шухова В.Г. на Шаболовке,
сооруженная из каркасов однополостных гиперболоидов, градирни
(трубы) ТЭЦ имеют такую форму и т. д.
На рис. 7.20 представлен элементарный чертеж однополостно
го гиперболоида вращения - заданы скрещивающиеся прямые
(образующая) и (ось вращения). На рис. 7.21 приведен основной
чертеж отсека рассматриваемой поверхности, образованный враще
нием отрезка образующей . Линиями обреза отсека являются
окружности и , проходящие через точки и соответственно.
-
-
l
j
[A,B] l
m m A B
1
2
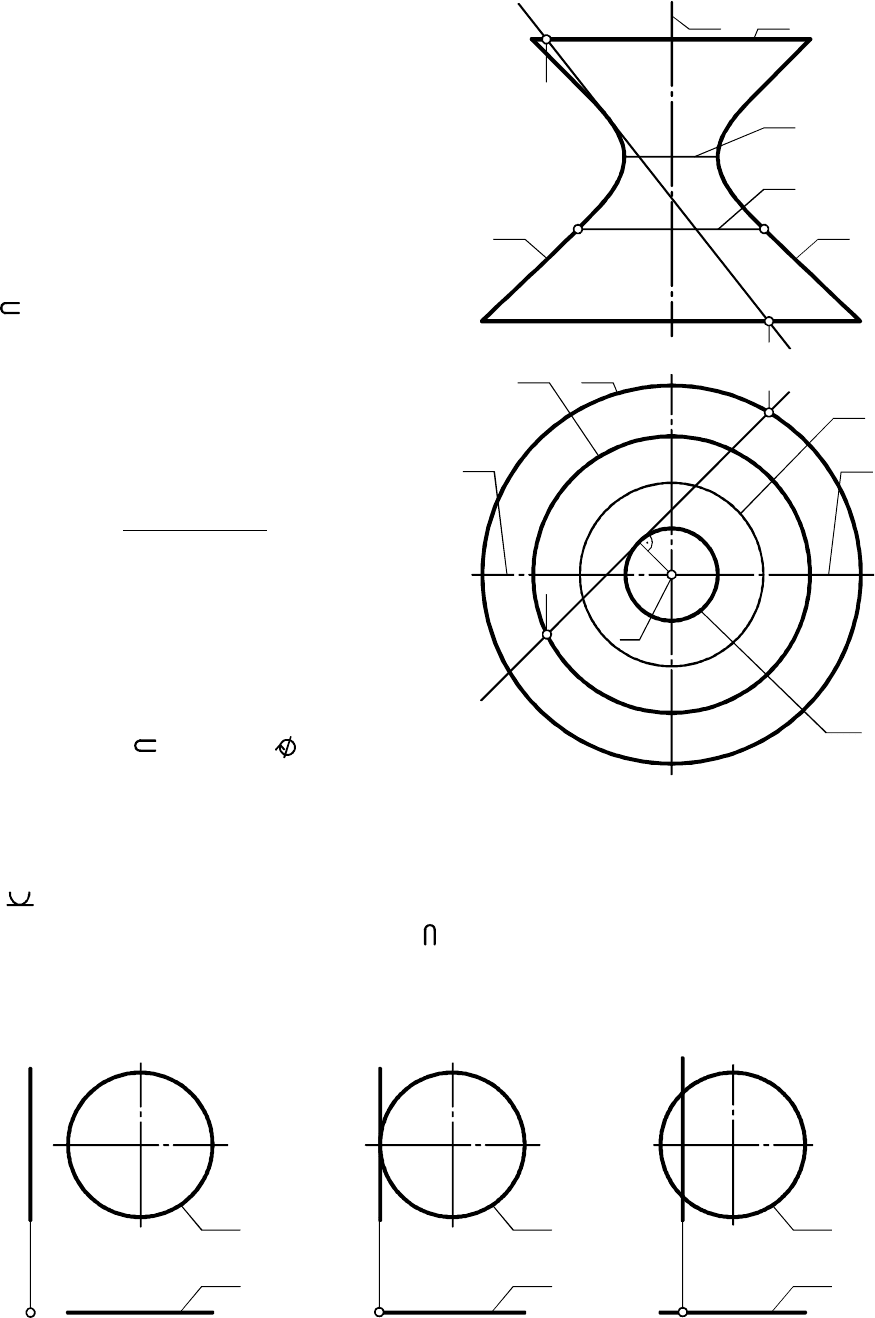
Поверхность тора получает
ся при вращении окружности или
её дуги вокруг оси , причем
образующая окружность и ось
расположены в одной плоскости:
.
Если окружность и ось не
имеют общих точек, то тор называ-
-
m
j
m j
{m(m,j; m,j )(m =m j)}
m j
67
B
2
j
2
m
A
2
l
l
B
1
i
A
1
Рис. 7.21
2
2
m
2
3
m
2
g
2
2
2
m
2
1
g
2
1
1
mm
1 1
12
g
1
1
g
1
2
m
3
1
j
1
i
m
1
Ветви и гиперболы на чертеже
- линии касания поверхности
проецирующими лучами, перпенди
кулярными , а горло - перпен-
дикулярными .
Для построения проекций и
ветвей гиперболы строят доста-
точно плотный каркас параллелей
(включая , , ), которые
на проецируются в окружности, а
на - в отрезки прямых. Проекции
и проводят через крайние ле-
вые и правые точки отрезков .
g g
m
g
g
m m m m
g g
m
-
1
2
2
Ï
Ï
1
2
1
2
2
i
Ô
2 31
Ï
1
2
Ï
2
1
2
2
i
2
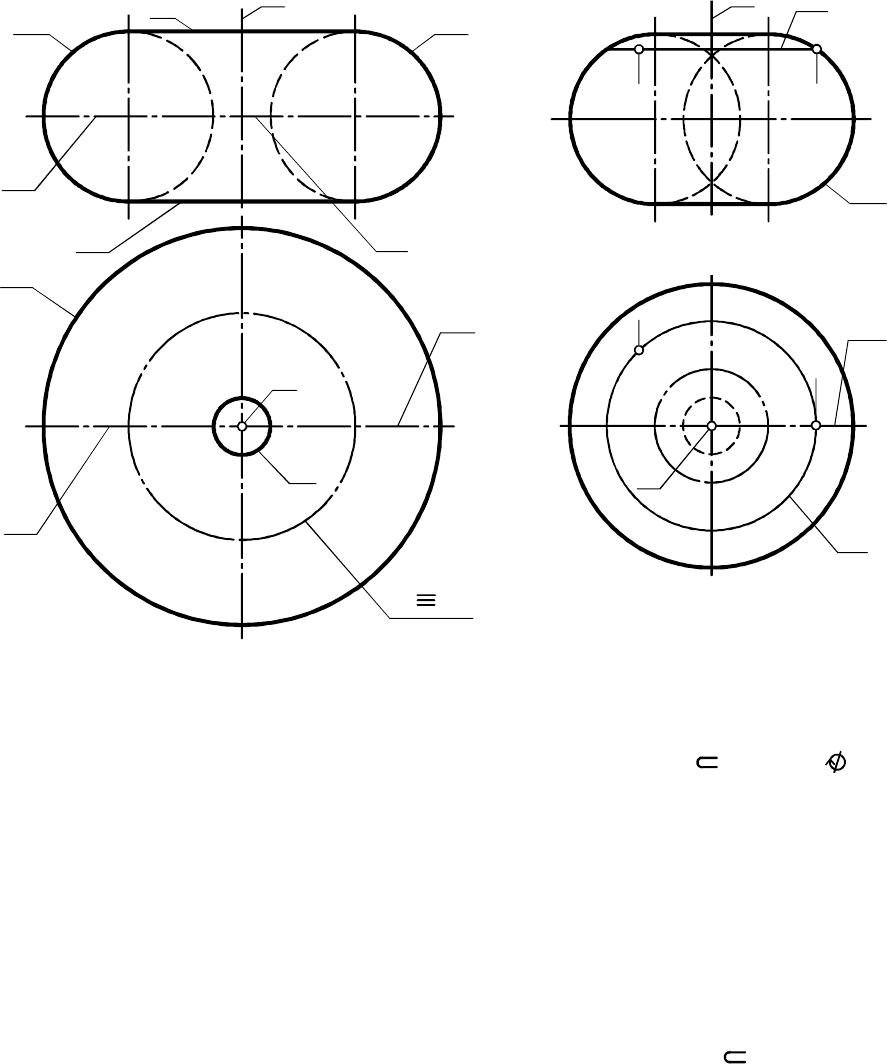
7.2.4. Торы
ют открытым или кольцом; если окружность и ось касаются
( ), то образуется закрытый тор с одной конической точкой; если
ось пересекает окружность ( ), то образуется закрытый тор с
двумя коническими точками, называемый также пересекающимся
тором. Элементарные чертежи перечисленных торов изображены
соответственно на рис. 7.22 - 7.24.
m j
m j
j m m j
Ô
Ô
i
Ã
Рис. 7.23Рис. 7.22 Рис. 7.24
m
j
1
2
2
m
j
1
m
1
2
m
m
1
2
m
j
2
j
1
j
2
j
1
68
На рис. 7.25 представлен основной чертеж открытого тора, а
на рис. 7.26 - пересекающегося. Контурными линиями открытого
тора относительно являются окружности экватора и горла,
а относительно - образующие окружности и , а также
окружности (параллели) и , получаемые при вращении верхней
и нижней точек образующей окружности . Контурными линиями
пересекающегося тора являются аналогичные линии.
q q
m m
q q
m
2
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
1
1 1
3
3
4
4
q
q
q
q
q
q
q
q
j
j
m
m
m
m
Ï
1
2
Ï
1 2
1
3 4
2
2
2
1
1
1
1
q
q
j
m
m
M
M
Рис. 7.26Рис. 7.25
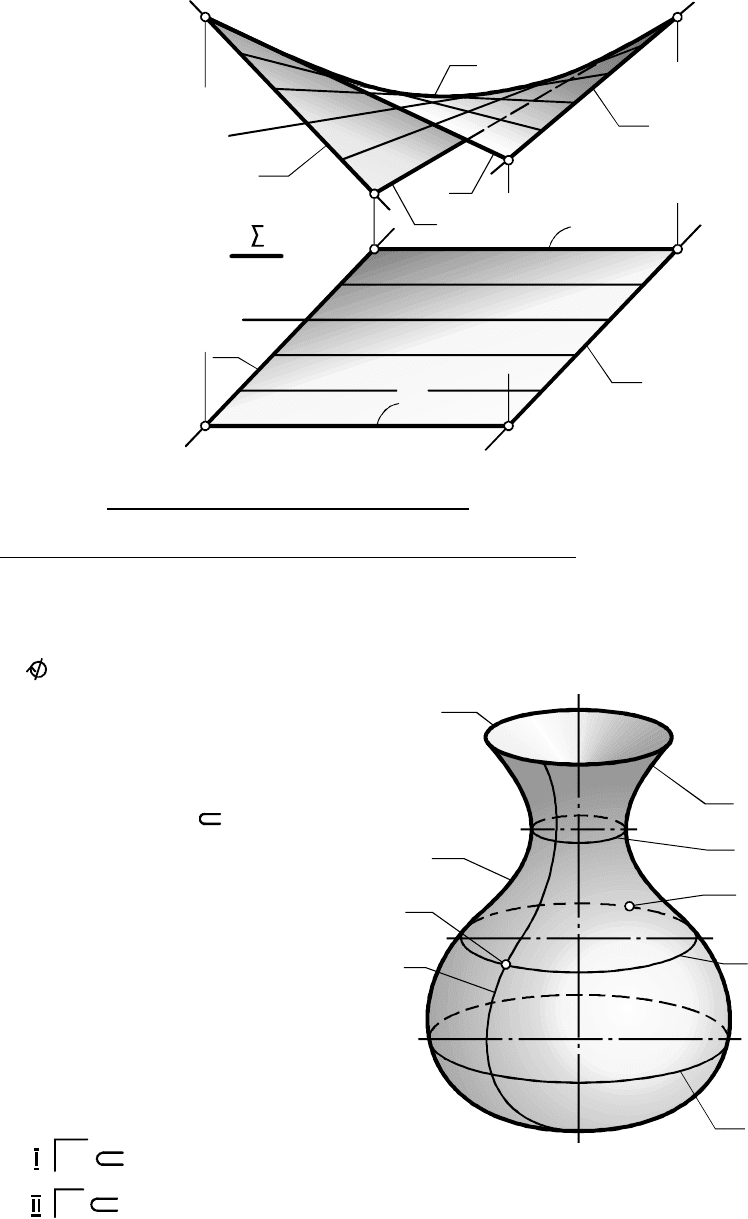
Частным случаем пересекающегося тора, у которого центр C
образующей окружности расположен на оси вращения, является сфе
ра. Формулу сферы часто записывают так: .
-
{m(m,j;C j)(m =m j)}
На рис. 7.27 и 7.28 показаны соответственно элементарный
и основной чертежи. На элементарном чертеже задана образующая
- главный меридиан и ось . Контурными линиями сферы на её ос-
новном чертеже являются окружность экватора и
уже упомянутая окружность главного меридиана .
На рис. 7.26 - 7.28 показано построение произвольной точки ,
принадлежащей соответствующей поверхности , для чего исполь
зовались проекции и произвольной окружности .
её
относительно
относительно
-
m j
g
m
M
q q q
Ô
i
m
Ï
1
2
Ï
Ô
1 2
Ô
2
j
m
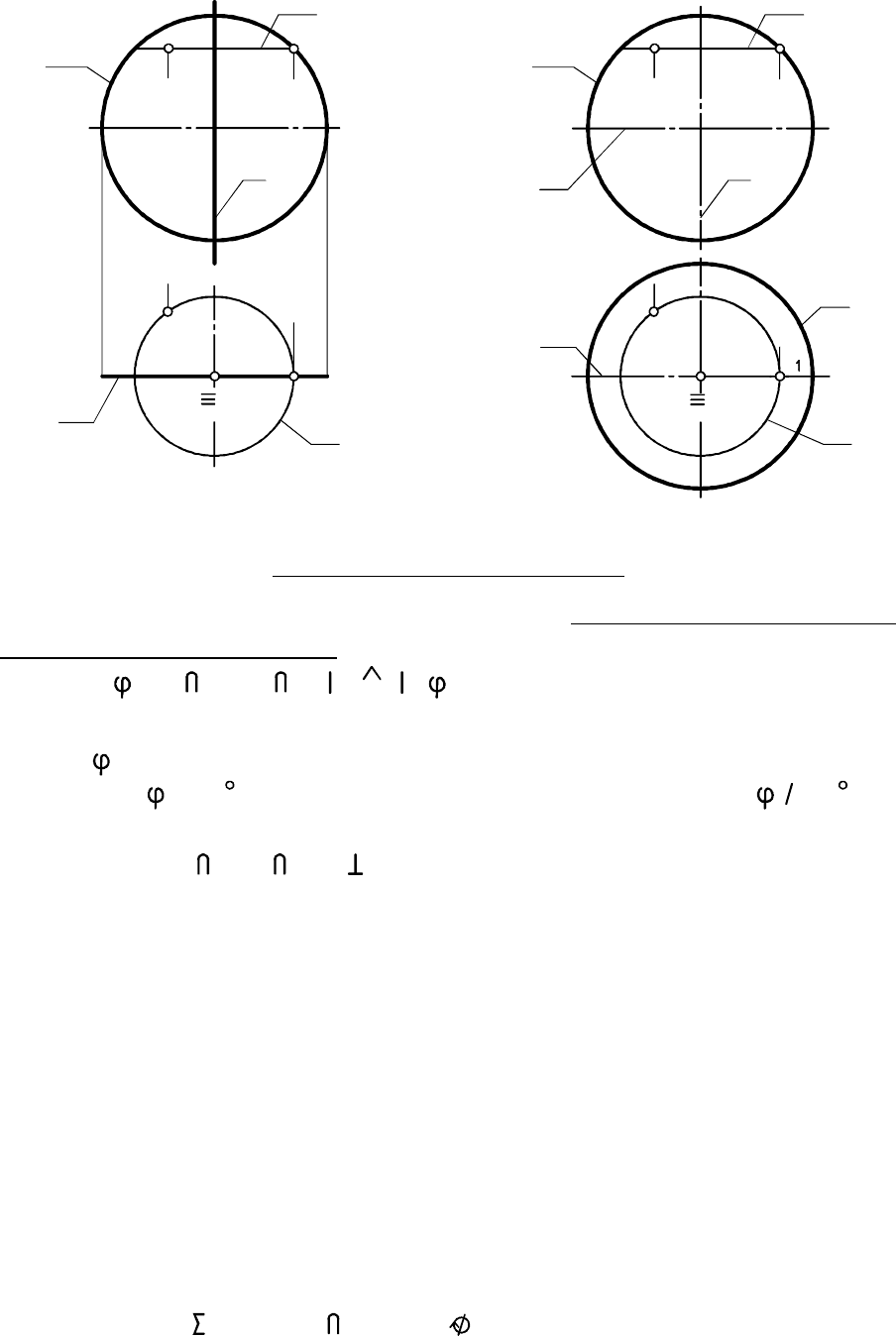
69
m
m
1 1
m
m
j j
C C
q q
j j
q q
g
g
m m
2 2
2
2
2 2
2 2
2 2
1
1
1
1
1 11 1
1
1 1
1
M
M
M
M
1 1
Рис. 7.27 Рис. 7.28
2
7.3. Винтовые поверхности
В курсе рассматривают только
, формула которых имеет вид:
линейчатые винтовые
поверхности - геликоиды
, где - образующая, прямая ли-
ния; - цилиндрическая винтовая линия; - прямая, ось винтовой
линии; - постоянный угол наклона образующей к оси .
{t(k,j, )(t k, t j, t j = )} t
k j
t j
Если = 90 , то геликоид называется прямым, если = 90 , то
наклонным (косым). Формулу прямого геликоида можно записать
так: . Если при вращении точки вокруг оси
по часовой стрелке, точка удаляется от наблюдателя, то винтовая
линия и геликоид являются правыми, а если приближается, то
левыми.
{t(k,j)(t k, t j, t j)}
На рис. 7.29 приведен элементарный чертеж прямого геликои-
да, а на рис. 7.30 - наклонного. На чертежах для наглядности
построены проекции нескольких образующих, а также заданы
направление вращения и проекции точки , определяющие направ-
ление винтовой линии (на рис. 7.29 линия правая, на рис. 7.30 -
левая).
A
Для построения образующих наклонного геликоида при-
нимают, что любая его образующая параллельна соответ-
ствующей образующей вспомогательной конической поверхнос-
t
l
ти вращения , у которой все образующие{ l (l, j; l j)(l = l j)}
Ô
i i i
i
Ô
i i i
i
i
i
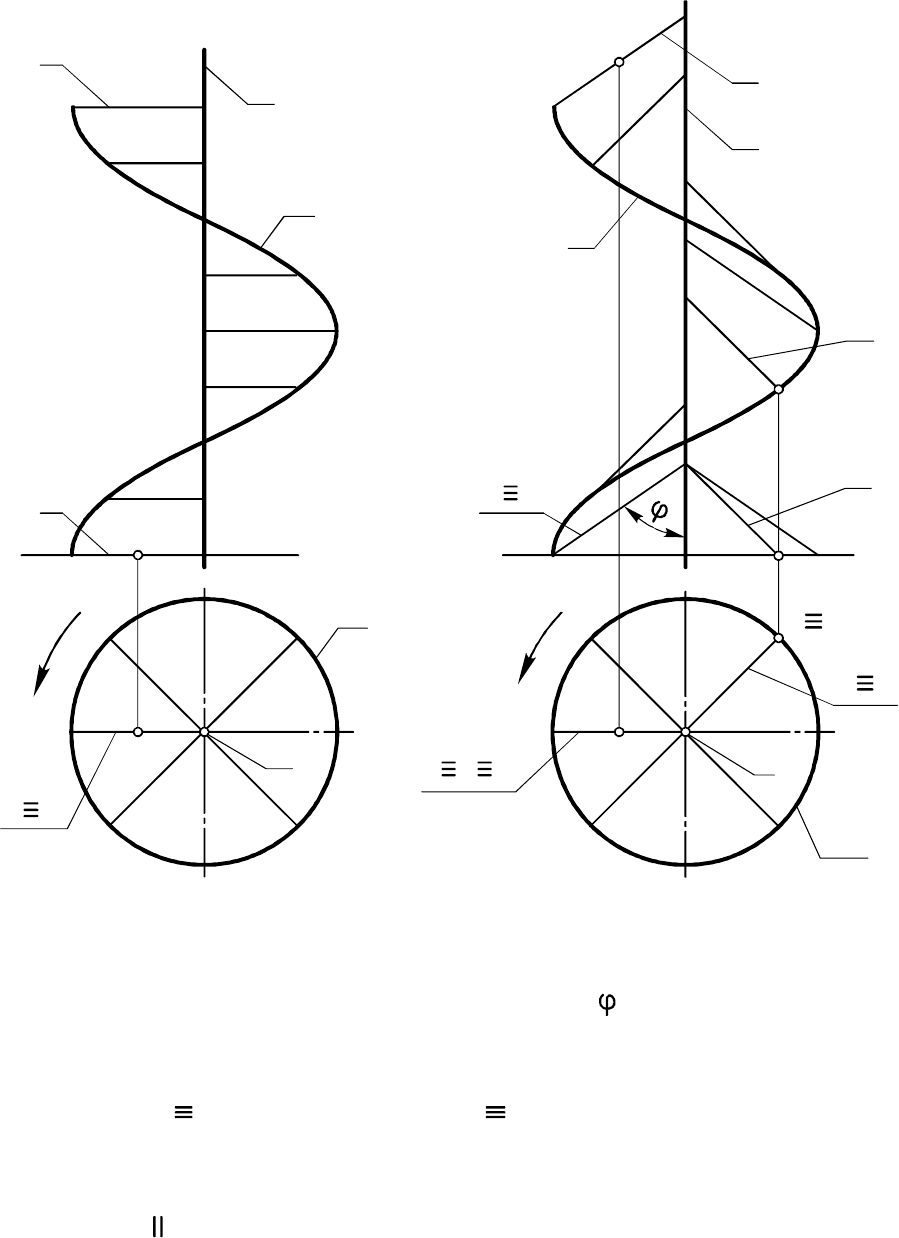
70
j
k
A
A
2
2
2
j
1
1
Рис. 7.29 Рис. 7.30
t
1
2
k
1
t
1
2
1 1
t
j
j
t
t
k
A
2
2
2
1
1
1
t
2
k
1
t
1
2
1 1
t
1
2
1
1
2
2
2
1
l
i
1
i
l
i
2
i
A
2
1
t
2
2
наклонены к оси вращения под тем же углом . Поскольку геликоид
и коническая поверхность имеют общую ось , перпендикуляр-
ную , то горизонтальные проекции образующих поверхностей
совпадают: . Задав проекции , строят проекцию обра-
зующей конической поверхности, проходящей через её точку и
вершину, а затем через проекцию точки винтовой линии
проводят .
Винтовые поверхности широко используются в технике: винты,
сверла, пружины, конструкции винтовых аппарелей и лестниц и
многое другое изготовлено с использованием этих поверхностей.
j
t l t l l
1
2 2 k
t l
Ï
1
1 1
i i
1 1
i i
2
i
2
i
2
i
t
2
2
l
1
l
2
2
