Оганесов О.А., Кайль В.А., Рябикова И.М., Кузенева Н.Н. Курс лекций по начертательной геометрии. Часть 1
Подождите немного. Документ загружается.

1
x
A
2
A
A
3
A
1
A
x
A
x
x
1.5. Введение новой плоскости проекций
При решении ряда инженерно-геометрических задач удобно
использовать дополнительные изображения ГО, позволяющие
упростить решение задачи, сделать его более точным и т. д. Получе-
ние новой проекции (новых проекций) ГО по уже имеющимся
является результатом преобразования КЧ. Из множества способов
преобразования КЧ здесь рассмотрим один: способ введения
(задания) новой ПП.
Суть этого способа заключается в том, что дополнительно к
ПП и вводится новая ПП , проецируя на которую ГО по-
лучают его новую проекцию. На новую ПП накладывают только одно
ограничение: она должна быть перпендикулярна хотя бы одной из
ПП или . Новое направление проецирования параллельно ,
если , или , если .
Ï Ï Ï
Ï Ï Ï
Ï Ï Ï Ï Ï
1 2 3
1
2
1
3 2 3 2
1
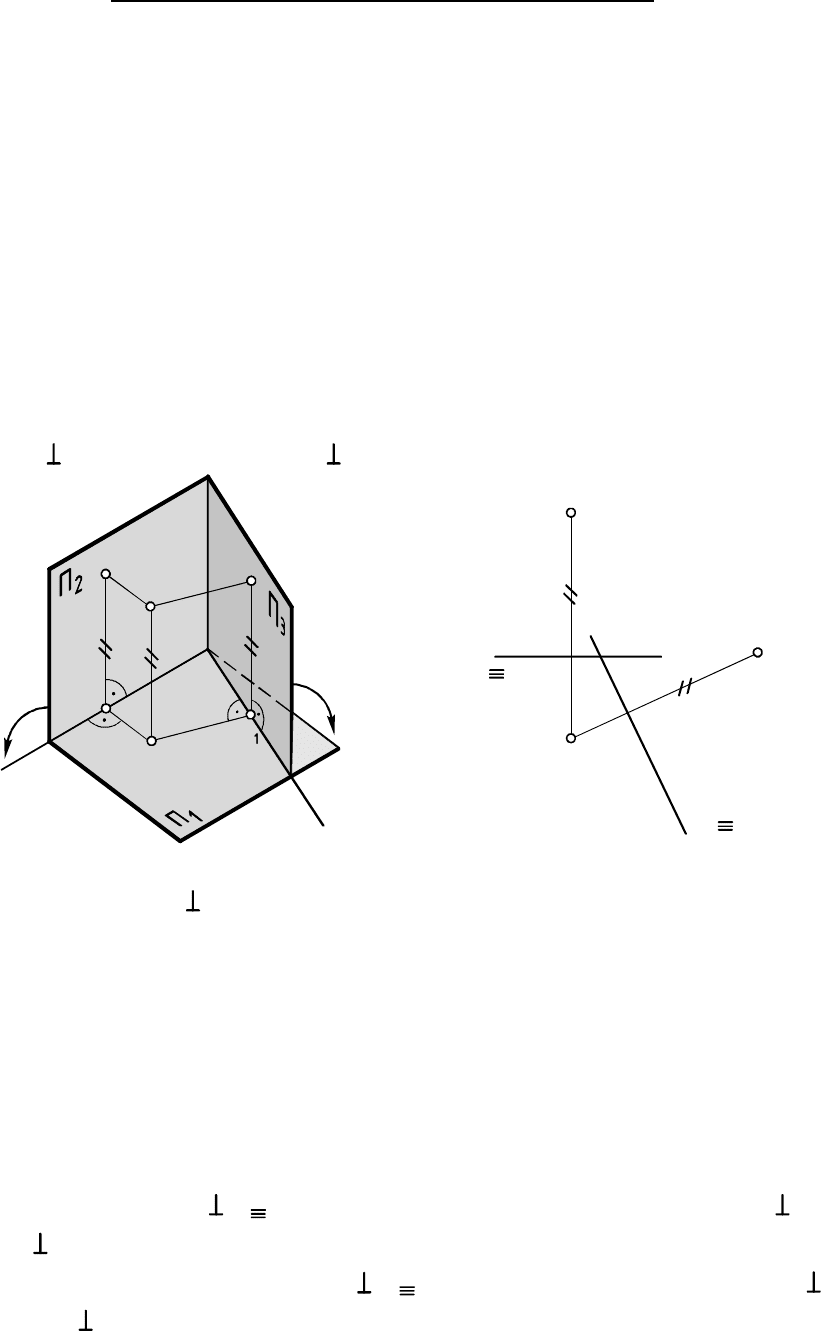
Зададим и найдем проекции и точки на
ПП , и (рис. 1.11). В старой системе ПП ( , ) точка
задавалась проекциями и , а в новой системе ПП ( , ) -
проекциями и . Для перехода к плоскому изображению повер-
нем и вокруг прямой (линия пересечения и ) до их
совпадения, а затем повернем вокруг (линия пересечения и
A A A A
A
A A
A A
x
x
,
) до совпадения с и . В результате получим трехкартинный КЧ
точки - плоскость, содержащую проекции точки на три ПП (рис. 1.12).
Линия связи ( на КЧ образуется линиями ( и
( при развороте ПП и в плоскость чертежа. Анало
гично новая линия связи ( образуется линиями (
и при совмещении с и .
A A A A x
A A x Ï Ï
A A A A x
A A x Ï Ï Ï
, ) , )
, ) -
, ) , )
( , )
Ï Ï
3 1
3
2
1
1 2 3
Ï Ï Ï
2
1
Ï Ï
1 2
1
Ï
3
Ï
1 3
2
1
Ï Ï
2
1
Ï
Ï
3
Ï
1
Ï
3
Ï
21
Ï Ï
1
1 2
x
21
1
x
2
x
21
1
3
x
31
1
x
1
1
x
1
1
3
3 1 2
11
Рис. 1.11 Рис. 1.12
A
2
A
1
A
3
x
21
x
31
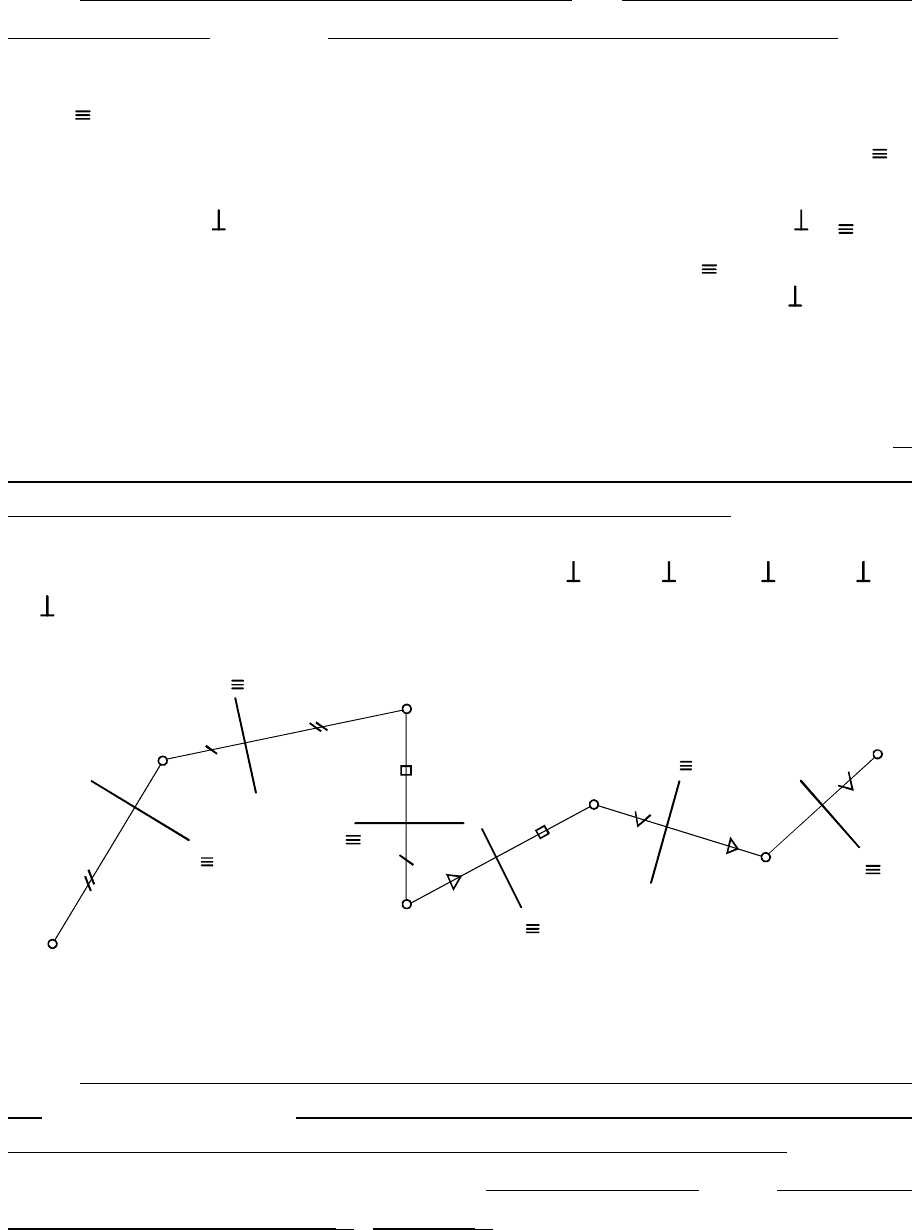
Аналогично можно последовательно задавать любое число
новых ПП и получать многокартинный КЧ, лишь бы вновь вводимая
ПП была перпендикулярна хотя бы одной из имеющихся ПП.
. На рис. 1.13
приведен семикартинный КЧ точки A, полученный при введении
новых ПП в такой последовательности: , , , ,
(все оси проекций задавались произвольно, а откладываемые
расстояния отмечены).
В
общем случае расстояние новой проекции точки от новой оси равно
расстоянию заменяемой проекции от предыдущей оси
Ï
23
Ï Ï
34
Ï Ï
15
Ï Ï
56
Ï
Ï
67
Ï
и :
Правило построения новой проекции точки по двум задан-
ным проекциям и новому направлению проецирования
À
A A
3
1 2
31
1. Перпендикулярно линии связи ( , ) проводят ось проекций
, если она на КЧ не задана.
2. В заданном направлении проводят новую ось проекций ,
являющуюся отображением линии пересечения и .
3. Из ( ) проводят новую линию связи ( , ) .
4. На новой линии связи ( от новой оси откладывают
расстояние от точки до плоскости , так как (см.
помеченные расстояния на рис. 1.11 и 1.12).
À À
õ
õ
x Ï Ï
A Ï Ï À À
A A x
A Ï Ï Ï
, )
1 2
21
1
1 3
1 3 1 1 3
x
31
1 3 31
1 3 1
Рис. 1.13
x
21
A
1
A
2
x
51
A
3
x
43
A
5
A
6
A
7
x
76
x
65
x
32
A
4
Новую ПП задают с точностью до параллельного переноса: уже
отмечалось, что при таком переносе проекция фигуры не меняется.
Решение любой задачи с применением преобразования черте-
жа сводится к решению четырех задач, называе-
мых основными задачами преобразования чертежа (ОЗПЧ)
в конечном счете
.
Наиболее часто используется -
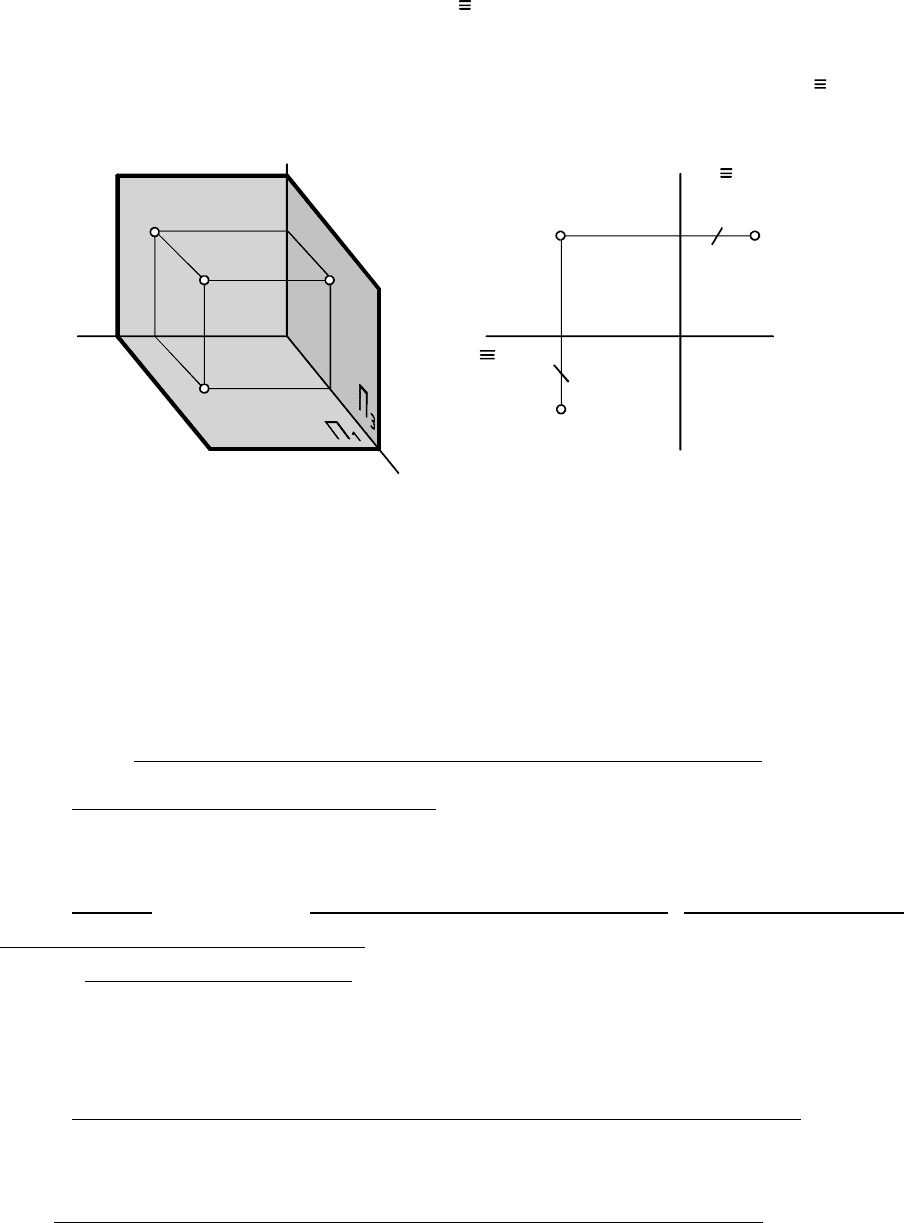
. Три взаимно перпендикуляр-
ные ПП обычно рассматривают как координатные (рис. 1.14).
профильная ПП новая ПП,
перпендикулярная и ПП , и ПП
Ï
Ï Ï
При переходе к плоскому изображению будем считать, что
система ПП мысленно разрезана по оси , а ПП жестко связанаy Ï
3
1
2
3
12
ЛИНИЯ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
Л Е К Ц И Я 2
2.1. Общие вопросы задания линии на чертеже
Линия - это одномерный ГО, имеющий одно измерение (длину)
и рассматриваемый как траектория точки, перемещающейся в
пространстве по определенному закону.
делятся на .
, если все их точки лежат в одной плос-
кости, . Из плоских кривых выделяют кривые
второго порядка - эллипс, его частный случай окружность, параболу
и гиперболу, а из пространственных - винтовую линию, широко
используемую в технике.
Линии кривые, ломаные и прямые Кривые и лома-
ные линии бывают плоские
и пространственные
- линия
задана на чертеже, если относительно любой точки пространства
можно однозначно ответить на вопрос, принадлежит точка линии или
нет, :
При задании линии используют критерий её заданности
и следующие свойства ортогонального проецирования
осью с ПП . Повернем и вокруг оси до их совпадения, а
затем вокруг оси развернем до совпадения с и и получим
трехкартинный КЧ (рис.1.15). Новая линия связи проводилась из
точки перпендикулярно оси (проекция оси на ПП и ),
после чего на ней откладывали координату точки и -
проекции оси на плоскости и . Вместо обозначений , и
применяют упрощенные обозначения и .
z Ï Ï Ï x
z Ï Ï Ï
À z z Ï Ï
Y A (y y
y Ï Ï ) z y
y z y
3
1 2
2
32
2 3
1 3
1
3
32
1
3
2 1
2
В заключении лекции отметим, что используемые в курсе
понятия “комплексный чертеж” и “чертеж” - синонимы.
13
x
y
y
z
z
Рис. 1.14 Рис. 1.15
1
x
21
A
A
2
A
3
A
1
Ï
2
32
A
3
3
y
1
A
2
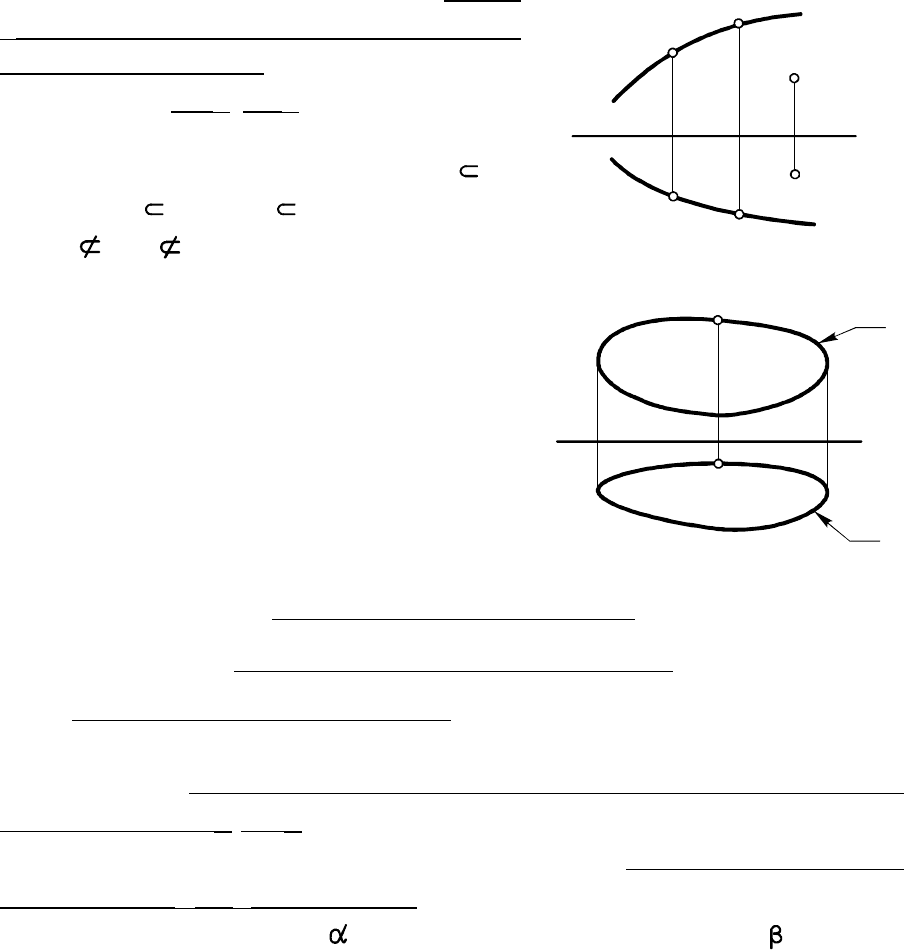
В общем случае (свойство 1)
(проекциями всех
своих точек) (рис. 2.1). Воз-
можность определить по чертежу, что
точка принадлежит линии ( ),
так как и , а точки и
нет (свойство 2), подтверж-
дает: линия своими проекциями
линия
на КЧ задается непосредственно
своими проекциями
на и
k
Ï Ï
M k M k
M k M k E N
E k N k
k k
( , )
и задана.k
Иногда для установления одно-
значного проекционного соответствия
точек линии помимо её проекций
необходимо задавать ещё проекции
какой-то точки (каких-то точек) линии
(рис. 2.2).
на КЧ
1. В общем случае проекцией кривой линии является кривая
линия, ломаной - ломаная, прямой - прямая.
2. Если точка принадлежит линии, то соответствующая проекция
точки принадлежит соответствующей проекции линии.
3. Если точка делит отрезок прямой в каком-то отношении, то
проекция точки делит проекцию отрезка в том же отношении.
4. Длина проекции отрезка прямой равна длине отрезка, умно-
женной на косинус угла его наклона к плоскости проекций.
5. Прямая, перпендикулярная плоскости проекций, проецируется
на эту ПП в точку.
6. Если прямые параллельны, то параллельны их проекции.
1 2
1
2
1 1 2 2
N
N
Рис. 2.1
k
1
k
2
E
2
M
1
M
2
x
2
1
E
1
Рис. 2.2
A
1
A
2
x
k
1
k
2
Прямая общего положения
Прямая общего положения задается на КЧ своими
проекциями на и
или проекциями двух
своих точек и на рис. 2.5)
- это прямая, не параллельная
и, следовательно, не перпендикулярная ни одной из ПП (прямая
на рис. 2.3).
- прямыми, не параллельными и не перпен-
дикулярными оси проекций ( и на рис. 2.4)
, определяющими положение проек-
ций прямой. На рис. 2.3 - угол наклона прямой к , - к .
a
a a
a Ï Ï
Ï Ï
A B(
2.2. Задание прямой линии
2.2.1. Прямая общего положения
21
1
2
21
14
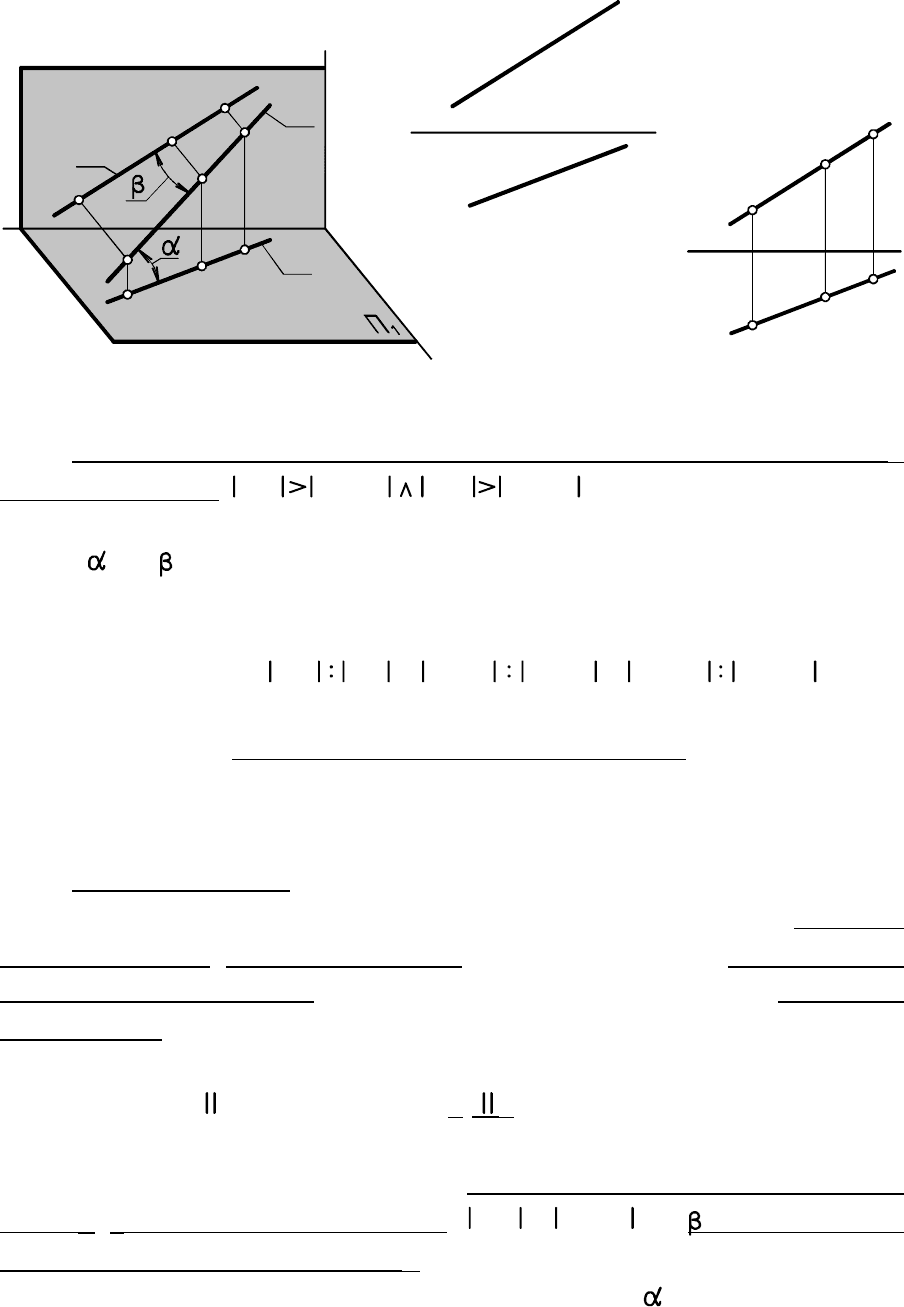
: (свойство 4 и рис. 2.3).
На КЧ (рис. 2.5) величины длин отрезков прямой общего положения,
углов и наклона её к и не заданы и при необходимости
ищутся путем построений на КЧ.
Для трех точек , , прямой (рис. 2.3, 2.5) справедливы отно
шения (свойство 3): .
Длина отрезка прямой общего положения всегда больше дли
ны его проекции
-
A,B A ,B A,B A ,B
Ï Ï
A B C
A,C C,B = A ,C C ,B = A ,C C ,B
-
Рис. 2.3
x
y
z
A
2
B
1
Ï
2
A
1
A
B
2
B
a
2
a
1
a
C
C
C
2
1
x
x
Рис. 2.4
Рис. 2.5
a
2
a
1
A
2
A
1
B
1
B
2
1 1
2 2
1
2
1 1
1
1 2 2 2 2
2.2.2. Прямые частного положения
К прямым частного пложения относятся прямые уровня и
проецирующие прямые.
- это прямая, параллельная какой-либо
плоскости проекций. Прямую, параллельную , называют
; параллельную -
; параллельную профильной ПП -
. Обычно горизонталь обозначают , фронталь - ,
профильную прямую - .
Так как , то (рис. 2.6) ( все точки горизонтали уда-
лены от
Прямая уровня
горизон-
тальной прямой или горизонталью фронтальной
прямой или фронталью профиль-
ной прямой
Ï
Ï
h f
p
h Ï
Ï
Z
h x
на одинаковое расстояние и на координированном КЧ
имеют одинаковые координаты ), отрезок горизонтали проецирует-
ся на Ï
Ï
A,B = A ,B
h h Ï
Ï
в натуральную величину - угол наклона
горизонтали к плоскости
: и
, определяемый углом между
горизонталью и её проекцией на (угол наклона горизон-
тали к равен 0 ).
О
1
2
1
1
2
1
1 1
1
2
2
2
C
1
C
2
15
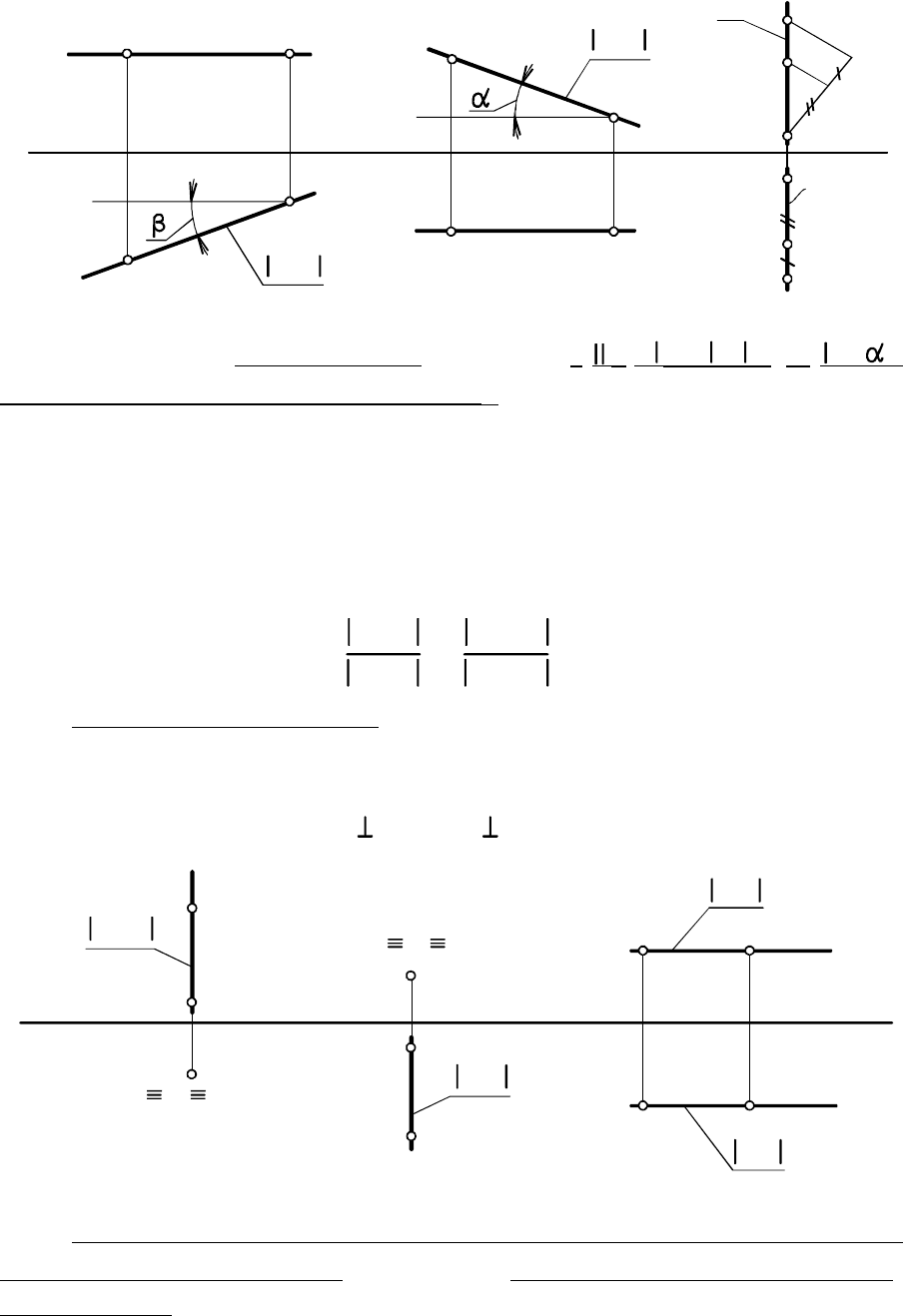
f
f
h
h
p
p
M
M
N
N
K
K
E
E
F
F
B
B
A
Рис. 2.6
A
1
x
2
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
1
2
Аналогично (рис. 2.6)
.
Для профильной прямой помимо проекций и надо
ещё задавать проекции двух её точек (точки и на рис. 2.6). Если
точка задана на прямой одной проекцией, например,
ищется с использованием профильной ПП или, как по-
казано на рис. 2.6, с использованием условия:
для фронтали и -
угол наклона фронтали к плоскости
f x M,N = M ,N
Ï
,
p p p
E F
K p K , то
проекция K
1
1
2 2
2
2
22
1
1
1
1
F ,K F ,K
K ,E K ,E
=
.
1
1 2
2
ая аяПроецирующ прям - это прямая, перпендикулярная какой-
либо ПП. Прямую, перпендикулярную , называют горизонтально
проецирующей прямой, а перпендикулярную - фронтально
проецирующей. Прямые и показаны на рис. 2.7.
Ï
Ï
a Ï b Ï
1
2
1
2
E,
A,
L,
L,
F
B
K
K
Рис. 2.7
x
a
2
A
2
B
2
a A
1
B
11
b F E
222
E
1
b
1
F
1
L
2
L
1
Ê
2
Ê
1
l
2
l
1
Проецирующая прямая проецируется на ПП, к которой она
перпендикулярна, в точку называемую основной проек
цией прямой
( и ),
, а на вторую ПП - в прямую, перпендикулярную оси
проекций ( и ).
a b
a b
-
1
2
A,B
M,N
2
1
16
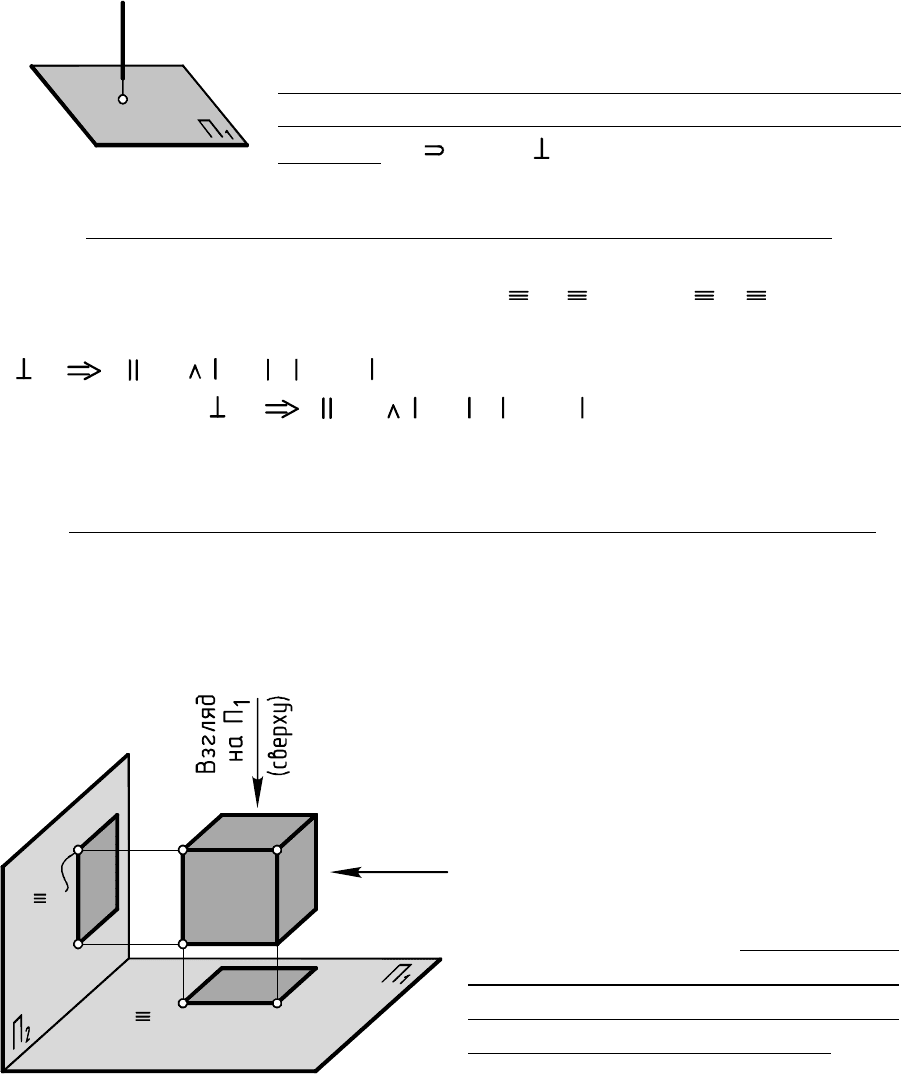
Чтобы задать проецирующую прямую,
достаточно однокартинного чертежа (рис. 2.8):
- и . Поэтому проекции и
на КЧ (рис. 2.7) давать не обязательно.
основная проекция проецирующей прямой
однозначно задает её положение в прост-
ранстве d d d Ï a
b
1 1 2
1
: все
точки проецирующей прямой проецируются на ПП, перпендикуляр-
ную к ней, в её основную проекцию ( и ).
Основная проекция обладает собирательным свойством
A B a E F b
Горизонтально проецирующая прямая является фронталью:
, а фронтально проецирующая прямая -
горизонталью: .
a Ï a Ï A,B = A ,B
b Ï b Ï A,B = A ,B
На рис. 2.7 задана также профильно проецирующая прямая ,
которая одновременно параллельна и .
l
Ï Ï
в
их видимости относительно той ПП, к которой прямая перпендику-
лярна и на которую все точки проецируются в основную проекцию.
На рис. 2.7 точки прямой конкурируют относительно , прямой -
относительно
Все точки проецирующей прямой являются конкурирующими
a Ï b
Ï . Конкурирующие точки используют для опреде-
1 1 1 2 2 2
2
1
2 2
2
1 1 1
1
2
1
2
ления видимости ГО и их
элементов . Решая вопрос
видимости, надо учитывать
направление взгляда (проеци-
рования) и то, что проецируе-
мый ГО всегда расположен
между ПП и наблюдателем
(рис. 2.9). Поэтому
. Так,
на рис. 2.9 из двух конкурирую-
щих относительно точек и
видимой из
конкурирующих точек является
точка, находящаяся дальше от
ПП и ближе к наблюдателю
Ï B
C B B C Ï
A B A
Ï A B a A
Ï
Ï
видна точка ( выше ), а конкурирующих относительно
- более удаленная от точка . Аналогично на рис. 2.7
относительно из двух точек и прямой видна точка
выше , см. на проекции и ), относительно из двух точек
и прямой видна точка ( дальше от , см. на проекции
и ).
точек
и
(A
B A B F
E b E E E
F
1
2
1
2 2
2
2
1
1
17
2
Ï
A
A
2
Ñ
B
Ñ
2
B
1
Ñ
1
A
1
B
2
Рис. 2.9
Âçãëÿä
íà Ï
2
d
1
d
Рис. 2.8
(ñïåðåäè)
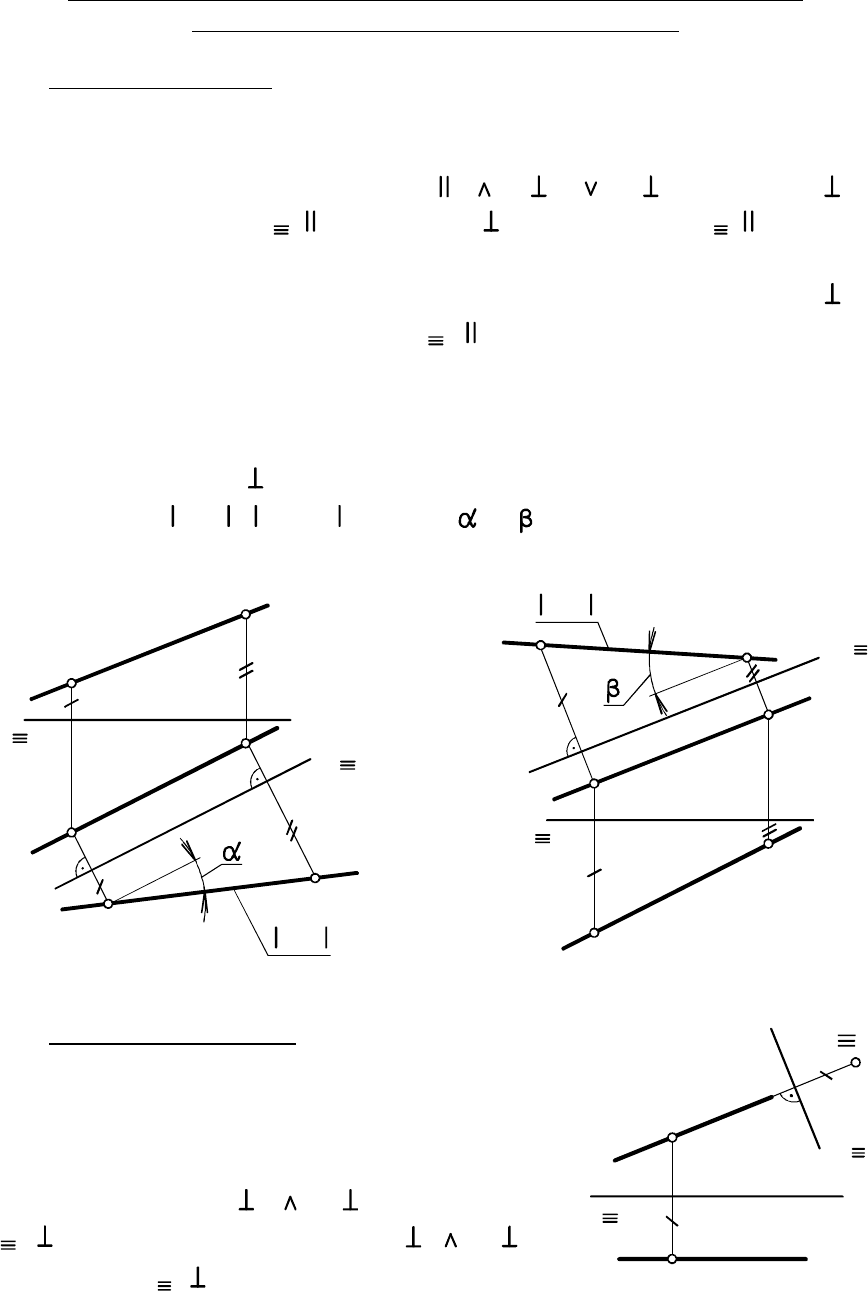
: прямую уровня
перевести в положение проецирующей
прямой.
Новую ПП задают перпендикулярно
прямой уровня. Горизонталь станет прое-
цирующей при (новая ось
), а фронталь - при
(новая ось ) На рис. 2.11
Условие 2ОЗПЧ
h
h
h f f
f . фронталь
, заданная проекциями и , переведена вf f f
: преобразовать КЧ так, чтобы прямая
общего положения стала прямой уровня.
Для решения 1ОЗПЧ новую ПП задают параллельно прямой
и перпендикулярно или ( ). При
новая ось проекций , а при новая ось .
На рис. 2.10,а прямая , заданная проекциями и
переведена в положение прямой уровня с использованием .
Для этого нанесли новую ось , на прямой взяли две
произвольные точки ( , ) и ( , ), нашли их проекции и
(используемые для этого расстояния помечены), через которые и
провели проекцию прямой . На рис 2.10,б та же задача решена
с применением . Заметим, что на рис. 2.10 найдены длина
отрезка ,
Условие 1ОЗПЧ a
Ï
a Ï Ï Ï a Ï Ï Ï Ï Ï Ï
a a a
a
A A A B B A B
a a
[A B] = A B a
,
,
B
( A B , ) и углы и наклона к и со-
ответственно.
2.3. Решение 1-й и 2-й основных задач преобразования
чертежа способом задания новой ПП
1 2 3 3 1 3 2 3 1
x
31
a
31
Ï
2
Ï x
32
a
2
1 2
x
31
a
1
3
Ï
1
Ï
Ï Ï
23
3 3
1 12 2
3
33
Ï Ï
21
x
21
x
31
x
32
B
2
B
1
A
1
a
1
a
2
A
2
A
3
B
3
a
3
x
21
B
2
B
1
A
1
a
1
a
2
A
2
A
3
B
3
a
3
A,B
A,B
Рис. 2.10
à) á)
1
1
x
31
3
Ï
3
Ï Ï
x
Ï Ï Ï
3
x
32
x
21
A
1
1
2
A
2
f
A
3
3
f
f
Рис. 2.11
3
3 2
32
2
21
18
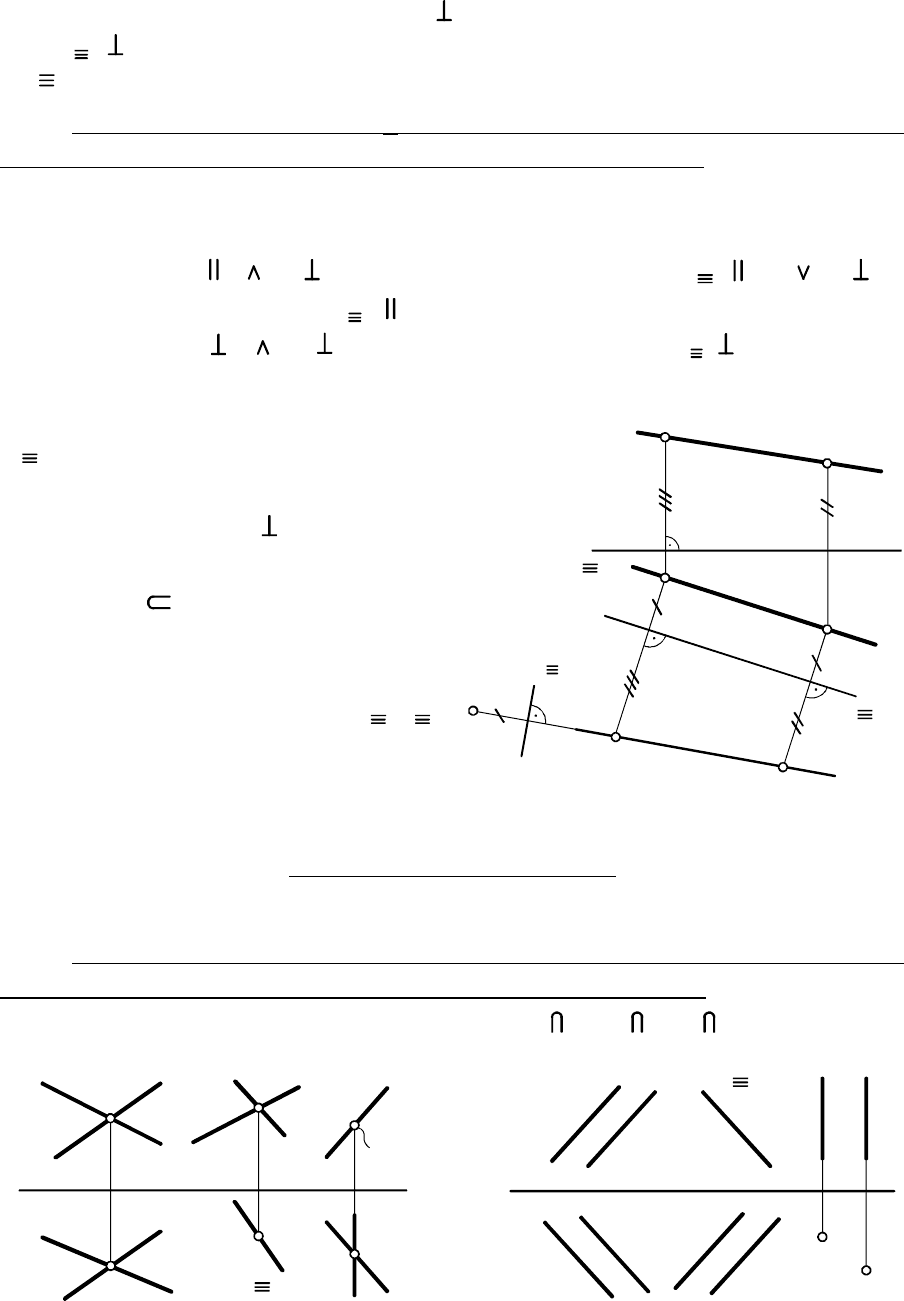
положение последовательно вводят две новые ПП (сразу задать
новую ПП перпендикулярно нельзя: такая ПП не перпендикулярна
ни , ни ):
a
Ï Ï
2. Задают (новая ось проекций )Ï a Ï Ï a - решают
2ОЗПЧ.
1. Задают (новая ось проекций )Ï a Ï Ï a Ï Ï
(новая ось проекций ) - решают 1ОЗПЧ.a
1
2
3 3 1
x
31
1
3
2
x
32
2
4
3
x
43
4
3
На рис. 2.12 (были заданы
для перевода прямой в
проецирующее положение на 1-м эта-
пе использовали . Проекции и
строили с помощью произвольных
точек , (откладываемые рас
стояния на рис. 2.12 обозначены).
a a
a
a
a
A B a
, ,
)
-
1 2
3
1
Ï Ï
3
4
2.4. Задание пар прямых
Прямые могут пересекаться, быть параллельными, скрещиваться.
. На рис. 2.13
заданы пары пересекающихся прямых
Если прямые пересекаются, то точки пересечения их однои-
менных проекций находятся на одной линии связи
a b d g l t, , .
g
g
b
b
d
d
Рис. 2.13
1
2
x
a
a
2
2
2
t
l
2
t
l
1
1 1
1
1
2
t
1
1
l
t
2
2
l
2
a
b
2
b
1
a
1
g
d
2 2
g
1
d
1
Рис. 2.14
x
проецирующее положение ( ). Для построения прове-
ли , на фронтали взяли точку , ) и нашли её проекцию
.
f
f A A A
A f
(
Для перевода прямой общего положения в проецирующееa
3
3
Ï
3
f
x
32
2
1 2
3
Рис. 2.12
x
31
x
43
a
1
2
A
2
B
1
B
2
A
1
4
A Ba
4 4
a
3
A
3
B
3
a
x
21
x
21
19
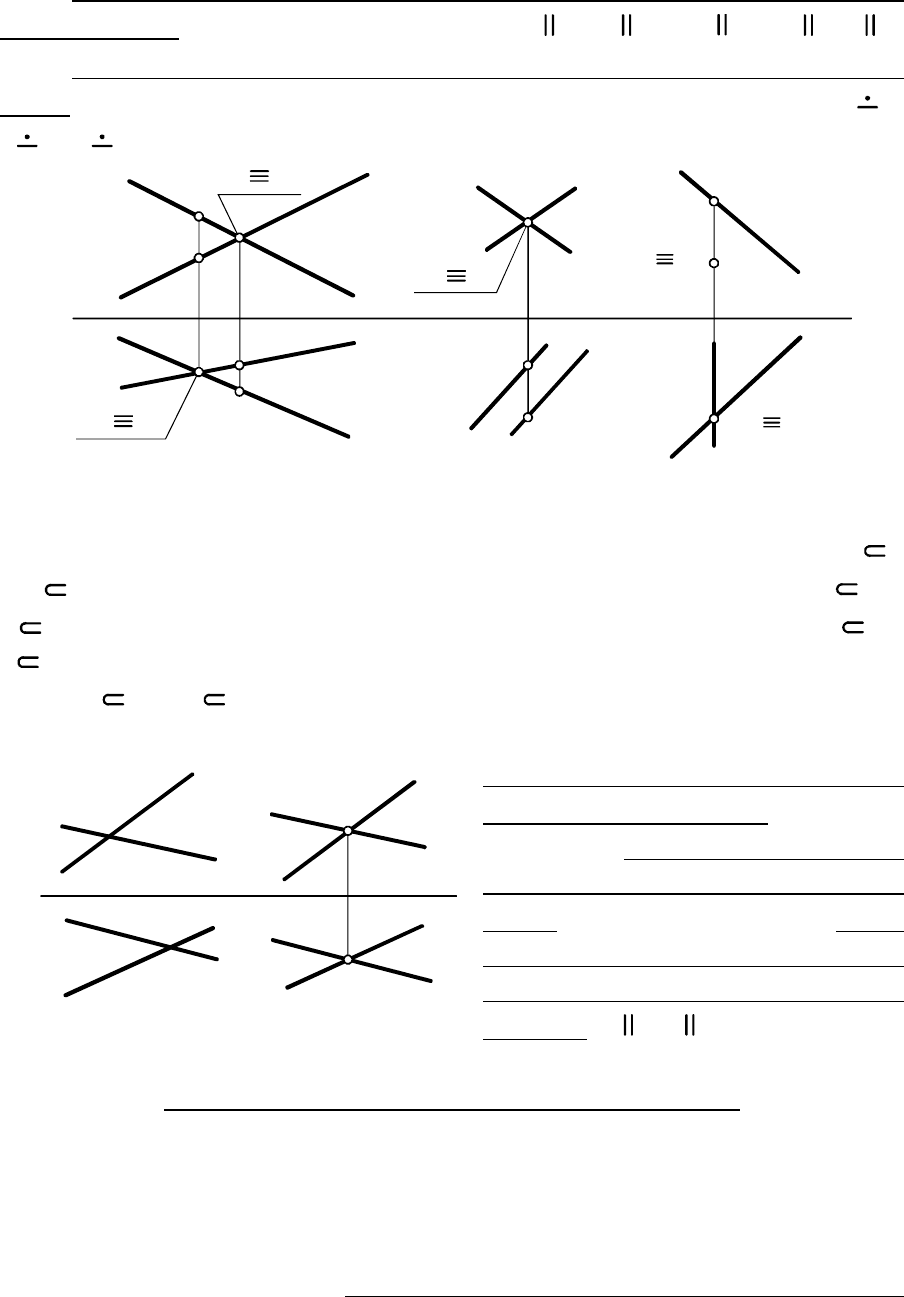
(свойство 6). На рис. 2.14 ( )
Если прямые параллельны, то параллельны их соответствую-
щие проекции a b a b a b d g l t; , , .
1
2
1
2
. На рис. 2.15 приведены пары скрещивающихся прямых
Скрещивающиеся прямые - прямые, не лежащие в одной плос-
кости a b
d g l t
,
, .
g
g
b
b
t
d
A
A
C
C
D
D
B
B
E
F
t
E
F
G
G
Q
a
1
2
l
2
x
a
2
2
22
2 2
d
2
Q
2
2
2
1
1
1 1
1
1
1
1
l
1
1
1
11
2
2
Скрещивающиеся прямые всегда имеют одну или две пары то-
чек, конкурирующих относительно и . У прямых и точки
и конкурируют относительно (видна точка ), а точки и
- относительно (видна точка ); у прямых и точки и
Ï Ï a b A a
B b Ï A C b
D a Ï C l t E l
Рис. 2.15
1
2
1
2
F t Ï F g d
G g Q d Ï G
конкурируют относительно (видна точка ), у прямых и
точки и конкурируют относительно (видна точка ).
Введем понятие угла между скрещивающимися прямыми.
1
2
Величина угла между скрещи-
вающимися прямыми
равна величине угла
между пересекающимися пря-
мыми соот-
ветственно параллельными
данным скрещиваю щимся
прямым
( и на
рис. 2.16)
( и на рис. 2.16),
( ).
a b
t l
t a l b,
b
b
Рис. 2.16
1
2
x
a
a
2
2
t
l
2
t
l
1
1
1
2.5. Теорема о проецировании прямого угла
В общем случае прямой угол между пересекающимися или
скрещивающимися прямыми проецируется на ПП с искажением.
Теорема о проецировании прямого угла выделяет частный, но
важный для практики случай, когда прямой угол проецируется на ПП
без искажения. Так как теорема о проецировании прямого угла
связывает три ГО (рис. 2.17) - прямой угол, некую плоскость
20
