Оганесов О.А., Кайль В.А., Рябикова И.М., Кузенева Н.Н. Курс лекций по начертательной геометрии. Часть 1
Подождите немного. Документ загружается.

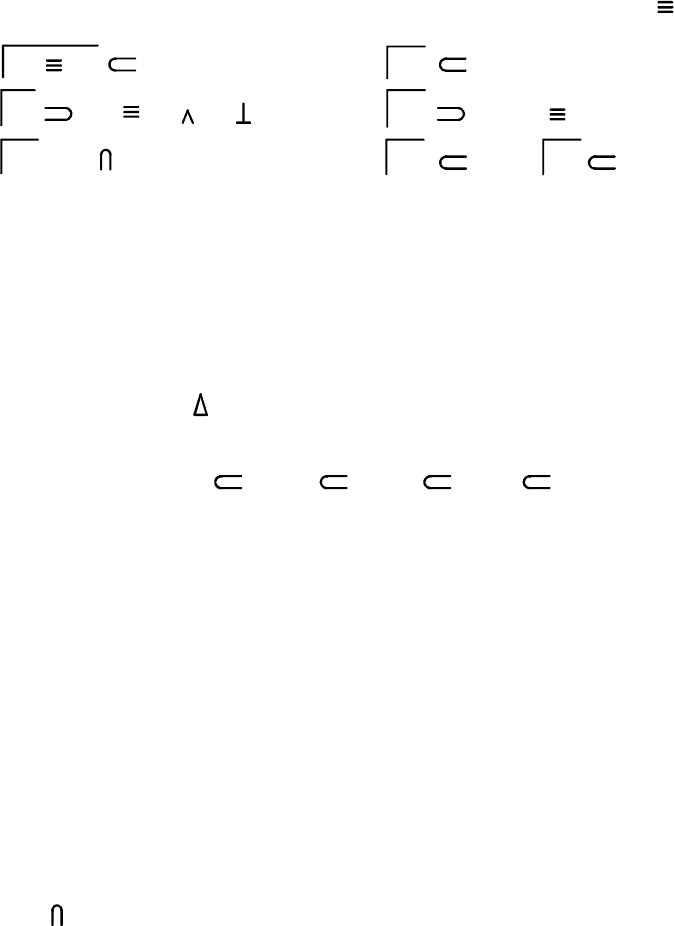
Горизонтальные проекции линий пересечения конической
поверхности и секущих плоскостей строят по их известным фрон
тальным проекциям и условию принадлежности линий пересечения
поверхности конуса. Для этого обычно используют окружности ,
проецирующиеся на и в отрезки прямых, а на - в окружности.
Ниже дан ГА построения горизонтальных проекций точек и
гиперболы по их произвольно взятой фронтальной проекции :
-
q
M P
M P
i
2
Ï
3
Ï Ï
1
2 2
1. M
2
1
3.
l
22
5.
6.
2.
4.
1
2
M
1
M
1
1
2
=
2
2
.
1
.
1
1
1
;
.
.
.
1
q
C
2 1
j
q
2
q
.
ÃÐ
2
q
Ð
2
q
l
1
q
1
Ð
1
1
q
Проекции и найдены с использованием их координат
и , взятых в поле и откладываемых в нужные стороны от оси
M P Y
Y z
по линии связи .(M ,M )
Аналогично строили проекции точек , , , , , , , и не
указанных промежуточных точек эллипса и гиперболы. Точки , , ,
, лежащие в плоскости и на образующих прямых, проходящих
через точки , и , (рис. 10.4), можно было строить с помощью
этих образующих. Точки , , , найдены на
проекциях соответствующих контурных образующих конуса.
Q G B C F K D E
B C D
E
T 3 T 4
A l S l N l L l
Относительно видны все точки конической поверхности.
Относительно всегда видны точки конической поверхности, рас-
положенные перед контурными образующими и и проецирую
щиеся на и левее соответствующих проекций этих образую-
щих. Поэтому относительно видны точки гиперболы, дуга эллип-
са и части дуг окружностей от точек и до образующих и
. Из-за сквозного выреза в конусе на видны также части
отрезков и .
l l
NGAQS F K l
l
[C,E] [B,D]
-
Отрезки, по которым пересекаются секущие плоскости,
находятся внутри конуса и поэтому относительно и не видны
(отрезок конкурирует на с гиперболой).[F,K]=
Контурные относительно образующие и вырезаны от
точек и до плоскости и показаны на этих участках тонкими
линиями как не существующие.
l l
N S
3
3
Ð
M
Ï
1
3
2 3
2 3 4
1
Ï
1
3
Ï
3
4
Ï
12
Ï
3
Ï
3
4
3
Ï
Ï
1 3
Ï
à Ô
Ô
Ï
1
3
Ï
3 4
91
j
,
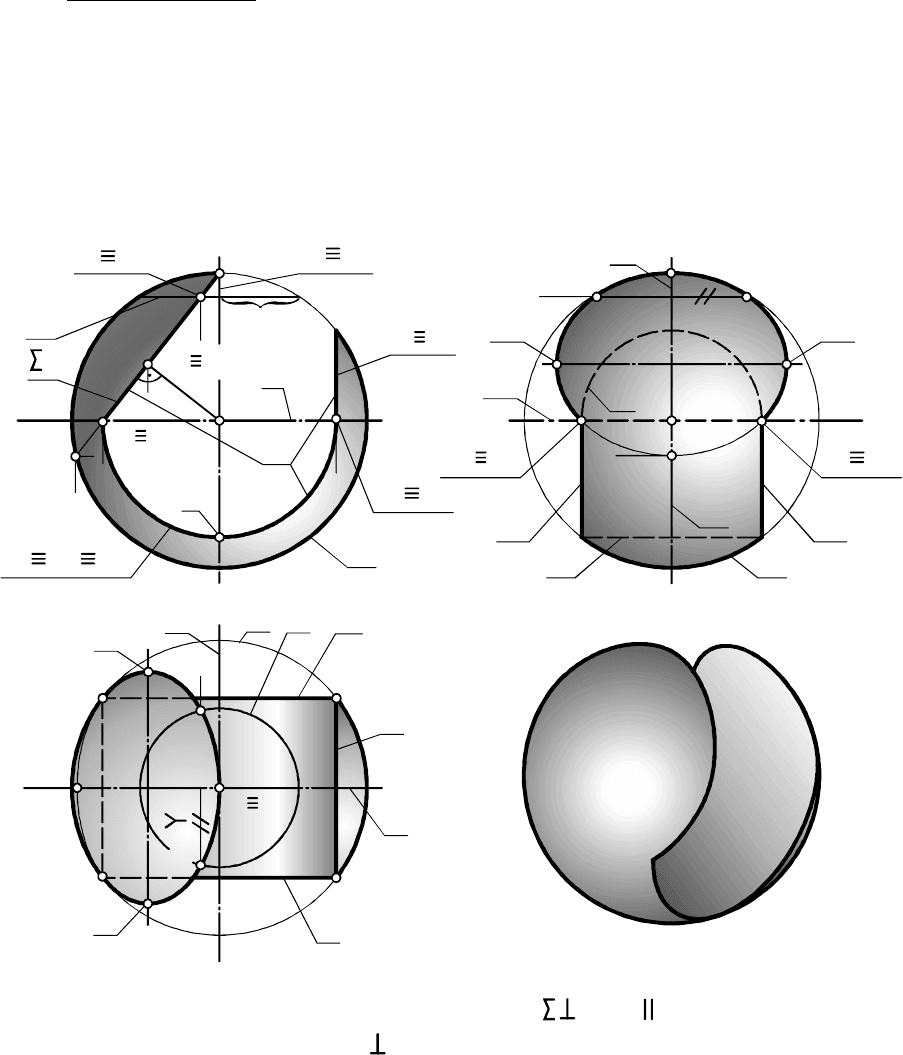
Задан вид шара со сквозным вырезом на
(см. вид шара на на рис. 10.5 без обозначений). Построить
изображения шара на и (рис. 10.5).
Изображением шара на является проекция его главного
меридиана , на - проекция его экватора , на - проекция
ПРИМЕР 10.3.
m
m q q g
его профильного меридиана . На рис. 10.5 также даны проекции
координатных осей и начала отсчета .
g
O
2
Ï
2
Ï
Ï
1 3
Ï
2
Ï
2
Ï
1
1
3
Ï
3
x
Рис. 10.5
m
g
Y
R
1 2
2
A
2
F
Ê
2
N
k
2
Ô
E
2
B
t
x
m
g
q
1
2 2
m
2
2
22
B
2
D
2
C
2
2
2
1
z
2 2
2
2
Ã
2
q
2
2
m
2
g
A
3
z
3
2
1
3
3
B
3
D
3
1
g
1
3
O
2
O
3
C Ê
3
3
N
3
E
3
m
2
3
m
3
1
t
3
g
3
y
3
3
m
3
F
3
N
A
1
O
E
1
C
1
D
1
F
1
Ê
1
q
2
q
g
1
1
1
1
2
1
1
1
q
1
1
1
1
1
1
1
m
1
1
y
1
m
1
2
Сквозной вырез образуют плоскости , и цилиндричес-
кая поверхность вращения , соосная со сферой.
Поскольку вырез образуют фронтально проецирующие поверх-
ности, то фронтальные проекции линий пересечения сферы
(поверхности шара) с секущими поверхностями и секущих
поверхностей между собой известны - они совпадают с основными
проекциями проецирующих поверхностей на (на рис. 10.5 обоз-
начены ). Поэтому решение задачи сводится к построению
горизонтальных и профильных проекций указанных линий
пересечения по их известным фронтальным проекциям.
k
2
Ï
Ô
Ã
2
Ï
3
Ï
2
Ï
92
2
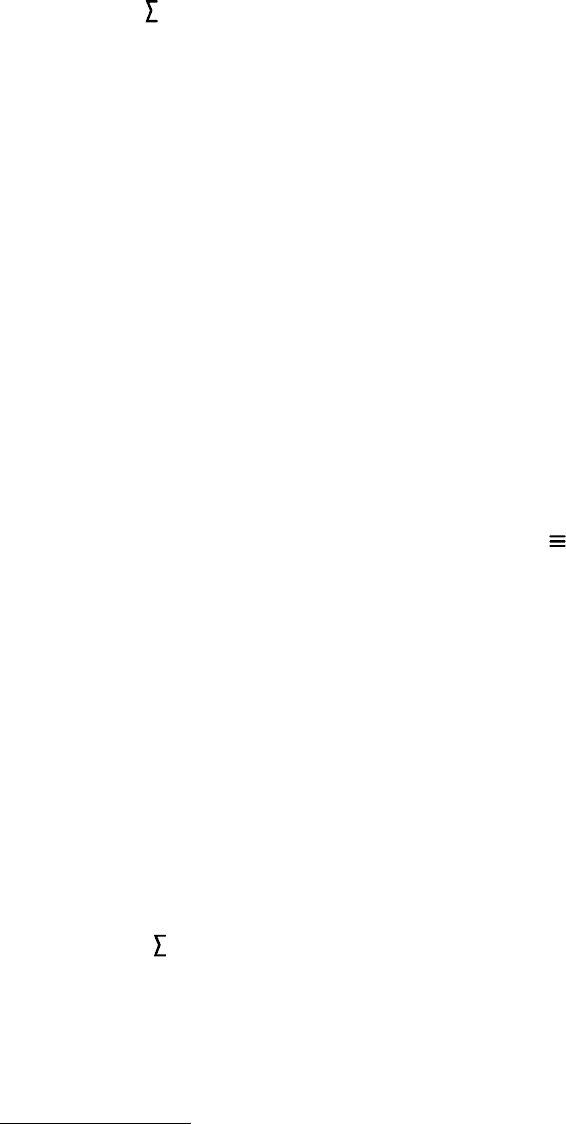
Плоскость пересекает сферу по окружности, проецирующей
ся на в отрезок , а на и - в эллипсы, не существую
щая которых показывается на чертеже тонкой линией.
Плоскость пересекает сферу по полуокружности , проецирую-
-
[A ,F ]
g
-
дуга EFC
2
Ï
2 2
3
Ï
1
Ï
Ã
1
Общая ось вращения сферы и цилиндрической поверхности
перпендикулярна . Поэтому сфера и поверхность соосны и
пересекаются по двум полуокружностям и , проходящим через
точки , и соответственно. На эти полуокружности проеци
руются в полуокружность , а на и - в отрезки прямых.
Ô
m m
C K E,N -
Характерные точки расположены на главном меридиане
сферы , а , , и на её экваторе .
A F
m C E K N q
и
Горизонтальные проекции промежуточных точек и для по-
строения эллипсов найдены по их взята на
произвольно) с помощью окружности и линии связи .
Профильные проекции этих точек построены по их фронтальным и
горизонтальным проекциям с использованием координаты . Анало-
гично определены проекции характерных точек и , задающих
положение второй оси эллипсов и других их произвольных точек
(при необходимости).
1 2
[A ,F ]
q (1 ,1 )
Y
B D
проекции 1 2 (
На видны все точки, расположенные выше экватора , а
также, благодаря вырезу, - часть дуг окружностей и .
q
m m
На видны все точки, расположенные перед профильным
меридианом и проецирующиеся на и левее и .g g g
Плоскость и цилиндрическая поверхность пересекаются
по отрезку , расположенному внутри шара и не видимому ни на
, ни на . На показана проекция нижней контурной обра
зующей цилиндрической поверхности .
[C,E]
t
t
-
2
Ï
Ï
1 3
Ï
2 2
2 2
2
1
Ï
1
2
1
3
Ï
Ï
1 2
Ï
1 2
Ô
Ï
1 3
Ï
3
Ï
3
Ô
2
Ï Ô
1
2
Задан вид цилиндра вращения на и основ-
ные проекции фронтально проецирующих плоскостей, образующих
в цилиндре сквозной вырез (см. вид цилиндра на на рис. 10.6 без
обозначений). Построить виды цилиндра с вырезом на ПП и
ПРИМЕР 10.4.
(рис. 10.6).
Цилиндр ограничен цилиндрической поверхностью вращения
и плоскостями верхнего и нижнего оснований.
Ï
1 3
Ï
2
Ï
2
Ï
93
Ô
2
1
щейся на в отрезок длиной, равной радиусу этой окруж-
ности, на - в отрезок , на - в полуокружность .
[K ,L ]
[K ,N ] g
2
Ï
2 2
Ï
1 3
Ï
1
3
1 1
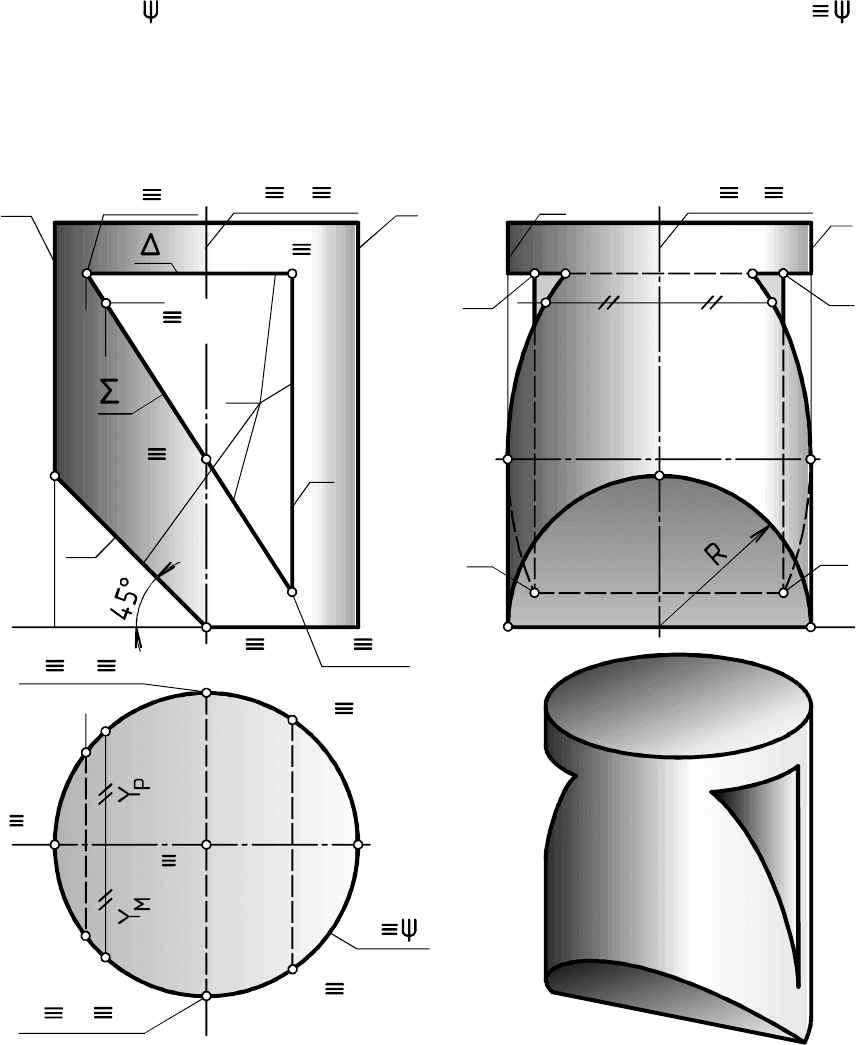
а на - в ломаную , образованную основными проекциями секу-
щих плоскостей. Поэтому в примере строили профильные проекции
указанных линий пересечения по их известным горизонтальным и
фронтальным проекциям.
k
2
Ï
2
Рис. .610
A
A
E
E
l
l
ll
l
l
l ll l
A
B
B
F
Ã
F
S
K
T
C
L
L
L
C
N
D
S
K
K
P
P
CN
T
E
S
F
T
M
M
D
N
D
B
P
M
Ô
2
1
3
4
2
2
2
2
2
2
2
2
2
2
2
2
2
2 2
2
z
2
k
2
2
2
2
2
2
x
2
1
3
4
3
4
2
l
2
3
1
3
3
3
3
3
3
Y
Ð
M
Y
3
3
3
3
3
3
3
3
3
3
1
1
1
1
1 1 1
1
1
1
1
1
1 1
1
O
1
y
1
y
3
z
3
x
1
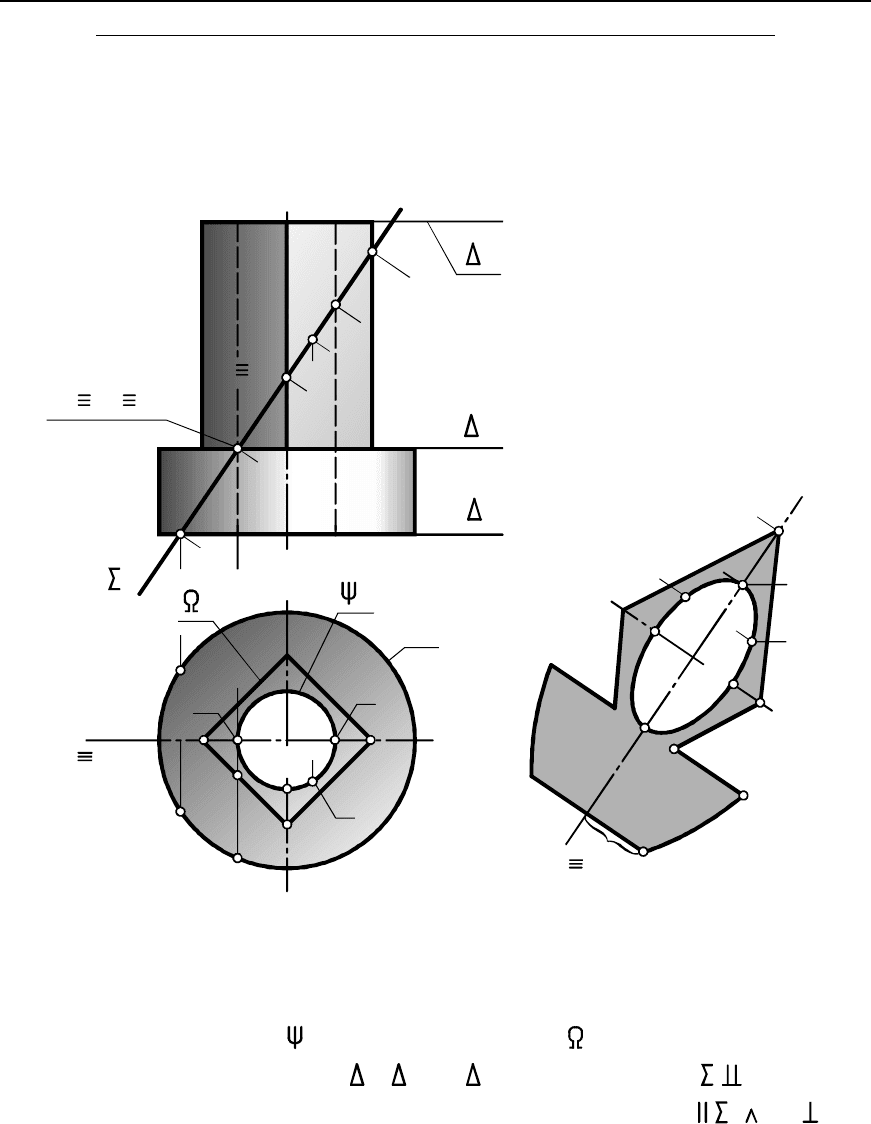
На рис. 10.6 помимо изображений цилиндра с вырезом
обозначены секущие плоскости, проекции контурных образующих
цилиндра, проекции координатных осей связанной с ним системы
координат, выделены и обозначены характерные и некоторые
промежуточные точки линий пересечения.
94
z
1
l
1
1
k
1
1
Особенность задачи: секущие плоскости являются проецирую-
щими на , а цилиндрическая поверхность на . Поэтому извест-
ны две проекции линий пересечения секущих плоскостей и
цилиндрической поверхности: на эти линии проецируются в
окружность - основную проекцию поверхности цилиндра ) ,
k
k(
2
Ï Ï
1
Ï
1
1
1 1
- на с помощью вертикальной линии связи, проведенной из
точки , найдены проекции и (точка видна относитель-
но , а точка не видна);
- из точки провели горизонтальную линию связи,
перпендикулярную ( ) и на ней от оси отложили коорди
наты и , взятые в поле , и получили проекции и
точек и .
Плоскость пересекает цилиндрическую поверхность по дуге
эллипса , который на проецируется в отрезок , на -
в дугу окружности , на - в дугу окружности радиу-
сом, равным радиусу вращения цилиндра, так как плоскость пе-
ресекает ось цилиндра под углом 45 .
M P M P M
P
M P
z
Y Y M P
M P
LKN [K ,L ]
L K N L K N
z
z z -
1
2
2
1 1
2 2
3
Ð
M
Ï
1
3 3
2
Ï
Ô
2
Ï
2 2
Ï
1
1 1 1
3
Ï
3 3 3
Ô
- в параллельные отрезки и .[E ,C ] [F ,D ]
Плоскости и пересекаются по отрезку , и - по
отрезку , и - по отрезку и, наконец, плоскость пере-
секает нижнюю плоскость основания цилиндра по отрезку .
[A,B]
[E,F] [C,D]
[L,N]
Относительно видно только верхнее основание цилиндра.
Относительно всегда видны точки, расположенные перед
контурными образующими и и проецирующиеся на и вl l
левую часть цилиндра, в частности точки , , , , , , , , .A B M P S T K L N
Кроме того, из-за выреза части геометрического тела могут быть
видны точки, расположенные за образующими и , например,l l
Плоскость перпендикулярна оси цилиндра и пересекает его
поверхность по дугам и окружности, которые на и прое-
цируются в отрезки прямых, а на - в дуги окружности. Плоскость
параллельна оси цилиндра и пересекает его поверхность по
отрезкам и образующих прямых, которые на проеци-
руются в отрезок , на - в точки и , на
AE BF
Ã
[ , ] [F ]
[E ,C ] C E D F
E C ,D
[F ,D ]
2
Ï
3
Ï
Ï
1
2
Ï
2 2
Ï
1
1
3
Ï
3
1
1 1
3 3 3
Ã
à Ô
Ï
1
3
Ï
3
4
Ï
1 2
Ï
3
4
95
3
2
2 2
Плоскость пересекает цилиндрическую поверхность по дугам
эллипса и , которые на проецируются в отрезок ,
на - в дуги и окружности , а на - в дуги эллипса
и , которые построены по точкам. Рассмотрим поря-
док построения профильных проекций точек на примере построения
произвольных точек эллипса и :
ATC BSD [A ,C ]
A C B D
M P
B S D A T C
- на взяли произвольную фронтальную проекцию кон-
курирующих точек и ;
M P
M P
2
Ï
2 2
Ï
1
1 1 1 1
1
3
Ï
2 22
3 3
3
3 3 3
}
10.3. Построение натурального вида плоской фигуры,
при пересечении геометрического тела плоскостью
получаемой
5
5
5
6
6
6
2
2
2
4
4
4
3
3
3
1
1
1
7
7
7
8
8
8
Ô
x
21
x
32
1
2
1
3
2 2
2 2
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
1
1
3
3
3
3
3
3
3
Рис. 1 .70
На рис. 10.7 строится натуральный вид сечения сложного
геометрического тела, ограниченного горизонтально проецирующими
цилиндрическими и и призматической поверхностями, гори-
зонтальными плоскостями , и и плоскостью . Задача
свелась к решению 4ОЗПЧ и заданию новой ПП . В
Такие задачи имеют практическое значение, так как при выпол-
нении производственных чертежей иногда возникает необходимость
определить натуральный вид фигуры сечения, получаемой при
рассечении изделия плоскостью, не параллельной ПП.
Ô
1
2
2
Ï
3
Ï
2
Ï
3
Ï
96
9
2
9
3
9
1
точки и . Поэтому части отрезков и , расположенные вE F [E,C] [F,D]
“задней” относительно половине цилиндра, “выглядывают” из-за
дуг эллипса и становятся видимыми.
Отрезки, по которым пересекаются секущие плоскости,
расположены внутри цилиндра и относительно не видны.
3
Ï
3
Ï

качестве оси задавалась ось симметрии фигуры на . При
построении натурального вида сечения симметричные точки не обоз-
начались. Расстояние, используемое для получения проекции ,1 на
рис. 10.7 очкаотмечено фигурной скобкой. Т - промежуточная для9
построения эллипса.
x
21
Ï
1
3
97
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Локтев О.В. Краткий курс начертательной геометрии: Учеб. для
втузов.-3-е изд., испр.-М.: Высш.шк., 1999.-136с.
2. Кузнецов Н.С. Начертательная геометрия: Учеб. для втузов.-2-е
изд., перераб. и доп.-М.: Высш.шк., 1981.-262с.
3. Нартова Л.Г. Начертательная геометрия: Учеб. для вузов / Л.Г.
Нартова, В.И.Якунин.-М.: Дрофа, 2003.-208с.
4. Фролов С.А. Начертательная геометрия: Учеб. для втузов.-2-е
изд., перераб. и доп.-М.: Машиностроение., 1983.-240с.
5. Оганесов О.А. Курс лекций по начертательной геометрии:
Учебное пособие для студентов механических специальностей /
6. Оганесов О.А. Курс лекций по начертательной геометрии:
Учебное пособие для студентов механических специальностей /
8. Оганесов О.А., Кузенева Н.Н. Инженерная графика. Справоч-
ные материалы: Учебное пособие / МАДИ(ГТУ). Часть 1. -М.,
2006. -94с.
МАДИ(ГТУ). Часть 1. -М., 2002.-101с.
МАДИ(ГТУ). Часть 2. -М., 2002.-79с.
7. Оганесов О.А., Кузенева Н.Н. Пересечение поверхностей.
Методическое пособие к выполнению расчетно-графической
работы для студентов механических специальностей
/ МАДИ(ГТУ). -М., 2002. -79с.

98
ОГЛАВЛЕНИЕ
Принятая система сокращений и обозначений. Используемые
типы линий...........................................................................................
Лекция 1. Комплексный чертеж точки ...............................................
Лекция 2. Линия на комплексном чертеже .......................................
Лекция 3. Плоскость ...........................................................................
Лекция 4. Основные метрические задачи. Главные позиционные
задачи для прямой и плоскости .......................................
Лекция 5. Комплексные позиционно-метрические задачи ..............
Лекция 6. Поверхности ......................................................................
Лекция 7. Поверхности (продолжение)..............................................
Лекция 8. Главные позиционные задачи ........................................
Лекция 9. Главные позиционные задачи (продолжение) ...............
Лекция 10. Геометрические тела ......................................................
Список рекомендуемой литературы .................................................
Олег Авакович ОГАНЕСОВ, Виктор Александрович КАЙЛЬ,
Ирина Михайловна РЯБИКОВА, Наталья Николаевна КУЗЕНЕВА
КУРС ЛЕКЦИЙ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Учебное пособие для студентов строительных специальностей
Часть 1
Редактор Ю.К.Фетисова
Тем. план 2009г., п. 17
Подписано в печать 03.02.09 г. Формат 60х84/16
Печать офсетная. Усл.печ.л. 6,1 Уч.-изд.л. 5,0
Тираж 1200 экз. Заказ Цена 50 р.
Ротапринт МАДИ(ГТУ). 125319, Москва, Ленинградский проспект, 64
3
6
22
97
13
30
39
50
59
72
79
86
