Оганесов О.А., Кайль В.А., Рябикова И.М., Кузенева Н.Н. Курс лекций по начертательной геометрии. Часть 1
Подождите немного. Документ загружается.

51
A
1
2
i
A
A
b
1
2
i
a
b
b
a
a
1
2
i
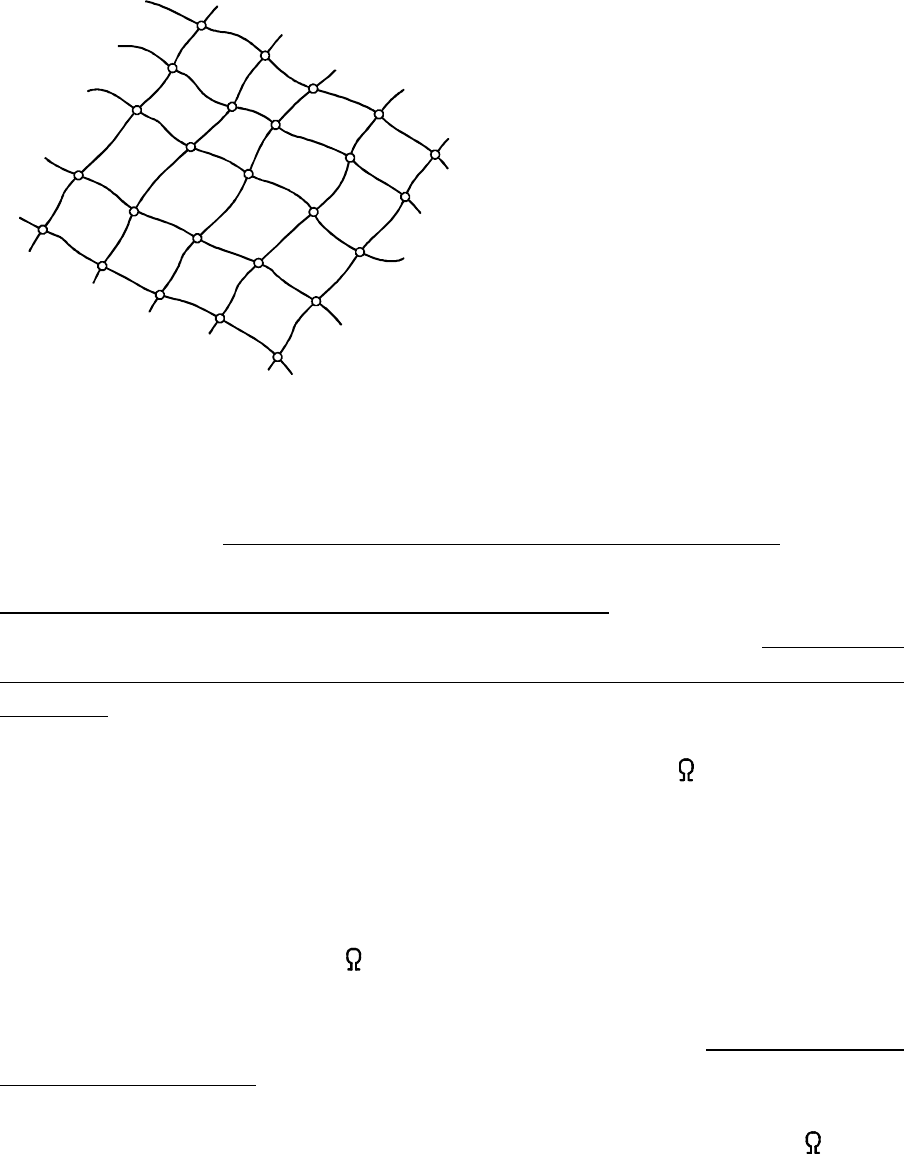
Рис. 6.1
У образующей при образо-
вании поверхности могут непре-
рывно меняться как параметры
положения, так и параметры
формы (сравните , , ..., ).
Различные элементы каркаса
связывают между собой величи-
ной, называемой параметром
каркаса. Каждому конкретному
параметру каркаса соответствует в
пространстве конкретная по фор-
ме и положению линия каркаса
a a a
(образующая). Если параметр каркаса меняется непрерывно, то
каркас поверхности непрерывен, а если дискретно, то каркас
поверхности дискретен.
Различают - каркас,
совокупность всех линий которого покрывает всю поверхность, и
- каркас, полностью
заполняющий часть поверхности, которой принадлежит.
, так как он состоит из бесконечного числа линий, а каждая
линия на чертеже должна иметь определенную толщину. Поэтому на
рис. 6.1 приведен дискретный каркас поверхности , в то время как
образующая перемещается непрерывно.
полный непрерывный каркас поверхности
неполный непрерывный каркас поверхности
Непрерыв-
ный каркас поверхности изобразить на чертеже нельзя принци-
пиально
a
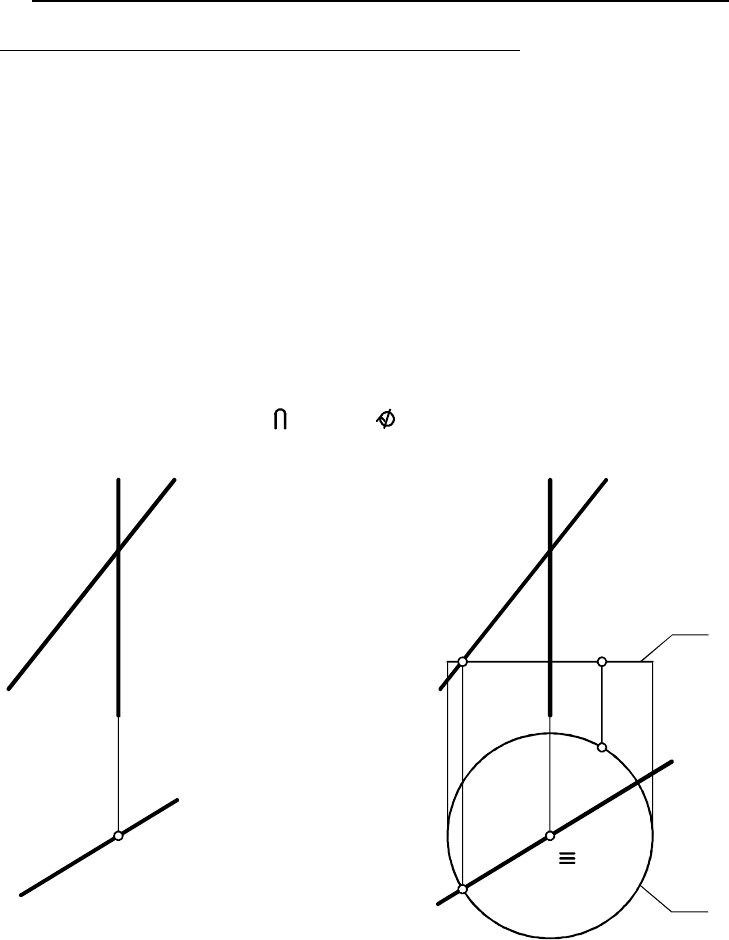
При движении образующей каждая её точка описывает в
пространстве некоторую линию ( , , ..., , ...). Например, линия
на рис. 6.1 образуется перемещением точки . Но тогда можно
считать, что поверхность образуется перемещением образующей
, которая при движении во всех своих положениях пересекает
линии , называемые направляющими линиями (
- линия, которую при перемещении постоянно
пересекает образующая поверхности).
a
b b b b
b A
a a
b направляющая
линия поверхности
Таким образом, на любой кинематической поверхности мож
но выделить два семейства линий - подвижные линии семейства
образующих и неподвижные линии семейства направляющих .
Каждая линия одного семейства пересекает линии другого
семейства, но никакие две линии одного семейства на пересекаются
между собой. В свою очередь, через любую точку поверхности
-
a b
1
2
i
1
i
1 2
i
c
1
c
2
1
M
m
t
j
52
можно провести линию семейства образующих и линию семейства
направляющих. Поменяв местами линии семейств и , считая
линии семейства неподвижными направляющими, по которым
скользят образующие семейства , получим ту же поверхность .
Дискретный каркас поверхности может быть линейным и
состоять из некоторого количества линий семейства или , либо
может формироваться одновременно линиями обоих семейств,
образующими на поверхности сетку (сетчатый каркас).
Всякая поверхность несет на себе сколько угодно каркасов
различных линий, так как образующая поверхности и закон её
образования могут быть самыми разными. Из возможных способов
образования поверхности выбирают такие, которые являются
наиболее простыми и удобными для изображения или решения
конкретной задачи.
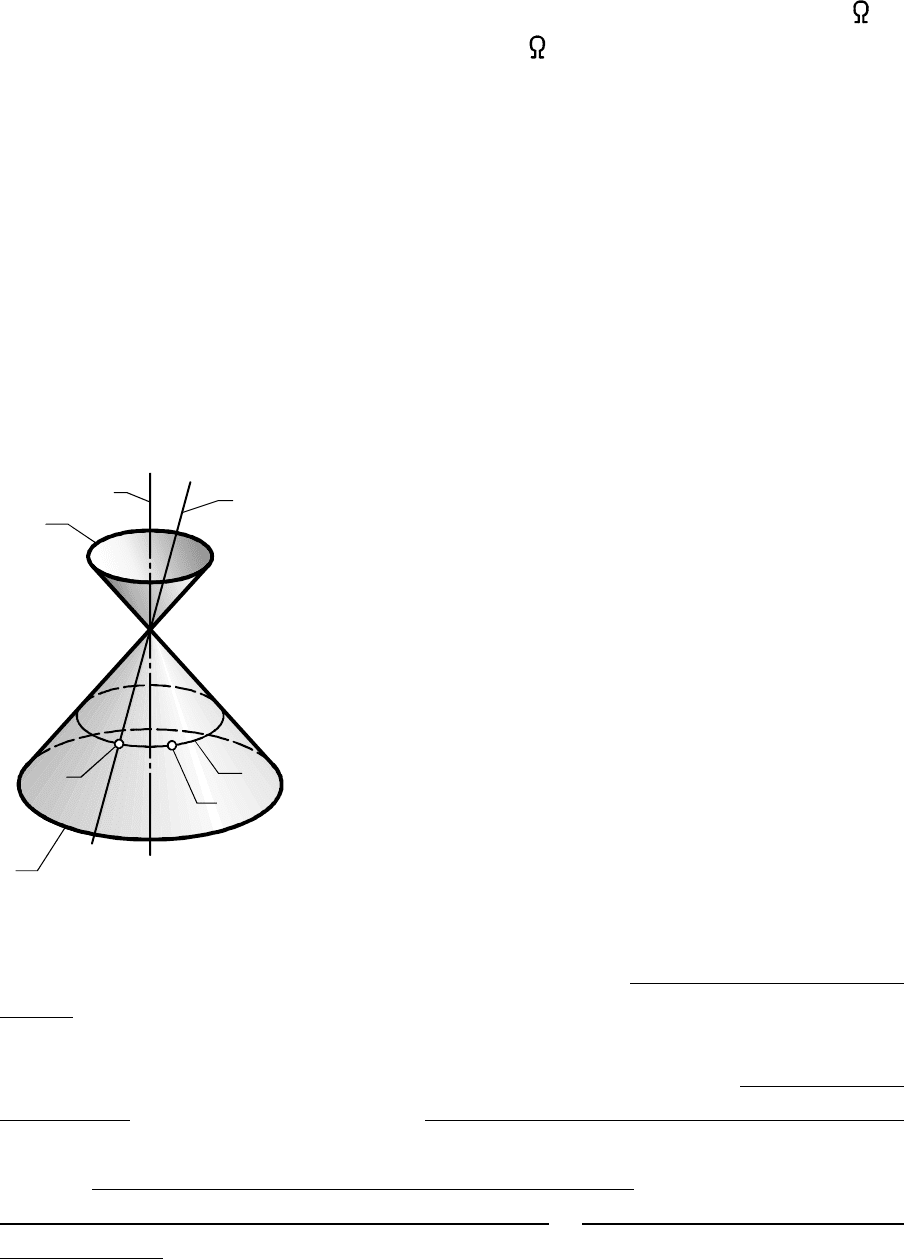
На рис. 6.2 дано наглядное изображение отсека (части) кони-
ческой поверхности вращения, ограниченного окружностями и .
a b
a
b
a b
c c
1
2
Рис. 6.2
Эта поверхность может быть образована
вращением прямой вокруг пересекающей её
оси вращения ; перемещением окружности
переменного радиуса, плоскость которой
перпендикулярна оси , а центр находится на
ней (к семейству этой образующей относятся
окружности и ); перемещением эллипса,
гиперболы или параболы по определенным
законам, а также перемещением любой
линии, расположенной на поверхности.
Окружность приведена на рис. 6.2
для иллюстрации решения основной пози-
t
j
j
c c
m
1
2
ционной задачи - построения произвольной
точки на поверхности.M
В данном пособии будут рассмотрены
- плоскость, цилиндрическая, призматическая, коническая и
пирамидальная поверхности, а также поверхности Каталана
(цилиндроид, коноид и гиперболический параболоид);
, к которым отнесем
(цилиндрическую, коническую, однополостный гиперболоид враще-
ния); (только торы) и
;
- геликоиды.
линейчатые поверх-
ности
поверхности
вращения линейчатые поверхности вращения
циклические поверхности вращения
поверхность вращения общего вида линейчатые винтовые
поверхности
53
Тот факт, что одна и та же поверхность может быть образована
различным образом, делает классификацию поверхностей весьма
условной. Так, упомянутая коническая поверхность вращения может
быть отнесена и к линейчатым поверхностям, и к циклическим
поверхностям (поверхностям, образованным перемещением
окружности), и к поверхностям вращения.
6.2. Определитель поверхности
при выполнении
следующих условий: образующая и направляющие линии геометри-
чески определены и заданы, а образование поверхности подчинено
определенному закону. У закономерных поверхностей информация
об образующей, изменении её формы при перемещении, взаимо-
расположении и форме направляющих и условиях перемещения
образующей выражена аналитически или четко сформулирована
словесно. Отсутствие хотя бы одного из указанных условий делает
. Обычно информация о незакономер
ных поверхностях задается графически или в словесной форме.
Поверхность считается закономерной
поверхность незакономерной -
Согласно кинематическому способу образования поверхность,
рассматриваемая как множество всех положений двигающейся
образующей, определена, если в любой момент движения
образующей известны её положение и форма. Это обстоятельство
приводит к понятию определителя поверхности.
- это совокупность геометрических образов и условий,
позволяющих реализовать заданный закон образования поверхнос-
ти (строить её образующую в любой момент перемещения) .
Определитель
поверхности
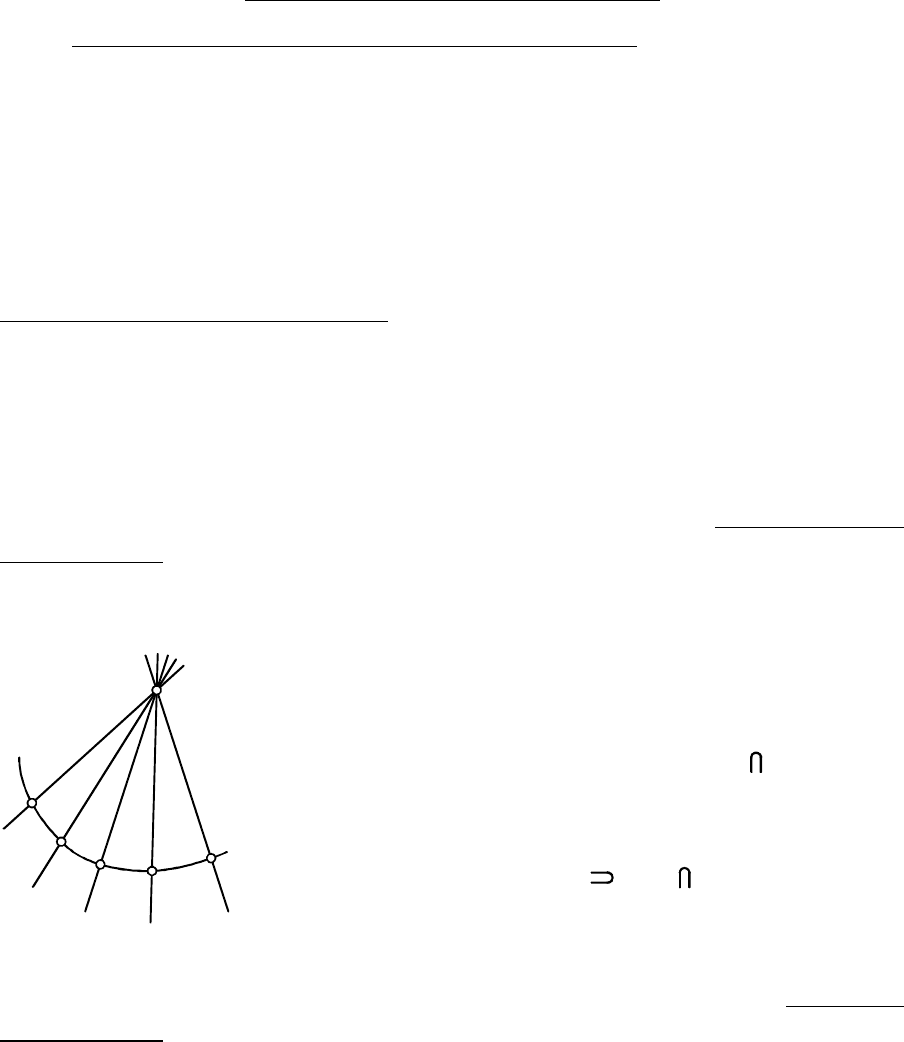
Так, определителем конической поверхнос-
ти вращения при образовании её вращением
прямой вокруг оси является образующая и
ось , а также уточняющее условие .
Коническая поверхность общего вида
может быть образована перемещением прямой
по закону образования , , где - точка,
- кривая линия (рис. 6.3). Определителем
поверхности являются и .
t j t
j t j
Ô
l
l T l a T
a
Ô T a
l
1
2
i
T
l
l
Рис. 6.3
i i
Часто для закономерных поверхностей используют
- специальным образом организованную знаковую
запись, в которой указаны: вид образующей, определитель и закон
образования поверхности. Формула поверхности имеет структуру:
формулу
поверхности
a
54
Ô{ ... ( ... ) ( ... ) }.
обозначение
поверхности
образующая
поверхности
определитель
поверхности
закон образования
поверхности
Примеры формул: - коническая поверх-
ность коническая поверхность
.
вращения; -
общего вида
{l(T,a)
(
l T, l a)}
i
i
Ô{ (t,j; t j)(t =t j)}
i
6.3. Задание поверхности на чертеже
Поверхности в отличие от точек и линий в общем случае не
задаются на чертеже своими проекциями - проекциями всех своих
точек. Дело в том, что чертеж в общем определении есть некая
точек и линий, изображенных на плоскости.
Но проекция поверхности представляет собой совокупность
проекций всех её точек, являющуюся в общем случае бесконечным
множеством точек, которое обычно на чертеже не задаётся
непосредственно из-за бессмысленности этого.
Существует : поверхность
задана на чертеже, если он содержит такие её элементы, которые
позволяют точно или с достаточной степенью приближенности ре-
шать для поверхности основную позиционную задачу - однозначно
строить любую точку поверхности и решать вопрос о принад-
лежности поверхности .
В свою очередь, существует
: точка принадлежит поверхности, если она принад-
лежит одной из линий поверхности; сначала на поверхности строят
линию, а затем на ней задают точку.
Таким образом,
. Тогда для того, чтобы задать поверхность,
достаточно задать на чертеже один из её полных непрерывных
каркасов, который полностью покрывает поверхность и целиком ей
принадлежит. В этом случае через каждую точку поверхности
проходит линия каркаса, что позволяет строить любую точку
поверхности. Принципиально каркасами можно представлять
любые поверхности, силовые поля, закономерные процессы и др.
Однако уже отмечалось, что полный непрерывный каркас
конечная совокупность
критерий заданности поверхности
условие принадлежности точки
поверхности
чертеж поверхности должен быть таким, чтобы
на нем можно было выделять и строить линии и точки, принадле-
жащие поверхности
заданной точки данной
t
55
задать графически нельзя. Поэтому для задания поверхности на
чертеже используют другие способы.
6.3.1. Задание поверхности элементарным чертежом
называют двухкартин-
ный чертеж её определителя.
Проекции элементов определителя являются чертежом
поверхности только при условии, что закон её образования задан.
Зная определитель и закон образования поверхности, принципиаль-
но можно строить проекции образующей линии в любой момент её
движения и, следовательно, реализовать критерий заданности
поверхности, строя на чертеже проекции любой её точки. Элемен-
тарный чертеж поверхности - обратимый и метрически определен-
ный чертеж, позволяющий решать любую задачу с поверхностью.
На рис. 6.4 задан элементарный чертеж конической поверх-
ности вращения (заданы и ). Покажем, как
Элементарным чертежом поверхности
Ô{t(t,t,j;t j)(t =t j)} t j
i
t
t
1
2
j
j
2
1
Рис. 6.4
t
t
1
2
j
j
2
1
Рис. 6.5
m
2
m
1
C
1
m
M
M
2
1
1
1
1
2
на элементарном чертеже решается ОПЗ, построив проекции произ-
вольной точки конической поверхности вращения (рис. 6.5).M
Нетрудно представить, что плоскости, перпендикулярные оси
вращения, пересекают коническую поверхность вращения по окруж-
ностям. Эти окружности, принадлежащие рассматриваемой поверх-
ности, удобно использовать для построения точек на ней (подробнее
см. раздел 7.2.1). Поэтому точку на конической поверхности задают
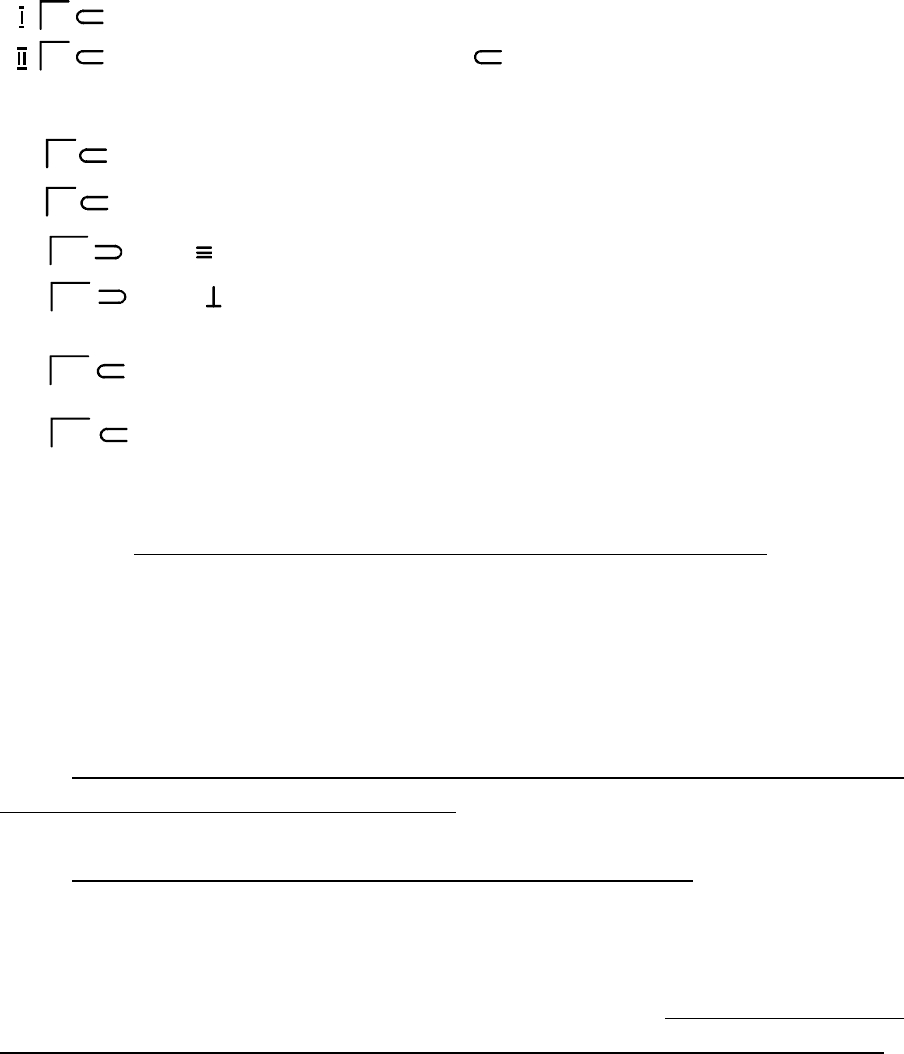
56
1. 1
1
2
3. m C,
11
5.
1
1
6.
2. 1
t
2
4. ,
2 2 2
1
t
2
}
- на проекциях и образующей берут
и произвольной точки .
t t t
1 1 1
проек-
ции
1 2
1
m
1
j
1
- через точку из центра проводят окружность .1 j m
1 1 1
- через точку перпендикулярно проводят1 j
отрезок , в который проецируется наm Ï окружность .m
m 1
2
m j
2 2
2 2
M
m
M m
2
- на окружности берут проекцию произвольнойm M
точки .M
1 1
- на отрезке находят проекцию точки .m M M
2 2
.
.
m
M
Ô
m
- строят произвольную окружность на поверхности .
Ô
- произвольную точку берут на окружности .
m
M
Ô
ГА построения проекций точки (рис. 6.5):M
Заметим, что задача имеет бесконечное множество решений.
6.3.2. Задание поверхности основным чертежом
Элементарный чертеж поверхности - самый простой по испол-
нению её чертеж. Но он обладает плохой наглядностью: по нему
достаточно сложно представить форму заданной поверхности,
особенно начинающим изучать НГ. Более наглядным является
основной чертеж поверхности.
называют элементарный чертеж
поверхности, дополненный проекциями контурных линий.
относят: линии
точек касания поверхности проецирующими лучами; линии обреза
или границы поверхности; ребра многогранных поверхностей
(призматических и пирамидальных); линии пересечения поверх-
ностей (для составных поверхностей) и т. д.
.
Для гладкой поверхности линия точек касания поверхности
проецирующими лучами является линией видимости, лежащей на
поверхности и отделяющей её видимую часть от невидимой.
Линия видимости образована множеством точек касания поверх-
ности проецирующими относительно ПП лучами (рис. 6.6).
Основным чертежом поверхности или её отсека (отсек
поверхности - часть поверхности)
К контурным линиям поверхности и её отсека
Контурные линии
принадлежат самой поверхности, а на чертеже даются их проекции
g
Ô Ï s
i
n
с помощью окружности (рис. 6.2 и 6.5), проецирующуюся на
плоскость в окружность, а на плоскость - в отрезок прямой.
Задача решалась согласно ПА:
m
Ï
1 2
Ï
1 2
57
Из множества контурных
линий выделяют
- это контурные
линии или их части, все точки
которых обладают свойством:
проецирующий луч, проведен-
ный через точку линии, не имеет
больше общих точек с поверх-
ностью (исключение - конкури-
рующие контурные линии).
крайние кон-
турные линии
Линия видимости является
крайней контурной линией гладкой
поверхности (линия на рис. 6.6) или
составной частью крайних контурных
линий поверхности. Какие контурные
линии поверхности являются крайни-
ми, а также положение и форма
линии видимости зависит от направ-
ления взгляда (проецирования).
g
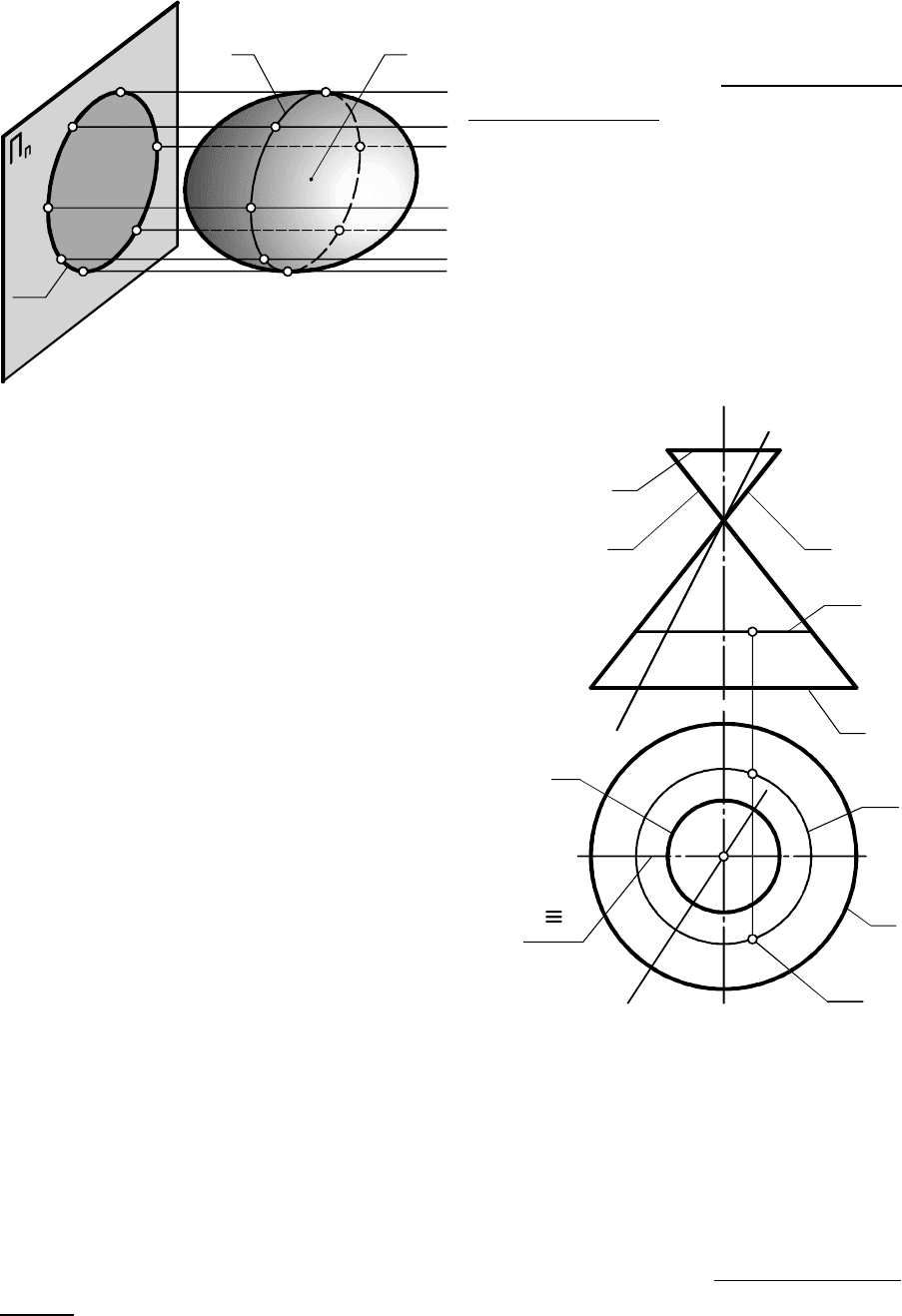
На рис. 6.7 приведен основной
чертеж отсека конической поверх-
ности вращения,
.
Контурными линиями отсека относи-
тельно являются линии , , отно-
сительно - линии , , , , где
и - линии точек касания поверх-
ности проецирующими лучами,
наглядное изобра-
жение которого показано на рис. 6.2
c c
c c g g
g g
t
t
1
2
j
j
2
1
m
2
m
1
M
M
2
1
M
1
c
2
2
c
2
1
1
c
1
1
g
1
g
1
1
2
Рис. 6.7
c
2
1
g
1
g
2 2
2
перпендикулярными . Л - крайние контурные
относительно ( и - конкурирующие линии: их видимые перед-
ние половины на конкурируют с невидимыми задними), а линия
- крайняя контурная относительно .
инии , , ,c c g g
c c
c
Крайние контурные линии всегда видны.
Проекции крайних контурных линий образуют
. Очерк поверхности - замкнутая линия на чертеже.
Поверхность рассматривается как тончайшая непрозрачная
оболочка.
очерк поверх-
ности
Ï
1
2
Ï
1 2
1
1
2
2
1 2
2
Ï
2
Ï
1 2
2
Ï
2
Ï
1
1 12 2
g
n
g
s
i
Ô
Рис. 6.6
58
Точки на поверхности строят одинаково, не зависимо от того,
задана она основным чертежом или элементарным. На рис. 6.7
проекцией была задана точка . Проекция точки строи-
лась с помощью окружности . Оказалось, что проекцией на
поверхности заданы две точки, одна из которых определяется
проекциями и , а вторая - и . Относительно видимой
является первая точка, расположенная в передней части
поверхности.
Элементарным и основным чертежами обычно задают
закономерные поверхности.
M M Ô M
m M
M M M M Ï
M
2
2
1
2
1
1
2
2
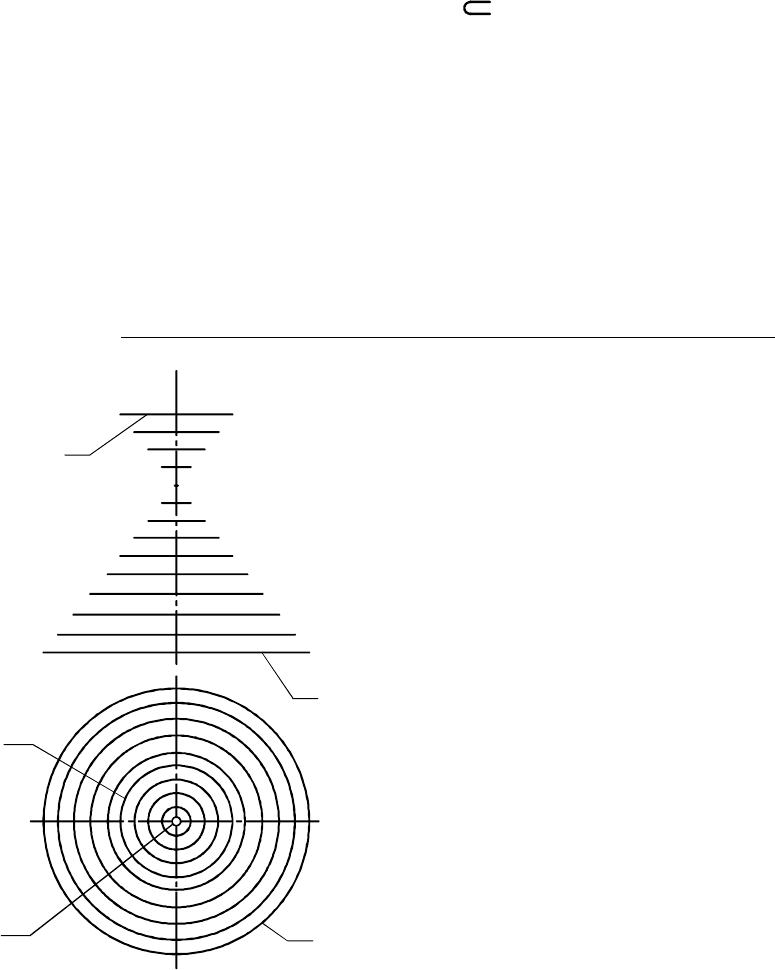
6.3.3. Задание поверхности дискретным каркасом
На рис. 6.8 тот же отсек конической
поверхности вращения задан дискретным
каркасом, элементами которого являются
концентрические окружности , , ...,
задаваемые на чертеже своими проек-
циями.
Обычно закономерные поверхности
таким способом не задаются, поскольку
поверхность, задаваемая дискретным кар-
касом, не вполне определена: поверхности
могут иметь один и тот же дискретный
каркас, но несколько отличаться друг от
друга, а точки таких поверхностей, не
лежащие на линиях каркаса, строятся
приближенно.
А вот незакономерные поверхности,
называемые иногда каркасными, графичес-
кими или нерегулярными, можно задать на
чертеже только дискретным каркасом -
c c
j
2
c
2
2
c
2
1
c
1
1
Рис. 6.8
c
2
1
j
1
1
2
некоторым числом принадлежащих им линий. Часто элементами
каркаса являются плоские кривые, расположенные в плоскостях,
параллельных друг другу. Для более точного задания нерегулярной
поверхности, её каркас задают двумя семействами линий, образую-
щих на поверхности сеть.
Примерами поверхностей, задаваемых каркасами, являются
поверхности корпусов судов, летательных аппаратов, автомобилей
и т. д. К каркасным поверхностям относятся и топографические
1

59
поверхности, раскрывающие рельеф земной коры и рассматривае-
мые во второй части курса.
Часто при изготовлении различных сооружений
некоторые поверхности . Например, при постройке
крыши сначала выполняют её каркас - обрешетку, которую затем
покрывают кровельным материалом.
дискретным
каркасом задают
Л Е К Ц И Я 7
7.1. Линейчатые поверхности
ПОВЕРХНОСТИ (продолжение)
К линейчатым поверхностям относят поверхности, которые
могут быть образованы перемещением прямой линии.
Точку на линейчатой поверхности удобно строить с по-
мощью её образующих - прямых линий согласно ПА:
M
l
Ô
.
.
l - по закону образования поверхности строят её образующую.
M
Ô
l - точку поверхности берут (ищут) на этой образующей.
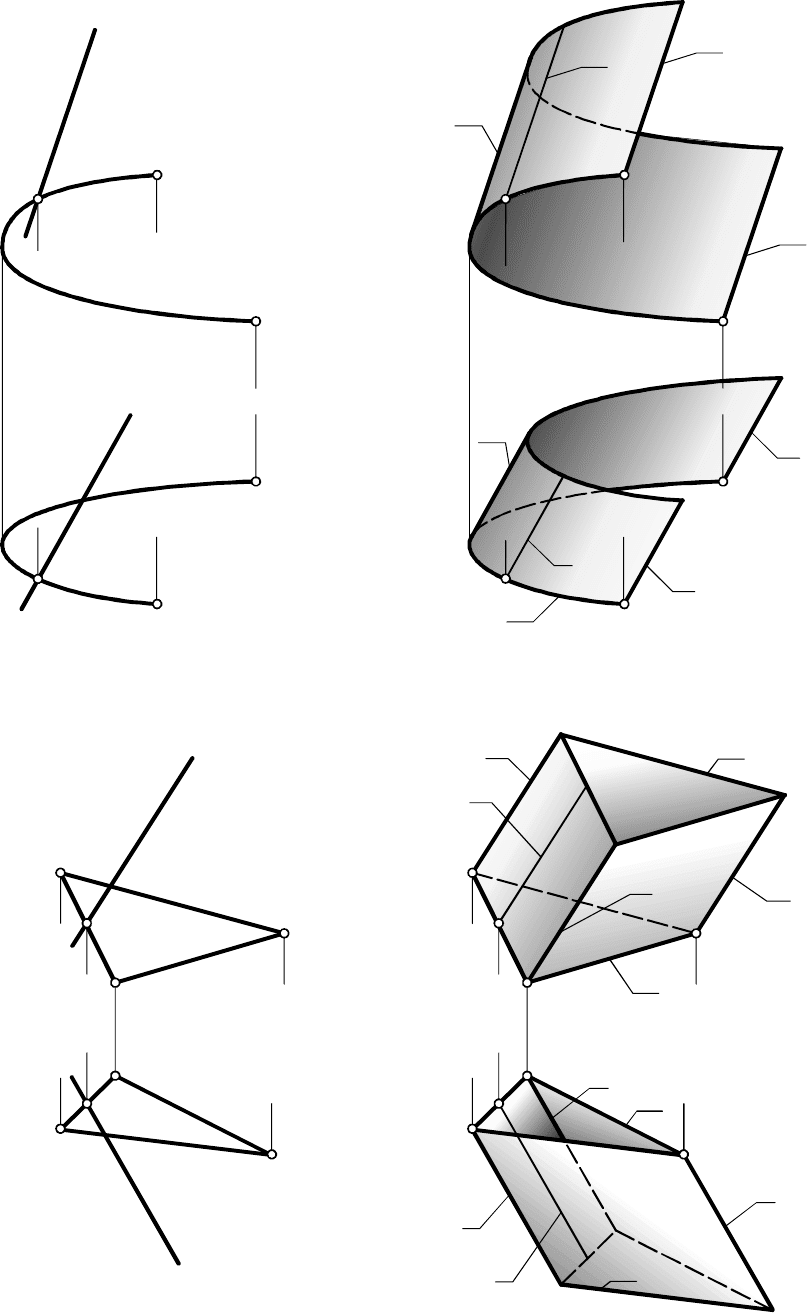
7.1.2. Цилиндрическая и призматическая поверхности
Формула цилиндрической поверхности имеет вид:
.{ l (a, l)(l a, l l)}
Когда - кривая линия, формула представляет цилиндричес-
кую поверхность; когда - ломаная линия, - призматическую ( в
обоих случаях направляющая и образующая не лежат в од-
ной плоскости); когда - прямая линия, формула представляет
плоскость.
a
a
a l
a
На рис. 7.1 приведен элементарный чертеж цилиндрической
поверхности общего вида (изображены только проекции элементов
её определителя), а на рис. 7.2 - основной чертеж отсека той же
поверхности. Линии , , и - линии обреза, а линия - линия,
по которой поверхности касаются проецирующие лучи, перпендику-
лярные и , и .
a a l l g
Аналогично на рис. 7.3 приведен элементарный чертеж
призматической поверхности, на рис. 7.4 - основной чертеж её
отсека. Контурными линиями отсека являются ломаные и (гра-
ницы отсека) и ребра , , .
a a
l l l
i i
1
2
Ï
1 2
Ï
1
1 2 3
1
Ô
7.1.1. Общие замечания
A
1
B
1
a
1
60
a
a
1
2
l
2
l
1
Рис. 7.1
A
1
D
B
2
B
A
1
2
l
l
2
1
D
1
2
Рис. 7.3
a
a
1
2
l
2
l
1
a
2
1
a
1
1
l
1
l
2
1
l
2
2
l
1
2
1
g
2
g
1
Рис. 7.2
D
B
2
A
2
l
2
D
1
2
l
2
l
2
1
a
1
l
l
1
1
1
l
1
2
l
1
3
l
2
3
1
a
2
a
2
1
Рис. 7.4
2
