Оганесов О.А., Кайль В.А., Рябикова И.М., Кузенева Н.Н. Курс лекций по начертательной геометрии. Часть 1
Подождите немного. Документ загружается.

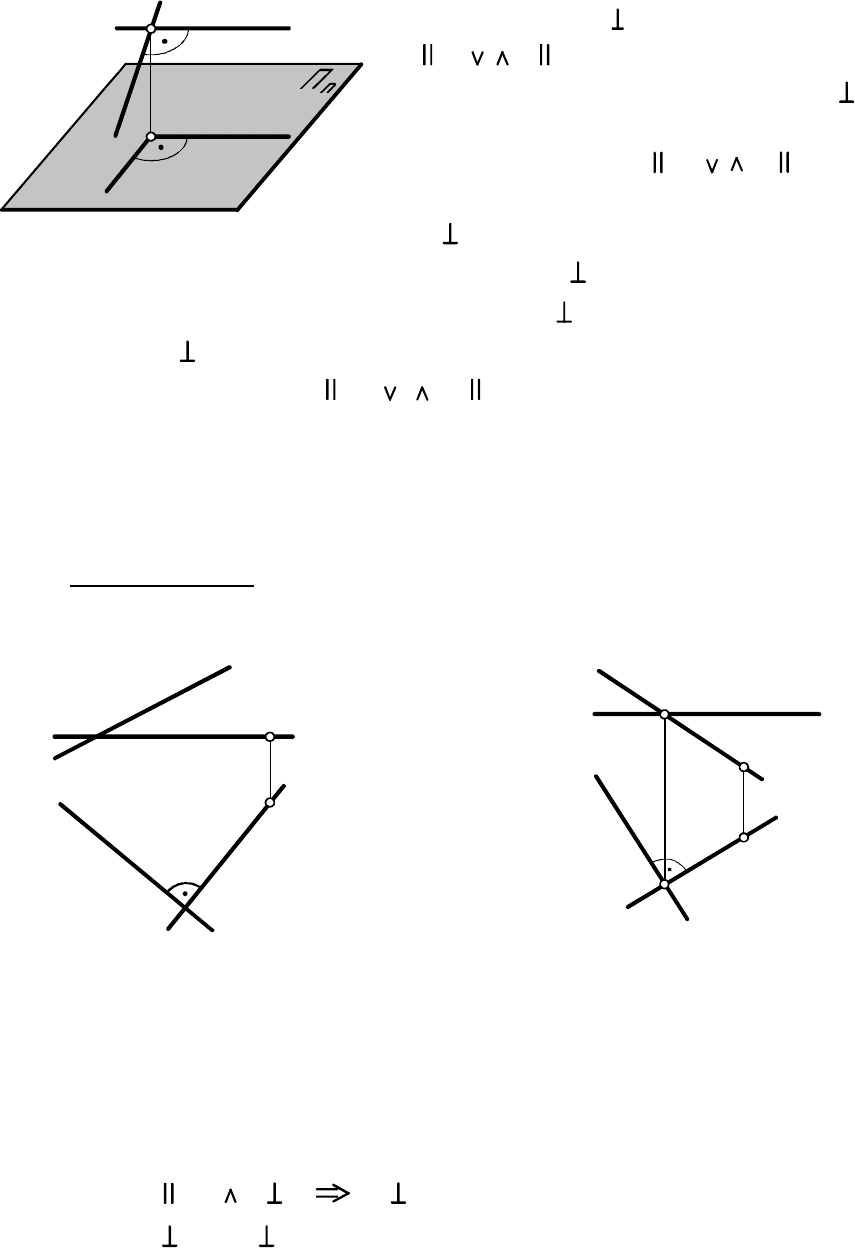
1. Если хотя бы одна из сторон
прямого угла ( ) параллельна ПП
( ( ) ), то прямой угол проеци-
руется на эту ПП в прямой угол ( ).
2. Если хотя бы одна из прямых
параллельна ПП ( ), а их
проекции на эту ПП перпендикулярны
( ), то данные прямые
a b
a b
a b
( )
перпен-
дикулярны ( ).a b
n n
3. Если перпендикулярны ( ) и перпендикулярны их
проекции ( ) на ПП ( ), то хотя бы одна из данных прямых
параллельна этой ПП ( ( ) ).
Через точку, не лежащую на прямой, можно провести
бесконечное множество прямых перпендикулярно данной прямой,
но только одна из этих прямых пересекает данную, а остальные
скрещиваются с ней.
прямые a b
a b
a b
n n
n n
Ï
n
Ï
n
Ï
n
проекций ( ) и проекцию прямого угла на эту ПП, то можноÏ
сформулировать три теоремы:
n
h
h
h
h
M
M
M
M
t
t
Рис. 2.18 Рис. 2.19
ПРИМЕР 2.1. Заданы прямая ( , ) и точка ( , ).
Через точку провести прямую перпендикулярно прямой (рис. 2.18).
a a a M M M
M a
1
2
1 2
2
2
2
2
2
2
2
a
a
1
1
1
1
1
1
K
K
1
Если дана прямая общего положения, то без дополнительных
построений, используя только теорему о проецировании прямого
угла, через точку можно провести лишь две прямые перпендику
лярно данной прямой, причем в общем случае обе они будут
скрещиваться с .
-
ней Одна из этих двух прямых - горизонталь на
рис. 2.18 ( ), а второй прямой могла бы быть
фронталь ( ).
h
h Ï h a h a
f a f a
1
1
1
2 2
a
Ï
n
b
Ï
n
a
Ï
n
b
Ï
n
21
A
A
b
b
Рис. 2.17
n
n
a
a
n
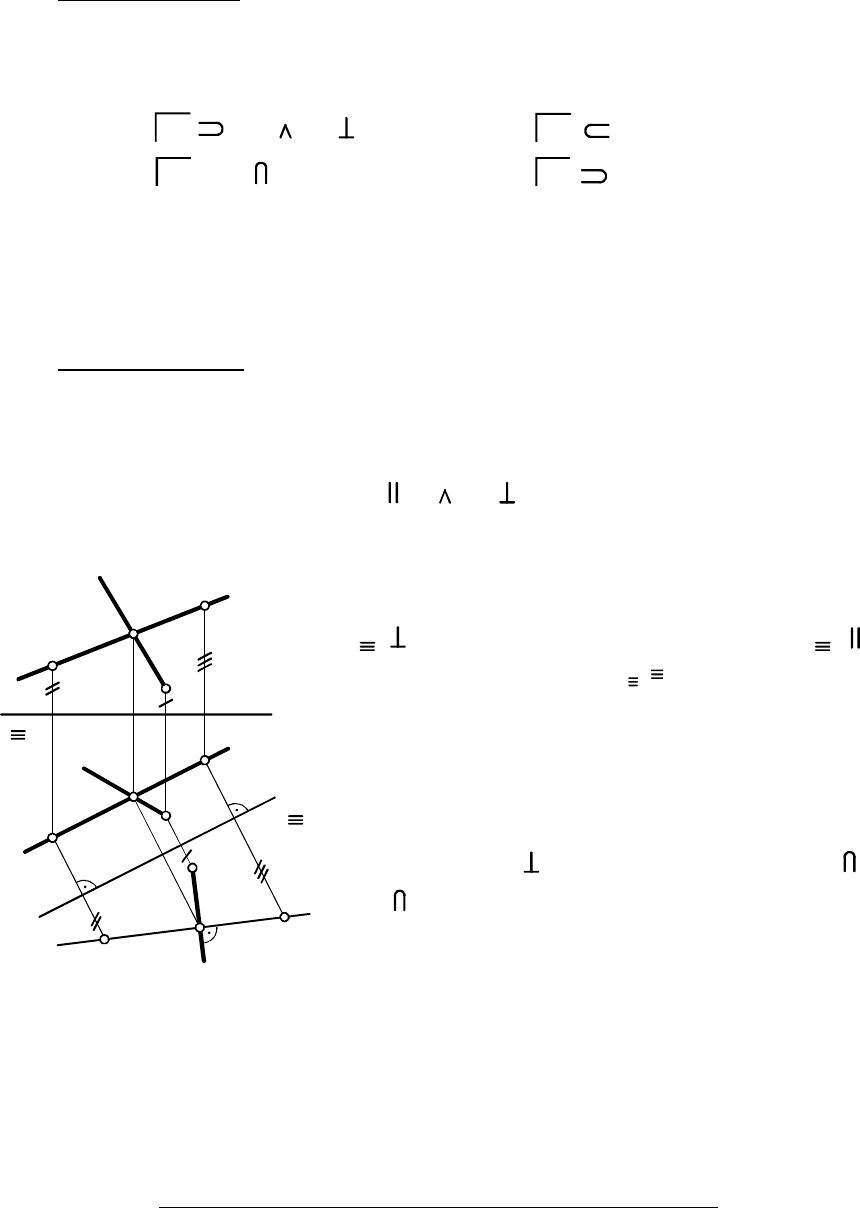
1. Задали новую ПП и перевели прямую в
положение прямой уровня. Для построения проекции на прямой
Ï a Ï a
a a
взяли произвольные точки и
,
A A A
B B B
( , )
( , ) нанесли старую ось проекций
( , и новую ось проекций
(можно было задать ), нашли проек-
ции точек , , и через и прове-
ли прямую .
M M
a
A B M A B
a
)
ПРИМЕР 2.2. Даны точка ( ) и горизонталь ).
Построить прямую , проходящую через точку и пересекающую
под прямым углом (рис. 2.19).
Порядок построения на рис. 2.19 был следующим:
M M M h h h
t M h
, ( ,
1 2 1 2
1. t M t h .
4. t M , .
1
3. K h .
2 2
1 1 1
2. .
=
K
1
h
1
t
1
2 2 2
K
В примере через точку без дополнительных построений
можно было провести любую из бесконечного множества прямых,
перпендикулярных горизонтали, причем горизонтальные проекции
всех перпендикуляров совпадали бы с .
M
t
1
ПРИМЕР 2.3. Даны прямая ( , ) и точка ( , ).
Через точку провести прямую , пересекающую под прямым
a a a M M M
M l a
углом (рис. 2.20).
Последовательность выполнения примера:
1 2
1 2
3
1
3
1 2
1 2
l
2
x
21
B
2
2
1
A
2
M
2
Ê
2
x
31
a
1
2
x
31
1
x
21
l
3
3
3
3
3
B
1
1
3
M
1
A
1
Ê
1
2. В поле применили теорему о
проецировании прямого угла: через точку
провели и нашли точку
( - точка пересечения прямых и ).
Проекции и определялись точками ,
и , соответственно.
Ï
M l a K =l a
K=l a l a
l l M
K M K
x
31
3
M
a
1
3
B
3
Ê
3
3 3 3 3 3 3
A
3
a
l
3
3
2 1
1
Рис. 2.20
1 2 2
ПЛОСКОСТЬ
Плоскость относят к линейчатым поверхностям, которые могут
образовываться при перемещении в пространстве прямой линии.
Подробнее вопросы образования и задания поверхностей рассмотрены
3.1. Задание плоскости общего положения
Л Е К Ц И Я 3
a
22
3
Ï
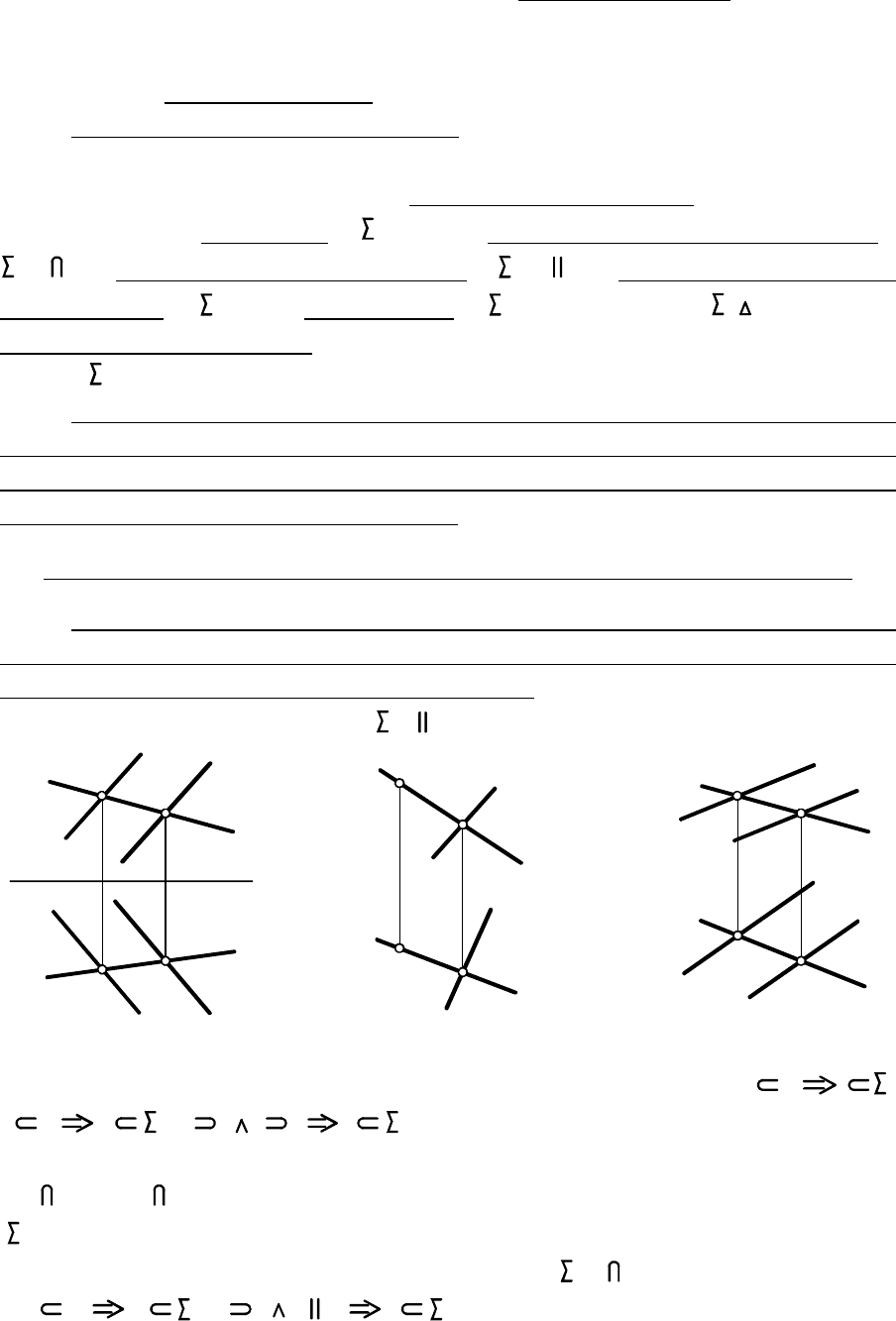
в лекции 6. Здесь отметим только, что плоскость и
другие поверхности не задаются на чертеже, как точки и линии,
своими проекциями (проекциями всех своих точек), представляю-
щими собой бесконечное множество точек.
в общем случае
в общем случае
- это плоскость, не
и, следовательно, не . Из элемен-
тарной геометрии известно, что не лежащие на
одной прямой - ( ); -
Плоскость общего положения
плоскость определяют
три точки две пересекающиеся прямые
перпендику-
лярная параллельная ни одной из ПП
A B D, ,
( ); - ( );
- ( , ); - ( , , , ) или ( ), реже
(в скобках после обозначающей плоскость
a b a b
a A A B D A ABD
две параллельные прямые прямая и не лежащая
на ней точка треугольник
другая плоская фигура
буквы условно указан способ задания плоскости).
.
Если плоскость задана не удобно для решения задачи, то надо
перейти к другому способу её задания. При этом от способа задания
плоскости тремя точками всегда переходят к какому-нибудь другому
способу, чаще всего треугольником
3.2. Построение прямой линии в плоскости общего положения
.
Прямая принадлежит плоскости, если она проходит через две
точки плоскости или если она проходит через точку плоскости
параллельно одной из прямых плоскости
На рис. 3.1 в плоскости ( ) построена произвольная прямая ,a b l
1
1
2
2
d
d
2
1
1
1
2
2
2
l
l
1
a
2
a
1
x
1
1
2
1
2
l
l
1
a
2
a
1
1
1
d
d
2
1
1
2
2
t
t
1
a
2
a
1
A
1
A
2
Рис. 3.1 Рис. 3.2 Рис. 3.3
проходящая через точку прямой и точку прямой : ;
; . Обычно одну из проекций или
проводят произвольно, а вторую строят, используя проекции точек
и . Если плоскость задана прямой и точкой (плоскость
( ) на рис. 3.2), то прямую целесообразно проводить через
данную точку ( ). На рис. 3.3 в плоскости ( ) построена прямая
: ;
1 a 2 b 1 a 1
2 b 2 l 1 l 2 l l l
1=l a 2=l b
a A l
A a b
t 1 a 1 t 1 t b t
,
.
1 2
23
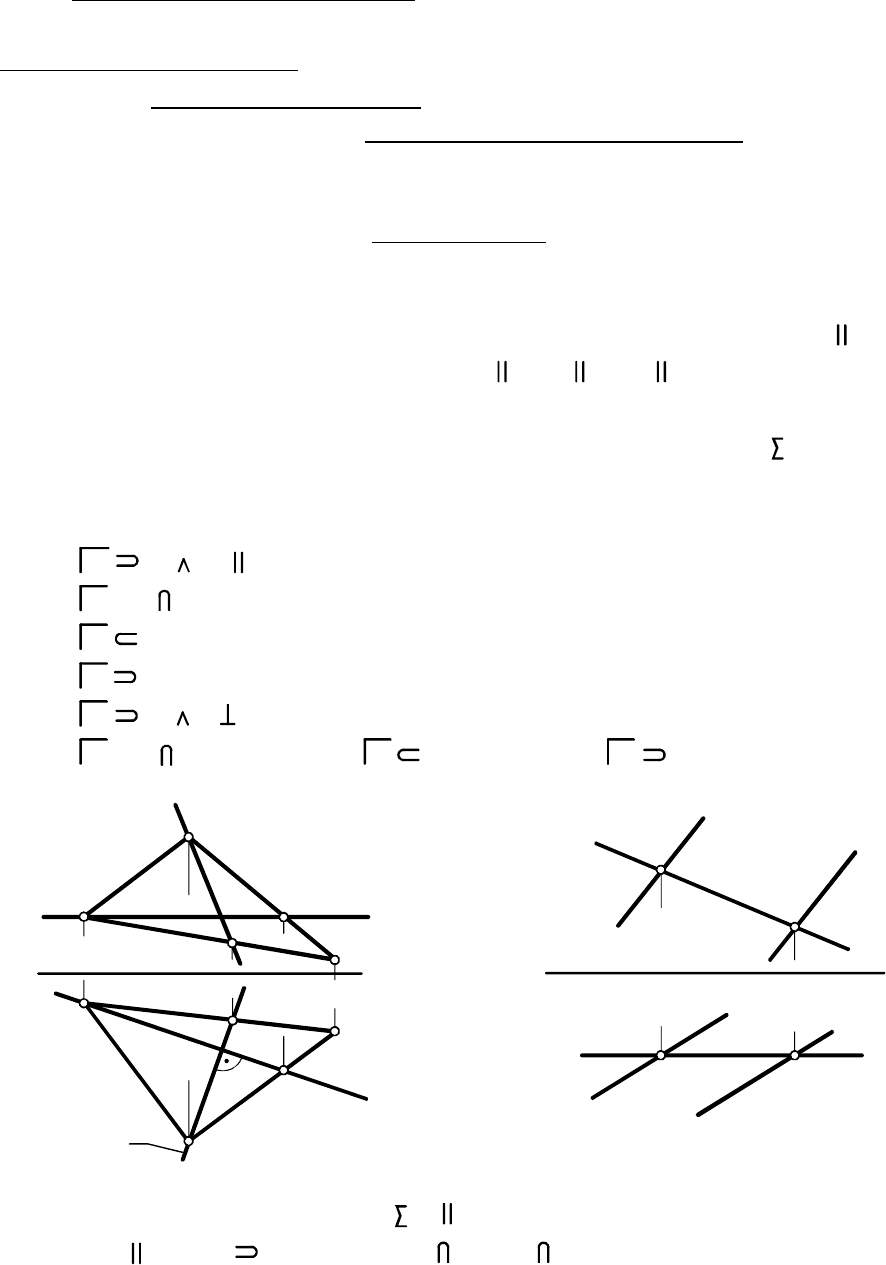
Горизонталь плоскости начинают строить с проекции , а
фронталь плоскости - с проекции ( , ). Проекции
и строят по точкам, используя проекции и и условие при-
надлежности и плоскости. На рис. 3.4 в плоск ти ( , , , )
построены горизонталь и линия ската , проходящие через
вершины и соответственно:
h h x
f f x h Ï f Ï h
f h f
h f A B D A
h t
A B
ос
- это горизонталь плоскости, фрон-
таль плоскости и линии наклона плоскости к плоскостям проекций.
- прямая, параллельная и принадлежащая
плоскости. - прямая, параллельная и при-
надлежащая плоскости.
Главные линии плоскости
Горизонталь плоскости
Фронталь плоскости
Ï
Ï
Линии наклона плоскости
линией ската
- прямые
плоскости, перпендикулярные к линиям уровня плоскости. Линию
наклона плоскости к плоскости , перпендикулярную горизонтали
плоскости, называют также . Линия наклона плоскости
образует с соответствующей плоскостью проекций угол, по величине
равный углу наклона плоскости к этой ПП.
1
2
2
1 1
2
1
2 2 1
B
A
A
D
D
h
h
t
t
1
1
2
2
x
1
1
2
2
b
f
f
1
2
x
2
2
2
2
2
2
1
1
1
1
1
a
2
a
1
1
1
1
1
2
2
2
b
2
Рис. 3.4 Рис. 3.5
1. - через параллельно оси провели .
2. - нашли точку пересечения и , .
3. - нашли из условия её принадлежности , .
4. провели через точки и .
5. - через перпендикулярно провели .
6. . .
h A h x A x h
1 =h [B ,D ] 1 h [B D ]
1 [B ,D ] 1 [B D ]
A ,1 h A 1
t B t h B h t
2 =t [A ,D ] 2 [A ,D ] t B ,2
-
7. 8. .
h
2
1
2 2 2
2 2 2
1 1
1 1 1
2 2
2
2 2 2
1 1 1
1 1 1
1 1 1 1 1 1 1
1 1 1 1
2 2 2 2 2 2
На рис. 3.5 в плоскости ( ) построена произвольная фрон-
таль : , а где
Все горизонтали плоскости параллельны друг другу. Это же от-
носится к фронталям плоскости и линиям наклона плоскости к ПП.
a b
f f x f 1 ,2 1=f a 2=f b, , .
1 2 2 2
24
Ï
1
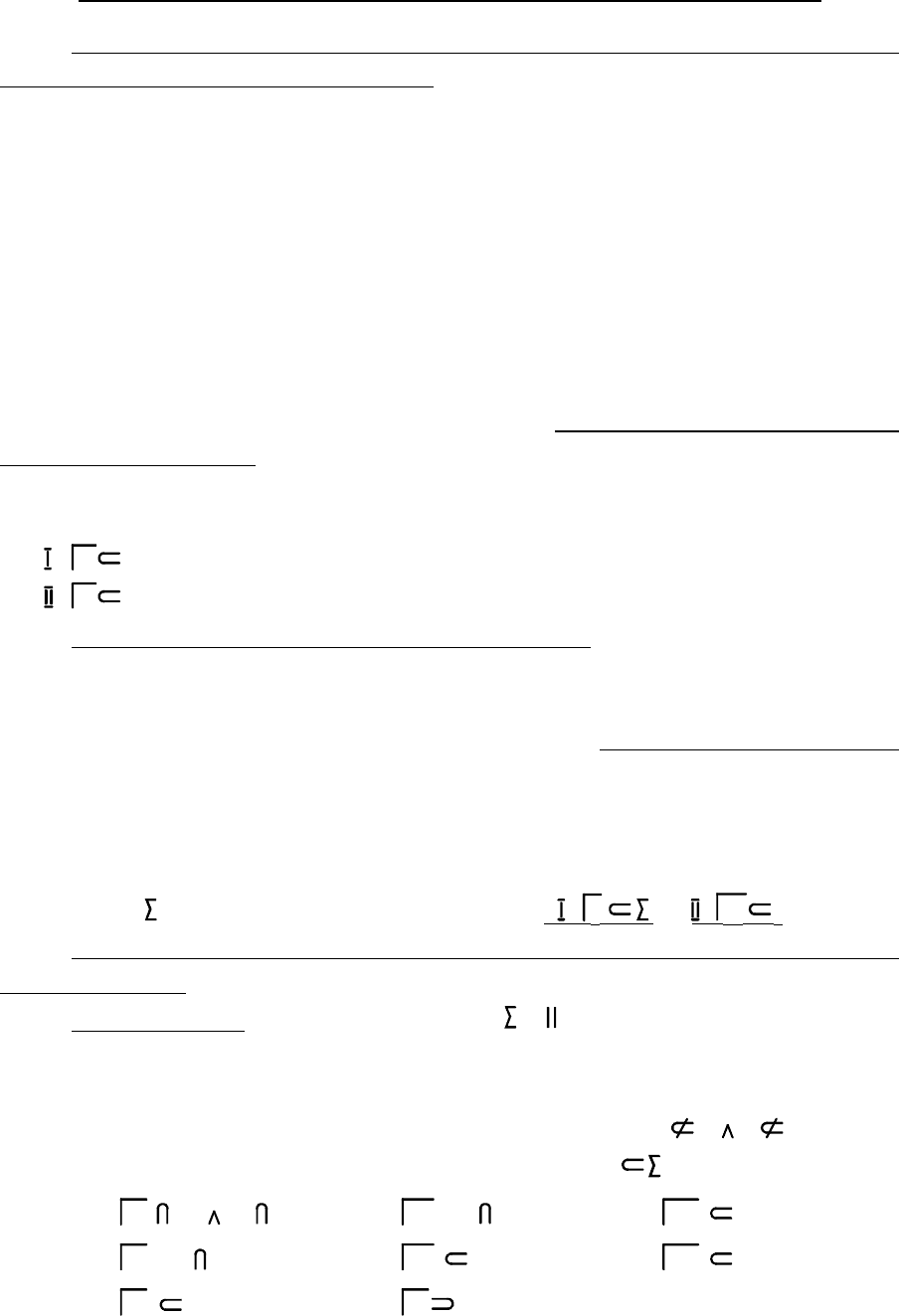
(ОПЗ). ОПЗ является одной из
ключевых задач НГ: возможность решения ОПЗ на чертеже под-
тверждает то, что поверхность на этом чертеже задана (лекция 6).
Существуют три формулировки ОПЗ:
Задача на принадлежность точки поверхности называется
основной позиционной задачей
3.3. Принадлежность точки плоскости общего положения
1. На чертеже задана поверхность. Построить проекции произ-
вольной точки, принадлежащей поверхности.
2. На чертеже заданы поверхность и одна проекция точки, при-
надлежащей поверхности. Построить вторую проекцию точки.
3. На чертеже заданы поверхность и точка. Определить, принад-
лежит точка поверхности или нет.
Для решения ОПЗ используется
: точка принадлежит поверхности, если она
принадлежит линии этой поверхности. Поэтому ОПЗ выполняется в
соответствии с таким пространственным алгоритмом (ПА):
условие принадлежности
точки поверхности
. - на поверхности строится некая линия .
. - на линии задается (ищется, берется) точка .
a Ô Ô a
M a a M
- последовательность
геометрических построений в пространстве, приводящих к решению
задачи. Для пояснения порядка выполнения многих задач на черте-
же условными знаками будет записываться
(ГА) их решения - последовательность графических построений на
чертеже, приводящих к решению задачи. При этом одна и та же
задача обычно имеет несколько ГА её выполнения.
В общем случае ПА решения задачи
графический алгоритм
В плоскости точки строят с помощью прямых линий, и для
плоскости ПА решения ОПЗ имеет вид: . l M l. ..
.
В дальнейшем буквами и будут обозначаться только
прямые линии
l t
Задана плоскость ( ). Построить проекцииПРИМЕР 3.1. a b M
и произвольной точки , принадлежащей этой плоскости (рис. 3.6).M M
2
1
Условимся, что точка считается произвольной, если она не
принадлежит ГО, задающему поверхность (здесь ). Точка
строилась с помощью произвольной прямой согласно ГА:
M a M b
M l
1. l a l b .
2 .. 1 =l a
3 .. 1 a
7 .. M l
8 .. M l
4 .. 2 =l b
5 .. 2 b
6 .. l 1 ,2
11 1 1
1 1 1
2 2
1 1 1
2 2
2 2 2
2 2
1 1
25
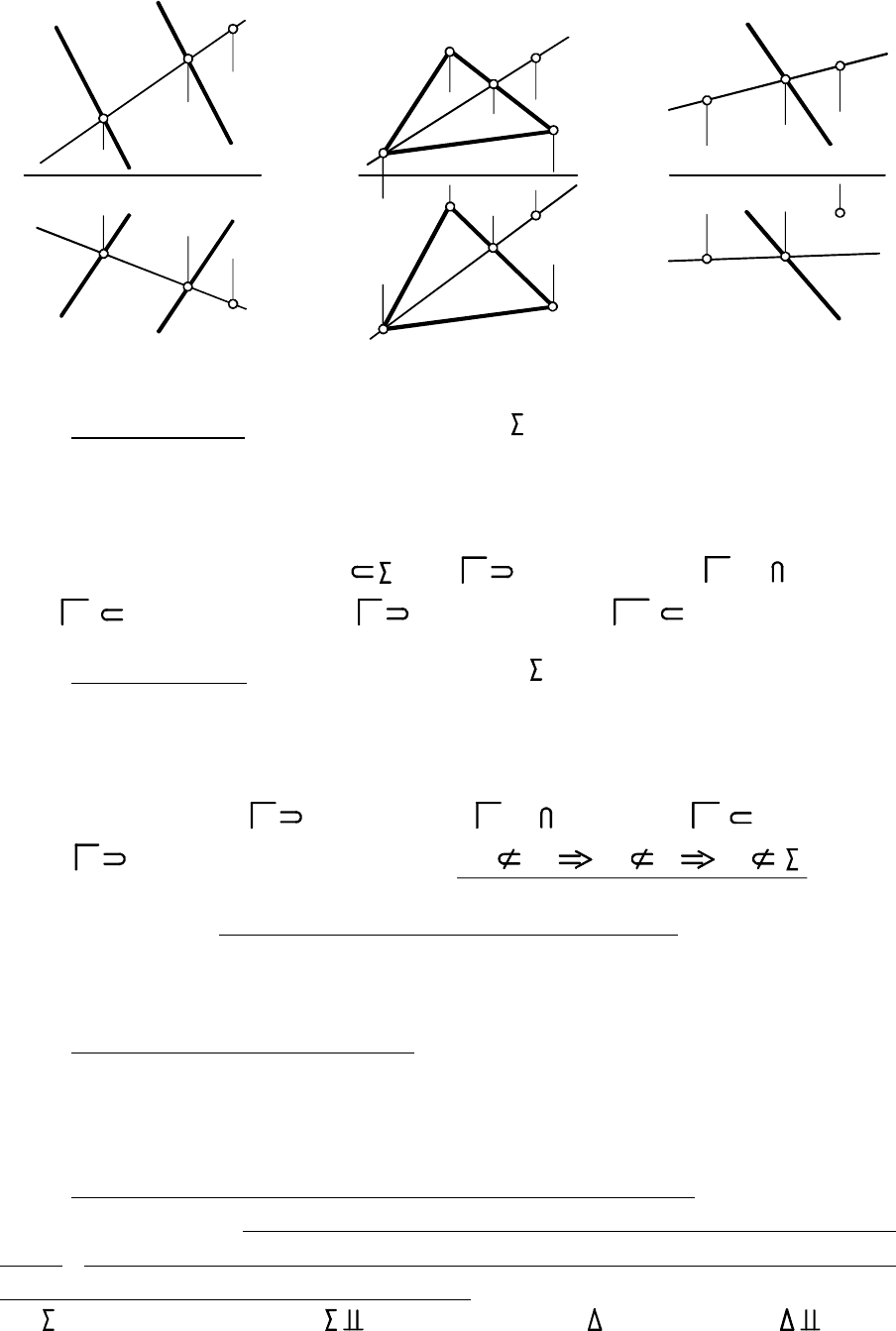
x x
M
M
M
M
M
M
1
1
1
1
1
1
2
2
b
b
A
A
A
A
B
B
D
D
l
1
2
l
2
a
2
2
2
2
a
1
1
1
1
1
x
l
1
l
2
l
2
l
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
a
a
Рис. 3.6 Рис. 3.7 Рис. 3.8
Заданы плоскость ( ) и проекция точки
, принадлежащей плоскости (рис. 3.7). Построить .
Сначала, соединив три точки , и , переходят к способу
задания плоскости треугольником. Далее задача решается с
использованием прямой :
ПРИМЕР 3.2. A,B,D M
M M
A B D
l
2
3. .1 [B ,D ] 5. M l .
1 1 1
1
1. l M ,A .
2 2 2
2. 1 =l [B ,D ].
2 2 2 2
1 1
4. .l A ,1
1 1 1
Заданы плоскость ( ) и точка (рис. 3.8).
Определить, принадлежит точка плоскости или нет.
При ответе на вопрос о принадлежности точки плоскости
делается попытка построить в плоскости прямую, проходящую
через точку :
ПРИМЕР 3.3. A,a M
M
M
M
M l M l M .
1 1
1. l A ,M .
2 2 2
2. 1 =l
a
.
2 2 2
3. 1 a .
1 1
4 .. Оказалось, чтоl A ,1
1 1 1
3.4. Плоскости частного положения
К плоскостям частного положения относят проецирующие
плоскости и плоскости уровня.
- это плоскость, перпендикулярная
какой-либо ПП. Плоскость, перпендикулярную , называют гори-
зонтально проецирующей, а перпендикулярную - фронтально
проецирующей.
, к которой она
перпендикулярна,
.
. На рис. 3.9 основной проекци-
ей задана плоскость , а проекцией - плоскость .
Проецирующая плоскость
Проецирующая плоскость проецируется на ПП
в прямую линию, называемую её основной проек-
цией Чтобы задать проецирующую плоскость, достаточно задать
основную проекцию этой плоскости
Ï
Ï
2
1
1
ÏÏ
1 2 2
1
26
x x
2
1
l
l
2
1 1 1
1
1
2
2
2
2
1
2
1
22
2
1
1
1
1
1
1
Основная проекция обладает собирательным свойством: на
ней расположены проекции всех точек и линий проецирующей
плоскости. Поэтому
. На рис. 3.10 в плоскости заданы
точка , прямая , горизонталь и фронталь : , ,
. При этом фронталь горизонтально проецирующей плоскости
. На рис. 3.10 в плоскости заданы точка , прямая ,
горизонталь ( ) фронталь
фигура принадлежит проецирующей плоскости,
если её соответствующая проекция принадлежит основной
проекции этой плоскости
M l h f M l h
f
f Ï N t
h f .h и
Плоскость уровня
Плоскость уровня - частный слу-
чай проецирующей плоскости
- это плоскость, параллельная какой-либо
ПП. Плоскость, параллельную , называют горизонтальной, а
параллельную - фронтальной.
: если , то , а если ,
то . Поэтому плоскости уровня задаются своими основными
проекциями, параллельными оси проекций: на рис. 3.11 проекци-
ей задана плоскость , а на рис. 3.12 проекцией -
плоскость . На рис. 3.11 также заданы прямые , и плоскос-
ти . Так как , то все эти прямые фронтали, а прямая еще и
горизонталь ( ).
Ï
Ï
x x
l t b
b
b b
Ï
1
1
1
1
1
1
1 1
Ï
1
2
1 11
2
Ï
1
Ï Ï
2
à Ï
2
à Ï
1
1
2
1
Ã
Ï
2
2
Ã
1
Ï
Ï
2
1
Ï
Ï
2
x
2
1
b
t
l
2
2
l
t
b
1
1 1
D
D
B
BA
A
x
Ã
1
2 2 2 2
1
1
Расположенная в плоскости уровня фигура проецируется на
ПП, которой эта плоскость параллельна, в натуральную величину.
27
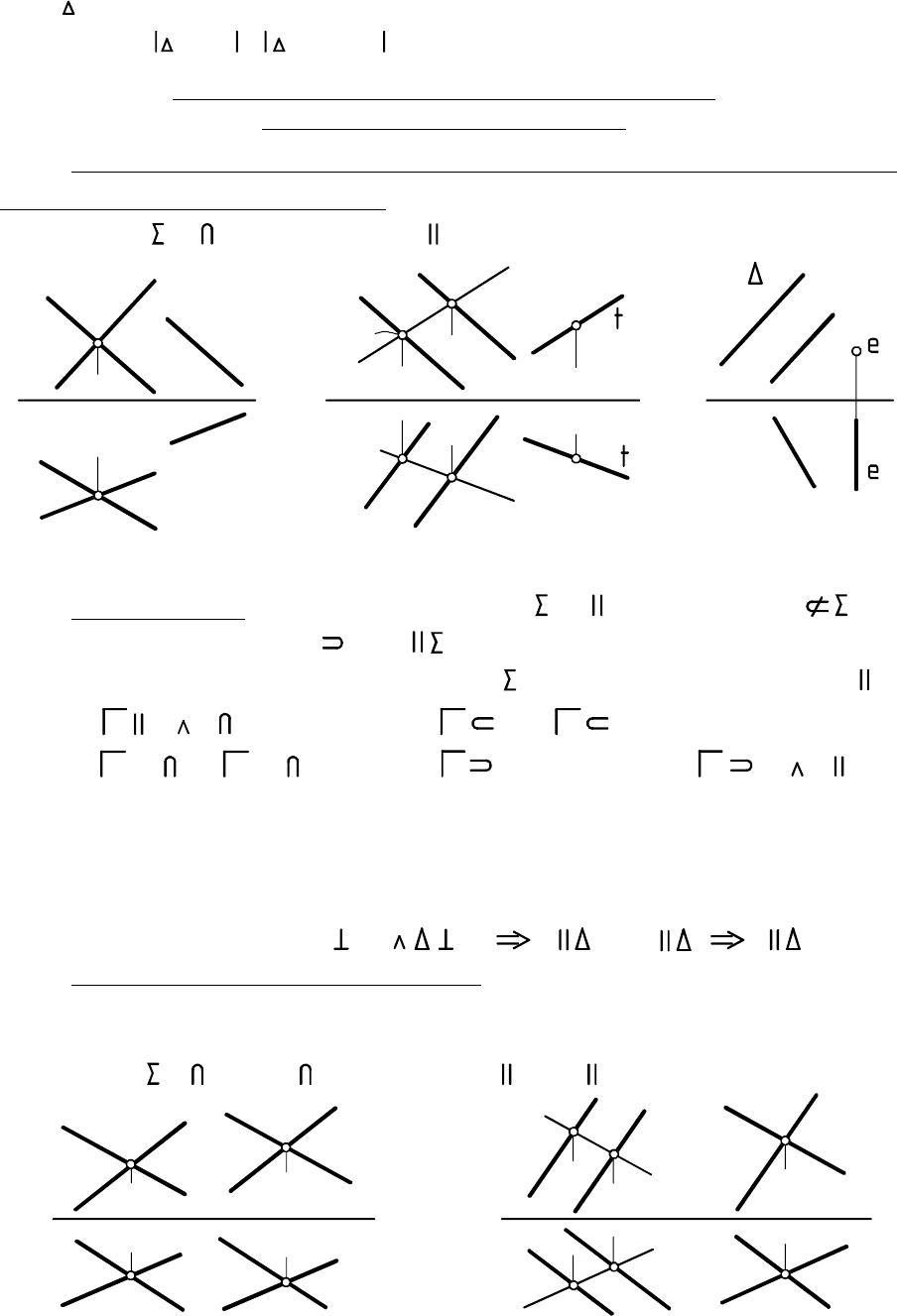
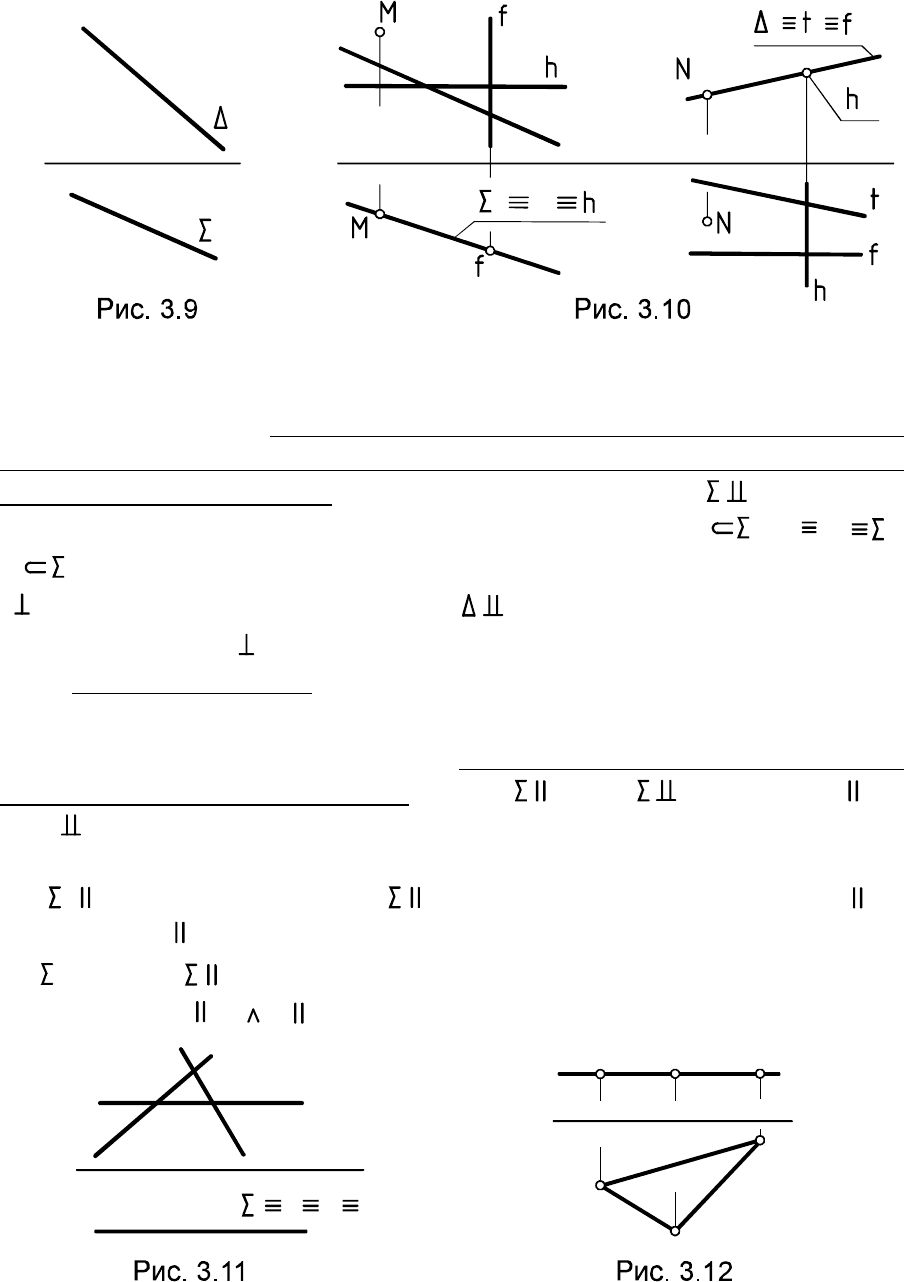
Проецирующая прямая параллельна проецирующей плоскости,
если прямая и плоскость перпендикулярны одной ПП. Непроецирую-
щая прямая параллельна проецирующей плоскости, если
соответствующая проекция прямой параллельна основной проекции
плоскости. На рис. 3.15 и .e e d d
Две плоскости параллельны, если две пересекающиеся
прямые одной плоскости соответственно параллельны двум пересе-
кающимся прямым другой. На рис. 3.16 заданы параллельные
плоскости ( ) и ( ), у которых и .a b à l t l a t b
Так, , расположенный в плоскости , проецируется на без
искажения: (рис. 3.12).
ABD
ABD = A B D
à Ï
1
1 1 1
3.5. Параллельность прямой и плоскости,
параллельность плоскостей
. На рис. 3.13 прямая параллельна
плоскости ( ), поскольку .
Прямая параллельна плоскости, если она параллельна какой-
либо прямой этой плоскости g
a b g a
x x
M
g
a
2
2
1
l
1
l
2
2
Рис. 3.13 Рис. 3.14
g
b
2
b
1
a
1
a
2
b
2
b
1
a
1
1
2
1
1
2
2
2
1
M
1
2
1
x
d
2
2
2
d
1
1
Рис. 3.15
Заданы плоскость ( ), точка ( ) и
проекция прямой , , . Построить .
ПРИМЕР 3.4. a b M M
t t t M t t(рис. 3.14)
Для решения задачи в плоскости строилась некая прямая :l t
1
2
1. l t l a b .
1 1 1 1
2. 1 =l ,
1 1
a
1
2 =l
1 1 1
b .
3. 1, a 2 b .
2 2 2 2
4 , .. l 1 2
2 2 2
5. t M t l .
2 2 2 2
Ï
2
Ï
2
2
2
b
b
b
b
t
t
d
d
t
t
Рис. 3.16 Рис. 3.17
Å
Å
a
l
2
1
l
a
1
x
2
2
2
1
1
a
2
x
2
2
a
1
l
1
l
2
1
1
1
1
2
2
28
1
,
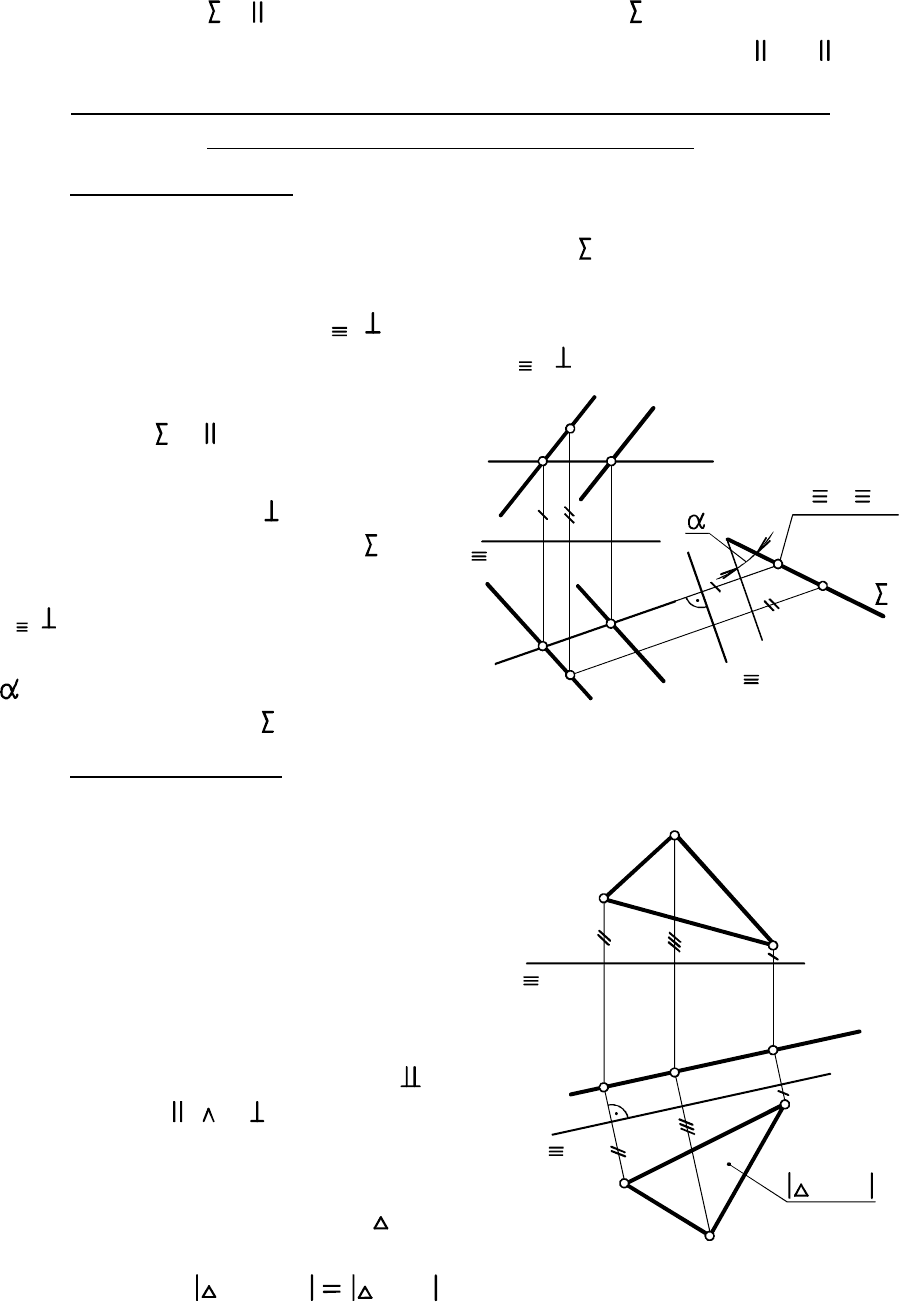
На рис. 3.17 через точку проведена плоскость , параллель-
ная плоскости ( ). Для этого в плоскости построили произ
вольную прямую и задали плоскость прямыми и , ).
E Ã
a b -
d à l t l d t a(
3.6. Решение 3-ей и 4-ой основных задач преобразования
чертежа способом задания новой ПП
: преобразовать КЧ так, чтобы плоскость
общего положения стала проецирующей плоскостью.
Чтобы плоскость общего положения стала проецирующей,
новую ПП задают перпендикулярно горизонтали плоскости и
(новая ось проекций ) или перпендикулярно фронтали
плоскости и (новая ось проекций ).
Условие 3ОЗПЧ
Ï h Ï
f
f
3 1
x
31
h
Ï
2
x
32
1
2
h
h
h
1
1
1
2
2
2
3
3
3
b
b
Рис. 3.18
x
31
x
21
a
a
1
2
3
2
2
2
2
2
1
1
1
1
1
3
3
3 3
В примере на рис. 3.18 в
плоскости ( ) проведена
произвольная горизонталь и
задана новая ПП . Основ-
ную проекцию плоскости
строили с использованием оси
и точек и ( - произ-
вольная точка плоскости). Угол
определяет величину угла
наклона плоскости к .
a b
h
Ï h
1 3 3
3
3
x
31
h
1
Ï
1
: преобразовать КЧ так, чтобы проецирующая
плоскость стала плоскостью уровня.
Условие 4ОЗПЧ
Для решения 4ОЗПЧ новую
ПП задают параллельно данной
плоскости и перпендикулярно той
ПП, на которую данная плоскость
является проецирующей (новую
ось проекций проводят параллель-
но основной проекции плоскости).
На рис. 3.19 плоскость
заданием переведена
в положение плоскости уровня.
При этом любая фигура, лежащая
в плоскости , например,
проецируется на ПП в натураль-
ную величину: .
à Ï
Ã
B
B
B
A
A
A
D
D
D
Ã
ABD
Рис. 3.19
x
31
x
21
2
1
2
2
1
1
1
3
3
3
Ï Ã
3
1
Ï
3
Ï
A B D
1
Ï
3
A B D ABD
3 3 3
29
ОСНОВНЫЕ МЕТРИЧЕСКИЕ ЗАДАЧИ. ГЛАВНЫЕ
ПОЗИЦИОННЫЕ ЗАДАЧИ ДЛЯ ПРЯМОЙ И ПЛОСКОСТИ
4.1. Основные метрические задачи
Л Е К Ц И Я 4
Всякая задача, в условии или в процессе решения которой
встречается численная характеристика, называется
. К метрическим задачам относят задачи на определение
расстояний, углов, натурального вида фигур и т. д.
Из множества метрических задач выделяют две, лежащие в
основе решения других метрических задач и называемые поэтому
.
1ОМЗ - задача на перпендикулярность прямой и плоскости.
2ОМЗ - задача на определение длины отрезка или расстояния
между двумя точками.
метрической
задачей
основными метрическими задачами (ОМЗ)
4.2. Решение 1ОМЗ
1ОМЗ имеет две возможные формулировки:
- через точку провести прямую перпендикулярно данной плос-
кости (точка может принадлежать плоскости или нет);
- через точку провести плоскость перпендикулярно данной
прямой (точка может принадлежать прямой или нет).
: прямая перпендикулярна плоскости (всем пря-
мым плоскости), если она перпендикулярна двум пересекающимся
прямым этой плоскости, .
Эта теорема позволяет использовать при построении взаимно
перпендикулярных прямой и плоскости на чертеже прямых уровня,
существенно облегчая решение 1ОМЗ. Сформулируем с учетом
теоремы
:
Решение 1ОМЗ базируется на признаке перпендикулярности
прямой и плоскости
и теореме о проецировании прямого угла
признак перпендикулярности прямой и плоскости для
чертежа
- : чтобы построить прямую , перпенди-первая формулировка l
кулярную плоскости , в строят горизонталь и фронтальà à h f
(если они не заданы) и проводят ;l h l f
- : плоскость , перпендикулярную прямой
, задают горизонталью и фронталью , проводя .
вторая формулировка
l h f h l f l
1
22
1
Ã
1
22
1
На рис. 4.1 через точку перпендикулярно прямой
проведена плоскость , заданная горизонталью ( ) и фрон-
талью ( ). На рис. 4.2 через точку проходит прямая ,
M a
h a h a
f a f a M l
Ã
1 1
2 2
30
