Никитин А.А. Управление техническими системами

Рис. 7

.1

8

.

Схема катаракта

z

1

z

2

p

1

p

2

m

1

3

4

Уравнение движения поршня можно записать в виде

2

ПТР2ПР21П

)(

dt

zd

mFzcppf =−−− , (7.181)

где f

П

– рабочая площадь поршня (т. е. площадь поршня минус площадь што-

ка); p

1

и p

2

– давление в левой и правой полостях гидроцилиндра; c

ПР

– жест-

кость пружины; F

ТР

– сила трения, действующая на поршень и шток; m

П

– мас-

са поршня, штока и пружины; z

2

– перемещение штока.

Если пренебречь массой m

П

и силой трения F

ТР

, то уравнение (7.181)

примет вид

0)(

2ПР21П

=

−

zcppf

. (7.182)

Принимая режим течения через дроссель ламинарным, зависимость рас-

хода Q

ДР

от перепада давления будет линейной:

)(

21ДРДР

ppkQ

−

=

, (7.183)

где

к

4

к

ДР

μ128

π

l

d

k

⋅⋅

⋅

= – проводимость дросселя; d

к

– диаметр канала дросселя (в

нашем случае диаметр отверстия в поршне); l

к

– длина канала дросселя; µ –

динамический коэффициент вязкости.

С другой стороны, расход через дроссель связан со скоростью переме-

щения цилиндра относительно поршня, без учета сжимаемости будем иметь

dt

zzd

fQ

)(

21

ПДР

−

= , (7.184)

где z

1

– перемещение цилиндра 2.

Принимая за входное воздействие перемещение цилиндра, а за выход-

ную величину перемещение поршня, систему уравнений (7.182)–(7.184) при-

ведем к одному уравнению в форме "вход-выход":

dt

dz

Tz

dt

dz

T

1

к2

2

к

=+ , (7.185)

где

ПРДР

2

П

к

ck

f

T = – постоянная времени катаракта.

Вопросы для самопроверки

3. Назовите типовые звенья.

4. Напишите уравнения звеньев первого порядка.

5. Напишите уравнения звеньев второго порядка.

6. Напишите формулу переходной функции интегрирующего звена.

7. Напишите формулу переходной функции апериодического звена перво-

го порядка.

8. Напишите формулу весовой функции интегрирующего звена.

9. Напишите формулу весовой функции апериодического звена первого

порядка.

10. Напишите формулу передаточной функции интегрирующего звена.

11. Напишите формулу передаточной функции апериодического звена пер-

вого порядка.

12. Напишите формулу передаточной функции колебательного звена.

13. Напишите формулу амплитудно-фазовой частотной характеристики ин-

тегрирующего звена.

14. Напишите формулу амплитудно-фазовой частотной характеристики

апериодического звена первого порядка.

15. Напишите формулу амплитудно-фазовой частотной характеристики ко-

лебательного звена.

16. Покажите на примере колебательного звена применение формулы Хе-

висайда для определения переходной функции.

17. Нарисуйте график переходной функции интегрирующего звена.

18. Нарисуйте графики переходной функции колебательного, консерватив-

ного и апериодического звеньев второго порядка.

8. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ

АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

Построение структурных схем. Преобразование структурных схем.

Передаточные функции замкнутой и разомкнутой систем. Передаточные

функции ошибки.

Математические модели систем автоматического регулирования и

управления для наглядности можно представить структурными схемами. В

этих схемах звенья изображают прямоугольниками, в поле которых записыва-

ют соответствующие передаточные функции, а связи между звеньями показы-

вают стрелками. Операции сложения и вычитания величин выносят в узлы ал-

гебраического суммирования.

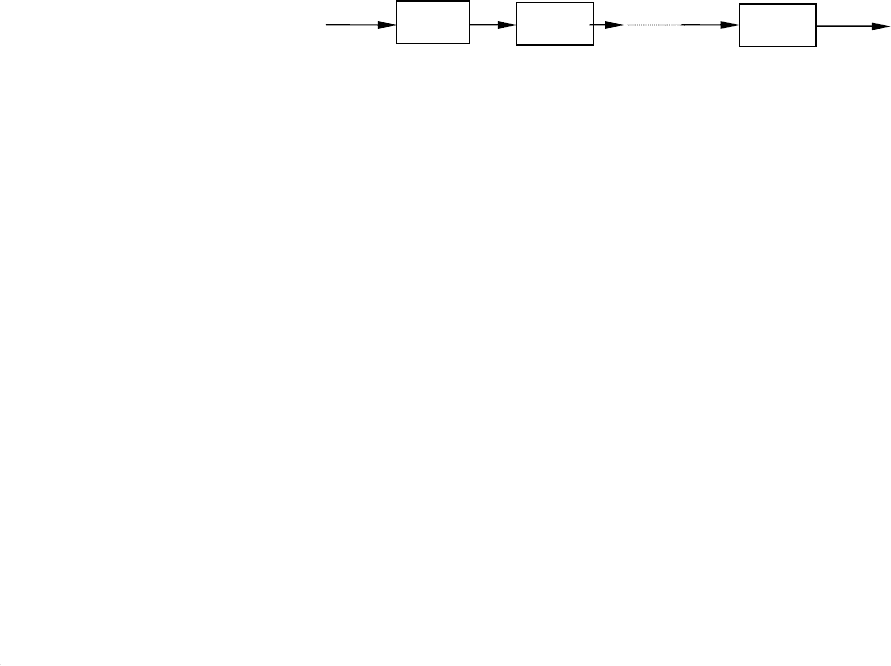
При последовательном соединении звеньев (рис. 8.1) выходная величина

Y s

k

()

предыдущего звена служит входной величиной

U s

k+1

()

для последую-

щего звена. Передаточная функция

W

s

(

)

цепи п последовательно соединен-

ных звеньев равна произведению передаточных функций звеньев:

Ws W s

k

n

() ()=

=

∏

1

, (8.1)

где

W s

k

()

– передаточная функция k-го звена.

Рис. 8.1. Последовательное соединение n звеньев

Амплитудно-фазовую частотную характеристику такой цепи находят

перемножением амплитудно-фазовых частотных характеристик отдельных

звеньев:

)ω()ω(

1

jWjW

n

k

∏

=

. (8.2)

Амплитудная частотная характеристика цепи и последовательно соеди-

ненных звеньев равна произведению амплитудных частотных характеристик

этих звеньев:

)ω()ω(

1

∏

=

n

k

АА

, (8.3)

W s

1

()

W s

2

()

W s

n

()

U

s

(

)

Y

s

(

)

а фазовая частотная характеристика цепи, составленная из последовательно

включенных звеньев, равна сумме фазовых частотных характеристик отдель-

ных звеньев:

)ω()ω(

1

∑

=

n

k

ϕϕ

. (8.4)

Логарифмическая амплитудная

)

ω

(

lg

20

)

ω

(

A

L

=

и логарифмическая

фазовая частотные характеристики будут суммой соответствующих логариф-

мических частотных характеристик всех последовательно включенных звень-

ев.

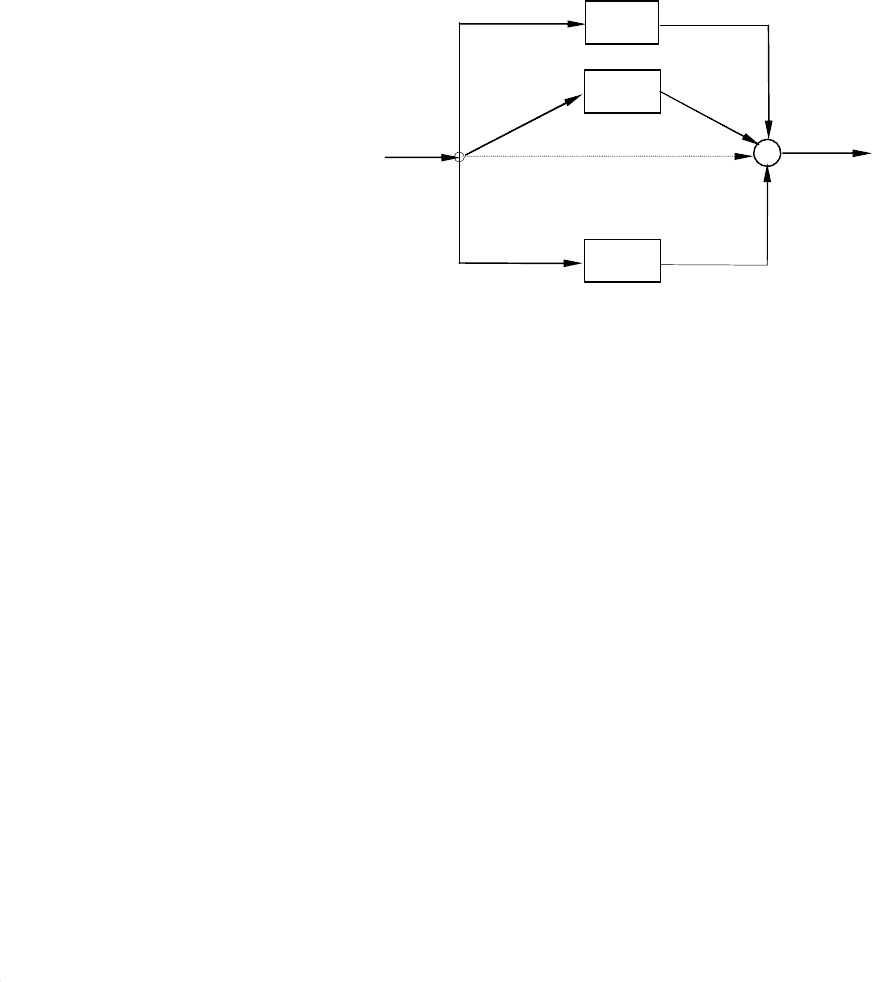
При параллельном соединении звеньев (рис. 8.2) входная величина (воз-

действие) имеет одинаковые значения для всех звеньев, а выходная величина

является алгебраической суммой выходных величин этих звеньев.

Рис. 8.2. Параллельное соединение звеньев

Передаточная функция n звеньев, соединенных параллельно, равна сум-

ме передаточных функций отдельных звеньев:

Ws W s

k

n

() ()=

=

∑

1

. (8.5)

Амплитудно-фазовая частотная характеристика

)

ω

(

j

W

параллельного

соединения звеньев определяется по правилу сложения комплексных

величин:

∑∑∑

===

+==

n

k

n

k

n

k

QjPjWjW

111

)ω()ω()ω()ω(

, (8.6)

где

)ω(

k

P

– вещественная часть амплитудно-фазовой частотной характеристи-

ки;

)ω(

k

Q

– мнимая часть.

Передаточная функция соединения с обратной связью определяется по

формуле

W s

1

()

W s

2

()

W s

n

()

U

s

(

)

Y

s

(

)

+

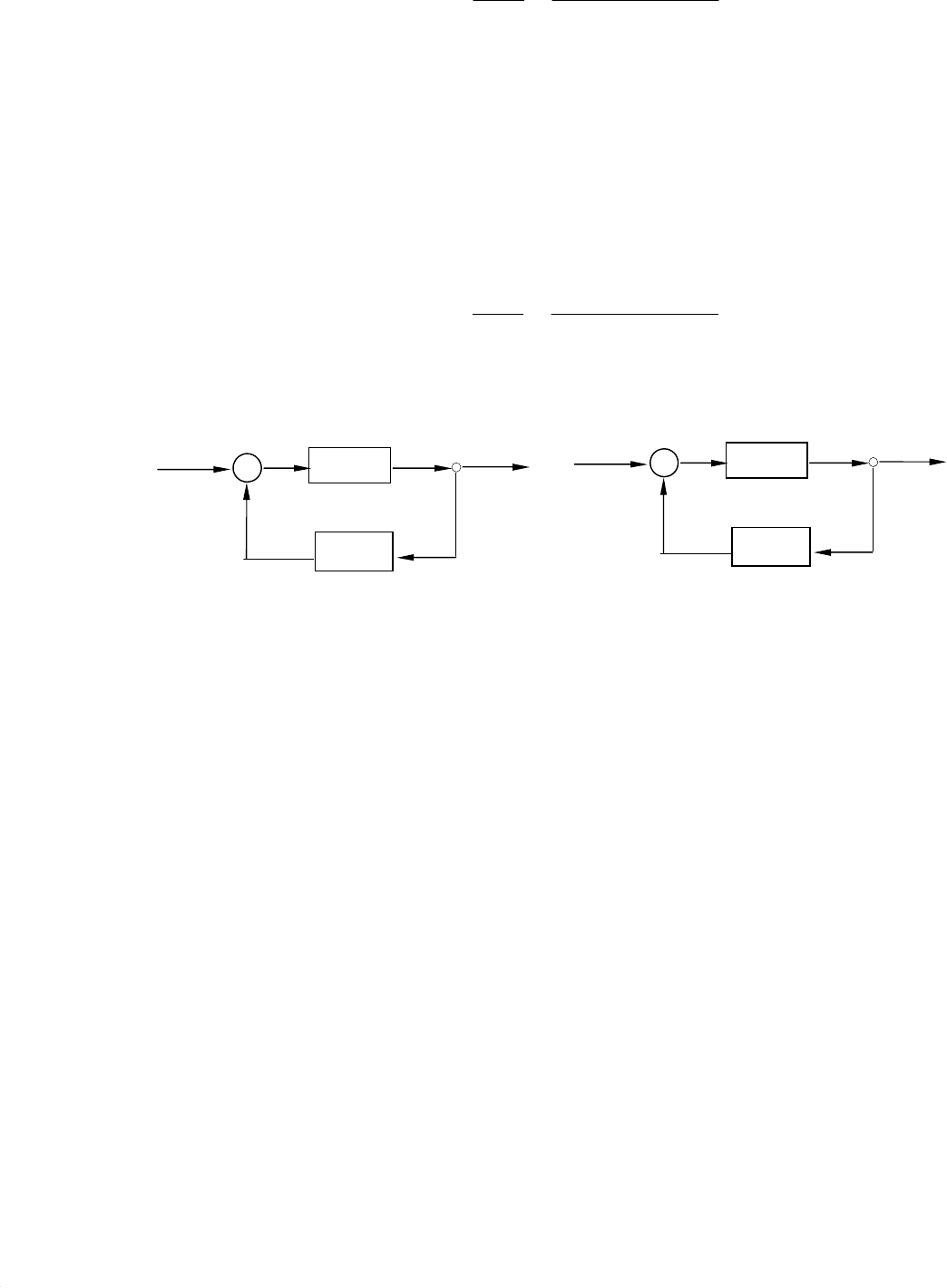
)()(1

)(

oб

sWsW

sW

sU

sY

sФ

⋅±

== , (8.7)

где знак “плюс” соответствует отрицательной обратной связи (рис. 8.3, а), а

знак “минус” – положительной обратной связи (рис. 8.3, б). Передаточная

функция разомкнутой цепи равна произведению передаточных функций пря-

мой цепи и обратной:

(

)

)()(

oб

sWsWsW

p

⋅

=

. (8.8)

Передаточная функция ошибки определяется по соотношению

)()(1

1

)(

об

sWsWsU

sE

sФ

EU

⋅+

== , (8.9)

где E(s) – изображение ошибки ε(t).

а б

Рис. 8.3. Соединение с обратной связью:

а – с отрицательной, б – с положительной

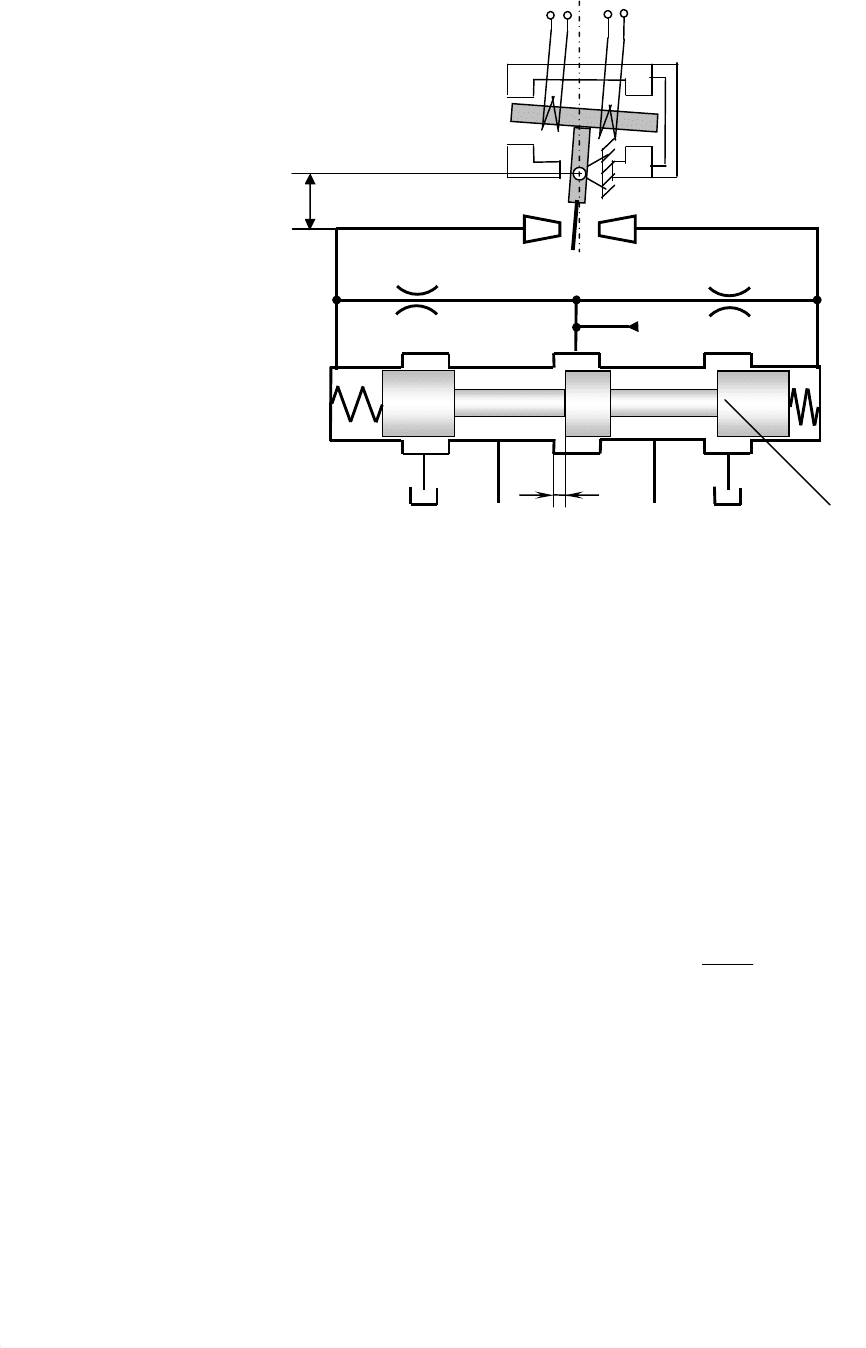
Построение структурных схем рассмотрим на примере электрогидравли-

ческого усилителя, схема которого приведена на рис. 8.4. Электрогидравличе-

ский усилитель с золотником, нагруженным пружинами, состоит из электро-

механического преобразователя (ЭМП) и гидроусилителя (ГУ), имеющего

усилительную ступень в виде сопла-заслонки и управляющую ступень в виде

золотникового распределителя. Гидроусилитель состоит из золотника 1, пру-

жин, нерегулируемых дросселей 3, заслонки 4 и сопел.

Электрогидравлический усилитель работает следующим образом. При

подаче напряжения на ЭМП в обмотке управления возникает ток, и якорь

ЭМП вместе с заслонкой 4 отклоняется от нейтрального положения. Отклоне-

ние заслонки 4 от нейтрального положения вызывает изменение расходов че-

рез сопла и перепад давлений в полостях А и Б, необходимый для управления

золотником 1.

Для обеспечения пропорциональной зависимости перемещений золотни-

ка от перемещений заслонки применены пружины 2. Усилие этих пружин при

W s

об

()

W

s

(

)

U

s

(

)

Y

s

(

)

W s

об

()

W

s

(

)

U

s

(

)

Y

s

(

)

-

+

смещении золотника от нейтрального положения уравновешивают силы дав-

лений, приложенные к нему со стороны жидкости в полостях А и Б.

Описание динамики электрогидроусилителя с золотником, нагруженным

пружинами, с учетом массы золотника, силы трения и сжимаемости жидкости

выполним при малых отклонениях заслонки от нейтрального положения. За

входное воздействие примем отклонение заслонки от нейтрального положе-

ния, а за выходную величину, т. е. регулируемую, – перемещение золотника.

Математическое описание начнём с процессов, происходящих в элек-

тромеханическом преобразователе. Уравнение вращения якоря запишем в виде

dt

d

JМММ

Я

ЯНСЯ

ϕ

=−− , (8.10)

где М

Я

– момент электромагнитных сил, поворачивающих якорь; М

С

– момент

сопротивления, обусловленный силами трения и электромагнитными силами

сопротивления, вызванными встречной ЭДС в обмотке управления ЭМП; М

Н

–

момент сил, действующих на заслонку и представляющих нагрузку на якорь;

J

Я

– момент инерции якоря вместе с заслонкой; φ

Я

– угол отклонения якоря от

среднего положения.

x

З

p

П

p

СЛ

1

p

1

p

2

Рис. 8.4. ЭГУ с золотником, нагруженным пружинами

l

Внешнюю моментную характеристику электромеханического преобра-

зователя будем использовать в виде линейной зависимости момента М

Я

, раз-

виваемого якорем от тока управления i

У

и угла φ

Я

поворота якоря:

ЯM.У.MЯ

ϕ

KiKM

i

−

=

, (8.11)

где

ϕM..M

,KK

i

– коэффициенты внешней моментной характеристики ЭМП.

Момент сопротивления М

С

, возникающий при вращении якоря, будем

определять по формуле

dt

d

KM

Я

СС

ϕ

= , (8.12)

где К

С

– коэффициент сопротивления, обычно определяется эксперименталь-

но.

Так как заслонка жестко связана с якорем и имеет возможность повора-

чиваться вокруг оси совместно с ним, то гидродинамическую силу, прило-

женную к заслонке, нужно учесть при составлении уравнения вращения якоря.

Момент нагрузки М

Н

определяется гидродинамической силой F

ГД1

, обу-

словленной воздействием на заслонку струй жидкости, истекающих из сопел:

lFМ

⋅

=

1ГДН

, (8.13)

где l – расстояние от центра вращения якоря вместе с заслонкой до оси сопел.

Гидродинамическую силу, действующую со стороны потока рабочей

жидкости на заслонку, можно определить по формуле

УCC1ГД

χ pfF = , (8.14)

где χ

С

– коэффициент, равный 1,03–1,06 для сопел с острыми кромками;

4

2

СС

df π= – площадь проходного сечения сопла (здесь d

C

– диаметр сопла);

p

y

– разность давлений в полостях А и Б (

2У1УУ

ppp

−

=

).

После подстановки моментов из формул (8.11)–(8.13) в уравнение (8.10)

с учетом соотношения (8.14) получим

2

Я

2

ЯУCC

Я

СЯМ.У.М

χ

dt

d

Jplf

dt

d

ККiК

i

ϕϕ

ϕ

⋅=⋅⋅⋅−⋅−⋅−⋅ . (8.15)

Уравнение (8.15) описывает процессы, происходящие в ЭМП. Для элек-

тромеханического преобразователя входной величиной является ток i

У

, пода-

ваемый на обмотки управления, а выходной – угол φ

Я

поворота якоря. Приве-

дем уравнение к форме “вход-выход”, т. е. в левую часть перенесем члены, со-

держащие выходную величину φ

Я

, а в правую – входную i

У

, в результате полу-

чим

yccУ.МЯМ.

Я

2

Я

2

Я

χ plfiКК

dt

d

К

dt

d

J

iС

⋅⋅⋅−⋅=⋅+⋅+⋅ ϕ

ϕϕ

ϕ

. (8.16)

В правой части уравнения (8.16) член, содержащий p

У

, представляет об-

ратную связь, обусловленную действием гидродинамической силы, стремя-

щейся вернуть заслонку с якорем в нейтральное положение.

Разделив все члены уравнения (8.16) на К

М.φ

, получим его стандартную

форму:

y.У.Я

Я

ЯЯ

2

Я

2

Я

ζ2 pКiК

dt

d

T

dt

d

T

pi

⋅−⋅=+⋅⋅⋅+⋅

ϕϕ

ϕ

ϕϕ

, (8.17)

где Т

Я

– постоянная якоря; ζ

Я

– коэффициент относительного демпфирования

якоря; Kφ.i – коэффициент преобразования тока i

У

управления в угол φ

я

пово-

рота якоря; К

φ.p

– коэффициент преобразования разности давления p

y

в угол φ

я

поворота. Постоянная времени якоря и коэффициенты преобразования опре-

деляются по соотношениям:

ϕМ.

Я

К

J

T =

, (8.18)

ϕ.МЯ

С

Я

2

ζ

КJ

К

⋅⋅

=

, (8.19)

ϕ

.М

.

К

i

= , (8.20)

ϕ

М.

CC

.

χ

К

lf

К

p

⋅

= . (8.21)

Теперь составим математическое описание гидроусилителя. Зависимость

расхода жидкости Q

у

, обеспечивающего перемещение золотника, от отклоне-

ния h

у

заслонки от нейтрального положения и разности давлений p

у

в полостях

А и Б примем линейной:

y.У.У

pKhKQ

pQhQ

⋅

−

⋅

=

, (8.22)

где К

Q.h

и К

Q.p

– коэффициенты расхода, можно определить эксперимен-

тально.

С другой стороны, расход связан с перемещением золотника:

dt

dp

B

V

dt

dx

SQ

У

Ж

УЗ

ЗУ

2

⋅

+⋅= , (8.23)

где 4π

2

ЗЗ

dS ⋅= – площадь торца золотника; d

З

– диаметр золотника; x

З

– пе-

ремещение золотника; V

У

– объем каждой из полостей А и Б; B

Ж

– модуль объ-

емной упругости жидкости. Второе слагаемое в правой части уравнения (8.23)

учитывает изменение объема жидкости, обусловленное её сжимаемостью.

Отклонение заслонки h

У

от нейтрального положения связано с углом φ

Я

поворота якоря, при малых отклонениях заслонки можно записать

ЯУ

ϕ

⋅

=

lh

. (8.24)

Уравнения (8.22)–(8.24) можно заменить одним уравнением в форме

“вход-выход”; приняв за входную величину φ

Я

, а за выходную – p

у

, получим

dt

dx

SlKpK

dt

dp

B

V

hQpQ

З

ЗЯ.У.

У

Ж

У

2

⋅−⋅⋅=⋅+⋅

⋅

ϕ . (8.25)

Разделив все члены уравнения (8.25) на К

Q.p

, получим его стандартную

форму:

dt

dx

ТКp

dt

dp

T

p

З

2ГУЯ.У

У

1ГУ

⋅−⋅=+⋅ ϕ

ϕ

, (8.26)

где Т

ГУ1

и Т

ГУ2

– постоянные времени гидроусилителя; К

φ.p

– коэффициент пре-

образования угла φ

Я

поворота в разность давлений p

У

. Постоянные времени

гидроусилителя и коэффициент преобразования определяются по соотноше-

ниям:

pQ

КB

V

T

.Ж

У

1ГУ

2 ⋅⋅

= , (8.27)

pQ

К

S

T

.

З

2ГУ

=

, (8.28)

pQ

hQ

p

K

lK

K

.

⋅

=

ϕ

. (8.29)

Уравнение движения золотника под действием разности давлений в по-

лостях А и Б (

2У1УУ

ppp

−

=

) можно записать в виде

2

З

2

ЗПРТР2ГДЗУ

dt

xd

mFFFSp ⋅=−−+⋅ , (8.30)

Никитин А.А. Управление техническими системами

Подождите немного. Документ загружается.