Никитин А.А. Управление техническими системами
Подождите немного. Документ загружается.


T
T
T
TTT
s
1ζ
ζ
)ζ(ζ
2
2
22
2
−
−−=
−⋅−⋅−
= . (7.137)
Для колебательного звена корни будут комплексные и их можно привести к
виду
T
j
T
s
2
1
ζ1
ζ
−
⋅+−= , (7.138)
T
j
T
s
2
2
ζ1
ζ
−
⋅−−= , (7.139)
где 1−=j .
С учетом обозначений
T
ζ
α = , (7.140)
T
2
c
ζ1
ω
−
= (7.141)
корни s
1
и s
2
можно записать в виде
c1
ωα
⋅
+
−
=
js , (7.142)
c2
ωα
⋅
−
−
=
js
. (7.143)
Подставим выражения (7.140), (7.142) и (7.143) корней в соотношения
(7.132) и (7.133), в результате получим
jTsD ⋅⋅⋅=
c
2
1
ω2)(
&
, (7.144)
jTsD ⋅⋅⋅−=
c
2
2
ω2)(
&
. (7.145)
Подставим в формулу (7.130) Хевисайда соотношения (7.134), (7.135),
(7.142), (7.143), (7.144) и (7.145), в результате получим выражение переходной
функции для колебательного звена
tjtj
e
jTj
K
e
jTj
K
Kty
⋅−−⋅+−
⋅
−−
+⋅
+−
+=
)ωα(
c
2
c
)ωα(
c
2
c
cc
ω)ωα(2ω)ωα(2
)( .
(7.146)
Вторая и третья составляющие переходной функции (7.146) являются
комплексно сопряженными выражениями, поэтому сумма их равна удвоенной
вещественной части одного из них:
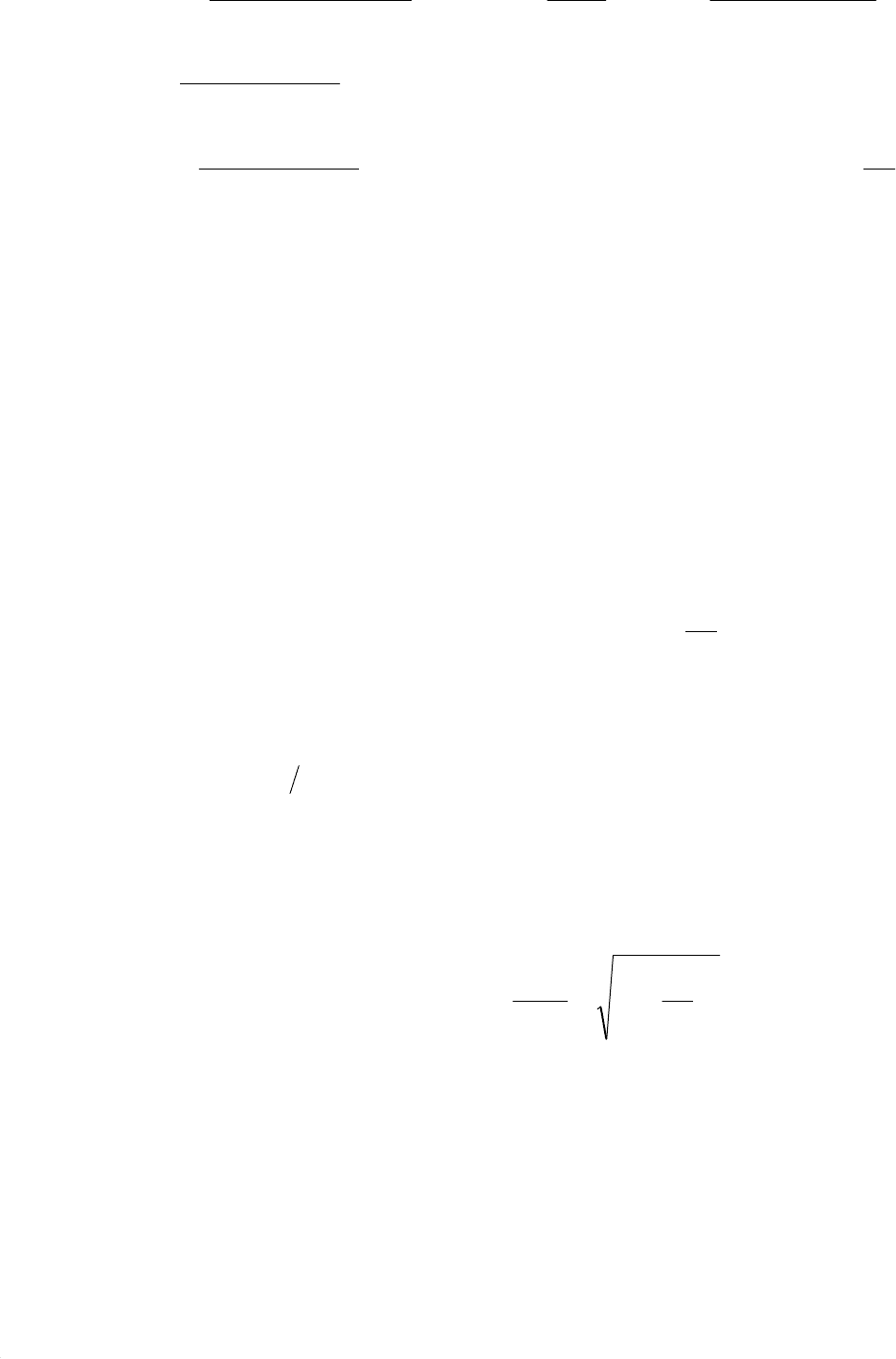
[ ]
⋅+⋅⋅−=+⋅
+
⋅
−=
=++−⋅
+
⋅
=
=⋅
+
−
−
−
⋅⋅=⋅
+−
−
−
−
−
⋅+−
tteKtt
T
eK
tjtj
T
eK
e
jj
e
T
K
e
jTj
K
t
t
t
tj
t
tj
c
c
c
α
ccc
2
c
2
c
2
α
ccc
2
c
2
c
2
ω
2
c
2
c
α
c
2
)ωα(
c
2
c
ωsin
ω
α
ωcos)ωsinαωcosω(
)ωα(ω
)ωsinω)(cosαω(Re
)ωα(ω
ωα
))(ωα(
Re
ωω)ωα(2
Re2
cc
α
(
7.147)
В уравнении (7.147) при преобразовании комплексной функции
использованы формула Эйлера
tjte
tj
cc
ω
ωsinωcos
c
+= (7.148)
и соотношение
1)ωα(
2
c
22
=+T , (7.149)
которое легко проверить подстановкой в (7.149) α и ω
с
из (7.140) и (7.141).
С учетом выражения (7.147) переходная функция (7.146) примет вид
⋅+⋅−⋅=
−
tteKty
t
c
c
c
α
ωsin
ω
α
ωcos1)( . (7.150)
Переходной функции (7.150) можно придать удобный для анализа вид.
Для этого умножим и разделим выражение в круглых скобках на sin φ при
)αω(arctg
c
=
ϕ
и, применив формулу для синуса суммы двух углов, в резуль-
тате получим
[
]
)ωsin(1)(
c
α
ϕ+⋅⋅−⋅=
−
teAKty
t
, (7.151)
где
2
c
ω
α
1
sin
1
+==
ϕ
A
. (7.152)
График переходной функции, построенный по формуле (7.150) или
(7.151), имеет вид затухающих колебаний (рис. 7.12). Колебания происходят
относительно горизонтальной прямой с ординатой y = K (в данном случае при
расчете переходной функции приняты следующие значения параметров: ко-
эффициент усиления K = 2, постоянная времени T = 0,2 и коэффициент отно-
сительного демпфирования ζ = 0,1). Интенсивность затухания процесса оцени-
вается по отношению
21
aa
амплитуд, взятых в моменты времени, отличаю-
щиеся на период
c
ωπ2
колебаний. В теории колебаний используют натураль-
ный логарифм этого отношения и называют логарифмическим декрементом
затухания
=
2
1
lnδ
a
a
. (7.153)
Амплитуда
1
a колебаний в момент времени t и амплитуда
2
a колебаний в мо-
мент времени (t + 2π/ω
c
), согласно формуле (7.151), соответственно равны:
t
eAa
⋅−
⋅=
α
1
, (7.154)
+⋅−
⋅=
c
ω
2π
α
2
t
eAa
. (7.155)
Подставив выражения для амплитуд
1
a
и
2
a
из формул (7.154) и (7.155)
в (7.153), получим логарифмический декремент затухания для колебательного
звена
c
ω
πα2
δ
⋅
⋅
= . (7.156)
При ζ = 0 уравнение (7.91) описывает консервативное звено. В этом слу-
чае согласно формулам (7.140), (7.141), α = 0 и ω
с
= 1/T и из уравнения (7.150)
получим переходную функцию консервативного звена
)ωcos1()(
c
tKty
−
=
, (7.157)
описывающую незатухающие колебания.
0
1 2
Р
3
4
0
2
4
y(t
)
t
2 π/ωс
a
1
a
2
Рис. 7.12. Переходная функция колебательного
звена

При ζ ≥ 1, согласно формулам (7.136) и (7.137), корни уравнения (7.131)
будут действительными числами и переходный процесс, описываемый реше-
нием y(t) уравнения (7.91), будет апериодическим. Если ζ = 1, корни s
1
и s
2
равны, переходную функцию вычисляют по формуле
+⋅−⋅==
−
T
t
eKthty
Тt
11)()(
. (7.158)
При ζ > 1 корни s
1
и s
2
отрицательные действительные числа, в этом случае пе-
реходную функцию вычисляют по соотношению
(
)
[
]
tsts
eСeСKthty
⋅−⋅−
⋅+⋅+⋅==
21
21
1)(
, (7.159)
где
21
2
1
ss
s
C
−
= ;
12
1
2
ss
s
C
−
= , (7.160)
причем в уравнение (7.159) должны быть подставлены абсолютные значения
s
1
и s
2
.
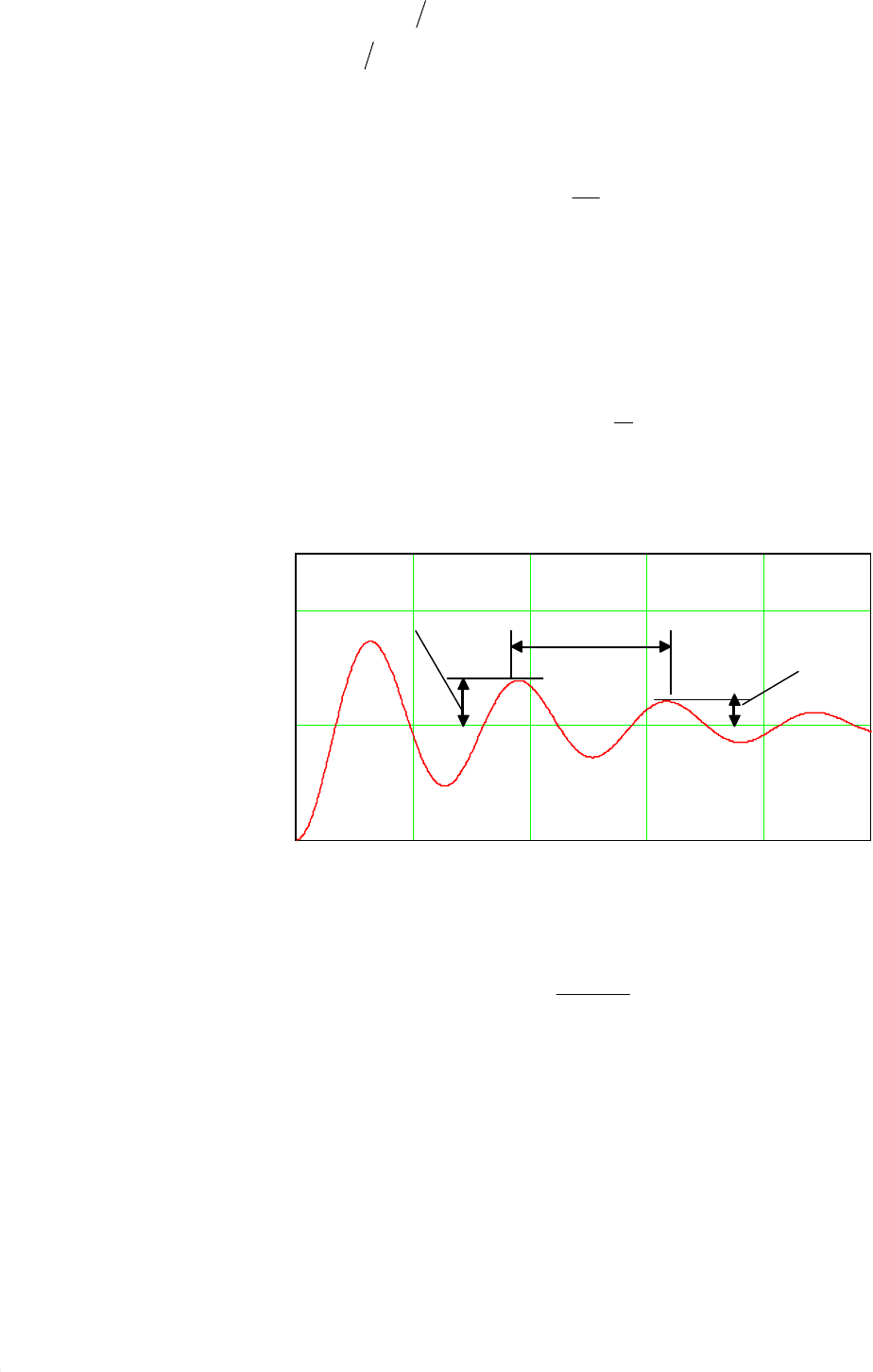
Графики переходных функций консервативного, колебательного и апе-
риодического звена 2-го порядка приведены на рис. 7.13.
Сравнение графиков переходных функций, приведенных на рис. 7.13,
показывает, что график переходной функции консервативного звена имеет вид
незатухающих колебаний (кривая 1), график переходной функции колебатель-
ного звена имеет вид затухающих колебаний (кривая 2), а график переходной
функции апериодического звена 2-го порядка имеет апериодический характер
(кривая 3).
Весовую функцию для колебательного и консервативного звена в соот-
ветствии с формулой (6.16) найдем дифференцированием переходной функции
(7.150) по времени. После несложных преобразований получим
teKteKtwty
tt
c
α
c
2
0
c
c
2
c
2
α
ωsin
ω
ω
ωsin
ω
ωα
)()( ⋅⋅⋅=⋅
+
⋅⋅==
⋅−⋅−
, (7.161)
где
T1ω
0
=
.
Если коэффициент относительного демпфирования находится в интер-
вале 0 < ζ < 1, то уравнение (7.161) описывает колебательное звено. При ζ = 0
уравнение (7.161) описывает консервативное звено. В этом случае согласно
формулам (7.140), (7.141), α = 0 и ω
с
= ω
0
= 1/T и из уравнения (7.161) получим
переходную функцию консервативного звена
tKty
00
ωsinω)(
=
, (7.162)
описывающую незатухающие колебания.
Весовую функцию для апериодического (ζ ≥ 1) звена легко найти диф-
ференцированием переходной функции (7.159) по времени, в результате полу-
чим:
)()()(
21
2211
tsts
eCseCsKtwty
−−
+==
, (7.163)
в уравнение (7.163) должны быть подставлены абсолютные значения s
1
и s
2
.
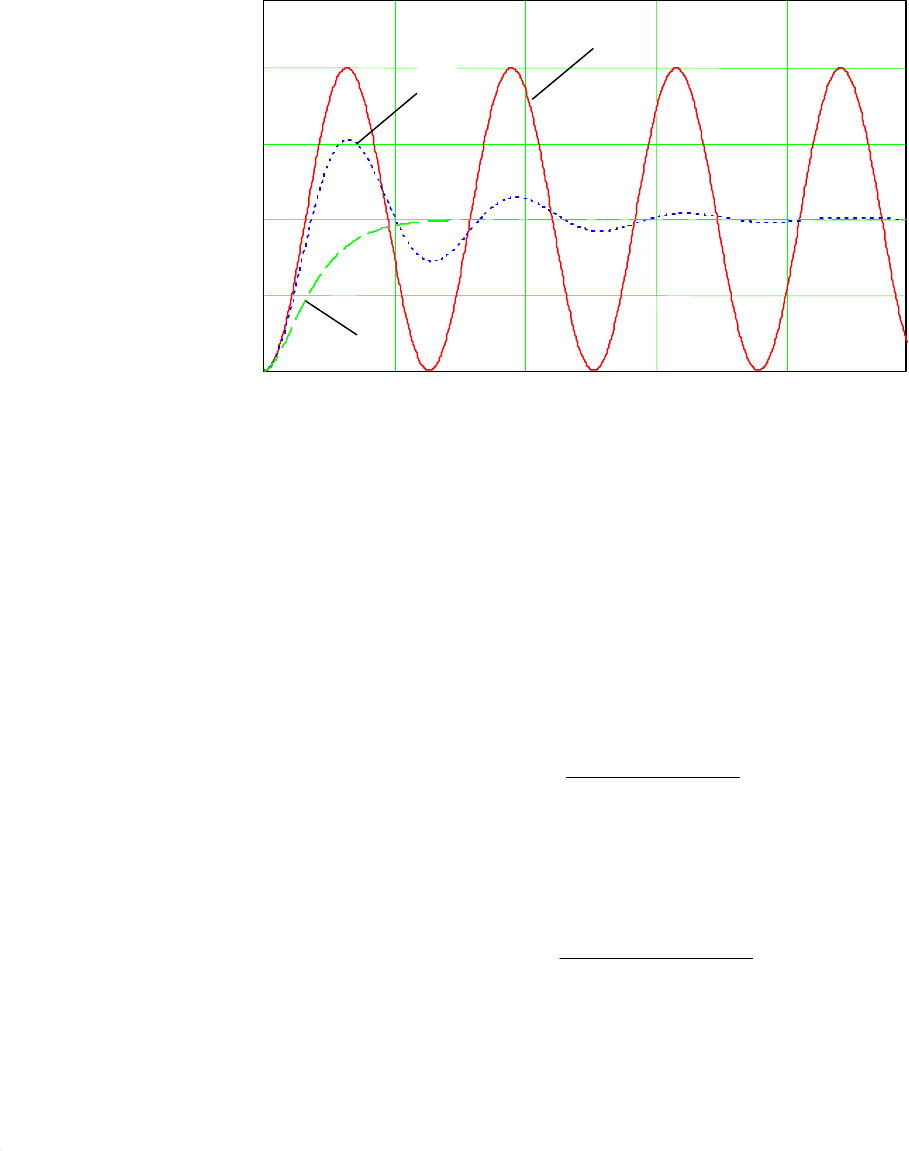
Графики весовых функций консервативного, колебательного и аперио-
дического звена 2-го порядка приведены на рис. 7.14. Из рис. 7.14 видно, что
графики весовых функций совершают колебания относительно оси абсцисс в
отличие от графиков (рис. 7.13) переходных функций.
Найдем передаточную функцию колебательного звена, подставив выра-
жения (7.128) и (7.129) для операторов D(s) и M(s) в формулу (6.23), по-
лучим:
1ζ2
)(
22
++
=
TssT
K
sW . (7.164)
Амплитудно-фазовую частотную характеристику (АФЧХ) можно найти
с помощью подстановки s = jω в передаточную функцию (7.164):
ωζ2ω1
)ω(
22
TjT
K
jW
+−
= . (7.165)
0
1
2
3
4
0
1
2
3
4
y
(t)
t
2
1
3
Рис. 7.13. Графики переходных функций звеньев 2-го порядка:
1 – консервативного, 2 – колебательного, 3 – апериодического
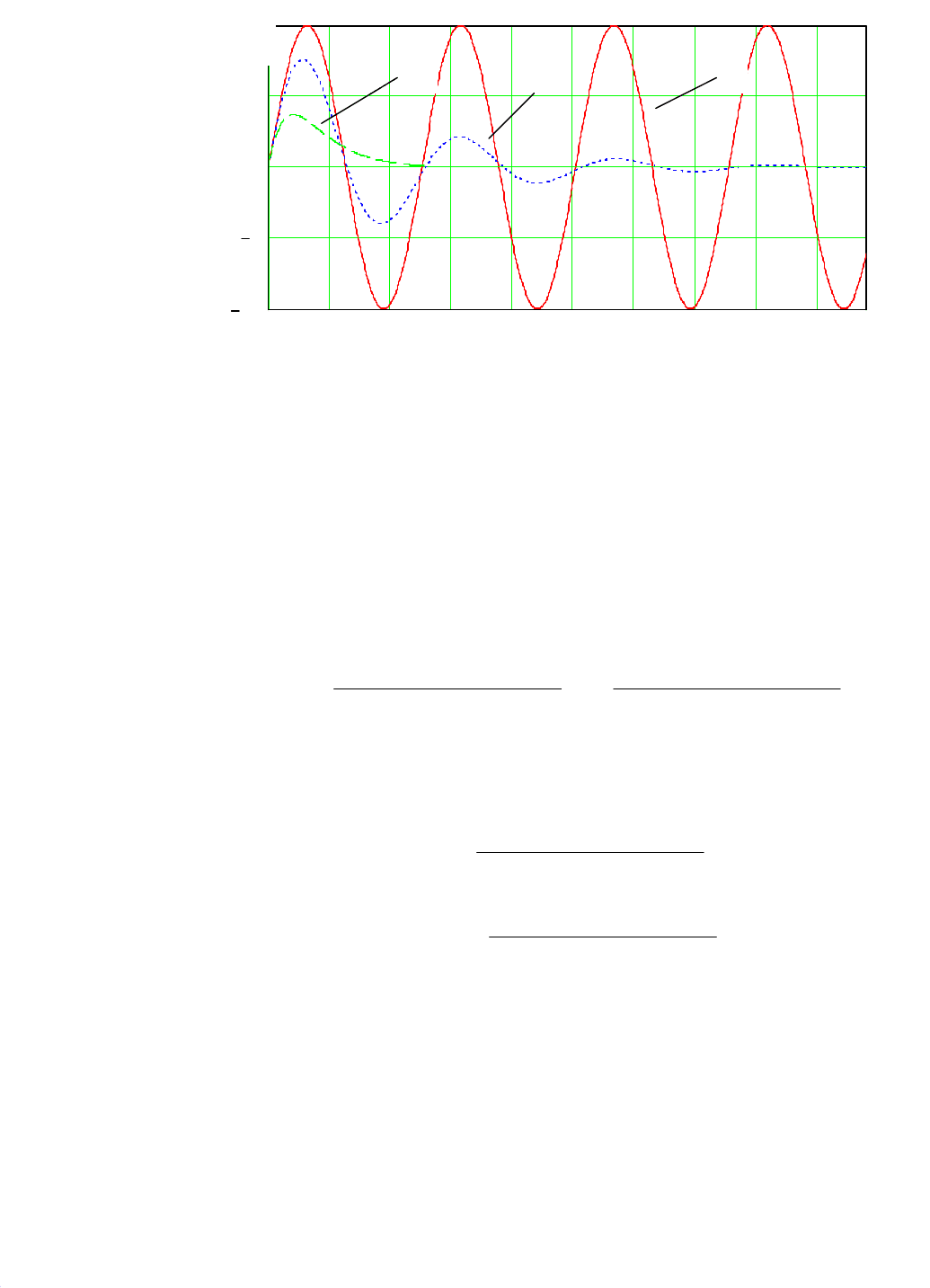
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
10
5
0
5
.
t
y(t)
2
1
3
Рис. 7.14. Графики весовых функций звеньев 2-го порядка:
1 – консервативного; 2 – колебательного; 3 – апериодического
АФЧХ, согласно формуле (6.27), можно представить как сумму вещест-
венной и мнимой частей:
(
)
(
)
(
)
ωωω jQPjW
+
=
. (7.166)
Умножив числитель и знаменатель АФЧХ (7.165) на сопряженную со
знаменателем функцию, выделим вещественную P(ω) и мнимую Q(ω) частот-
ные характеристики:
22222222
22
)ζω2()ω1(
ζω2
)ζω2()ω1(
)ω1(
)ω(
TT
TK
j
TT
TK
jW
+−
⋅−
+−
−
=
. (7.167)
Из формулы (7.167) следует, что вещественная и мнимая частотные ха-
рактеристики определяются соотношениями
2222
22
)ζω2()ω1(
)ω1(
)ω(
TT
TK
P
+−
−
=
; (7.168)
2222
)ζω2()ω1(
ζω2
)(
TT
TK
Q
+−
−=ω . (7.169)
Графики амплитудно-фазовой частотной характеристики колебательного звена
для двух значений коэффициента ζ относительного демпфирования приведены
на рис. 7.15. При изменении частоты ω в диапазоне от 0 до + ∞ амплитудно-
фазовые характеристики расположены ниже вещественной оси, а при отрица-
тельных частотах расположены выше вещественной оси.
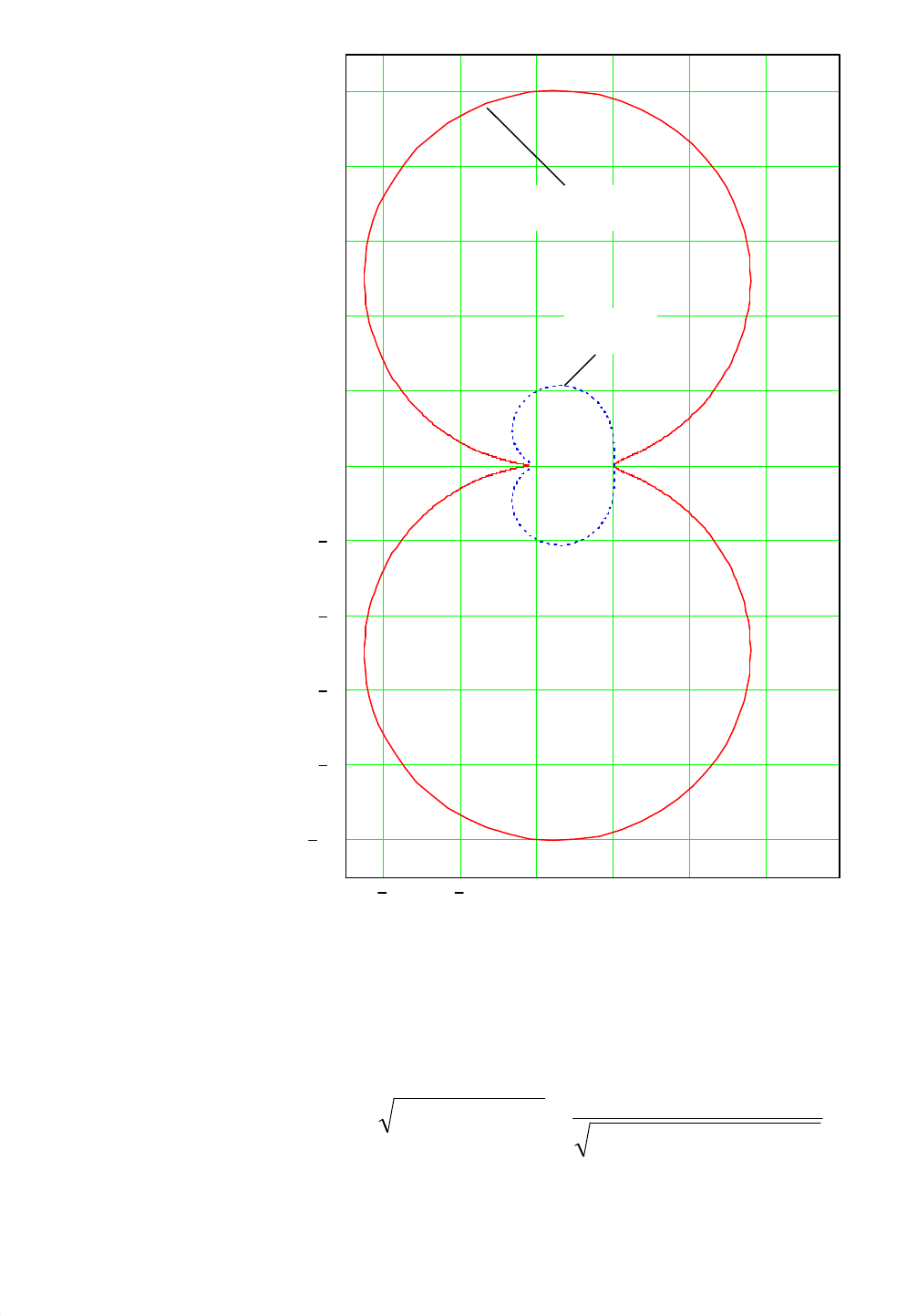
Амплитудную и фазовую частотные характеристики определяем по из-
вестным из комплексного анализа соотношениям:
() () ()
2222
22
)ζω2()ω1(
ωωω
TT
K
QPA
+−
=+=
; (7.170)
Рис. 7.15. Амплитудно-фазовая частотная характеристика
колебательного звена
4 2 0 2 4 6
10
8
6
4
2
0
2
4
6
8
10
.
jQ(ω)
P(ω)
ζ = 0,5
ζ = 0,1

()
(
)
()
22
ω1
ζω2
arctgπ
ω
ω
arctgω
T
T
k
Q
P
−
−=+=ϕ , (7.171)
при ωT < 1 k = 0;
()
(
)
()
π
ω1
ζω2
arctgπ
ω
ω
arctgω
22
−
−
−=+=
T
T
k
Q
P
ϕ , (7.172)
при ωT > 1 k = – 1.
Логарифмическую амплитудную частотную характеристику найдем,
подставив в формулу (6.32) выражение (7.170) амплитудной характеристики. В
результате получим:
(
)
(
)
[
]
2222
)ζω2()ω1(lg10lg20ωlg20ω TTKAL +−−== . (7.173)
Логарифмическая амплитудная частотная характеристика колебательно-
го звена имеет две асимптоты. При низких (ω < 1/T) частотах в формуле
(7.173) пренебрегаем членами, содержащими ωT, в результате получим первую
асимптоту:
KL lg20)ω(
1
=
. (7.174)
При высоких (ω > 1/T) частотах в формуле (7.173) пренебрегаем 1 и 2ζωT, в ре-
зультате получим вторую асимптоту:
TKL ωlg40lg20)ω(
2
−
=
. (7.175)
Первая асимптота параллельна оси абсцисс и проходит выше оси при K
> 1 или ниже оси при K < 1, а при K = 1 совпадает с осью абсцисс. Вторая
асимптота имеет наклон 40 дБ/дек. Это легко проверить, вычислив по формуле
(7.175) разность L
2
(ω
i
) и L
2
(10ω
i
). Обе асимптоты пересекаются в точке, где
частота ω равна частоте ω
0
собственных недемпфированных колебаний (ζ =
0):
T
1
ω
0
= . (7.176)
Логарифмические амплитудная и фазовая частотные характеристики,
построенные соответственно по формулам (7.173) и (7.171), (7.172) при K = 1 и
ω
0
= 100, приведены на рис. 7.16 и 7.17.
Наибольшее отклонение ЛАЧХ (7.173) от своих асимптот имеет в окре-
стности ω
0
. Величина этого отклонения зависит от коэффициента ζ относи-
тельного демпфирования.
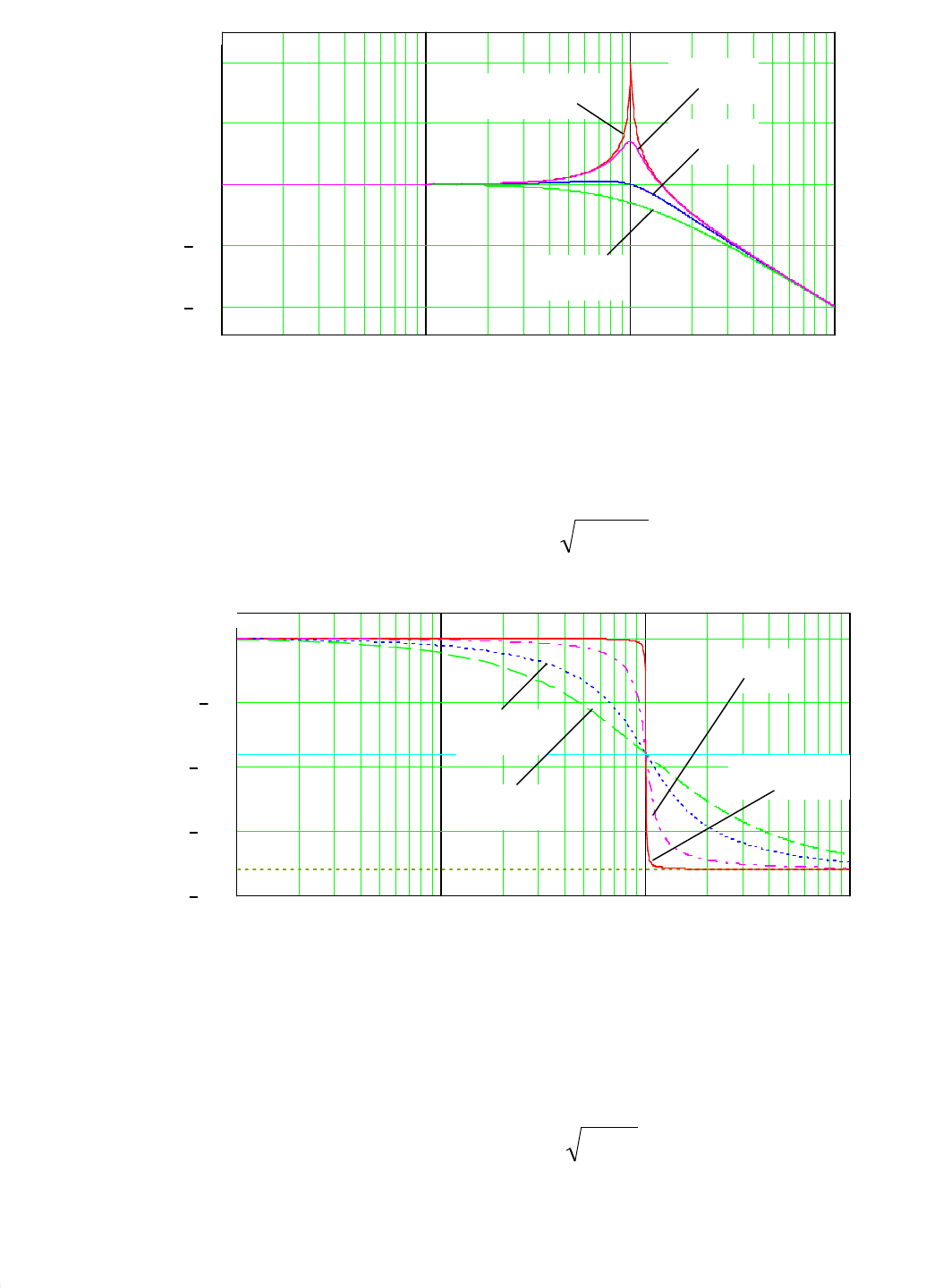
1 10 100 1
.
10
3
200
150
100
50
0
.
φ(ω)
ζ = 1
ω
ζ = 0,1
ζ = 0,5
ζ = 0,005
Рис. 7.17. Логарифмическая фазовая частотная
характеристика колебательного звена
При 0 < ζ < 0,5 на характеристике (7.173) наблюдается резонансный пик.
Максимального значения ЛАЧХ (7.173) достигает при резонансной частоте:
2
0р
21ωω ζ−⋅= . (7.177)
Колебательное звено (0 < ζ < 1) имеет три характерные частоты: резо-
нансную частоту ω
р
, частоту ω
с
свободных колебаний при переходном процес-
се
2
0
ζ1ωω −⋅=
c
(7.178)
L(ω)
ζ = 0,005
ζ = 0,5
Рис. 7.16. Логарифмическая амплитудная частотная
характеристика колебательного звена
1 10 100 1
.
10
3
40
20
0
20
40
.
ζ = 0,5
ζ = 1
ζ = 0,005
ζ = 0,1
L
(
ω
)
ω

и частоту ω
0
собственных недемпфированных колебаний. При ζ = 0 все три
частоты равны ω
0
, а логарифмическая амплитудная частотная характеристика
имеет разрыв.
7.7. Форсирующее звено 2-го порядка
Форсирующее звено 2-го порядка описывается уравнением
++= u
dt
du
T
dt
ud
TKy ζ2
2
2
2
, (7.179)
где y(t) – функция времени, описывающая закон изменения выходной величи-
ны; u(t) – функция времени, описывающая закон изменения входной величи-
ны; T – постоянная времени, зависящая от параметров звена, задается препо-
давателем;
ζ
– коэффициент относительного демпфирования; K – коэффици-
ент усиления.
7.8. Реальное дифференцирующее звено
Реальное дифференцирующее звено описывается уравнением
dt
du
Ty
dt
dy
T =+ , (7.180)
где y(t) – функция времени, описывающая закон изменения выходной величи-
ны; u(t) – функция времени, описывающая закон изменения входной величи-
ны; T – постоянная времени, зависящая от параметров звена, задается препо-
давателем.
Одним из примеров реального дифференцирующего звена может слу-
жить гидравлическое устройство, показанное на рис. 7.18. Его называют ката-
рактом и применяют в автоматических регуляторах для осуществления изо-
дромной обратной связи. Катаракт состоит из пружины 1, цилиндра 2 и порш-
ня 3, имеющего дроссельное отверстие 4.
