Никитин А.А. Управление техническими системами

где F

ГД2

– гидродинамическая сила, действующая на золотник со стороны

жидкости, протекающей через распределитель; F

ТР

– сила трения; F

ПР

– сила,

действующая на торцы золотника со стороны пружин; m

З

– масса золотника.

Гидродинамическую силу F

ГД2

будем считать линейной зависимостью от

смещения золотника и определять по формуле

ЗГД2ГД

2 xcF

−

=

, (8.31)

где

ГД

c – коэффициент жесткости гидродинамической пружины (гидродина-

мическая сила имеет линейную зависимость аналогично силе пружины отсюда

и название коэффициента).

Силу трения будем считать вызванной жидкостным трением и опреде-

лять по формуле

dt

dx

kF

З

ТРТР

⋅= , (8.32)

где k

ТР

– коэффициент трения.

Силу от действия пружин на торцы золотника будем определять по фор-

муле

ЗПРПР

2 xcF

⋅

=

, (8.33)

где с

ПР

– жесткость каждой из пружин.

Подставив в уравнение (8.29) выражения для сил, определяемых соот-

ношениями (8.30)–(8.32), и преобразовав его к форме “вход-выход”, получим:

УЗЗПРГД

З

ТР

2

З

2

З

)(2 pSxcc

dt

dx

k

dt

xd

m ⋅=⋅+⋅+⋅+⋅ . (8.34)

Разделив все члены уравнения (8.34) на коэффициент )(2

ПРГД

cc

+

⋅

при

выходной величине x

З

, получим:

y.З

З

ГУ3ГУ

2

З

2

3ГУ

ζ2 pКx

dt

dx

Т

dt

xd

T

px

⋅=+⋅⋅⋅+⋅ , (8.35)

где Т

ГУ3

– постоянная времени гидроусилителя; ζ

ГУ

– коэффициент относи-

тельного демпфирования гидроусилителя; К

φ.p

– коэффициент преобразования

разности давления p

у

в перемещение золотника x

З

.

Постоянная времени гидроусилителя, коэффициент относительного

демпфирования и коэффициент преобразования определяются по соотношени-

ям:

)(2

ПРГД

З

3ГУ

сс

m

T

+⋅

=

, (8.36)

ЗПРГД

ТР

ГУ

)(22 mсс

k

⋅+⋅⋅

=ζ

, (8.37)

)(2

ПРГД

З

.

сс

S

K

px

+⋅

= . (8.38)

Уравнения (8.17), (8.26) и (8.35) с учетом соотношений (8.18)–(8.21),

(8.27)–(8.29) и (8.36)–(8.38) составляют математическую модель электрогид-

равлического усилителя.

Преобразуем уравнения (8.17), (8.26) и (8.35) по Лапласу, в результате

получим:

)()()()1ζ2(

y.У.ЯЯЯ

22

Я

spКsiКssTsT

pi

⋅−⋅=⋅+⋅⋅⋅+⋅

ϕϕ

ϕ , (8.39)

)()()()1(

З2ГУЯ.y1ГУ

sxsТsКspsT

p

⋅

−

⋅

=

⋅

+

⋅

ϕ

, (8.40)

)()()1ζ2(

y.З3ГУГУ

22

3ГУ

spКsxsТsT

px

⋅=⋅+⋅⋅⋅+⋅ . (8.41)

Найдем из каждого полученного уравнения изображение выходной

величины:

[

]

)()(

)1ζ2(

1

)(

y.У.

ЯЯ

22

Я

spКsiК

sTsT

s

pi

⋅−⋅⋅

+⋅⋅⋅+⋅

=

ϕϕ

ϕ

, (8.42)

[

]

)()(

)1(

1

)(

ЗГУ2Я.

1ГУ

y

sxsТsК

sT

sp

p

⋅⋅−⋅⋅

+⋅

= ϕ

ϕ

, (8.43)

)(

)1ζ2(

)(

y

3ГУГУ

22

3ГУ

.

З

sp

sТsT

К

sx

px

⋅

+⋅⋅⋅+⋅

= . (8.44)

Введем обозначения:

)1ζ2(

1

)(

ЯЯ

22

Я

1

+⋅⋅⋅+⋅

=

sTsT

sW , (8.45)

)1(

1

)(

1ГУ

2

+⋅

=

sT

sW , (8.46)

)1ζ2(

)(

3ГУГУ

22

3ГУ

.

3

+⋅⋅⋅+⋅

=

sТsT

К

sW

px

. (8.47)

Уравнения (8.42)–(8.44) с учетом соотношений (8.45)–(8.47) примут вид

[

]

)()()()(

y.У.1Я

spКsiКsWs

pi

⋅

−

⋅

=

ϕϕ

ϕ

, (8.48)

[

]

)()()()(

З2ГУЯ.2y

sxsТsКsWsp

p

⋅

−

⋅

=

ϕ

, (8.49)

)()()(

У3З

spsWsx

⋅

=

. (8.50)

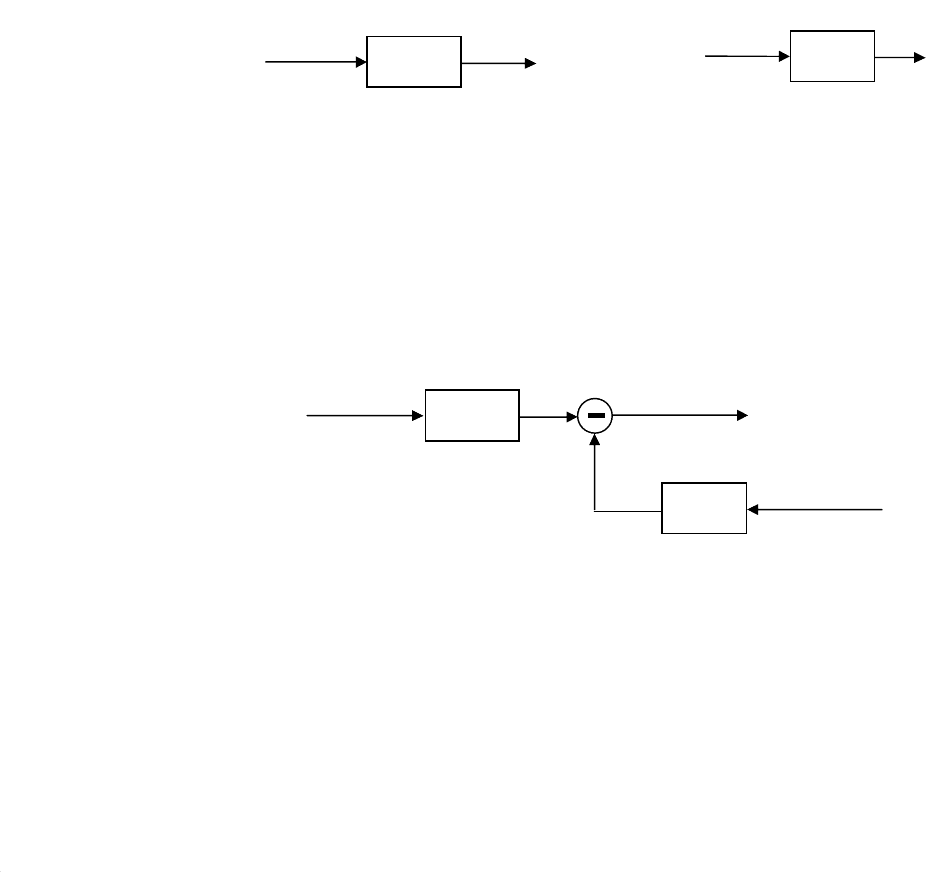
По уравнениям (8.48)–(8.50) построим структурную схему электрогид-

равлического усилителя. Построение начнём с уравнения (8.48), так как в него

входит изображение входной величины i

У

(s). На схеме, показанной на рис. 8.5,

а, входная величина i

У

(s) должна пройти через пропорциональное звено с пе-

редаточной функцией, равной коэффициенту К

φ.i

, – это соответствует пер-

вому члену К

φ.i

∙ i

У

(s) в квадратной скобке уравнения (8.48), содержащему

изображение переменной величины, умноженное на постоянный коэффициент.

Второй член К

φ.p

∙ p

У

(s) в квадратной скобке содержит изображение p

У

(s), ум-

ноженное на постоянный коэффициент К

φ.p

, поэтому ему на структурной схеме

(рис. 8.5, б) соответствует такой же элемент.

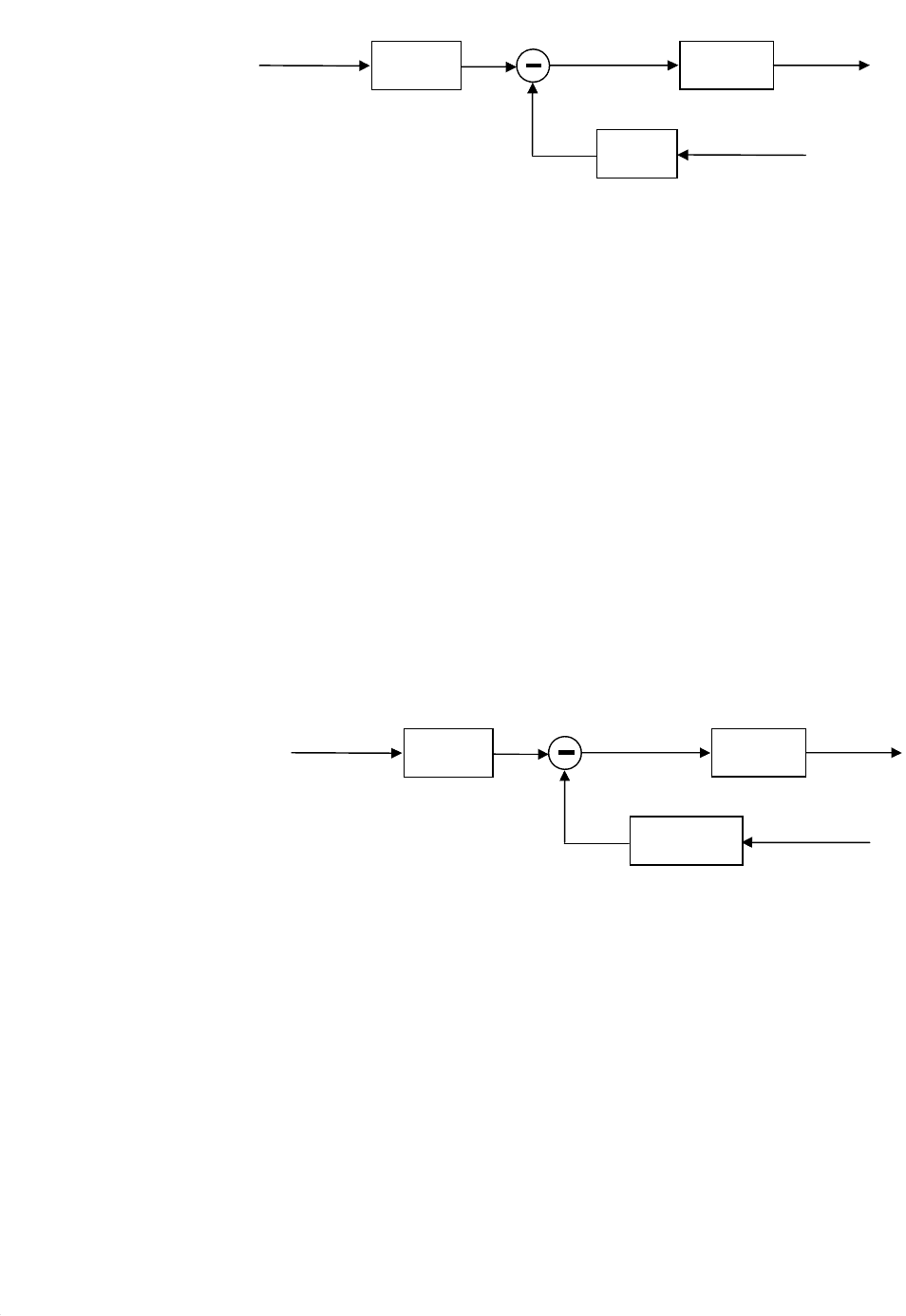
Квадратной скобке в правой части уравнения (8.48) на структурной схе-

ме (рис. 8.6) соответствуют первый и второй элементы, объединенные в узле

алгебраического суммирования (на схеме изображается кружочком со знаком

внутри “+” для операции сложения или “─” для операции вычитания).

Квадратная скобка в правой части уравнения (8.48) умножается на пере-

даточную функцию W

1

(s), поэтому на структурной схеме третий элемент (рис.

8.6) должен пройти через звено с передаточной функцией W

1

(s) (рис. 8.7),

а на выходе, согласно уравнению (8.48), получим φ

Я

(s).

К

φ.i

i

У

(s)

Рис. 8.5. Первый (а) и второй (б) элементы структурной схемы

К

φ.p

p

У

(s)

а

б

К

φ.i

i

У

(s)

К

φ.p

p

У

(s)

Рис. 8.6. Третий элемент структурной схемы

Аналогично строим структурную схему (рис. 8.8), соответствующую

уравнению (8.49). Построение начнём с входной величины, её изображение

φ

Я

(s) входит в состав квадратной скобки. Входная величина φ

Я

(s) (рис. 8.8)

должна пройти через пропорциональное звено с передаточной функцией, рав-

ной коэффициенту К

p.φ

– это соответствует первому члену К

p.φ

∙ φ

Я

(s) в квад-

ратной скобке уравнения (8.49), содержащему изображение переменной вели-

чины, умноженное на постоянный коэффициент.

Второй член

)(

З2ГУ

sxsТ

⋅

в квадратной скобки уравнения (8.49) соот-

ветствует обратной цепи (рис. 8.8). Вычитание из первого члена квадратной

скобки уравнения (8.49) второго происходит в алгебраическом узле суммиро-

вания. Далее сигнал должен пройти через звено с передаточной функцией

W

2

(s), так как квадратная скобка уравнения (8.49) умножается на W

2

(s). В ре-

зультате на выходе получим изображение управляющего давления p

У

(s), что

соответствует левой части уравнения (8.49).

Двум уравнениям (8.48) и (8.49) на структурной схеме (рис. 8.9) соответ-

ствует объединение четвёртого (рис. 8.7) и пятого (рис. 8.8) элементов.

К

φ.i

i

У

(s)

К

φ.p

p

У

(s)

Рис. 8.7. Четвёртый элемент структурной схемы

W

1

(s)

φ

Я

(s)

К

p.φ

φ

Я

(s)

Т

ГУ2

∙ s

x

З

(s)

Рис. 8.8. Пятый элемент структурной схемы

W

2

(s)

p

У

(s)

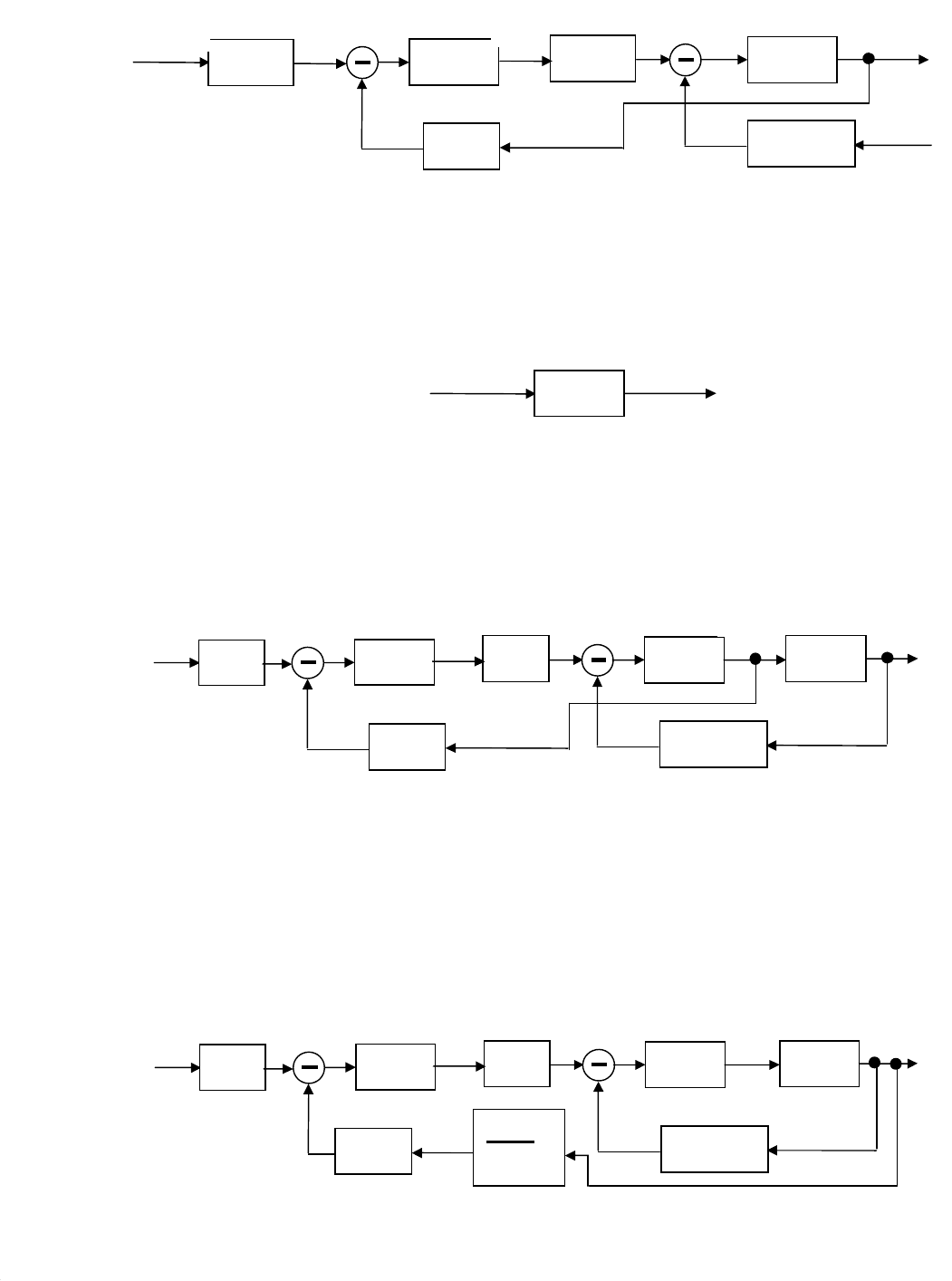
Строим элемент структурной схемы (рис. 8.10) соответствующий урав-

нению (8.49).

Трём уравнениям (8.48), (8.49) и (8.50) на структурной схеме (рис. 8.11)

соответствует объединение шестого (рис. 8.9) и седьмого (рис. 8.10) элемен-

тов.

Для проверки ЭГУ усилителя на устойчивость с помощью логарифмиче-

ских частотных характеристик удобнее структурную схему, приведенную на

рис. 8.11, преобразовать к виду, в котором обратные связи не пересекают-

ся.

x

З

(s)

Рис. 8.10. Седьмой элемент структурной схемы

W

3

(s)

p

У

(s)

К

φ.i

i

У

(s)

К

φ.p

p

У

(s)

Рис. 8.9. Шестой элемент структурной схемы

W

1

(s)

φ

Я

(s)

К

p.φ

Т

ГУ2

∙ s

x

З

(s)

W

2

(s)

p

У

(s)

К

φ.i

i

У

(s)

К

φ.p

p

У

(s)

Рис. 8.11. Структурная схема ЭГУ

W

1

(s)

φ

Я

(s)

К

p.φ

Т

ГУ2

∙ s

x

З

(s)

W

2

(s)

p

У

(s)

x

З

(s)

W

3

(s)

К

φ.i

i

У

(

s

)

К

φ.p

p

У

(s

)

Рис. 8.12. Структурная схема ЭГУ

W

1

(s)

φ

Я

(s)

К

p.φ

Т

ГУ2

∙ s

x

З

(s)

W

2

(s)

p

У

(s)

x

З

(s)

W

3

(s)

_1__

W

3

(s)

Перенесём левый узел разветвления вправо через звено с передаточной

функцией W

3

(s). Чтобы в обратной связи получить изображение p

у

(s), нужно

сигнал, забираемый из полученного узла разветвления, пропустить через звено

с передаточной функцией 1/W

3

(s) обратной W

3

(s). Полученная после эквива-

лентного преобразования структурная схема ЭГУ показана на рис. 8. 12.

Вопросы для самопроверки

1. Постройте структурную схему ЭМП.

2. Постройте структурную схему ГУ.

3. Найдите передаточную функцию прямой цепи ГУ.

4. Найдите передаточную функцию замкнутого контура ГУ.

5. Найдите передаточную функцию разомкнутого контура ГУ.

6. Дайте пример переноса узла разветвления на примере схемы ЭГУ.

9. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ.

КРИТЕРИИ УСТОЙЧИВОСТИ

Понятие устойчивости линейных систем. Критерий устойчивости

Рауса - Гурвица. Критерий Михайлова. Критерий устойчивости Найквиста.

Использование логарифмических характеристик для исследования устойчиво-

сти. Понятие о запасе устойчивости. Оценка влияния коэффициента усиле-

ния на устойчивость систем. Способы обеспечения устойчивости.

Под устойчивостью понимается способность системы сохранять задан-

ные состояния равновесия или заданные виды движения.

Устойчивая система при отклонениях от равновесного состояния или ус-

тановившегося движения вследствие внешних воздействий должна возвра-

щаться к нему с заданной точностью.

В неустойчивой системе автоматического регулирования после любого

случайного возмущения возникают незатухающие колебания, или колебания с

нарастающей во времени амплитудой, или отклонение регулируемой величи-

ны монотонно нарастает во времени.

Для линейных стационарных систем условие устойчивости заключается

в том, чтобы все корни характеристического уравнения, полученного по диф-

ференциальному уравнению этой системы, имели бы отрицательные вещест-

венные части, т. е. располагались на комплексной плоскости слева от мнимой

оси.

Расположение корней на комплексной плоскости относительно мнимой

оси может быть установлено по критериям устойчивости без решения харак-

теристического уравнения. Критерии устойчивости разделяют на алгебраиче-

ские и частотные.

9.1. Алгебраические критерии устойчивости

Среди алгебраических критериев устойчивости известны критерий Э.

Рауса (1875 г.) и критерий А. Гурвица (1895 г.). В технических расчетах широ-

кое распространение получил критерий Гурвица. Согласно этому критерию

для устойчивости системы необходимо и достаточно, чтобы все коэффициен-

ты характеристического уравнения (9.2) и определители ∆

n

, ∆

n-1

,…, ∆

1

были

положительными.

Пусть система описывается линейным дифференциальным уравнением в

форме “вход-выход”:

ub

dt

du

b

dt

ud

b

dt

ud

bya

dt

dy

a

dt

yd

a

dt

yd

a

m

n

n 01

1

101

1

...... +++=+++

−

,(9.1)

где u = u(t) – входная величина (закон изменения параметра, характеризующе-

го воздействие на систему, – входной сигнал); y = y(t) – выходная величина

(закон изменения параметра, характеризующего состояние системы, – выход-

ной сигнал); a

1

, …, a

n

, b

1

, …, b

m

– постоянные коэффициенты.

Уравнению (9.1) соответствует характеристическое уравнение n-й сте-

пени, составленное из коэффициентов его левой части:

0λ...λλ

01

1

=++++

−

aaaa

n

. (9.2)

Определители составляются из коэффициентов характеристического

уравнения (9.2). Вначале составляют определитель ∆

n

.

0

2345

123

1

...0000

..................

......

0...00

a

aaaa

aa

nnnn

nn

n −−−−

−−−

−

=∆ . (9.3)

Все последующие определители (∆

n-1

, ∆

n-2

…, ∆

1

) являются минорами

элементов определителя ∆

n

, которые получаются вычеркиванием столбцов и

строк, на пересечении которых стоят элементы главной диагонали, начиная с

а

0

.

Для характеристического уравнения n-й степени условие устойчивости

системы по критерию Гурвица можно записать в виде неравенств:

.0...,,0,0,0

;0...,,0,0,0

321

210

>∆>∆>∆>∆

>

n

aaaa

(9.4)

При составлении определителя ∆

1

мы должны в определителе ∆

n

вычеркнуть

все столбцы кроме 1-го и вычеркнуть все строки кроме 1-й, согласно формуле

(9.3); останется только один элемент a

n-1

. Следовательно, ∆

1

= a

n-1

. Поэтому ес-

ли a

n-1

> 0, то условие ∆

1

> 0 в неравенствах (9.4) становится лишним. Так как

в нижней строке определителя ∆

n

все элементы равны нулю, кроме a

0

, то ∆

n

=

а

0

∙ ∆

n-1

, поэтому если a

0

> 0 и ∆

n-1

> 0, то условие ∆

n

> 0 в неравенствах (9.4)

тоже становится лишним.

Таким образом, условие устойчивости (9.4) можно заменить следующи-

ми неравенствами:

.0...,,0,00

;0...,,0,0,0

1432

210

>∆>∆>∆>∆

>

−n

n

aaaa

(9.5)

Условие устойчивости систем по Гурвицу будет иметь вид:

1) при n = 1

a

0

> 0, a

1

> 0; (9.6)

2) при n = 2

a

0

> 0, a

1

> 0, a

2

> 0; (9.7)

3) при n = 3

a

0

> 0, a

1

> 0, a

2

> 0, a

3

> 0, ∆

2

> 0. (9.8)

Так как определитель ∆

3

равен

0

210

32

3

00

0

a

aaa

aa

=∆ , (9.9)

то, вычеркивая столбец и строку, на пересечении которых находится элемент

a

0

, получаем определитель ∆

2

3012

10

32

2

aaaa

aa

⋅−⋅==∆ , (9.10)

следовательно, условие устойчивости можно записать в виде

a

0

> 0, a

1

> 0, a

2

> 0, a

3

> 0, (9.11)

0

3012

>

⋅

−

⋅

aaaa

; (9.12)

4) при n = 4

a

0

> 0, a

1

> 0, a

2

> 0, a

3

> 0, a

4

> 0, ∆

2

> 0, ∆

3

> 0; (9.13)

так как ∆

4

равен

0

210

4321

43

4

000

0

00

a

aaa

aaaa

aa

=∆

, (9.14)

то, вычеркивая столбец и строку, на пересечении которых находится элемент

a

0

, получаем определитель ∆

3

2

304

2

1321

10

321

43

3

0

aaaaaaa

aa

aaa

aa

⋅−⋅−⋅⋅==∆

. (9.15)

А вычеркивая столбцы и строки, на пересечении которых находятся элементы

a

0

и a

1

, получаем определитель ∆

2

.

4132

21

43

2

aaaa

aa

⋅−⋅==∆ . (9.16)

Следовательно, условие устойчивости можно записать в виде

a

0

> 0, a

1

> 0, a

2

> 0, a

3

> 0, a

4

> 0, (9.17)

0

4132

>

⋅

−

⋅

aaaa

, (9.18)

0

2

304

2

1321

>⋅−⋅−⋅⋅ aaaaaaa

. (9.19)

Как видно, уже для уравнения 4-й степени условия устойчивости по кри-

терию Гурвица получаются громоздкими. Поэтому использование этого кри-

терия практически ограничивается уравнениями третьего или четвертого по-

рядка.

9.2. Частотные критерии устойчивости

Частотные критерии устойчивости основаны на связи между формой

частотной характеристики системы автоматического регулирования и характе-

ром расположения корней характеристического уравнения. К частотным кри-

териям устойчивости относятся: критерии Михайлова и Найквиста. Для про-

верки систем на устойчивость применяют также логарифмические частотные

характеристики.

Критерий устойчивости Михайлова

Рассмотрим критерий устойчивости Михайлова (1938 г.). Левая часть

характеристического уравнения (9.2) представляет характеристический много-

член

01

1

λ...λλ)λ( aaaaD

n

++++=

−

. (9.20)

Из характеристического многочлена (9.20) подстановкой λ = j ∙ ω можно

получить комплексную функцию

Никитин А.А. Управление техническими системами

Подождите немного. Документ загружается.