Никитин А.А. Управление техническими системами
Подождите немного. Документ загружается.


линдр называется ненагруженным. При перечисленных допущениях из урав-
нения (7.65) следует равенство давлений:
p
1
= p
2
. (7.69)
При равенстве рабочих площадей поршня из уравнений (7.66) и (7.67) следует
равенство расходов, которые можно обозначить одной буквой:
ЗЗЗ
QQQ
=
=
21
. (7.70)
На основании соотношений (7.70), (7.63) и (7.64) следует равенство
2
СЛП
СЛ21П
pp
pppp
−
=−=− . (7.71)
На основании соотношений (7.70), (7.71) и принятых выше допущений о сим-
метричности распределителя и гидроцилиндра систему уравнений (7.63)–
(7.67) можно заменить системой двух уравнений:
ρ
µ
СЛП
ОК2
pp
xbQ
ЗЗЗ
−
= , (7.72)
dt
dy
fQ
З
ШТ
Ц
= . (7.73)
Система уравнений (7.68), (7.72)–(7.73) является математической моде-
лью гидропривода при принятых выше допущениях. Эту систему уравнений
легко привести к одному уравнению (уравнению апериодического звена 1-го
порядка). Для этого приравняем правые части уравнений (7.72) и (7.73) и за-
меним x
З
согласно соотношению (7.68), в результате получим
AШТ
ШТ
Г
Khy
dt
dy
T =+ , (7.74)
где
ρ
μ
СЛП
ОКЗО.С
Ц
Г
pp
bK
f
T
−
⋅⋅⋅
= – постоянная времени гидравлического
механизма;
О.С
KKK
xh
=
– коэффициент усиления.

7.5. Форсирующее звено 1-го порядка
Форсирующее звено 1-го порядка описывается уравнением
+⋅⋅= u
dt
du
TKy
, (7.75)
где y(t) – функция времени, описывающая закон изменения выходной величи-
ны; u(t) – функция времени, описывающая закон изменения входной величи-
ны; K – коэффициент передачи; T – постоянная времени, зависящая от пара-
метров звена.
Переходную и весовую функции форсирующего звена можно найти как
суммы соответствующих функций дифференцирующего и пропорционального
звеньев:
)]
1
(
1
)
(
δ
[
)
(
)
(
+
⋅
⋅
=
=
t
T
K
t
h
t
y
, (7.76)
+⋅⋅== )(δ
)(δ
)()( t
dt
td
TKtwty . (7.77)
Применив преобразования Лапласа и его свойства, дифференциальное
уравнение (7.75) при нулевых начальных условиях можно заменить алгебраи-
ческим:
)
(
)
1
(
)
(
s
U
s
T
K
s
Y
⋅
+
⋅
⋅
=
(7.78)
или
)
(
)
(
)
(
)
(
s
U
s
M
s
Y
s
D
⋅
=
⋅
, (7.79)
где
1
)
(
=
s
D
и
)
1
(
)
(
+
⋅
⋅
=
s
T
K
s
M
. (7.80)
Передаточная функция W(s) определяется как отношение Y(s) к U(s). Для апе-
риодического звена из уравнения (7.78) или (7.79) получим
)1(
)(
)(
)(
)(
)( +⋅⋅=== sTK
sD
sM
sU
sY
sW
. (7.81)
Используя передаточную функцию W(s), уравнение (7.78) можно запи-
сать в следующем виде:
)
(
)
(
)
(
s
U
s
W
s
Y
⋅
=
. (7.82)
Амплитудно-фазовую частотную характеристику можно найти с помо-
щью подстановки s = jω в передаточную функцию (7.81):
)
ω
1
(
)
ω
(
T
j
K
j
W
⋅
⋅
+
⋅
=
. (7.83)

Из формулы (7.83) следует, что вещественная и мнимая частотные ха-
рактеристики определяются соотношениями
K
P
=
)
ω
(
, (7.84)
T
K
Q
⋅
⋅
=
ω
)
ω
(
. (7.85)
Амплитудную частотную характеристику звена определим как модуль
амплитудно-фазовой частотной характеристики W(jω), с учетом соотношений
(7.84) и (7.85) получим
222
)ω(1)ω()ω()ω()ω( TKQPjWA ⋅+⋅=+==
. (7.86)
Фазовую частотную характеристику можно найти, используя формулу
(6.29), с учетом соотношений (7.84) и (7.85) получим
)ω(arctg
)ω(
)ω(
arctg)ω(arg)ω( T
P
Q
jW ⋅===ϕ (7.87)
Логарифмическую амплитудную частотную характеристику можно най-
ти с помощью формул (6.32) и (7.86), в результате получим
[
]
2
)ω(1lg10lg20)ω(lg20)ω( TKAL ⋅+⋅+⋅=⋅= . (7.88)
Логарифмическая амплитудная частотная характеристика имеет две
асимптоты. При частоте ω, стремящейся к нулю, пренебрегая вторым слагае-
мым в квадратных скобках формулы (7.88), получаем уравнение первой асим-
птоты
K
L
lg
20
)
ω
(
⋅
≈
. (7.89)
При частоте
T1ω
>>
, пренебрегая первым слагаемым в квадратных
скобках формулы (7.88), получаем уравнение второй асимптоты
)
ω
lg(
20
lg
20
)
ω
(
T
K
L
⋅
⋅
+
⋅
≈
. (7.90)
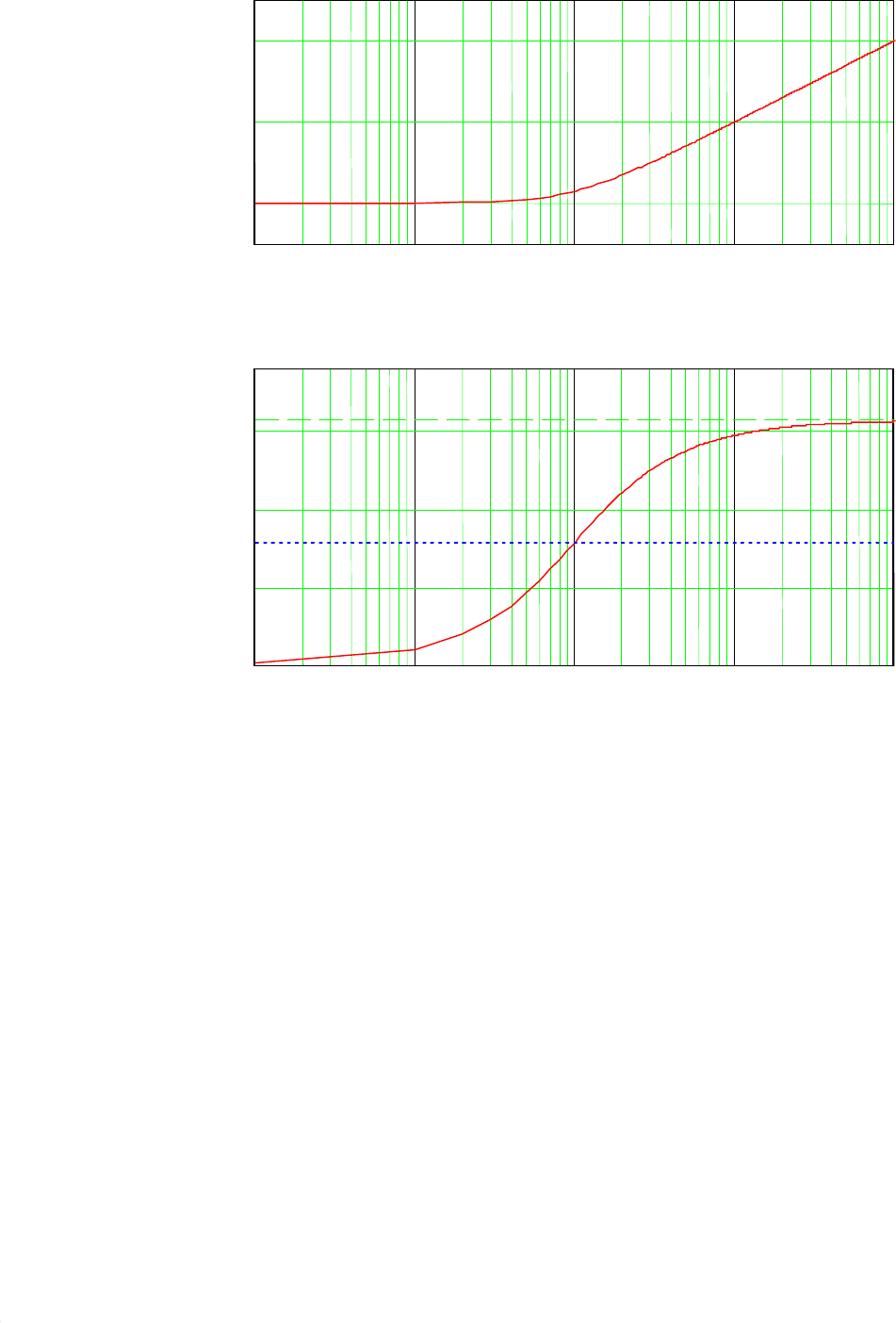
График логарифмической амплитудной частотной характеристики для K
= 1 приведен на рис. 7.10.
1
10
100
1
.
10
3
1
.
10
4
0
0.5
1
1.5
φ(ω)
ω
Рис.7.11. Логарифмическая фазовая частотная характеристика
Лога-
рифмическая фазовая частотная характеристика (рис. 7.11) форсирующего
звена первого порядка, построенная по уравнению (7.87), при положительных
значениях частоты изменяется от 0 до π/2, проходя через точку φ(ω) = π/4 при
ω = 1/T .
Графики (рис. 7.9 и 7.10) частотных характеристик форсирующего звена
первого порядка являются зеркальным отражением относительно оси частот
графиков (рис. 7.7 и 7.8) частотных характеристик апериодического звена пер-
вого порядка.
1 10
100
1
.
10
3
1
.
10
4
0
20
40
L
ω
(
)
ω
Рис. 7.10. Логарифмическая
амплитудная частотная характеристика

7.6. Колебательное и апериодическое звенья 2-го порядка
Уравнения звеньев 2-го порядка имеют вид
Kuy
dt
dy
T
dt
yd
T =+ζ+ 2
2
2
2
, (7.91)
где y(t) – функция времени, описывающая закон изменения выходной величи-
ны; u(t) – функция времени, описывающая закон изменения входной величи-
ны; T – постоянная времени, зависящая от параметров звена, задается препо-
давателем; ζ – коэффициент относительного демпфирования; K – коэффициент
усиления.
Звено называется колебательным, если коэффициент ζ относительного
демпфирования лежит в интервале 0 < ζ < 1, а при ζ ≥ 1 – апериодическим. Ес-
ли ζ = 0, то звено становится консервативным. Названия звеньев связаны с ви-
дом переходного процесса (т. е. законом изменения y(t)), вызванного измене-
нием входного сигнала в виде единичной ступенчатой функции 1(t).
Одним из примеров звена второго порядка может служить следящий
гидропривод, схема которого изображена на рис. 7.9.
Составим математическое описание гидравлического механизма, пред-
полагая, что питание его рабочей жидкостью осуществляется при постоянном
давлении (p
П
= const) от источника с неограниченным расходом. Гидролинии
от золотникового распределителя к гидроцилиндру будем принимать настоль-
ко короткими, чтобы в них можно было бы не учитывать потери давления и
волновые процессы.
Для гидрораспределителя, когда окна распределителя имеют равные ко-
эффициенты расхода, при нулевых перекрытиях золотника, без учета утечек и
перетечек рабочей жидкости в распределителе, можно записать два уравнения
расходов:
ρ
)(2
μ
1П
ЗОКЗ1
pp
xbQ
З
−
=
, (7.92)
ρ
)(2
μ
СЛ2
ЗОКЗ2
pp
xbQ
З
−
=
, (7.93)
где Q
З1
– расход рабочей жидкости, втекающей в гидроцилиндр; Q
З2
– расход
рабочей жидкости, вытекающей из гидроцилиндра; µ
З
– коэффициент расхода

окон золотникового распределителя; b
ОК
– ширина окон во втулке (если окно,
расположенное напротив бурта золотника, занимает весь периметр втулки, то
b
ОК
= πd
З
; x
З
– смещение золотника от нейтрального положения; p
З
– давление
питания в напорной гидролинии; p
СЛ
– давление в сливной гидролинии; p
1
и p
2
– давления в левой и правой полостях гидроцилиндра; ρ – плотность жидко-
сти.
Для гидроцилиндра можно записать уравнение движения поршня и
уравнения расходов (втекающего и вытекающего) без учета сжимаемости
жидкости:
2
П
2
ПРТР22Ц11Ц
dt
yd
mFFpfpf =−−− , (7.94)
dt
dy
fQ
З
П
1Ц1
=
, (7.95)
dt
dy
fQ
З
П
2Ц2
= , (7.96)
где f
Ц1
и f
Ц2
– рабочие площади поршня (т. е. площадь поршня минус площадь
штока) в левой и правой полостях гидроцилиндра; F
ТР
– сила трения, дейст-
вующая на поршень и шток; F – внешняя нагрузка; m
ПР
– суммарная масса
поршня, штока и приведенной массы рабочих органов, приводимых в движе-
ние штоком; y
П
– перемещение штока.
Для завершения построения математической модели следящего гидро-
привода необходимо еще записать уравнение, устанавливающее связь между
перемещением точки A рычага AOB, которое является управляющим сигна-
лом, перемещением золотника и перемещением штока гидроцилиндра. Если
корпуса распределителя и гидроцилиндра закреплены неподвижно, то имеем
следующее кинематическое соотношение:
ПО.С.AЗ
yKhKx
xh
−
=
, (7.97)
где
AOOBK
xh
=
,
CD
AO
DOAB
K
⋅
⋅
=
О.С.
, (7.98)
K
xh
– коэффициент передачи механизма управления гидроприводом; K
O.C
– ко-
эффициент обратной связи гидропривода.
Система уравнений (7.92)–(7.97) является нелинейной математической
моделью рассматриваемого гидравлического механизма. В некоторых случаях
ее можно заменить более простой моделью.

Пусть гидроцилиндр выполнен с одинаковыми значениями рабочих
площадей в левой и правой полостях (f
Ц1
= f
Ц2
), обозначим эти площади через
f
Ц
. Пусть также в уравнении (7.94) можно пренебречь силой трения и внешней
нагрузкой по сравнению с инерционной нагрузкой, равной произведению при-
веденной массы на ускорение. В этом случае уравнение (7.94) примет сле-
дующий вид:
2
П
2
ПР21Ц
)(
dt
yd
mppf =− . (7.99)
При равенстве рабочих площадей поршня из уравнений (7.95) и (7.96)
следует равенство расходов, которые можно обозначить одной буквой:
ЗЗ21З
QQQ
=
=
. (7.100)
На основании соотношений (7.100), (7.92), (7.93) и принятых выше до-
пущениях следует равенство
2
НСЛП
СЛ21П
ppp
pppp
−
−
=−=− , (7.101)
где
21Н
ppp
−
=
– перепад давлений в полостях гидроцилиндра. На основа-
нии соотношений (7.100), (7.101) и принятых выше допущениях о симметрич-
ности распределителя и гидроцилиндра уравнения расходов (7.92), (7.93),
(7.95) и (7.96) можно заменить двумя уравнениями:
ρ
μ
НСЛП
ЗОКЗЗ
ppp
xbQ
−−
=
, (7.102)
dt
dy
fQ
П
ЦЗ
= . (7.103)
Система уравнений (7.97), (7.99), (7.102) и (7.103) является также нели-
нейной математической моделью гидропривода при принятых выше допуще-
ниях (хотя и более простой). Для получения линейной модели необходимо не-
линейное уравнение (7.102) линеаризовать путем перехода к малым отклоне-
ниям переменных от значений, которые они имеют на установившемся режиме
гидропривода. Значения переменных на установившемся режиме будем отме-
чать индексом 0 (h
A.0
, x
З.0
, y
П.0
, p
Н.0
, Q
З.0
). Малые отклонения переменных бу-
дем отмечать штрихом (
A
h
′
,
З
x
′
,
П
y
′
,
Н
p
′
,
З
Q
′
). Тогда переменные можно выра-
зить через малые отклонения переменных и значения переменных на устано-
вившемся режиме:
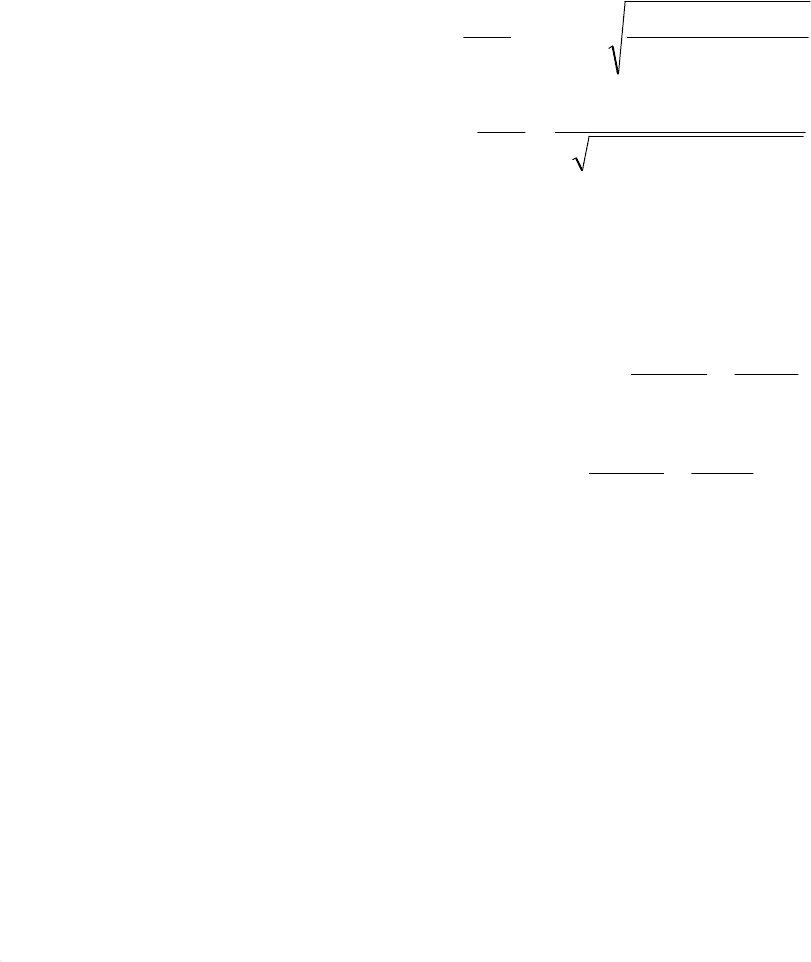
A0.AA
hhh
′
+
=
, (7.104)
З0.ЗЗ
xxx
′
+
=
, (7.105)
П0.ПП
yyy
′
+
=
, (7.106)
Н0.НН
ppp
′
+
=
, (7.107)
З0.ЗЗ
QQQ
′
+
=
. (7.108)
Проведем линеаризацию уравнения (7.102): разложим его в ряд Тейлора
в окрестности установившихся значений переменных и отбросим нелинейные
члены ввиду их малости, в результате получим
НЗ0.ЗЗ
pKxKQQ
QpQx
′
⋅
−
′
⋅
+
=
, (7.109)
где
ρ
μ
0.НСЛП
ОКЗ
З
З
ppp
b
x
Q
K
Qx
−−
=
∂
∂
=
; (7.110)
)(ρ2
μ
0.НСЛП
0.ЗОКЗ
Н
З
ppp
xb
p
Q
K
Qp
−−
=
∂
∂
= . (7.111)
Система уравнений (7.97), (7.99) и (7.103) после подстановки в нее вы-
ражений для переменных из соотношений (7.104)–(7.107) примет вид
)()(
П0.ПО.С.A0.AЗ0.З
yyKhhKxx
xh
′
+
−
′
+
=
′
+
, (7.112)
′
+=
′
+
2
П
2
2
0.П
2
ПРЦ0.НЦ
dt
yd
dt
yd
mpfpf
Н
, (7.113)
′
+=
′
+
dt
yd
dt
dy
fQQ
ШТ0.ШТ
ЦЗ0.З
. (7.114)
Система уравнений (7.109), (7.112)–(7.114) описывает переходный про-
цесс в окрестности установившегося режима. При равенстве нулю малых от-
клонений переменных
0
A
=
′
h
,
0
З
=
′
x
,
0
П
=
′
y
,
0
Н
=
′
p
,
0
З
=
′
Q
система
уравнений (7.109), (7.112)–(7.114) описывает установившийся режим, в этом
случае она принимает вид
0.З0.З
QQ
=
, (7.115)
0.ПО.С.0.A0.З
yKhKx
xh
−
=
, (7.116)

2
0.П
2
ПР0.Н
dt
yd
mpf
Ц
= , (7.117)
dt
dy
fQ
0.П
Ц0.З
= . (7.118)
Вычитая из системы уравнений (7.109), (7.112)–(7.114), описывающей
переходный процесс, систему уравнений (7.115)–(7.118), описывающую уста-
новившийся режим, получим систему уравнений, описывающую переходный
процесс в малых отклонениях:
НЗЗ
pKxKQ
QpQx
′
⋅
−
′
⋅
=
′
, (7.119)
ПО.С.AЗ
yKhKx
xh
′
⋅
−
′
⋅
=
′
, (7.120)
2
П
2
ПРНЦ
dt
yd
mpf
′
=
′
, (7.121)
dt
yd
fQ
П
ЦЗ
′
=
′
. (7.122)
Систему уравнений (7.119)–(7.122) нетрудно привести к одному уравне-
нию в форме "вход-выход". Для этого исключим переменные
З
x
′
,
Н
p
′
,
З
Q
′
и пе-
ренесем в левую часть уравнения члены, содержащие выходную величину, а
члены, содержащие входную величину, – в правую, в результате получим
AП
П
1
2
П
2
2
2
hKy
dt
yd
T
dt
yd
T
′
⋅=
′
+
′
+
′
, (7.123)
где
О.СЦ
2
KKf
mK
T
Qx
Qp
= – постоянная времени;
О.С
Ц
1
KK
f
T
Qx
=
– постоянная
времени;
О.С
K
K
K
xh
= – коэффициент усиления.
Уравнение (7.123) описывает систему второго порядка, принимая
TT
=
2
и вводя новую величину
T
T
2
ζ
1
= , (7.124)
которая называется коэффициентом относительного демпфирования, прида-
дим уравнению (7.123) форму уравнения колебательного звена
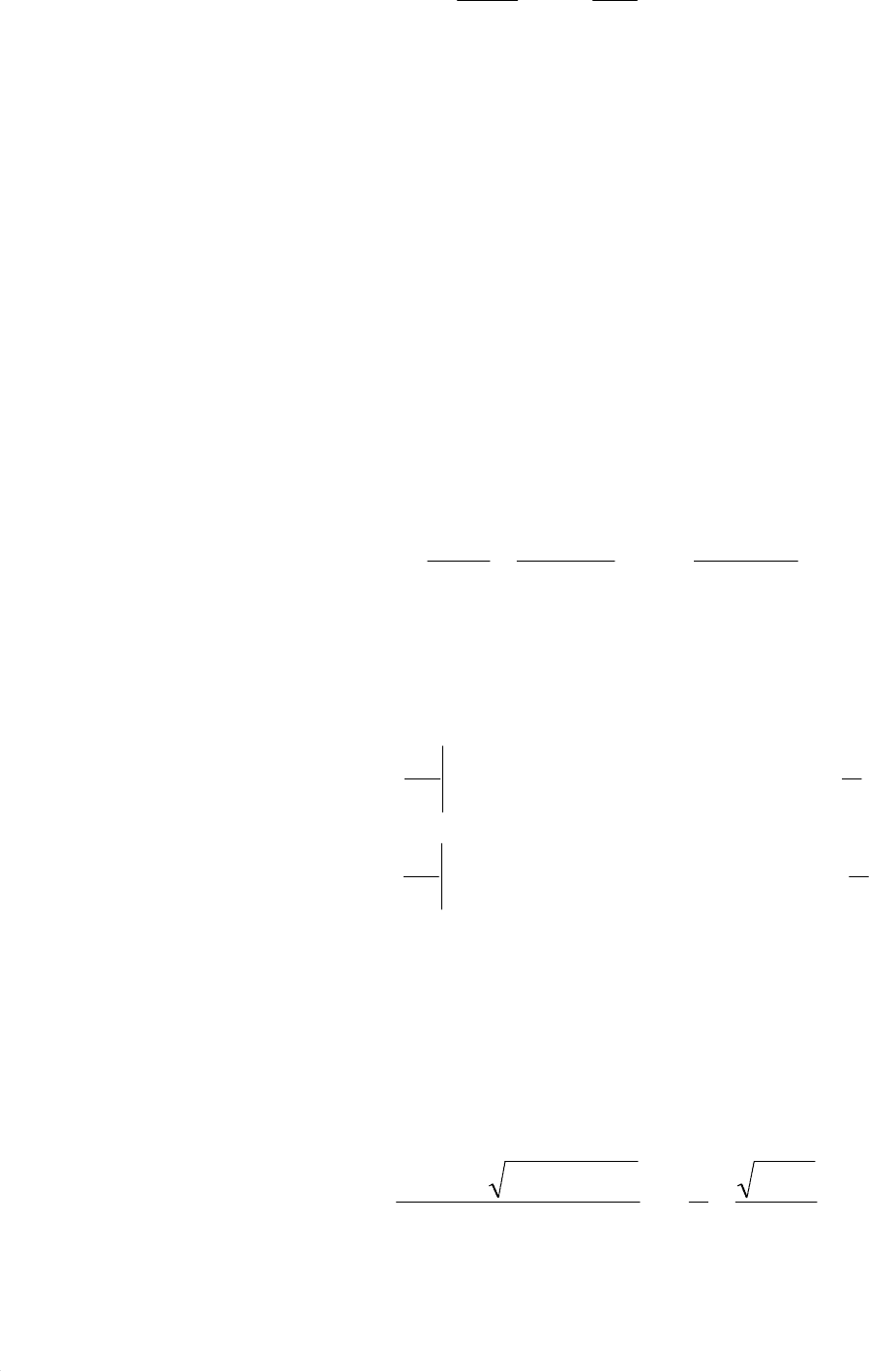
AП
П
2
П
2
2
ζ2 hKy
dt
yd
T
dt
yd
T
′
⋅=
′
+
′
+
′
. (7.125)
Закон изменения y(t), вызванный изменением входного сигнала в виде
единичной ступенчатой функции 1(t), можно найти, решив непосредственно
уравнение (7.91), или воспользоваться формулой Хевисайда (6.36).
Воспользуемся вторым способом. Для этого преобразуем уравнение
(7.91) по Лапласу:
)()()12(
22
sUKsYsTsT ⋅=⋅+⋅⋅⋅+⋅ ζ
(7.126)
или
)
(
)
(
)
(
)
(
s
U
s
M
s
Y
s
D
⋅
=
⋅
, (7.127)
где
12)(
22
+⋅⋅⋅+⋅= sTsTsD ζ , (7.128)
K
s
M
=
)
(
. (7.129)
Для уравнения (7.126) второго порядка формула Хевисайда имеет вид
tsts
e
sDs
sM
e
sDs
sM
D
M
thty
⋅⋅
⋅
⋅
+⋅
⋅
+==
21
)(
)(
)(
)(
)0(
)0(
)()(
22
2
11
1
&&
, (7.130)
где s
1
, s
2
– корни уравнения
01ζ2)(
22
=+⋅⋅⋅+⋅= sTsTsD
; (7.131)
)(
1
sD
&
,
)(
2
sD
&
– производные от оператора D(s):
+⋅⋅=⋅⋅+⋅⋅=
∂
∂
=
T
sTTsT
s
D
sD
s
ζ
2ζ22)(
1
2
1
2
1
1
&
, (7.132)
+⋅⋅=⋅⋅+⋅⋅=
∂
∂
=
T
sTTsT
s
D
sD
s
ζ
2ζ22)(
2
2
2
2
2
2
&
. (7.133)
Операторы M(s) и D(s), согласно соотношениям (7.128) и (7.129), при
0
=
s
равны
K
M
s
M
=
=
)
0
(
)
(
, (7.134)
1
)
0
(
)
(
=
=
D
s
D
. (7.135)
Уравнение (7.131) 2-го порядка имеет два корня:
T
T
T
TTT
s
1ζ
ζ
)ζ(ζ
2
2
22
1
−
+−=
−⋅+⋅−
= , (7.136)
