Никитин А.А. Управление техническими системами
Подождите немного. Документ загружается.


⋅=⋅+−⋅
⋅+⋅=
=
′
⋅−=
+=
2
0
2
0ПР0.ПР0.2
0.2
Ж
00
0.3
200.2
2.10.1
0.30.20.1
)(
dt
yd
mycFSp
dt
dp
E
W
dt
dy
SQ
QQ
pKQ
QQQ
pQ
. (5.35)
Вычтем из системы уравнений (5.34) систему (5.35), в результате получим
′
⋅=
′
⋅−⋅
′
′
⋅+
′
⋅=
′
′
⋅+
′
⋅=
′
′
⋅−=
′
′
+
′
=
′
2
2
ПР2
2
Ж
0
3
2.2.22
2.11
321
dt
yd
mycSp
dt
pd
E
W
dt
yd
SQ
pKxKQ
pKQ
QQQ
pQxQ
pQ
. (5.36)
Система линейных уравнений (5.36) представляет собой линейную ма-
тематическую модель и при малых отклонениях переменных может с доста-
точной точностью описывать переходные процессы, протекающие в гидравли-
ческой системе (рис. 5.2).
Математическое описание гидравлической системы, схема которой по-
казана на рис. 5.2, можно представить в форме “вход-выход”.
Принимая за входное воздействие перемещение x подвижного элемента
(золотника) регулируемого дросселя, а выходной величиной считая переме-
щение y массы m, систему уравнений (5.36) приведём к одному уравнению в
форме “вход-выход”. Для этого исключим функции
1
Q
′
,
2
Q
′
и
3
Q
′
, описываю-
щие малые отклонения расходов, и переменную p′
2
. Подставим в первое урав-
нение системы (5.36)
1
Q
′
,
2
Q
′
и
3
Q
′
из второго, третьего и четвёртого, в резуль-
тате вместо системы (5.36) пяти уравнений получим систему двух уравнений:
′
⋅=
′
⋅−⋅
′
′
⋅+
′
⋅+
′
⋅+
′
⋅=
′
⋅−
2
2
ПР2
2
Ж
0
2.2.22.1
dt
yd
mycSp
dt
pd
E
W
dt
yd
SpKxKpK
pQxQpQ
. (5.37)
Из второго уравнения системы (5.37) найдём
2
p
′
и подставим его в пер-
вое, перенесём члены, содержащие выходную величину y, в левую часть урав-

нения, а члены, содержащие входную x, в правую часть, в результате получим
уравнение в форме “вход-выход”
( )
( )
xKy
S
c
KK
dt
yd
SE
cW
S
dt
yd
mKK
dt
yd
E
mW
xQpQpQ
pQpQ
′
⋅=
′
⋅⋅++
+
′
⋅
⋅
⋅
++
′
⋅⋅++
′
⋅
⋅
.
ПР
..
Ж
ПР0
2
2
..
3
3
Ж
0
221
21
. (5.38)
Введём обозначения:
(
)
S
c
KKa
pQpQ
ПР
..0
21
⋅+= ; (5.39)
⋅
⋅
+=
SE
cW
Sa
Ж
ПР0
1
; (5.40)
(
)
mKKa
pQpQ
⋅
+
=
..2
21
; (5.41)
Ж
0
3
E
mW
a
⋅
= ; (5.42)
xQ
Kb
.0
2
=
. (5.43)
С учётом обозначений (5.39) – (5.43) уравнение (5.38) примет вид
xbya
dt
yd
a
dt
yd
a
dt
yd
a
′
⋅=
′
⋅++
′
⋅+
′
⋅+
′
⋅
001
2
2
2
3
3
3
. (5.44)
Таким образом, процессы, протекающие в гидравлической системе (рис. 5.2),
при учете сжимаемости жидкости и массы и малых отклонениях переменных,
описываются линейным дифференциальным уравнением (5.44) третьего по-
рядка.
Процессы, протекающие в гидравлической системе (рис. 5.2), без учета сжи-
маемости жидкости (Е
Ж
= ∞), но с учётом массы при малых отклонениях пе-
ременных, описываются линейным дифференциальным уравнением второго
порядка:
xbya
dt
yd
a
dt
yd
a
′
⋅=
′
⋅++
′
⋅+
′
⋅
001
2
2
2
. (5.45)
Коэффициенты
0
a
,
2
a
и
0
b
, входящие в уравнение (5.45), определяются соот-
ветственно по формулам (5.39), (5.41) и (5.43), а коэффициент
1
a
– по соотно-
шению, приведённому ниже:

Sa
=
1
. (5.46)
При исследовании процессов, протекающих в системах, с помощью нелиней-
ных математических моделей часто приходится применять ЭВМ и пакеты
прикладных программ, основанные на численных методах. В этом случае ма-
тематическое описание удобнее выполнять в переменных состояния и системы
уравнений приводить к дифференциальным уравнениям первого порядка, за-
писанным в форме Коши.
Для примера выполним математическое описание процессов, протекающих в
гидравлической системе (рис. 5.2) в переменных состояния.
Введем обозначение
dt
dy
=υ , (5.47)
где υ – скорость поршня и массы m, так как y – перемещение поршня.
С учетом формулы (5.47) система уравнений (5.9)–(5.12) и (5.15) примет вид
⋅+⋅=
−⋅
⋅⋅⋅⋅⋅=
−⋅
⋅⋅=
+=
⋅=⋅+−⋅
=
dt
dp
E
W
SQ
pp
xkdQ
pp
fQ
QQQ
dt
d
mycFSp
dt
dy
2
Ж
0
3
32
22
21
111
321
ПР0.ПР2
ρ
)(2
πμ
ρ
)(2
μ
)(
υ
υ
υ
. (5.48)
В качестве переменных состояний примем y, p
2
и υ. Подставим в третье урав-
нение системы (5.48) выражения для расходов Q
1
, Q
2
и Q
3
из четвёртого, пято-
го и шестого уравнений, затем члены, содержащие производные от перемен-
ных состояний, перенесём в левые части уравнений, в результате получим сис-
тему дифференциальных уравнений первого порядка в форме Коши:
y(t)
t
υ(t)
[ ]
⋅−
−⋅
⋅⋅⋅⋅⋅−
−⋅
⋅⋅⋅=
⋅+−⋅⋅=
=
υ
ρ
)(2
πμ
ρ
)(2
μ
)(
1υ
υ
32
2
21
11
0
Ж2
ПР0.ПР2
S
pp
xkd
pp
f
W
E
dt
dp
ycFSp
mdt
d
dt
dy
.
(5.49)
При заданных начальных условиях, т. е. при заданных значениях переменных
состояний в начальный момент времени t
0
:
00
)( yty
=
; (5.50)
00
υ)(υ
=
t ; (5.51)
0.202
)( ptp
=
(5.52)
и известном входном воздействии – перемещении золотника x для все t > t
0
, т.
е.
)
(
t
x
x
=
, (5.53)
можно найти зависимости y(t), υ(t) и p
2
(t) для всех t > t
0
.
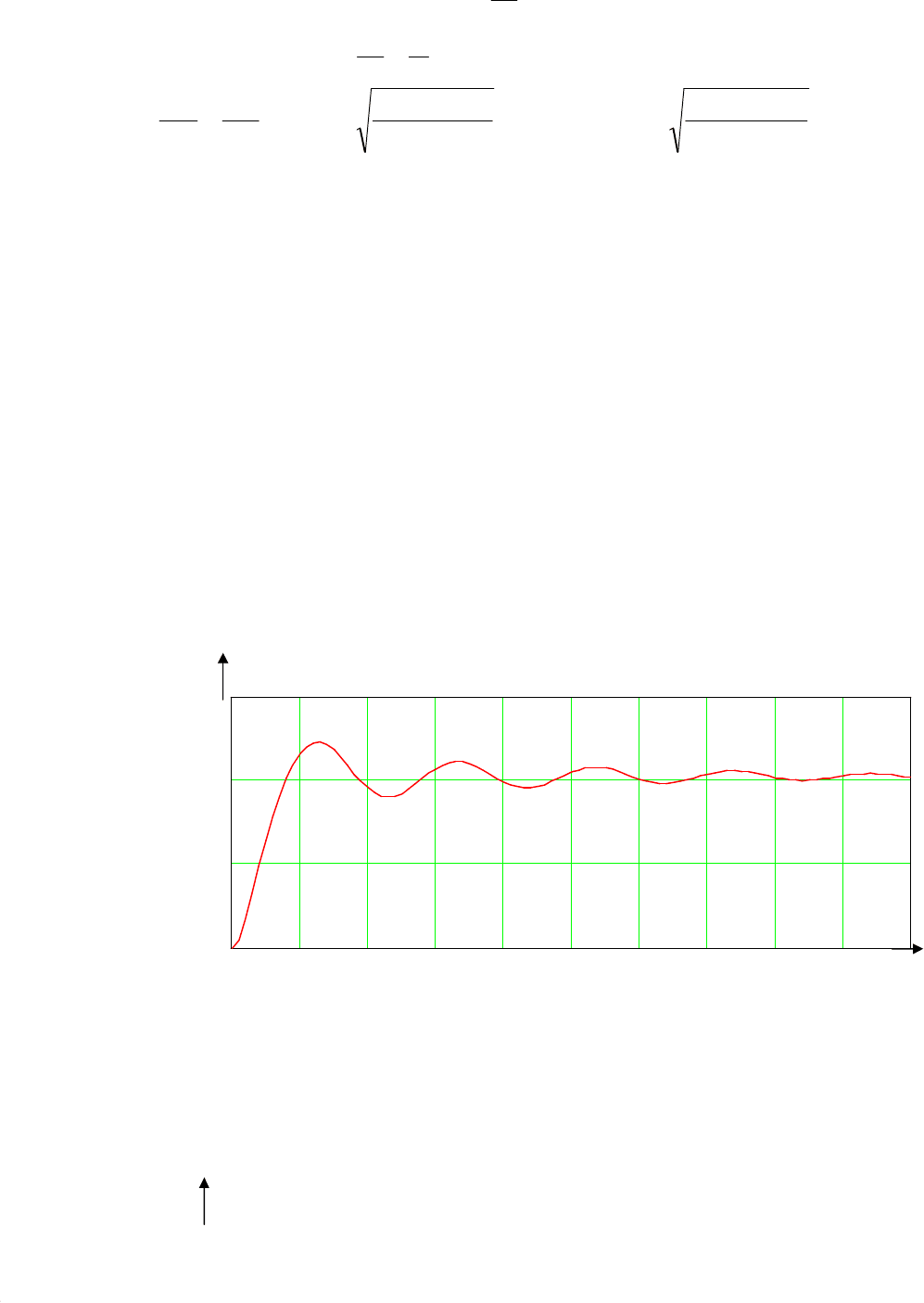
Результаты численных расчетов математической модели (5.49) в MathCAD
приведены на рис. 5.3–5.5.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
0
0.05
0.1
0.15
.
Из графика (рис. 5.3) можно определить вид переходного процесса (движения
поршня), время переходного процесса, количество колебаний, динамическую
ошибку и другие параметры переходного процесса.
Рис. 5.3. Зависимость перемещения поршня от
времени
t
p
2
(t)
t
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
0
1
2
.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
5
.
10
6
1
.
10
7
1.5
.
10
7
2
.
10
7
.
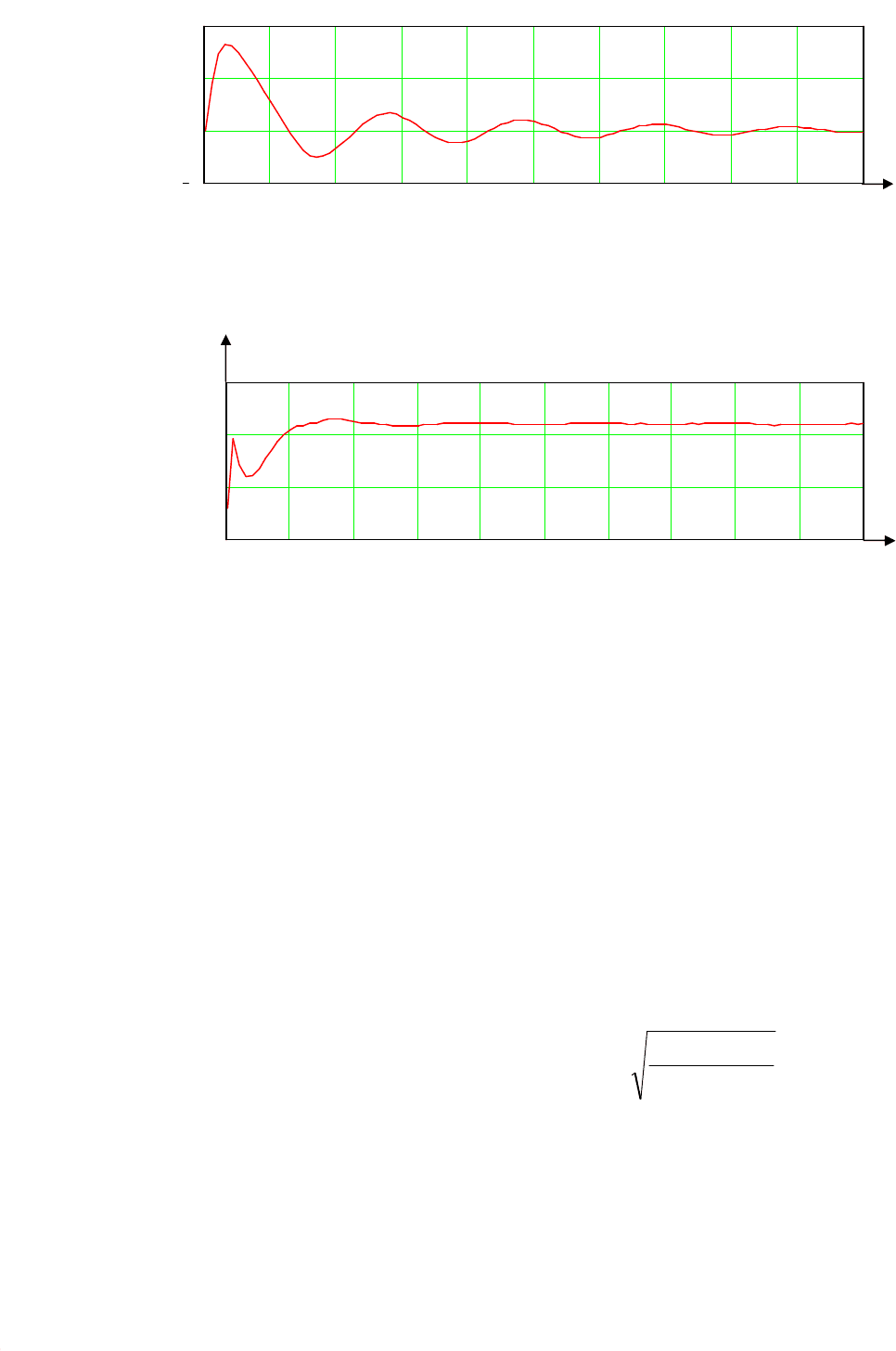
Зависимости, приведенные на рис. 5.4 и 5.5, позволяют проанализировать ха-
рактер изменения скорости поршня и колебаний давления в полости гидроци-
линдра.
Вопросы для самопроверки
1. Привести примеры линейных зависимостей.
2. Привести примеры нелинейных зависимостей.
3. Методы линеаризации нелинейных зависимостей.
4. Напишите формулы для определения коэффициентов линеаризации.
5. Линеаризировать функцию расхода
ρ
)(2
πμ),,(
21
21
pp
xdppxQ
−⋅
⋅⋅⋅⋅=
.
Рис. 5.4. Зависимость скорости поршня от вре-
мени
Рис. 5.5. Зависимость давления в полости гидроцилиндра
от врем
е
ни

6. ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ
Передаточная функция. Переходная и весовая функции. Общие сведения
о частотных характеристиках. Логарифмические характеристики.
6.1. Передаточная функция
На основании физических законов составляют систему уравнений, опи-
сывающих процессы, протекающие в отдельных звеньях. Полученную систему
уравнений приводят к одному уравнению в форме “вход-выход”, т. е. исклю-
чая промежуточные переменные и оставляя только входную и выходную ве-
личины. Все члены с выходной величиной обычно переносят в левую часть
уравнения, а все члены с входной величиной – в правую часть уравнения.
Уравнение в форме “вход-выход” обычно имеет вид
ub
dt
du
b
dt
ud
bya
dt
dy
a
dt
yd
a
m
m
m
n
n
n 0101
...... +++=+++
, (6.1)
где
0
a
,
a
1
, …,
a
n
,
0
b
,
b
1
, …,
b
m
– коэффициенты;
u
– входная величина;
y
–
выходная величина.
Для определения передаточной функции уравнение (6.1) нужно преобра-
зовать по Лапласу (основано на интегральном преобразовании):
∫
∞
⋅−
⋅⋅=
0
)()( dttfesF
ts
. (6.2)
Преобразование (6.2) переводит функцию-оригинал f(t) действительного пере-
менного t в функцию-изображение F(s) комплексного переменного s. Соот-
ветствие между оригиналами и изображениями будем обозначать символом
“=” (равно), к которому добавлены точки, расположенные по диагонали. В
этом случае соответствие между функциями f(t) и F(s) будет иметь вид
)()( sFtf
•
•
=
. (6.3)
Основные свойства преобразования Лапласа, применяемые при замене
линейных дифференциальных уравнений алгебраическими, следующие.
1. Умножение аргумента оригинала (изображения) не некоторое число
приводит к делению аргумента изображения (оригинала) и изображения (ори-
гинала) на это же число:
⋅=⋅
•
•
a
s
F
a
taf
1
)( , (6.4)

⋅=⋅
•
•
a
f
f
a
saF
1
)(
. (6.5)
2. Изображение суммы конечного числа оригиналов равно сумме их
изображений, если
)()(
11
sFtf
•
•
=
и
)()(
22
sFtf
•
•
=
, (6.6)
то
)()()()(
2121
sFsFtftf +=+
•
•
. (6.7)
3. Изображение произведения оригинала на постоянную величину равно
произведению изображения на эту постоянную:
)()( sFatfa ⋅=⋅
•
•
. (6.8)
4. Если оригинал смещается вдоль оси t на величину τ, причем
0
)
τ
(
=
−
t
f
при t < τ и )()( sFtf
•
•
= , то
)()τ(
τ
sFetf
s
⋅=−
⋅−
•
•
. (6.9)
5. Смещение изображения на s
0
приводит к умножению оригинала на
ts
e
⋅
0
:
)()(
0
0
ssFtfe
ts
−=
•
•
⋅
, (6.10)
где s
0
– любое комплексное число.
6. Произведение двух изображений F
1
(s) и F
2
(s) также является изобра-
жением, которому соответствует свертывание оригиналов:
∫
⋅−⋅=⋅
•
•
t
dtffsFsF
0
2121
τ)τ()τ()()( . (6.11)
Интеграл в правой части этого соотношения называется сверткой функ-
ций f
1
(s) и f
2
(s) и обозначается следующим образом:
∫
⋅−⋅=∗
t
dtffff
0
2121
τ)τ()τ( , (6.12)
где τ – вспомогательное время, изменяющееся от нуля до текущего значения t.
Свертка, как и произведение, обладает свойством коммутативности:
1
2
2
1
ffff
∗
=
∗
или
∫∫
⋅−⋅=⋅−⋅
tt
dtffdtff
0
12
0
21
τ)τ()τ(τ)τ()τ( , (6.13)
и свойством ассоциативности:
)()(
321321
ffffff
∗
∗
=
∗
∗
. (6.14)
7. Теорема о предельном значении приводит к условию

)
(
lim
lim
0
)(
s
F
s
s
t
tf
⋅
→
∞→
=
. (6.15)
8. Теорема о начальном значении дает соотношение
)
(
lim
lim
)(
0
s
F
s
s
t
tf
⋅
∞→
→
=
. (6.16)
9. Изображение производных от оригиналов при нулевых начальных ус-
ловиях находится по соотношению
)()(
)(
sFstf
n
n
⋅=
•
•
, (6.17)
где )()( sFtf
•
•
= ;
)(
)(
n
tf
– производная n-го порядка от функции f(t) по t.
10. Интегрирование оригинала от нуля до переменной t соответствует в
пространстве изображений делению изображения s при нулевых начальных
условиях:
)(
1
)(
0
sF
s
df
t
⋅=⋅
•
•
∫
ττ
. (6.18)
Проведем преобразование по Лапласу дифференциального уравнения
(6.1). Принимая нулевые начальные условия и используя свойства 2, 3, 9, по-
лучаем
(
)
(
)
(
)
(
)
sUbsbsbsYasasa
m
m
n
n
⋅+++=⋅+++
0101
......
, (6.19)
где s – комплексная переменная; Y(s) – изображение выходной величины; U(s)
– изображение входной величины.
Для краткости записи обычно вводят операторы воздействия
(
)
Ms и
собственный оператор
(
)
Ds:
(
)
01
1
1
... bsbsbsbsM
m
m
m
m
++++=
−
−
; (6.20)
(
)
01
1
1
... asasasasD
n
n
n
n
++++=
−
−
. (6.21)
С учетом (6.20) и (6.21) уравнение (6.19) можно записать в виде
(
)
(
)
(
)
(
)
sUsMsYsD
⋅
=
⋅
. (6.22)
Отсюда легко найти передаточную функцию как отношение изображе-
ния выходной величины к изображению входной:
()
(
)
()
(
)
()
sD
sM
sU
sY
sW ==
. (6.23)

6.2. Частотные характеристики
Если входное воздействие
(
)
ut на элемент или систему имеет вид гармо-
нической функции
(
)
tj
u
etu
ω
α= , (6.24)
то для линейных систем (описываемых линейными уравнениями) выходная
величина
(
)
yt
будет тоже гармонической функцией:
(
)
(
)
ϕ+
=
tj
y
ety
ω
α
, (6.25)
где
u
α и
ω
– амплитуда и угловая частота входного воздействия;
α
y
и
ϕ
–
амплитуда выходной величины и сдвиг ее по фазе относительно входной ве-
личины; j – мнимая единица ( 1−=j ).
Комплексную функцию
(
)
W jω от действительного переменного часто-
ты
ω
( )
(
)
()
()
ω
ωω
⋅
⋅==
j
eA
tu
ty
jW (6.26)
называют амплитудно-фазовой частотной характеристикой звена или системы
(здесь
(
)
uy
aaA
=
ω
).
Зависимость от частоты
ω
отношения амплитуды
a
y
выходной величи-
ны к амплитуде
a
u
входной величины называют амплитудной частотной ха-
рактеристикой
(
)
A a a
y u
ω= .
Зависимость
(
)
ϕω сдвига по фазе между выходной величиной
(
)
yt и
входной величиной
(
)
ut в зависимости от частоты
ω
называют фазовой час-
тотной характеристикой.
Амплитудно-фазовую частотную характеристику можно найти по пере-
даточной функции
(
)
Ws, используя подстановку
s
j
=
⋅
ω
в формулу (6.23).
Амплитудно-фазовую частотную характеристику как комплексную
функцию можно задать вещественной частотной характеристикой
(
)
P ω и
мнимой частотной характеристикой
(
)
Q ω :
(
)
(
)
(
)
W j P jQω ω ω= + . (6.27)

В этом случае амплитудную и фазовую частотные характеристики мож-
но определить по известным из комплексного анализа соотношениям:
(
)
(
)
(
)
A P Qω ω ω= +
2 2
; (6.28)
()
(
)
()
ϕω
ω
ω
π= +arctg
P
Q
K ,
K
=
0
;
±
1
;
±
2
;
.
.
.
. (6.29)
Для нахождения амплитудной и фазовой частотных характеристик мож-
но применить систему MathCAD и использовать встроенные в неё функции
|W(jω)| (определяющей модуль комплексной функции W(jω)) и arg(W(jω)) (оп-
ределяющей аргумент комплексной функции W(jω)):
)(:)( ωω WA = , (6.30)
))(arg(:)(
ω
ω
ϕ
W
=
. (6.31)
В правых частях формул (6.30) и (6.31) функция W(jω) записана в виде W(ω),
так как аргументом является только частота ω, а мнимая единица j подчерки-
вает, что функция W(jω) комплексная.
Логарифмическая амплитудная частотная характеристика определяется
по соотношению
(
)
(
)
ω
=
ω
AL lg20
. (6.32)
6.3. Переходная и весовая функции
Вид функции y(t), являющийся решением уравнения (6.1), зависит от ви-
да функции u(t), входящей в правую часть уравнения (6.1). Закон изменения
выходной величины
y
t
(
)
во времени при заданном законе изменения входной
величины
u
t
(
)
(входного воздействия) в виде единичной ступенчатой функ-
ции
1
(
)
t
называется переходной функцией и обозначается
h
t
(
)
, т. е. если
u
t
t
(
)
(
)
=
1
, то
y
t
h
t
(
)
(
)
=
, где
≥
<
=
0
0
при
при
1
0
)(1
t
t
t
. (6.33)
Закон изменения выходной величины
y
t
(
)
во времени при заданном
законе изменения входной величины
u
t
(
)
(входного воздействия) в виде еди-
