Никитин А.А. Управление техническими системами
Подождите немного. Документ загружается.


ничной импульсной функции
)
(
δ
t
называется весовой функцией
w
t
(
)
, т. е. ес-
ли
ut t() ()
=
δ
, то
y
t
w
t
(
)
(
)
=
, где
1)(δ
ε
ε
=
∫
+
−
dtt
при любом
ε
>
0
. (6.34)
Зная переходную функцию
h
t
(
)
, легко найти весовую функцию
w
t
(
)
из
соотношения
dt
dh
tw =)( , (6.35)
т. е. весовая функция является производной от переходной функции.
Согласно теории обобщенных функций единичная импульсная функция
)
(
δ
t
является производной от единичной ступенчатой функции
1
(
)
t
.
Если передаточная функция
Ws
Ms
Ds
()
()
()
=
известна и является дробно-
рациональной функцией, причем степень полинома
M
s
(
)
в числителе меньше
степени полинома
D
s
(
)
в знаменателе и
D
s
(
)
=
0
имеет простые, отличные
от нуля корни, то переходную функцию можно найти по формуле Хевисай-
да:
ts
n
k
kk
k
k
e
sDs
sM
D
M
th
⋅
=
•
∑
⋅⋅
⋅
+=
1
)(
)(
)0(
)0(
)( , (6.36)
где
s
k
– корни уравнения
D
s
(
)
=
0
;
k
ss
k
s
D
sD
=
•
=
∂
∂
)(
.
Если полином
D
s
(
)
– второго порядка (т. е. имеет вид as as a
2
2
1 0
+ + ;
поделив все члены последнего полинома на
а
0
, можно перейти к полиному
Ts Ts
2
22
1
1+ + ), а полином
M
s
K
(
)
=
, то для определения переходной функции
h
t
(
)
можно воспользоваться следующими соотношениями.
А. Корни
s
k
уравнения
D
s
(
)
=
0
– комплексные, что имеет место при
(
)
T T
1 2
2 1< , в этом случае корни можно представить в виде
c1
ωα
⋅
+
−
=
js
, (6.37)
c2
ωα
⋅
−
−
=
js
, (6.38)
где
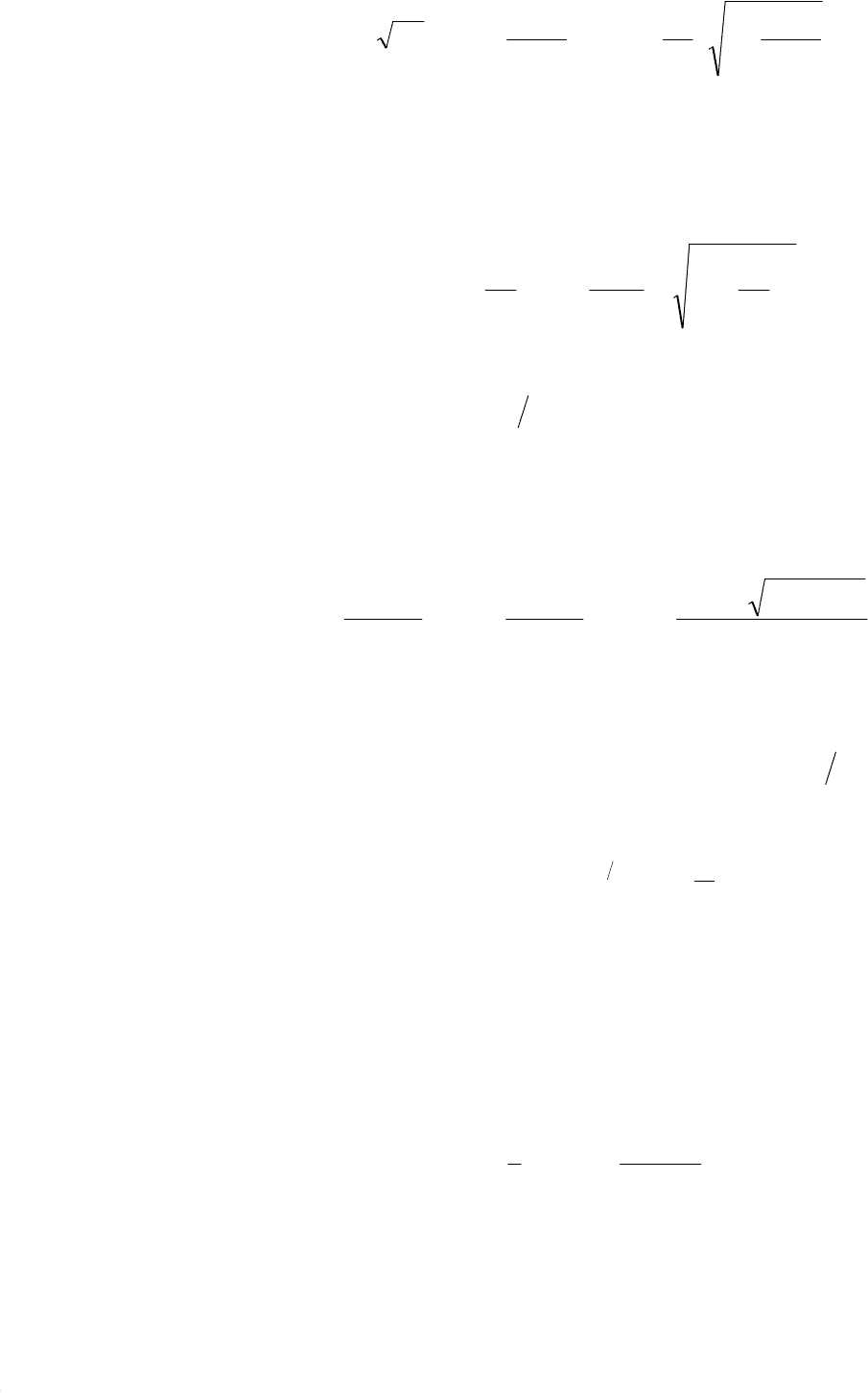
1−=j
;
2
2
1
2
α
Т
Т
⋅
=
;
2
2
2
1
2
с
4
1
1
ω
T
T
Т
⋅
−⋅=
. (6.39)
При этом переходную функцию вычисляют по формуле
(
)
(
)
[
]
ϕ+⋅⋅−⋅=
⋅−
teAKth
t
c
α
ωsin1 , (6.40)
где
α
ω
arctg
c
=ϕ ;
2
c
ω
α
1
sin
1
+==
ϕ
A . (6.41)
Б. Корни
s
k
уравнения
D
s
(
)
=
0
– отрицательные действительные числа
λ
1
и
λ
2
, что имеет место при
(
)
T T
1 2
2 1≥ ; в этом случае переходную функ-
цию вычисляют по соотношению
(
)
[
]
tt
eСeСKth
⋅−⋅−
⋅+⋅+⋅=
21
λ
2
λ
1
1 , (6.42)
где
21
2
1
λλ
λ
−
=C ;
12
1
2
λλ
λ
−
=C ;
2
2
2
2
2
11
2,1
2
4
λ
Т
ТТТ −±−
=
, (6.43)
причем в уравнение (6.7) должны быть подставлены абсолютные значения
λ
1
и
λ
2
.
В. Если корни
λ
1
и
λ
2
равны, что имеет место при
(
)
T T
1 2
2 1= , пере-
ходную функцию вычисляют по формуле
+⋅−⋅=
−
T
t
eKth
Тt
11)( . (6.44)
Для некоторых частных случаев, когда порядок полинома
D
s
(
)
не пре-
вышает двух, а порядок полинома
M
s
(
)
не выше первого, переходную функ-
цию можно найти по таблице соответствия между функциями времени и их
изображениями по Лапласу. Вначале по передаточной функции
W
s
(
)
находят
изображение
H
s
(
)
переходной функции по Лапласу с помощью соотношения
Hs
s
Ws
Ms
sDs
() ()
()
()
= ⋅ =
⋅
1
, (6.45)
а затем по таблице соответствия по изображению
H
s
(
)
находят оригинал пе-
реходной )(th функции.

Если известна вещественная частотная характеристика P
З
(ω) замкнутой
системы, то переходную h(t) и весовую w(t) функции можно найти по приве-
денным ниже соотношениям:
∫
∞
⋅
⋅
⋅
⋅=
0
ω
ω
)ωsin()ω(
π
2
)( d
tP
th
З
(6.46)
∫
∞
⋅⋅⋅⋅=
0
ω)ωcos()ω(
π
2
)( dtPtw
З
(6.47)
Вопросы самопроверки
1. Дайте определение передаточной, переходной и весовой функций.
2. Как найти передаточную, переходную и весовую функции?

7. ТИПОВЫЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ
Элементарные динамические звенья, их уравнения и передаточные
функции. Переходные и весовые функции элементарных звеньев. Частотные
характеристики звеньев. Логарифмические характеристики элементарных
звеньев. Применение цифровых вычислительных машин для расчета частот-
ных характеристик.
При определенной степени идеализации различных устройств удается
получить достаточно простые математические модели (уравнения), отражаю-
щие общие динамические свойства устройств независимо от особенностей
протекающих в них физических процессов. Звенья, описываемые такими ма-
тематическими моделями, относятся к типовым. Это пропорциональные, ин-
тегрирующие, дифференцирующие, апериодические, форсирующие первого
порядка, колебательные и апериодические второго прядка, форсирующие вто-
рого порядка. Первые три вида звеньев являются наиболее простыми по дина-
мическим характеристикам.
7.1. Пропорциональное звено
Пропорциональным называется звено, описываемое уравнением
u
K
y
⋅
=
, (7.1)
где K – коэффициент усиления, если входной и выходной сигналы являются
безразмерными или величинами, имеющими одинаковую размерность; коэф-
фициент K называют коэффициентом передачи или преобразования, если
входной и выходной сигналы имеют разные размерности; y(t) – функция вре-
мени, описывающая закон изменения выходной величины; u(t) – функция вре-
мени, описывающая закон изменения входной величины.
Пропорциональное звено передает сигналы от входа к выходу без сдвига
по фазе, отношение амплитуд выходной и входной величин, при этом сохраня-
ется постоянным во всем диапазоне частот.
Значение коэффициента K находят по статическим характеристикам зве-
на (системы) или по передаточной функции (6.23), подставляя в неё операторы
M(s) и D(s), определяемые соотношениями (6.20) и (6.21) при s = 0.
Примером пропорциональных звеньев могут служить рычажные и зуб-
чатые механизмы, если при их математическом описании можно пренебречь
влиянием инерции, упругих деформаций трением в механизме. К пропорцио-

нальным звеньям относятся также малоинерционные датчики, преобразующие
перемещения механических элементов, или давления, или расходы жидкостей
в электрические сигналы (напряжения или токи).
7.2. Интегрирующее звено
Интегрирующее звено описывается дифференциальным уравнением
u
dt
dy
T =⋅ , (7.2)
где T – постоянный коэффициент, имеющий размерность времени при одина-
ковых размерностях входного и выходного сигналов, поэтому данный коэф-
фициент называют постоянной времени. Постоянная времени T зависит от па-
раметров звена.
Уравнение (7.2) можно представить в виде
uK
dt
dy
⋅=
υ
, (7.3)
где
TK 1
=
υ
– коэффициент усиления, определяемый отношением скорости
выходного сигнала к величине входного сигнала.
При изменении входного сигнала в виде единичной ступенчатой функ-
ции
u = 1(t) (7.4)
переходную функцию интегрирующего звена можно найти, решив уравнения
(7.2) или (7.3):
∫
=⋅==
T
t
dt
T
thty
1
)()(
или
tKty
⋅
=
υ
)(
, (7.5)
где
υ
K – коэффициент усиления.
В решении (7.5) произвольная постоянная равна нулю, так как началом
отсчета выходной величины (выходного сигнала) принято ее значение до сту-
пенчатого единичного воздействия, т. е. y(0) = 0.
Весовую функцию интегрирующего звена можно найти, решив уравне-
ния (7.2) или (7.3) при изменении входного сигнала в виде единичной им-
пульсной функции u = δ(t), или в соответствии с формулой (6.35) определить
дифференцированием переходной (7.5):

T
twty
1
)()( ==
. (7.6)
Переходная и весовая функции интегрирующего звена приведены на
рис. 7.1. График (рис. 7.1, а) переходной функции при t ≥ 0 имеет вид наклон-
ной прямой, а график (рис. 7.1, б) весовой функции при t ≥ 0 имеет вид гори-
зонтальной прямой.
Передаточную функцию интегрирующего звена найдем согласно фор-
муле (6.6), предварительно преобразовав уравнение (7.2) по Лапласу при на-
чальных нулевых условиях, в результате получим
s
T
sW
⋅
=
1
)( . (7.7)
Амплитудно-фазовую частотную характеристику (АФЧХ) найдем с по-
мощью подстановки s = jω в передаточную функцию (7.7):
ω
)ω(
⋅
−=
T
j
jW . (7.8)
Из формулы (7.8) следует, что вещественная частотная характеристика
равна нулю:
P(ω) = 0, (7.9)
а мнимая частотная характеристика определяется соотношением
ω
)ω(
⋅
−=
T
j
Q . (7.10)
Амплитудная частотная характеристика звена определяется как модуль
W(jω):
ω
1
)ω()ω()ω()ω(
22
⋅
=+==
T
QPjWA . (7.11)
0 0.5
0
50
0 5
0
100
h(t)
w(t)
t
t
б
D
Рис. 7.1. Временные характеристики интегрирующего звена:
а – переходная функция; б – весовая функция

Фазовая частотная характеристика является аргументом комплексной
функции W(jω). Используя формулу (6.12) и учитывая соотношения (7.9) и
(7.10), получаем:
2
π
)ω(
)ω(
arctg)ω(arg)(ω −===
P
Q
jWϕ
. (7.12)
Из формулы (7.12) видим, что фазовая частотная характеристика имеет
постоянное значение при всех частотах больше нуля (ω ≥ 0).
Логарифмическую амплитудную частотную характеристику можно най-
ти, используя формулу (6.13) и учитывая соотношение (7.11):
)
ω
lg(
20
)
ω
(
lg
20
)
ω
(
⋅
⋅
−
=
⋅
=
T
A
L
. (7.13)
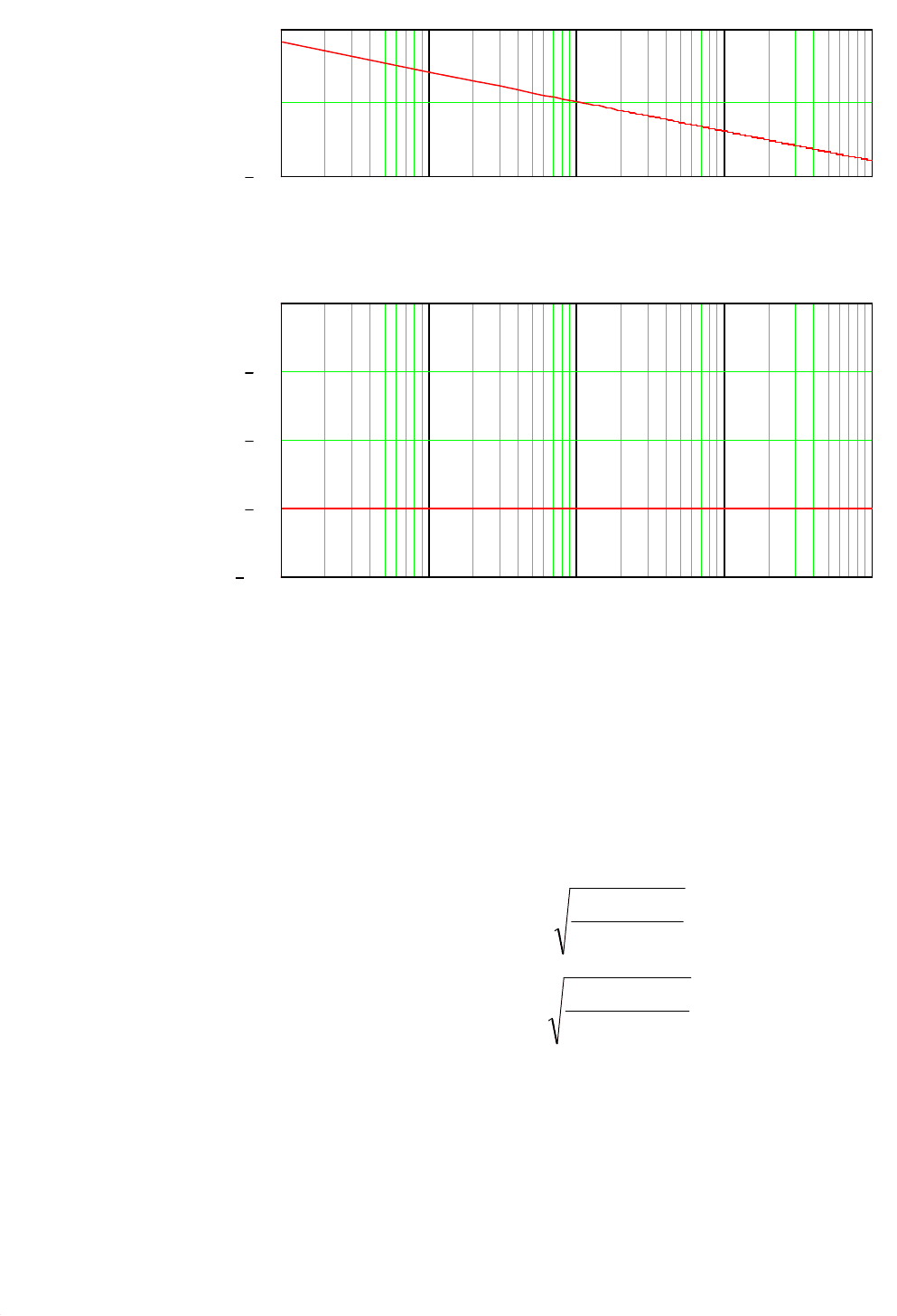
Частотные характеристики интегрирующего звена приведены
на рис. 7.2. Из рис. 7.2, а видно, что логарифмическая амплитудная частотная
характеристика имеет вид прямой с наклоном –20 дБ/дек, пересекающей ось
частот при частоте среза, равной ω
ср
= 1/T. Рис. 7.2, б показывает, что ампли-
тудная частотная характеристика имеет вид горизонтальной прямой, располо-
женной ниже оси частот и пересекающей ось ординат при значении фазы ϕ =
–90° (–π/2). Таким образом, сигнал на выходе интегрирующего звена имеет
сдвиг по фазе на –90° по сравнению с сигналом на входе при любой частоте
входного сигнала.
Одним из примеров интегрирующего звена может служить гидравличе-
ский механизм, состоящий из золотникового гидрораспределителя и ненагру-
женного гидроцилиндра (рис. 7.3). Составим математическое описание гид-
равлического механизма, предполагая, что питание его рабочей жидкостью
осуществляется при постоянном давлении (p
П
= const) от источника с неогра-
ниченным расходом. Гидролинии от золотникового распределителя к гидро-
цилиндру будем принимать настолько короткими, чтобы в них можно было бы
не учитывать потери давления и волновые процессы.
Для гидрораспределителя, когда окна распределителя имеют равные ко-
эффициенты расхода, при нулевых перекрытиях золотника, без учета утечек и
перетечек рабочей жидкости в распределителе, можно записать два уравнения
расходов:
ρ
)(2
μ
1П
ЗОКЗ1З
pp
xbQ
−
=
(7.14)
ρ
)(2
μ
СЛ2
ЗОКЗ2З
pp
xbQ
−
= , (7.15)
где Q
З1
– расход рабочей жидкости, втекающей в гидроцилиндр; Q
З2
– расход
рабочей жидкости, вытекающей из гидроцилиндра; µ
З
– коэффициент расхода
окон золотникового распределителя; b
ОК
– ширина окон во втулке (если окно,
расположенное напротив бурта золотника, занимает весь периметр втулки, то
b
ОК
= πd
З
; x
З
– смещение золотника от нейтрального положения; p
П
– давление
1 10 100 1
.
10
3
1
.
10
4
50
0
а)
1 10 100 1
.
10
3
1
.
10
4
100
90
80
70
60
б)
L(ω)
ϕ(ω)
ω
ω
Рис. 7.2. Частотные характеристики интегрирующего звена:
а – логарифмическая амплитудная; б – фазовая
a
б

питания в напорной гидролинии; p
СЛ
– давление в сливной гидролинии; p
1
и p
2
– давления в левой и правой полостях гидроцилиндра; ρ – плотность жидкости.
Для гидроцилиндра можно записать уравнение движения поршня и
уравнения расходов (втекающего и вытекающего):
2
ШТ
2
ПРТР22Ц11Ц
dt
yd
mPPpFpF =−−−
(7.16)
dt
dy
FQ
ШТ
1Ц1З
= (7.17)
dt
dy
FQ
ШТ
2Ц2З
= , (7.18)
где F
Ц1
и F
Ц2
– рабочие площади поршня (т.е. площадь поршня минус площадь
штока) в левой и правой полостях гидроцилиндра; P
ТР
– сила трения, дейст-
вующая на поршень и шток; P – внешняя нагрузка; m
ПР
– суммарная масса
поршня, штока и приведенной массы рабочих органов, приводимых в движе-
ние штоком; y
ШТ
– перемещение штока.
Система уравнений (7.14)–(7.18) является математической моделью рас-
сматриваемого гидравлического механизма. В некоторых случаях ее можно
заменить более простой моделью.
Пусть гидроцилиндр выполнен с одинаковыми значениями рабочих
площадей в левой и правой полостях (F
Ц1
= F
Ц2
), обозначим эти площади через
x
З
p
П
p
СЛ
y
П
p
2
p
1
1
2
F
m
ПР
Рис. 7.3. Гидравлический механизм
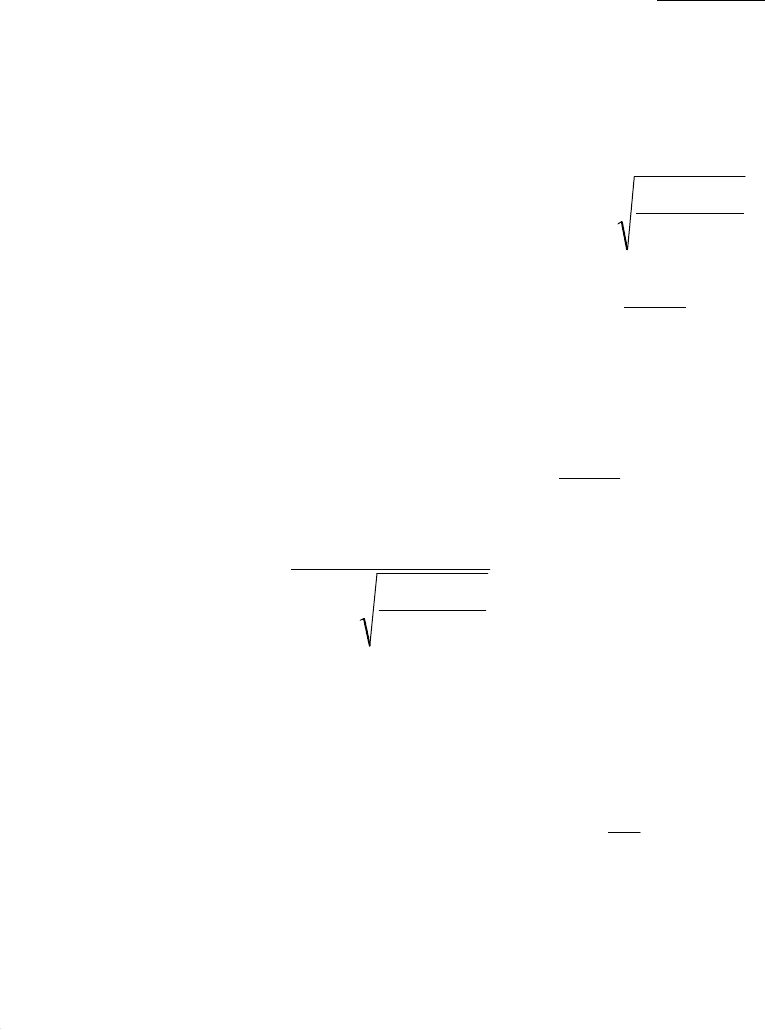
F
Ц
. Если в уравнении (7.16) можно пренебречь силой трения, внешней нагруз-
кой и произведением приведенной массы на ускорение, то такой гидроци-
линдр называется ненагруженным. При перечисленных допущениях из урав-
нения (7.16) следует равенство давлений:
p
1
= p
2
. (7.19)
При равенстве рабочих площадей поршня из уравнений (7.17) и (7.18) следует
равенство расходов, которые можно обозначить одной буквой:
З2З1З
QQQ
=
=
. (7.20)
На основании соотношений (7.20), (7.14) и (7.15) следует равенство
2
СЛП
СЛ21П
pp
pppp
−
=−=− . (7.21)
На основании соотношений (7.20), (7.21) и принятых выше допущений о
симметричности распределителя и гидроцилиндра систему уравнений (7.14)–
(7.18) можно заменить системой двух уравнений:
ρ
μ
СЛП
ЗОКЗ2З
pp
xbQ
−
=
, (7.22)
dt
dy
FQ
З
ШТ
Ц
= . (7.23)
Систему уравнений (7.22)–(7.23) можно привести к одному уравнению (урав-
нению интегрирующего звена)
З
x
dt
dy
T =
ШТ
Г
, (7.24)
где
ρ
μ
СЛП
ОКЗ
Ц
Г
pp
b
F
T
−
=
– постоянная времени гидравлического меха-
низма.
7.3. Дифференцирующее звено
Дифференцирующее звено описывается уравнением
dt
du
Ty = , (7.25)
где T – постоянная времени дифференцирующего звена.
