Никитин А.А. Управление техническими системами
Подождите немного. Документ загружается.

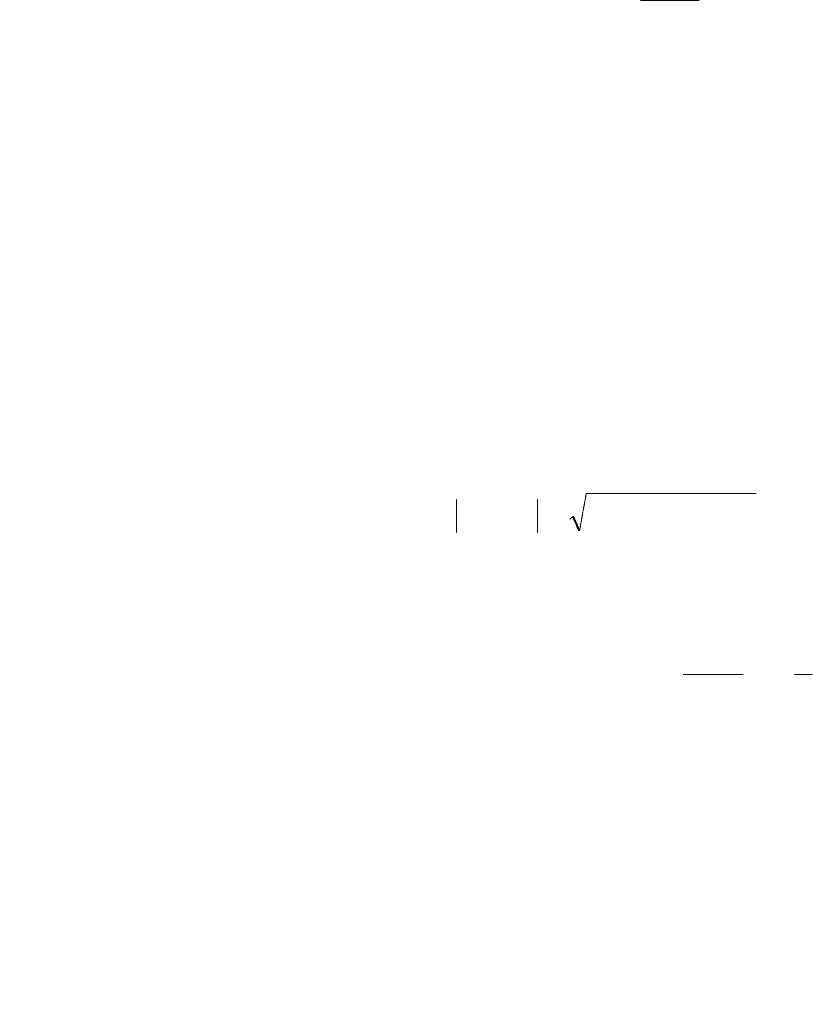
Передаточную функцию интегрирующего звена найдем с помощью
формулы (6.23), предварительно преобразовав уравнение (7.25) по Лапласу
при нулевых начальных условиях, в результате получим
sTsW
⋅
=
)(
. (7.26)
Переходную функцию можно найти непосредственно из уравнения
(7.25) при u = 1(t). Согласно теории обобщенных функций производная от
единичной ступенчатой функции 1(t) является дельта-функция δ(t)
)
(
δ
)
(
)
(
t
T
t
h
t
y
⋅
=
=
. (7.27)
Весовая функция в соответствии с формулой (6.35) определяется диффе-
ренцированием переходной h(t):
dt
td
twty
)(δ
)()( == . (7.28)
Амплитудно-фазовую частотную характеристику найдем с помощью
подстановки s = jω в передаточную функцию (7.26):
ω
)
ω
(
⋅
⋅
=
T
j
j
W
. (7.29)
Из формулы (7.29) видно, что вещественная частотная характеристика
равна нулю:
P(ω) = 0, (7.30)
а мнимая частотная характеристика определяется соотношением
ω
)
ω
(
⋅
=
T
Q
. (7.31)
Амплитудная частотная характеристика звена определяется как модуль
W(jω):
ω)ω()ω()ω()ω(
22
⋅=+== TQPjWA (7.32)
Фазовую частотную характеристику можно найти, используя формулу
(6.29), с учетом соотношений (7.30) и (7.31) получим
2
π
)ω(
)ω(
arctg)ω(arg)ω( +===
P
Q
jWϕ . (7.33)
Из формулы (7.33) видим, что фазовая частотная характеристика имеет посто-
янное значение при всех частотах больше нуля (ω ≥ 0).
Логарифмическую амплитудную частотную характеристику можно най-
ти, используя формулу (6.32), с учетом соотношений (7.32) получаем
ω
lg
20
)
ω
(
lg
20
)
ω
(
⋅
⋅
=
⋅
=
T
A
L
. (7.34)
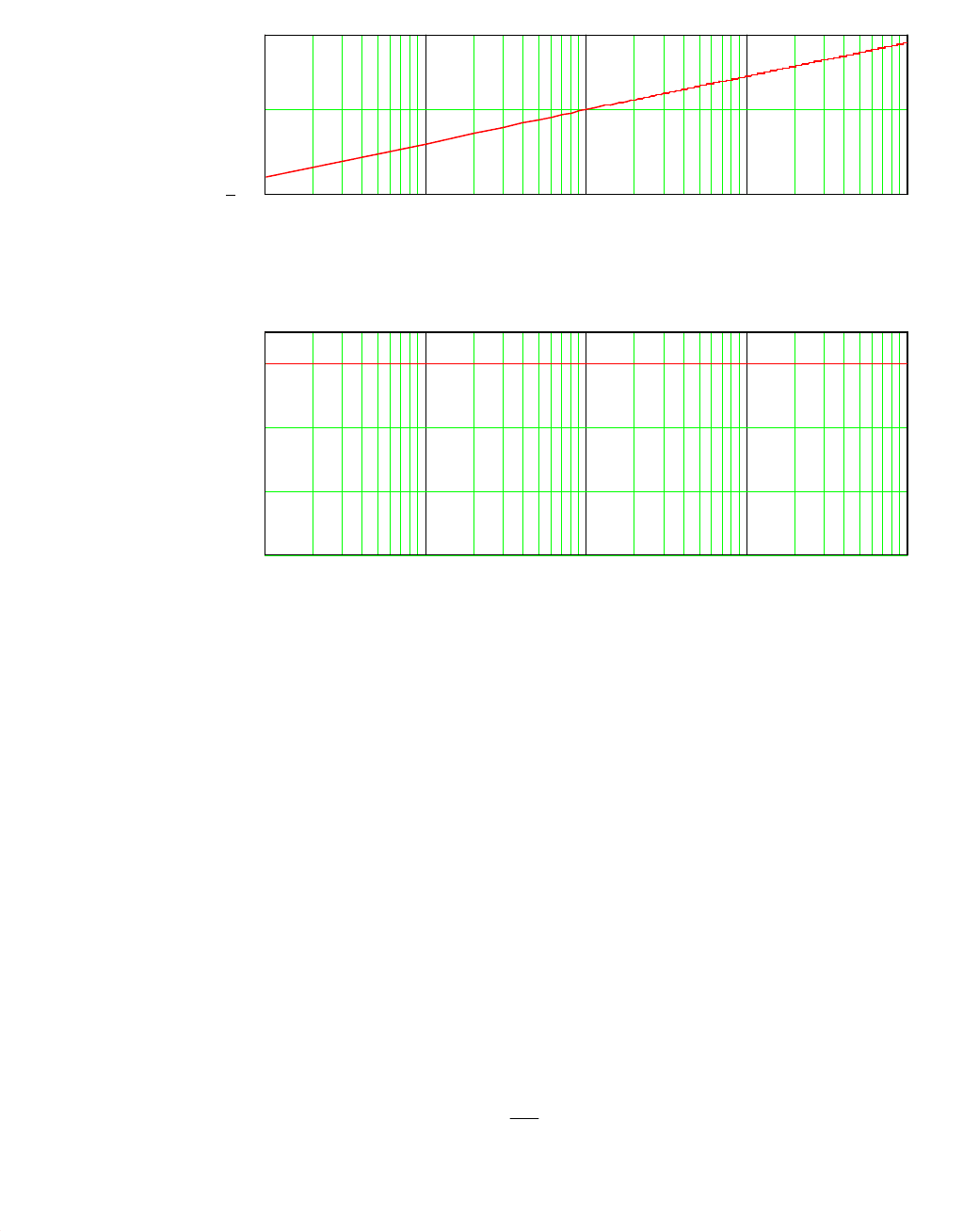
На рис. 7.4 показаны частотные характеристики дифференцирующего
звена. Логарифмическая амплитудная (рис. 7.4, а) частотная характеристика
имеет вид прямой с наклоном 20 дБ/дек, пересекающей ось частот при частоте
среза, равной ω
ср
= 1/T.
Логарифмическая фазовая частотная характеристика имеет вид горизон-
тальной прямой, расположенной выше оси частот и пересекающей ось ординат
при значении фазы, равной ϕ = 90° (π/2). Таким образом, сигнал на выходе
дифференцирующего звена имеет сдвиг по фазе на 90° по сравнению с сигна-
лом на входе при всех частотах ω ≥ 0.
7.4. Апериодическое звено 1-го порядка
Апериодическое звено 1-го порядка описывается дифференциальным
уравнением 1-го порядка
Kuy
dt
dy
T =+ , (7.35)
1 10 100 1
.
10
3
1
.
10
4
50
0
1
10
100
1
.
10
3
1
.
10
4
60
70
80
90
Рис. 7.4. Логарифмические амплитудная (а) и фазовая (б)
частотные характеристики
а
б
ω
ω
L(ω)
φ(ω)
a
б
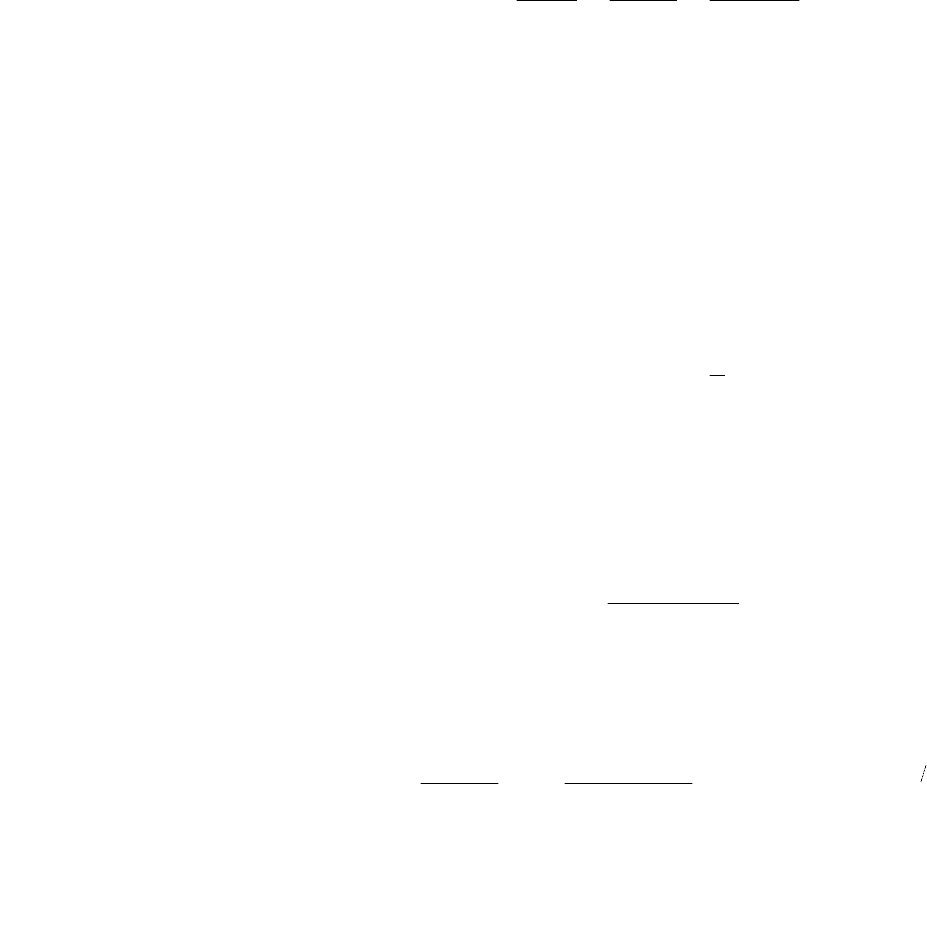
где y(t) – функция времени, описывающая закон изменения выходной величи-
ны; u(t) – функция времени, описывающая закон изменения входной величи-
ны; T – постоянная времени; K – коэффициент передачи или преобразования;
если коэффициент безразмерный, то его называют коэффициентом усиления.
Применив преобразования Лапласа и его свойства, дифференциальное
уравнение (7.35) при нулевых начальных условиях можно заменить алгебраи-
ческим
)()()1( sUKsYsT
⋅
=
⋅
+
⋅
(7.36)
или
)()()()( sUsMsYsD
⋅
=
⋅
, (7.37)
где
1)(
+
⋅
=
sTsD
и M(s) = K. (7.38)
Передаточная функция W(s) определяется как отношение Y(s) к U(s). Для апе-
риодического звена из уравнения (7.37) получим
1)(
)(
)(
)(
)(
+⋅
===
sT
K
sD
sM
sU
sY
sW
. (7.39)
Используя передаточную функцию W(s), уравнение (7.36) можно запи-
сать в следующем виде:
)()()( sUsWsY
⋅
=
. (7.40)
Переходную функцию можно найти, решив уравнение (7.25) при u
= 1(t). Второй способ определения переходной функции заключается в сле-
дующем. С помощью интеграла Лапласа (6.2) находим изображение входного
сигнала u(t), описываемого единичной ступенчатой функцией 1(t):
s
dttesU
ts
1
)(1)(
0
=⋅⋅=
∫
∞
⋅−
. (7.41)
Подставив в уравнение (7.40) полученные выражения для изображения
входного сигнала (7.41) и передаточной функции (7.39), получим изображение
переходной функции:
)1(
)()(
+⋅⋅
==
sTs
K
sHsY . (7.42)
Применив обратное преобразования Лапласа к изображению переходной
функции (7.42), получим оригинал переходной функции:
)1(
)1(2
1
)()(
Tt
jc
jc
ts
eKdse
sTs
K
j
thty
−
∞⋅+
∞⋅−
⋅
−⋅=⋅⋅
+⋅⋅
⋅
⋅⋅
==
∫
π
. (7.43)
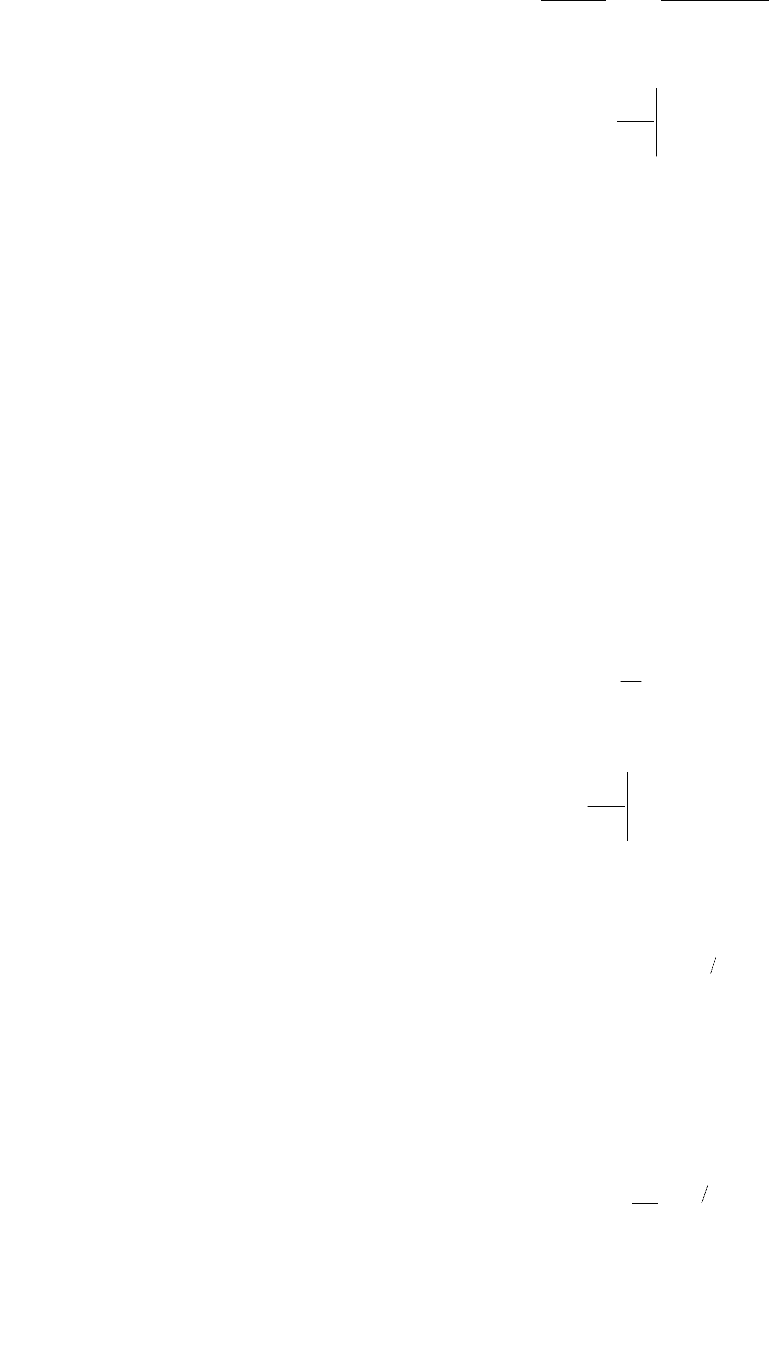
Переходную функцию можно также получить, используя формулу раз-
ложения Хевисайда
∑
⋅
⋅
⋅
+==
ts
kk
k
k
e
sDs
sM
D
M
thty
)(
)(
)0(
)0(
)()(
&
, (7.44)
где s
k
– корни уравнения D(s) = 0;
k
s
k
s
D
sD
∂
∂
=)(
&
.
Для передаточной функции W(s) (7.39) апериодического звена операто-
ры M(s) и D(s) согласно соотношению (7.38) равны
K
s
M
=
)
(
, (7.45)
1
)
(
+
⋅
=
s
T
s
D
, (7.46)
поэтому при s = 0
K
M
=
)
0
(
(7.47)
1
)
0
(
=
D
. (7.48)
Так как оператор D(s) является многочленом 1-го порядка, то n = k = 1 и
корень уравнения
0
1
)
(
=
+
⋅
=
s
T
s
D
(7.49)
всего один
T
s
1
1
−=
. (7.50)
Производная от оператора D(s) по s при s = s
1
согласно (7.46) равна
T
s
D
sD
s
=
∂
∂
=
1
)(
1
&
. (7.51)
Подставив в формулу (7.44) соотношения (7.47), (7.48), (7.50) и (7.51),
получим выражение для переходной функции
)1()()(
Tt
eKthty
−
−⋅==
, (7.52)
совпадающее с (7.43), так как решение не зависит от метода, которым оно по-
лучено.
Весовая функция в соответствии с формулой (6.16) определяется диффе-
ренцированием переходной h(t):
Tt
e
T
K
twty
−
⋅== )()( . (7.53)

График переходной функции (7.52) для апериодического звена имеет
апериодический характер (рис. 7.5, а), с чем связано название данного звена.
Из графика (рис. 7.5, а) видно, что выходной сигнал плавно возрастает по апе-
риодическому закону, несмотря на то, что он вызван ступенчатым изменением
входного сигнала.
График весовой функции (7.53) приведен на рис. 7.5, б.
Амплитудно-фазовую частотную характеристику можно найти с помо-
щью подстановки s = jω в передаточную функцию (7.39):
Tj
K
jW
⋅⋅+
=
ω1
)ω( . (7.54)
Умножив числитель и знаменатель АФЧХ (7.54) на сопряженное со зна-
менателем число, выделим вещественную P(ω) и мнимую Q(ω) частотные ха-
рактеристики:
22
)ω(1
ω
)ω(1
)ω(
T
TK
j
T
K
jW
⋅+
⋅
⋅
⋅−
⋅+
= . (7.55)
0 2 4 6 8 10 12 14 16 18
0
5
10
y(t)
t
а
0 2 4 6 8 10 12 14 16 18
0
2
y(t)
t
б
Рис. 7.5. Переходная (а) и весовая (б) характеристики апериодического звена
Из формулы (7.55) следует, что вещественная и мнимая частотные ха-
рактеристики определяются соотношениями
б
Рис. 7.5. Переходная (а) и весовая (б) функции апериодического звена
а
2
)ω(1
)ω(
T
K
P
⋅+
= , (7.56)
2
)ω(1
ω
)ω(
T
TK
Q
⋅+
⋅
⋅
= . (7.57)
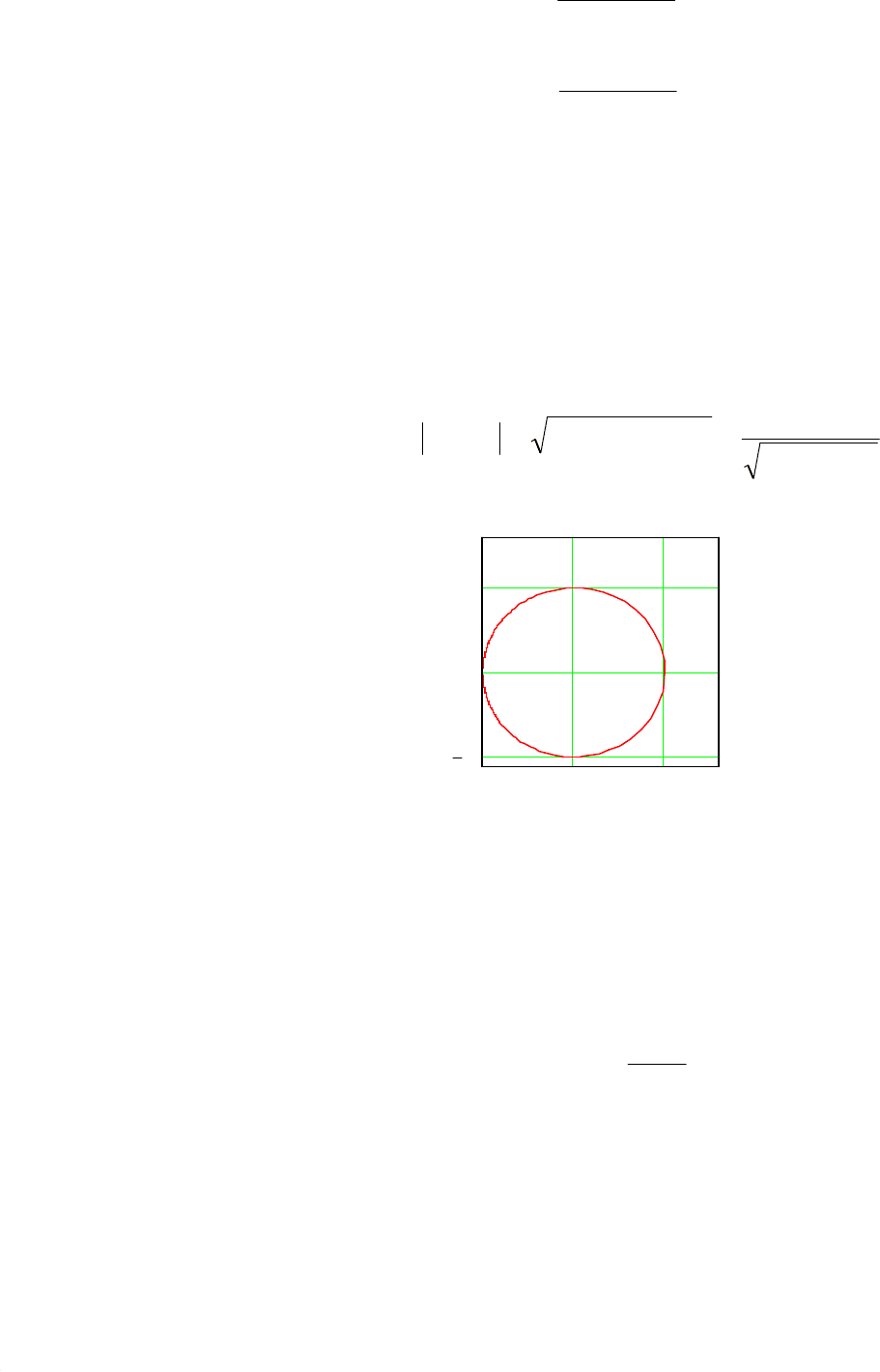
График амплитудно-фазовой частотной характеристики W(jω), постро-
енный по уравнению (7.55) при изменении частоты ω от –
∞
до +
∞
, имеет вид
окружности диаметром K с центром в точке P(ω) = K/2, Q(ω) = 0 (рис.
7.6).
Амплитудную частотную характеристику звена определяем как модуль
амплитудно-фазовой частотной характеристики W(jω), с учетом соотношений
(7.56) и (7.57) получим
2
22
)ω(1
)ω()ω()ω()ω(
T
K
QPjWA
⋅+
=+==
. (7.58)
0 5 10
5
0
5
jQ(ω
)
P(ω
)
Рис. 7.6. Амплитудно-фазовая
частотная характеристика
апериодического звена
Фазовую частотную характеристику находим, используя формулу (6.28);
с учетом соотношений (7.56) и (7.57) получим
)ω(arctg
)ω(
)ω(
arctg)ω(arg)ω( T
P
Q
jW ⋅−===ϕ . (7.59)
Логарифмическую амплитудную частотную характеристику можно най-
ти с помощью формул (6.32) и (7.58), в результате получим
[
]
2
)ω(1lg10lg20)ω(lg20)ω( TKAL ⋅+⋅−⋅=⋅= . (7.60)
Логарифмическая амплитудная частотная характеристика имеет две
асимптоты. При частоте ω, стремящейся к нулю, пренебрегая вторым слагае-
мым в квадратных скобках формулы (7.60), получаем уравнение первой асим-
птоты
K
L
lg
20
)
ω
(
⋅
≈
. (7.61)
При частоте
T1ω
>>
, пренебрегая первым слагаемым в квадратных
скобках формулы (7.60), получаем уравнение второй асимптоты
)
ω
lg(
20
lg
20
)
ω
(
T
K
L
⋅
⋅
−
⋅
≈
. (7.62)
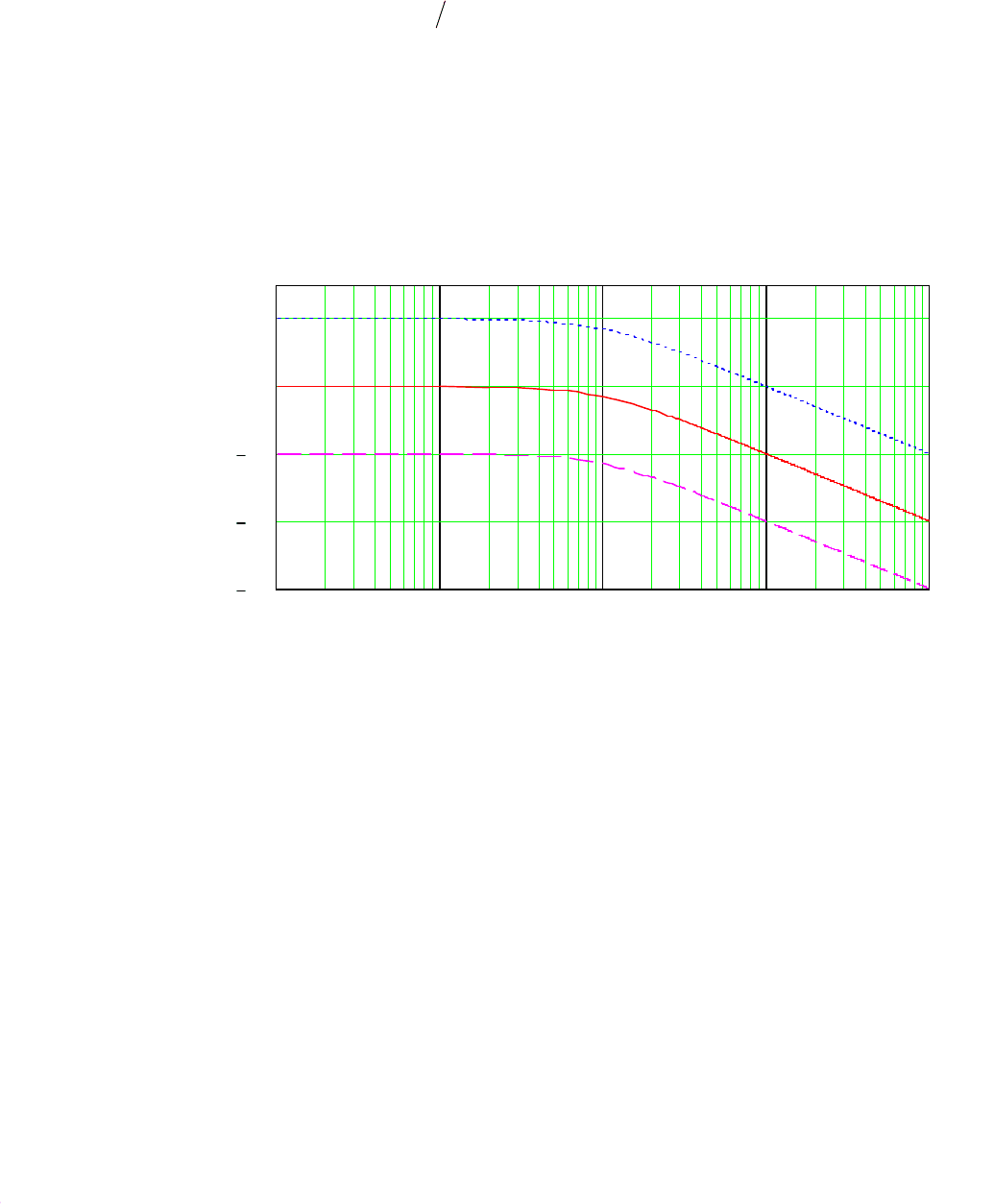
График логарифмической амплитудной частотной характеристики
апериодического звена первого порядка для трех значений K приведен на рис.
7.7.
1 10 100 1
.
10
3
1
.
10
4
60
40
20
0
20
L(ω
)
K=10
K=1
K=0,1
Рис. 7.7. Логарифмическая амплитудная частотная
характеристика апериодического звена
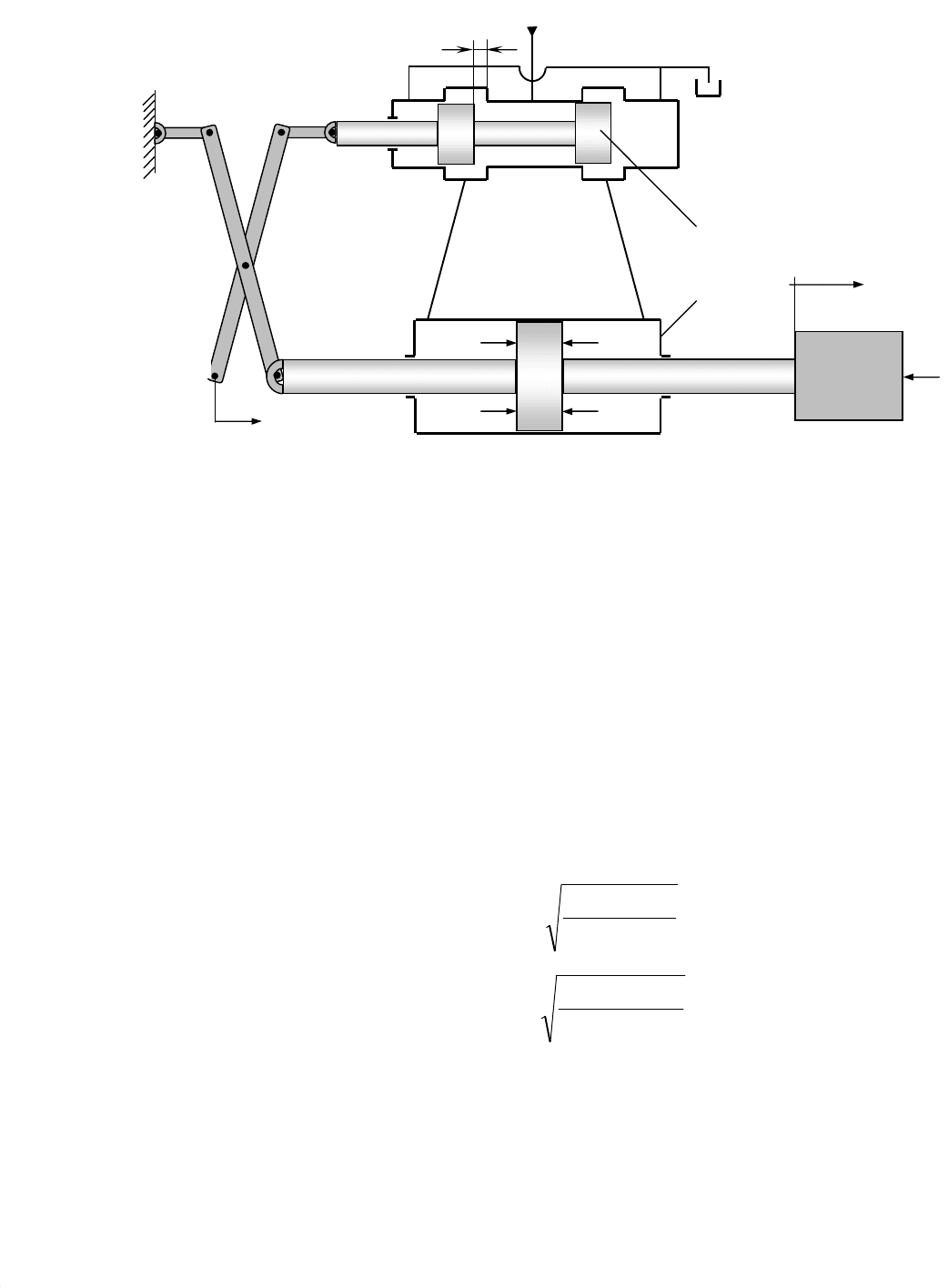
Логарифмическая фазовая частотная характеристика (рис. 7.8) аперио-
дического звена первого порядка, построенная по уравнению (7.59), при поло-
жительных значениях частоты изменяется от 0 до – π/2, проходя через точку
φ(ω) = – π/4 при ω = 1/T .
ω

Одним из примеров апериодического звена может служить следящий
гидропривод, состоящий из золотникового гидрораспределителя и ненагру-
женного гидроцилиндра (рис. 7.9). Механизм управления гидроприводом со-
стоит из рычагов AOB и COD. При смещении точки A рычага AOB в направле-
нии, показанном на схеме стрелкой, золотник 1 смещается влево, соединяя ле-
вую полость гидроцилиндра 2 с напорной линией, а правую полость гидроци-
линдра – со сливной линией. Под действием возникшего в полостях перепада
давления поршень гидроцилиндра перемещается вправо. При этом точка C
рычага COD, связанная со штоком, также перемещается вправо. Перемещение
поршня гидроцилиндра пропорционально перемещению точки A.
Таким образом, перемещением точки A рычага AOB осуществляется
входное воздействие на данный следящий привод, а рычагом COD обеспечи-
вается отрицательная обратная связь от выходного звена (штока гидроцилинд-
ра) к золотнику. Выходной (регулируемой) величиной является перемещение
штока. Коэффициенты передачи механизма управления зависят от отношения
плеч рычагов AOB и COD.
F
φ(ω)
Рис. 7.8. Логарифмическая фазовая частотная характеристика
1
10
100
1
.
10
3
1
.
10
4
2
1.5
1
0.5
0
ω
Составим математическое описание гидравлического механизма, пред-
полагая, что питание его рабочей жидкостью осуществляется при постоянном
давлении (p
П
= const) от источника с неограниченным расходом. Гидролинии
от золотникового распределителя к гидроцилиндру будем принимать настоль-
ко короткими, чтобы в них можно было бы не учитывать потери давления и
волновые процессы.
Для гидрораспределителя, когда окна распределителя имеют равные ко-
эффициенты расхода, при нулевых перекрытиях золотника, без учета утечек и
перетечек рабочей жидкости в распределителе, можно записать два уравнения
расходов:
ρ
)(2
μ
1П
ЗОКЗ1
pp
xbQ
З
−
=
, (7.63)
ρ
)(2
μ
СЛ2
ЗОКЗ2
pp
xbQ
З
−
= , (7.64)
где Q
З1
– расход рабочей жидкости, втекающей в гидроцилиндр; Q
З2
– расход
рабочей жидкости, вытекающей из гидроцилиндра; µ
З
– коэффициент расхода
окон золотникового распределителя; b
ОК
– ширина окон во втулке (если окно,
расположенное напротив бурта золотника, занимает весь периметр втулки, то
D
B
O
C
A
h
A
x
З
p
П
p
СЛ
y
П
p
2
p
1
1
2
F
m
ПР
Рис. 7.9. Следящий гидропривод с дроссельным регулированием
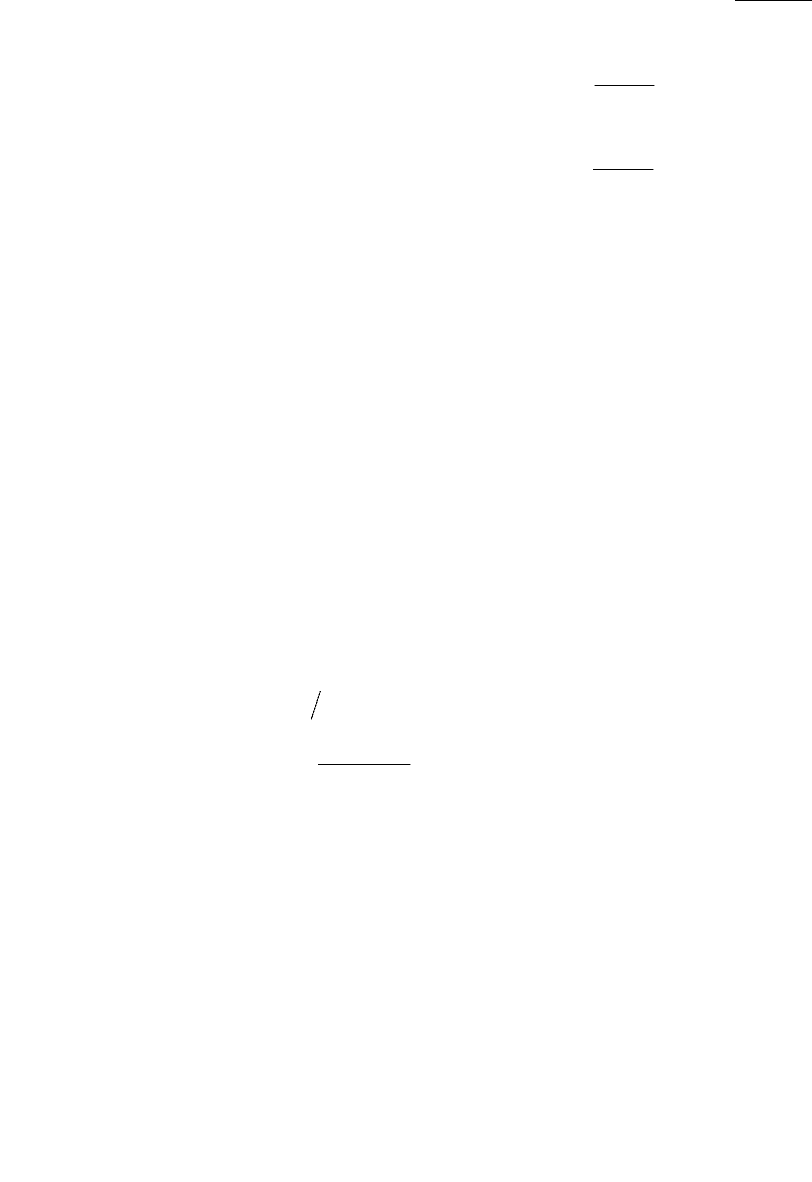
b
ОК
= πd
З
; x
З
– смещение золотника от нейтрального положения; p
П
– давление
питания в напорной гидролинии; p
СЛ
– давление в сливной гидролинии; p
1
и p
2
– давления в левой и правой полостях гидроцилиндра; ρ – плотность жидко-
сти.
Для гидроцилиндра можно записать уравнение движения поршня и
уравнения расходов (втекающего и вытекающего):
2
ШТ
2
ПРТР22Ц11Ц
dt
yd
mFFpfpf =−−− (7.65)
dt
dy
fQ
ШТ
1Ц1З
= (7.66)
dt
dy
fQ
ШТ
2Ц2З
= , (7.67)
где f
Ц1
и f
Ц2
– рабочие площади поршня (т. е. площадь поршня минус площадь
штока) в левой и правой полостях гидроцилиндра; F
ТР
– сила трения, дейст-
вующая на поршень и шток; F – внешняя нагрузка; m
ПР
– суммарная масса
поршня, штока и приведенной массы рабочих органов, приводимых в движе-
ние штоком; y
ШТ
– перемещение штока.
Для завершения построения математической модели следящего гидро-
привода необходимо еще записать уравнение, устанавливающее связь между
перемещением точки A рычага AOB, которое является управляющим сигна-
лом, перемещением золотника и перемещением штока гидроцилиндра. Если
корпуса распределителя и гидроцилиндра закреплены неподвижно, то имеем
следующее кинематическое соотношение:
ШТО.С.З
yKhKx
Axh
−
=
, (7.68)
где
AOOBK
xh
=
– коэффициент передачи механизма управления гидропри-
водом;
CD
AO
DOAB
K
⋅
⋅
=
О.С
– коэффициент обратной связи гидропривода.
Уравнения (7.63)–(7.68) являются математической моделью рассматри-
ваемого гидравлического механизма. В некоторых случаях ее можно заменить
более простой моделью.
Пусть гидроцилиндр выполнен с одинаковыми значениями рабочих
площадей в левой и правой полостях (f
Ц1
= f
Ц2
), обозначим эти площади через
f
Ц
. Если в уравнении (3.65) можно пренебречь силой трения, внешней нагруз-
кой и произведением приведенной массы на ускорение, то такой гидроци-
