Никитин А.А. Управление техническими системами
Подождите немного. Документ загружается.


где Q
ДР
– расход жидкости через дроссель; )(
21ДР
ppp
−
=
∆
– перепад давле-
ния на дросселе; k
ДР
– проводимость дроссельного отверстия в поршне демп-
фера.
Для ламинарного режима течения жидкости в цилиндрическом канале
диаметром d и длиной l
l
d
k
⋅⋅
⋅
=
μ128
π
4
ДР
(4.6)
(здесь μ – динамический коэффициент вязкости жидкости).
На основании неразрывности потока несжимаемой жидкости можно за-
писать
dt
dz
SQ
2
ДР
⋅= . (4.7)
Система уравнений (4.1), (4.5) и (4.7) с учетом соотношений (4.2) – (4.4)
и (4.6) составляет математическую модель рассматриваемой системы. Полу-
ченную систему уравнений можно привести к одному уравнению в форме
“вход-выход”, исключив промежуточные переменные и оставив только вход-
ную и выходную величины, соответственно z
1
и z
2
. При этом все члены с вы-
ходной величиной переносят в левую часть уравнения, а все члены с входной
величиной – в правую.
Для системы (рис. 4.1) уравнение в форме “вход-выход” будет иметь вид
1ПР2ПР
2
ДР
2
2
2
2
zczc
dt
dz
k
S
dt
zd
m ⋅=⋅+⋅+⋅ . (4.8)
Уравнение (4.8) можно записать в общем виде:
ubya
dt
dy
a
dt
yd
a ⋅=⋅+⋅+⋅
001
2
2
2
, (4.9)
где
ma
=
2
;
ДР
2
1
k
S
a = ;
ПР0
ca
=
;
ПР0
cb
=
; (4.10)
y = z
2
, u = z
1
. (4.11)
Уравнение (4.9) обычно приводят к стандартному виду. Для этого все
члены уравнения делим на коэффициент
0
a
при выходной величине, в резуль-
тате получим
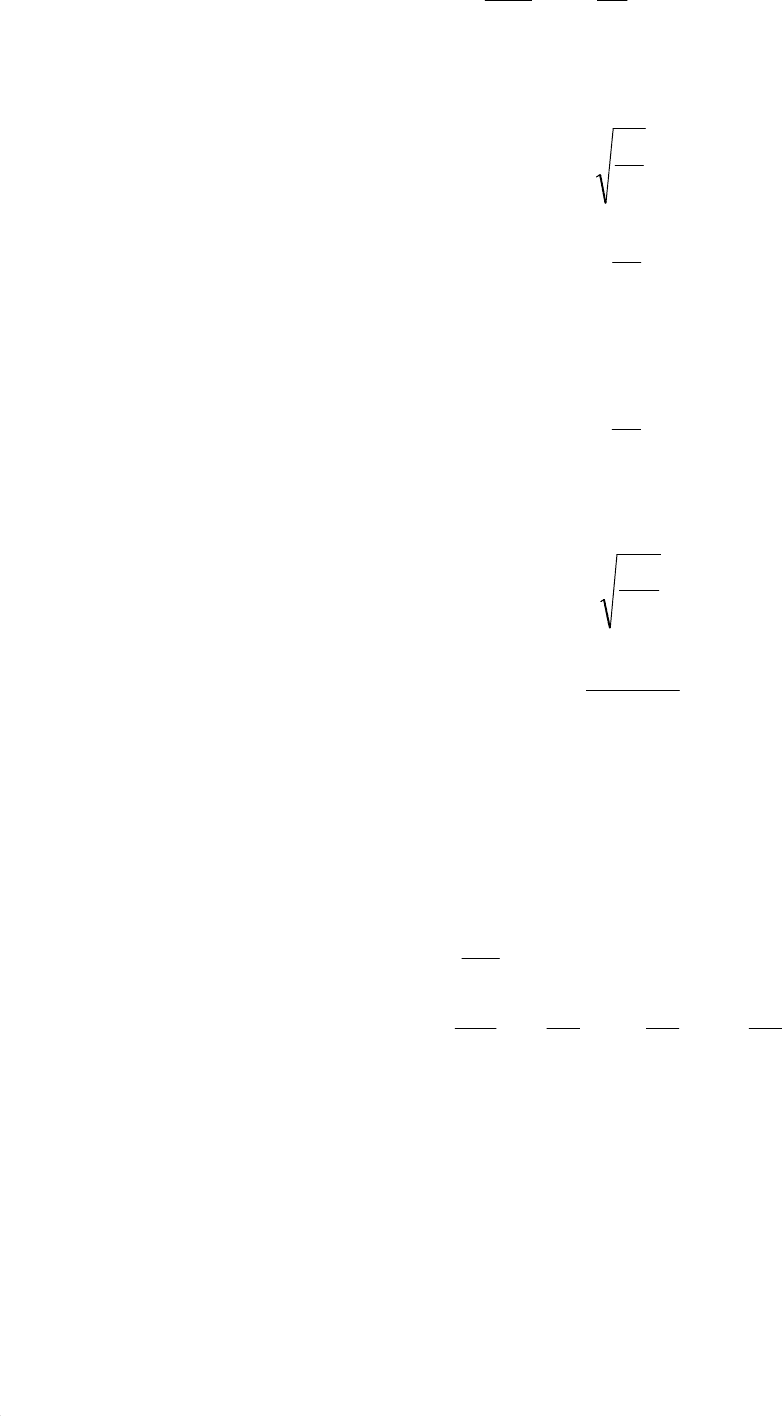
uKy
dt
dy
T
dt
yd
T ⋅=+⋅+⋅
1
2
2
2
2
. (4.12)
Коэффициенты T
1
и T
2
имеют размерность времени, поэтому называются
постоянными времени:
0
2
2
a
a
T = , (4.13)
0
1
1
a
a
T = . (4.14)
Коэффициент K называется коэффициентом передачи или преобразования,
или коэффициентом усиления если он является безразмерной величиной:
0
0
a
b
K = . (4.15)
Для системы (рис. 4.1), описываемой уравнением (4.8), можно получить
выражения для коэффициентов, используя соотношения (4.10) и (4.13) – (4.15):
ПР
2
c
m
T = , (4.16)
ПРДР
2
1
ck
S
T
⋅
= , (4.17)
1
=
K
. (4.18)
Для математического описания системы с использованием переменных
состояния дифференциальное уравнение (4.12) второго порядка заменим сис-
темой двух уравнений первого порядка:
⋅+⋅−⋅−=
=
u
T
K
x
T
T
x
Tdt
dx
x
dt
dx
2
2
2
2
2
1
1
2
2
2
2
1
1
(4.19)
и соотношением
yx
=
1
. (4.20)
Зная пару переменных x
1
и x
2
в некоторый момент времени t
0
и входное
воздействие u для всех t > t
0
, можно определить состояние системы в любой
момент времени всех t > t
0
и найти значение выходной величины y(t). Величи-
ны x
1
и x
2
называются переменными состояния данной системы, а уравнения

(4.19) – дифференциальными уравнениями состояния. Соотношение (4.20) ус-
танавливает связь выходной величины с переменной состояния.
Вопросы для самопроверки
1. Привести пример математического описания системы в форме “вход-
выход”.
2. Уравнение, записанное в форме “вход-выход”, привести к стандарт-
ному виду.
3. Дать определение математической модели системы.
4. Привести пример математического описания системы в переменных
состояния.

5. УРАВНЕНИЯ СТАТИКИ И ДИНАМИКИ
Уравнения элементов, статические и динамические свойства элементов.
Принципы линеаризации характеристик нелинейных зависимостей. Диффе-
ренциальная и операторная формы.
Систему или ее элементы можно рассматривать как звено направленного дей-
ствия, пропускающего сигналы в одном направлении. При этом входную ве-
личину, характеризующую воздействие на систему (элемент), будем обозна-
чать u, а выходную величину, определяющую состояние системы (регулируе-
мую) или воздействие элемента на последующий элемент, через y.
До тех пор пока величины, определяющие состояние системы, не изменяются
во времени, система находится в равновесии. Соотношения, связывающие ме-
жду собой входные и выходные величины при разных состояниях системы или
ее элементов, называются уравнениями статики. Уравнения статики элемента
или системы записываются в виде
0),(
00
=
yuF , (5.1)
где
0
u
,
0
y
– входная и выходная величины при равновесии элемента или сис-
темы.
График, построенный по уравнению (5.1), называется статической характери-
стикой элемента или системы. Статические характеристики элементов или
системы можно получить экспериментально или теоретически (рассчитать).
Статические характеристики могут быть линейными или нелинейными.
Примером может служить статическая характеристика золотникового
распределителя, сопла-заслонки или клапана, связывающая между собой раз-
личные установившиеся значения либо двух, либо трех величин: расхода ра-
бочей жидкости, перепада давления, перемещения подвижного элемента уст-
ройства.
Для несжимаемой жидкости установившийся расход через перечислен-
ные устройства определяется зависимостью
ρ
)(2
πμ
21
pp
xkdQ
−⋅
⋅⋅⋅⋅⋅=
, (5.2)
где μ – коэффициент расхода; d – диаметр регулируемого канала; k – коэффи-
циент, зависящий от конструктивного исполнения устройства; x – перемеще-
ние запорно-регулирующего элемента; p
1
и p
2
– давление соответственно до и
после устройства; ρ – плотность рабочей жидкости.

Нелинейные функции можно линеаризовать с помощью разложения в
ряд Тейлора и пренебрегая нелинейными членами.
В качестве примера линеаризуем зависимость (5.2) расхода от давления
и перемещения запорно-регулирующего элемента. При постоянных коэффи-
циентах μ и k расход Q будет функцией трех переменных: x, p
1
и p
2
. Разло-
жив нелинейную функцию Q (x, p
1
, p
2
) в ряд Тейлора и отбросив нелинейные
члены, получим
2
2
1
1
2010021
202
101
0
202
101
0
202
101
0
),,(),,( p
p
Q
p
p
Q
x
x
Q
ppxQppxQ
pp
pp
xx
pp
pp
xx
pp
pp
xx
′
⋅
∂
∂
+
′
⋅
∂
∂
+
′
⋅
∂
∂
+=
=
=
=
=
=
=
=
=
=
,
(5.3)
где x
0
, p
10
, p
20
– значения переменных в точке линеаризации, соответствующей
одному из установившихся режимов течения жидкости через устройство; x΄,
p΄
1
, p΄
2
– малые отклонения переменных от установившихся значений.
Введем обозначения:
),,(
21
ppxQQ
=
; (5.4)
),,(
201000
ppxQQ
=
; (5.5)
ρ
)(2
πμ
2010
202
101
0
pp
kd
x
Q
K
pp
pp
xx
Qx
−⋅
⋅⋅⋅⋅=
∂
∂
=
=
=
=
; (5.6)
)(ρ2
1
πμ
2010
0
21
202
101
0
202
101
0
pp
xkd
p
Q
p
Q
K
pp
pp
xx
pp
pp
xx
Qp
−⋅⋅
⋅⋅⋅⋅⋅=
∂
∂
−=
∂
∂
=
=
=
=
=
=
=
. (5.7)
Тогда зависимость (5.4) с учетом соотношений (5.5)–(5.7) можно запи-
сать в виде
210
pKpKxKQQ
QpQpQx
′
⋅
−
′
⋅
+
′
⋅
+
=
, (5.8)
где K
Qx
, K
Qp
– коэффициенты линеаризации, определяемые соотношениями
(5.6) и (5.7).
Линеаризацию можно проводить и графически. Если нелинейная одно-
значная статическая характеристика плавно изменяет свою форму, то ее мож-
но заменить приближенной линейной статической характеристикой в виде
прямой – касательной к исходной характеристике. График функции (5.2) при
постоянных x (x = x
0
) и p
1
(p
1
= p
10
) приведен на рис. 5.1. Проведя касательную
к заданной кривой в точке p
2
= p
20
, лежащей в исследуемом диапазоне измене-
ния переменных, найдем коэффициент линеаризации K
Qp
, который равен тан-
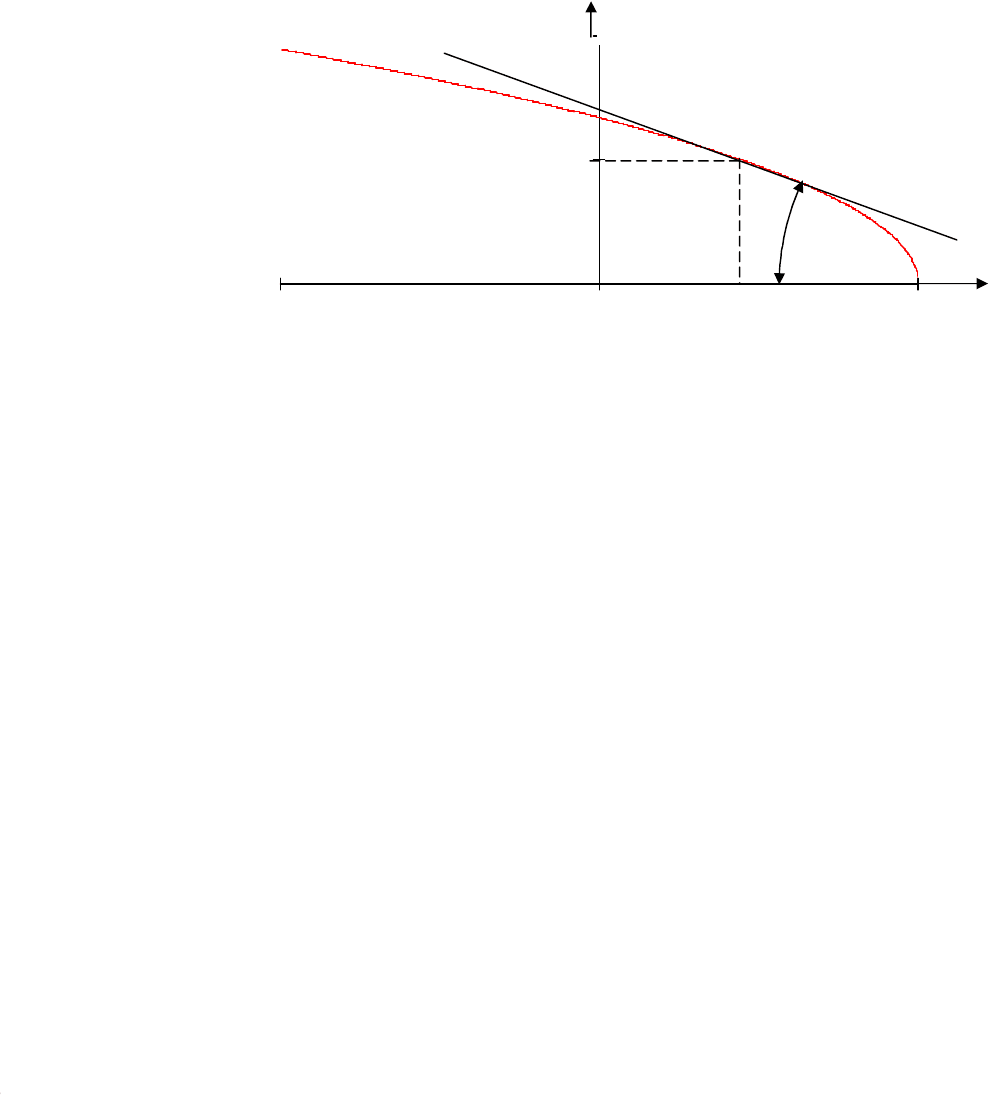
генсу
tg
φ
наклона касательной. Аналогично можно определить коэффициент
K
Qx
.
Уравнения, описывающие изменяющиеся во времени состояния систем
или элемента, называются уравнениями динамики. Они могут быть дифферен-
циальными, интегральными и алгебраическими.
При математическом описании элементов и систем чаще всего исполь-
зуют дифференциальные уравнения. Если эти уравнения линейные, то основ-
ные задачи автоматического регулирования и управления решаются наиболее
просто.
.
Однако уравнения динамики реальных элементов и систем вследствие
сложности протекающих в них физических процессов обычно получаются не-
линейными. Когда это возможно, нелинейные уравнения заменяют прибли-
женными линейными уравнениями.
Одним из методов линеаризации уравнений является метод малых от-
клонений переменных, который основан на описании физических процессов,
протекающих в элементах и системах, в малых отклонениях переменных от
тех значений, которыми определяются невозмущенные состояния элементов и
систем. Используя разложения в ряд Тейлора и пренебрегая нелинейными
членами, нелинейные функции заменяют линейными.
В качестве примера приведем описание простой гидравлической систе-
мы, схема которой показана на рис. 5.2. Система состоит из распределителя 1 с
постоянным гидравлическим сопротивлением, регулируемого дросселя 2 с пе-
ременным гидравлическим сопротивлением, гидроцилиндра 3 с поршнем 4 и
массы m. Сопротивлением гидролиний будем пренебрегать. В этом случае
давление после распределителя 1, перед регулируемым дросселем и в гидро-
Q(x, p
1
, p
2
)
Q
0
p
20
p
2
φ
Рис. 5.1. Аппроксимация нелинейной статической характер
и-
стики
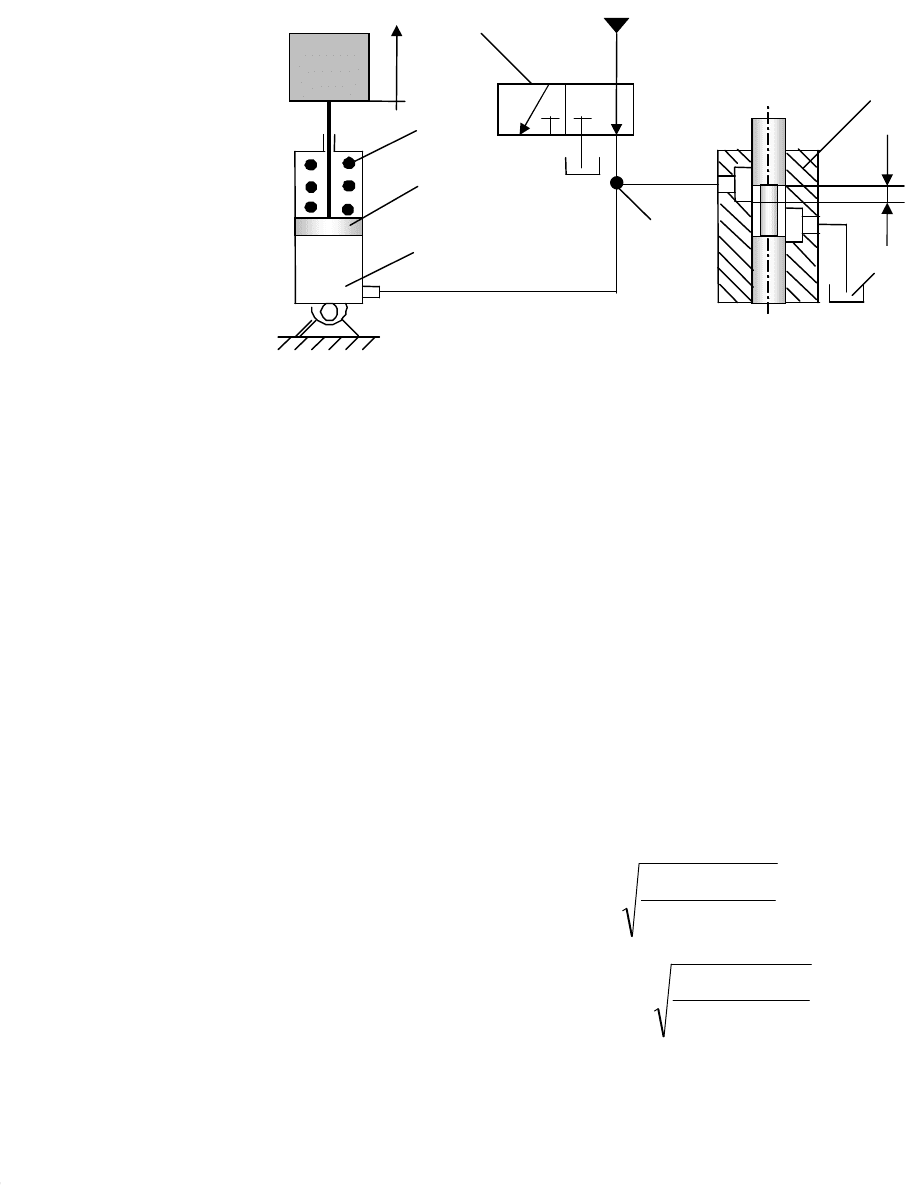
цилиндре будет одинаковым (p
2
). На поршень с одной стороны действует сила
давления жидкости, а с другой – сила пружины 5, жесткость которой равна с
ПР
.
Поршень находится в равновесии, когда эти силы равны. Изменяя гидравличе-
ское сопротивление регулируемого дросселя, можно изменять давление p
2
. Это
приводит к нарушению равновесия сил, действующих на поршень, и к его пе-
ремещению.
Масса m с помощью штока жестко связана с поршнем, поэтому при пе-
ремещении поршня будет перемещаться и масса m.
Гидравлическое сопротивление регулируемого дросселя можно изменять
за счет изменения его проходного сечения. Таким образом, изменяя проходное
сечение регулируемого дросселя 2, перемещением x золотника, можно управ-
лять положением y массы m (рис. 5.2).
Будем считать давление p
1
перед распределителем и давление p
3
после
дросселя постоянными, причем p
1
> p
3
.
При показанных на схеме направлениях течения жидкости с расходами
Q
1
, Q
2
и Q
3
можно записать:
321
QQQ
+
=
, (5.9)
ρ
)(2
μ
21
111
pp
fQ
−⋅
⋅⋅= , (5.10)
ρ
)(2
πμ
32
22
pp
xkdQ
−⋅
⋅⋅⋅⋅⋅=
, (5.11)
1
5
3
Рис. 5.
2
.
Гидравлическая сист
е
ма
m
x
p
1
p
2
2
4
y
p
3

где μ
1
– коэффициент расхода распределителя; f
1
– площадь поперечного сече-
ния канала нерегулируемого дросселя; μ
2
– коэффициент расхода регулируе-
мого дросселя; d – диаметр регулируемого канала; k – коэффициент, завися-
щий от конструктивного исполнения устройства. Коэффициенты расхода μ
1
и
μ
2
будем считать постоянными.
На основании неразрывности течения, с учетом сжимаемости жидкости
в гидроцилиндре можно записать:
dt
dp
E
W
dt
dy
SQ
2
Ж
0
3
⋅+⋅= , (5.12)
где S – площадь поршня; y – перемещение поршня (массы m); W
0
– объем ра-
бочей полости гидроцилиндра, соответствующий установившемуся режиму;
E
Ж
– модуль объемной упругости жидкости.
Уравнение движения поршня можно записать в виде
2
2
ТРПР2
dt
yd
mFFSp ⋅=−−⋅ , (5.13)
где F
ПР
– сила, приложенная к поршню со стороны пружины; F
ТР
– сила трения
между поршнем и цилиндром.
При линейной характеристике пружины
ycFF
⋅
+
=
ПР0.ПРПР
, (5.14)
где F
ПР.0
– сила, развиваемая пружиной при равновесии поршня в положении
0
=
y
.
Если силой трения между поршнем и цилиндром пренебречь, то с уче-
том соотношения (5.14) уравнение (5.13) примет вид
2
2
ПР0.ПР2
)(
dt
yd
mycFSp ⋅=⋅+−⋅
. (5.15)
Система уравнений (5.9)–(5.12) и (5.15) представляет собой нелинейную
математическую модель рассматриваемой гидравлической системы, потому
что содержит нелинейные функции (5.10) и (5.11).
Для получения линейной модели будем рассматривать малые отклоне-
ния y′, x′ и p′
2
переменных y, x и p
2
относительно установившихся значений y
0
,
x
0
и p
2.0
, которые они принимают при
0
xx
=
. Тогда можно записать:
yyy
′
+
=
0
; (5.16)
xxx
′
+
=
0
; (5.17)

20.22
ppp
′
+
=
. (5.18)
Проведем линеаризации функций расхода Q
1
(p
2
) и Q
2
(x, p
2
), с учетом
формулы (5.8) получим
2.1101
pKQQ
pQ
′
⋅
−
=
, (5.19)
2.2.2202
pKxKQQ
pQxQ
′
⋅
+
′
⋅
+
=
, (5.20)
где Q
1.0
и Q
2.0
– расходы на установившемся режиме соответственно через
распределитель и регулируемый дроссель;
ρ
)(2
μ
0.21
110.1
pp
fQ
−⋅
⋅⋅=
, (5.21)
ρ
)(2
πμ
30.2
020.2
pp
xkdQ
−⋅
⋅⋅⋅⋅⋅=
. (5.22)
Коэффициенты расхода K
Q1.p
, K
Q2.x
, K
Q2.p
, согласно соотношениям (5.6) и (5.7),
определим по формулам:
)(ρ2
1
πμ
0.21
0111
2
1
.1
202
0
pp
xkd
p
Q
K
pp
xx
pQ
−⋅⋅
⋅⋅⋅⋅⋅=
∂
∂
−=
=
=
; (5.23)
ρ
)(2
πμ
30.2
222
2
.2
202
0
pp
kd
x
Q
K
pp
xx
xQ
−⋅
⋅⋅⋅⋅=
∂
∂
=
=
=
; (5.24)
)(ρ2
1
πμ
30.2
0222
2
2
.2
202
0
pp
xkd
p
Q
K
pp
xx
pQ
−⋅⋅
⋅⋅⋅⋅⋅=
∂
∂
−=
=
=
. (5.25)
Уравнение (5.12) с учетом соотношений (5.16), (5.17) и (5.18) можно записать
в виде
dt
pd
E
W
dt
dp
E
W
dt
yd
S
dt
dy
SQ
2
Ж
00.2
Ж
00
3
′
⋅+⋅+
′
⋅+⋅= . (5.26)
Подставим в уравнение (5.15) выражения для давления p
2
из формулы (5.18) и
для перемещения y из формулы (5.16), в результате получим
2
2
2
0
2
ПР0ПР0.ПР20.2
)(
dt
yd
m
dt
yd
mycycFSpSp
′
⋅+⋅=
′
⋅+⋅+−⋅
′
+⋅ . (5.27)

Система уравнений (5.9), (5.19), (5.20), (5.26) и (5.27) представляет собой
линейную математическую модель рассматриваемой гидравлической системы,
которая описывает процессы, протекающие в системе, при малых отклонениях
переменных. Из этих уравнений можно исключить члены, содержащие уста-
новившиеся значения переменных. Для этого введем малые отклонения расхо-
дов от установившихся значений:
0.111
QQQ
−
=
′
; (5.28)
0.222
QQQ
−
=
′
; (5.29)
0.333
QQQ
−
=
′
, (5.30)
где
1
Q
′
,
2
Q
′
и
3
Q
′
– малые отклонения расходов соответственно Q
1
, Q
2
и Q
3
от-
носительно установившихся значений Q
1.0
, Q
2.0
и Q
3.0
.
Из соотношений (5.28)–(5.30) найдем выражения для расходов:
10.11
QQQ
′
+
=
; (5.31)
20.22
QQQ
′
+
=
; (5.32)
30.33
QQQ
′
+
=
. (5.33)
После подстановки в уравнения (5.9), (5.19), (5.20), (5.26) выражения для
расходов соответственно Q
1
, Q
2
и Q
3
из формул (5.28)–(5.30) система уравне-
ний (5.9), (5.19), (5.20), (5.26) и (5.27) примет следующий вид:
′
⋅+⋅=
′
⋅+⋅+−⋅
′
+⋅
′
⋅+⋅+
′
⋅+⋅=
′
+
′
⋅+
′
⋅+=
′
+
′
⋅−=
′
+
′
+
+
′
+
=
′
+
2
2
2
0
2
ПР0ПР0.ПР20.2
2
Ж
00.2
Ж
00
30.3
2.2.22020.2
2.1100.1
30.320.210.1
)(
dt
yd
m
dt
yd
mycycFSpSp
dt
pd
E
W
dt
dp
E
W
dt
yd
S
dt
dy
SQQ
pKxKQQQ
pKQQQ
QQQQQQ
pQxQ
pQ
. (5.34)
Система уравнений (5.34) описывает переходный процесс, происходя-
щий в гидравлической системе (рис. 5.2). В частном случае, когда малые от-
клонения равны нулю, система уравнений (5.34) будет описывать установив-
шейся процесс. При этом система уравнений (5.34) примет вид
