Математическое моделирование, численные методы и комплексы программ 2007 Вып.13

160 161

( ) ( )

{ }

{ } { }

( ) ( ) ( )

[ ]

{

;0,0,

;,max,max

),,(),,,(max|),,(|

;0,0,0;1,,0,,0

21112

1111

2

1

11

1

niiiii

iiii

nii

ii

i

ddcod

dyardyardyar

da

dy

d

j-e+j+e+j--e+j=j

e+j-e+j=e+j-j=

=e+-=e+=j

=j=

÷

ø

ö

ç

è

æ

¶

j¶

¶

j¶

=j

( ) ( ) ( )

[ ]

}

( ) ( )

[ ]

{

( ) ( )

[ ]

}

=e

/

--e

/

+j-+---

e

/

--e

/

+j+-=

=j-e+j-+e+j-e+j-

0,0,|),,(|0,0,01,,0

;0,0,|),,(|0,0,01,,0

0,0,

1

2111

n

i

n

i

niini

niiii

dyara

dyaraco

dd

(

)

(

)

{

( ) ( )}

=--+--

-

+

=

0,0|,),,(|),,(1,,0

;0,0|,),,(|),,(1,,0

n

i

niii

dyardyara

dyardyaraco

(

)

(

)

{

}

( ) ( ) ( )

=

j

jj-jj

=

=e+j-+e+j=j

-

=

2

2112

1

112

;0,0,0

;1,|,),,(|),,(,1,|,),,(|),,(

i

iiii

i

niii

iiiiii

dd

fd

ddd

adyardyaradyardyarco

( ) ( )( ){ }

( )

.0,0,0

;1,|,|,1,|,|1,,0

2

2112

1

1111

2

1

2

1

n

i

iiii

i

iiiiii

i

dd

fd

aacoa

=

j

jj-jj

=

--j-j-j-j

j

-

j

=

Следовательно,

{

}

{

}

{

}

=-+-+-= 0,0,;0,0,

111111 niiiniii

FffdFfdcoFd

( ) ( )( ){ }

+--j-j-j-j

j

-

j

ï

î

ï

í

ì

þ

ý

ü

î

í

ì

þ

ý

ü

î

í

ì

j

-=

1,|,|,1,|,|1,,0

;0,0,,0max

1111

2

1

2

1

2

1

iiiiii

i

n

i

aacoa

co

( )( ){ }

=

ï

þ

ï

ý

ü

--j-j-j-j

j

-

÷

ø

ö

ç

è

æ

j

þ

ý

ü

î

í

ì

j

-

j

ï

î

ï

í

ì

þ

ý

ü

î

í

ì

þ

ý

ü

î

í

ì

j

-=

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-

j

+

1,|,|,1,|,|

,,,0max

;0,0,,0max0,0,,0max

1111

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

iiiiii

i

n

i

n

i

aaco

a

co

;0,0,,0max

2

1

ï

î

ï

í

ì

þ

ý

ü

î

í

ì

þ

ý

ü

î

í

ì

j

-=

n

i

co

( )( ){ }

( )

ç

è

æ

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

j

j-j×

j

-

ï

î

ï

í

ì

þ

ý

ü

î

í

ì

þ

ý

ü

î

í

ì

j

-=

=

ï

þ

ï

ý

ü

÷

ø

ö

--j-j-j-j

j

+

ç

è

æ

+

÷

ø

ö

ç

è

æ

j

þ

ý

ü

î

í

ì

j

-

j

--

;,,||0,0,,0max

1,|,|,1,|,|

,,,0max

2

1

2

1

11

2

1

2

1

1111

2

1

2

1

2

1

2

1

2

1

i

ii

i

n

i

iiiiii

i

acoco

aaco

a

( )

;,,,0max,,||

;0,0,,0max,,,0max

2

1

2

1

2

1

2

1

2

1

2

1

11

2

1

2

1

2

1

2

1

2

1

2

1

ç

è

æ

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

j

þ

ý

ü

î

í

ì

j

-

j

-

÷

ø

ö

ç

è

æ

j

j-j

j

-

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-=

÷

ø

ö

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

j

þ

ý

ü

î

í

ì

j

-

j

-

i

ii

i

n

i

aaco

coa

( )

=

ï

þ

ï

ý

ü

÷

ø

ö

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

j

þ

ý

ü

î

í

ì

j

-

j

-

÷

ø

ö

ç

è

æ

j

-

j

-j-j-

j

2

1

2

1

2

1

2

1

2

1

2

1

11

2

1

,,,0max,,||

i

ii

i

aa

;0,0,,0max

2

1

î

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-=

n

i

co

162 163

( )

î

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-=

=

ï

þ

ï

ý

ü

÷

ø

ö

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

j

þ

ý

ü

î

í

ì

j

-

j

-

÷

ø

ö

ç

è

æ

j

-

j

-j-j-

j

ç

è

æ

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

j

þ

ý

ü

î

í

ì

j

-

j

-

÷

ø

ö

ç

è

æ

j

j-j

j

-

;0,0,,0max

,,,0max,,||

;,,,0max,,||

2

1

2

1

2

1

2

1

2

1

2

1

2

1

11

2

1

2

1

2

1

2

1

2

1

2

1

2

1

11

2

1

n

i

ii

i

ii

i

co

aa

aaco

( )

=

ï

þ

ï

ý

ü

÷

ø

ö

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

j

-

j

-

þ

ý

ü

î

í

ì

j

+

j

-j-j-

j

ç

è

æ

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

+

j

-j-j

j

-

2

1

2

1

2

1

2

1

11

2

1

2

1

2

1

11

2

1

2,2,,0max||

;0,0,,0max||

i

ii

i

n

i

ii

i

a

co

( )

ç

è

æ

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

+

j

-j-j

j

-

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-=

;0,0,,0max||

;0,0,,0max

2

1

2

1

11

2

1

2

1

n

i

ii

i

n

i

co

( )

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-=

=

ï

þ

ï

ý

ü

÷

ø

ö

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

j

-

j

-

þ

ý

ü

î

í

ì

j

+

j

-j-j-

j

;0,0,,0max

2,2,,0max||

2

1

2

1

2

1

2

1

2

1

11

2

1

n

i

ii

i

co

a

;0,0,,0max

||

2

1

2

1

2

11

2

1

ç

è

æ

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

+

j

-

j

jj

-

j

-

n

i

ii

i

co

=

ï

þ

ï

ý

ü

÷

ø

ö

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

j

-

j

-

þ

ý

ü

î

í

ì

j

+

j

-

j

jj

-

j

-

2

1

2

1

2

1

2

1

2

11

2

1

2,2,,0max

||

i

ii

i

a

=

ï

þ

ï

ý

ü

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

j

þ

ý

ü

î

í

ì

j

-

j

+

j

jj

+

j

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-

j

+

j

jj

+

j

-

î

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-=

2

1

2

1

2

1

2

1

2

11

2

1

2

1

2

1

2

11

2

1

2

1

2,2,,0max

||

;0,0,,0max

||

;0,0,,0max

i

ii

i

n

i

ii

i

n

i

a

co

=

ï

þ

ï

ý

ü

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

j

þ

ý

ü

î

í

ì

j

-

j

+

j

jj

+

j

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-

j

+

j

jj

+

j

-

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-=

2

1

2

1

2

1

2

1

2

11

2

1

2

1

2

1

2

11

2

1

2

1

2,2,,0max

||

;0,0,,0max

||

;0,0,,0max

i

ii

i

n

i

ii

i

n

i

a

co

;2,2,,0max

||

;0,0,,0max

||

;0,0,,0max

2

1

2

1

2

1

2

1

2

11

2

1

2

1

2

1

2

11

2

1

2

1

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

j

þ

ý

ü

î

í

ì

j

-

j

+

j

jj

+

j

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-

j

+

j

jj

+

j

-

î

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-=

i

ii

i

n

i

ii

i

n

i

a

co

( )

.0,0,00

1

n

i

fddFd =+=

164 165

Аналогично выведем формулу для

:,

22 jj

FdFd

( )

{ }

{ } { }

( ) ( ) ( )

[ ]

{

( ) ( ) ( )

[ ]

}

( )

[ ]

{

( )

[ ]

}

=e

/

--e

/

+y-+-

e

/

--e

/

+y+---=

=y-e+y-+e+y-e+y-

y-e+y+e+y--e+y=y

e+y-e+y=e+y-y=

=e+-=e+-=y

=y--=

÷

ø

ö

ç

è

æ

¶

y

¶

y

¶

=y

0,0,|),,(|0,0,01,,0

;0,0,|),,(|0,0,01,,0

0,0,

;0,0,

;,max,max

),,(),,,(max|),,(|

;0,0,0;1,,0,,0

1

2111

2112

1111

2

1

11

1

njjnj

njjjj

njjjjij

jjjj

njj

jj

j

dybrb

dybrbco

dd

ddcod

dybrdybrdybr

db

dy

d

=-+ )}0,0,),,(),,(()1,,0(

njjj

dybrdybrb

( )( ){ }

+y-y---y-y

y

-

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

ï

þ

ï

ý

ü

ï

î

ï

í

ì

y

-=

1,|,|,1,|,|

;0,0,,0max

1111

2

1

2

1

jjjjjj

j

n

j

bbco

co

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

ï

þ

ï

ý

ü

ï

î

ï

í

ì

y

-=

=

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

ï

þ

ï

ý

ü

ï

î

ï

í

ì

y

-

y

+

÷

ø

ö

ç

è

æ

y

-

y

-+

;0,0,,0max

0,0,,0max,,0

2

1

2

1

2

1

2

n

j

n

j

co

b

;2,2,,0max

||

;0,0,,0max

||

2

1

2

1

2

1

2

1

2

11

2

1

2

1

2

1

2

11

2

1

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

y

-

y

-

ï

þ

ï

ý

ü

ï

î

ï

í

ì

y

-

y

+

y

yy

+

y

÷

ø

ö

ç

è

æ

ï

þ

ï

ý

ü

ï

î

ï

í

ì

y

-

y

+

y

yy

+

y

-

j

jj

j

n

j

jj

j

b

( )

.0,0,00

22 njj

fddFd =+=

Следовательно, можно теперь выписать гипо- и гипердифференци-

алы для функционала

(

)

yF

e

1

:

()

;0,0,,0max

||

;0,0,,0max

2

1

2

1

2

11

2

1

2

1

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-

j

+

j

jj

+

j

-

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

þ

ý

ü

î

í

ì

j

-=

å

Î

e

n

i

ii

i

Ii

n

i

coyFd

;0,0,,0max

||

;0,0,,0max

2,2,,0max

||

2

1

2

1

2

11

2

1

2

1

2

1

2

1

2

1

2

1

2

11

2

1

÷

ø

ö

ç

è

æ

ï

þ

ï

ý

ü

ï

î

ï

í

ì

y

-

y

+

y

yy

+

y

-

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

ï

þ

ï

ý

ü

ï

î

ï

í

ì

y

-+

+

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

j

þ

ý

ü

î

í

ì

j

-

j

+

j

jj

+

j

å

Î

n

j

jj

j

Jj

n

j

i

ii

i

co

a

ï

þ

ï

ý

ü

÷

ø

ö

ç

è

æ

y

-

y

-

ï

þ

ï

ý

ü

ï

î

ï

í

ì

y

-

y

+

y

yy

+

y

2

1

2

1

2

1

2

1

2

11

2

1

2,2,,0max

||

j

jj

j

b

,

где

;|),,(|);,,(

2

1

e

+

=

j

=

j

dyardyar

i

.|),,(|);,,(

21

e

+

=

y

-

=

y

dybrdybr

jjjj

() ( )

.0,0,0

1

n

yFd =

e

Таким образом, установлено, что функционал является гиподиф-

ференцируемым и найден вид его гиподифференциала.

Замечание 2. Учитывая, что данное кодифференциальное отобра-

жение является непрерывным в метрике Хаусдорфа, можно строить схо-

дящиеся методы. Однако это не является задачей настоящей работы.

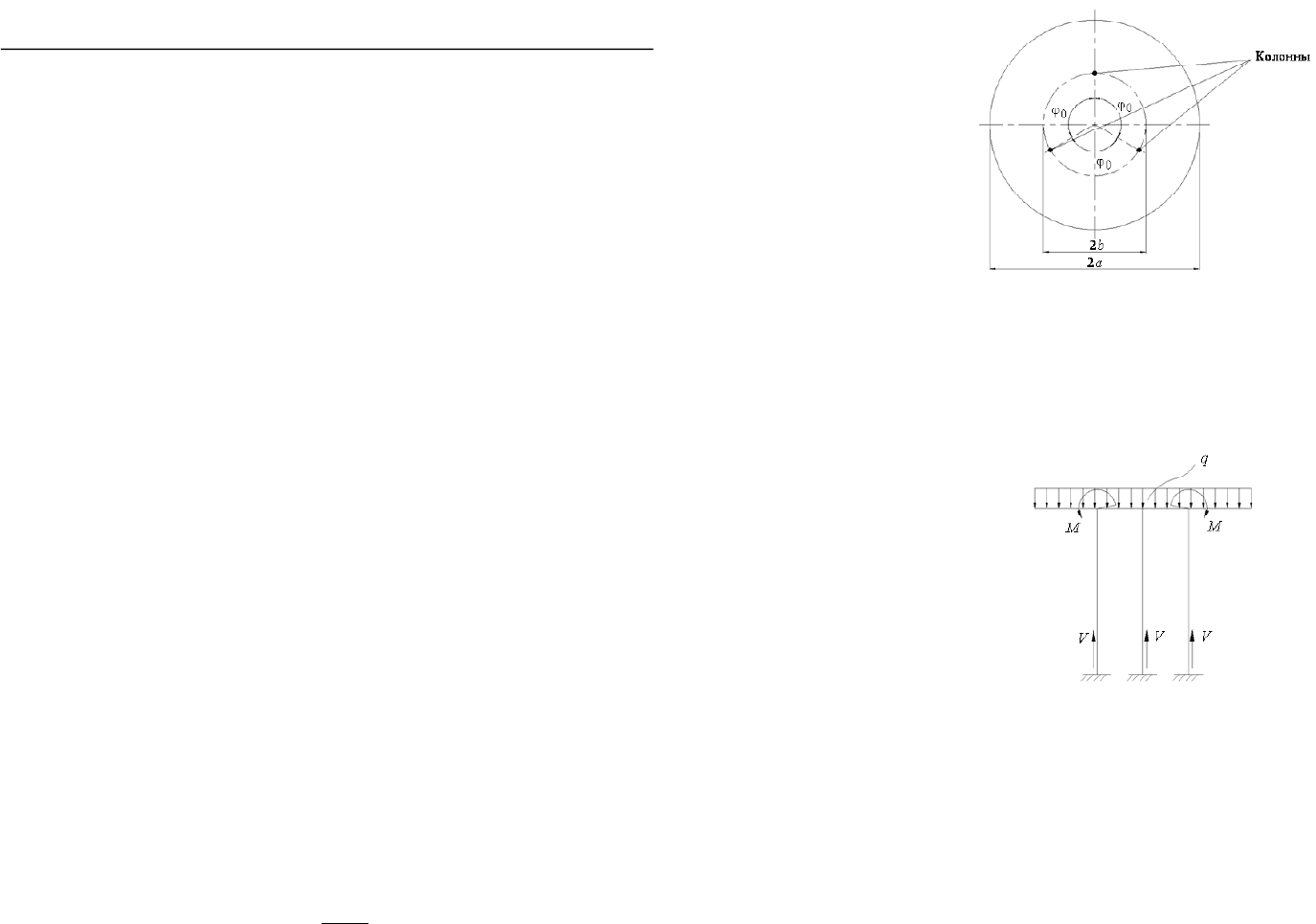
166 167

Список литературы

1. Григорьева К. В. Использование суррогатных функционалов

в математической диагностике // Математическое моделирование, чис-

ленные методы и комплексы программ: Межвуз. темат. сб. тр. / СПбГАСУ.

Вып 12. СПб., 2006. – С. 218–234.

2. Григорьева К. В. Метод проектирования в одной задаче иденти-

фикации // Процессы управления и устойчивость: Тр. XXXIV науч. конф.

аспирантов и студентов. – СПб.: СПбГУ, 2003. – С. 268–271.

3. Демьянов В. Ф., Рубинов А. М. Основы негладкого анализа и ква-

зидифференциальное исчисление. – М.: Наука, 1990. – 432 с.

Получено 17 апреля 2007 года.

УДК 624.073-422.11:624.042.62

С. А. Видюшенков, Е. В. Соколов (ГОУ ВПО «ПИМаш (ЛМЗ–

ВТУЗ)»)

КРУГЛАЯ ПЛАСТИНКА, ЛЕЖАЩАЯ НА КОЛОННАХ,

РАСПОЛОЖЕННЫХ НА ОКРУЖНОСТИ С ЦЕНТРОМ

В ПОЛЮСЕ ПЛАСТИНКИ

Рассматривается круглая пластинка, лежащая на колоннах, расположен-

ных на окружности с центром в полюсе пластинки. Построены разрешающие

дифференциальные уравнения осесимметричных и циклически симметричных

деформаций и получены расчетные зависимости для прогибов и изгибающих

моментов.

Рассмотрим круглую пластинку с наружным диаметром, равным

2 а, находящуюся под действием равномерного давления интенсивнос-

тью q и лежащую на нескольких колоннах, расположенных на одинако-

вых расстояниях друг от друга и от центра пластинки (рис. 1).

Если количество колонн равняется N, то вследствие одинаковых

условий их работы вертикальные усилия, возникающие в колоннах,

.

2

N

aq

V

p

=

(1)

Математическое моделирование, численные методы и комплексы

программ. СПб., 2007

Рис. 1. Пластинка, лежащая на колоннах

В то же время в местах контакта пластинки с колоннами наряду

с усилиями V будут возникать радиальные моменты M, препятствующие

деформированию пластинки в направлении, указанном на рис. 2.

Рис. 2. Схема деформирования пластинки

Схема деформирования, приведенная на рис. 2, соответствует слу-

чаю, когда размер b значительно превышает размер консольной части

пластинки (a – b). В противном случае схема деформирования будет иметь

выпуклость, направленную вверх, и изменяется направление действия

моментов M.

Сосредоточенные силы V и моменты M войдут в правую часть ис-

ходного разрешающего дифференциального уравнения пластинки, ко-

торое в данном случае примет вид

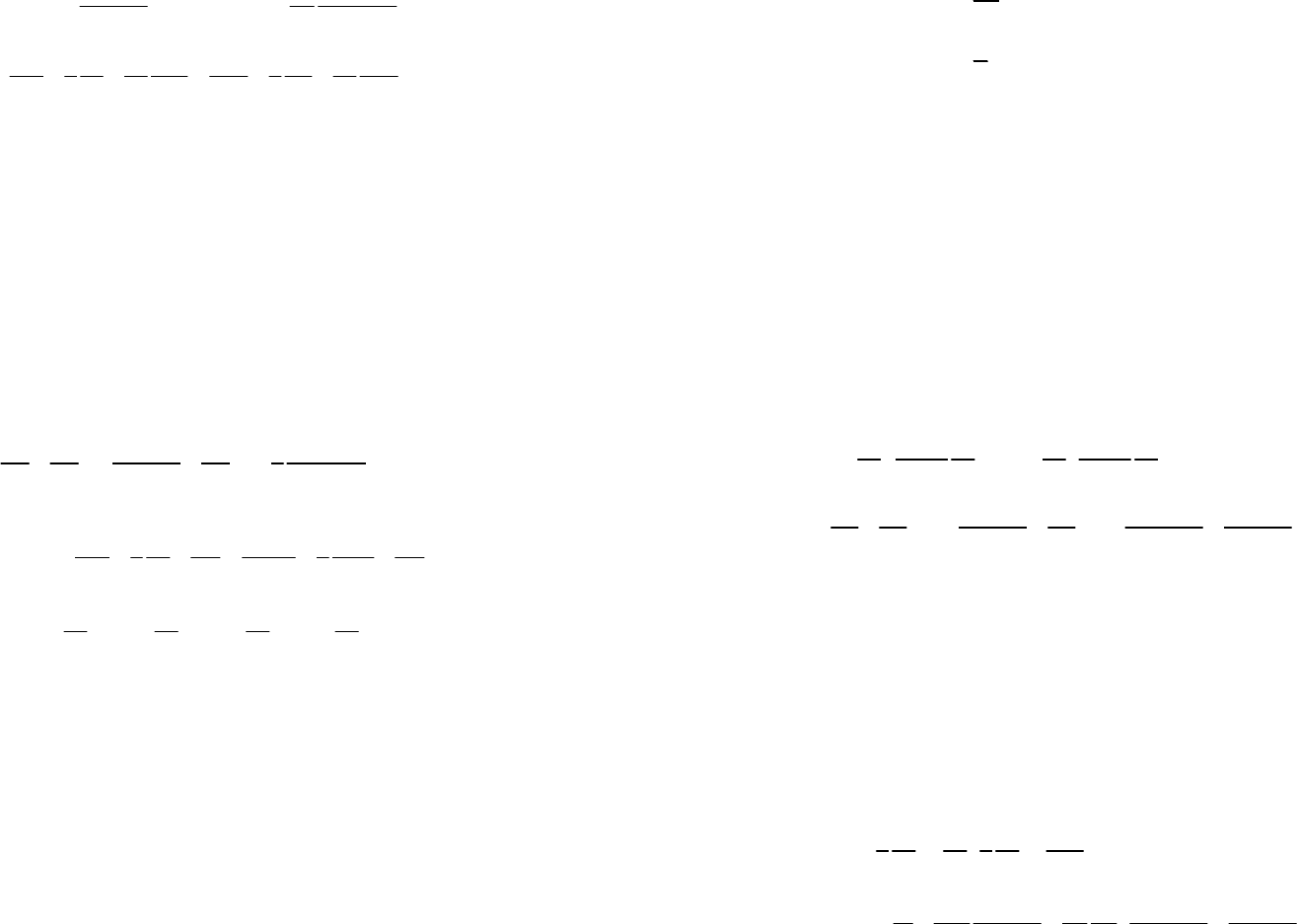
168 169

(

)

( )

(

)

( )

åå

==

j-jd

¶

-d¶

+j-jd

-d

-=Ñ

N

n

N

n

r

br

r

M

n

r

br

VqwD

1

0

1

0

4

,

(2)

где

÷

ø

ö

ç

è

æ

j¶

¶

+

¶

+

¶

÷

ø

ö

ç

è

æ

j¶

¶

+

¶

+

¶

=Ñ

2

22

2

22

2

4

1111 w

r

w

r

w

r

rr

r

w

есть бигармонический дифференциальный оператор в полярных коор-

динатах.

Так как пластинка замкнута в окружном направлении, все характе-

ристики ее напряженно-деформированного состояния будут периодичес-

кими функциями относительно угловой координаты φ с периодом 2р,

и тогда, представляя прогиб пластинки w в форме

()

å

¥

=

j=

0

cos

m

mrww

(3)

и раскладывая правую часть дифференциального уравнения (2) в ряд

Фурье по косинусам mφ, получим бесконечную систему обыкновенных

дифференциальных уравнений следующего вида:

(

)

(

)

( )

...,2,1,0

1

4

=

-

d

+

-

d

-=Ñ m

dr

brd

r

MN

D

a

r

br

VN

D

a

D

q

w

mmm

, (4)

где

( )

,

11

2112211

2

4

þ

ý

ü

î

í

ì

þ

ý

ü

î

í

ì

ú

û

ù

ê

ë

é

=

÷

ø

ö

ç

è

æ

-+

÷

ø

ö

ç

è

æ

-+=Ñ

----

m

mmmmm

m

mm

wr

dr

d

r

dr

d

r

dr

d

r

dr

d

r

w

r

m

dr

dw

r

dr

wd

r

m

dr

d

r

dr

d

w

(5)

а правая часть уравнения (4) получена в результате разложения в ряд

Фурье по косинусам mц распределенной нагрузки q и дельта-функций

δ(φ – nφ

0

).

При этом коэффициенты Фурье q

m

от q следующие:

ï

î

ï

í

ì

³

=

.1при0

0при

m

mq

q

m

(6)

В то же время коэффициенты Фурье a

m

от функций

( )

å

=

j-jd

N

n

1

0

примут вид

ï

î

ï

í

ì

³j

p

=

p

=

.1приcos

1

0при

2

1

0

mmn

m

a

m

(7)

Поскольку при разложении в ряд Фурье по косинусам mц дельта-

функций δ(φ – nφ

0

) не равными нулю остаются лишь коэффициенты a

m

,

кратные числу колонн N, можно считать, что m = kN (k = 1, 2, 3,…). Тогда

cos mnφ

0

= cos knNφ

0

= cos kn2р и так как числа k и т – целые числа, то

все cos mnφ

0

= 1.

В силу фильтрующих свойств дельта-функции и ее первой произ-

водной, имеющих вид

(

)

(

)

(

)

(

)

() ( ) () ( ) ()( )

,

;

brbbrbbrr

brbbrr

rrr

-dj

¢

--d

¢

j=-d

¢

j

-

d

j

=

-

d

j

(8)

и с учетом того, что в данном случае φ(r) = 1/r, уравнение (4) может быть

записано в такой форме:

(

)

( ) ( ) ( )

.

11

2

12

1

ú

û

ù

ê

ë

é

-d

+

-d

¢

+

-d

p-=

=

þ

ý

ü

î

í

ì

þ

ý

ü

î

í

ì

ú

û

ù

ê

ë

é

-

b

br

b

br

MN

D

a

b

br

aq

D

a

D

q

wr

dr

d

r

dr

d

r

dr

d

r

dr

d

r

rmmm

m

(9)

При построении дифференциального уравнения (9) учтено соот-

ношение (5) и формула (1). Дальнейшее построение решения дифферен-

циального уравнения (9) целесообразно производить по отдельности для

случаев осесимметричных деформаций (m = 0) и циклически симмет-

ричных деформаций (m ³ 1).

Осесимметричная деформация (m = 0)

Полагая в уравнении (9) m = 0 и учитывая значения коэффициентов

Фурье q

m

и a

m

, с помощью соотношений (6) и (7) при m = 0 получим

такое дифференциальное уравнение для осесимметричной деформации:

( ) ( ) ( )

.

22

11

2

0

ú

û

ù

ê

ë

é

-d

+

-d

¢

p

+

-d

-=

=

þ

ý

ü

î

í

ì

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

b

br

b

brN

D

M

b

br

D

qa

D

q

dr

dw

r

dr

d

rdr

d

r

dr

d

r

(10)

170 171

Последовательно четыре раза интегрируя уравнение (10), получим

соотношения для угла поворота пластинки dw

0

/dr и для ее прогиба w

0

.

Они имеют вид

( )

;

1

24

1ln2

816

32

2

223

0

r

C

r

C

r

b

r

D

MN

brH

b

r

b

D

rqa

brH

D

qr

dr

dw

++

÷

ø

ö

ç

è

æ

-

p

-+

+

÷

ø

ö

ç

è

æ

-+--=

(11)

( )

,ln

4

1ln2

8

1ln1

864

43

2

2224

0

C

b

r

C

r

C

b

r

b

r

D

MNb

brH

b

r

b

r

b

r

D

bqa

brH

D

qr

w

+++

÷

ø

ö

ç

è

æ

--

p

-+

+

ú

û

ù

ê

ë

é

+-

÷

ø

ö

ç

è

æ

+--=

(12)

где H(r – b) – единичная функция.

Для пластинки, не имеющей отверстия в центре, т. е. при r = 0,

C

3

= 0. Так же, как и всегда, для осесимметричной деформации С

1

= 0.

Произвольные постоянные интегрирования С

2

и С

4

определяются

из граничных условий задачи, имеющих вид

(

)

(

)

.0

0,10

=

aMbw

(13)

При этом радиальный изгибающий момент M

1,0

(r) определяется по

формуле

() ( )

( ) ( )

,

2

1

11

4

1

2

1

ln1

4

3

16

2

22

2

0

2

0

2

0,1

n+

+

÷

ø

ö

ç

è

æ

÷

ø

ö

ç

è

æ

n-+n+

p

--

-

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

-

n-

+n+-+

+n+-=

÷

ø

ö

ç

è

æ

n

+-=

C

r

b

MN

brH

r

b

rqa

brH

qr

dr

dw

r

dr

wd

DrM

(14)

где ν – коэффициент Пуассона.

Используя граничные условия (13), определим величины произволь-

ных постоянных интегрирования С

2

и С

4

.

,

8

4

64

;

2

11

224

411

2

B

D

MNb

A

D

bqa

D

qb

CB

Db

MN

A

D

qa

C

p

+--=

p

-=

(15)

где

.1

1

;1

1

ln2

4

1

3

8

1

2

1

2

1

+

÷

ø

ö

ç

è

æ

n+

n-

=

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

-

n+

n-

++

n+

×-=

a

b

B

a

b

a

A

Величину изгибающего момента определим из условия равенства

углов поворота пластинки и любой из поддерживающих ее колонн в месте

их контакта, т. е. при r = b:

.

EI

Ml

dr

dw

br

m

=

÷

ø

ö

ç

è

æ

=

(16)

Тогда с учетом соотношений (11) и (15) получим

( )

×=

÷

ø

ö

ç

è

æ

n+

n-

+

p

-

n+

-

EI

Ml

M

a

b

D

N

D

bqa

D

qb

2

223

1

41416

Отсюда определяется величина изгибающего момента М.

.

42

1

16

1

11

2

3

/

÷

ø

ö

ç

è

æ

p

+

÷

ø

ö

ç

è

æ

+= B

N

EI

Dl

A

b

a

qbM

(17)

Циклически симметричные деформации (m = N, 2N,…)

С учетом соотношений (5)–(7) дифференциальное уравнение

циклически симметричных деформаций примет вид

(

)

( ) ( ) ( )

( )

.,...2,

2

2112211

Nnm

b

br

b

brN

D

M

b

br

D

qa

wr

dr

d

r

dr

d

r

dr

d

r

dr

d

r

m

mmmmm

=

ú

û

ù

ê

ë

é

-d

+

-d

¢

p

-

-d

=

þ

ý

ü

î

í

ì

þ

ý

ü

î

í

ì

ú

û

ù

ê

ë

é

----

(18)

Умножая уравнение (18) на r

1 – m

, получим

(

)

( )

( ) ( )

.

2

211221

ú

û

ù

ê

ë

é

-d+-d

¢

p

-

-d

=

þ

ý

ü

î

í

ì

þ

ý

ü

î

í

ì

ú

û

ù

ê

ë

é

-

---

br

b

m

brb

N

D

M

b

br

D

qa

wr

dr

d

r

dr

d

r

dr

d

r

dr

d

r

m

mmmm

(19)

172 173

Правая часть уравнения (19) получена с учетом соотношений (8).

Последовательно четыре раза интегрируя уравнение (19), будем иметь

( )

.

22

1

81

1

18

22

43

2

1

ï

þ

ï

ý

ü

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

-

÷

ø

ö

ç

è

æ

-

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

+

÷

ø

ö

ç

è

æ

+

-

´

p

-+

ï

þ

ï

ý

ü

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

-

÷

ø

ö

ç

è

æ

+

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

-

÷

ø

ö

ç

è

æ

+

-

´

-

-++++=

-+-

--+

mmmm

m

mm

b

r

b

r

m

b

r

b

r

m

D

MNb

brH

b

r

b

r

b

r

b

r

m

mDm

bqa

brHrCrCrCrCw

(20)

В силу замкнутости пластинки в центре произвольные постоянные

C

2m

= C

4m

= 0.

С учетом соотношения (20) угол поворота пластинки

( ) ( )

( )

( ) ( )

( )

.

1

2

1

2

8

22

1

18

2

1111

2

1

3

1

ï

þ

ï

ý

ü

ï

î

ï

í

ì

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

-

÷

ø

ö

ç

è

æ

-

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

-

÷

ø

ö

ç

è

æ

+

p

-+

+

ï

þ

ï

ý

ü

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

-+

÷

ø

ö

ç

è

æ

+

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

+-

÷

ø

ö

ç

è

æ

-

+

-

´

-

-+++=

-+--+

---

-+

mmmm

m

b

r

b

r

m

b

r

b

r

m

D

MN

brH

b

r

m

b

r

m

b

r

m

b

r

m

mDm

rqa

brHmrCrmC

dr

dw

(21)

Радиальный изгибающий момент определяется по формуле

( )

1

18

14

2

1112

2

13

2

113121

2

1

-

ï

þ

ï

ý

ü

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

+

÷

ø

ö

ç

è

æ

+

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

-

÷

ø

ö

ç

è

æ

+

-

´

-

----=

=

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

-

n

+-=

--+

-

MN

r

b

d

r

b

d

r

b

d

r

b

d

m

mm

qa

brHrdDCrdDC

w

r

m

dr

dw

r

dr

wd

DM

mmmm

m

mm

m

( )

.

22

1

8

14

2

1112

2

13

ï

þ

ï

ý

ü

ï

î

ï

í

ì

÷

ø

ö

ç

è

æ

+

÷

ø

ö

ç

è

æ

-

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

+

÷

ø

ö

ç

è

æ

+

-

´

-p

--

--+

m

r

b

d

r

b

d

m

r

b

d

r

b

d

m

mb

MN

brH

mmm

(22)

Здесь d

11

, d

12

, d

13

, d

14

– некоторые постоянные, вид которых указан

ниже:

(

)

(

)

( ) ( ) ( )

[ ]

;1121

;11

12

11

n-+n++=

n

-

=

mmd

(

)

(

)

( ) ( ) ( )

[ ]

.1121

;11

14

13

n--n+-=

n

-

+

=

mmd

Постоянные интегрирования C

1m

и C

3m

определяются с помощью

граничных условий

() () ()

,0

1

=+= aH

a

m

aQaM

(23)

где

( )

.

1

;1

2

÷

ø

ö

ç

è

æ

-+-=Ñ-=

÷

ø

ö

ç

è

æ

-n-=

m

mm

m

w

r

m

dr

dw

r

dr

wd

dr

d

Dw

dr

d

DQ

w

r

m

dr

dw

r

m

DH

Тогда постоянные интегрирования будут следующими:

( ) ( )

,

1

,

1

,1

1

,

1818

,

1818

2112

11

3

14

2

1112

2

132

2

21

23

22

21

22

1

3

12

3

4

3

1

2

1

ú

û

ù

ê

ë

é

+

÷

ø

ö

ç

è

æ

=

÷

ø

ö

ç

è

æ

+

÷

ø

ö

ç

è

æ

+

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

-

÷

ø

ö

ç

è

æ

+

-

=

÷

ø

ö

ç

è

æ

+

ú

û

ù

ê

ë

é

+

÷

ø

ö

ç

è

æ

-

+

-

=

-p

-

-p

-=

-p

+

-

=

--+

+

---

mm

m

mmmm

m

mm

m

AA

b

a

d

A

a

b

d

a

b

d

a

b

d

a

b

d

m

A

a

b

d

a

b

d

m

A

B

mD

bMNa

A

mmD

qa

C

B

mD

MNb

A

mDm

bqa

C

174 175

( )

[ ]

( ) ( ) ( )

[ ]

.2112,12

,212,

1

,

22

1

,1

2

1

23

3

22

212112

11

3

14

2

1112

2

132

2

21

23

22

21

22

1

+n--=n-=

+n+=

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

+=

÷

ø

ö

ç

è

æ

+

÷

ø

ö

ç

è

æ

-

ú

û

ù

ê

ë

é

÷

ø

ö

ç

è

æ

+

÷

ø

ö

ç

è

æ

+

-

=

÷

ø

ö

ç

è

æ

+

ú

û

ù

ê

ë

é

-

÷

ø

ö

ç

è

æ

+

-

+

-

=

--+

+

mmmdmd

mmdB

a

b

Bd

d

B

a

b

d

a

b

d

m

a

b

d

a

b

d

m

B

a

b

d

a

b

d

m

B

m

mm

mmmm

m

mm

m

Получено 2 мая 2007 года.

УДК 531.44

П. М. Огар, Е. А. Ключев, О. В. Максимова (БрГУ)

ОПРЕДЕЛЕНИЕ УПРУГОЙ ХАРАКТЕРИСТИКИ СЛОИСТОГО

ПОЛУПРОСТРАНСТВА

В работе на основании жесткостной модели слоистого полупространства

излагается инженерная методика определения его упругой характеристики в зави-

симости от упругих характеристик покрытия и основного материала, толщины

покрытия и степени деформации.

Рассмотрим слоистое упругое тело (рис. 1), которое состоит из

покрытия толщиной d с упругими характеристиками m

1

и

E

1

и основного

материала с упругими характеристиками m

2

и

E

2

. Задача определения

напряжений и деформаций при нагружении слоистого упругого тела

чрезвычайно актуальна, в частности для трибомеханики. Точное решение

этой задачи при осесимметричном нагружении приведено в [1], однако

оно трудоемко для инженерных расчетов. В работе [2] для этой цели

предложено использовать теорию Герца. Имея достоверные результаты

для крайних значений d = 0 и d = ¥ и используя двухточечную

аппроксимацию Паде получили выражение для безразмерного

упругогеометрического параметра, при помощи которого определяется

упругая постоянная слоистого полупространства и все основные

характеристики при его осесимметричном нагружении.

Целью настоящей работы является определение упругой характери-

стики слоистого полупространства на основании его жесткостной модели

для любых значений д. Рассмотрим нагружение слоистого полупростран-

ства (см. рис. 1) нормальными напряжениями в круговой области

,1)(

22

0

app r-=r

.

0

a

£

r

£

(1)

С учетом классического подхода, основанного на применении по-

тенциальных функций Буссинеску перемещение любой точки по оси

симметрии внутрь однородного полупространства для случая его нагру-

жения распределенной нагрузкой [3]

( )

,12

2

1

ú

û

ù

ê

ë

é

y

-ym-

p

m

+

=

dz

d

z

E

u

z

(2)

где

E

и

m

– модуль упругости и коэффициент Пуассона соответственно;

()

,

1

òò

jrrr=y

s

dd

R

p

,

22

zR +r=

или с учетом выражения (1) и того, что

a

r

=

r

и

azz

=

,

1

4

2

0

1

0

2

0

òò

p

+r

jrrr-

=y

z

dd

ap

[

]

.arcctg)1(

0

zzzap

-

+

p

=

y

(3)

Подставляя выражение (3) в (2) получим

),,(

0

m

q

=

zaKpu

z

(4)

где

(

)

,1

2

Em-=q

( )

.arcctg1

1

arcctg),( zzzzK -

m-

m

-=m

Перемещения точки

O

(см. рис. 1), находящейся на оси z под

нагрузкой, можно представить в виде суммы перемещений слоя ω

д

и основания ω

a

: ω

0

= ω

д

+ ω

a

.

Математическое моделирование, численные методы и комплексы

программ. СПб., 2007

176 177

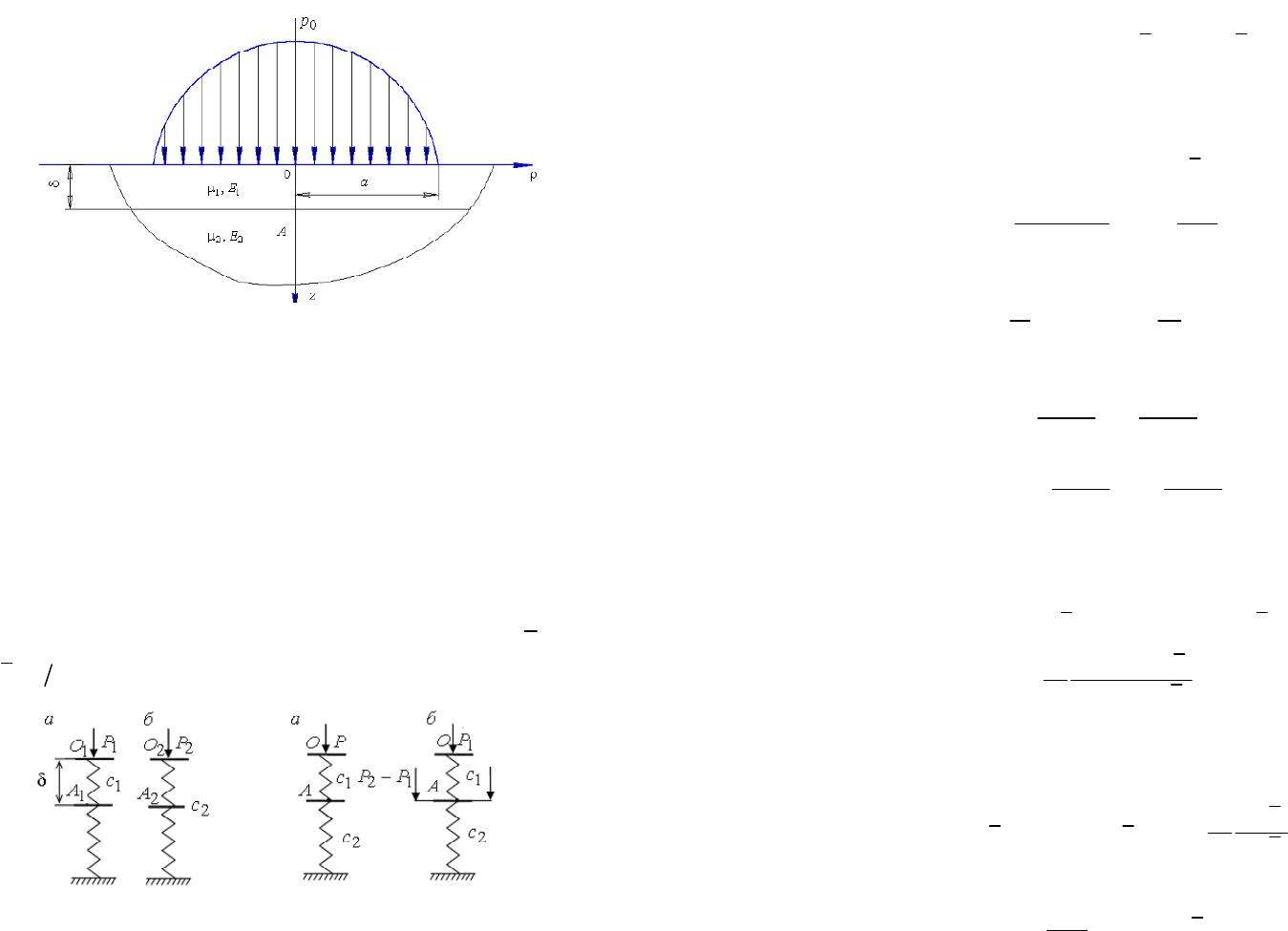
Рис. 1. Схема нагружения слоистого полупространства

Схему (см. рис. 1) можно представить в виде рис. 3, а. Тогда получим

перемещения

,

1

Pc

=

w

d

2

Pc

a

=

w

,

(

)

,

210

ccP

+

=

w

где с

1

, с

2

– жесткости слоя и основного материала.

Введем два однородных полупространства с упругими характе-

ристиками m

1

, Е

1

и m

2

, Е

2

, нагруженных соответственно силами P

1

и P

2

(рис. 2).

Силы P

1

и P

2

, а соответственно максимальные давления р

01

и р

02

выбираются из условия равенства перемещений

,

1

w

=

w

d

.

2

w

=

w

a

Для схемы (рис. 3, а):

(

)

(

)

[

]

1111111111

,,0

m

d

-

m

q

=

-

=

w

-

w

=

w

d

KKapuu

OzAzOAO

,

где

a

d

=

d

.

Рис. 2. Схемы однородных Рис. 3. Эквивалентная схема

полупространств нагружения слоистого

полупространства

Упростим обозначения, приняв

(

)

(

)

0,0

iii

KK

=

m

,

(

)

(

)

d

=

m

d

iii

KK ,

.

Тогда

(

)

(

)

[

]

d

-

q

=

w

d 11011

0 KKap

.

Для схемы, представленной на рис. 2, б,

(

)

d

q

=

w

202222

aKpu

zAA

;

1

11

1

P

uu

c

zAzO

-

=

;

.

2

P

u

c

zA

=

(5)

Для схемы, представленной на рис. 3, а,

( )

.

2

11

1

0 zAzAzO

u

P

uu

P

+-=w

Из эквивалентности схем нагружения на рис. 4, а и 4, б следует

2

1

2

1

cc

c

P

cc

c

PP

+

=

, (6а)

или

2

1

2

02

2

1

010

cc

c

p

cc

c

pp

+

=

. (6б)

Значение р

01

определим из условий равенства сжатия покрытия

толщиной δ для слоистого тела под нагрузкой р

0

и однородного материала

под нагрузкой р

01

:

(

)

(

)

[

]

(

)

(

)

[

]

d-q=d-q

110110000

00 KKapKKap

,

(

)

(

)

()

.

0

1

00

1

0

01

p

KK

p

d-

q

=

(7)

Значение р

02

определим из условия равенства перемещений при

z = δ слоистого тела под нагрузкой р

0

и однородного материала при

z = δ под нагрузкой р

02

:

(

)

(

)

d

q

=

d

q

2022000

aKpaKp

,

(

)

()

0

2

0

2

0

02

p

K

p

d

q

=

. (8)

Выражения (5) представим в виде

()

[

]

,0

2

3

11

1

d-

p

q

= KK

a

c

(9а)

178 179

() ()

.

2

3

2

3

1

02

01

1

2

d

p

q

=d

p

q

= K

p

a

K

a

c

С учетом выражений (7) и (8) имеем

(

)

(

)

()

(

)

()

.

0

2

3

1

0

2

11

00

2

d

d-

p

q

= K

K

KK

a

c

(9б)

Подставляя выражения (7), (8), (9а) и (9б) в (6б) и с учетом того,

что

(

)

(

)

00

01

KK

=

, получим

,

10 d

q

=

q

F

где

()

(

)

(

)

()

(

)

()

.

0

1

2

0

2

1

00

2

11

1

ú

û

ù

ê

ë

é

q

×

d

d+

d-

=

d

K

KK

K

F

(10)

При

0

=

d

20

q

=

q

, при

¥

=

d

10

q

=

q

, т. е. граничные условия вы-

полняются.

Так как значения функции

(

)

md,K

для м = 0.3,…, 0.5 изменяются

незначительно, то с большой степенью точности (менее 1 %) можно при-

нять

d

×

qq-

m

-

m

-m=m F

1

2

21

10

1

и решать уравнение (10) относительно F

д

с начальным приближением

( )

2

1

5.0

0

m+m=m

dd

=

FF

.

Рассмотрим контакт жесткой сферы радиусом R со слоистым

полупространством (см. рис. 4). Согласно данным [3] радиус площадки

контакта

.

4

3

1

÷

ø

ö

ç

è

æ

q

=

PR

a

(11)

Перемещение точки О (см. рис. 4, а) может быть представлено

в виде суммы перемещений покрытия и основания под нагрузкой P:

a

w

+

w

=

w

d0

.

Введем две новые схемы контактирования (см. рис. 4, б, в) сферы

с радиусом R под нагрузками P

1

и P

2

с однородными полупространства-

ми с упругими характеристиками м

1

, E

1

и м

2

, E

2

соответственно.

Рис. 4. Расчетные схемы: а – контактирования; б – контакта сферы с однородным

полупространством с характеристиками m

1

,

E

1

; в – с характеристиками m

2

,

E

2

Математическое моделирование, численные методы и комплексы программ 2007 Вып.13

Подождите немного. Документ загружается.