Математическое моделирование, численные методы и комплексы программ 2007 Вып.13
Подождите немного. Документ загружается.

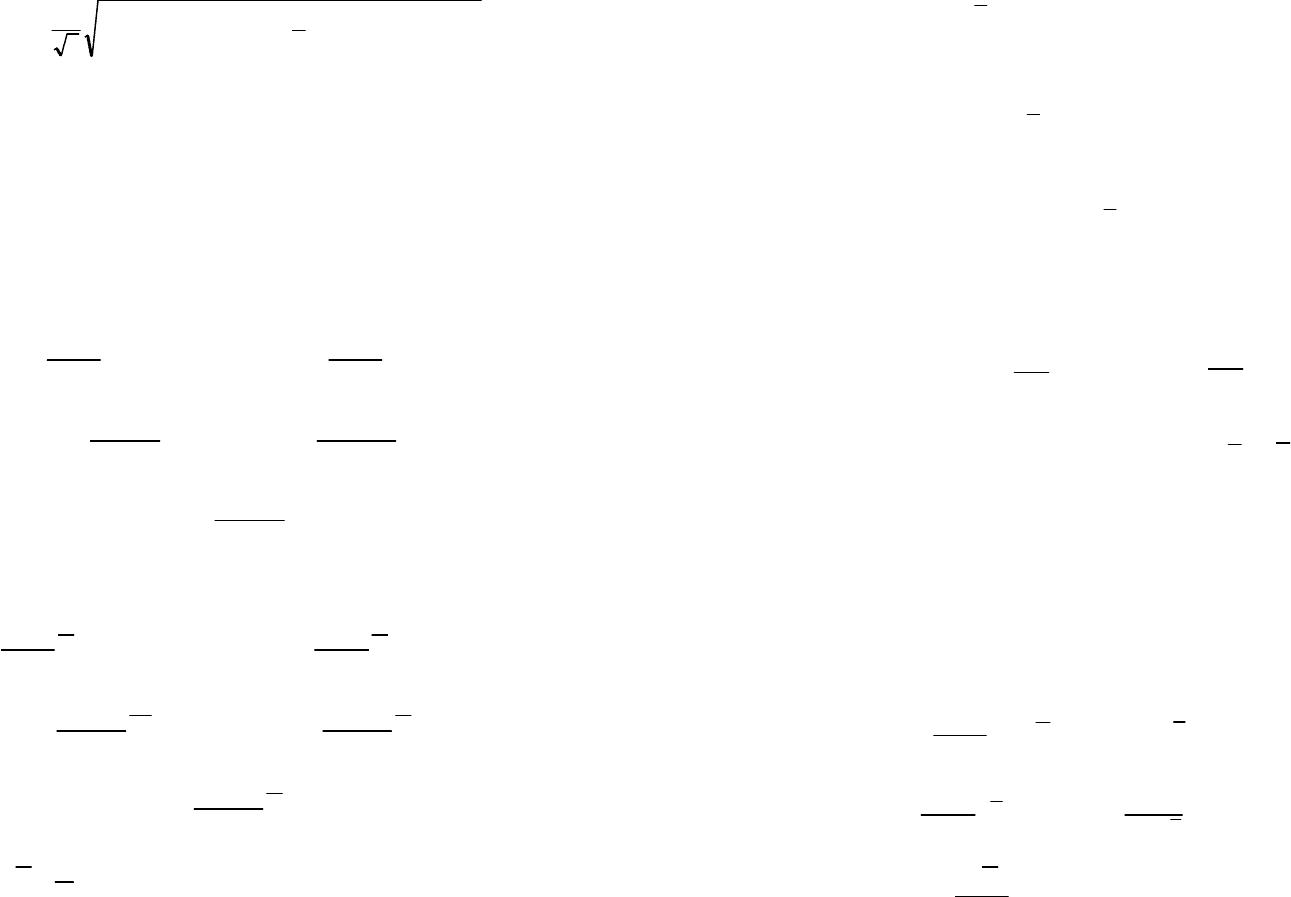
40 41
где
(
)
i
e
w
– функция А. А. Ильюшина.
Интенсивность деформации записывается в виде
(
)
(
)
(
)
ú
û
ù
ê
ë
é
g+g+g+e+ee+e=e
22
222
4
1
3
2
yzxz
z
xy
z
y
z
y
z
x
z
xi
. (6)
Если зависимость
(
)
i
e
s
взять в виде (4), тоо
2
c i
mEE e-=
и выражения (1) примут вид
пл
xxx
s-s=s
;
пл
yyy
s-s=s
;
пл
xyxyxy
t-t=t
;
пл
xzxzxz
t-t=t
;
пл
yzyzyz
t-t=t
.
(7)
Здесь соотношения с индексом «л» (линейно-упругие составляю-
щие) будут иметь вид
)(
1
2
л z
y
z
xx
E
me+e
m-
=s
;
)(
1
2
л z
x
z
yy
E
me+e
m-
=s
;
z
xyxy
E
g
m+
=t
)1(2
л
;
xzxz
E
g
m+
=t
)1(2
л
; (8)
yzyz
E
g
m+
=t
)1(2
л
,
а соотношения с индексом «п» (пластические составляющие)
примут вид
)(
1
2
2
п z
y
z
xix
m
E
me+ee
m-
=s
;
)(
1
2
2
п z
x
z
yiy
m
E
me+ee
m-
=s
;
z
xyixy
m
E
ge
m+
=t
2п
)1(2
;
xzixz
m
E
ge
m+
=t
2п
)1(2
; (9)
yziyz
m
E
ge
m+
=t
2п
)1(2
.
Здесь
E
m
m =
. (Эта безразмерная величина имеет для металлов
значение порядка 10
5
.)
Выражение
2
i
e
, где
i
e
имеет вид (6), можно представить в виде
()
[
]
zfbzbzbb
i
2
4
2
321
2
3
4
+++=e
.
В работе А. С. Вольмира [1] принимается
xxz
b
=
g
,
yyz
b
=
g
, и тогдада
(
)
2
321
2
3
4
zbzbb
i
++=e
, (10)
где
(
)
22222
1
4
1
yxxyyyxx
b b+b+g+e+ee+e=
;
1221212
22 cg+ce+ce+ce+ce=
xyyyxx
b
; (11)
2
12
2
221
2
13
c+c+cc+c=b
;
x
W
xx
¶
¶
+y=b
;
y
W
yy
¶
¶
+y=b
.
Интегрируя выражения (7) по z в пределах от
2
h
-
до
H
h
+
2
, получим
усилия и моменты, приведенные к координатной поверхности и прихо-
дящиеся на единицу длины сечения,
п
x
y
xx
NNN -=
;
п
y
y
yy
NNN -=
;
п
xy
y
xyxy
NNN -=
;
п
x
y
xx
MMM -=
;
п
y
y
yy
MMM -=
;
п
xy
y
xyxy
MMM -=
;
п
x
y
xx
QQQ -=
;
п
y
y
yy
QQQ -=
,
где составляющие с индексом y имеют вид
( )
(
)
( )
[
]
21
2
1
mc+c+me+e+
m-
= SFh
E
N
yx
y
x
;
( )
( )
ú
û
ù
ê
ë
é
mc+c
÷
ø
ö
ç
è
æ
+
+me+e
m-
=
21
2
12
1
J
h
S
E
M
yx
y
x
;
( )
( )
[
]
2121
2
1
mc+c+me+e
m-
= II
mE
N
yx
y
y ;
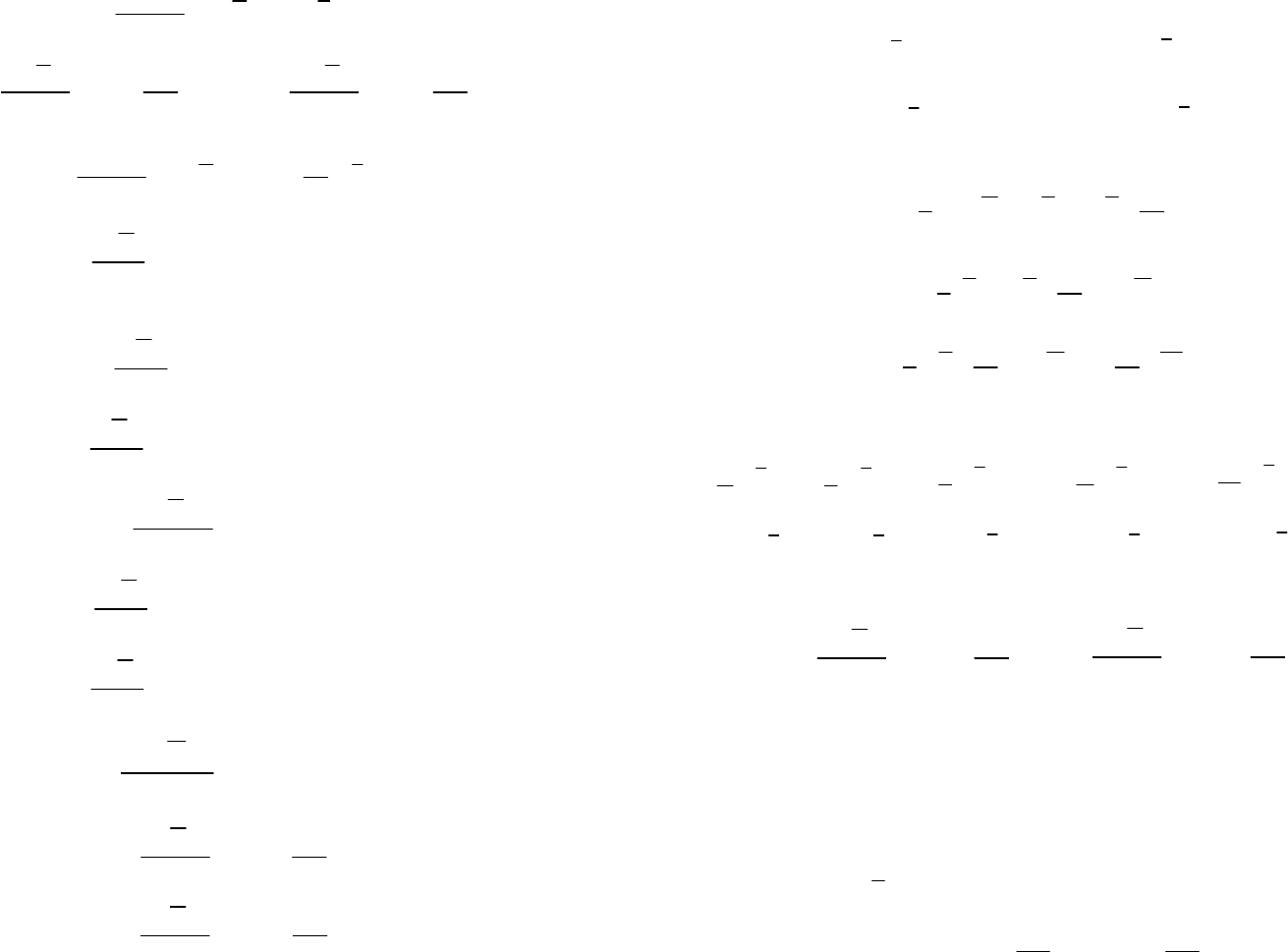
42 43
( )
[
]
12
2
)1(2
c+g+
m+
= SFh
E
N
xy
y
xy
; (12)
÷
ø
ö
ç
è
æ
¶
¶
+y
m+
=
x
W
k
FE
Q
x
y
x
)1(2
;
÷
÷
ø
ö
ç
ç
è
æ
¶
¶
+y
m+
=
y
W
k
FE
Q
y
y
y
)1(2
;
( )
ú
ú
û
ù
ê
ê
ë
é
c
÷
÷
ø
ö
ç
ç
è
æ
++g+
m+
=
12
3
12
2
)1(2
J
h
SFh
E
M
xy
y
xy
;
( )
( )
[
]
2132
2
1
mc+c+me+e
m-
= II
mE
M
yx
y
y ,
а составляющие с индексом «п» имеют вид
( )
( )
[
]
2121
2
п
1
mc+c+me+e
m-
= II
mE
N
yxx ;
( )
( )
[
]
1221
2
п
1
mc+c+me+e
m-
= II
mE
N
xyy ;
(
)
1221
2
п
2
)1(2
c+g
m-
= II
mE
N
xyxy ;
( )
( )
[ ]
2132
2
п
1
mc+c+me+e
m-
= II
mE
M
yxx ;
(13)
( )
( )
[ ]
1232
2
п
1
mc+c+me+e
m-
= II
mE
M
xyy ;
(
)
1232
2
п
2
)1(2
c+g
m-
= II
mE
M
xyxy ;
÷
ø
ö
ç
è
æ
¶
¶
+y
m+
=
x
W
I
kmE
Q
xx 4
п
)1(2
;
÷
÷
ø
ö
ç
ç
è
æ
¶
¶
+y
m+
=
y
W
I
kmE
Q
yy 4
п
)1(2
.
Здесь
ò
+
-
-
e=
H
h
h
i
ik
dzzI
2
2
12
;
()
.
2
2
2
4
ò
+
-
e=
H
h
h
i
dzzfI
(14)
В развернутом виде жескостные параметры принимают вид
( )
ú
ú
û
ù
ê
ê
ë
é
÷
÷
ø
ö
ç
ç
è
æ
++++=
3
3
211
123
4
b
h
JbSbFhI
;
ú
ú
û
ù
ê
ê
ë
é
+
÷
÷
ø
ö
ç
ç
è
æ
++=
32
3
12
123
4
bKb
h
JbSI
; (15)
ú
ú
û
ù
ê
ê
ë
é
÷
÷
ø
ö
ç
ç
è
æ
+++
÷
÷
ø
ö
ç
ç
è
æ
+=
3
5
21
3
3
80123
4
bM
h
bKb
h
JI
,
где
ò
+
=
H
h
h
dzF
2
2
;
ò
+
=
H
h
h
zdzS
2
2
;
ò
+
=
H
h
h
dzzJ
2
2
2
;
ò
+
=
H
h
h
dzzK
2
2
3
;
ò
+
=
H
h
h
dzzM
2
2
4
.
В работе А. С. Вольмира [1] вместо
4
I
берется
1
I
, поэтому для
yx
QQ ,
соотношения примут вид
÷
ø
ö
ç
è
æ
¶
¶
+y
m+
=
x
W
kI
mE
Q
xx 1
п
)1(2
;
÷
÷
ø
ö
ç
ç
è
æ
¶
¶
+y
m+
=
y
W
kI
mE
Q
yy 1
п
)1(2
. (16)
Функционал полной энергии деформации оболочки ступенчато-
переменной толщины с учетом упругопластических деформаций будет
иметь вид
пл
ЭЭЭ
-
=
,
где
п
Э
выражается соотношением
{
,2
2
1
Э
пп
12
п
00
2
п
1
пппп
п
dxdy
y
W
Q
x
W
QM
MMNNN
yyxxx
ab
xxxyxyyyxx
þ
ý
ü
÷
÷
ø
ö
ç
ç
è
æ
¶
¶
+y+
÷
ø
ö
ç
è
æ
¶
¶
+y+c+
+c+c+g+e+e=
òò
(17)

44 45
а функционал
Л
Э
принимает вид
{
.2
2
2
1
Э
п
л
12
л
00
2
л
1
лллл
л
dxdyqW
y
W
Q
x
W
QM
MMNNN
yy
xxx
ab
xxxyxyyyxx
þ
ý
ü
-
÷
÷
ø
ö
ç
ç
è
æ
¶
¶
+y+
+
÷
ø
ö
ç
è
æ
¶
¶
+y+c+
+c+c+g+e+e=
òò
(18)
Таким образом, получена математическая модель деформирования
пологой ребристой оболочки с учетом упруго-пластических деформаций.
Список литературы
1. Вольмир А. С. Нелинейная динамика пластин и оболочек. – М.:
Наука, 1972. – 432 с.
2. Карпов В. В. Математическое моделирование, алгоритмы иссле-
дования модели, вычислительный эксперимент в теории оболочек /
СПбГАСУ. – СПб., 2006. – 330 с.
Получено 1 июня 2007 года.
УДК 593.3
А. Н. Панин (СПбГАСУ)
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЕФОРМИРОВАНИЯ
РЕБРИСТЫХ ПОЛОГИХ ЖЕЛЕЗОБЕТОННЫХ ОБОЛОЧЕК
С УЧЕТОМ ПОЛЗУЧЕСТИ МАТЕРИАЛА
Рассматривается модель деформирования пологой ребристой железобетон-
ной оболочки с учетом жесткости арматуры и возможности развития деформаций
ползучести.
Оболочечные конструкции находят большое применение в различ-
ных областях техники, в том числе и в строительстве. Железобетонные
оболочки, подкрепленные ребрами жесткости, применяются для покры-
тия большепролетных строительных сооружений и могут длительное
время находиться под действием нагрузки. При длительном нагружении
может проявиться свойство ползучести материала (рост деформаций при
неизменной нагрузке), поэтому расчеты напряженно-деформированно-
го состояния (НДС) оболочек должны вестись с учетом возможности
развития ползучести материала.
Рассматривается пологая прямоугольная в плане оболочка двоякой
кривизны, подкрепленная со стороны вогнутости перекрестной систе-
мой ребер, направленных параллельно координатным линиям (рисунок).
Срединная поверхность оболочки (обшивки) толщиной h прини-
мается за координатную поверхность. Оси х, у ортогональной системы
координат проходят по линиям главных кривизн оболочки, ось z – орто-
гональна координатной поверхности в сторону вогнутости.
Слой подкреплений задается функцией
( )
)()()()(,
1 111
ij
n
i
m
j
ij
i
n
i
i
j
m
j
j
yyxxhyyhxxhyxH -d-d--d+-d=
-
-
= =
-
=
-
=
åååå
.
Здесь
mrh
j
j
,,
- соответственно высота, ширина и число ребер,
параллельных оси у;
nrh
i
i
,,
- то же для ребер, параллельных оси х;
)(
j
xx -d
-
- единичная столбчатая функция, равная единице при
jj
bxa
£
£
;
÷
÷
ø
ö
ç
ç
è
æ
+=-=
2
;
2
j
jj
j
jj
r
xb
r
xa
и равная нулю при
Математическое моделирование, численные методы и комплексы
программ. СПб., 2007
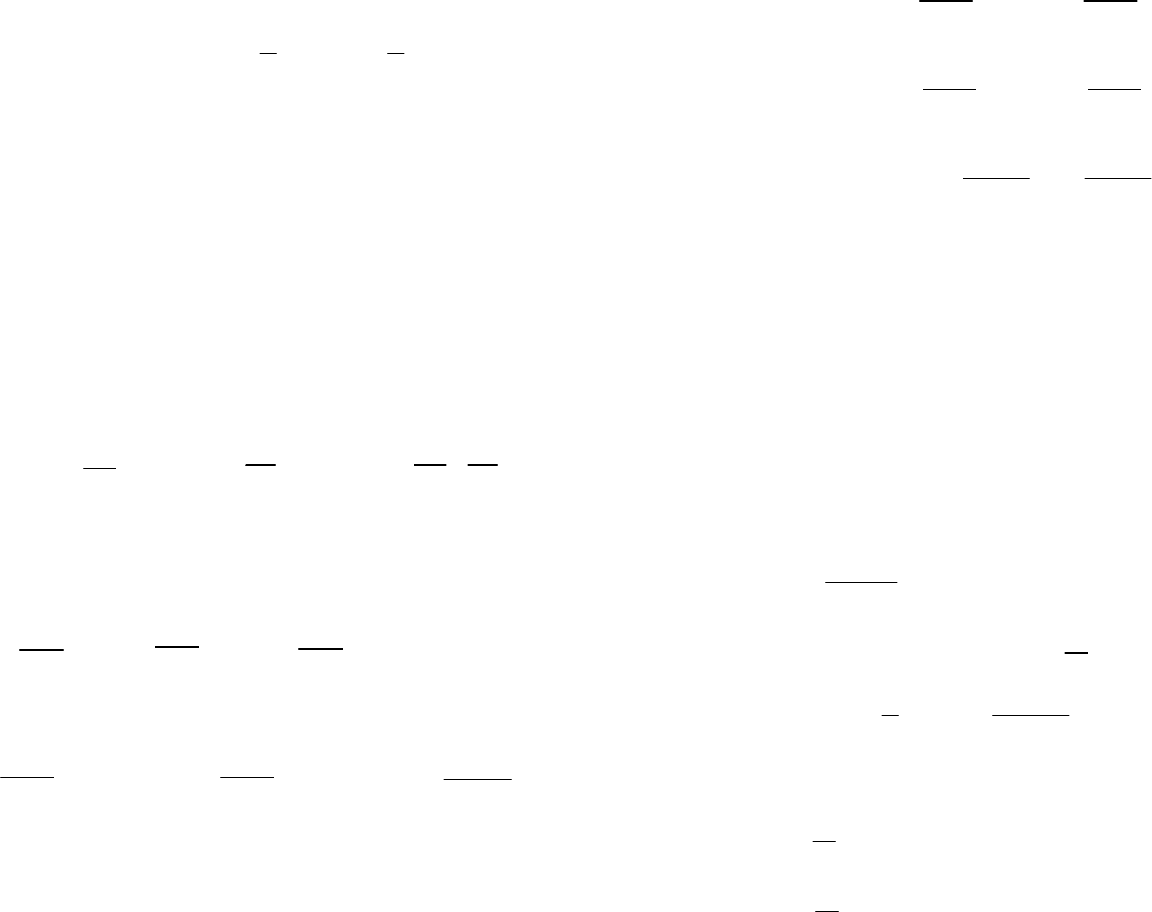
46 47
других значениях х;
( )
i
yy -d
-
- единичная столбчатая функция, равная
единице при
ii
dyc
£
£
;
÷
ø
ö
ç
è
æ
+=-=
2
;
2
i
ii
i
ii
r
yd
r
yc
и равная нулю при
других значениях у;
},{
jiij
hhh =
.
Таким образом, толщина всей конструкции равна h + H.
Математическая модель деформирования любой оболочки состоит
из трех групп соотношений:
геометрических соотношений;
физических соотношений;
уравнений равновесия или функционала полной энергии деформа-
ции конструкции.
Так как железобетонные оболочки в основном имеют прогибы, су-
щественно меньшие их толщины, то геометрические соотношения (связь
деформаций и перемещений) принимаются линейными (в срединной
поверхности) и будут следующими:
;Wk
x
U
xx
-
¶
¶
=e
;Wk
y
V
yy
-
¶
¶
=e
x
V
y
U
xy
¶
¶
+
¶
¶
=g
. (1)
В поверхности, отстоящей на расстоянии z от срединной, исходя из
гипотез Кирхгофа – Лява они примут вид
;
1
c+e=e z
x
z
x
;
2
c+e=e z
y
z
y
,2
12
c+g=g z
xy
z
xy
(2)
где
;
2
2
1
x
W
¶
¶
-=c
;
2
2
2
y
W
¶
¶
-=c
.
2
12
yx
W
¶¶
¶
-=c
Физические соотношения (связь напряжений и деформаций) для
упругого изотропного материала задаются исходя из закона Гука:
);(
1
2
z
y
z
xx
E
me+e
m-
=s
);(
1
2
z
x
z
yy
E
me+e
m-
=s
( )
z
xyxy
E
g
m+
=t
12
, (3)
где
m
,
E
- упругие характеристики материала.
При учете ползучести материала (бетона), используя наследствен-
ную теорию старения, физические соотношения можно взять в виде (бу-
дем рассматривать нестареющий материал, неустановившуюся незату-
хающую ползучесть)
(
)
(
)
( )
ttme+e
m-
-me+e
m-
=s
ò
t
dtR
EE
t
z
y
z
x
z
y
z
xx
,
11
1
22
1
;
( ) ( )
( )
ttme+e
m-
-me+e
m-
=s
ò
t
dtR
EE
t
z
x
z
y
z
x
z
yy
,
11
1
1
22
; (4)
( ) ( )
( )
ttg
m+
-g
m+
=t
ò
t
dtR
EE
t
z
xy
z
xyxy
,
1212
2
1
.
Здесь
(
)
(
)
t
t
,,,
2
1
tRtR
- функции влияния (ядра релаксации)
материала при растяжении (сжатии) и сдвиге соответственно. Эти
функции исходя из экспериментальных данных и подходов разных
авторов принимаются в различном виде.
Уравнения равновесия получаются из условия минимума
функционала полной энергии деформации и представляют собой сложные
системы интегро- дифференциальных уравнений. Функции перемещений
),
,
,
(
t
y
x
u
)
,
,
(
),
,
,
(
t
y
x
w
t
y
x
v
можно найти, используя метод Ритца, для
минимизации функционала полной энергии деформаций оболочки,
который после некоторых преобразований может быть записан в виде
( )
(
)
}
]
]
( )}
.,4
12
22)(),()2()
12
(
)(2
)2)((
)1(2
)1(2
)42)(
12
()2
(22
12
Э
2
2
121
3
121
2
1
2
221
2
1
3
1221
22
00
1
2
2
2
121
2
221
2
1
3
12112
21
2
1
22
00
2
ttcm
÷
÷
ø
ö
ç
ç
è
æ
++
+cgm+mg
ê
ë
é
++tc+cmc+c++
+cme+ce+cme+ce+
+e+eme+e
î
í
ì
ê
ë
é
+
m-
-m--
-cm+c+cmc+c++cgm+cme+ce+
+cme+ce+gm+e+eme+e
î
í
ì
÷
÷
ø
ö
ç
ç
è
æ
+
m-
=
-
---
-
t
-
-
--
òòò
òò
dtRJ
h
SFhtRJ
h
S
Fh
E
dydxW
E
q
J
h
SFh
E
xyxy
yyxx
yyxx
abt
xyyy
xxxyyyxx
ab
(5)

48 49
Здесь
-
-
-
JSF ,,
- площадь поперечного или продольного сечения
ребер, приходящаяся на единицу длины сечения, статический момент
и момент инерции сечения, соответственно.
Представленная математическая модель оболочки учитывает диск-
ретное расположение ребер, их сдвиговую и крутильную жесткость, воз-
можность развития деформаций ползучести и может быть использована
для исследования напряженно-деформированного состояния пологих
ребристых железобетонных оболочек при их длительном нагружении.
Так как рассматриваются железобетонные оболочки, жесткость ар-
матуры в направлении осей
x
и
y
может быть разной и тогда физичес-с-
кие соотношения (3) должны учитывать ортотропию материала:
)(
)1)(1(
2
2
1
1
z
x
z
yx
E
em+e
m-m-
=s
;
)(
)1)(1(
1
2
1
2
z
x
z
yy
E
em+e
m-m-
=s
; (6)
z
xyxy
G g=t
12
.
С учетом ползучести физические соотношения перепишутся в виде
(
)
( )
( )
;,
)1)(1(
)1)(1(
1
1
2
21
1
2
21
1
ttem+e
m-m-
-
-em+e
m-m-
=s
ò
t
dtR
E
E
t
z
y
z
x
z
y
z
xx
(
)
( )
( )
;,
)1)(1(
)1)(1(
1
1
1
21
2
1
21
2
ttem+e
m-m-
-
-em+e
m-m-
=s
ò
t
dtR
E
E
t
z
x
z
y
z
x
z
yy
(7)
.),(
212
1
ttg=t
ò
t
dtRG
z
xy
t
xy
Здесь характеристики материалов
,
1
E
,
2
E
1
m
,
2
m
,
12
G
– разные
в направлениях осей
x
и
y
, определяются с учетом жесткости арматуры.
Функционал полной энергии деформации оболочки запишется
в виде
.,,)2(
2
1
Э
00
4
2
dzdydxqw
z
xyxy
z
yy
а b
H
h
h
z
xx
-gt+es+es=
òò ò
+
-
(8)
Список литературы
1. Карпов В. В. Математическое моделирование, алгоритм исследо-
вания модели, вычислительный эксперимент в теории оболочек / СПбГА-
СУ. – СПб., 2006. – 330 с.
Получено 20 июня 2007 года.
УДК 519.24
Е. В. Седунов, Е. А.Седунова (СЗИП СПбГУТД)
УПРАВЛЕНИЕ ДИНАМИЧЕСКИМ ЭКСПЕРИМЕНТОМ НА
МНОЖЕСТВЕ ЭЛЕМЕНТАРНЫХ ОПЕРАТОРОВ
Рассматриваются аналитические методы решения задачи оптимального уп-
равления динамическим экспериментом с использованием непараметрической
априорной информации при непрерывном во времени наблюдении за объектом на
множестве элементарных операторов.
1. Математическая формулировка двухкритериальной задачи.
На практике встречаются задачи [1–3], когда необходимо изучить пове-
дение объекта во времени
t
Î
t
при различных внешних условиях
Χ
x
Î
, причем при фиксированном
x
из
Χ
результаты измерений мож-ж-
но регистрировать непрерывно во времени. Формализуем эту практи-
ческую ситуацию, следуя работам [3, 4].
Пусть
(
)
mÌ ,
2
ΧLF
и
(
)
vLG ,
2
tÌ
– конечномерные гильбертовы
пространства;
s
F
=
dim
;
v
G
=
dim
;
Χ
– компакт в
κ
R
;
t
– отрезок пря-
мой;
m
– конечная мера на
Χ
;
v
– мера Лебега на
t
. Введем простран-ран-
ство
G
F
H
Ä
=
, состоящее из функций
(
)
txh ,
таких, что о
(
)
Fth
Î
×
,
v
–
Математическое моделирование, численные методы и комплексы
программ. СПб., 2007

50 51
п. в. и
(
)
Gxh
Î
×
,
m
– п. в., и снабженное скалярным произведением
( ) ( ) () ()
xdtdtxhtxhhh
Χ
m
÷
÷
ø
ö
ç
ç
è
æ
n=
òò
t
,,,
2121
.
По предположению искомая функция
(
)
Htx
Î
h
,
,
Χ
x
Î
,
t
Î
t
.
Областью планирования
U
в рассматриваемой ниже постановке служит
множество элементарных операторов
z
Q
{
}
ΧzQUU
ze
Î
=
=
:
,
GHQ
z
®
:
, (1)
(
)
(
)
(
)
(
)
(
)
(
)
t
Î
Î
"
=
m
=
ò
tHhtzhdxtxhxhthQ
Χ
zz
,,,,
,
где
(
)
xh
z
– воспроизводящее ядро пространства
F
, задаваемоее
равенством
() () ()
xfzfxh
l
m
l
lz
å
=
=
1
. (2)
Здесь
{
}
m
l
l
f
1
=
– любая
m
-ортонормированная система функций из
F
.
При этом планы экспериментов – вероятностные меры
x
на мно-
жестве
e
U
вида (1) с конечным носителем:
(
)
GHQUQppQQ
j
ze
j
zn
n
zz
®
Î
=
x
:,,,,;,,
1
1
KK
, (3)
{ }
å
=
=
=Î>
n
j
n
j
jjj
ppnjp
1
1
,1;:1,0
– веса наблюдений.
При плане
x
схема измерений неизвестного элемента
h
из
H
имеет
вид
(
)
(
)
(
)
(
)
(
)
(
)
njttzttQty
jjjzj
j
:1,,,,,
Î
w
e
+
h
=
w
e
+
h
=
w
, (4)
где
t
Î
x
Î
tQ
j
z
,supp
,
(
)
w
,ty
j
и
(
)
w
e
,t
j
– случайные процессы;
w
– элемент из множества случайных событий, причем
(
)
(
)
(
)
t
Î
¹
"
=
w
e
w
e
=
w
e
tijttEtE
ijj
,0,,,0,
,
а ковариационный оператор
(
)
njGGED
jjj
:1,:][
Î
®
e
Ä
e
=
e
задан своей матрицей
(
)
j
D
e
в некотором
n
-ортонормированном базисее
(
)
{
}
v
u
u
tg
1
=
пространства
G
:
( )
( )
v
wu
j
wu
j
j
p
D
1,
,
=
÷
÷
ø
ö
ç
ç
è
æ
s
=e
,
.
:
1
n
j
Î
Здесь запись
h
h
Ä
обозначает оператор вида
hzhz
z
>
®<
,
,
где
h
,
z
– из некоторого гильбертова пространства а
Z
.
В силу условия ограниченности ресурсов, характерного для рас-
сматриваемого класса задач,
(
)
Fsn dimsuppсard
=
<
=
x
, (5)
несмещенно оценить неизвестный элемент
h
из
H
в эксперименте (4)
по плану (3) не представляется возможным. По этой причине оценку
h
)
неизвестного элемента
H
Î
h
будем искать в конечномерном аффинномм
подпространстве
HH
d
Í
с помощью аффинного оператора
( )
ded
HULS ®x,:
2
:
yS
d
=
h
)
, (6)
где
0
HdH
d
+
=
;
^
Î
0
Hd
;
0
H
– линейное подпространство о
H
;
^
0
H
–
ортогональное дополнение в
H
к
0
H
;
0
SdS
d
+
=
;
( )
0
2
0
: HULS
e
®x
–
линейный оператор,
( )
x,
2
e
UL
– пространство
G
-значных функций на
пространстве с мерой
(
)
x
,
e
U
.
Оценку
h
)
подчиним условию несмещенности по отношению к наи-
лучшему приближению
h
из
d
H
:
HPE
d
Î
h
"
h
=
h
,
)
, (7)
где
dd
HHP
®
:
– аффинный ортогональный проектор.
Далее при условии (7) на множестве
АН
P
аффинных несмещенных
процедур
(
)
x
=
p
,,,
00
SHd
формируется двухкритериальная задача
минимизации систематической ошибки
() ( ) ()
hdHB
H
d
ò
gh=p
g
,dist
2
, (8)
усредненной по априорной мере
g
в
H
, и случайной ошибки, характе-
ризуемой некоторым функционалом
[
]
(
)
h
F
)
D
от ковариационногоо
оператора
[
]
h
)
D
оценки
h
)
вида (6).
Указанная двухкритериальная задача оптимизации рассматривает-
ся далее с приоритетом, предоставляемым систематической ошибке (8):

52 53
()
,infArg
*
p=p
g
PÎp
B
АН
(9)
)(ФinfArg
*
*
p
Õ
=p
Îp
AH
, (10)
где
АН
АН
PÍP
*
– множество решений задачи (9).
2. Основные аналитические результаты. На данный случай мож-
но перенести результаты работы [5] и их обобщения на задачи с вектор-
нозначным откликом [6].
Теорема 1. При решении задачи (9) для схемы измерений (4) мож-
но ограничиться процедурами восстановления
h
вида
(
)
(
)
{
}
.suppcard,supp:;,,, nUSHd
en
=
x
Ì
x
X
Î
x
=
X
Î
x
x
=
p
xxxx
При этом параметр сдвига
^
xx
Î Hd
в аффинном операторе оценива-
ния
( )
xx
x
xx
x
+=®x+= HdHULSdS
ded
,:
2
вычисляется по формуле
( )
,g=
^
xx
EPd
(11)
где
^
x
^
x
® HHP :
– ортогональный проектор.
Линейное пространство оценивания имеет вид
(
)
(
)
{
}
.:1,supp,,Span njUQGgtgxhH
ezz
jj
Î
Ì
x
Î
Î
=
x
(12)
Линейный оператор оценивания
(
)
xx
®x HULS
e
,:
2
задается
равенством
[
]
e=
-
x
-
xx
1*1
DJMS
, (13)
где
x
J
– сужение оператора измерения
x
I
:
(
)
x® ,
2
e
ULH
на подпро-
странство
x
H
; оператор
x
I
определяется посредством м
h
=
h
x
QI
;
H
Î
h
;
x
Î
supp
Q
;
[
]
xxx
-
xx
®e= HHJDJM :
1*
– информационный операторор
оценки
(
)
tx,
h
)
.
Значение
АН
-оценки
(
)
tx,
h
)
для
C
Î
"
x
и
t
Î
"
t
в эксперименте
по плану
x
, элементы носителя которого
{
}
n
j
j
z
Q
1=
линейно независимы,
находится по формуле
( ) ( )( )
[
]
( ) ( )( ){ } ()
,,,,,
1,
1
xhtzEtyΗtxEtx
j
zii
ji
n
ij
g-w+g=h
å
=
-
)
(14)
где
( )
(
)
;
1,
n
iji
j
z
zhΗ
=
=
(
)
w
,ty
i
– усредненное значение наблюдений
в i-м опыте с учетом весов наблюдений.
На множестве процедур
x
П
вида (11)–(13) задача (9) может быть,
как и в работе [5], сведена к максимизации функционала
()
[
]
*
:
xx
g=xY PDPtr
,
где
[
]
HHD
®
g
:
– ковариационный оператор меры
g
,
[
]
(
)
(
)
(
)
(
)
dhEhEhD
H
ò
g
g
-
Ä
g
-
=
g
:
.
Теорема 2. Если найдется план
*
x
из
n
X
такой, что выполнено
условие (5) и
(
)
nv
HH =
x
*
– подпространство
H
, натянутое на соб-
ственные векторы оператора
[
]
g
D
, соответствующие
nv
наибольшим егоо
собственным числам, то процедура
*
x
p
решает задачу (9).
При этом
å
+=
x
g
l=
÷
ø
ö
ç
è
æ
p
m
vni
i
B
1
*
, где
0
1
³
l
³
³
l
³
³
l
mnv
KK
–
последовательность собственных чисел оператора
[
]
g
D
.
Следствие. Пусть спектр
{
}
**
1
,,
n
zz K
плана
*
x
из
n
X
удовлетворяет
ограничению (5) и условиям
(
)
(
)
( )
ï
î
ï
í
ì
tÎ"=+==y
tÎ"¹y
=
,,,,1;,,1,0,
,,0,det
*
1,
*
tnjmvnitz
ttz
ji
n
ji
ji
KK
(15)
где
(
)
tx
i
,
y
,
m
i
,
,
1
K
=
– ортонормированные собственные функции
оператора
[
]
g
D
, упорядоченные по убыванию его собственных чисел.
Тогда
*
x
p
– решение задачи (9).
Пусть далее носитель плана
(
)
nzz
ppQQ ,,;,,
1
2
1
KK
=
x
выбран по
результатам решения задачи (9) и зафиксирован, а свободу в выборе весов

54 55
наблюдений
{
}
n
jj
p
1=
в плане
(
)
p
x
используем для решения задачи (10)
в следующей формулировке
( )
[
]
,infArg
*
p
Pp
Dp
x
Î
F=
(16)
где
( )
;1;,,2,1,10:,,:
1
1
þ
ý
ü
î
í
ì
==£<==
å
=
n
j
jjn
pnjppppP KK
( )
][
p
D
x
F
– заданный дифференцируемый выпуклый функционал отт
ковариационного оператора
( ) ( )
1
-
xx
=
pp
MD
оценки
(
)
tx,
h
)
. Выберем
в пространстве
x
H
ортонормированный базис
() ()
{
}
vn
ul
ul
tgxf
,
1,1
~
~
==
, гдеде
()
{
}
n
ll
xf
1
~
=
и
()
{
}
v
uu
tg
1
~
=
– ортонормированные базисы пространств
(
)
{
}
,:1,Span njxhF
j
z
Î
=
x
и
G
соответственно. Запишем в этом базисее
матрицу
(
)
pD
оператора
()
p
D
x
:
()
T
AΡApD
åå
-
=
21
1
21
,
где
(
)
n
j
v
F
n
zjv
F
zj
IhfIhfA
1
1
,
~
,,,
~
=
+
+
= K
;
(
)
vnv
IpIp ,,diag
1
K
=
R
;
(
)
å
å
å
=
n
1
,,diag K
,
(
)
(
)
å
=
s=
j
v
wu
wu
j
1,
,
;
{
}
n
j
j
z
h
1=
+
– биортогональная
система к линейно независимой системе
{
}
n
j
j
z
h
1=
, задаваемая
равенствами
njihh
ij
j
z
i
z
,,2,1,,, K=d=
+
; (17)
v
I
– единичная диагональная
(
)
n
´
v
-матрица.
Теорема 3. При сделанных предположениях существует, по край-
ней мере, одно решение задачи (16).
Необходимым и достаточным условием оптимального выбора весов
наблюдений
**
1
,,
n
pp K
в задаче (16) служит выполнение равенств
(
)
(
)
nj
D
D
j
,,2,1,tr
**
K=x
¶
F
¶
=xj
, (18)
где
() ()
,)(tr
2
jj
T
jj
A
D
Ap åx
¶
F
¶
=xj
g
-
n
j
,
,
2
,
1
K
=
;
;:
1,
nv
li
il
DD
=
÷
ø
ö
ç
è
æ
¶
F¶
=
¶
F¶
T
v
F
j
znv
F
j
zj
IhfIhfA
÷
ø
ö
ç
è
æ
=
++
,
~
,,,
~
1
K
,
;
:
1
n
j
Î
(
)
**
1,
1
*
,,,,
n
n
zz
ppQQ KK=x
.
По отношению к критериям
D
-оптимальности
(
)
[
]
(
pD
=
F
(
)
)
pDdet
=
и линейным критериям оптимальности (
(
)
[
]
(
)
pLDpD tr
=
F
,
где
L
– заданная положительно полуопределенная матрица) выбор весов
наблюдений дается, соответственно формулами
njnp
j
,,2,1,1
*
K==
; (19)
(
)
(
)
( )( )
.,,1
,
tr
tr
1
21
21
*
nj
LAA
LAA
p
n
r
rr
T
r
jj
T
j
j
K=
å
å
=
å
=
(20)
Пример. Пусть
G
F
H
Ä
=
,
{
}
2
,,1pan xxSF =
,
( )
mÌ ,
2
XLF
,
[
]
1,1
-
=
Î
Xx
,
( )
dxdx
2
1
=m
,
{
}
tG Span
=
,
[
]
1,0
=
t
Î
t
;
e
UU
=
;
dim
=
F
3
=
=
s
;
1
dim
=
=
v
G
,
3
dim
=
=
=
sv
m
H
;
3
2
=
<
=
s
n
;
÷
ø
ö
ç
è
æ
=g
3
1
,
3
1
,
3
1
;,,
2
txxtt
;
(
)
å
=
5.0;1.0diag
;
(
)
[
]
(
)
pDpD tr
=
F
– А-опти-
мальность.
Решение в условиях примера задачи (9), (10) начнем с введения
в пространстве
H
ортонормированного базисаа
( ) ( ) ( ) ( )( )
(
)
(
)
(
)
txtxttxtxtxtx
T
13215,3,3,,,,,,
2
321
-=jjj=j
.
Запишем в этом базисе матрицу оператора
[
]
g
D
:
()
(
)
( )
(
)
dhEhEhD
m
ji
H
j
H
i
H
gjg-jg-=g
=
=
ò
3
1,
,,
,

56 57
где
(
)
txxttE
2
3
1
++=g
.
Несложные расчеты дают
()
÷
÷
÷
÷
÷
÷
ø
ö
ç
ç
ç
ç
ç
ç
è
æ
--
--
--
=g
15
8
15
2
53
2
15
2
2
3
4
53
2
3
4
3
14
81
1
D
.
Минимальному собственному числу
0
3
=
l
оператора
[
]
g
D
соответствуют собственный вектор
(
)
T
q 5,3,1
3
=
и собственная
функция
( ) ( )
( )
=-++=j=y txtxtqtxtx
T
13
2
35
333,,
2
33
(
)
12533
2
-+= xxt
. Теперь из условий (15) находим, что операторам
*
supp
*
xÎ
j
z
Q
,
2
,
1
=
j
, соответствуют т
(
)
5
16
*
1
+
-=z
и
(
)
5
16
*
2
-
=z
– нулили
многочлена
1
2
5
2
-
+
x
x
.
Зафиксируем носитель плана
*
x
и перейдем к вычислению
A
-оптимальных весов наблюдений
*
1
p
и
*
2
p
по формуле (20). Для этогоого
с помощью соотношения (2) при
(
)
1
1
=
xf
,
(
)
xxf 3
2
=
,
()
(
)
13
2
5
2
3
-= xxf
получим
()
(
)
2222
551543
4
3
zxzxxzxh
z
--++=
,
откуда
()
465,0070,2605,1
2
*
1
+-= xxxh
z
;
()
935,1870,0804,2
2
*
2
++-= xxxh
z
.
Учитывая, что
()
0,
*
2
*
1
=
F
zz
hxh
, легко найти
m
-ортонормирован-
ный базис пространства
x
F
:
()
285,0270,1985,0
~
2
*
1
+-= xxxh
z
;
()
385,1623,0007,2
~
2
*
2
++-= xxxh
z
.
В рассматриваемом случае можно упростить соотношения (20),
приведя их к виду
(
)
( )
,,,1,
tr
tr
1
21
21
*
nj
h
h
p
n
r
F
r
z
r
F
j
z
j
j
K==
åå
å
=
+
+
где биортогональная система
{
}
n
jz
j
h
1=
+
с учетом (17) выражается черезз
элементы исходной системы
{
}
n
j
j
z
h
1=
посредствомм
[
]
njhh
n
r
z
rj
z
rj
:1,
1
1
ÎH=
å
=
-+
.
В условиях данного примера несложные вычисления дают
()
;613.0,175.0778.0603.0
1
1
2
=+-=
+
+
z
z
hxxxh
()
.715,0,991.0445.0436/1
2
2
2
=++-=
+
+
z
z
hxxxh
Отсюда легко находим
( )
.723.01;277.0
715.05.0613.01.0
613,01.0
*
1
*
2
*
1
=-==
×+×
×
= ppp
Далее пространство оценивания имеет вид
(
)
(
)
(
)
[
{
]
( ) ( )
[
]
}
.))12(и)11(см.(64612263,64
612263Span125
6
1
2
22
**
*
txxt
xxtxxHdH
d
++----×-+
++--+-+=+=
xx
x
Для оценки
(
)
tx,
h
)
получаем по формуле (14) следующее выраже-
ние:
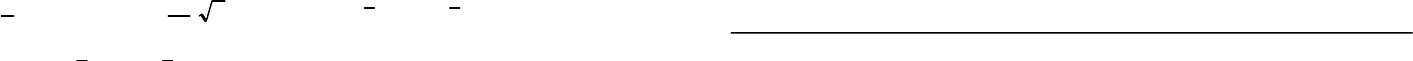
58 59
( )
(
)
[
(
)
( ) ( )( )
( )
( ) ( )( )
]
.,,725
,,2356
12
1
125
6
1
,
2
1
2
21
22
w+w-+-
-w-w--+-+=h
tytyxx
tytyxxtxxtx
)
В заключение отметим, что в реальных ситуациях рассчитывать на
аналитические методы при решении задачи (9)–(10) не приходится
и остается обратиться к численным методам. Детальное рассмотрение
такого рода процедур не вписывается в рамки данной статьи.
Список литературы
1. Дубова И. С., Федоров В. В., Федорова Г. С. Выбор оптимальных
траекторий при отклике, зависящем от времени // Регрессионные экспе-
рименты. Сб. тр. / МГУ. – М., 1977. – С. 30–38.
2. Седунов Е. В., Седунова Е. А. Оптимизация эксперимента в об-
ратных коэффициентных задачах математической физики // Математи-
ческое моделирование, численные методы и комплексы программ: Меж-
вуз. темат. сб. тр. / СПбГАСУ. – СПб., 2002. – Вып. 8. – С. 205–211.
3. Седунов Е. В., Седунова Е. А. Задача управления экспериментом
при наблюдении за объектом во времени // Математическое моделирова-
ние, численные методы и комплексы программ: Межвуз. темат. сб. тр. /
СПбГАСУ. – СПб., 2002. – Вып. 12. – С. 212–218.
4. Седунов Е. В., Сидоренко Н. Г., Соловьева С. А. Несмещенное
планирование эксперимента при непрерывном во времени наблюдении
за объектом // Тезисы докладов III Всесоюзн. конф. «Перспективные
методы планирования и анализа экспериментов при исследовании слу-
чайных полей и процессов» / МЭИ. – М., 1988. – Ч. 1. – С. 175–176.
5. Седунов Е. В., Сидоренко Н. Г. Несмещенное планирование экс-
перимента в гильбертовом пространстве // Теория вероятностей и ее при-
менение. – 1987. – Т. 32. – № 4. – С. 804–808.
6. Сидоренко Н. Г. Планирование и анализ экспериментов с вектор-
ным откликом при ограниченных ресурсах //Автореф. дисс…. канд. физ.-
мат. наук. – Л.: ЛГУ, 1988. – 16 с.
Получено 15 февраля 2007 года.
Математическое моделирование, численные методы и комплексы
программ. СПб., 2007
УДК 681.325.5
М. И. Самохина, Ю. Ю. Стебенькова (БрГУ)
НОВЫЙ ПОДХОД К МОДЕЛИРОВАНИЮ ДЛЯ ПОДДЕРЖКИ
ПРИНЯТИЯ РЕШЕНИЙ
Рассматриваются возможности использования систем поддержки принятия
решений и экспертных систем при проектировании и управлении большими со-
циально-техническими и экологическими системами, относящимися к области
прикладного системного анализа операционных исследований.
В основе понятия системы поддержки принятия решений, и в час-
тности экспертных систем, лежит осознание того факта, что есть класс
проблемных ситуаций, которые не до конца понимаются заинтересован-
ной группой людей. В этом случае проблемы не могут быть решены по-
средством обращения к сильно структурированным машинным методам.
Такие проблемы не являются уникальными, что оправдало бы большие
разовые усилия для их решения, и в то же время они не так часто встре-
чаются в схожих постановках, чтобы использовать формальные матема-
тические методы. Из-за этой смеси неопределенности в научных аспек-
тах задач и субъективных, основанных на соображениях здравого смыс-
ла, элементов в социально-экономических аспектах нельзя указать пол-
ностью объективно обоснованный метод нахождения лучших решений.
Одним из подходов к этому классу неопределенных проблемных
ситуаций является итеративная последовательность применения мето-
дов системного анализа и процессов обучения, производимая эксперт-
ной системой или системой поддержки решений. По Филиппсу, основ-
ными составляющими такой системы являются владельцы проблемы,
технология предпочтений, помогающая выразить оценочные суждения
и формализовать временные предпочтения, предпочтения риска и соот-
ношения между ними, а также информационная технология, которая
представляет и организует данные, информацию и модели.
В настоящее время нет общепринятого определения систем под-
держки принятия решения (СППР). Почти любая система с использова-
нием ЭВМ – от управления БД или информационных систем и систем
моделирования до методов математического программирования и опти-
