Математическое моделирование, численные методы и комплексы программ 2007 Вып.13

Подождите немного. Документ загружается.

20 21

пример, статические задачи о нагружении тел при столь малых напря-

жениях и температурах, когда пластические и вязкие эффекты пренеб-

режимо малы. В этих случаях характеристика поведения материала под-

чиняется закону Гука, а при больших деформациях принимаются нели-

нейные зависимости, устанавливающие, однако, взаимно однозначное

соответствие между деформациями и напряжениями. Соответственно

и механическая система в целом практикуется как вполне упругая.

Однако такая «чисто упругая» постановка задачи далеко не уни-

версальна. Существует большое число динамических задач, при кото-

рых нельзя игнорировать различные сопротивления неупругого харак-

тера. Последние можно разделить на две группы:

внешние сопротивления: трение в опорах систем; аэро- или гидро-

динамическое сопротивление среды; сопротивление, создаваемое спе-

циально вводимыми в систему демпферами;

внутренние сопротивления – внутреннее трение в материале; тре-

ние в так называемых неподвижных соединениях (заклепочных, прессо-

вых, шлицевых, резьбовых и т. п.).

Сопротивления указанного вида неизбежно сопровождают всякий

процесс деформирования реальных механических систем, таким обра-

зом, кривые зависимости между напряжением и деформацией при уве-

личении нагрузки и при ее уменьшении, строго говоря, не совпадают

между собой.

Работа, затрачиваемая на деформацию больше, чем работа, отдава-

емая материалом при разгрузке. Таким образом, при каждом цикле коле-

бания рассеивается (превращается в теплоту) энергия, соответствующая

площади петли гистерезиса. Рассеивание энергии становится особенно

значительным, если в процессе деформации возникают пластические

деформации; однако потери энергии имеют место и при напряжениях,

меньших предела упругости (упругий гистерезис).

Игнорируя неупругие сопротивления, мы лишаемся возможности

объяснить многие реально наблюдаемые явления. Так, в интересующей

нас области колебаний наглядным примером явлений этого типа может

служить затухание свободных колебаний. Учет неупругих сопротивле-

ний приобретает также первостепенное значение при определении амп-

литуд вынужденных колебаний в резонансной зоне и в ряде других за-

дач динамики деформируемых тел.

Очевидно, что решение различных задач о колебании систем с внут-

ренним трением требует отчетливых представлений о закономерностях,

описывающих соответствующие неупругие сопротивления. Эти экспе-

риментально устанавливаемые закономерности неизбежно приходится

описывать таким образом, чтобы облегчить последующее решение со-

ответствующих дифференциальных уравнений.

Введем в рассмотрение внутреннее трение и заменим «чисто упру-

гую» задачу моделью вязкоупругого тела Бокка – Сорокина (эллипти-

ческая форма петли гистерезиса), приводящей к наиболее простым ре-

шениям. Запишем связь между напряжением и деформацией для одно-

осного напряженного состояния в виде

+e=s

, (14)

где s – нормальные напряжения в поперечном сечении бруса;

e – деформация; Е – модуль упругости материала стержня (модуль Юнга);

w – круговая частота; y

– коэффициент поглощения, определяемый как

= DW/W; W – амплитудное значение потенциальной энергии;

DW – рассеянная за один цикл деформирования энергия.

Перепишем уравнение (14) в виде

)()(

+e=

ZEFZN

или с учетом (4)

)()(

¶¶

ZEFZN

(15)

Решим систему (3), (15) для гармонического возбуждения с круговой

частотой w.

Выполним подстановку:

[

]

[ ]

;e)()(),(

ZjNZNtZN

ZjUZUtZU

×w×

(16)

где j – мнимая единица; U

, U

, N

– подлежащие определению

действительные функции смещения и усилия.

Подставим выражения (16) в систему уравнений (3) и (15) и, разде-

лив действительную и мнимую части, получим систему уравнений

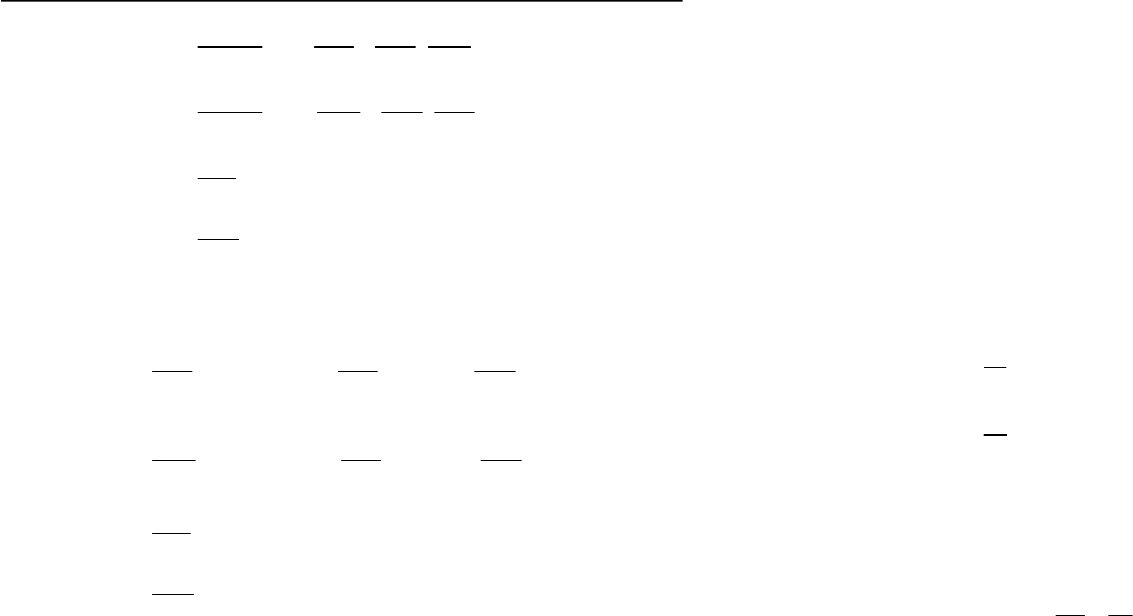
22 23

,)(

2)(

UZF

ZEF

rw-=

или окончательно

rw-=

+×=

.)(

,)(

1)(

UZF

NNZEF

(17)

Получено 4 апреля 2007 года.

УДК 504.3.054

И. А. Гаранина (БрГУ)

МОДЕЛЬ РАСПРЕДЕЛЕНИЯ ИОНОВ ПРИ НАЛИЧИИ

АЭРОЗОЛЕЙ И ИСТОЧНИКОВ ИОНИЗАЦИИ В ПРИЗЕМНОМ

СЛОЕ АТМОСФЕРЫ

Представлена разработка численной модели электрического состояния при-

земного слоя, исследование возможности контроля антропогенного воздействия

на атмосферу.

В настоящее время антропогенное воздействие на среду обитания

в виде аэрозольных выбросов промышленных предприятий, выхлопов ав-

тотранспорта, радиоактивного загрязнения приводит к изменению электро-

физического состояния приземного слоя атмосферы. Следствием этого яв-

ляется количественное и качественное изменение аэроионного состава воз-

духа, что существенным образом влияет на жизнедеятельность человека.

Определенный прогресс в оценке влияния техногенных аэрозолей

на электрическое состояние приземного слоя атмосферы вносит мате-

матическое моделирование. Теоретическое исследование принципиаль-

но расширяет возможности изучить объект, воспроизвести который

в лабораторных условиях нельзя.

Для моделирования горизонтально-однородного приземного слоя

атмосферы распределение ионов в присутствии аэрозолей и источников

ионизации имеет вид [1]

()

0122112111

)( NnNnnnzqEnb

h-h-a-=

;

()

0221212122

)( NnNnnnzqEnb

h-h-a-=-

;

121012

NnNn

;

(1)

211022

NnNn

;

const

021

NNNN

;

( )

2121

NNnn

-+-

где

2,1

– концентрации положительных и отрицательных легких ионов;

2,1

– их подвижность; Е – напряженность электрического поля;

i – плотность электрического тока; q – интенсивность ионообразования;

a – коэффициент рекомбинации легких ионов; е – элементарный заряд;

z – ось координат, перпендикулярная поверхности Земли;

–

концентрации положительных, отрицательных тяжелых ионов;

–

концентрация нейтральных аэрозольных частиц;

2,1

– коэффициенты

взаимодействия легких ионов соответственно с заряженными и ней-

тральными тяжелыми ядрами;

– электрическая постоянная.

Математическое моделирование, численные методы и комплексы

программ. СПб., 2007

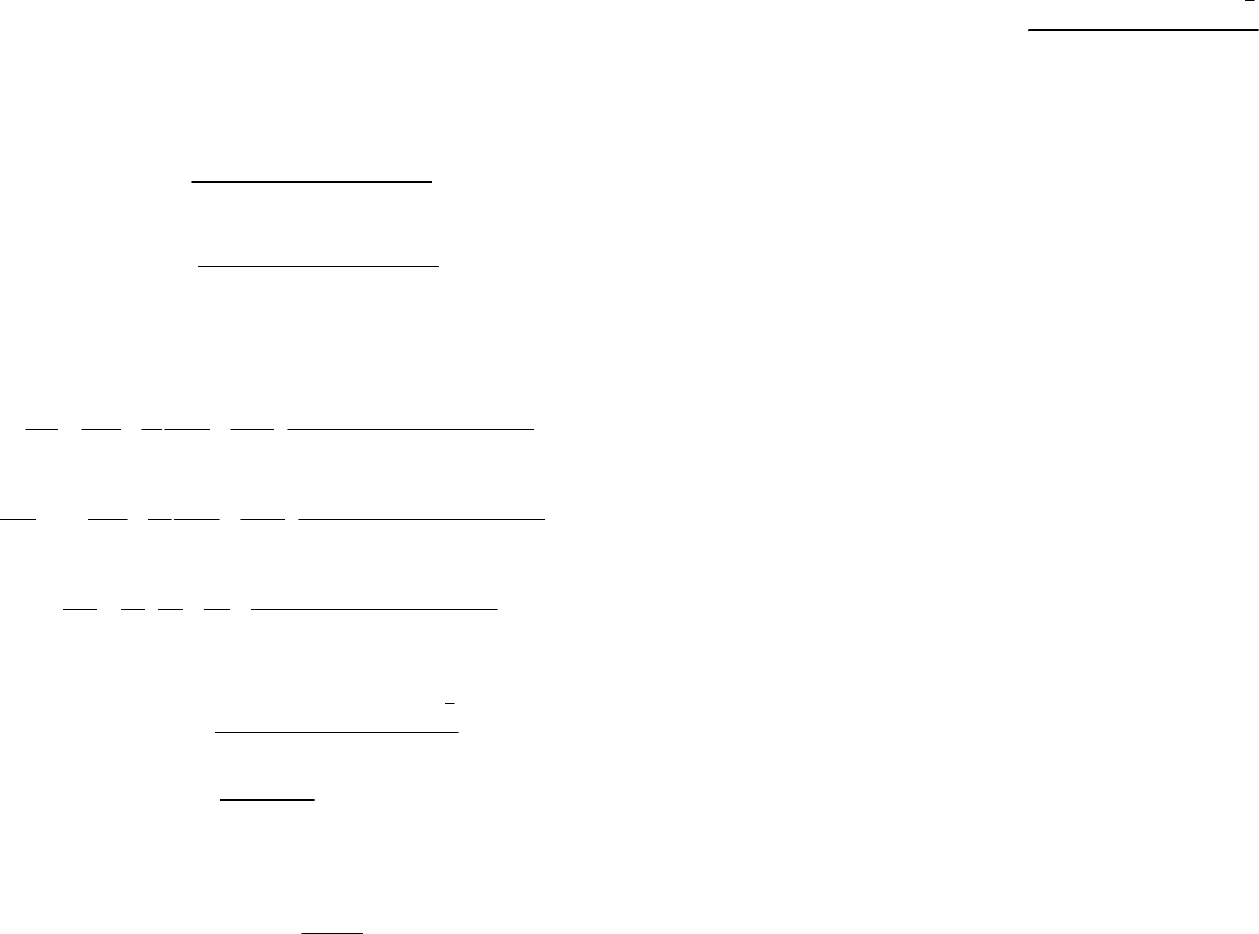
24 25

При этом предполагалось, что присутствие ядер конденсации в ат-

мосфере приводит к образованию тяжелых ионов, подвижность кото-

рых на несколько порядков меньше, чем легких. Предполагалось, что

ядра стационарны и имеют постоянную концентрацию.

Решая совместно третье, четвертое и пятое уравнения системы (1)

получаем функции

121

nnnn

hh+h+hh

; (2)

221

nnnn

hh+h+hh

. (3)

Подставляем (2), (3) в (1) и, вводя обозначения

Eny

EyEny

322

, получаем следующую систему уравнений:

(

)

hh+h+hh

h+hh

22121

121

2112

yyyy

;

()

hh+h+hh

h+hh

--=

22121

121

2112

yyyy

; (4)

(

)

hh+h+hh

-hh

22121

121

yyyy

yyN

Граничные условия с учетом новых обозначений приобретают вид

() () ()

()

( )

()

;

321

¥a++×

=¥¥=¥ y

qNBNB

yyy

( )

()

.00;

h+h

= yB

(5)

В стационарном случае, учитывая инвариантность плотности элек-

трического тока, получаем

() ()

=¥

(6)

Подставляем (6) в (5) получаем

()

( )

()

qNBBN

¥a++

=¥

(7)

Таким образом, исходной системой для проведения численных

решений является система (4) с граничными условиями (5). Значения

параметров, входящих в уравнения, задавались следующими:

= 1.4×10

– 12

– 1

;

= 4×10

– 12

–

;

= 1.6×10

– 12

– 1

;

= 1.2×10

– 4

– 1

;

= 1.4×10

– 4

– 1

;

= 8.85×10

–12

Ф м

– 1

;

= 1.6×10

– 19

Кл.

Полученная система дифференциальных уравнений первого

порядка с граничными условиями представляет собой краевую задачу

[2]. Система решалась численно методом Рунге – Кутта четвертого

порядка [2, 3]. При этом значение

(

)

подбиралось таким образом,

чтобы выполнялись соотношения (5), (6), (7). Шаг интегрирования

выбирался равным 10

– 3

– 10

– 4

м.

Расчеты показывают, что при

– 3

аэрозоль практически не

влияет на распределение

2,1

в приземном слое. Такая ситуация

наблюдается в экологически чистых районах. Увеличение

до значений

порядка 5×10

–10

–3

приводит к тому, что объемный заряд в равной мере

создается как легкими, так и тяжелыми ионами. При N ~ 10

–10

– 3

роль легких ионов незначительна и весь объемный заряд обусловлен

тяжелыми ионами. Предположение о том, что аэрозоли являются стоком

для аэроионов подтверждается.

Таким образом, наличие в атмосфере концентрации аэрозольных

частиц более (5–15)×10

– 3

оказывает заметное влияние на распределение

2,1

вблизи поверхности земли.

Список литературы

1. Морозов В. Н. Атмосферное электричество // Атмосфера. Справоч-

ник (справочные данные, модели). – Л.: Гидрометеоиздат, 1991. – С. 394–408.

2. Корн Г., Корн Т. Справочник по математике для научных работ-

ников и инженеров. – М.: Наука, 1984. – 831 с.

3. Хайрер Э., Нёрсет С., Ваннер Г. Решение обыкновенных диффе-

ренциальных уравнений. Нежесткие задачи. – М.: Мир, 1990. – 512 с.

Получено 3 апреля 2007 года.

26 27

УДК 624.012.3

О. А. Калаш, Г. В. Коваленко, Р. П. Курамшина (БрГУ)

АЛГОРИТМ ОПИСАНИЯ ПРОГРАММЫ ПО ИССЛЕДОВАНИЮ

НДС ЖЕЛЕЗОБЕТОННЫХ ФЕРМ С УЧЕТОМ НЕЛИНЕЙНОГО

ХАРАКТЕРА ИХ ДЕФОРМИРОВАНИЯ

Приводится алгоритм расчета железобетонных ферм по нелинейной дефор-

мационной модели. При загружении ферм используются шагово-итерационные

методы. Физическая нелинейность учитывается путем аналитического описания

диаграмм деформирования бетона и арматуры.

Обработка экспериментальных данных испытаний преднапряжен-

ных ферм на комбинате «Братскжелезобетон» позволила выявить опре-

деленный процент брака для ферм сегментного очертания ФСМ-18

и ФСМ-24. Было установлено, что основной причиной неудовлетвори-

тельных результатов является существенное снижение трещиностойко-

сти нижнего пояса – 35 % бракованных ферм. Это происходит вслед-

ствие неравномерности натяжения канатов и приводит к эксцентрисите-

ту общего усилия от центра тяжести нижнего пояса [1]. Но также проис-

ходит и выход из строя элементов верхнего пояса или решетки, поэтому

возникает необходимость в написании программы по исследованию на-

пряженно-деформированного состояния отдельных элементов ферм

и оценке эксплуатационной пригодности фермы в целом.

Анализ расчетных моделей показал, что более точно отразить фак-

тическое состояние элементов фермы под нагрузкой позволит деформа-

ционная нелинейная модель на основе реальных диаграмм деформиро-

вания материалов, предложенная В. Н. Байковым, Н. И. Карпенко [2, 3].

Данная модель основывается на условиях равновесия нормального се-

чения, разбитого на дискретные участки бетона и арматуры. Железобе-

тон – упруго-пластический материал, для которого учет физической не-

линейности осуществляется путем аналитического описания диаграмм

деформирования бетона и арматуры, принятых в данной расчетной мо-

дели по предложению Н. И. Карпенко:

e×n×=s

ssss

bbbb

(1)

где

– соответственно напряжения в бетоне и арматуре;

–

модули упругости;

– деформации;

– коэффициенты

упругости данных материалов.

Выбранный для исследования способ описания диаграмм дефор-

мирования материалов является наиболее оптимальным, поскольку

он позволяет вычислять напряжения в бетоне и арматуре по единообраз-

ным зависимостям на каждом этапе кратковременного нагружения. При

этом переменной величиной будут являться коэффициенты упругости

бетона и арматуры, которые характеризуют постепенное снижение секу-

щих модулей вплоть до разрушения.

Программа ориентирована на поэтапный расчет элементов ферм

с максимальными усилиями, которые испытывают разное напряженно-

деформированное состояние. Для элемента нижнего пояса на первом

этапе прикладывается усилие обжатия с эксцентриситетом в обоих на-

правлениях. Это связано с тем, что результаты исследований ферм на

комбинате «Братскжелезобетон» показали: в процессе изготовления кон-

струкций часто происходит обрыв прядей канатов в пролете, перекос

натяжных устройств, проскальзывание арматуры вследствие длительной

эксплуатации анкерных приспособлений. Следовательно, общее усилие

преднапряжения смещается по отношению к центру тяжести попереч-

ного сечения и меняет картину распределения напряжений. Далее рас-

чет выполняется шагово-итерационным методом, т. е. внешняя нагрузка

прикладывается ступенями и на каждой ступени решается система урав-

нений, построенная на условиях равновесия сечения, представленного

в дискретном виде: n – количество элементарных участков бетона;

k – количество участков арматурных стержней.

В матричном виде уравнения равновесия запишем в виде

{

}

[

]

{

}

, (2)

где

{

}

– вектор внешних сил;

[

]

– матрица жесткости железобетонногоо

сечения, элементы которой корректируются на каждом этапе загружения

с учетом изменения модулей деформаций материалов;

{

}

– вектор

деформаций, получаемый в результате решения системы уравнений (2).

Математическое моделирование, численные методы и комплексы

программ. СПб., 2007

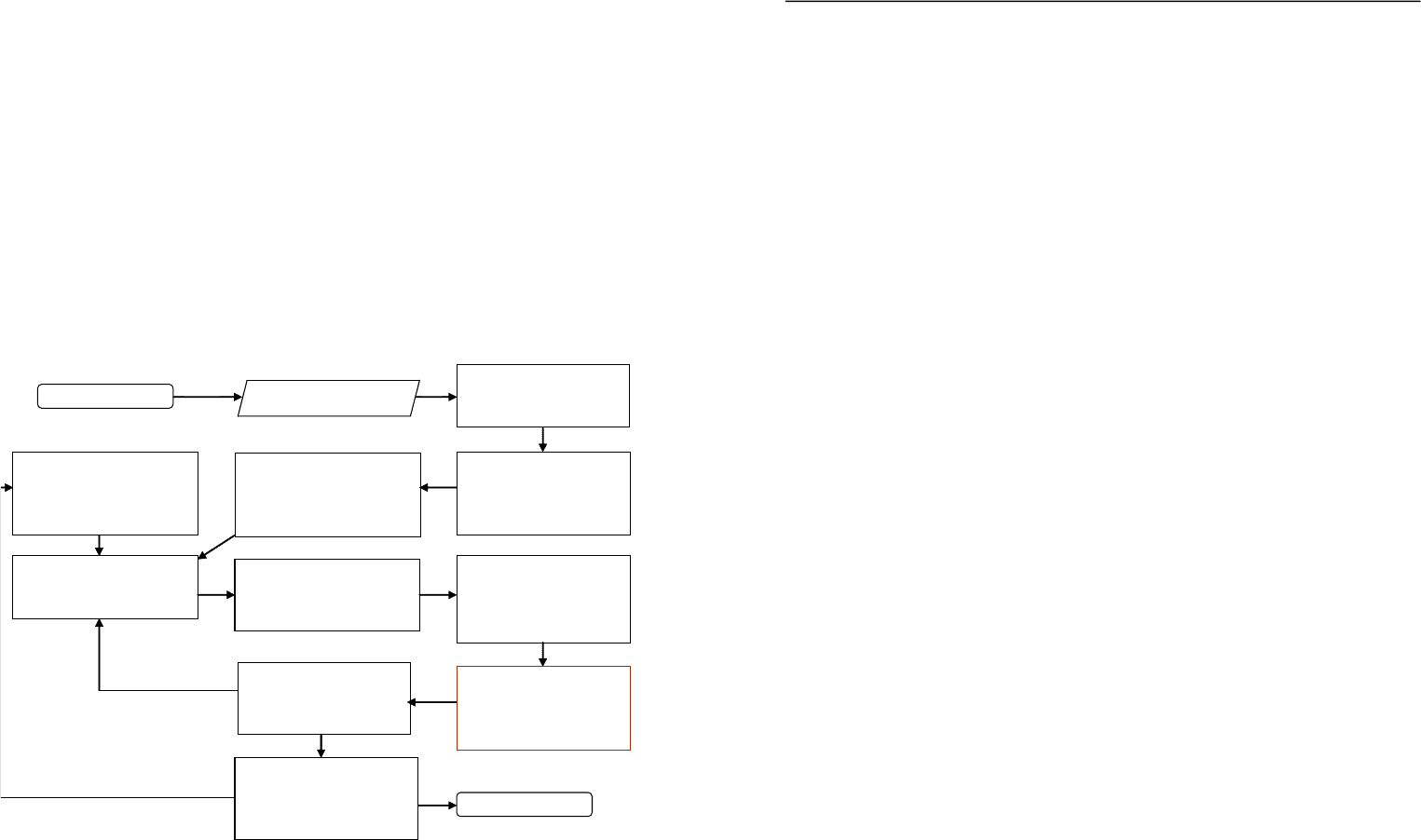
28 29

Затем исходя из гипотезы плоского деформирования вычисляются

деформации в бетоне и арматуре для каждого дискретного участка:

skyskxzsk

bnybnxzbn

ykxk

×-×-e=e

(3)

где

– деформации элемента на уровне продольной оси z;

kk ,

–

соответственно кривизны в направлении осей x и y;

bnbn

yx ,

– координаты

центра тяжести бетонных дискретных элементов, которые вычисляются

в программе при дискретизации поперечного сечения на заданное

количество n участков;

sksk

yx ,

– координаты центра тяжести арматурных

дискретных элементов (стержней), которые вводятся в программу наряду

с остальными данными.

Блок-схема алгоритма оценки НДС нижнего пояса преднапряжен-

ных ферм представлена на рисунке.

Нет

Приращение вектора

внешних сил по

заданному шагу

Вызов подпрограммы

«БЕТОН»,

«АРМАТУРА»

Определение вектора

внешних сил от усилия

обжатия после отпуска

арматуры

Формирование

жесткостных

коэффициентов

Ввод исходных данных

Начало расчета

Да

Нет

Конец расчета

Выбор элементов с

максимальным

усилием

Разбивка сечения на

элементарные

площадки, их

привязка к осям

Проверка заданной

точности вычисления

предельной нагрузки

(ε ≤ 0.03)

Решение системы

уравнений

относительно вектора

деформаций

Вычисление

относительных

продольных

деформаций

Проверка сходимости

итерационного

процесса (≤ 0.001)

Блок-схема оценки НДС преднапряженного нижнего пояса ферм

Для сжатого элемента верхнего пояса или решетки расчет ведется

с учетом случайного эксцентриситета по тому же алгоритму, как для ниж-

него пояса, за исключением первого этапа, поскольку эти элементы яв-

ляются непреднапряженными.

В результате расчета по разработанной программе на основе дан-

ной модели возможно оценить несущую способность элемента фермы,

на каждом этапе загружения получить распределение напряжений по

сечению с учетом влияния эксцентриситетов. Для оценки эксплуатаци-

онной пригодности ферм разрабатывается программа на основе вероят-

ностного расчета с использованием модуля программы по оценке напря-

женно-деформированного состояния элементов фермы.

Список литературы

1. Самарин Ю. А., Романчук В. Э. Исследование напряженного со-

стояния нижних поясов ферм с канатной арматурой в процессе их про-

изводства // Известия вузов. Строительство и архитектура. – 1980. – № 2. –

С. 17–20.

2. Байков В. Н., Додонов М. И. и др. Общий случай расчета проч-

ности элементов по нормальным сечениям // Бетон и железобетон. – 1987. –

№ 5. – С. 16–18.

3. Карпенко Н. И., Мухамедиев Т. А., Сапожников М. И. К построе-

нию методики расчета стержневых элементов на основе диаграмм дефор-

мирования материалов // Совершенствование методов расчета статически

неопределимых железобетонных конструкций / – М.: НИИЖБ, 1987.

Получено 3 апреля 2007 года.

УДК 624.012.3

С. А. Жердева, И. В. Дудина, Е. А. Чевская (БрГУ)

МОДЕЛИРОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО

СОСТОЯНИЯ НЕСУЩИХ СТЕНОВЫХ ПАНЕЛЕЙ ПРИ

КРАТКОВРЕМЕННОМ НАГРУЖЕНИИ

Приводится методика расчета несущих стеновых панелей по разным рас-

четным моделям. Наиболее актуальной расчетной моделью для описания косого

Математическое моделирование, численные методы и комплексы

программ. СПб., 2007

30 31

изгиба является расчет по нелинейно-деформационной теории с учетом реальных

диаграмм деформирования бетона и арматуры.

Производство бетонных и железобетонных конструкций требует

к себе особого внимания. Во-первых, они отличаются большим разно-

образием видов бетона и арматуры, характера силовых и несиловых воз-

действий, типов конструктивных решений и т. д. Во-вторых, методы рас-

чета и конструирования бетонных и железобетонных конструкций со-

гласно СНиП содержат набор эмпирических зависимостей и конструк-

тивных правил, из которых трудно выделить конкретные положения,

относящиеся к требованиям для стеновых панелей.

При расчете по предельным состояниям степень надежности желе-

зобетонных конструкций в нормативных документах [1] оценивается по-

лувероятностным способом, по которому в расчет вводятся норматив-

ные характеристики материалов и нагрузок, учитывающие их изменчи-

вость с определенной обеспеченностью, а изменчивость остальных фак-

торов учитывается детерминированным путем с помощью обобщенных

коэффициентов надежности.

Такой способ не позволяет оценить надежность железобетонных

конструкций в целом. В связи с этим на комбинате «Братскжелезобетон»

предложена автоматизированная система контроля качества на основе

вероятностных методов, которая позволяет учитывать изменчивость тех-

нологического процесса и ежесменно давать интегральную оценку экс-

плуатационной пригодности выпускаемой продукции. Внедрение тако-

го способа оценки эксплуатационной пригодности стеновых конструк-

ций на стадии изготовления требует выбора оптимальной расчетной

модели по оценке напряженно-деформированного состояния (НДС) ис-

следуемых конструкций и эффективного вероятностного метода, на базе

которого разрабатывается программа и выполняется оценка начальной

надежности стеновых панелей. При этом следует отметить, что расчет

наружных стеновых панелей производится при совместном действии

вертикальной и горизонтальной нагрузок, т. е. на косой изгиб (рис. 1).

Учет недостатков расчета по общим зависимостям СНиП при ис-

следовании НДС стеновых панелей позволяет использовать нелинейно-

деформационную модель с учетом диаграмм деформирования материа-

лов [2, 3].

Сущность данного метода заключается в следующем (рис. 2): по-

перечное сечение разбивается на n элементарных участков бетона с пло-

щадями A

и k элементарных участков арматуры с площадями A

Число участков бетона » 100, число участков арматуры равно числу стер-

жней в сечении. В дальнейшем учет физической нелинейности работы

конструкции основывается на следующих положениях:

используются диаграммы деформирования для бетона и арматуры,

полученные при эталонных испытаниях образцов;

принимается гипотеза плоского деформирования в нормальных

сечениях на всех стадиях загружения;

напряжения в бетоне у

и арматуры у

считают равномерно

распределенными на элементарных площадках A

и A

;

записываются три условия равновесия внешних и внутренних сил

в следующем виде:

Рис. 1. Схема испытания стеновых панелей

на вертикальную и горизонтальную нагрузки

Рис. 2. Схема нормального сечения

по дискретной схеме

Ось симметрии

32 33

RRR

333231

232221

131211

, (1)

или

{

}

{

}

(

)

{

}

{

}

(

)

{

}

SFUSFRF ,,

, (2)

где

{

}

{

}

yxz

MMNF ,,=

– вектор-столбец внешних сил;

{

}

(

)

{

}

SFU , =

}

{

}

yxz

kk ,,e=

– вектор-столбец деформаций, являющийся функцией

внешних сил

{

}

и геометрических характеристик сечения S;

{

}

(

)

{

}

SFR ,

–

матрица жесткости нормального сечения конструкции.

Для реализации данной расчетной модели на основе реальных ди-

аграмм деформирования бетона и арматуры написана программа

DIASTEN по оценке НДС несущих стеновых панелей с учетом нелиней-

ного характера их деформирования, которая готовится к регистрации

в Роспатенте. Для оценки адекватности выбранных расчетных моделей

по описанию фактического НДС стеновых панелей и для контроля каче-

ства их на стадии изготовления разработана программа вероятностного

расчета стеновых панелей, которая позволяет более точно и достоверно

оценить эксплуатационную пригодность исследуемых конструкций.

Анализ сопоставления результатов расчета по разным расчетным

моделям [3] с экспериментальными данными, полученными на комби-

нате «Братскжелезобетон» при натурных испытаниях стеновых панелей,

произведен для более чем шести видов панелей (с разными геометри-

ческими параметрами и армированием). Исходя из анализа рассмотрен-

ных моделей более точно НДС описывает деформационно-нелинейная

модель на основе реальных диаграмм деформирования материалов.

СНиП резко занижает развитие прогибов по сравнению с развитием их

по экспериментальным данным. Анализ показателей надежности [3] так-

же свидетельствует, что по обеим методикам показатели надежности

конструкций дают близкие результаты, которые удовлетворительно со-

гласуются с экспериментальными данными, полученными при оценке

эксплуатационной пригодности исследуемых стеновых панелей.

В заключение следует отметить, что моделирование на ЭВМ явля-

ется наиболее эффективным средством анализа надежности исследуе-

мых конструкций и более точно отражает фактическое НДС конструк-

ций. Учет физической и геометрической нелинейности позволяет более

адекватно оценить разрушающие нагрузки, а также проанализировать

поведение конструкции в аварийных ситуациях.

Список литературы

1. СП 52-10–2003. Бетонные и железобетонные конструкции без

предварительного напряжения арматуры / Свод правил по проектирова-

нию и строительству. – М.: НИИЖБ, 2004. – 70 с.

2. Дудина И. В., Жердева С. А. Особенности расчета стеновых па-

нелей с учетом нелинейных свойств материалов / Материалы межрегио-

нальной научно-технической конференции. – Братск: ГОУ ВПО «БрГУ»,

2003. –73 с.

3. Жердева С. А., Дудина И. В., Чевская Е. А. Анализ результатов

вероятностной оценки эксплуатационной пригодности несущих стено-

вых панелей // Эффективные строительные конструкции: теория и прак-

тика: Сборник статей V Международной научно-технической конферен-

ции. – Пенза, 2006.

Получено 4 апреля 2007 года.

УДК 666.97.033

С. Н. Герасимов, А. С. Беспрозванных, Р. В. Назаров (БрГУ)

ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ПАРАМЕТРОВ ЛОПАСТНЫХ

БЕТОНООТДЕЛОЧНЫХ МАШИН ВИБРАЦИОННОГО ТИПА

Приведен обзор конструкции дискового рабочего органа заглаживающей

машины с вертикальными колебаниями и противоположно вращающимися эле-

ментами диска; уточнена методика определения полной мощности привода, зат-

рачиваемой на обработку поверхности незатвердевшей бетонной смеси заглажи-

вающей машины, и определена заглаживающая способность рабочего органа.

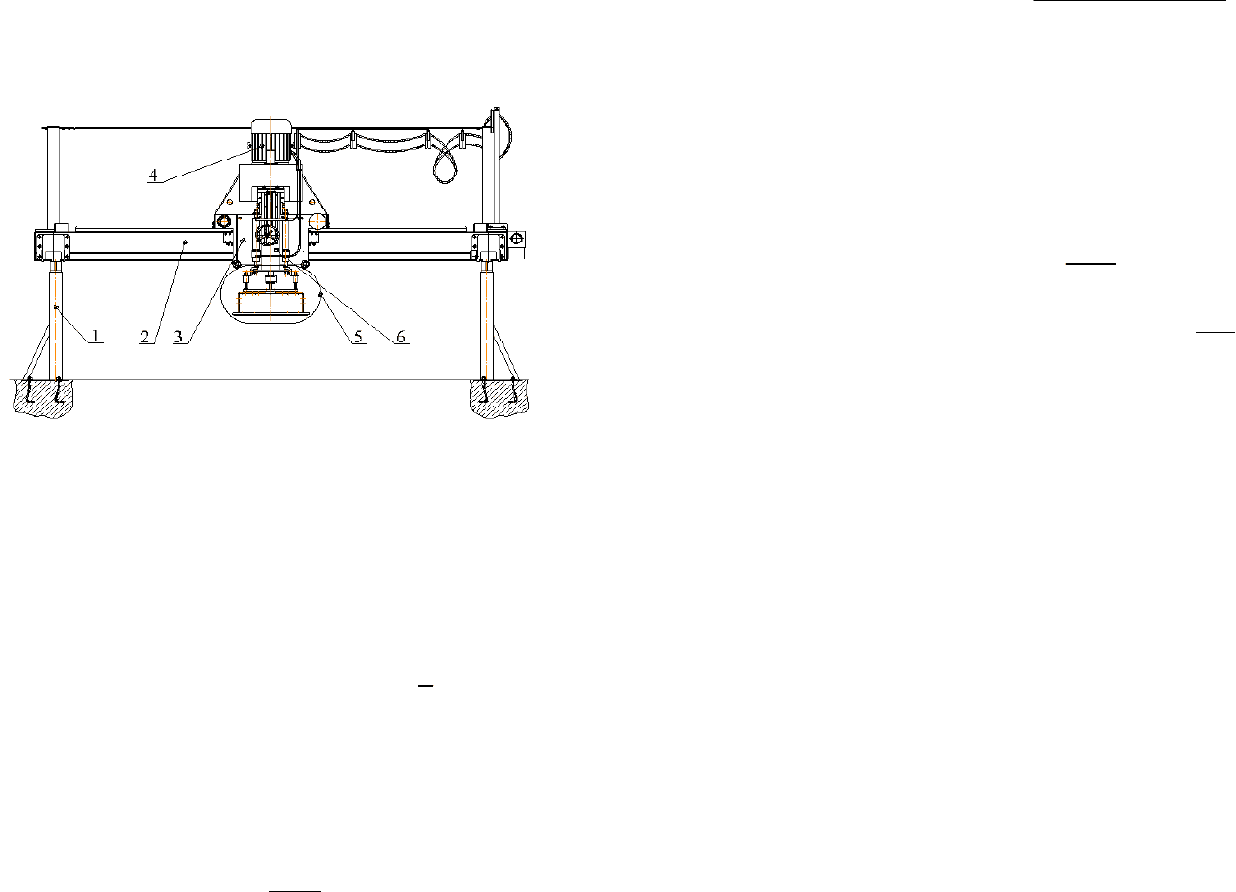
Рабочий орган заглаживающей машины (рис. 1) относится к облас-

ти строительной промышленности и может быть использован для каче-

ственной обработки незатвердевших поверхностей железобетонных из-

делий с получением требуемого класса шероховатости на лицевой по-

Математическое моделирование, численные методы и комплексы

программ. СПб., 2007

34 35

верхности изделий, отформованных из жестких бетонных смесей

не сложной конфигурации в плане и любых геометрических размеров

для гражданского и промышленного строительства.

Получение высокого качества обработки поверхностей и снижение

энергоемкости процесса заглаживания достигаются тем, что рабочий

орган заглаживающего устройства содержит приводной вал, упругую

муфту, дебалансный механизм, демпфер, цилиндрический корпус пла-

нетарного механизма и заглаживающий диск, состоящий из внешнего

кольца и внутреннего диска, вращающихся в противоположных направ-

лениях с разными угловыми скоростями, имеющих в смежной зоне вра-

щения цилиндрические углубления с расположенными в них лопастя-

ми, образуя при этом радиальное кольцо.

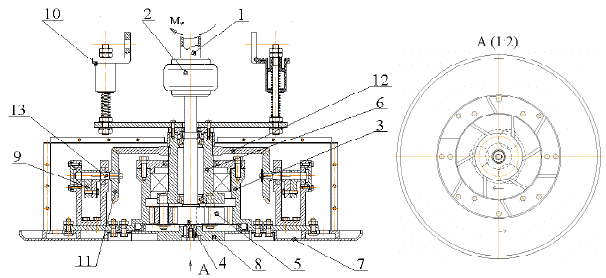
На рис. 1, а показан продольный разрез дискового рабочего органа

заглаживающей машины с вертикальными колебаниями и противопо-

ложно вращающимися элементами диска. Вид рабочего органа снизу

изображен на рис. 1, б.

Дисковый рабочий орган заглаживающей машины с вертикальны-

ми колебаниями и противоположно вращающимися элементами диска

работает следующим образом. При включении электродвигателя через

соединительную муфту 2, планетарному механизму передается враще-

ние с приводного вала 1, который жестко закреплен с внутренним дис-

ком 8 при помощи шпоночного соединения. Планетарный механизм пе-

редает вращательное движение, противоположное направлению враще-

ния приводного вала 1 корпусу 3, который находится в жестком соеди-

нении с внешним кольцом 7 при помощи болтов. Стакан 6 крепится

к каретке заглаживающей машины и в процессе работы рабочего органа

остается неподвижным, на нем установлена коническая шестерня 12,

которая заставляет вращаться коническую шестерню 11 и приводит

в движение дебалансный механизм, который и создает вертикальные ко-

лебания внешнего кольца 7.

При таком воздействии рабочего органа на обрабатываемую повер-

хность происходит передача энергии колебаний нижележащим слоям

бетонной смеси, при этом связи между частицаtми нарушаются, снижа-

ется сопротивление их сдвига. Жесткая заглаживаемая поверхность при-

обретает подвижность, а зерна заполнителя и цемента получают возмож-

ность занять более устойчивое пространственное взаиморасположение,

чем достигается плотная упаковка зерен заполнителя. Одновременно

с этим из бетонной смеси отжимается некоторое количество воды.

а б

Рис. 1. Дисковый рабочий орган заглаживающей машины с

вертикальными колебаниями и противоположно вращающимися

элементами диска:

1 – приводной вал; 2 – упругая муфта; 3 – корпус; 4 – зубчатое колесо;

5 – сателлиты; 6 – стакан; 7 – наружное кольцо; 8 – внутренний диск;

9 – дебалансный механизм; 10 – демпфера; 11 и 12 – конические шестерни;

13 – вал

Дисковый рабочий орган заглаживающей машины с вертикальны-

ми колебаниями и противоположно вращающимися элементами диска

устанавливается на экспериментальную лабораторную установку с це-

лью проверки и подтверждения выводов и заключений теоретических

исследований, а также для дополнительных экспериментальных иссле-

дований при обработке свежеуложенной бетонной поверхности. На рис. 2

представлен общий вид экспериментального стенда дисковой заглажи-

вающей машины. В основе всей конструкции лежит заглаживающая

машина, которая состоит из рамы 1, расположенного на ней подвижного

моста 2, по которому передвигается каретка 3 с установленным на нем

электродвигателем 4 и стандартным приводом 6 с дисковым рабочим

органом 5.

Описанная заглаживающая машина позволит проводить исследо-

вания, связанные с получением оптимальных параметров обработки бе-

тонных поверхностей.

Полная мощность, затрачиваемая на обработку поверхности незат-

вердевшей бетонной смеси заглаживающей машиной, определяется как

3210

NNNN

36 37

где N

– мощность, затрачиваемая на преодоление трения диска с обра-

батываемой бетонной поверхностью при поступательном движении;

– мощность, затрачиваемая на перемещение рабочего органа при по-

ступательном движении; N

– мощность, затрачиваемая на перемешива-

ние бетонной смеси лопастями при обработке бетонной поверхности.

Рис. 2. Общий вид экспериментального стенда дисковой загла-

живающей машины с вертикальными колебаниями и противо-

положно вращающимися элементами диска

Рабочий орган в процессе заглаживания трется не только о бетон-

ную смесь своей нижней плоскостью, но еще и передней кромкой о вол-

ну, движущуюся перед ним. Тогда выражение для определения мощнос-

ти привода (Вт) с учетом его КПД (

) в случае трения будет иметь вид

+D+=

)()(1.2

вдк

тp1

KVVPrRfN

где R – радиус кольца, м; r – радиус диска, м; f

тp

– коэффициент трения;

DP – удельное давление рабочего органа, Па; V

и V

– окружная скорость

кольца и диска, м/с; K

– коэффициент, учитывающий сопротивление

волны бетонной смеси; K

= 1.1.

Мощность, расходуемая на перемещение машины,

зк

где

– КПД трансмиссии; P

– сопротивление качению колес и трению

в подшипниках.

ир2м

)

(

где G

– масса машины, Н;

– коэффициент трения качения (0.03…0.05);

d – диаметр подшипника ходового колеса, м; K

– коэффициент трения

скольжения в ребордах колеса (1.45…2.20); D

– диаметр ходового колеса, м;

– коэффициент трения в подшипниках (0.015…0.1); K

– коэффициент

инерции покоя (3.0…4.0).

Мощность N

, Вт, затрачиваемая на перемешивание бетонной сме-

си лопастным смесителем, определится следующим образом:

)(

н3

N -

где z – число смесительных лопастей;

– коэффициент;

–

коэффициент, учитывающий зависимость между длиной лопасти и ее

шириной;

– объемная масса перемешиваемого раствора, кг/м

; g –

ускорение свободного падения, м/с

; r

, r

– наружный и внутренний

радиус лопасти.

Эффективность воздействия рабочего органа на заглаживаемую

поверхность в основном определяется длиной линии, на протяжении

которой рабочий орган воздействует на каждую точку (элементарную

площадку) обрабатываемой площадки (необходимо также учитывать

возникающие при этом силы трения). Длина этой линии, обозначаемая

через S

р.о

(м), названа «заглаживающей способностью рабочего органа».

);;(

3р.ор.о

DuUfS

где U

р.о

– собственная скорость рабочего органа; u

– скорость

поступательного движения машины; D – диаметр рабочего органа.

Рассматриваемый рабочий орган имеет сложную конструкцию,

состоящую из двух противоположно вращающихся элементов (кольцо

и диск), определяющих сумму заглаживающих способностей для загла-

живающего кольца и заглаживающего диска.

Средняя заглаживающая способность диска может быть определе-

на уравнением

3дд

/94.0 uRuS

Средняя заглаживающая способность кольца может быть опреде-

лена уравнением

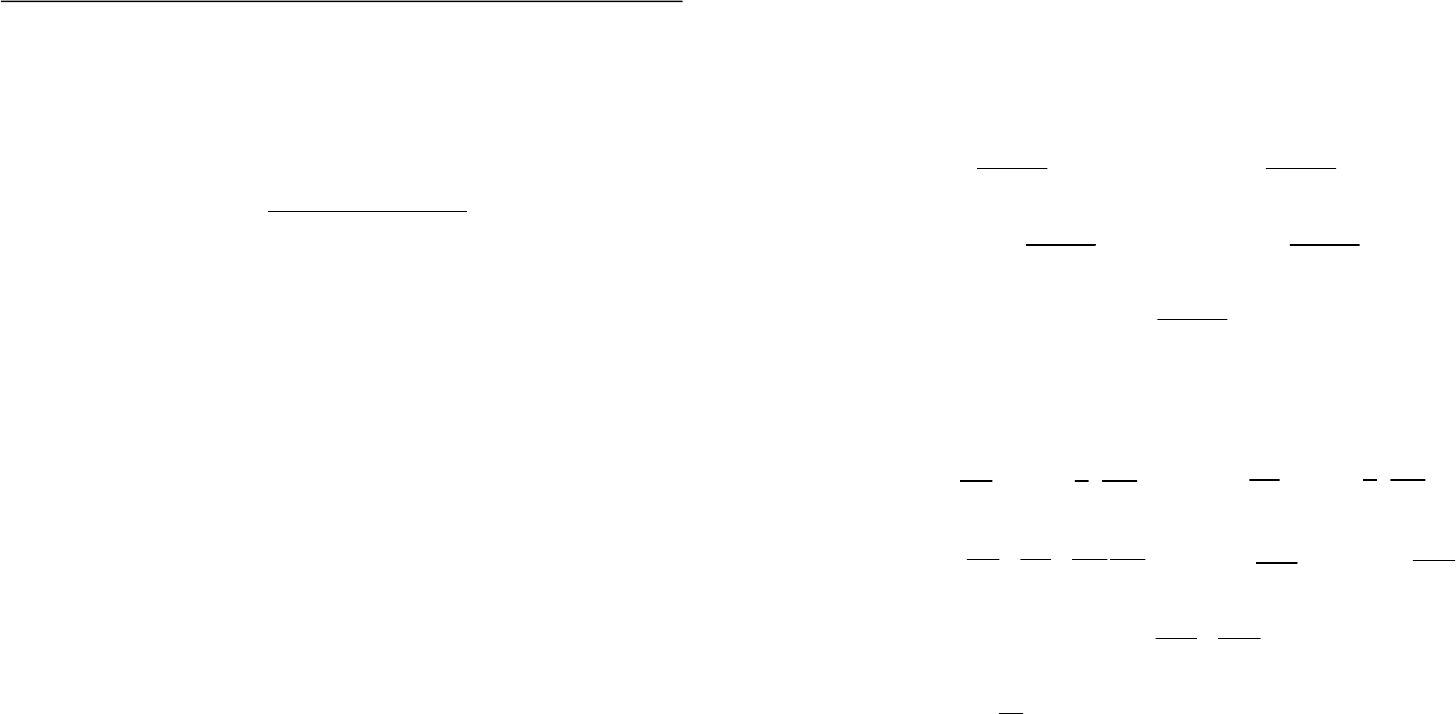
38 39

3кк

/313.0 uRuS

где 0.313 – среднее значение k

; u

– скорость вращения диска; u

– скорость

вращения кольца.

Таким образом, для данного рабочего органа среднюю заглажива-

ющую способность можно определить по следующей формуле:

ккдд

ср

р.о

313.094.0

RuRu

где R

– радиус диска; R

– радиус кольца.

Список литературы

1. Болотный А. В. Заглаживание бетонных поверхностей. – Л.:

Стройиздат. 1979. – 128 с.

2. Мамаев Л. А. Динамические процессы взаимодействия вибраци-

онных заглаживающих машин с обрабатываемой средой. – Иркутск: Изд-

во ИрГТУ, 2006. – 114 с.

Получено 3 апреля 2007 года.

УДК 539.3

Д. Е. Мухин (СПбГАСУ)

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЕФОРМИРОВАНИЯ

ПОЛОГИХ ОБОЛОЧЕК СТУПЕНЧАТО-ПЕРЕМЕННОЙ

ТОЛЩИНЫ С УЧЕТОМ УПРУГОПЛАСТИЧЕСКИХ

ДЕФОРМАЦИЙ

На основе деформационной теории пластичности и геометрической нели-

нейности получена математическая модель деформирования пологих ребристых

оболочек.

Рассматриваются пологие оболочки двойной кривизны, находящи-

еся под действием поперечной нагрузки. Срединная поверхность обо-

лочки принимается за координатную. Оси х и y ортогональной системы

координат направлены по линиям главных кривизн. Ось z – ортогональ-

но координатной поверхности в сторону вогнутости. Со стороны вогну-

тости оболочка подкреплена системой ребер, параллельных координат-

ным линиям.

Будем использовать деформационную теорию пластичности. В этом

случае физические соотношения для оболочек ступенчато-переменной

толщины с учетом поперечных сдвигов принимают вид (изотопный ма-

териал):

)(

)1(

me+e

;

)(

)1(

me+e

;

xyxy

)1(2

;

xzxz

)1(2

; (1)

yzyz

)1(2

где

c+e=e z

;

c+e=e z

;

2 c+g=g z

; (2)

;

; (3)

y¶

Здесь

– секущий модуль упругости, который представляет

собой нелинейную функцию интенсивности деформации

и находит-

ся опытным путем для различных материалов.

Существуют различные аппроксимации

(

)

, например

)(

mE e-e=s

(4)

или

(

)

[

]

iii

, (5)

Математическое моделирование, численные методы и комплексы

программ. СПб., 2007