Математическое моделирование, численные методы и комплексы программ 2007 Вып.13
Подождите немного. Документ загружается.

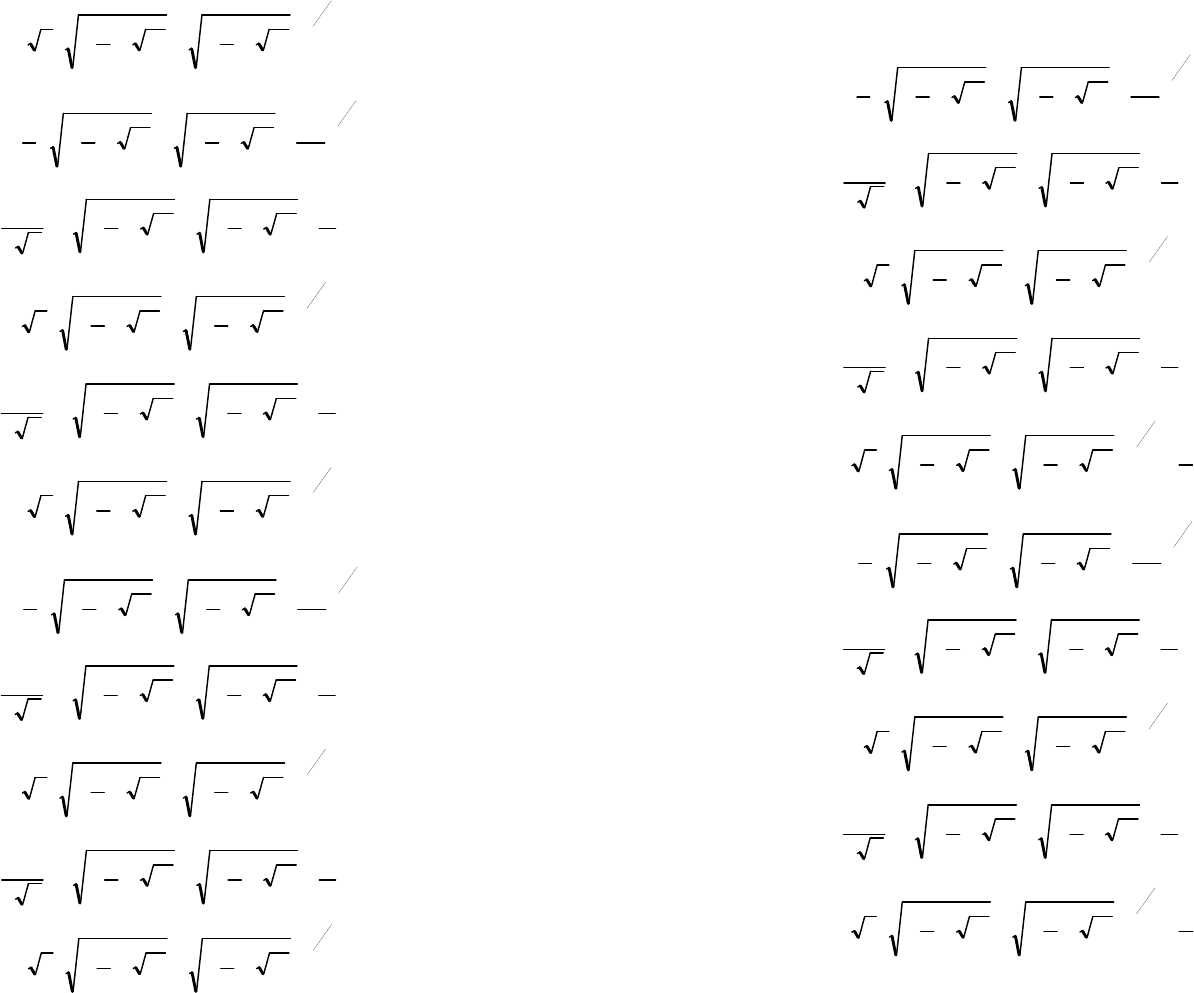
100 101
2
1
33
22
3
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-- D
n
D
n
j
;
+
÷
÷
ø
ö
ç
ç
è
æ
---++--=
2
1
33
3
3
2
222
1 p
D
n
D
n
y
ê
ë
é
+----+--+
322
22
1
33
p
D
n
D
n
-
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-+
2
1
33
22
3 D
n
D
n
j
ê
ë
é
-----+---
322
22
1
33
p
D
n
D
n
2
1
33
22
3
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-- D
n
D
n
j
;
-
÷
÷
ø
ö
ç
ç
è
æ
---++--=
2
1
33
4
3
2
222
1 p
D
n
D
n
y
ê
ë
é
+----+---
322
22
1
33
p
D
n
D
n
+
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-+
2
1
33
22
3 D
n
D
n
j
ê
ë
é
-----+--+
322
22
1
33
p
D
n
D
n
2
1
33
22
3
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-- D
n
D
n
j
,
а учитывая использованную ранее подстановку (4), определить корни
уравнений (3)
+
÷
÷
ø
ö
ç
ç
è
æ
---++-=l
2
1
33
1
3
2
222
1 p
D
n
D
n
ê
ë
é
+----+--+
322
22
1
33
p
D
n
D
n
+
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-+
2
1
33
22
3 D
n
D
n
j
ê
ë
é
-----+--+
322
22
1
33
p
D
n
D
n
422
3
2
1
33
a
D
n
D
n
j -
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+--
;
-
÷
÷
ø
ö
ç
ç
è
æ
---++-=l
2
1
33
2
3
2
222
1 p
D
n
D
n
ê
ë
é
+----+---
322
22
1
33
p
D
n
D
n
-
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-+
2
1
33
22
3 D
n
D
n
j
ê
ë
é
-----+---
322
22
1
33
p
D
n
D
n
422
3
2
1
33
a
D
n
D
n
j -
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+--
;
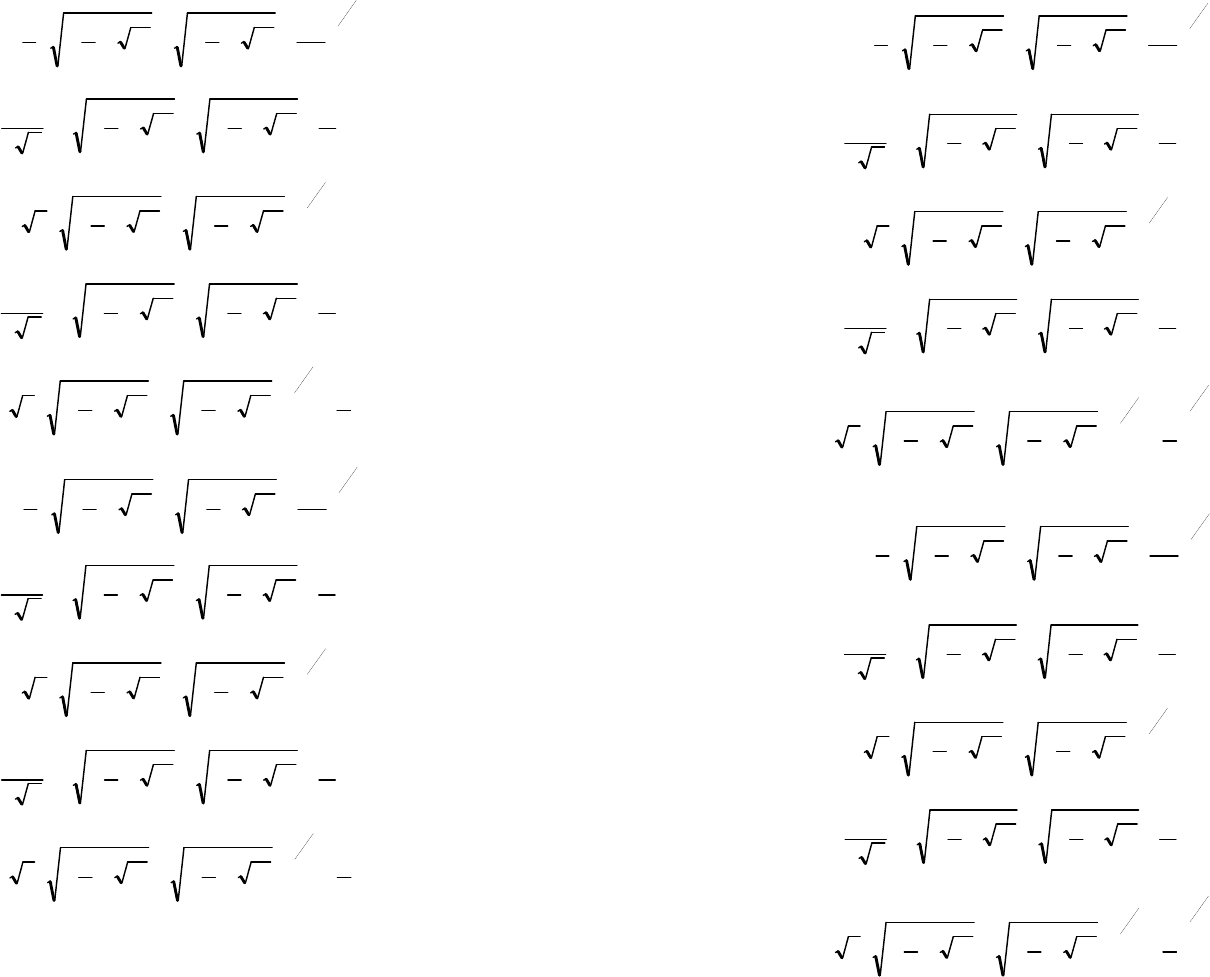
102 103
+
÷
÷
ø
ö
ç
ç
è
æ
---++--=l
2
1
33
3
3
2
222
1 p
D
n
D
n
ê
ë
é
+----+--+
322
22
1
33
p
D
n
D
n
-
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-+
2
1
33
22
3 D
n
D
n
j
ê
ë
é
-----+---
322
22
1
33
p
D
n
D
n
422
3
2
1
33
a
D
n
D
n
j -
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+--
;
-
÷
÷
ø
ö
ç
ç
è
æ
---++--=l
2
1
33
4
3
2
222
1 p
D
n
D
n
ê
ë
é
+----+---
322
22
1
33
p
D
n
D
n
+
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-+
2
1
33
22
3 D
n
D
n
j
ê
ë
é
-----+--+
322
22
1
33
p
D
n
D
n
422
3
2
1
33
a
D
n
D
n
j -
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+--
.
И теперь, наконец, с учетом равенства (2) можно определить корни
характеристического уравнения (1):
ï
î
ï
í
ì
+
÷
÷
ø
ö
ç
ç
è
æ
---++-±=
2
1
33
2,1
3
2
222
1 p
D
n
D
n
x
ê
ë
é
+----+--+
322
22
1
33
p
D
n
D
n
+
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-+
2
1
33
22
3 D
n
D
n
j
ê
ë
é
-----+--+
322
22
1
33
p
D
n
D
n
2
1
2
1
33
422
3
ï
þ
ï
ý
ü
-
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+--
a
D
n
D
n
j
;
ï
î
ï
í
ì
-
÷
÷
ø
ö
ç
ç
è
æ
---++-±=
2
1
33
4,3
3
2
222
1 p
D
n
D
n
x
ê
ë
é
+----+---
322
22
1
33
p
D
n
D
n
-
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-+
2
1
33
22
3 D
n
D
n
j
ê
ë
é
-----+---
322
22
1
33
p
D
n
D
n
2
1
2
1
33
422
3
ï
þ
ï
ý
ü
-
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+--
a
D
n
D
n
j
;
104 105
ï
î
ï
í
ì
+
÷
÷
ø
ö
ç
ç
è
æ
---++--±=
2
1
33
6,5
3
2
222
1 p
D
n
D
n
x
ê
ë
é
+----+--+
322
22
1
33
p
D
n
D
n
-
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-+
2
1
33
22
3 D
n
D
n
j
ê
ë
é
-----+---
322
22
1
33
p
D
n
D
n
2
1
2
1
33
422
3
ï
þ
ï
ý
ü
-
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+--
a
D
n
D
n
j
;
ï
î
ï
í
ì
-
÷
÷
ø
ö
ç
ç
è
æ
---++--±=
2
1
33
8,7
3
2
222
1 p
D
n
D
n
x
ê
ë
é
+----+---
322
22
1
33
p
D
n
D
n
+
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+-+
2
1
33
22
3 D
n
D
n
j
ê
ë
é
-----+--+
322
22
1
33
p
D
n
D
n
2
1
2
1
33
422
3
ï
þ
ï
ý
ü
-
ú
û
ù
÷
÷
ø
ö
ç
ç
è
æ
+--+--
a
D
n
D
n
j
.
Величины постоянных распределения каждой пары волн электро-
магнитного поля определятся следующим образом:
2,11
x=g
n
;
4,32
x=g
n
;
6,53
x=g
n
;
8,74
x=g
n
.
Анализ характеристического уравнения однородного участка рай-
онной электрической сети позволяет оценить физическую сущность элек-
тромагнитных процессов, происходящих в конструктивных элементах
ЛЭП.
Список литературы
1. Большанин Г. А. Способ прогнозирования гармонических состав-
ляющих электрической энергии по неразветвленным участкам электро-
энергетической системы: Патент 2210154. Россия, МКИ
7
Н 02 J 3/01. –
№ 2001106402. Заявл. 06.03.01; опубл. 10.08.03.
2. Корн Г., Корн Т. Справочник по математике для научных работ-
ников и инженеров: Определения, теоремы, формулы. – М.: Наука, 1973.
– 832 с.
3. Бронштейн И. Н., Семендяев К. А. Справочник по математике
для инженеров и учащихся втузов. 13-е изд., испр. – М.: Наука, 1986. –
544 с.
Получено 4 апреля 2007 года.
УДК 621.315.1.001.63
Г. А. Большанин, Л. Ю. Большанина, Т. Г. Коробова, С. И. Харин
(БрГУ)
ОПТИМИЗАЦИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
ОДНОРОДНОГО СИММЕТРИЧНОГО УЧАСТКА
ТРЕХФАЗНОЙ ТРЕХПРОВОДНОЙ ЛЭП В УСЛОВИЯХ
ПОНИЖЕННОГО КАЧЕСТВА ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ
Приведены результаты оптимизации математической модели однородного
симметричного участка трехфазной линии электропередач трехпроводного испол-
нения в условиях пониженного качества электрической энергии. Отмечено умень-
шение громоздкости процедуры оптимизации из-за симметрии анализируемого
участка ЛЭП.
Математическое моделирование, численные методы и комплексы
программ. СПб., 2007
106 107
Симметричной трехфазную систему можно назвать в случае абсо-
лютного (по величине и характеру) равенства продольных и соответству-
ющих поперечных параметров каждого линейного провода между со-
бой на частоте каждой гармонической составляющей напряжения и тока.
Условия ее построения на частоте
n
-й гармонической составляющей
основных характеристик электрической энергии выразятся следующи-
ми равенствами:
nnn
=
=
CBA
RRR
000
;
nnn
=
=
CBA
LLL
000
;
nnn
=
=
CBA
CCC
000
;
nnn
=
=
CABCAB
GGG
000
;
nnn
=
=
CABCAB
MMM
000
;
nnn
=
=
CABCAB
CCC
000
;
nnn
=
=
000000 CBA
GGG
;
nnn
=
=
000000 CBA
CCC
.
Иначе эти равенства можно представить в виде
nnnn
=
=
=
0ф0000000
YYYY
CBA
;
n
n
n
n
=
=
=
л
0
0
0
0
YYYY
CA
BC
AB
;
nnnn
=
=
=
ф0000
ZZZZ
CBA
;
n
n
n
n
=
=
=
м
0
0
0
0
ZZZZ
CA
BC
AB
.
В таком случае несколько упростится процедура определения по-
стоянных распространения каждой пары электромагнитной энергии по
проводам линии электропередач, входящей в состав выделенного участ-
ка ЛЭП. Они определяются из решения характеристического уравнения
однородного участка трехфазной трехпроводной ЛЭП
0
246
=
+
+
+
c
bx
ax
x
,
где в данном случае оказывается, что
(
)
nnnnnn
+
-
-
=
л0м00ф0ф0ф0
213 YZYZYZa
л
;
[
+
-
-
-
=
nnnnnn л0м00ф00ф0ф0
44213 YZYZYZb
л
(
)
--++
nnnnnn
2
л0м00ф00ф0ф0
22 YZYZYZ
л
(
)
]
2
л0м00ф0м00л0ф0 nnnnnn
--- YZYZYZ
;
++--=
nnnnnn
2
0л0
2
м0л0ф0ф0ф0
6631 YZYZYZc
(
)
--++
nnnnnn
2
л0м0л0ф00ф0ф0
223 YZYZYZ
(
)
----
nnnnnn
2
л0м00ф0м00л0ф0
3 YZYZYZ
(
)
+-+-
nnnnnn
3
л0м00ф00ф0ф0
22 YZYZYZ
л
(
)
(
-
-
+
+
nnnnnnnn 0л0ф0л0м0л0ф00ф0ф0
223 YZYZYZYZ
)
---
nnnn
2
л0м00ф0м0
YZYZ
(
)
3
л0м00ф0м00л0ф0
2
nnnnnn
--- YZYZYZ
.
Собственные волновые сопротивления для каждой пары волн элек-
тромагнитной энергии в линейных проводах здесь оказываются тоже
одинаковыми:
n
n
n
n
=
=
=
1
1
1
1
с
сC
сB
сA
ZZZZ
;
n
n
n
n
=
=
=
2
2
2
2
с
сC
сB
сA
ZZZZ
;
n
n
n
n
=
=
=
3
3
3
3
с
сC
сB
сA
ZZZZ
.
О взаимных волновых сопротивлениях, которые проявляются лишь
при равновеликости магнитных связей между проводами ЛЭП, здесь
говорить не приходится.
С учетом этих равенств фазные и линейные напряжения и токи в
конце участка ЭЭС, отстающего от начала этого же участка на расстоя-
ние
l
, при условии известности спектрального состава основных харак-
теристик в начале выделенного участка и абсолютной симметрии фаз-
ных проводов оказываются следующими:
-g+g-g=
nnn
n
nnnn
lUlZIlUU
A
c
AAA 211
1
111
chshch
&&&&
lZIlUlZI
с
c
AA
c
A n
n
nnnn
n
n
g-g+g-
3
3
1312
2
1
shchsh
&
&
&
;
-g+g-g=
nnn
n
nnnn
lUlZIlUU
B
c
BBB 211
1
111
chshch
&
&
&
&
lZIlUlZI
с
c
BB
c
B n
n
nnnn
n
n
g-g+g-
3
3
1312
2
1
shchsh
&&&
;
-g+g-g=
nnn
n
nnnn
lUlZIlUU
C
c
CCC 211
1
111
chshch
&
&
&
&
lZIlUlZI
с
c
CC
c
C n
n
nnnn
n
n
g-g+g-
3
3
1312
2
1
shchsh
&&&
;
(
)
(
)
+g--g-=
n
n
nnnnnn
lZIIlUUU
c
BABAAB 1
1
11111
shch
&
&
&
&
&
(
)
(
)
+g--g-+
n
n
nnnnn
lZIIlUU
c
BABA 2
2
11211
shch
&&&&
(
)
(
)
lZIIlUU
c
BABA n
n
nnnnn
g--g-+
3
3
11311
shch
&
&
&
&
;
(
)
(
)
+g--g-=
n
n
nnnnnn
lZIIlUUU
c
CBCBBС 1
1
11111
shch
&&&&&
(
)
(
)
+g--g-+
n
n
nnnnn
lZIIlUU
c
CBCB 2
2
11211
shch
&
&
&
&
(
)
(
)
lZIIlUU
c
CBCB n
n
nnnnn
g--g-+
3
3
11311
shch
&
&
&
&
;

108 109
(
)
(
)
+g--g-=
n
n
nnnnnn
lZIIlUUU
c
ACACСA 1
1
11111
shch
&&&&&
(
)
(
)
+g--g-+
n
n
nnnnn
lZIIlhUU
c
ACAC 2
2
11211
shch
&
&
&
&
(
)
(
)
lZIIlUU
c
ACAC n
n
nnnnn
g--g-+
3
3
11311
shch
&&&&
;
l
Z
U
lII
c
A
AA n
n
n
nnn
g-g=
1
1
1
11
shch
&
&&
+g-g+
n
n
n
nn
l
Z
U
lI
c
A
A 2
2
1
21
shch
&
&
l
Z
U
lI
c
A
A n
n
n
nn
g-g+
3
3
1
31
shch
&
&
;
+g-g=
n
n
n
nnn
l
Z
U
lII
c
B
BB 1
1
1
11
shch
&
&&
+g-g
n
n
n
nn
l
Z
U
lI
c
B
B 2
2
1
21
shch
&
&
l
Z
U
lI
c
B
B n
n
n
nn
g-g+
3
3
1
31
shch
&
&
;
l
Z
U
lII
c
C
CC n
n
n
nnn
g-g=
1
1
1
11
shch
&
&&
+g-g+
n
n
n
nn
l
Z
U
lI
c
C
C 2
2
1
21
shch
&
&
l
Z
U
lI
c
A
C n
n
n
nn
g-g+
3
3
1
31
shch
&
&
,
где
nA
U
1
&
,
nB
U
1
&
,
nC
U
1
&
и
nA
I
1
&
,
nB
I
1
&
,
nC
I
1
&
– изображения на комплекснойсной
плоскости фазных напряжений и линейных токов на частоте
n
-й
гармонической составляющей в начале выделенного участка ЛЭП;
n
g
1
,
n
g
2
и
n
g
3
– постоянные распространения волн электромагнитного поляля
по проводам ЛЭП;
l
– протяженность анализируемого участка от егоо
начала до места определения напряжений и токов.
При известном спектральном составе основных характеристик элек-
трической энергии в конце анализируемого участка ЛЭП фазные и ли-
нейные напряжения и токи в любом месте, отстоящем от конца выде-
ленного участка на расстоянии
y
, следует определять по формулам
yZIyUU
c
AAA n
n
nnnn
g+g=
1
1
212
shсh
&
&
&
+g+g+
n
n
nnn
yZIyU
c
AA 2
2
222
shсh
&
&
yZIyU
с
c
AA n
n
nnn
g+g+
3
3
232
shсh
&
&
;
yZIyUU
c
BBB n
n
nnnn
g+g=
1
1
212
shсh
&&&
+g+g+
n
n
nnn
yZIyU
c
BB 2
2
222
shсh
&&
yZIyU
с
c
BB n
n
nnn
g+g+
3
3
232
shсh
&
&
;
+g+g=
n
n
nnnn
yZIyUU
c
CCC 1
1
212
shсh
&&&
yZIyU
c
CC n
n
nnn
g+g+
2
2
222
shсh
&
&
yZIyU
с
c
CC n
n
nnn
g+g+
3
3
232
shсh
&
&
;
(
)
(
)
+g-+g-=
n
n
nnnnnn
yZIIlUUU
c
BABAAB 1
1
22122
shсh
&&&&&
(
)
(
)
+g-+g-+
n
n
nnnnn
yZIIyUU
c
BABA 2
2
22222
shсh
&
&
&
&
(
)
(
)
yZIIyUU
c
BABA n
n
nnnnn
g-+g-+
3
3
22322
shсh
&&&&
;
(
)
(
)
+g-+g-=
n
n
nnnnnn
yZIIlUUU
c
CBCBBС 1
1
22122
shсh
&&&&&
(
)
(
)
+g-+g-+
n
n
nnnnn
yZIIyUU
c
CBCB 2
2
22222
shсh
&
&
&
&
(
)
(
)
yZIIyUU
c
CBCB n
n
nnnnn
g-+g-+
3
3
22322
shсh
&&&&
;
(
)
(
)
+g-+g-=
n
n
nnnnnn
yZIIlUUU
c
ACACCA 1
1
22122
shсh
&
&
&
&
&
(
)
(
)
+g-+g-+
n
n
nnnnn
yZIIyUU
c
ACAC 2
2
22222
shсh
&&&&
(
)
(
)
yZIIyUU
c
ACAC n
n
nnnnn
g-+g-+
3
3
22322
shсh
&
&
&
&
;
y
Z
U
yII
c
A
AA n
n
n
nnn
g+g=
1
1
2
12
shсh
&
&&
+g+g+
n
n
n
nn
y
Z
U
yI
c
A
A 2
2
2
22
shсh
&
&
y
Z
U
yI
c
A
A n
n
n
nn
g+g+
3
3
2
32
shсh
&
&
;
y
Z
U
yII
c
B
BB n
n
n
nnn
g+g=
1
1
2
12
shсh
&
&&
+g+g+
n
n
n
nn
y
Z
U
yI
c
B
B 2
2
2
22
shсh
&
&
y
Z
U
yI
c
B
B n
n
n
nn
g+g+
3
3
2
32
shсh
&
&
;
y
Z
U
yII
c
С
СС n
n
n
nnn
g+g=
1
1
2
12
shсh
&
&&
+g+g+
n
n
n
nn
y
Z
U
yI
c
С
С 2
2
2
22
shсh
&
&
y
Z
U
yI
c
С
С n
n
n
nn
g+g+
3
3
2
32
shсh
&
&
,

110 111
где
nA
U
2
&
,
nB
U
2
&
,
nC
U
2
&
и
nA
I
2
&
,
nB
I
2
&
,
nC
I
2
&
– изображения на комплекснойсной
плоскости фазных напряжений и линейных токов на частоте
n
-й гармо-
нической составляющей в конце выделенного участка ЛЭП.
Судя по приведенным здесь равенствам, снижение громоздкости
процесса прогнозирования распределения основных характеристик элек-
трической энергии вследствие достижения симметрии на анализируе-
мом участке ЛЭП весьма существенное. Это следует из сопоставления
полученных здесь результатов оптимизации математической модели
с результатами подобной оптимизации математической модели распре-
деления электрической энергии пониженного качества по несимметрич-
ному участку трехфазной трехпроводной ЛЭП [1].
На первый взгляд кажется, что можно объединить ранее известные
величины напряжений и токов соответствующих частот, например, че-
рез оператор поворота. Но такая операция будет возможна лишь при ра-
венстве соответствующих фазных и линейных напряжений и токов меж-
ду собой по модулю. В этом случае симметричной должна быть вся элек-
троэнергетическая система, что практически невозможно или, по мень-
шей мере, маловероятно.
Список литературы
1. Большанин Г. А. Распределение электрической энергии пониженно-
го качества по участкам электроэнергетической системы // Труды Братского
государственного университета: Сер. Естественные и инженерные науки –
развитию регионов Сибири. Братск: БрГУ, 2006. – Т. 2. – С. 129–140.
Получено 4 апреля 2007 года.
УДК 621.315.1.001.63
Г. А. Большанин, Л. Ю. Большанина, С. И. Харин (БрГУ)
ОПТИМИЗАЦИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
СИММЕТРИЧНОГО ОДНОРОДНОГО УЧАСТКА РАЙОННОЙ
СЕТИ В УСЛОВИЯХ ПОНИЖЕННОГО КАЧЕСТВА
ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ
Приведены результаты оптимизации математической модели однородного
симметричного участка трехфазной линии электропередач четырехпроводного
Математическое моделирование, численные методы и комплексы
программ. СПб., 2007
исполнения в условиях пониженного качества электрической энергии. Отмечено
уменьшение громоздкости процедуры оптимизации из-за симметрии анализируе-
мого участка ЛЭП.
Районные электрические сети, как правило, представляют собой
трехфазные четырехпроводные линии электропередач (ЛЭП), или ли-
нии с изолированной нейтралью.
Выделенный участок электроэнергетической системы можно счи-
тать симметричным, если продольные и поперечные параметры каждо-
го линейного провода на частоте каждой гармонической составляющей
напряжения и тока равны между собой по величине и по характеру.
То есть должны соблюдаться равенства
nnn
=
=
CBA
RRR
000
;
nnn
=
=
CBA
LLL
000
;
nnn
=
=
CBA
CCC
000
;
nnn
=
=
CABCAB
GGG
000
;
nnn
=
=
CABCAB
MMM
000
;
nnn
=
=
CABCAB
CCC
000
;
nnn
=
=
CNBNAN
GGG
000
;
nnn
=
=
CNBNAN
MMM
000
;
nnn
=
=
CNBNAN
CCC
000
;
nnn
=
=
000000 CBA
GGG
;
nnn
=
=
000000 CBA
CCC
.
В реальных линиях электропередач, даже если они и считаются
симметричного исполнения, продольные и поперечные параметры фаз-
ных и нейтрального проводов могут оказаться неодинаковыми.
Эти равенства можно представить и в ином виде:
nnnn
=
=
=
0ф0000000
YYYY
CBA
;
n
n
n
n
=
=
=
л
0
0
0
0
YYYY
CA
BC
AB
;
nnnn
=
=
=
ф0000
ZZZZ
CBA
;
n
n
n
n
=
=
=
м
0
0
0
0
ZZZZ
CA
BC
AB
;
nnnn
=
=
=
NCNBNAN
YYYY
ф0000
;
nnnn
=
=
=
NCNBNAN
ZZZZ
ф0000
.
Постоянные распространения электромагнитной энергии по про-
водам ЛЭП следует определять из характеристического уравнения одно-
родного участка районной электрической цепи на частоте каждой гар-
монической составляющей напряжения и тока
0
2468
=
+
+
+
+
d
cx
bx
ax
x
,
где a , b, c и d – коэффициенты, учитывающие первичные параметры
однородного участка анализируемой ЛЭП на частоте
n
-й гармонической
составляющей напряжения и тока.
При этом собственные волновые сопротивления фазных проводов
для каждой разновидности электромагнитных волн оказываются одина-
ковыми:
112 113
nnnn
=
=
=
1
1
1
1
c
cC
cB
cA
ZZZZ
;
nnnn
=
=
=
2
2
2
2
c
cC
cB
cA
ZZZZ
;
nnnn
=
=
=
3
3
3
3
c
cC
cB
cA
ZZZZ
;
nnnn
=
=
=
4
4
4
4
c
cC
cB
cA
ZZZZ
.
О взаимных волновых сопротивлениях симметричного участка ЛЭП
здесь не может быть и речи, поскольку эти величины имеют сколько-
нибудь заметные значения лишь при разновеликих электромагнитных
связях между проводами.
В таком случае при условии известности напряжений и токов на
частоте n-й гармонической составляющей в начале рассматриваемого
участка основные характеристики электрической энергии на расстоянии
l
от его начала следует определять так:
+g-g=
n
n
nnnn
lZIlUU
c
AAA 1
1
111
shch
&&&
+g-g
n
n
nnn
lZIlU
c
AA 2
2
121
shch
&&
+g-g+
n
n
nnn
lZIlU
c
AA 3
3
131
shch
&
&
lZIlU
c
AA n
n
nnn
g-g
4
4
141
shch
&
&
;
+g-g=
n
n
nnnn
lZIlUU
c
BBB 1
1
111
shch
&
&
&
+g-g
n
n
nnn
lZIlU
c
BB 2
2
121
shch
&
&
+g-g+
n
n
nnn
lZIlU
c
BB 3
3
131
shch
&
&
lZIlU
c
BB n
n
nnn
g-g
4
4
141
shch
&
&
;
+g-g=
n
n
nnnn
lZIlUU
c
CCC 1
1
111
shch
&
&
&
+g-g
n
n
nnn
lZIlU
c
CC 2
2
121
shch
&
&
+g-g+
n
n
nnn
lZIlU
c
CC 3
3
131
shch
&
&
lZIlU
c
CC n
n
nnn
g-g
4
4
141
shch
&
&
;
+g+g=
n
n
nnnn
lZIlUU
cN
NNN 1
1
111
shch
&
&
&
+g+g
n
n
nnn
lZIlU
cN
NN 2
2
121
shch
&
&
+g+g+
n
n
nnn
lZIlU
cN
NN 3
3
131
shch
&
&
lZIlU
cN
NN n
n
nnn
g+g
4
4
141
shch
&
&
;
(
)
(
)
+g--g-=
n
n
nnnnnn
lZIIlUUU
c
BABAAB 1
1
11111
shch
&
&
&
&
&
(
)
(
)
+g--g-+
n
n
nnnnn
lZIIlUU
c
BABA 2
2
11211
shch
&
&
&
&
(
)
(
)
+g--g-+
n
n
nnnnn
lZIIlUU
c
BABA 3
3
11311
shch
&&&&
(
)
(
)
lZIIlUU
c
BABA n
n
nnnnn
g--g-+
4
4
11411
shch
&&&&
;
(
)
(
)
+g--g-=
n
n
nnnnnn
lZIIlUUU
c
CBCBBC 1
1
11111
shch
&
&
&
&
&
(
)
(
)
+g--g-+
n
n
nnnnn
lZIIlUU
c
CBCB 2
2
11211
shch
&
&
&
&
(
)
(
)
+g--g-+
n
n
nnnnn
lZIIlUU
c
CBCB 3
3
11311
shch
&
&
&
&
(
)
(
)
lZIIlUU
c
CBCB n
n
nnnnn
g--g-+
4
4
11411
shch
&
&
&
&
;
(
)
(
)
+g--g-=
n
n
nnnnnn
lZIIlUUU
c
ACACCA 1
1
11111
shch
&
&
&
&
&
(
)
(
)
+g--g-+
n
n
nnnnn
lZIIlUU
c
ACAC 2
2
11211
shch
&
&
&
&
(
)
(
)
+g--g-+
n
n
nnnnn
lZIIlUU
c
ACAC 3
3
11311
shch
&
&
&
&
(
)
(
)
lZIIlUU
c
ACAC n
n
nnnnn
g--g-+
4
4
11411
shch
&
&
&
&
;
(
)
(
)
+g+-g-=
n
n
n
n
nnnnn
lZIZIlUUU
cN
N
c
ANAAN 1
1
1
1
1111
shch
&
&
&
&
&
(
)
(
)
+g+-g-+
n
n
n
n
nnnn
lZIZIlUU
cN
N
c
ANA 2
2
1
2
1211
shch
&&&&
(
)
(
)
+g+-g-+
n
n
n
n
nnnn
lZIZIlUU
cN
N
c
ANA 3
3
1
3
1311
shch
&
&
&
&
(
)
(
)
lZIZIlUU
cN
N
c
ANA n
n
n
n
nnnn
g+-g-+
4
4
1
4
1411
shch
&
&
&
&
;
(
)
(
)
+g+-g-=
n
n
n
n
nnnnn
lZIZIlUUU
cN
N
c
BNBBN 1
1
1
1
1111
shch
&
&
&
&
&
(
)
(
)
+g+-g-+
n
n
n
n
nnnn
lZIZIlUU
cN
N
c
BNB 2
2
1
2
1211
shch
&&&&
(
)
(
)
+g+-g-+
n
n
n
n
nnnn
lZIZIlUU
cN
N
c
BNB 3
3
1
3
1311
shch
&
&
&
&
(
)
(
)
lZIZIlUU
cN
N
c
BNB n
n
n
n
nnnn
g+-g-+
4
4
1
4
1411
shch
&
&
&
&
;
(
)
(
)
+g+-g-=
n
n
n
n
nnnnn
lZIZIlUUU
cN
N
c
CNCCN 1
1
1
1
1111
shch
&
&
&
&
&
(
)
(
)
+g+-g-+
n
n
n
n
nnnn
lZIZIlUU
cN
N
c
CNC 2
2
1
2
1211
shch
&
&
&
&
(
)
(
)
+g+-g-+
n
n
n
n
nnnn
lZIZIlUU
cN
N
c
CNC 3
3
1
3
1311
shch
&
&
&
&
(
)
(
)
lZIZIlUU
cN
N
c
CNC n
n
n
n
nnnn
g+-g-+
4
4
1
4
1411
shch
&
&
&
&
;
+g-g=
n
n
n
nnn
l
Z
U
lII
c
A
AA 1
1
1
11
shch
&
&&
+g-g
n
n
n
nn
l
Z
U
lI
c
A
A 2
2
1
21
shch
&
&
+g-g+
n
n
n
nn
l
Z
U
lI
c
A
A 3
3
1
31
shch
&
&
l
Z
U
lI
c
A
A n
n
n
nn
g-g
4
4
1
41
shch
&
&
;
+g-g=
n
n
n
nnn
l
Z
U
lII
c
B
BB 1
1
1
11
shch
&
&&
+g-g
n
n
n
nn
l
Z
U
lI
c
B
B 2
2
1
21
shch
&
&
+g-g+
n
n
n
nn
l
Z
U
lI
c
B
B 3
3
1
31
shch
&
&
l
Z
U
lI
c
B
B n
n
n
nn
g-g
4
4
1
41
shch
&
&
;

114 115
+g-g=
n
n
n
nnn
l
Z
U
lII
c
C
CC 1
1
1
11
shch
&
&&
+g-g
n
n
n
nn
l
Z
U
lI
c
C
C 2
2
1
21
shch
&
&
+g-g+
n
n
n
nn
l
Z
U
lI
c
C
C 3
3
1
31
shch
&
&
l
Z
U
lI
c
C
C n
n
n
nn
g-g
4
4
1
41
shch
&
&
;
+g+g=
n
n
n
nnn
l
Z
U
lII
cN
N
NN 1
1
1
11
shch
&
&&
+g+g
n
n
n
nn
l
Z
U
lI
cN
N
N 2
2
1
21
shch
&
&
+g+g+
n
n
n
nn
l
Z
U
lI
cN
N
N 3
3
1
31
shch
&
&
l
Z
U
lI
cN
N
N n
n
n
nn
g+g
4
4
1
41
shch
&
&
,
где
nA
U
1
&
,
nB
U
1
&
,
nC
U
1
&
,
nN
U
1
&
и
nA
I
1
&
,
nB
I
1
&
,
nC
I
1
&
,
nN
I
1
&
– изображения наения на
комплексной плоскости фазных напряжений и линейных токов, а также
напряжения и тока в нейтральном проводе на частоте
n
-й гармонической
составляющей в начале выделенного участка ЛЭП;
n
g
1
,
n
g
2
,
n
g
3
и
n
g
4
–
постоянные распространения волн электромагнитного поля по проводам
ЛЭП.
Если известны напряжение и токи на частоте n-й гармонической
составляющей в конце рассматриваемого симметричного участка ЭЭС,
то основные характеристики электрической энергии на этой же частоте
на расстоянии
y
от конца анализируемого участка определяют следую-
щим образом:
+g+g=
n
n
nnnn
yZIyUU
c
AAA 1
1
212
shch
&&&
+g+g
n
n
nnn
yZIyU
c
AA 2
2
222
shch
&&
+g+g+
n
n
nnn
yZIyU
c
AA 3
3
232
shch
&&
yZIlU
c
AA n
n
nnn
g+g
4
4
242
shch
&&
;
yZIyUU
c
BBB n
n
nnnn
g+g=
1
1
212
shch
&&&
+g+g+
n
n
nnn
yZIlU
c
BB 2
2
222
shch
&&
yZIyU
c
BB n
n
nnn
g+g+
3
3
232
shch
&&
yZIlU
c
BB n
n
nnn
g+g+
4
4
242
shch
&&
;
yZIyUU
c
CCC n
n
nnnn
g+g=
1
1
212
shch
&&&
+g+g+
n
n
nnn
yZIlU
c
CC 2
2
222
shch
&&
yZIyU
c
CC n
n
nnn
g+g+
3
3
232
shch
&&
yZIlU
c
CC n
n
nnn
g+g+
4
4
242
shch
&&
;
+g-g=
n
n
nnnn
yZIyUU
cN
NNN 1
1
212
shch
&&&
+g-g
n
n
nnn
yZIyU
cN
NN 2
2
222
shch
&&
yZIyU
cN
NN n
n
nnn
g-g+
3
3
232
shch
&&
yZIyU
cN
NN n
n
nnn
g-g+
4
4
242
shch
&&
;
(
)
(
)
+g-+g-=
n
n
nnnnnn
yZIIyUUU
c
BABAAB 1
1
22122
shch
&
&
&
&
&
(
)
(
)
+g-+g-+
n
n
nnnnn
yZIIlUU
c
BABA 2
2
22222
shch
&
&
&
&
(
)
(
)
+g-+g-+
n
n
nnnnn
ysZIIyUU
c
BABA 3
3
22322
hch
&
&
&
&
(
)
(
)
yZIIlUU
c
BABA n
n
nnnnn
g-+g-+
4
4
22422
shch
&
&
&
&
;
(
)
(
)
+g-+g-=
n
n
nnnnnn
yZIIyUUU
c
CBCBBC 1
1
22122
shch
&
&
&
&
&
(
)
(
)
+g-+g-+
n
n
nnnnn
yZIIyUU
c
CBCB 2
2
22222
shch
&
&
&
&
(
)
(
)
+g-+g-+
n
n
nnnnn
yZIIyUU
c
CBCB 3
3
22322
shch
&
&
&
&
(
)
(
)
yZIIlUU
c
CBCB n
n
nnnnn
g-+g-+
4
4
22422
shch
&
&
&
&
;
(
)
(
)
+g-+g-=
n
n
nnnnnn
yZIIyUUU
c
ACACCA 1
1
22122
shch
&
&
&
&
&
(
)
(
)
+g-+g-+
n
n
nnnnn
yZIIyUU
c
ACAC 2
2
22222
shch
&
&
&
&
(
)
(
)
+g-+g-+
n
n
nnnnn
yZIIyUU
c
ACAC 3
3
22322
shch
&
&
&
&
(
)
(
)
yZIIyUU
c
ACAC n
n
nnnnn
g-+g-+
4
4
22422
shch
&
&
&
&
;
(
)
(
)
+g++g-=
n
n
n
n
nnnnn
yZIZIyUUU
cN
N
c
ANAAN 1
1
2
1
2122
shch
&
&
&
&
&
(
)
(
)
+g++g-+
n
n
n
n
nnnn
yZIZIyUU
cN
N
c
ANA 2
2
2
2
2222
shch
&
&
&
&
(
)
(
)
+g++g-+
n
n
n
n
nnnn
yZIZIyUU
cN
N
c
ANA 3
3
2
3
2322
shch
&
&
&
&
(
)
(
)
yZIZIyUU
cN
N
c
ANA n
n
n
n
nnnn
g++g-+
4
4
2
4
2422
shch
&
&
&
&
;
(
)
(
)
+g++g-=
n
n
n
n
nnnnn
yZIZIyUUU
cN
N
c
BNBBN 1
1
2
1
2122
shch
&
&
&
&
&
(
)
(
)
+g++g-+
n
n
n
n
nnnn
yZIZIyUU
cN
N
c
BNB 2
2
2
2
2222
shch
&
&
&
&
(
)
(
)
+g++g-+
n
n
n
n
nnnn
yZIZIyUU
cN
N
c
BNB 3
3
2
3
2322
shch
&
&
&
&
(
)
(
)
yZIZIyUU
cN
N
c
BNB n
n
n
n
nnnn
g++g-+
4
4
2
4
2422
shch
&
&
&
&
;
(
)
(
)
+g++g-=
n
n
n
n
nnnnn
yZIZIyUUU
cN
N
c
CNCCN 1
1
2
1
2122
shch
&
&
&
&
&
(
)
(
)
+g++g-+
n
n
n
n
nnnn
yZIZIyUU
cN
N
c
CNC 2
2
2
2
2222
shch
&
&
&
&

116 117
(
)
(
)
+g++g-+
n
n
n
n
nnnn
yZIZIyUU
cN
N
c
CNC 3
3
2
3
2322
shch
&
&
&
&
(
)
(
)
yZIZIyUU
cN
N
c
CNC n
n
n
n
nnnn
g++g-+
4
4
2
4
2422
shch
&
&
&
&
;
y
Z
U
yII
c
A
AA n
n
n
nnn
g+g=
1
1
2
12
shch
&
&&
+g+g+
n
n
n
nn
y
Z
U
yI
c
A
A 2
2
2
22
shch
&
&
y
Z
U
yI
c
A
A n
n
n
nn
g+g+
3
3
2
32
shch
&
&
y
Z
U
yI
c
A
A n
n
n
nn
g+g+
4
4
2
42
shch
&
&
;
y
Z
U
yII
c
B
BB n
n
n
nnn
g+g=
1
1
2
12
shch
&
&&
+g+g+
n
n
n
nn
y
Z
U
yI
c
B
B 2
2
2
22
shch
&
&
+g+g+
n
n
n
nn
y
Z
U
yI
c
B
B 3
3
2
32
shch
&
&
y
Z
U
yI
c
B
B n
n
n
nn
g+g
4
4
2
42
shch
&
&
;
+g+g=
n
n
n
nnn
y
Z
U
yII
c
C
CC 1
1
2
12
shch
&
&&
+g+g
n
n
n
nn
y
Z
U
yI
c
C
C 2
2
2
22
shch
&
&
+g+g+
n
n
n
nn
y
Z
U
yI
c
C
C 3
3
2
32
shch
&
&
y
Z
U
yI
c
C
C n
n
n
nn
g+g
4
4
2
42
shch
&
&
;
+g-g=
n
n
n
nnn
y
Z
U
yII
cN
N
NN 1
1
2
12
shch
&
&&
+g-g
n
n
n
nn
y
Z
U
yI
cN
N
N 2
2
2
22
shch
&
&
+g-g+
n
n
n
nn
y
Z
U
yI
cN
N
N 3
3
2
32
shch
&
&
y
Z
U
yI
cN
N
N n
n
n
nn
g-g
4
4
2
42
shch
&
&
,
где
nA
U
2
&
,
nB
U
2
&
,
nC
U
2
&
,
nN
U
2
&
и
nA
I
2
&
,
nB
I
2
&
,
nC
I
2
&
,
nN
I
2
&
– изображения наения на
комплексной плоскости фазных напряжений и линейных токов, а также
напряжения и тока в нейтральном проводе на частоте v-й гармонической
составляющей в конце выделенного участка ЛЭП.
Таким образом, получается, что факт симметрии выделенного уча-
стка ЛЭП достаточно существенно снижает громоздкость процедуры
прогнозирования распространения электромагнитных волн.
Получено 3 апреля 2007 года.
Математическое моделирование, численные методы и комплексы
программ. СПб., 2007
УДК 621.315.1.001.63
Г. А. Большанин, Л. Ю. Большанина, Т. Г. Коробова, С. И. Харин
(БрГУ)
ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ ОДНОРОДНОГО
УЧАСТКА ТРЕХФАЗНОЙ ТРЕХПРОВОДНОЙ ЛЭП В
УСЛОВИЯХ ПОНИЖЕННОГО КАЧЕСТВА ЭЛЕКТРИЧЕСКОЙ
ЭНЕРГИИ
Представлено характеристическое уравнение однородного участка трехфаз-
ной трехпроводной электрической цепи в условиях пониженного качества элект-
рической энергии. Предложен вариант его решения.
Трехфазная трехпроводная линия электропередач (ЛЭП) предназ-
начена для транспортировки электрической энергии напряжением ме-
нее 1000 В и более 35 кВ. Иначе ее называют линией с глухозаземленной
нейтралью.
Электрическая энергия пониженного качества отличается заметны-
ми уровнями несинусоидальности, несимметрии, отклонения и колеба-
ния напряжений и токов. ЛЭП, предназначенная для транспортировки
такой энергии, при анализе ее функционирования должна быть пред-
ставлена линией с распределенными параметрами в полнофазном вари-
анте.
В теории электротехники имеется аппарат анализа распределения
гармонически изменяющихся токов и напряжений по однородному уча-
стку ЛЭП [1], поэтому перед выполнением подобного анализа распреде-
ления электрической энергии пониженного качества по реальной ЛЭП
последнюю необходимо разделить на хотя бы относительно однород-
ные участки и выполнить спектральный анализ известных напряжений
и токов [2]. Анализ следует выполнять для каждого однородного участ-
ка ЛЭП на частоте каждой гармонической составляющей спектральных
составов основных характеристик электрической энергии.
Математическая модель однородного участка трехфазной трехпро-
водной ЛЭП на частоте
n
-й гармонической составляющей напряжения
и тока представляет собой совокупность девяти интегро-дифференци-
альных уравнений [3]. В результате совместного решения этих уравне-

118 119
ний можно получить характеристическое уравнение однородного участ-
ка трехфазной трехпроводной ЛЭП в условиях пониженного качества
электрической энергии. Оно представляет собой уравнение шестого по-
рядка
0
246
=
+
+
+
c
bx
ax
x
, (1)
где
(
)
-
+
+
-
=
nnnn
CA
AB
A
A
YYYZa
0
0
0
0
0
3
(
)
(
)
+
+
+
-
+
+
-
n
n
n
n
n
n
n
n
BC
CA
C
C
AB
BC
B
B
YYYZYYYZ
0
0
0
0
0
0
0
0
0
0
(
)
n
n
n
n
n
n
n
+
+
+
+
CA
CA
BC
BC
CA
AB
AB
YZYZYYZ
0
0
0
0
0
0
0
22
;
(
)
-
+
+
-
=
n
n
n
n
CA
AB
A
A
YYYZb
0
0
0
0
0
23
(
)
(
)
+
+
+
-
+
+
-
n
n
n
n
n
n
n
n
BC
CA
C
C
AB
BC
B
B
YYYZYYYZ
0
0
0
0
0
0
0
0
0
0
22
(
)
+
+
+
+
+
n
n
n
n
n
n
n
CA
CA
BC
BC
CA
AB
AB
YZYZYYZ
0
0
0
0
0
0
0
2422
(
)
[
-
-
+
+
+
n
n
n
n
n
n
AB
AB
CA
AB
A
A
YZYYYZ
0
0
0
0
0
0
0
]
(
)
[
-
+
+
-
n
n
n
n
n
n
AB
BC
B
B
CA
CA
YYYZYZ
0
0
0
0
0
0
0
]
+
-
-
n
n
n
n
BC
BC
AB
AB
YZYZ
0
0
0
0
(
)
[
-
-
+
+
+
n
n
n
n
n
n
AB
AB
CA
AB
A
A
YZYYYZ
0
0
0
0
0
0
0
]
(
)
[
-
+
+
-
n
n
n
n
n
n
BC
CA
С
С
CA
CA
YYYZYZ
0
0
0
0
0
0
0
]
+
-
-
n
n
n
n
BC
BC
CA
AB
YZYZ
0
0
0
0
(
)
[
-
-
+
+
+
n
n
n
n
n
n
AB
AB
AB
BC
B
B
YZYYYZ
0
0
0
0
0
0
0
]
(
)
[
-
+
+
-
n
n
n
n
n
n
BC
CA
С
С
BC
BC
YYYZYZ
0
0
0
0
0
0
0
]
n
n
n
n
-
-
BC
BC
CA
AB
YZYZ
0
0
0
0
[
-
+
-
n
n
n
n
BC
CA
AB
A
YZYZ
0
0
0
0
(
)
]
[
-
+
+
+
-
n
n
n
n
n
n
n
n
CA
BC
AB
B
AB
BC
B
AB
YZYZYYYZ
0
0
0
0
0
0
0
0
0
(
)
]
n
n
n
n
+
+
-
CA
AB
A
AB
YYYZ
0
0
0
0
0
[
-
+
-
n
n
n
n
CA
AB
BC
B
YZYZ
0
0
0
0
(
)
]
[
-
+
+
+
-
n
n
n
n
n
n
n
n
AB
AB
BC
C
BC
CA
C
BC
YZYZYYYZ
0
0
0
0
0
0
0
0
0
(
)
]
n
n
n
n
+
+
-
AB
BC
B
BC
YYYZ
0
0
0
0
0
[
-
+
-
n
n
n
n
BC
AB
СA
A
YZYZ
0
0
0
0
(
)
]
[
-
+
+
+
-
n
n
n
n
n
n
n
n
AB
BC
CA
C
BC
CA
C
CA
YZYZYYYZ
0
0
0
0
0
0
0
0
0
(
)
]
n
n
n
n
+
+
-
CA
AB
A
AB
YYYZ
0
0
0
0
0
;
(
)
-
+
+
-
=
n
n
n
n
CA
AB
A
A
YYYZc
0
0
0
0
0
21
(
)
n
n
n
n
+
+
-
AB
BC
B
B
YYYZ
0
0
0
0
0
(
)
+
+
+
-
n
n
n
n
BC
CA
C
C
YYYZ
0
0
0
0
0
(
)
+
+
+
+
+
n
n
n
n
n
n
n
CA
CA
BC
BC
CA
AB
AB
YZYZYYZ
0
0
0
0
0
0
0
2
(
)
[
-
-
+
+
+
n
n
n
n
n
n
AB
AB
CA
AB
A
A
YZYYYZ
0
0
0
0
0
0
0
]
(
)
[
-
+
+
-
n
n
n
n
n
n
AB
BC
B
B
CA
CA
YYYZYZ
0
0
0
0
0
0
0
]
+
-
-
n
n
n
n
BC
BC
AB
AB
YZYZ
0
0
0
0
(
)
[
-
-
+
+
+
n
n
n
n
n
n
AB
AB
CA
AB
A
A
YZYYYZ
0
0
0
0
0
0
0
]
(
)
[
-
+
+
-
n
n
n
n
n
n
BC
CA
С
С
CA
CA
YYYZYZ
0
0
0
0
0
0
0
]
+
-
-
n
n
n
n
BC
BC
CA
AB
YZYZ
0
0
0
0
(
)
[
-
-
+
+
+
n
n
n
n
n
n
AB
AB
AB
BC
B
B
YZYYYZ
0
0
0
0
0
0
0
]
(
)
[
-
+
+
-
n
n
n
n
n
n
BC
CA
С
С
BC
BC
YYYZYZ
0
0
0
0
0
0
0
]
n
n
n
n
-
-
BC
BC
CA
AB
YZYZ
0
0
0
0
[
-
+
-
n
n
n
n
BC
CA
AB
A
YZYZ
0
0
0
0
(
)
]
[
-
+
+
+
-
n
n
n
n
n
n
n
n
CA
BC
AB
B
AB
BC
B
AB
YZYZYYYZ
0
0
0
0
0
0
0
0
0
(
)
]
n
n
n
n
+
+
-
CA
AB
A
AB
YYYZ
0
0
0
0
0
[
-
+
-
n
n
n
n
CA
AB
BC
B
YZYZ
0
0
0
0
(
)
]
[
-
+
+
+
-
n
n
n
n
n
n
n
n
AB
AB
BC
C
BC
CA
C
BC
YZYZYYYZ
0
0
0
0
0
0
0
0
0
(
)
]
n
n
n
n
+
+
-
AB
BC
B
BC
YYYZ
0
0
0
0
0
[
-
+
-
n
n
n
n
BC
AB
СA
A
YZYZ
0
0
0
0
(
)
]
[
-
+
+
+
-
n
n
n
n
n
n
n
n
AB
BC
CA
C
BC
CA
C
CA
YZYZYYYZ
0
0
0
0
0
0
0
0
0
(
)
]
n
n
n
n
+
+
-
CA
AB
A
AB
YYYZ
0
0
0
0
0
(
)
[
-
+
+
-
n
n
n
n
CA
AB
A
A
YYYZ
0
0
0
0
0
]
(
)
[
-
+
+
-
-
n
n
n
n
n
n
n
n
AB
BC
B
B
CA
CA
AB
AB
YYYZYZYZ
0
0
0
0
0
0
0
0
0
]
(
)
[
-
+
+
-
-
n
n
n
n
n
n
n
n
BC
CA
C
C
BC
BC
AB
AB
YYYZYZYZ
0
0
0
0
0
0
0
0
0
]
n
n
n
n
-
-
BC
BC
CA
AB
YZYZ
0
0
0
0
(
)
[
-
+
+
+
n
n
n
n
CA
AB
A
A
YYYZ
0
0
0
0
0
]
[
-
+
-
-
n
n
n
n
n
n
n
n
СA
AB
BС
B
CA
CA
AB
AB
YZYZYZYZ
0
0
0
0
0
0
0
0
(
)
]
[
-
+
+
+
-
n
n
n
n
n
n
n
n
AB
AB
BC
C
BC
CA
С
BС
YZYZYYYZ
0
0
0
0
0
0
0
0
0
(
)
]
n
n
n
n
+
+
-
AB
BC
B
BC
YYYZ
0
0
0
0
0
(
)
[
-
+
+
+
n
n
n
n
BC
CA
C
C
YYYZ
0
0
0
0
0
]
[
-
+
-
-
n
n
n
n
n
n
n
n
BС
CA
AB
A
BC
BC
CA
AB
YZYZYZYZ
0
0
0
0
0
0
0
0
(
)
]
[
-
+
+
+
-
n
n
n
n
n
n
n
n
CA
BC
AB
B
AB
BC
B
AB
YZYZYYYZ
0
0
0
0
0
0
0
0
0
(
)
]
n
n
n
n
+
+
-
CA
AB
A
AB
YYYZ
0
0
0
0
0
(
)
[
-
+
+
+
n
n
n
n
AB
BC
B
B
YYYZ
0
0
0
0
0
]
[
-
+
-
-
n
n
n
n
n
n
n
n
BС
AB
СA
A
CA
CA
AB
AB
YZYZYZYZ
0
0
0
0
0
0
0
0
(
)
]
[
-
+
+
+
-
n
n
n
n
n
n
n
n
AB
BC
CA
C
BC
CA
С
СA
YZYZYYYZ
0
0
0
0
0
0
0
0
0
