Математическое моделирование, численные методы и комплексы программ 2007 Вып.13

Подождите немного. Документ загружается.

80 81

Для оценки статической устойчивости электроэнергетической сис-

темы существует несколько способов, наиболее часто применяют непос-

редственное решение уравнений Парка – Горева, описывающих пере-

ходные процессы в энергосистеме. Расчет корней характеристического

уравнения системы позволяет оценить запас устойчивости. Метод

Д-разбиения используют для получения оптимальных настроек АРВ. Вы-

бор электростанций в энергосистеме, наиболее сильно влияющих на ста-

тическую устойчивость, целесообразно проводить, анализируя частот-

ные характеристики параметров стабилизации. Для решения перечис-

ленных задач авторами был разработан программный комплекс ISUEES.

Программный комплекс состоит из нескольких модулей, решаю-

щих следующие задачи: расчет режима, составление системы линеари-

зованных уравнений Парка – Горева, расчет и построение областей

Д-разбиения по двум параметрам (искомые значения коэффициентов ре-

гулирования АРВ), расчет и построение частотных характеристик, рас-

чет корней характеристического полинома, расчет и построение облас-

тей Д-разбиения по трем параметрам (первым и вторым параметрами

выступают искомые значения коэффициентов регулирования АРВ, тре-

тий параметр – затухание α). Перечисленные модули объединены одним

исполняемым файлом.

Внешний вид модуля расчета режима показан на рис. 1. Подобная

реализация программы расчета режима позволяет наглядно видеть схе-

му исходной электроэнергетической системы (ЭЭС), легко просматри-

вать и изменять параметры.

Рис. 1. Внешний вид модуля расчета режима

Модуль, в котором происходит составление линеаризованной сис-

темы уравнений, не имеет визуальной формы. Коэффициенты данной

системы рассчитываются без участия пользователя, задаётся только ге-

нератор, для которого будет проводиться исследование.

В модуле расчета частотных характеристик и областей Д-разбие-

ния по двум параметрам можно задать и изменить параметры расчета, а

также значения настроечных коэффициентов АРВ генераторов.

Модуль построения частотных характеристик и областей

Д-разбиения по двум параметрам имеет визуальную форму, представ-

ленную на рис. 2. В изображенном окне осуществляется построение рас-

считанных кривых, а также возможен расчет корней характеристическо-

го полинома, предусмотрена возможность изменять значение искомых

коэффициентов регулирования АРВ. Все расчеты и построенные харак-

теристики можно свести в один отчет (в формате MS Word), выбрав со-

ответствующий пункт меню.

Рис. 2. Внешний вид модуля построения частотных характеристик

и областей Д-разбиения по двум параметрам

В программном комплексе имеется возможность построения трех-

мерной области Д-разбиения. По осям абсцисс и ординат откладывают-

ся искомые коэффициенты регулирования, а по оси аппликат – затуха-

82 83

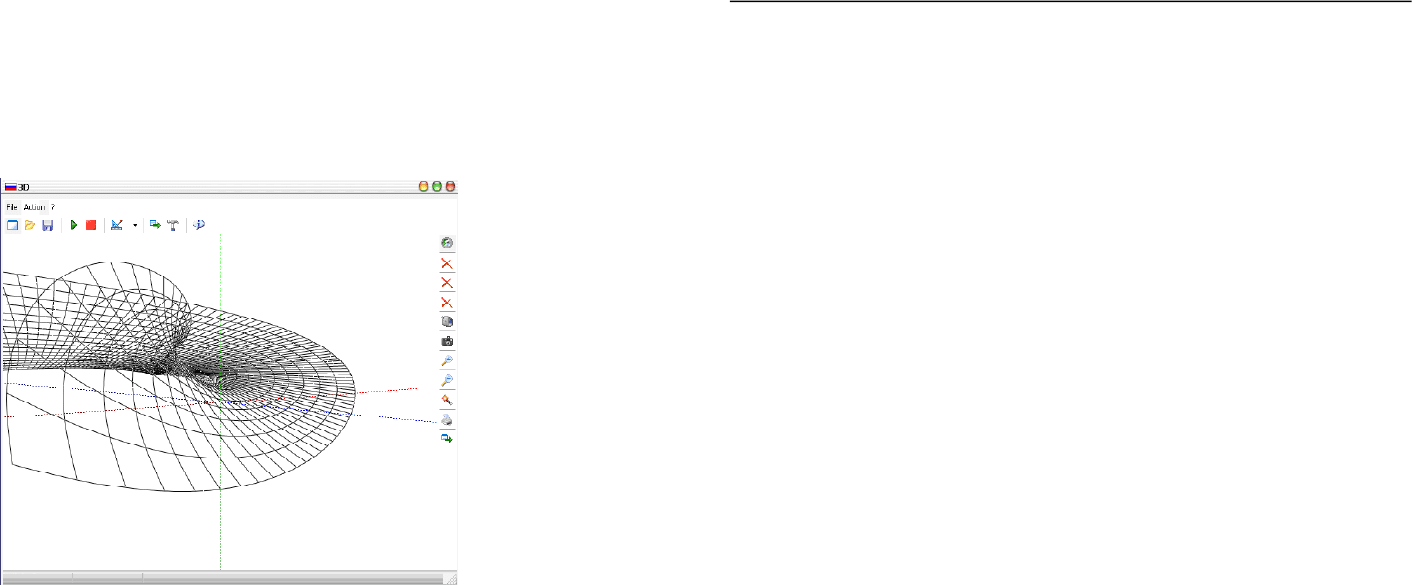
ние (рис. 3). Трехмерная область Д-разбиения может быть использована

для исследования характера изменения границы устойчивости.

Функции модуля следующие: построение функций, заданных

аналитически; построение функций, заданных графически (координатами

точек); трассировка полученных поверхностей; печать результатов;

сохранение результатов в графическом (*.bmp, *.jpg), видео (*.avi

с выбираемым кодеком) форматах.

Рис. 3. Макет трехмерной области Д-разбиения в перспективе

Для параметрического описания областей Д-разбиения в простран-

стве используются B-сплайны (NURBS). Такой выбор обусловлен тем,

что NURBS имеет наиболее широкий набор полезных математических

свойств (возможность локального управления кривизной сплайна, на-

личие весов для управляющих точек) и, следовательно, с их помощью

можно наиболее точно приблизить функцию.

Использование NURBS дало возможность строить трехмерные об-

ласти наиболее быстро. При построении нет необходимости рассчиты-

вать каждую точку кривой Д-разбиения, рассчитываются лишь некото-

рые точки с задаваемым пользователем интервалом, что позволяет зна-

чительно уменьшить время построения модели.

Прикладные возможности модуля:

1) выделение интересующих участков на построенных областях

с возможностью нахождения площади участка;

2) аппроксимация функций, заданных графически;

3) графическое решение уравнений, заданных аналитически, либо

графически.

Разработанный программный комплекс прошел официальную ре-

гистрацию в Федеральной службе по интеллектуальной собственности,

патентам и товарным знакам [1].

Список литературы

1. Игнатьев И. В., Пьянников Е. Д. Исследование статической ус-

тойчивости электроэнергетических систем (ISUEES v.1.00): Свидетель-

ство об официальной регистрации программы для ЭВМ от 25 сентября

2006 г. № 2006612627.

Получено 4 апреля 2007 года.

УДК 621.311

А. А. Бушин (БрГУ)

ИСПОЛЬЗОВАНИЕ ИТЕРАЦИОННОГО МЕТОДА

ПРИ АНАЛИЗЕ РАСПРЕДЕЛЕНИЯ ВЫСШИХ ГАРМОНИК

В ПРОМЫШЛЕННЫХ ЭЛЕКТРИЧЕСКИХ СЕТЯХ

Рассматриваются вопросы использования итерационного метода при ана-

лизе распределения гармоник в промышленных электрических сетях как допол-

нение к методу обратной матрицы с целью упрощения расчета нагрузок потреби-

телей для высших гармоник.

До настоящего времени острой продолжает оставаться проблема

качества электроэнергии как в России, так и в мире в целом. В связи

с ростом мощностей потребителей с нелинейными нагрузками, внося-

щих искажения в сеть (преобразовательные установки, электротяга, ду-

говые печи), и широким распространением электронных систем автома-

тического управления, чувствительных к искажениям в сети, внимание

ученых многих стран мира привлечено как к проблеме качества электро-

Математическое моделирование, численные методы и комплексы

программ. СПб., 2007

84 85

энергии в целом, так и к проблеме высших гармоник (ВГ) в напряжении

электрических сетей в частности.

Измерения коэффициентов искажения синусоиды напряжения К

и коэффициента гармоник напряжения К

u(n)

в распределительных сетях

показывают, что их величины часто превышают нормально допустимые

значения, установленные ГОСТ 13109–97 [1].

Для снижения уровней высших гармоник необходимо знать закон

их распределения в рамках рассматриваемой сети для эффективного при-

нятия мер по нормализации показателей качества.

Одна из главных проблем при анализе распределения гармоник

в сети состоит в достаточно сложном взаимодействии сети и нелиней-

ных нагрузок.

Возможно использование для такого анализа статистического ме-

тода, к примеру метода обратной матрицы. Этот метод весьма удобен в

применении и относительно прост. Его эффективно используют при ана-

лизе режимов распределения энергии на основной частоте [2].

Сложность применения этого метода для анализа распределения

ВГ состоит в том, что мощность нагрузок для высоких частот неизвест-

на, поскольку в качестве нагрузки может выступать электрооборудова-

ние, весьма различающееся по характеру.

Это значительно усложняет расчеты в рамках данного метода, так

как законы изменения сопротивления в зависимости от частоты для раз-

личных элементов нагрузки потребителя (трансформаторы, асинхрон-

ные двигатели и т. д.) различны и достаточно сложны. К тому же нет

единых выражений для описания таких закономерностей и в разных ис-

точниках приводятся различные варианты с различным набором усло-

вий [3, 4].

Вместо вычисления множества законов изменения элементов на-

грузки потребителя в зависимости от частоты можно воспользоваться

итерационным методом для определения мощности нагрузок, где в пер-

вом приближении нагрузки приравниваются нулю (холостой ход), а за-

тем во втором приближении и далее находятся величины мощностей

нагрузок для каждой гармонической составляющей.

Это позволит значительно упростить расчеты и, переориентировав

программу по расчету режимов сети с основной частоты на ВГ, анализи-

ровать распределение уже высших гармоник в рассматриваемой сети

с достаточно высокой точностью.

Список литературы

1. ГОСТ 13109–97. Электрическая энергия. Совместимость техни-

ческих средств электромагнитная. Нормы качества электрической энер-

гии в системах электроснабжения общего назначения. – М., 1997. – 60 с.

2. Проектирование районной электрической сети: Методические

указания к курсовому проекту / Сост. И. В. Игнатьев; БрГТУ. – Братск,

2000. – 90 с.

3. Арриллага Дж., Брэдли Д., Боджер П. Гармоники в электричес-

ких системах. – М.: Энергоатомиздат, 1990. – 320 с.

4. Жежеленко И. В. Высшие гармоники в системах электроснабже-

ния промпредприятий. – М.: Энергоатомиздат, 2000. – 331 с.

Получено 4 апреля 2007 года.

УДК 621.315.1.001.63

Г. А. Большанин, Л. Ю. Большанина, Т. Г. Коробова, С. И. Харин

(БрГУ)

ОСОБЕННОСТИ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ

МОДЕЛИ ОДНОРОДНОГО УЧАСТКА ТРЕХФАЗНОЙ

ТРЕХПРОВОДНОЙ ЛЭП В УСЛОВИЯХ ПОНИЖЕННОГО

КАЧЕСТВА ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ

Отмечены основные отличия процедуры построения математической моде-

ли однородного участка трехфазной линии электропередач трехпроводного испол-

нения, связанные с понижением качества электрической энергии, от традицион-

ных методик.

Трехпроводные трехфазные линии электропередач (ЛЭП) предназ-

начены для транспортировки электрической энергии напряжением до

1000 В и свыше 35 кВ. Иначе их называют линиями с глухозаземленной

нейтралью.

Однородный участок ЛЭП отличается неизменными на всем его

протяжении продольными и поперечными параметрами.

Электрическая энергия пониженного качества характеризуется за-

метными по величине отклонениями, несимметрией, несинусоидально-

Математическое моделирование, численные методы и комплексы

программ. СПб., 2007

86 87

стью и колебаниями напряжений и токов. К сожалению, для современ-

ных электроэнергетических систем такая электрическая энергия стала

практически традиционной. Именно с этим обстоятельством и связано

своеобразие математического моделирования многофазной ЛЭП.

Математическое моделирование ЛЭП выполняется на основании

анализа ее схемы замещения.

Схему замещения ЛЭП обычно представляли как совокупность

продольных и поперечных параметров: продольные параметры – как

совокупность активного и индуктивного элементов, а поперечные – как

совокупность активного и емкостного элементов. Причем в последнем

случае активный элемент учитывали далеко не всегда. Об электромаг-

нитных процессах, происходящих в ЛЭП, судили по результатам анали-

за распределения электрической энергии лишь по одному линейному

проводу.

Такие схемы замещения действительно с достоверностью, пригод-

ной для инженерных расчетов, описывали электромагнитные процессы,

происходившие в ЛЭП. Но лишь на частоте 50 Гц и при условии абсо-

лютной симметрии электроэнергетических систем.

В настоящее время, когда качество электрической энергии в ЭЭС

ни в коей мере нельзя назвать удовлетворительным, когда в спектраль-

ном составе электрической энергии содержится множество гармоничес-

ких составляющих, частота которых отлична от основной, характеризу-

ющихся ощутимыми амплитудными значениями, такую схему замеще-

ния ЛЭП, а следовательно, и прежние методики математического моде-

лирования использовать на практике нельзя.

Теперь при сложившихся обстоятельствах, когда из-за наличия вы-

сокочастотных составляющих в спектральном составе электрической

энергии длина волны электромагнитной энергии, распространяемой по

ЛЭП, резко уменьшилась, действующие линии электропередач следует

рассматривать не как линии с сосредоточенными, а как линии с распре-

деленными параметрами, даже при их относительно небольшой протя-

женности [1].

Кроме того, согласно результатам экспериментов, выполненных

специалистами в данной отрасли науки, продольные параметры ЛЭП

могут иметь как активно-индуктивный, так и активно-емкостной, а по-

перечные параметры этой же ЛЭП – как активно-емкостной, так и ак-

тивно-индуктивный характер [2]. Здесь необходимо учитывать всевоз-

можные электромагнитные связи между линейными проводами, а также

между линейными проводами и заземленными конструкциями ЛЭП. То

есть электрическая схема замещения ЛЭП должна включать в свой со-

став все ее конструктивные элементы и выглядит сравнительно громоз-

дко. Громоздкость проявляется и в математической модели распределе-

ния по этому участку электрической энергии пониженного качества. Она

включает в свой состав девять интегро- дифференциальных уравнений

по двум переменным [1]:

iddidii

ACAABAA

++-+=

;

idididii

BBCABBB

+++-=

;

idididii

CBCCACC

++-+=

;

dlM

dlLdlRiu

AAAA 0000

uti

dlC

++¶+

;

dlM

dlLdlRiu

BBBB 0000

uti

dlC

++¶+

;

dlM

dlLdlRiu

BС

CCCC 0000

uti

dlC

++¶+

;

dlM

dlLdlRiu

AAAAB 0000

--¶+

dlM

dlLdlRiti

dlC

BBBA

0000

uti

dlC

ABB

++¶-

;

88 89

dlM

dlLdlRiu

BBBBС 0000

--¶+

dlM

dlLdlRiti

dlC

BС

CCCB

0000

uti

dlC

BCC

++¶-

;

dlM

dlLdlRiu

BС

ССССA 0000

--¶+

dlM

dlLdlRiti

dlC

AAAС

0000

uti

dlC

CAC

++¶-

где

– фазные и линейные напряжения; ения;

– линейные токи;

– элементарные токи по электро-тро-

магнитным связям между линейными проводами и заземленными

конструкциями ЛЭП;

– элементарные токи по электро-ро-

магнитным связям между линейными проводами;

– погонные продольные параметры линейных

проводов;

– взаимные индуктивности линейных

проводов;

– протяженность однородного участка ЛЭП.

Поперечные параметры электрической схемы замещения ЛЭП уча-

ствуют в формировании элементарных токов через соответствующие

электромагнитные связи:

udlC

dlGdl

udi

AAA

AA 0000

;

+= dl

udlC

dlGdl

udi

BBB

BB 0000

;

+= dl

udlC

dlGdl

udi

CCC

CC 0000

;

+= dl

udlC

dlGdl

udi

ABABAB

ABAB 00

;

+= dl

udlC

dlGdl

udi

BCBCBC

BCBC 00

;

+= dl

udlC

dlGdl

udi

CACACA

CACA 00

где

00 A

00B

00C

– погонные поперечныечные

параметры, характеризующие электромагнитные связи между линейными

проводами и заземленными конструкциями ЛЭП;

00 AB

00AB

00 BC

00BC

00CA

– погонные поперечные параметры, характе-те-

ризующие электромагнитные связи между линейными проводами.

Временные характеристики напряжения и тока, представляющие

собою электрическую энергию пониженного качества, отличны от ха-

рактеристик синусоидальной формы, поэтому оптимизация математи-

ческой модели трехфазной ЛЭП с глухозаземленной нейтралью, пред-

полагающая совместное решение интегро- дифференциальных уравне-

ний, оказывается непростой операцией.

В этом случае следует вспомнить, что неперегруженная ЛЭП пред-

ставляет собой линейную систему, для которой вполне применим прин-

цип суперпозиции.

Иными словами, предлагается построение математической модели

для каждой составляющей спектров напряжения и тока. Оптимизация

таких моделей вполне осуществима при использовании соответствую-

щего математического аппарата. Результаты оптимизации несложно рас-

пространить на весь спектр напряжения и тока.

Описанная операция позволит выполнять прогнозирование распре-

деления электрической энергии пониженного качества по участкам со-

временных электроэнергетических систем.

Список литературы

1. Большанин Г. А. Распределение электрической энергии понижен-

ного качества по участкам электроэнергетической системы // Труды Брат-

ского государственного университета: Сер. Естественные и инженерные

науки – развитию регионов Сибири. Т. 2. – Братск: БрГУ, 2006. – С. 129–140.

90 91

2. Арриллага Дж., Брэдли Д., Боджер П. Гармоники в электричес-

ких системах / Пер. с англ. / Дж. Арриллага, Д. Брэдли, П. Боджер. – М.:

Энергоатомиздат, 1990. – 320 с.

Получено 4 апреля 2007 года.

УДК 621.315.1.001.63

Г. А. Большанин, Л. Ю. Большанина, С. И. Харин (БрГУ)

ОСОБЕННОСТИ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ

МОДЕЛИ ОДНОРОДНОГО УЧАСТКА РАЙОННОЙ СЕТИ

В УСЛОВИЯХ ПОНИЖЕННОГО КАЧЕСТВА

ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ

Отмечены основные отличия процедуры построения математической моде-

ли однородного участка трехфазной линии электропередач четырехпроводного

исполнения, связанные с понижением качества электрической энергии, от тради-

ционных методик.

Районные электрические сети, как правило, представляют собой

трехфазные четырехпроводные линии электропередач (ЛЭП) напряже-

нием от 1000 В до 35 кВ. В их состав входят три линейных и один нейт-

ральный провода. Нейтральный провод при установившихся неаварий-

ных режимах работы электроэнергетической системы изолирован от за-

земленных конструктивных элементов ЛЭП. Такую линию электропе-

редач называют линией с изолированной нейтралью.

ЛЭП с изолированной нейтралью составляют свыше 45 % от коли-

чества всех средств для транспортировки электрической энергии.

Однородность ЛЭП обеспечивается однозначностью продольных

и поперечных параметров линии электропередач на протяжении всего

рассматриваемого участка.

Электрическая энергия пониженного качества характеризуется за-

метными по величине отклонениями, несимметрией, несинусоидально-

стью и колебаниями напряжений и токов. К сожалению, для современ-

ных электроэнергетических систем такая электрическая энергия стала

практически традиционной. Именно с этим обстоятельством и связано

своеобразие математического моделирования многофазной ЛЭП.

Математическое моделирование ЛЭП выполняется на основании

анализа ее схемы замещения. Схему замещения ЛЭП в условиях пони-

женного качества электрической энергии следует представлять как со-

вокупность продольных и поперечных параметров линейных и нейтраль-

ного проводов. Причем эти параметры должны быть представлены ре-

зистивными, индуктивными и емкостными элементами.

Районные электрические сети представляют собой ЛЭП сравнитель-

но небольшой протяженности. Их протяженность редко превышает не-

сколько десятков километров. Но, тем не менее, в условиях повышенно-

го уровня несинусоидальности напряжений и токов при построении ма-

тематической модели районных сетей их следует воспринимать как ли-

нии с распределенными параметрами [1].

В состав электрической схемы замещения однородного участка ЛЭП

с глухозаземленной нейтралью входят погонные продольные параметры

линейных проводов

, а

также погонные продольные параметры нейтрального провода

; погонные поперечные параметры, иллюстрирующие электромаг-

нитные связи между линейными проводами,

, а также погонные поперечные пара-

метры, иллюстрирующие электромагнитные связи между каждым ли-

нейным проводом и заземленными конструктивными элементами ЛЭП,

00 A

00B

00C

; погонные поперечные параметры,ры,

иллюстрирующие электромагнитные связи между каждым линейным и

нейтральным проводами,

АN

, а также погонные поперечные параметры, иллюс-

трирующие электромагнитные связи между изолированным нейтраль-

ным проводом и заземленными конструктивными элементами ЛЭП,

00N

Так, здесь в начале рассматриваемого участка ЭЭС имеют место:

напряжения между линейными проводами (линейные)

;

напряжения между линейными и нейтральным проводами (фазные)

; напряжения между линейными проводами и заземленными

конструктивными элементами ЛЭП

; напряжение между

нейтральным проводом и поверхностью земли

, которое условно мож-

Математическое моделирование, численные методы и комплексы

программ. СПб., 2007

92 93

но назвать напряжением смещения нейтрали; линейные токи

;

а также ток в нейтральном проводе

Из этого следует, что рабочая математическая модель однородного

элементарного участка ЛЭП трехфазного четырехпроводного исполнения

протяженностью

содержит четырнадцать уравнений:

ididididii

AANCAABAA

+++-+=

;

ididididii

BBNABBCBB

+++-+=

;

ididididii

CCNBCCACC

+++-+=

;

ididididii

NNCNBNANN

-+-++=

;

dlM

dlLdlRiu

AAAA 0000

+++

- dl

udti

dlCdt

dlM

;

dlM

dlLdlRiu

BBBB 0000

+++

- dl

udti

dlCdt

dlM

;

dlM

dlLdlRiu

CCCC 0000

+++

- dl

udti

dlCdt

dlM

;

--=

dlM

dlLdlRiu

NNNN 0000

++-

+ dl

udti

dlCdt

dlM

;

dlM

dlLdlRiu

AAAAN 0000

- dti

dlCdt

dlM

dlLdlRi

NNN 0000

+++

- dl

udti

dlCdt

dlM

ANN

;

dlM

dlLdlRiu

BBBBN 0000

- dti

dlCdt

dlM

dlLdlRi

NNN 0000

+++

- dl

udti

dlCdt

dlM

BNN

;

dlM

dlLdlRiu

CCCCN 0000

- dti

dlCdt

dlM

dlLdlRi

NNN 0000

+++

udti

dlCdt

dlM

CNN

;

dlM

dlLdlRiu

AAAAB 0000

- dti

dlCdt

dlM

94 95

dlM

dlLdlRi

BBB 0000

++-

+ dl

udti

dlCdt

dlM

ABB

;

dlM

dlLdlRiu

BBBBC 0000

- dti

dlCdt

dlM

dlLdlRi

CCC 0000

++-

+ dl

udti

dlCdt

dlM

BCC

;

dlM

dlLdlRiu

CCCCA 0000

- dti

dlCdt

dlM

dlLdlRi

AAA 0000

++-

+ dl

udti

dlCdt

dlM

ACA

где

– элементарные токи по электромагнитным связям

между линейными проводами и заземленными конструкциями ЛЭП;

– элементарные токи по электромагнитным связям между нейтраль-

ным проводом и заземленными конструкциями ЛЭП;

–

элементарные токи по электромагнитным связям между линейными про-

водами;

– элементарные токи по электромагнитным

связям между каждым линейным проводом и заземленными конструк-

циями ЛЭП.

Величины элементарных токов следует определять по формулам

dlCdlGudi

AAAA

0000

;

dlCdlGudi

BBBB

0000

;

dlCdlGudi

CCCC

0000

;

dlCdlGudi

NNNN

0000

;

dlCdlGudi

ANANANAN

;

dlCdlGudi

BNBNBNBN

;

dlCdlGudi

CNCNCNCN

;

dlCdlGudi

ABABABAB

;

dlCdlGudi

BCBCBCBC

;

dlCdlGudi

CACACACA

Несинусоидальная форма временных диаграмм напряжений и то-

ков существенно усложняет процедуру оптимизации построенной мо-

дели. Понизить громоздкость предстоящей оптимизации поможет факт

представления однородного участка районной электрической сети ли-

нейной схемой замещения. Это обстоятельство делает возможным ис-

пользование принципа суперпозиций.

Благодаря этому принципу предоставляется возможность построе-

ния математической модели однородного участка районной электричес-

кой сети на частоте каждой гармонической составляющей спектров на-

пряжений и токов. Есть смысл в построении математической модели и

для постоянных составляющих спектров, если таковые имеются. Мате-

матический аппарат оптимизации математических моделей ЛЭП при

постоянных либо гармонически изменяющихся напряжениях и токах

известен [2], поэтому такая оптимизация вполне осуществима, особен-

но при использовании средств вычислительной техники. Результаты оп-

тимизации следует обобщить на весь спектр соответствующего напря-

жения или тока.

Список литературы

1. Большанин Г. А. Распределение электрической энергии пони-

женного качества по участкам электроэнергетической системы // Тру-

ды Братского государственного университета: Сер. Естественные и

инженерные науки – развитию регионов Сибири. Т. 2. – Братск: БрГУ,

2006. – С. 129–140.

96 97

2. Большанин Г. А. Способ прогнозирования гармонических состав-

ляющих электрической энергии по неразветвленным участкам электро-

энергетической системы: Патент 2210154. Россия, МКИ

Н 02 J 3/01/

Г. А. Большанин. – № 2001106402. Заявл. 06.03.01; Опубл. 10.08.03.

Получено 6 апреля 2007 года.

УДК 621.315.1.001.63

Г. А. Большанин, Л. Ю. Большанина, С. И. Харин (БрГУ)

ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ ОДНОРОДНОГО

УЧАСТКА РАЙОННОЙ СЕТИ В УСЛОВИЯХ ПОНИЖЕННОГО

КАЧЕСТВА ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ

Представлено характеристическое уравнение однородного участка трехфаз-

ной четырехпроводной электрической цепи в условиях пониженного качества элек-

трической энергии. Предложен вариант его решения.

Районная электрическая сеть обычно исполняется в трехфазном

варианте в виде совокупности четырех проводов: трех линейных и од-

ного нейтрального, т. е. представляет собой трехфазную четырехпровод-

ную линию электропередач (ЛЭП). Иначе ее называют линией с изоли-

рованной нейтралью. Она предназначена для транспортировки электри-

ческой энергии напряжением от 1000 В до 35 кВ.

В случае визуально заметных уровней несинусоидальности, несим-

метрии, отклонения и колебания напряжений и токов говорят об элект-

рической энергии пониженного качества. При анализе распределения

такой энергии по участкам электроэнергетических систем ЛЭП должна

быть представлена линией с распределенными параметрами в полно-

фазном варианте.

Анализировать распределение электрической энергии пониженно-

го качества целесообразно по каждому однородному участку ЛЭП на

частоте каждой гармонической составляющей напряжения и тока [1].

Результаты такого анализа следует обобщить на всю ЛЭП и на весь спектр

основных характеристик электрической энергии.

Математическая модель однородного участка трехфазной четырех-

проводной ЛЭП на частоте

-й гармонической составляющей напряже-

Математическое моделирование, численные методы и комплексы

программ. СПб., 2007

ния и тока представляет собой совокупность четырнадцати интегродиф-

ференциальных уравнений. В результате совместного решения этих урав-

нений можно получить характеристическое уравнение однородного уча-

стка трехфазной трехпроводной ЛЭП в условиях пониженного качества

электрической энергии. Оно представляет собой уравнение восьмого

порядка

2468

, (1)

где a, b, c и d – коэффициенты, учитывающие первичные параметры

однородного участка анализируемой ЛЭП на частоте

-й гармонической

составляющей напряжения и тока.

Восьмая степень характеристического уравнения (1) трехфазной

трехпроводной ЛЭП свидетельствует о том, что в каждом линейном про-

воде линии электропередач присутствует восемь волн электромагнитно-

го поля: четыре падающие и четыре отраженные. Постоянные распреде-

ления волн определятся в результате решения этого уравнения.

Для определения корней характеристического уравнения (1) необ-

ходимо принять, что

. (2)

Тогда уравнение примет вид

234

. (3)

Для его решения вполне можно использовать метод Декарта – Эй-

лера [2]. Тогда в результате введения подстановки

y -=l

(4)

характеристическое уравнение (3) сведется к «неполному» виду:

=+++ rqypyy

, (5)

где

bp -=

;

aba

q ++=

;

acaba

r +--=

256

Кубическая резольвента уравнения (5) имеет вид [3]

(

)

042

2223

=--++ qzrppzz

. (6)

Для решения уравнения (6), как и в случае анализа трехпроводного

участка ЭЭС, есть смысл применить формулу Кардано [3]. Для этого

следует выполнить замену

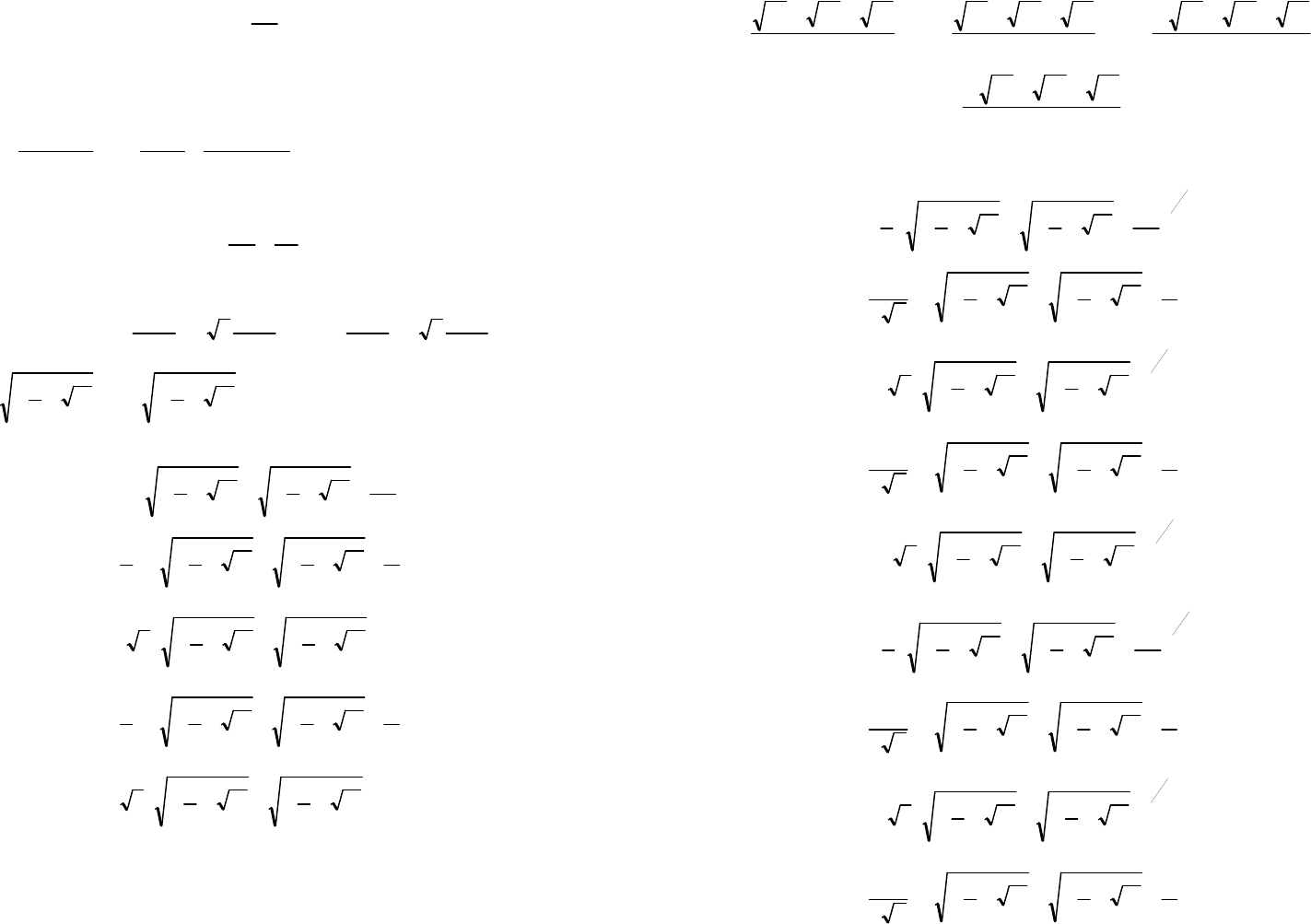
98 99

2 p

zk +=

. (7)

Тогда формула (6) примет вид

, (8)

где

;

prpp

n -

Дискриминант полученного уравнения можно определить так:

D +=

Корни уравнения (8) можно вычислить по формулам [3]

;

где

u +-=

;

--=n

Из равенства (7) определятся корни уравнения (6)

z ---++-=

; (9)

+----+--=

3222

+--+-+

3 D

; (10)

-----+--=

3222

+--+--

3 D

, (11)

а корни «неполного» уравнения (5) – по формулам [3]

zzz

;

zzz

;

zzz

-+-

;

zzz

+--

Принимая во внимание равенства (9), (10) и (11), можно уточнить

корни этого уравнения:

---++-=

222

1 p

+----+--+

322

+--+-+

3 D

-----+--+

322

+--+-- D

;

---++-=

222

1 p

+----+---

322

+--+-+

3 D

-----+---

322