Ляпидов В.C. Теоретические основы кибернетики. Методы оптимизации
Подождите немного. Документ загружается.


показать, что нормальная система уравнений, соответствующая
(4.21), представляется структурной схемой (рис. 4.2, в).
Рассмотрим оптимальное управление объектами, которые содер-
жат нелинейные звенья (рис. 4.2, е). Объект, состоящий из линейного
1 и нелинейного звена 2, описывается следующей системой
уравнений:
,,f
;f
212
21
2212
1
1
xx
x
xx
dt
dx
uu
dt
dx
(4.22)
где
.
max
Uu
Функции
21
x
и
22
x
непрерывны вместе со своими про-
изводными, причем
0
22
x
и
0
21
x
. Начальное состояние объекта
0x
21
x
, конечное состояние
n
xx
11
,
n
xx
22
.
Требуется за минимальное время перевести объект из начального
состояния в конечное.
Запишем функцию Гамильтона
.,ff
221211
xxuH
(4.23)
Возьмем частную производную от Н по u
1
u
H
(4.24)
и определим функцию
.
max1
Utsigntu
Для нахождения
1
составляем уравнения сопряженных функций
1
:
.,
ff
;
1
ff
2212
2
21
212212221
2
2
2
1
2
12
2
21
2
1
2
1
1
11
xx
x
xxxxx
xxdt
d
xxxdt
d
(4.25)
Решим уравнения (4.25):
.
;
1
21
2
1
,
22
0
21
C
x
dtt
t
eCt
dxx
(4.26)
Для определения алгоритма проанализируем поведение функций
t
2
и
t
1
. Функция
t
2
знака не меняет, так как экспоненциальный
член всегда положителен. Таким образом, производная от функций
dt
d
1
знакопостоянна, а сама функция
1
по теореме Ролля только
один раз меняет знак. Значит, оптимальное управление должно иметь
51

два интервала (разгон — торможение) с одной сменой знака. Данный
пример показывает, что если в объекте управления имеются
нелинейные звенья, то для нахождения оптимальных управлений
необходимо исследовать свойства нелинейных функций, их
производных и интегралов. В большинстве случаев эти исследования
могут быть очень сложными. Без доказательства укажем, что если
функции, описывающие нелинейные звенья, обладают ранее
указанными свойствами, то все выводы, сделанные для схем (см. рис.
4.2), справедливы и для нелинейных звеньев. Так как свойства таких
нелинейных объектов совпадают со свойствами линейных, то их
можно назвать квазилинейными.
Выше были рассмотрены оптимальные управления для случая
нулевых начальных и ненулевых конечных условий. Часто рассмат-
риваются оптимальные управления по ошибке системы, т. е. по
отклонению от конечного состояния. Тогда задача несколько изме-
няется, так как начальные условия будут ненулевыми, а конечные -
нулевыми. Для рассмотренных объектов такая трансформация не
вызывает изменений в определении оптимальных алгоритмов.
4.2. Физическая сущность управления, оптимального по
быстродействию.
Оптимальное управление по быстродействию имеет глубокий
физический смысл, связанный с балансом энергии в объекте.
Вспомним основную формулу, связывающую мощность и работу,
.
A
N
t
(4.27)
Из (4.27) видно, что для совершения одной и той же работы за
меньшее время потребуется большая мощность. Обычно в объектах
управления работу А представляют в виде суммы
,ААА
з п
(4.28)
52

где А
з
— энергия, запасенная в самом объекте (электрическая,
тепловая, механическая и т. д.);
А
п
— полезная работа, совершаемая в объекте. Объекты,
обладающие свойствами, выраженными формулами (4.27) и (4.28),
описываются различными дифференциальными уравнениями
(линейными, нелинейными, в частных производных и т. д.).
Запишем формулу (4.27) с учетом (4.28) в виде
.
N
A
N
A
пз
t
(4.29)
В оптимальном управлении наибольший интерес представляет
член
N
А
з
, характеризующий энергию, запасенную в объекте. Нор-
мально функционировать объект может только тогда, когда энергия,
запасенная в нем, соответствует номинальному режиму. Например,
допустим, что двигатель будет работать с постоянной скоростью
вращения
тогда, когда кинетическая энергия, запасенная в его
маховых массах, соответствует
. Теплообменник будет работать
нормально тогда, когда его пластины нагреваются до заданной
температуры
и ей соответствует некоторое количество тепловой
энергии, запасенной в пластинах и контурах теплообменника. Расход
жидкости при свободном истечении из резервуара, равный заданному
Q, соответствует определенной ее высоте, а значит и объему
резервуара. Таким образом, в резервуаре имеется запас веществ, в
частности жидкости.
Из приведенных примеров видно, что несоответствие запасенной
энергии номинальному режиму вызывает изменение управляемых
координат.
Увеличивая мощность N, можно ускорить процессы запасания
вещества и энергии в объекте, соответствующие номинальному ре-
жиму, и тем самым ускорить изменение управляемых координат.
Однако совершенно очевидно, что беспредельно увеличивать ее
нельзя. Мощность N, развиваемая объектом, ограничивается по двум
причинам: ограничением мощности источника питания и
53
ограничением, вызванным конструкцией объекта управления.
Поясним это примерами. Если электрический двигатель управляется
каким-либо усилителем (электронный, магнитный,
электромашинный), то мощность управления ограничивается
мощностью усилителя. Если двигатель управляется от сети
практически неограниченной мощности, то мощность управления
ограничивается конструкцией обмоток или коллектора.
Тепловая мощность, подводимая к теплообменнику, ограничи-
вается или проходными сечениями управляющих органов, или теп-
ловыми нагрузками, допустимыми для пластин.
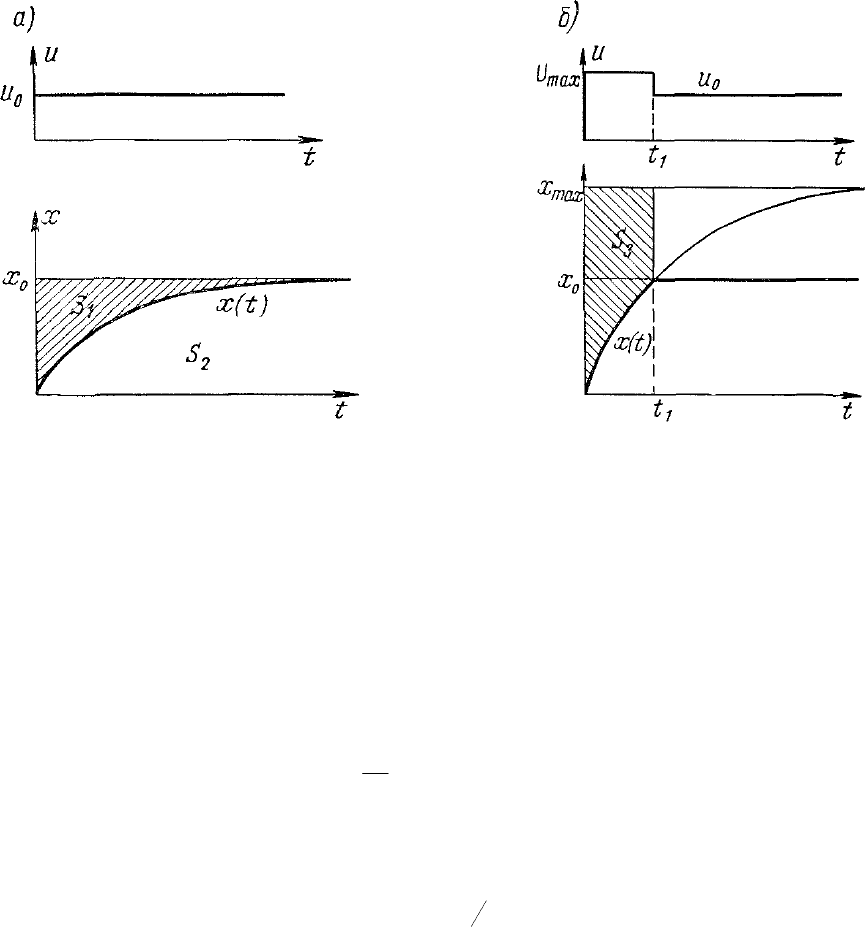
Рис. 4.3. Процессы в объекте управления, который описывается
дифференциальным уравнением первого порядка
Рассмотрим энергетические соотношения при оптимальном уп-
равлении некоторыми объектами. Начнем с объектов управления,
которые описываются линейными дифференциальными уравнениями
первого порядка,
.kux
dt
dx
T
(4.30)
Уравнение (4.30) описывает инерционное звено первого порядка.
Решение его хорошо известно при скачкообразном изменении и
.1 kuetx
T
t
(4.31)
54

Изменение координат и и х во времени показано на рис. 4.1, а.
Рассмотрим площадь
1
S
, ограниченную линией установившегося
состояния
0
x
и кривой
tx
, которая пропорциональна энергии,
запасенной в объекте управления. Возьмем электрическую цепь,
содержащую последовательно включенные индуктивность и
сопротивление. Тогда х будет соответствовать току
i
, а и —
приложенному напряжению, и решение (4.31) будет иметь вид
,i1i
0
T
t
et
где
.;i
0
R
L
T
R
u
Определяем площадь
.ii
0
0
01
TdteS
T
t
Возьмем половину произведения
uS
1
.
2
i
2
i
2
i
2
А
2
000
1
L
R
RLuT
uS
з
Получили хорошо известную формулу, которая дает величину
магнитной энергии, запасенной в индуктивности.
Площадь
2
S
, очевидно, пропорциональна полезной работе, со-
вершаемой на активном сопротивлении. Таким образом, энергия,
подведенная к объекту, расходуется на изменение запаса внутренней
энергии и на полезную работу. При отключении объекта запасенная
энергия превращается в полезную работу, вызывая изменение коор-
динаты х.
Увеличим управляющее воздействие до значения
max
U
. Коорди-
ната х должна принять установившееся значение
max
x
при том же
характере изменения
tx
(рис.4.3, б). Определим площадь
3
S
,
которая ограничена кривой
tx
до значения
0
x
.
Для определения площади нужно знать время
1
t
, легко
определяемое из решения (4.31),
,ln
0max
max
1
xkU
kU
Tt
55

или
,ln
0max
max
1
xx
x
Tt
так как
maxmax
xkU
.
При этом
.1
1
1
max
0
max3
T
t
t
T
t
eTxdtxeS
Покажем, что эта площадь равна площади
1
S
.11
0
ln
maxmax3
0max
max
1
TxeTxeTxS
xx
x
T
t
Энергия, запасенная объектом к моменту времени
1
t
, равна энер-
гии, соответствующей значению
0
x
. Это положение справедливо для
любых значений
0
x
и любых максимальных управляющих воз-
действий. Если теперь в момент
1
t
сделать переключение управляю-
щего воздействия от значения
max
U
до значения
0
U
, то управляемая
координата х сразу примет установившееся значение
0
x
. Это
произойдет потому, что запас энергии в объекте точно равен тому
запасу энергии, который необходим в номинальном режиме, а раз это
так, то нет причин, вызывающих изменение х. Для оптимального по
быстродействию управления требуется один интервал управления
длительностью
1
t
.
По истечении интервала
1
t
управление прекращать нельзя, его
нужно поддерживать на уровне
0
U
, чтобы удерживать координату на
значении
0
x
.
Многие объекты управления, содержащие интегрирующие
звенья, описываются уравнением вида
.ku
dt
dx
(4.32)
Запишем решение уравнения (4.32) при нулевых начальных ус-
ловиях и скачкообразном изменении U
.kuttx
(4.33)
Если задано значение
0
x
, то из (4.33) легко находится время
56
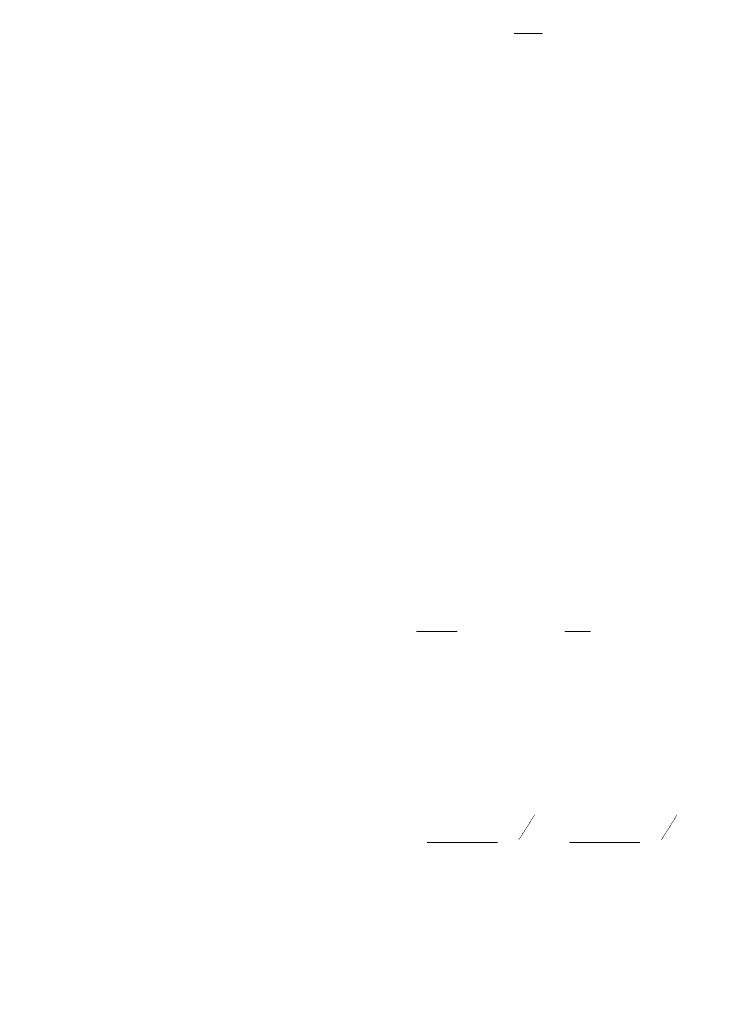
.
0
1
ku
x
t
Таким образом, интегрирующее звено совершает только полез-
ную работу, и в нем не запасается энергия. Для оптимального уп-
равления, т. е. для достижения
0
x
за минимальное время, требуется
максимальное значение воздействия
max
U
. Для объекта, который
описывается уравнением (4.32), необходим один интервал управления
длительностью
1
t
. После достижения заданного значения
координаты
0
x
управление должно прекращаться, т. е. и = 0.
Рассмотрим оптимальное управление объектами, которые опи-
сываются линейными дифференциальными уравнениями второго
порядка. Для наглядности представим себе объект, состоящий из двух
инерционных звеньев, включенных последовательно. Уравнение
такого объекта имеет вид
.
21
2
2
21
kux
dt
dx
TT
dt
xd
TT
(4.34)
Запишем решение (4.34) при нулевых начальных условиях и
скачкообразном управляющем воздействии
.1
21
21
2
21
1
kue
TT
T
e
TT
T
tx
T
t
T
t
(4.35)
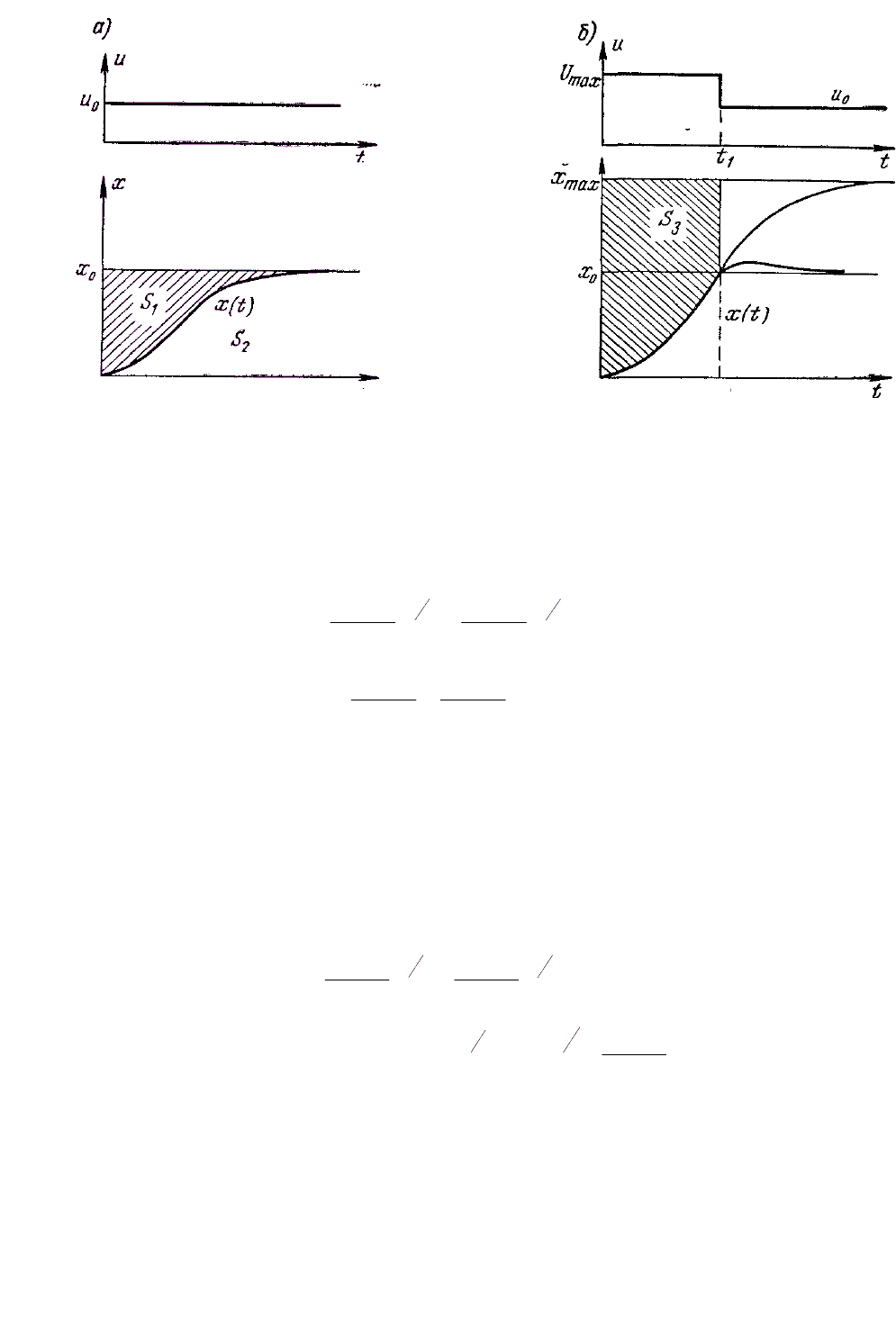
Изменения
tx
и м показаны на рис. 4.4, а. Очевидно, что пло-
щадь
1
S
пропорциональна энергии, запасенной в объекте, а площадь
2
S
— полезной работе.
57
Определим площадь
.
021
21
2
2
21
2
1
0
0
0
21
2
21
1
1
21
xTT
TT
T
TT
T
ku
dtkUe
TT
T
e
TT
T
S
T
t
T
t
Как и следовало ожидать, запасенная энергия пропорциональна
сумме энергий, запасенных в отдельных звеньях.
Увеличим входной сигнал до максимально допустимого значения
max
U
(рис. 4.4, б). Определим площадь
.
1
21
2
1
2
2maxmax21
0
max
21
2
21
1
3
2
1
2
1
21
TT
eTeTxxTT
dtkUe
TT
T
e
TT
T
S
T
t
T
t
t
T
t
T
t
Когда координата достигнет значения
0
x
, изменим
u
скачком от
max
U
до
0
U
. Определим время
1
t
(каким-либо численным методом),
за которое координата достигнет значения
0
x
из уравнения
58
Рис. 4.4. Процессы в объекте управления, который описывается
дифференциальным уравнением второго порядка
.1
max
21
2
21
1
0
2
1
1
1
kUe
TT
T
e
TT
T
x
T
t
T
t
Подставив значение
1
t
, найдем величину
3
S
.
Если сравнить площади
1
S
и
3
S
, то можно убедиться, что
13
SS
при любых
21
,TT
и
0max
UU
.
Таким образом, энергия, запасенная в объекте, будет
превосходить энергию, соответствующую номинальному режиму.
Вследствие этого выходная координата будет изменяться до тех пор,
пока запасенная энергия не станет
соответствовать номинальному
режиму, т.е. до значения
координаты
0
x
. Изменение
управляемой координаты
происходит в сторону ее
увеличения, как показано на рис.
4.4, б. Выясним подробнее
причины движения управляемой
координаты и выскажем некоторые
соображения по оптимальному
процессу.
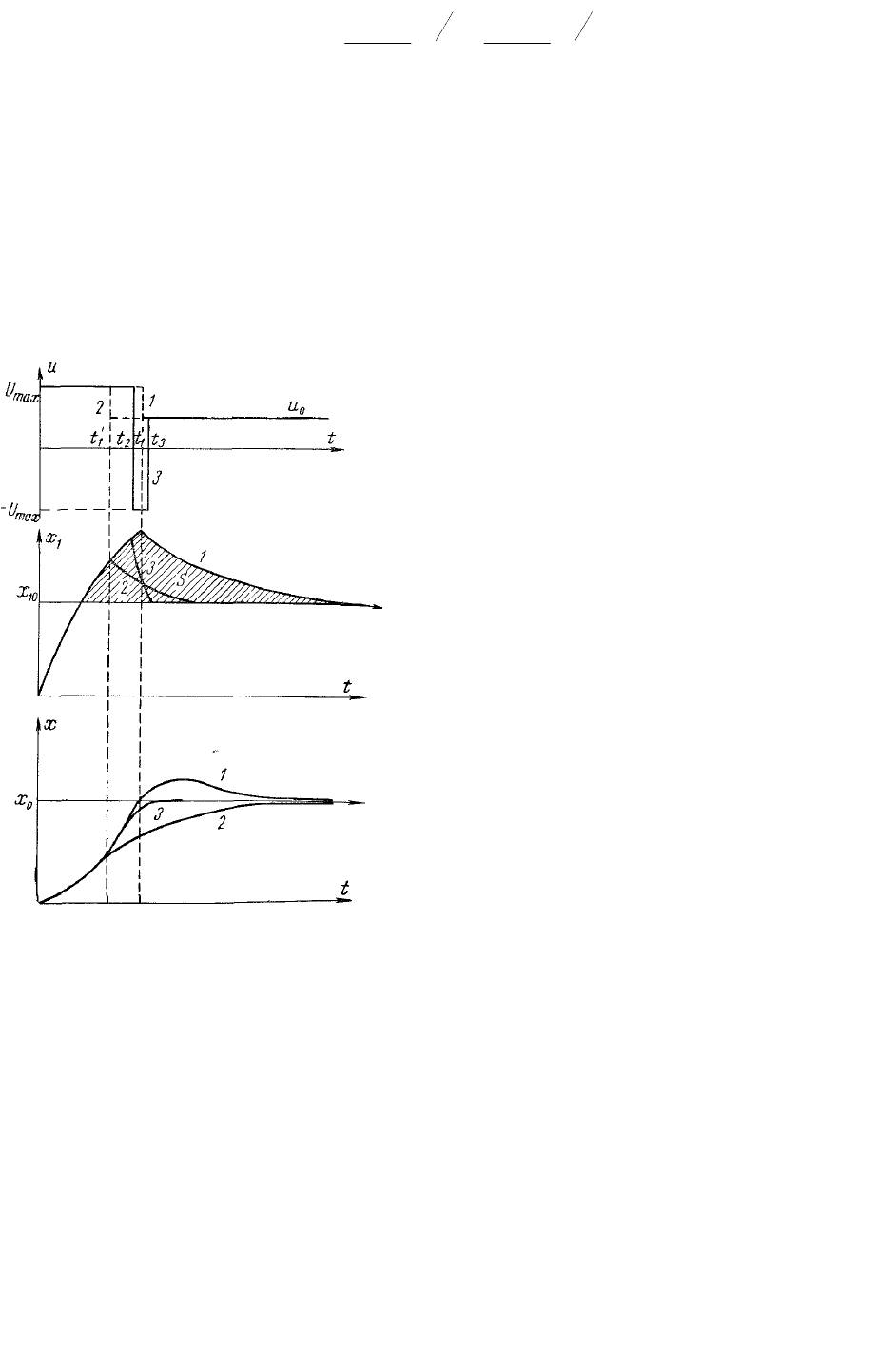
На рис. 4.5 показано изменение
всех координат, характеризующих
объект управления, и,
1
x
и х. При
длительности интервала
1
t
в звене
1 накапливается значительный
избыток энергии,
пропорциональный площади
3
S
. Этот избыток в первом звене
вызывает изменение координаты во втором звене в сторону ее
увеличения (траектории 1).
Сделаем переключение в момент времени
1
t
. В этот момент запас
энергии в системе равен запасу энергии при установившемся режиме,
т.е.
31
SS
,
59
Рис. 4.5. Анализ процессов при
различных алгоритмах
управления и нахождение
оптимального алгоритма

1
1
2
1
2
1
2
2
21
max
21max210
T
t
T
t
eTeT
TT
x
TTxTTx
На рис. 4.5 этому случаю соответствуют траектории 2. При этом
координата х не достигает значения
0
x
за конечное время. Очевидно,
траектории 1 и 2 не будут оптимальными, так как они не окан-
чиваются за конечное время, имеют перерегулирования и
дотягивания.
Управление координатой х можно осуществить другим путем.
Дадим объекту управления запас энергии, несколько больший, чем
требуется при номинальном режиме. При подходе к номинальному
значению управляемой координаты отнимем этот излишек путем
подачи отрицательного управляющего воздействия, равного макси-
мально допустимому, т. е.
max
U
. К моменту окончания управления
энергия и координата х должны быть равны заданным значениям.
Этот случай показан на рис. 4.5 траекториями 3. При этом процесс
заканчивается за конечное время и протекает без перерегулирований.
Этот процесс и будет оптимальным.
Из приведенного примера видно, что для оптимального управле-
ния требуется два интервала управления
max
U
, где управление
должно один раз менять знак. Для удержания координаты в
номинальном режиме управление прекращать нельзя, его следует
сделать соответствующим номинальному режиму
k
x
ux
0
0
.
Рассмотрим теперь объект, который описывается дифференци-
альным уравнением
.
2
2
ku
dt
xd
(4.36)
Объект представляет собой два интегрирующих звена, включен-
ных последовательно. Схема, на которой показано последовательное
соединение двух маломощных двигателей, изображена на рис. 4.6, а.
Если пренебречь их электромеханическими постоянными времени, а
за выходные координаты принять перемещение движков
1
x
и х, то
такая система будет описываться уравнением вида (4.36).
60
