Ляпидов В.C. Теоретические основы кибернетики. Методы оптимизации

Подождите немного. Документ загружается.

Напомним основные положения классического вариационного

исчисления. Вариации функционалов считались непрерывными и

линейными. Переменные, входящие в функционал или в уравнение

связи, ограничений не имели.

В практических задачах управления эти условия не всегда

соблюдались. Известно, что управляющие воздействия, которые

входят в функционалы, могут быть кусочно-непрерывными, т.е.

претерпевать разрывы первого рода. Примером таких управляющих

воздействий являются релейные. При некоторых условиях не только

управляющие воздействия, но и координаты объекта, в частности

производные, при управлении претерпевают разрывы. А это значит,

что нарушаются условия непрерывности.

Как указывалось ранее, на координаты и управления практически

всегда накладываются ограничения. Это соответствует тому, что

координаты и управления могут находиться в некоторых замкнутых

областях и даже находиться на границах этих областей.

Нарушение основных условий, на которых строится классическое

вариационное исчисление, не позволяет решать широкий круг задач

автоматического управления такими простыми способами, какие

были описаны выше.

Эти трудности преодолевает принцип максимума, разработанный

академиком Л.С. Понтрягиным и его коллегами.

Изложение принципа максимума встречает большие трудности,

т.к. его доказательство базируется на теории множеств и

функциональном анализе, которые не изучаются в курсе математики

вузов. Поэтому приведём упрощённое доказательство его, а основное

внимание уделим геометрическому и физическому толкованию

принципа.

Сделаем несколько предварительных замечаний. Запишем

уравнение системы управления:

 

nuuuxxx

,...,2,1i;,...,,,,...,,f

2121i



(3.6)

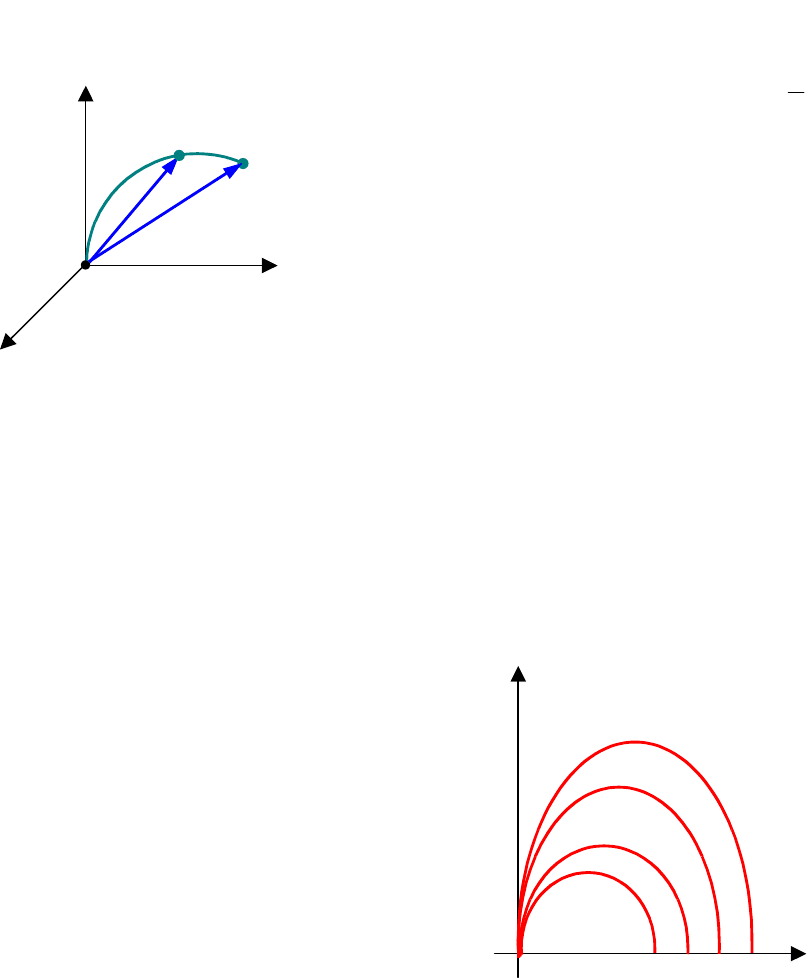
Введём n-мерное Евклидово пространство, которое образовано

координатами объекта, входящими в (3.6). Такое пространство в

теории управления называется фазовым. В качестве координат

пространства можно выбрать любые величины, характеризующие

объект управления. Положение точки в фазовом пространстве

определяется вектором, проведённым в неё из начала координат

пространства. В процессе управления фазовые координаты меняются,

а значить будет и меняться положение вектора.

Кривая, которая прочерчивается концом вектора, называется

фазовой траекторией, фазовое пространство, образованное

координатой и её производными

xxx



, показано на рис. 3.4.

Здесь же представлена фазовая

траектория АВС и вектор

Если придавать управлениям

различные значения, но так, чтобы

они не превосходили ограничений,

то в фазовом пространстве

образуется область, заполненная

траекториями (рис. 3.5).

Область фазовых

траекторий при

ограничении управления

приведена на рис. 3.5.

При дополнительных

ограничениях на координаты

в области фазовых





Рис. 3.4.

u=U

max



Рис. 3.5.

траекторий появляются подобласти, в которые не должны попадать

фазовые траектории.

Область фазовых траекторий при ограничении управления и при

дополнительном ограничении на координату

доп





приведена на рис.

3.6.

Из всего множества траекторий

нужно найти оптимальные траектории

и определить соответствующие им

управления.

Для нахождения оптимального

управления, кроме системы уравнений

объекта (3.6) задаётся ещё функционал,

определяющий цель управления:

 

min,...,,,,...,,fJ

21210





dtuuuxxx

(3.7)

Введём новую координату:

 

uuuxxx

,...,,,,...,,f

21210



(3.8)

Будем рассматривать систему из (n+1) уравнений, т.е.

 

nuuuxxx

,...,1,0i;,...,,,,...,,f

2121i



(3.9)

Соответственно системе будем иметь (n+1)-мерное фазовое

пространство, а систему уравнений (3.9) запишем в векторной форме:

 



(3.10)

Знак “” поставлен для того, чтобы отличать векторы в “n” и

(n+1)- мерных пространствах.

Допустим, применено управление

 

. Тогда

 

tх

будет

решением уравнения при известных начальных условиях. Представим

это решение графически в трехмерном фазовом пространстве рис. 3.7.

Начальное значение координат при

;

tt 

;

101

xx 

;

202

xx 

x

u= U

m ax



доп



Рис. 3.6.

конечное значение при

;

tt 

;

111

xx 

;

212

xx 

x

. Проведём через

точку

2111

,,0 xx

прямую N, параллельную оси

Начнём управление, в результате которого получим две

траектории: одну в плоскости х

,х

, которая в момент t

исходит из

начальной точки х

,х

и в момент t

проходит через точку х

,х

;

другую в пространстве всех координат, которая исходит из начальной

точки х

,х

и пересекает прямую N. Так как на прямой N

откладывается значение функционала J, то фазовая траектория,

пересекая N, даёт значение функционала J

в момент t

Для оптимального управления отрезок J

должен иметь

экстремальное значение. Рис. 3.7 даёт графическое толкование

решения системы (3.9).

Найдём теперь в пространстве (n+1) координат траектории,

которые являются оптимальными, и соответствующие им

управления. Для этого воспользуемся приёмами классического

вариационного исчисления. Кроме непрерывных управлений, нужно

рассматривать и кусочно-непрерывные. Это значит, что вариация

функции u, в частности

 

, может быть большой из-за разрывов

первого рода, поэтому будет большой и вариация функционала.

В линейном плане такие вариации рассматривать уже нельзя и

это сильно усложняет задачу, Однако Л.С. Понтрягиным и его

коллегами была предложена так называемая игольчатая вариация.

Смысл её состоит в том, что вариации функции рассматриваются

в виде импульса, действующего очень короткое время

 



рис. 3.8.

= J

m in

0 ,x

0,x

1 0

 

Рис. 3.7.

Импульс по амплитуде может

быть большим, но так как он

действует очень короткое время, то

вариация функционала J будет

малой. Поэтому приращение

функционала можно рассматривать

в линейном плане, а это уже сильно

упрощает задачу.

Рассмотрим нахождение

оптимального управления для

следующих условий. Задано уравнение объекта, имеющего “n”

координат:

 

,f

(3.

11)

и задан функционал:

 





dtux

min,fJ

(3.12)

Это задача со свободным концом траектории. Ей соответствует

случай, представленный на рис.3.7., если учесть, что при t

=T=const

координаты х

(Т) и х

(Т) могут принимать любые значения. При

изменении закона управления

будут меняться как значения

функционала J(T)=x

(T), так и значения координат х

(Т), х

(Т). Из

всего уравнения берётся то, при котором будет выполнено условие

(3.12).

Введём новую координату:

 



(3.13)

Будем рассматривать задачу в пространстве (n+1) координат с

уравнением:

 



(3.14)

где

 

xxxxx ,...,,,

210



 

uuuu ,...,,



Рис. 3.8.

Начальные условия известны в виде вектора

   

02010

,...,,,00

xxxx 

Предположим, что найдены оптимальное управление и траектория.

Обозначим их соответственно

 



 



. Оптимальная траектория

показана на рис. 3.7. (линия 1). В момент времени (Т) оптимальная

траектория проходит через точку с координатами х

,х

,…,х

отсекает на линии N отрезок J

min

В момент времени t=





T) введём игольчатую вариацию

длительностью (). В результате вариации дальнейшее движение

отклоняется от оптимальной траектории (см. рис. 3.7. линия 2). На

прямой N новая, варьируемая, траектория отсечёт новый отрезок J

Новый отрезок J

min

так как J

min

отсекается оптимальной

траекторией.

Запишем результат вариации:

     

   

 

   

 

 

tuxtux

txd

txtxtx

























~~~







(3.15)

Так как время  мало, то путь

 



приближённо можно

представить как произведение скорости

 



на время . Выразим

 

через вариацию и оптимальную траекторию, получим:

     

txtxtx

~~~







(3.16)

Подставим полученное выражение в уравнение объекта (3.13):

   

 

   

 

tutx

txtxd









Перейдём от векторов к координатам:

   

 

 

mnjj

uuuxxxtxtx

,...,,,,...,,f

2121j







(3.17)

Разложим полученную функцию в ряд Тейлора и сделаем

преобразования, аналогичные преобразованиям в разделе 3.3.

   

.,...,2,1,0

,,,...,,,,...,,f

2121

xuuuxxx

mnj









(3.18)

Полученное выражение есть не что иное, как линейная часть

приращения аргумента. Обратимся теперь к концу траектории при

Tt 

. Определим вариацию функционала в момент Т:

0JJJ

min2



Tt



Это соотношение можно записать так:



 TtTt



Введём вектор

 



таким образом, чтобы при

Tt 

скалярное

произведение

 



на

 



было равно

 



. Вектор

 



состоит из

непрерывных функций

 



, имеющих всюду, кроме точек разрыва

управления, непрерывные производные по t,

     





TTxTx



(3.19)

Так как

x



, то для того, чтобы выполнялось написанное

соотношение, координаты вектора

 



при

Tt 

должны быть равны:

   

,0,1

 TT



где

.,...,2,1i n

Получаем, что для неоптимальных управлений

0J 



и только при оптимальном

0J 



т.е. для оптимальных управлений вариация должна быть равна

нулю.

Свяжем вектор

 



с управлением и координатами объекта.

Найдём такой вектор

 



, который удовлетворяет условию:

       

constTTxttx 



Отсюда:

   

 

 tx

txd

ttx









Перейдём к координатам:

 

   

 

 

 



txt

txd

0 0i







(3.20).

Подставим в (3.20) значения производной

 



     

 

 

 



txxuuuxxx

ii2121

0 0i

0,...,,,...,,f





(3.21)

Изменим порядок суммирования в (3.21):

     

 

 

















n n

jmnjj

uuuxxx

0i 0

2121

0,...,,,...,,f



(3.22)

Так как



могут быть любыми, то равенства (3.22) соблюдаются

при равенстве нулю квадратных скобок. Тогда окончательно имеем:

     

tuuuxxx

jmn

,...,2,1i

,,...,,,,...,,f

2121











(3.23)

Следовательно, вектор

 



выражен через координаты векторов

управления и объекта.

Обратимся опять к вариации функционала

   

J  ttx



Заменим вариацию

 



выражением (3.15) и сократим на ξ.

   

 

     

 

 

,xf

f 



ttutttutx



(3.24)

Введём функцию

   

 

 

 ttutxH



(3.25)

Из равенства следует, что величина

достигает максимума

тогда, когда управление оптимально, т.е.

   

tutu





Значит, нужно в любой момент времени иметь такое значение

 



, при котором функция

достигает максимума.

Покажем на примере задачи о быстродействии, как использовать

полученные результаты.

Запишем уравнение объекта и функционал:

min

J Tdt







Введём координату

, пусть



Запишем функцию

 

0110





Равенство нулю функции

свидетельствует о том, что процесс

оптимальный.

Определим функции



 











Отсюда

2011

 CconsteC



Тогда

 

2110

CeCxuHH





Учитывая, что

C

, получим:

 



eCxuH

(3.26)

Таким образом, для рассматриваемого примера функция Н

должна быть максимальной и неотрицательной.

Функция Н, введённая для характеристики оптимальных

процессов, имеет вполне определённый физический смысл.





Так, если анализировать оптимальное управление для

механических систем, то функция Н есть не что иное, как полная

энергия системы, которая должна оставаться постоянной и

максимальной в процессе управления. Функции



является

импульсами, и задают направление движения. Для электрических,

например, систем функция Н является мощностью, а функция



импульсами.

Отсюда ясен физический смысл оптимального управления:

нужно в объект вводить такое количество энергии, которое

обеспечивало бы экстремум функционала и заданный закон

движения.

Энергия вводится с помощью управления

, поэтому и Н есть

функция от

Итак, было рассмотрено управление, когда граничные точки в

начале и конце управления строго ориентированы в фазовом

пространстве. Такая задача называется задачей с закреплёнными

концами фазовой траектории. Однако начальное и конечное

положения вектора

при t

и t

могут находиться на некоторых

поверхностях в фазовом пространстве. Очевидно, нужно знать те

точки на поверхностях, через которые должна пройти оптимальная

фазовая траектория. Точки эти находятся из условия

трансверсальности на концах траектории.

Сделаем несколько предварительных замечаний. Множество всех

точек

 

xxxx ,...,,



, которое задаётся уравнением

   

0,...,,ff



xxxx

(3.27)

называется гиперповерхностью пространства Х, а соотношение

(3.27)-уравнением этой гиперповерхности. Если функция

 

имеет

первые частные производные, то вектор

 















xgrad

,...,

(3.

28)

называется градиентом функции

 

Точки, в которых

 

xgrad f

обращается в нуль, называются

особыми точками. Гиперповерхность, не содержащая особых точек,

называется гладкой гиперповерхностью. Далее будем рассматривать

только гладкие гиперповерхности.

Если функция

 

линейна

 

0...f

11001



xaxaxax

(3.29)

то совокупность её точек в пространстве образуют

гиперплоскость. Для гиперплоскости вектор

 

xgrad

во всех точках

одинаков.

   

aaaxgrad ,...,,f

101



Возьмём на гиперповерхности точку “n” и определим в ней

градиент

 

ngrad f

. Если через точку “n” провести гиперплоскость так,

чтобы она была нормальна к

 

ngrad f

, то это будет касательная

гиперплоскость к гиперповерхности в точке “n”.

Оказывается, что оптимальная траектория и оптимальное

управление должны быть такими, чтобы вектор

 



в начальной

точке n

и конечной n

был параллелен векторам градиента в этих

точках. Или чтобы был ортогонален касательным векторам, лежащим

в касательных гиперплоскостях, проходящих через эти точки.

Таким образом, условие трансверсальности для оптимальных

процессов сводится к условию ортогональности векторов

 



 

