Ляпидов В.C. Теоретические основы кибернетики. Методы оптимизации
Подождите немного. Документ загружается.


процесс. Однако этот критерий плохо учитывает колебательность
процесса. Поэтому применяют более сложный обобщённый
интегральный критерий.
Если
2
12
1
22
1
2
...,,f
n
n
xxx)zux(
, то:
0
2
1
2
1
2
2
1
2
3
min...J dtxxx
n
n
(2.3)
Первый член в интеграле (2.3) запрещает длительное
существование отклонения х, а последующие члены длительное
существование производных.
Поэтому минимуму интеграла J
3
соответствуют достаточно
быстрые и плавные переходные процессы.
Значит, имея дифференциальное уравнение системы и задавая
весовые коэффициенты
i
можно вычислить значение интеграла J
3
.
Можно решить и обратную задачу, т.е. выбрать параметры замкнутой
системы таким образом, чтобы интеграл принимал минимальное
значение при заданных
i
. Интегральные критерии качества
подразумевают минимизацию свободного движения системы.
2.3. Задача ограничения энергетических ресурсов.
В подобных задачах требуется найти максимум функционала
T
xdt
0
4
maxJ
, если
T
AdtRy
0
2
5
J
т.е. постановка задачи аналогична, допустим, нахождение
максимального угла поворота вала двигателя
= J
4
при ограничении
количества тепла, которое выделяется в его якоре, Q =J
5
.
Все перечисленные задачи управления решаются с помощью:
1) классического вариационного исчисления;
11
2) принцип максимума Понтрягина;
3) динамического программирования Беллмона.
Классическое вариационное исчисление целесообразно
применять к задачам, у которых области изменения
Xx
и
Uu
открытые, т.е. не содержат ограничений. Это справедливо в случаях,
когда рассматриваются малые отклонения
x
и
u
от их
установившихся значений.
Принцип максимума Понтрягина применяется, когда области
Xx
и
Uu
замкнутые, а координаты векторов
x
и
u
могут
находиться на границах этих областей.
12

3. Математические основы теории оптимальных систем.
3.1. Функционалы, вариации и их свойства.
Методы решения вариационных задач схожи с методами
исследования функций на max и min.
Рассмотрим некоторую функцию
tx f
. Каждому значению
аргумента t соответствует число х. Допустим, х=е
-t/T
, тогда каждому
n
ttt ,...,,
21
соответствует числа
n
xxx ,...,,
21
.
Теперь возьмём функционал:
0
J dttx
Каждой функции х(t) будет соответствовать число J. Если х(t) =
е
-t/T
,тогда:
0
J dte
T
t
Каждому набору функций е
-t/T
будут соответствовать числа
i
J
.
Приращением (или вариацией) функции х(t) называется разность
между двумя функциями
х = x
1
(t) – x
2
(t). В данном примере вариация
х может быть равна
х = е
-t/T1
- е
-t/T2
.
Функция х(t) непрерывна, если малому изменению t
соответствует малое изменение х(t). Функционал непрерывен, если
малому изменению х(t) соответствует малое изменение J.
Если функционалы содержат производные, то в этом случае
понятие непрерывности усложняется. Поэтому рассматривают не
только разности самих функций, но и их производных, т.е.
txtxtxtxtxtx
kk
212121
,...,,
.
Считается, что функционал непрерывен, если малому изменению
функции и её производных соответствует малое приращение
функционала.
13

3.2. Понятие линейности функционала.
Линейными функционалами называются такие, для которых
справедливы следующие условия:
txctxc JJ
;
txtxtxtx
2
1
21
JJJ
.
Если приращение функции х(t) представляется в виде
txttxx
то и приращение функционала получается аналогично
txxtx JJJ
Линейная часть приращения функционала по отношению к
х
называется вариацией функционала и обозначается J. Вариация
функционала аналогична дифференциалу функции dx. Известно, что
если некоторая функция в точке t
0
имеет экстремум, то dx=0. Так как
вариация аналогична дифференциалу, то для того, чтобы функционал
имел экстремум, его вариация должна равняться нулю, т.е.
J=0.
Таким образом, если имеются несколько функций, и одна из них
доставляет экстремум функционалу, то эту функцию и нужно
выбирать в качестве решения задачи. Функции, на которых вариация
функционала
J=0, называются экстремалями.
3.3. Уравнение Эйлера. Уравнение Эйлера-Пуассона. Условия
трансверсальности.
Впервые вариационные задачи были поставлены в 1696г И.
Бернулли. Решались они многими видными математиками (Г.
Лейбниц, И. Ньютон, Г. Лопиталь), Однако наибольший вклад внёс
Леонард Эйлер, действительный член Петербургской Академии наук,
который и считается основоположником вариационного исчисления.
14
.

Было установлено, что для некоторых функций функционалы
принимают экстремальные значения. Как же среди множества
функций найти те, которые дают экстремум функционалу? Ответ на
этот вопрос даёт уравнение Эйлера, решение которого является
экстремалью. Приведём упрощённый вывод уравнения Эйлера. Пусть
задан функционал вида
1
0
,,fJ
t
t
dtxxt
(3.1)
Требуется найти функцию, которая даёт минимум функционалу
(3.1). Геометрически эта задача трактуется на рис. 3.1. Даны две
точки х(t
0
) и х(t
1
). Нужно найти уравнение такой линии 1, которое при
подстановке в функционал J. Давало бы ему экстремум.
Предположим, что такая линия найдена, т.е. найдена функция, её
описывающая. Проварьируем эту функцию и определим приращение
функционала.
1
0
1
0
,,f,,fJ
t
t
t
t
dtxxtdtxxxxt
(3.2)
Вариацию аргумента выберем таким
образом, чтобы δх(t
0
)=0 и δх(t
1
)=0, т.е.
варьируемая линия 2 должна проходить
через точку х(t
0
)=х
0
и х(t
1
)=х
1
.
Разложим проварьированную функцию вряд Тейлора.
15
Рис 3.1.

n
Rx
xd
fd
xx
xddx
fd
x
dx
fd
x
dx
df
x
dx
df
xxtxxxxt
2
2
22
2
2
2
2
2
1
,,f,,f
(3.3)
где R
n
- остаток порядка малости больше двух.
Первый член разложения (3.3) в фигурных скобках называется
первой вариацией, она линейна. Второй член называется второй
вариацией, она нелинейная. Ранее было условленно, что
рассматривается только линейная часть приращения функционала,
т.е. первая вариация, а поэтому всеми высшими вариациями можно
пренебречь.
Учитывая это, получим выражение для вариации функционала.
1
0
1
0
J
t
t
t
t
dtx
xd
df
xdt
dx
df
(3.
4)
Проинтегрируем по частям второе слагаемое в (3.4)
1
0
1
0
1
0
0
1
t
t
t
t
t
t
xdt
xd
df
dt
d
t
t
x
xd
df
dtx
xd
df
dtx
xd
df
(3.5)
Первое слагаемое в (3.5) равно нулю, т.к.
х(t
0
)
=
х(t
1
)
=0 по
условию задачи. Тогда вариация будет равна
0J
1
0
1
0
1
0
t
t
t
t
t
t
xdt
xd
df
dt
d
dx
df
xdt
xd
df
dt
d
xdt
dx
df
(3.6)
так как согласно свойствам функционалов, чтобы J имел
экстремум, его вариация J должна быть равна нулю. По лемме
Лагранжа интеграл (3.6) равен нулю тогда, когда подынтегральная
функция равна нулю, т.е.
0
,,,,
xx
F
dt
d
F
x
xxtf
dt
d
x
xxtf
(3.7)
Уравнение (3.7) называется уравнением Эйлера. Среди решений
этого уравнения следует искать экстремами. Чтобы установить,
16

действительно ли имеет место экстремаль, часто прибегают к
рассмотрению физической картины явления.
Покажем методику использования уравнения Эйлера. Требуется
определить, какое уравнение соответствует минимуму функционала
00
222
,,fJ dtxxtdtxTx
Находим производные, входящие в уравнение Эйлера.
xTxT
dt
d
xTx
xd
d
dt
d
F
dt
d
xxTx
dx
d
dx
df
F
x
x
22222
222
22
2
Получим уравнение Эйлера:
022
2
xTx
или
0
2
2
2
x
dt
xd
T
.
Решение уравнения:
T
t
T
t
eCeCtx
21
.
Если рассматривать некоторый затухающий процесс, то при
0; txt
. Это возможно тогда, когда
0
2
C
. Постоянную
1
C
найдём
из начальных (граничных) условий при
0
,0 xxt
. Отсюда
01
xC
.
Поэтому окончательно получим решение вида:
T
t
extx
0
. Это
уравнение экстремали. Однако, нетрудно заметить, что экстремаль
соответствует решению однородного дифференциального уравнения
вида:
0 x
dt
dx
T
т.о. для затухающих процессов решение уравнения Эйлера
(экстремаль) соответствует общему решению однородного линейного
дифференциального уравнения с постоянными коэффициентами.
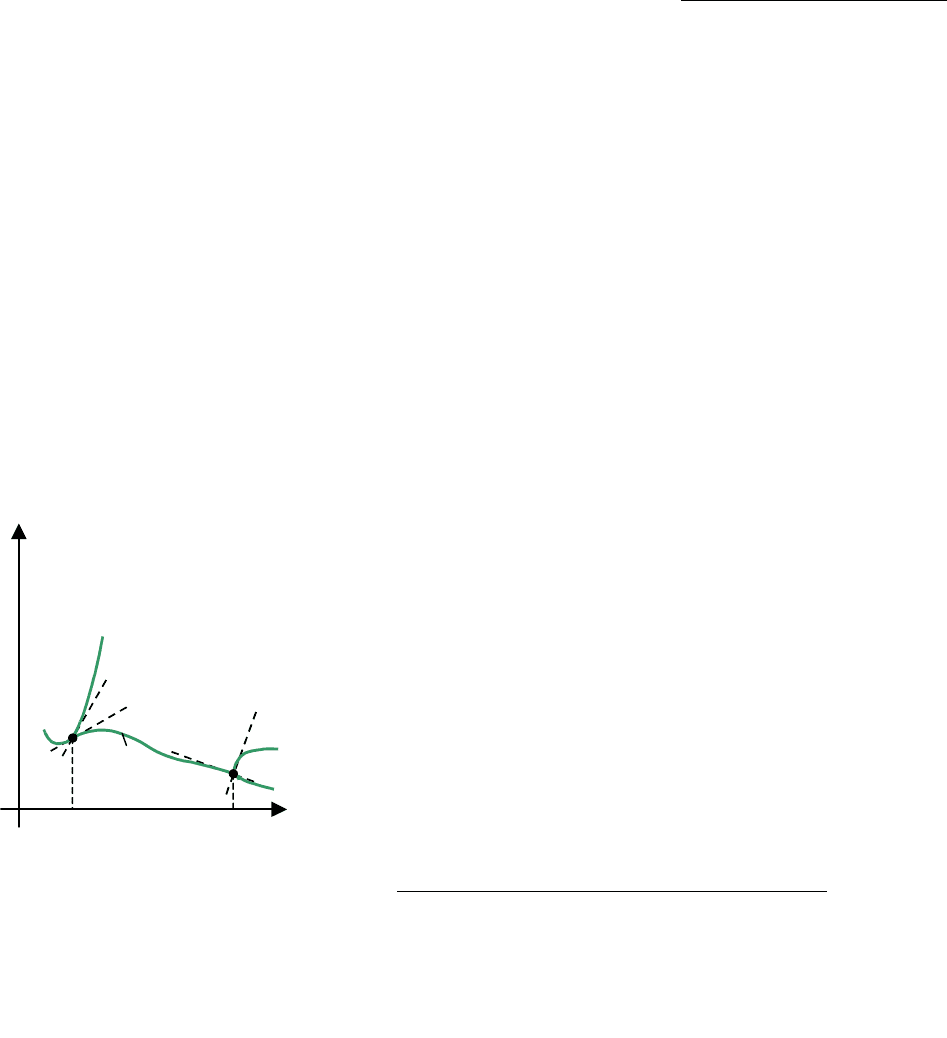
Меняя в функционале значение Т,
получим поле экстремалей (рис. 3.2).
Из этого поля выбирается та
экстремаль, которая удовлетворяет
требуемым условиям.
17
Рис. 3.2.

Итак, мы переходим к простейшей задаче вариационного
исчисления.
Теорема. Для того, чтобы функционал (3.1), определённый на
множестве функций
txx
, имеющих непрерывную первую
производную и удовлетворяющих граничным условиям
11
00
xtx
xtx
(3.8)
достигал на данной функции
tx
экстремума, необходимо, чтобы
эта функция удовлетворяла уравнению Эйлера:
0
xx
F
dt
d
F
Интегральные кривые уравнения Эйлера называются
экстремалями (лагранжевыми кривыми). При этом экстремум
функционала (3.1) может реализовываться только на тех экстремалях,
которые удовлетворяют уравнениям (3.8).
Надо иметь в виду, что кривая задача
1100
)(;)(
0
xtxxtx
F
dt
d
F
xx
(3.9)
не всегда имеет решение, а если решение существует, то оно
может быть не единственным.
Мы рассмотрели случай, когда в функционале (3.1) входила
только первая производная, однако (в общем случае) в функционал
могут входить и производные высших порядков.
Проводя для таких функционалов аналогичные рассуждения,
придём к уравнению Эйлера – Пуассона.
01...
2
2
n
x
n
n
n
xxx
F
dt
d
F
dt
d
F
dt
d
F
(3.10)
18
Сложнее обстоит дело, когда граничные точки не закреплены, а
могут находиться на некоторых поверхностях или линиях. Уравнение
Эйлера в этом случае дополняется условиями трансверсальности.
Смысл их заключается в следующем. Когда рассматривалось
уравнение Эйлера, то граничные точки были заданы. Такая задача
называется задачей с закреплёнными концами. Из граничных условий
находились постоянные интегрирования, и тем самым получалось
конкретное решение уравнения Эйлера. Если же экстремаль должна
проходить между поверхностями или линиями, то никаких
определённых граничных точек не задаётся. Они могут находиться в
любой точке поверхности или линии. Поэтому для определения
постоянных интегрирования нужно иметь некоторые условия.
Поясним с помощью построений, изображённых на рис. 3.3,
геометрический смысл этих условий.
Пусть имеются две линии,
t
и
)(t
. Требуется найти экстремаль,
которая соединила бы их по
кратчайшему пути. Экстремаль может
начинаться в любой точке на
)(t
и
оканчиваться в любой точке на
t
.
Точки эти находятся из следующих
соотношений, которые называются
условиями трансверсальности:
0
0
0
1
tt
xx
tt
xx
FxF
FxF
(3.11)
Условия трансверсальности дают возможность определить
постоянные интегрирования в уравнении Эйлера и тем самым
получить конкретное решение.
19
0
φ(t)
ψ(t)
x(t)
x(t
0
)
ψ(t
0
)
x(t
1
)
φ(t
1
)
t
t
1
t
2
x
.
.
.
.
Рис. 3.3

Часто условия трансверсальности сводятся к условиям
ортогональности, т.е. экстремаль и заданные линии или поверхности
должны пересекаться под прямым углом.
3.4. Задачи на условный экстремум.
Пусть задан функционал:
dtxxxxxxt
t
t
nn
1
0
,...,,,,...,,,fJ
2121
(3.12)
и дополнительные уравнения, называемые уравнениями связи:
nmmxxxt
ni
;,...,2,1i,0,...,,,
21
(3.13)
Подобные задачи встречаются в автоматическом управлении, так как
обычно задаётся функционал и система уравнений, описывающий
объект. Решаются такие задачи путём сведения их к безусловному
экстремуму. Для этого вводится новая функция:
xtF
i
m
i
i
,f
1
(3.14)
где
i
- множители Лагранжа.
Для функции F решают систему уравнений Эйлера:
.,...,2,1;0 njF
dt
d
F
jxxj
(3.15)
Эта система дополняется заданными уравнениями связи (3.13).Таким
образом, имеется “n” уравнений Эйлера и “m” уравнений связи. Их
достаточно для определения “n” неизвестных (x
j
) и “m” неизвестных
множителей (
i
) если заданы граничные условия. Необходимо только,
чтобы уравнения связи (3.13) не противоречило граничным условиям,
что в технических задачах всегда выполняется.
3.5. Принцип максимума.
20
