Ляпидов В.C. Теоретические основы кибернетики. Методы оптимизации
Подождите немного. Документ загружается.


натных осях
1
x
,
2
x
. точку
2
с
, а в координатных осях точку
1
x
, u точку
1
с
, т. е. точку стыкования приближенных решений. Для более
точного решения в окрестности точек
1
с
и
2
с
желательно уменьшить
приращение времени
t
. Это приведет к уменьшению угла наклона
лучей и к более точному стыкованию.
Возьмем координатные оси
1
x
,
t
и
2
x
,
t
и отложим в них прира-
щения
1
x
и
2
x
соответствующие приращениям
t
. Очевидно, что
это будут оптимальные процессы по координатам и
1
x
,
2
x
которые
показаны на рис. , б. Моменты переключения определяются
суммированием
t
для положительного и отрицательного
интервалов.
Если соединить точки, соответствующие приращениям
1
x
и
2
x
,
то получим фазовую траекторию
)(
21
xfx
(см. рис. , а), где точки
11
x
и
21
x
являются координатами переключения.
Из построения можно найти аналог производной
dt
dx
t
x
t
nxfnxf
2222
)()1(
Откладывая в координатных осях
2
x
и
2
x
аналог производной
соответственно
t
x
2
, построим приближенно фазовую траекторию
(рис. 4.16, в).
Таким образом, за одно построение удалось получить исчерпыва-
ющие сведения об оптимальном управлении, т.е. найдены моменты
переключения
1
t
и
2
t
, переходные процессы по всем координатам,
фазовые траектории и координаты переключения
11
x
и
21
x
. Это
является большим преимуществом метода. Даже при расчете
линейной системы пришлось бы решить систему трансцендентных
уравнений для определения
1
t
и
2
t
, четыре дифференциальных
уравнения для получения процессов
)(
1
tx
и
)(
2
tx
а также фазовых
траекторий
)(
22
xfx
и
)(
11
xfx
.
Несколько сложнее найти моменты переключения и фазовые тра-
ектории для объектов, которые описываются дифференциальными
91
уравнениями выше второго порядка. Моменты смены знака управ-
ляющего воздействия, в этом случае ищутся методом последователь-
ных приближений.
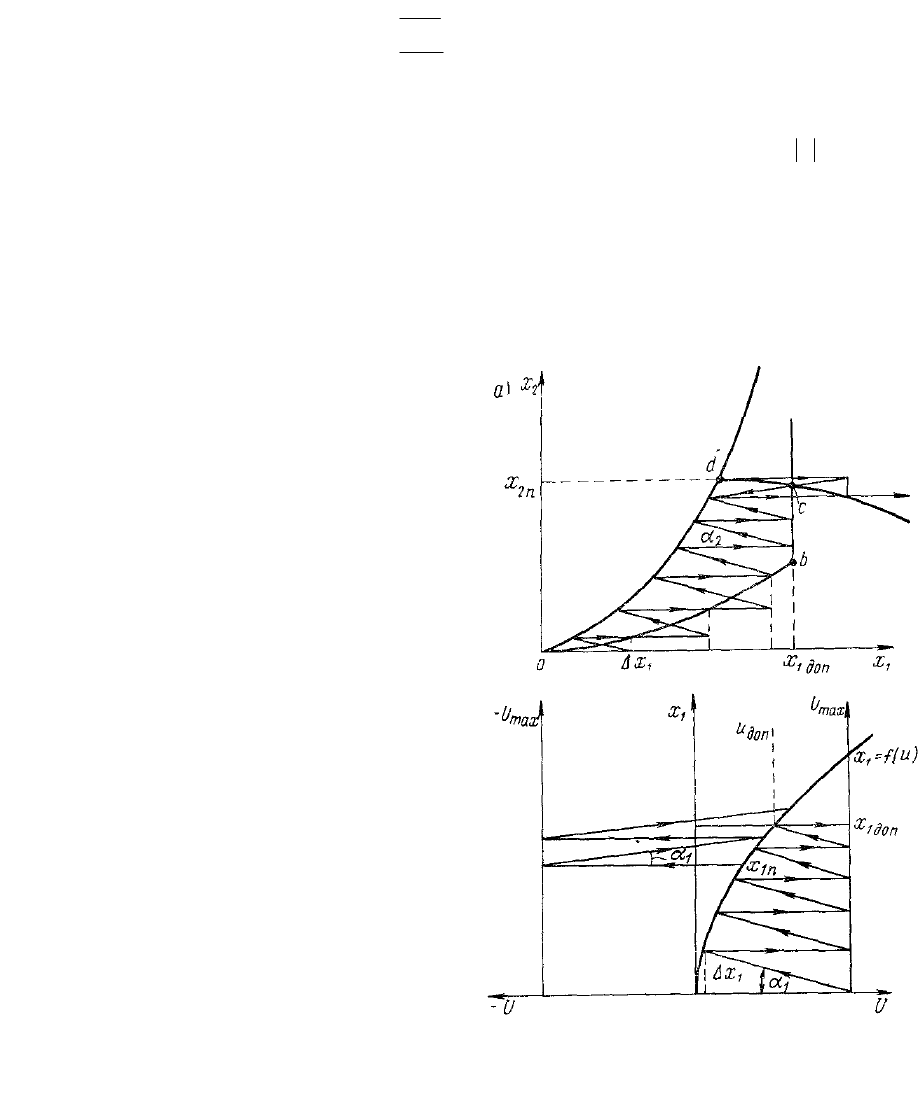
Графоаналитическим способом можно легко рассчитать моменты
переключения при ограничении координат. Пусть система состоит из
двух последовательно включенных звеньев, каждое из которых
описывается нелинейным дифференциальным уравнением:
122
2
11
1
)(
)(
xxf
dt
dx
uxf
dt
dx
(4.89)
Считаем, что начальные условия нулевые, а конечные
На управляющее воздействие наложено ограничение
max
Uu
.
Требуется перевести
систему из начального
состояния в конечное за
минимальное время при
ограничении
доп
xx
11
. Для
этого необходимо два
интервала и один участок
постоянства
доп
x
1
. Возьмем
две координатные системы и
отложим в них нелинейные
характеристики
)(
11
xfx
и
)(
22
xfx
(рис.4.17,а). В первой
координатной системе
отложим
max
U
и
max
U
,
наметим ограничения
n
x
2
и
n
x
1
. Определим углы
построения
1
и
2
для
первого и второго уравнений.
Начнем построение из
граничных точек при
max
U
и
92
б)
Рис.4.17. Нахождение фазовых
траекторий и алгоритма управления
графоаналитическим методом.

max
U
. Дальнейший ход указан стрелками. При достижении значения
доп
x
1
управление меняется скачком от
max
U
до
доп
U
. На фазовой
плоскости
1
x
,
2
x
получаем траекторию а, b, с, d c ограничением
координаты
1
x
. Времена переключения подсчитываются по
количеству приращений
t
на отдельных участках: время разгона до
доп
x
1
находится суммированием
t
на участке от
до b; время
движения при
доп
x
1
суммированием
t
на участке фазовой
траектории b, с; время торможения — суммированием
t
на участке
с, d. Зная моменты переключения, построим алгоритм управления
(рис.4.17 ,6).
93
4.6. Определение знака первого интервала.
Во всех рассмотренных примерах первый интервал произвольно
выбирался положительным. Очевидно, что знак первого интервала
надо выбирать, исходя из начальных и конечных условий. Если
начальные условия нулевые, то знак первого интервала определяется
знаком заданной координаты. Иначе говоря, если задана координата
n
x
, то управление следует начинать с положительного интервала,
если задана координата
n
x
, то с отрицательного интервала. При
ненулевых начальных условиях знак первого интервала выбирается
из следующих соотношений:
при
0
0
xx
n
первый интервал положительный;
при
0
0
xx
n
первый интервал отрицательный.
Данные соотношения справедливы только при равенстве нулю
всех производных в начальный и конечный моменты управления, т. е.
тогда, когда начальная и конечная точки фазовых траекторий лежат
на оси х или на линии установившихся состояний.
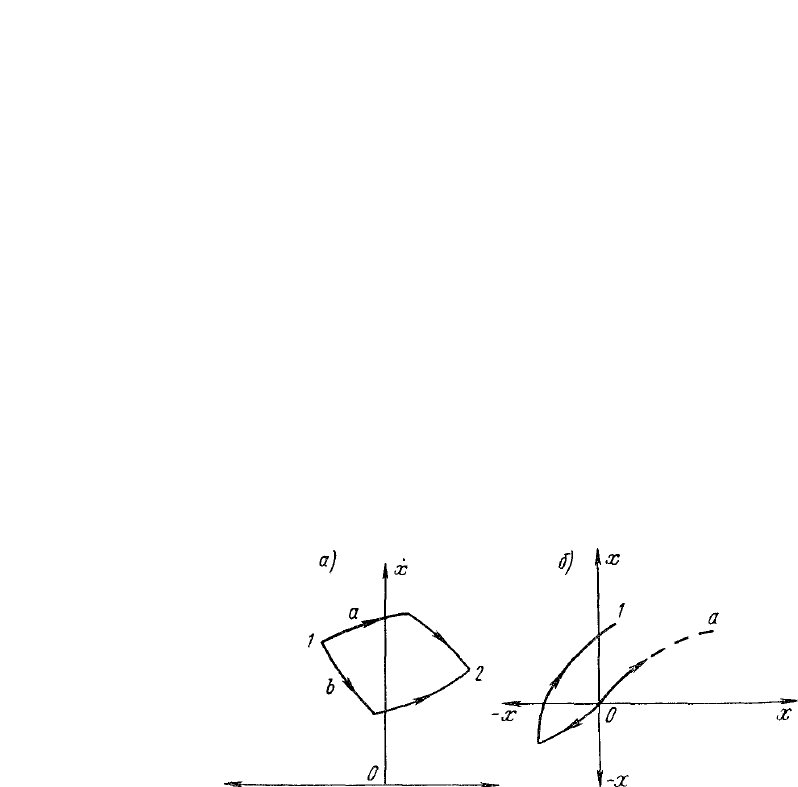
Рис.4.18. Определение знака первого интервала
Несколько сложнее определить знак первого интервала, когда
начальные и конечные точки фазовых траекторий лежат в фазовом
пространстве. На рис.4.18, а показана фазовая плоскость, где даны
две точки: начальная 1 и конечная 2. Из точки 1 в точку 2 можно
94
попасть по двум траекториям - a или b. Для движения по траектории
а управление следует начинать с положительного интервала, а по
траектории b - с отрицательного. Однако чем выше лежит фазовая
траектория, тем быстрее протекает процесс. Поэтому время движения
по траектории а будет меньшим, чем по траектории b. Естественно,
что процесс, характеризующийся траекторией а, будет оптимальным.
В данном простом случае легко определить знак первого интервала. В
более сложных случаях, когда трудно изобразить фазовые
траектории, приходится рассчитывать алгоритмы оптимального
управления для положительного и отрицательного первого интервала.
Алгоритм управления, дающий меньшее время, и будет
оптимальным.
Рассмотрим еще случай, показанный на рис.4.18, б. По фазовой
траектории а, соответствующей максимально допустимому поло-
жительному управляющему воздействию, попасть в точку 1 из начала
координат нельзя. Однако если сдвинуть фазовую траекторию влево
первым отрицательным интервалом, то можно достичь точки 1. При
затруднениях в получении фазовых траекторий нужно проделать
расчет для двух алгоритмов управления: с положительным и
отрицательным первым интервалом.
В примере (см. рис.4.18, б) функция оптимального управления
для первого положительного интервала вообще не имеет решения, т.
е. не существует алгоритма управления, начинающегося с
положительного интервала при данном ограничении и данных
граничных условиях. Следовательно, необходимость выбора знака
первого интервала в некоторых случаях может усложнить получение
оптимального алгоритма управления.
При рассмотрении оптимальных систем были использованы
простые примеры, в которых порядок дифференциальных уравнений
не превышал двух. Естественно, что трудоемкость расчетов с повы-
шением порядка дифференциальных уравнений сильно возрастает. В
таких случаях желательно применять цифровую вычислительную
95

машину. С ее помощью можно решать системы трансцендентных
уравнений, определяющих функцию оптимального управления. Для
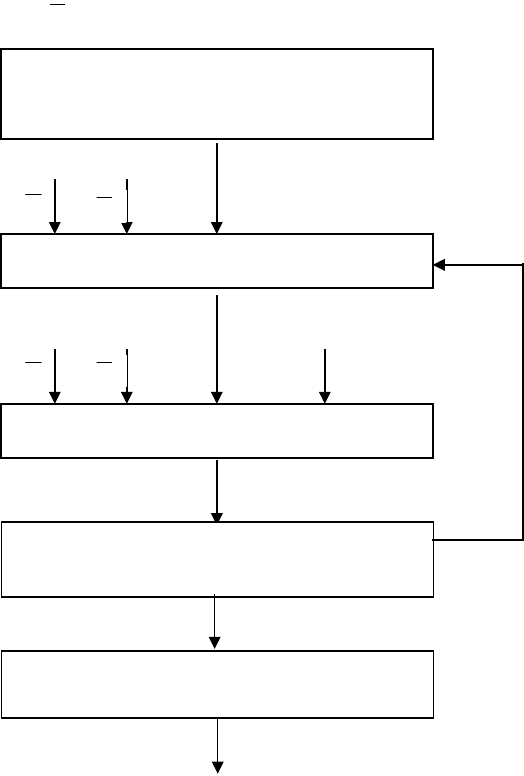
расчетов оптимальных управлений были предложены блок-схемы
вычислений на цифровой машине, одна из которых показана на рис.
4.19. Заметим, что вводить данные в ЦВМ нужно в цифровой форме;
при этом результаты вычислений получаются также в цифровой
форме. Для непосредственного управления это не совсем удобно, так
как требует преобразования непрерывных величин в цифровые и
наоборот.
Рассмотренные вопросы оптимального управления предполагали
реализацию алгоритмов разомкнутыми системами. В таких системах
не контролируется вектор состояния
x
и предполагается, что он
точно соответствует ожидаемому результату. Такие системы могут
применяться только в идеальных случаях, т. е. когда отсутствует
вектор возмущающих воздействий
z
, не меняются коэффициенты
дифференциальных уравнений и структура объекта управления. В
реальных системах трудно соблюсти все эти условия, а,
следовательно, и осуществить оптимальное управление в
разомкнутой системе.
При жестком алгоритме управления, т.е. при постоянных мо-
ментах переключения и действии возмущающих факторов, объект
будет попадать в заданную точку фазового пространства с избытком
или недостатком внутренней энергии. Это приведет к тому, что после
управления вектор состояния
x
сможет совершать свободные
движения, удаляясь при этом от заданной точки. Если величина
отклонений вектора
x
от заданной точки укладывается в заданную
точность при действии возмущающих факторов, то применить для
оптимального управления разомкнутую систему возможно. Однако
для этого следует проанализировать все возможные возмущающие
факторы и ошибки, которые они могут вызвать. Так как многие
возмущающие факторы, т.е. составляющие вектора
z
, часто не
известны, то и провести такой анализ нельзя. Реализация алгоритмов
96
управления в разомкнутых системах не так проста, как это кажется на
первый взгляд. Особенно она усложняется для реверсивных объектов
и объектов, которые требуют изменения моментов переключения.
Синтез оптимальных алгоритмов и анализ изменения координат
по изложенной методике лучше всего проводить на стадии проекти-
рования, выбирая, допустим, наиболее целесообразный агрегат или
технологическую схему. Очень полезно проделать расчеты оп-
тимального управления для выяснения возможностей объекта уп-
равления, даже если он и не автоматизируется.
Учитывая недостатки, которые присущи разомкнутым оптималь-
ным системам, их можно рекомендовать только в сугубо специаль-
ных случаях, допустим тогда, когда нельзя получить информацию
вектора состояния
x
.
)(tu
Рис.4.19. Блок-схема определения моментов переключения с помощью
цифровой вычислительной машины.
97
Выбор знака первого интервала
Определение
Проверка
Прерывание цифровых величин в
непрерывные
Память Функция оптимального
управления
o
x
n
x
max
U
o
x
n
x
5. Управление, близкое к оптимальному.
Рассмотренные выше системы оптимальны только в идеальных
случаях. Реальные системы всегда будут системами, близкими к
оптимальным. Это объясняется многими причинами. Так, например,
реализовать моменты переключения нельзя с большой точностью, так
как современные реле имеют зону нечувствительности, гистерезис,
конечное время срабатывания, т.е. не идеальные релейные
характеристики, необходимые для оптимального управления. Звенья
с насыщением, которые используются в качестве релейных
элементов, имеют зоны линейности и их нужно учитывать при
приближении к конечной цели управления. При малых входных
сигналах такие оптимальные системы работают, как обыкновенные
замкнутые линейные системы. Значительные упрощения и
идеализация допускаются и при математическом описании объектов.
Имеющиеся средства контроля фазовых координат также имеют
определенные погрешности измерения, из-за которых не удается
получить оптимальное управление. Кроме того, часто реализация
оптимальной системы бывает настолько сложна, что ее изготовление
и эксплуатация экономически невыгодны. Поэтому можно сразу
спроектировать не оптимальную систему, а систему, близкую к
оптимальной. Как правило, это приводит к упрощению системы за
счет снижения ее качества. Но в большинстве случаев выигрыш от
упрощения значительно превосходит проигрыш от ухудшения
качества.
Если теория оптимальных процессов, как это было видно, доста-
точно разработана, то вопросом реализации систем, близких к опти-
мальным, уделяется меньшее внимание, несмотря на их перспектив-
ность.
98

5.1. Уменьшение количества интервалов управления.
Сокращение количества интервалов управления возможно в двух
случаях. Первый случай предусматривает понижение порядка
дифференциального уравнения. Действительно, любой объект или
систему можно разбить на апериодические или интегрирующие
звенья. Апериодические звенья будут иметь разные постоянные
времени. Часто бывает, что некоторые из постоянных времени
значительно меньше остальных. Значит в звеньях, которые имеют
малые постоянные времени, будет запасаться относительно малое
количество энергии или вещества. Эти малые количества будут
незначительно сказываться на векторе состояния
x
, а поэтому ими
можно пренебречь. Правда, нет четких критериев, которые позволили
бы определенно решить, какими постоянными времени можно
пренебречь. По аналогии с теорией регулирования рекомендуется
пренебрегать теми постоянными времени, которые в 10 раз и более
меньше остальных. Если объект нельзя разбить на звенья, то следует
найти корни характеристического уравнения, соответствующего
дифференциальному уравнению. Некоторые корни могут быть более
чем в 10 раз больше остальных, поэтому ими пренебрегают. Большим
корням соответствуют быстро затухающие переходные процессы,
которые оказывают незначительное влияние на вектор состояния
x
.
Таким образом, пренебрегая некоторыми постоянными времени,
понижают порядок дифференциального уравнения, т.е. описывают
объект, допустим, не уравнением третьего порядка, а уравнением
второго порядка. Этим самым сокращается количество интервалов с
трех до двух, а это уже значительно упрощает реализацию алгоритма.
99

Второй случай связан с пренебрежением отдельными
интервалами. Встречаются такие соотношения параметров объекта,
граничных условий и вектора управления, что, наряду с достаточно
большими интервалами, некоторые интервалы становятся очень
малыми, допустим, десятые и сотые доли секунд. Если такие
интервалы нельзя реализовать с помощью имеющейся аппаратуры, то
ими приходится пренебрегать. Ошибка при этом получается
достаточно малой, так как за малый промежуток времени вектор
состояния не может сильно измениться. Кроме того, можно
сознательно пренебречь некоторыми интервалами управления,
обычно последними, которые, как правило, значительно меньше
первых, но так, чтобы цель управления достигалась с заданной
точностью. Иными словами, вектор состояния
x
должен попасть не в
точку, а в заданную область фазового пространства. На конкретном
примере покажем методику определения моментов переключения для
управления, близкого к оптимальному.
Рассмотрим объект, который описывается дифференциальным
уравнением второго порядка:
kux
dt
dx
TT
dt
xd
TT )(
21
2
2
21
(5.1)
Для оптимального управления необходимо иметь два интервала
управления и одну смену знака. Зададимся целью управлять объектом
с помощью одного интервала. При таком управлении может
возникать нежелательное отклонение вектора
x
. Значит,
переключение управляющего воздействия следует делать так, чтобы
отклонения вектора
x
не превосходили допустимых границ. Зададим
эту границу в виде ошибки
x
.
Для определения моментов переключения за конечное состояние
объекта примем значение координаты
xx
n
. При этом значении
координаты
0x
(рис.5.1).
Воспользуемся методом исключения постоянных
интегрирования. Допустим, что известно время
2
t
, за которое
100
