Ляпидов В.C. Теоретические основы кибернетики. Методы оптимизации
Подождите немного. Документ загружается.

к касательным гиперплоскостям в некоторых точках
гиперповерхности. Условия ортогональности и дают возможность
определить точки
0
tn
и
1
tn
на гиперповерхностях и тем самым
определить оптимальный процесс и оптимальную траекторию.
3.6. Динамическое программирование.
Метод динамического программирования разработан
американским математиком Р. Беллманом и его школой. Метод
развивался в процессе решения вариационных задач на
вычислительных машинах, поэтому содержит элементы
дискретности. Постановка основной вариационной задачи в
динамическом программировании такая же, как и в принципе
максимума Понтрягина. При изложении используются материалы
источников [8].
Рассмотрим пример решения вариационной задачи.
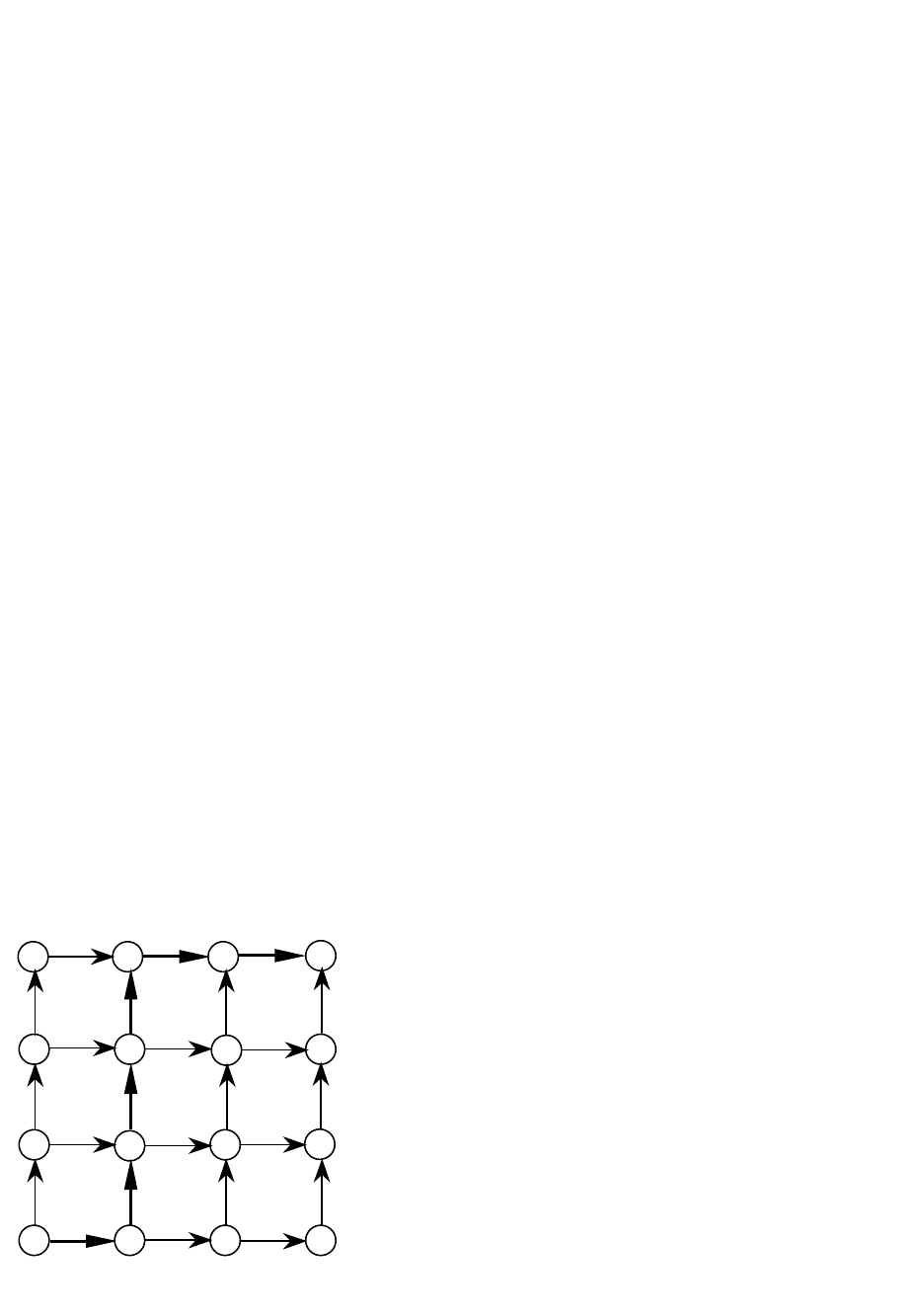
Пусть, между пунктами А и В (рис. 3.9) необходимо провести
железную или шоссейную дорогу так, чтобы стоимость строительства
была минимальной. Разобьём путь между А и В на горизонтальные и
вертикальные участки. Обозначим стоимость строительства на
каждом горизонтальном и вертикальном участке в некоторых
условных единицах (стоимость строительства можно заранее
подсчитать по карте). Обозначим узловые точки
i
C
,
i
D
,
i
E
,
i
F
,
i
G
.
31
38
25
10
0
12
26
37
46
24
39
54
37
44
52
59
56
Е
1
D
1
C
1
B
F
1
E
2
D
2
C
2
G
1
F
2
E
3
D
3
A
G
2
F
3
E
4
10
12
12
15
15
18
18
16
16
14
14
13
10
9
9
9
8
8
17
11
7
7
12
11
Начнём решение задачи с конечного пункта, за который примем
точку В.
В точку В можно попасть за один (последний) шаг или из точки
С
1
или из точки С
2
. Предположим, что каким-либо способом удалось
попасть в С
1
или С
2
. Затраты на последний шаг будут 12 или 10 ед.
Поставим величину затрат в кружки и
укажем направление последнего шага стрелками. Сместимся теперь в
точку D
i
. Опять считаем, что каким то образом эти точки уже
достигнуты. Проследим возможные пути в точку В. Из D
1
есть один
путь через С
1
, затраты при этом будут равны 25.
Из D
2
есть уже два пути: через С
1
и С
2
. Один путь даёт затраты
28, а другой 26. Через С
1
в В путь менее рационален, поэтому его из
дальнейших рассуждений исключаем. Ставим в D
2
кружок с
затратами 26 и стрелку оптимального управления в сторону С
2
. Также
анализируем точку D
3
. Из D
3
есть только один путь через С
2
. Ставим в
D
3
кружок с затратами 24 и стрелку оптимального управления в
сторону С
2
. Обратим внимание на то, что неоптимальная траектория
сразу исключается из рассмотрения. В этом и состоит смысл
динамического программирования. Перейдём к точке E
i
. Точки Е
1
и
Е
4
дают единственно возможные траектории.
Точки Е
2
и Е
3
дают по две траектории каждая, из которых
выбираем оптимальные, т.е. дающие минимум затрат. Причём из
точки Е
2
используем только оптимальную траекторию. Из всех
возможных путей из точек Е
1
, Е
2
, Е
3
, Е
4
остаются только четыре
(показаны стрелками). Переход таким же образом к точкам F
i
, G
i
и,
наконец, к А, получаем оптимальный путь, который на рисунке
отмечен жирной линией и даёт минимально возможный расход в
условных единицах- 59. Оптимальный путь можно трактовать как
оптимальную траекторию в принятой системе координат. Отметим
ещё раз, что по мере продвижения от В к А последовательно
исключились неоптимальные траектории. Это исключение
значительно упростило нахождение оптимальной траектории. При
Рис. 3.9.
32

простом переборе пришлось бы рассчитывать все траектории от А до
В, которых всего 25. Заметим ещё особенность, которая заключается
в том, что оптимальная траектория рассматривается не только на
одном шаге, но и учитываются другие шаги. На каждом шаге
траектория может быть и неоптимальной, но вся траектория в целом
оптимальна. Сформулирован принцип оптимальности, который
гласит, что любой отрезок оптимальной траектории также является
оптимальным, а будущее поведение процесса не зависит от его
предыстории, т.е. поведение системы в прошлом до начала
управления.
Следует, однако, сделать оговорку. Для примера был взят очень
простой случай. В реальных ситуациях даже разбиение на шаги и то
представляет большие трудности, причём шагов может быть многие
сотни. Поэтому идея метода динамического программирования в
большинстве случаев реализуется сложным образом. Дадим
математическую запись методу динамического программирования.
Пусть заданы динамические свойства объекта управления:
ux
dt
xd
,f
(3.30)
и начальные условия
0
0 xx
и
0
0 uu
. Выбираем критерий
оптимальности:
dtuxG ,J
0
(3.31)
где
u
- функция управления, которая доставляет минимум
функционалу J.
Обозначим через
minJ
0
xS
минимальное значение функционала,
которое зависит от начальных условий и вида управления.
Допустим, имеется оптимальная траектория
tx
, которая
обеспечивает минимальное значение интегралу J. Разобьем эту
траекторию на два участка: первый от
0t
до
t
, второй от
t
до
t
. Р. Беллманом был сформулирован принцип оптимальности,
согласно которому будущее поведение системы, т.е. при
t
, не
зависит от «предыстории», т.е. поведение системы в прошлом, и
33

определяется лишь её настоящее состоянием, т.е. в момент времени
t
. Поэтому если траектория от
0t
до
t
, оптимальная, то второй
участок оптимальной траектории также является оптимальным.
Кроме этого, второй участок может рассматриваться и как
самостоятельная траектория с начальными условиями
x
.
Используя принцип оптимальности, представим интеграл J в виде:
dtuxGdtuxGxS ,,min
0
0
(3.32)
.
Согласно принципу оптимальности Беллмана, если
tu
доставляет min интегралу
0
, dtuxG
,
то она будет доставлять также min интегралу
dtuxG ,
.
Поэтому, учитывая (3.32) получим
xSdtuxGxS
0
0
,min
(3.33)
где
xS
- функция от начального состояния
x
в момент
t
.
Будем считать τ достаточно малой величиной.
Тогда
uxxSxxSxS ,f
00
(3.34)
Применим к (3.34) формулу конечных приращений
dx
dS
uxxSuxxS ,f,f
00
(3.35)
Из (3.32) с учётом (3.35) можно записать
xd
dS
uxxSuxGxS
000000
,f,min
(3.36)
Вычтем из обеих частей последнего равенства
0
xS
0,f,min
0000
xd
dS
uxuxG
34
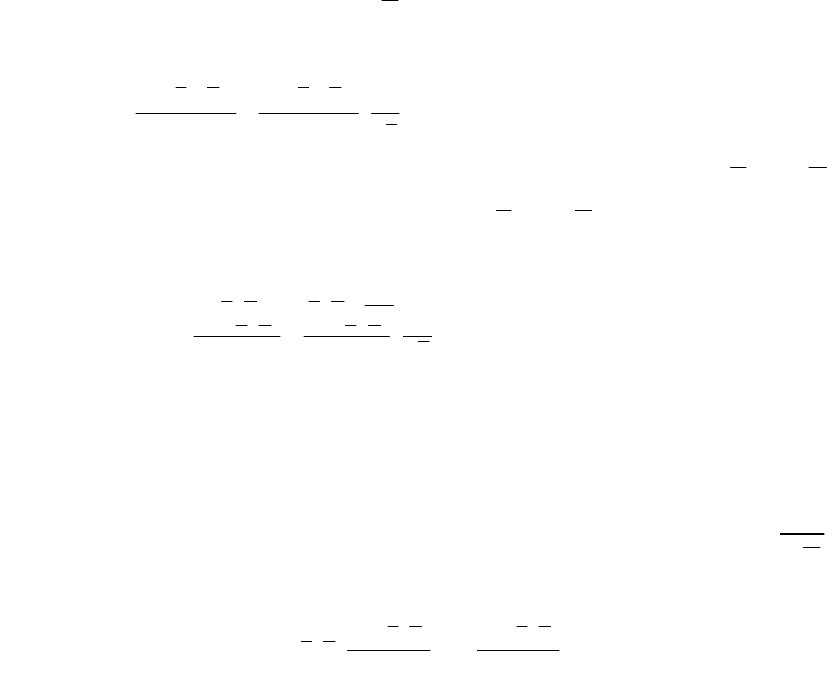
(3.37)
Для получения минимума по
u
нужно продифференцировать
(3.37) по
0
u
.
0
,f,
0
00
0
00
xd
dS
du
uxd
du
uxdG
(3.38)
Согласно принципу оптимальности начальные условия
0
x
и
0
u
можно заменить на текущие координаты
x
и
u
. Тогда получим
окончательно функциональные уравнения Беллмана:
0
,f,
0,f,
xd
dS
du
uxd
du
uxdG
dx
dS
uxuxG
(3.39)
Выражения (3.39) представляют собой нелинейные
дифференциальные уравнения в частных производных. Поэтому
применение этого метода в некоторых случаях требует сложных
расчётов и не всегда возможно в таком виде. Исключив из (3.39)
xd
dS
,
получим соотношение
du
uxd
G
du
uxdG
ux
,f,
,f
(3.40)
Заметим здесь, что функция S должна быть дифференцируемой
по х.
3.7. Способы нахождения фазовых траекторий.
Синтез оптимальных систем обычно проводится в фазовом
пространстве, поэтому необходимо уметь получать фазовые
траектории, т.е. находить их уравнения. При получении уравнений
фазовых траекторий предполагается, что управляющие воздействия
имеют вид единого скачка.
Предположим, что объект управления состоит из двух
последовательно включенных звеньев, уравнения которых имеют
вид:
35

1
2
11
x
dt
dx
T
xu
dt
dx
(3.41)
Требуется определить уравнение фазовой траектории, т.е.
функцию
12
f xx
.
Первый способ. Разделим почленно уравнения звеньев
1
1
1
212
xu
Tx
dx
dx
dt
dx
dt
dx
(3.42)
Проинтегрируем полученное выражение
CTxuux
xu
dxx
Tx
11
1
11
2
ln
(3.43)
Постоянную интегрирования С определяем из начальных
условий при
202101
,,0 xxxxt
.
CTxuuxx
101020
ln
, отсюда
101020
ln xuTuTxxC
(3.44)
Подставляя значение постоянной интегрирования (3.44) в (3.43),
окончательно получим уравнение фазовой траектории.
20110
1
10
2
ln xTxx
xu
xu
uTx
(3.45)
Второй способ. Уравнения для фазовых траекторий не, всегда
интегрируются. Тогда можно получить выражение для фазовой
траектории, исключая время из решений для отдельных координат.
Записываем решение для х
1
из (3.41)
T
t
eCCx
101
(3.46)
Определяем постоянную интегрирования С
1
из начальных
условий при t=0, x
1
=x
10
uxCuC
1010
;
.
Подставим С
1
в (3.46):
T
t
euxux
101
. (3.47)
Решаем второе уравнение из (3.41), учитывая х
1
:
36

T
t
euxu
dt
dx
10
2
;
.
210
2102
CeuxT
utCdteuxudtx
T
t
T
t
(3.48)
Из начальных условий при t=0, x
2
=x
20
находим постоянную C
2
:
.
10202
TuxxC
Подставим значение С
2
в решение (3.48):
.
1020102
uxTxeuxTutx
T
t
(3.49)
Из решения для x
1
определяем:
;ln
;
1
10
10
1
xu
xu
Tt
ux
ux
e
T
t
Подставляем эти значения в решение для х
2
:
.ln
ln
20110
1
10
10201
1
10
2
xTxx
xu
xu
uT
uxTxuxT
xu
xu
uTx
(3.50)
Естественно, что уравнение (3.50) для фазовой траектории не
отличается от уравнения (3.10), полученного первым способом.
Третий способ. Покажем другой вариант исключения времени из
решений дифференциальных уравнений.
Возьмем объект, который описывается следующей системой
уравнений:
.
;
2
212
1
11
T
xx
dt
dx
T
xu
dt
dx
(3.51)
Запишем решения для х
1
и х
2
.
,
;
21
1
2102
101
T
t
T
t
T
t
eCeCCx
eCCx
(3.52)
где
.
00
uСС
Определив постоянные интегрирования из начальных условий
при t=0, x
1
=x
10
, x
2
=x
20
подставив в (3.52), получим:
37
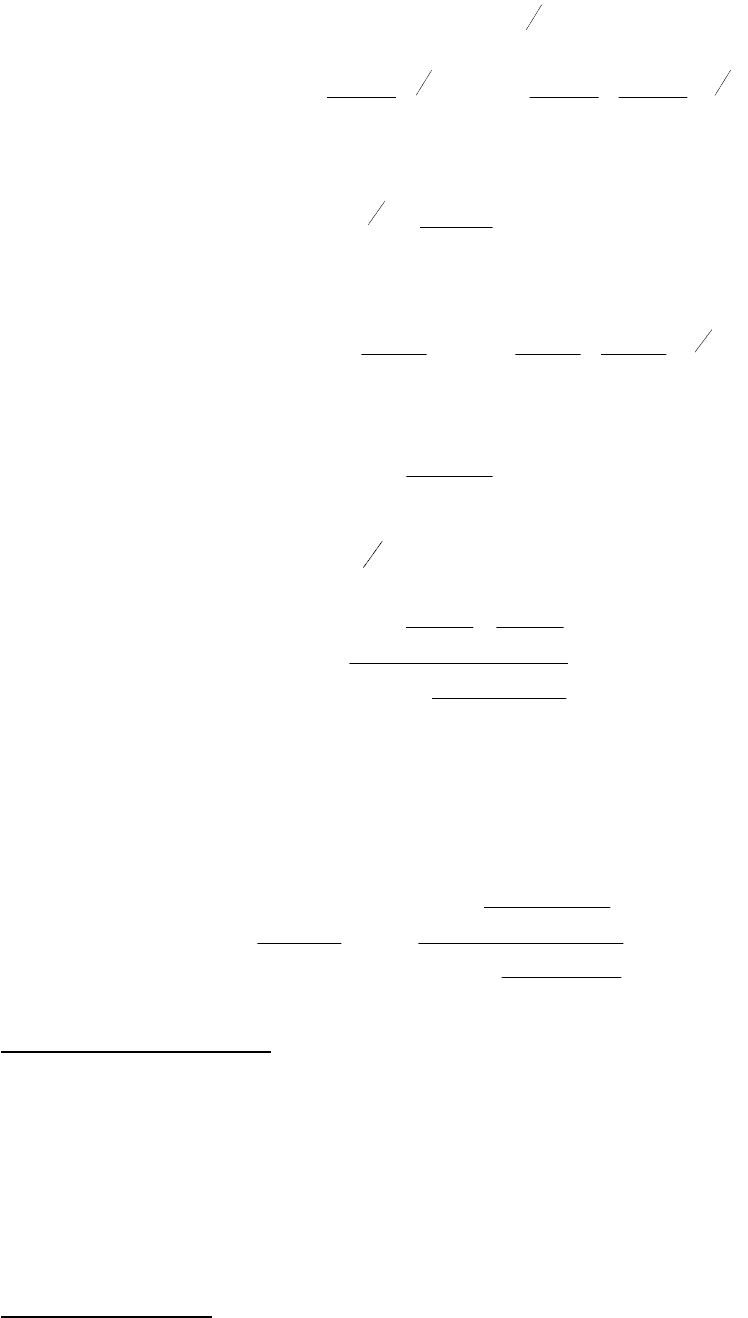
.
;
21
1
21
110
21
2
20
21
1
102
101
T
t
T
t
T
t
e
TT
Tx
TT
uT
xe
TT
T
uxux
euxux
(3.53)
Из решения (3.53) для x
1
определяем
.
10
1
1
ux
ux
e
T
t
(3.54)
Подставляем (3.54) в решение (3.53) для x
2
.
2
21
110
21
2
20
21
1
12
T
t
e
TT
Tx
TT
uT
x
TT
T
uxux
(3.55)
Из выражения (3.54) определяем время
.ln
1
10
1
xu
xu
Tt
(3.56)
Аналогично исключаем
T
t
e
из решения (3.53) для x
2
.ln
21
112
2
21
110
21
2
20
2
TT
TxuT
ux
TT
Tx
TT
uT
x
Tt
(3.57)
Так как фазовая траектория строится при одинаковых моментах
времени, то выражения (3.56) и (3.57) можно приравнять, получив
уравнение фазовой траектории:
.lnln
21
112
2
21
1102
20
2
1
10
1
TT
TxuT
ux
TT
TxuT
x
T
xu
xu
T
(3.58)
Четвертый способ. Выражение (3.58) довольно сложно и
неудобно для расчетов, так как относительно переменных оно
получилось в неявной форме. Поэтому иногда удобно задавать
уравнения фазовых траекторий в параметрической форме. Примером
такого задания может служить система решений (3.52). Находя при
одинаковых t значения x
1
и x
2
, можно построить фазовую траекторию.
Пятый способ. Бывают случаи, когда уравнение для фазовой
траектории не интегрируется, а из решений не исключается время.
Особенно часто встречаются такие случаи, когда объект описывается
38

системой нелинейных уравнений. Для качественной оценки фазового
портрета применяется метод изоклин.
Рассмотрим объект, который описывается следующей системой
уравнений:
.
;
21
2
1
xx
dt
dx
u
dt
dx
(3.59)
Разделим второе уравнение на первое:
.
21
1
2
u
xx
dx
dx
(3.60)
Проинтегрировать полученное уравнение фазовой траектории
довольно сложно. Поэтому построим фазовый портрет методом изо-
клин. Сущность метода состоит в следующем. Приравняем произ-
водную
1
2
dx
dx
некоторому постоянному числу m. Этому же числу будет
равна и правая часть уравнения (3.60)
.
21
m
u
xx
(3.61)
Уравнение (3.61) является уравнением некоторой кривой в
плоскости x
2
, x
1
. В любой точке этой кривой производная
1
2
dx
dx
постоянна и равна m.
Задаемся числами m
0
=0, m=m
1
, m=m
2
,…m=m
i
. Для этих чисел
решаем уравнение (3.61). В результате получим семейство парабол
(рис.3.10). На каждой параболе
отложим отрезки с наклоном,
соответствующим производной
i
1
2
m
dx
dx
.
Примем, что начальные условия
нулевые, т. е. при t=0, x
1
=x
2
=0. В
нулевой точке производная равна нулю,
так как т
о
=0. Плавной кривой
соединим отрезки на параболах т
1
, m
2
, .
39
x
2
x
1
m
2
m
1
m
0
m
3
2
1
Рис. 3.10 Фазовые траектории,
построенные методом изоклин
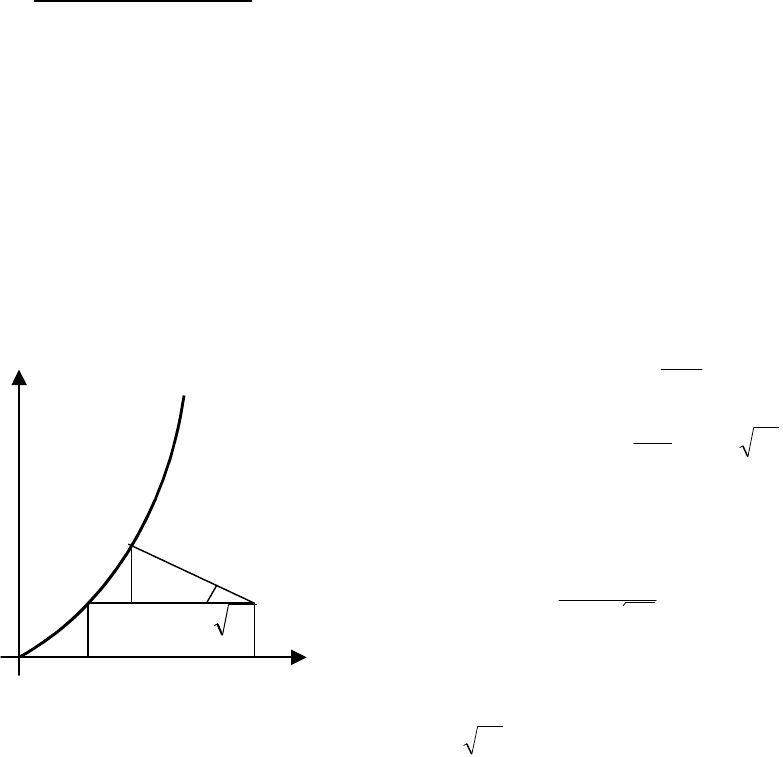
. ., т
i
(см. рис. 3.10, кривая 1). Получим интегральную кривую,
которая является фазовой траекторией. Если взять другие начальные
условия, то найдем другую фазовую траекторию (кривая 2).
Для точного построения фазовой траектории необходимо
построить много изоклин, т.е. линий равных значений производных.
Это связано с большим объемом вычислительной работы. Поэтому
метод изоклин удобно применить для выяснения качественной
стороны некоторого процесса. Обратим внимание на то, что методом
изоклин строятся фазовые портреты только на плоскости, т. е. для
объектов, которые описываются уравнениями не выше второго
порядка.
Шестой способ. Для расчетов процессов весьма полезными могут
быть графо-аналитические приближенные методы решения
дифференциальных уравнений. Наиболее распространен метод А. В.
Башарина, который был успешно использован для анализа и синтеза
нелинейных систем электропривода.
Сущность метода состоит в следующем. Заменим в системе урав-
нений (3.59) дифференциалы приращениями:
;
1
u
t
x
21
2
xx
t
x
После несложных
преобразований получим
.
;
21
2
1
t
xx
x
tux
(3.62)
Построим в координатных осях
х
1
, х
2
статическую характеристику
21
xx
(рис. 3.11).
40
21
xx
х
2
х
1
0
С
А
B
a
x
1
x
2
Рис. 3.11 Графо-аналитический
метод решения нелинейного
уравнения
