Лещинський О.Л. Економетрія
Подождите немного. Документ загружается.


91
íîâêè ìîæóòü áóòè íåïðàâèëüíèìè. Çðîçóì³ëî, ãåòåðîñêåäàñ-
òè÷í³ñòü º ñóòòºâîþ ïðîáëåìîþ, à òîìó ïîòð³áíî âì³òè çÿñîâóâàòè
¿¿ íàÿâí³ñòü.
5.2. Òåñòóâàííÿ íàÿâíîñò³ ãåòåðîñêåäàñòè÷íîñò³
ßê ³ â ðàç³ ìóëüòèêîë³íåàðíîñò³, ºäèíèõ ïðàâèë âèÿâëåííÿ ãåòå-
ðîñêåäàñòè÷íîñò³ íåìàº, à º ð³çíîìàí³òí³ òåñòè (êðèòåð³¿): êðèòåð³é µ,
ïàðàìåòðè÷íèé òà íåïàðàìåòðè÷íèé òåñòè Ãîëüäôåëüäà Êâàíäòà,
òåñò Ãëåéñåðà, òåñò ðàíãîâî¿ êîðåëÿö³¿ Ñï³ðìàíà òà ³í. Ðîçãëÿíåìî
ëèøå äåÿê³ ç íèõ.
Çàóâàæèìî, ùî ³íêîëè â õîä³ ïðîâåäåííÿ åêîíîìåòðè÷íèõ äîñë³ä-
æåíü ãåòåðîñêåäàñòè÷í³ñòü âãàäóºòüñÿ ³íòó¿òèâíî àáî âèñóâàºòüñÿ ÿê
àáñîëþòíå ïðèïóùåííÿ:
2
12
(
, , ...,
)
ii
up
f
xx x
σ=
.
Íàïðèêëàä, âèâ÷àþ÷è áþäæåò ñ³ì¿, ìîæíà ïîì³òèòè, ùî äèñïåð-
ñ³ÿ çàëèøê³â çðîñòຠâ³äïîâ³äíî äî çðîñòàííÿ äîõîäó. Îòæå, ïåðøèé
êðîê äî âèÿâëåííÿ ãåòåðîñêåäàñòè÷íîñò³ ãëèáîêèé àíàë³ç çì³ñòó
äîñë³äæóâàíî¿ ïðîáëåìè.
Êð³ì òîãî, ³ñíóº ãðàô³÷íèé ìåòîä òåñòóâàííÿ íàÿâíîñò³ ãåòåðîñêåäà-
ñòè÷íîñò³, ùî ´ðóíòóºòüñÿ íà âñòàíîâëåíí³ íàÿâíîñò³ ñèñòåìàòè÷íîãî
çâÿçêó êâàäðàò³â çàëèøê³â ðåãðåñ³éíî¿ ìîäåë³, ïîáóäîâàíî¿ íà îñíîâ³
ïðèïóùåííÿ ïðî â³äñóòí³ñòü ãåòåðîñêåäàñòè÷íîñò³ (ãðàô³÷íèé àíàë³ç).
5.2.1. Ïàðàìåòðè÷íèé òåñò Ãîëüäôåëüäà Êâàíäòà
Çàóâàæåííÿ. 1. Öåé òåñò çàñòîñîâóºòüñÿ äî âåëèêèõ âèá³ðîê.
2. Òåñò ïðèïóñêຠíîðìàëüíèé ðîçïîä³ë ³ íåçàëåæí³ñòü âèïàäêîâèõ
âåëè÷èí u
³
.
1-é êðîê:
ñïîñòåðåæåííÿ (âèõ³äí³ äàí³) âïîðÿäêóâàòè â³äïîâ³äíî äî âåëè÷è-
íè åëåìåíò³â âåêòîðà x
i
, ÿêèé ìîæå ñïðè÷èíèòè çì³íó äèñïåðñ³¿ çà-
ëèøê³â.
2-é êðîê:
â³äêèíóòè ñ ñïîñòåðåæåíü, ÿê³ ðîçì³ùåí³ âñåðåäèí³ âåêòîð³â âèõ³ä-
íèõ äàíèõ, äå
4
15
n
c
=
, n ê³ëüê³ñòü åëåìåíò³â âåêòîðà x
i
.

92
3-é êðîê:
ïîáóäóâàòè äâ³ ìîäåë³ íà îñíîâ³ çâè÷àéíîãî ÌÍÊ çà äâîìà ñòâî-
ðåíèìè ñóêóïíîñòÿìè ñïîñòåðåæåíü îáñÿãîì
2
nc
−
çà óìîâè, ùî
,
2
nc
m
−
≥
äå m ê³ëüê³ñòü çì³ííèõ.
4-é êðîê:
çíàéòè ñóìó êâàäðàò³â çàëèøê³â S
1
³ S
2
çà ïåðøîþ ³ äðóãîþ ìîäå-
ëÿìè:
111
tr
Suu
=
,
222
tr
Suu
=
,
äå u
1
³ u
2
çàëèøêè â³äïîâ³äíî çà ïåðøîþ ³ äðóãîþ ìîäåëÿìè.
5-é êðîê:
ðîçðàõóâàòè êðèòåð³é
*
2
1
,
S
F
S
=
ÿêèé ó ðàç³ âèêîíàííÿ ã³ïîòåçè
ïðî ãîìîñêåäàñòè÷í³ñòü â³äïîâ³äàòèìå F-ðîçïîä³ëó ç
1
(
2
)
2
nc m
−−
γ=
,
2
(
2
)
2
nc m
−−
γ=
ñòóïåíÿìè ñâîáîäè;
çíà÷åííÿ êðèòåð³þ
*
F
ïîð³âíÿòè ç òàáëè÷íèì çíà÷åííÿì F-êðè-
òåð³þ ïðè âèáðàíîìó ð³âí³ çíà÷óùîñò³ α ³ â³äïîâ³äíèõ ñòóïåíÿõ ñâî-
áîäè; ÿêùî
*
òàáë
FF
≤
, òî ãåòåðîñêåäàñòè÷í³ñòü â³äñóòíÿ.
Çàóâàæåííÿ: ÷èì á³ëüøå çíà÷åííÿ
*
F
, òèì á³ëüøà ãåòåðîñêåäàñ-
òè÷í³ñòü çàëèøê³â.
5.2.2. Íåïàðàìåòðè÷íèé òåñò
Ãîëüäôåëüäà Êâàíäòà
Öåé òåñò áàçóºòüñÿ íà âñòàíîâëåíí³ ê³ëüêîñò³ ï³ê³â çíà÷åíü çà-
ëèøê³â ï³ñëÿ âïîðÿäêóâàííÿ (ðàíæóâàííÿ) ñïîñòåðåæåíü çà x
ij
. ßêùî
äëÿ âñ³õ çíà÷åíü çì³ííî¿ x
ij
çàëèøêè ðîçïîä³ëÿþòüñÿ ïðèáëèçíî îä-
íàêîâî, òî äèñïåðñ³ÿ ¿õ îäíîð³äíà ³ ãåòåðîñêåäàñòè÷í³ñòü â³äñóòíÿ.
ßêùî âîíà çì³íþºòüñÿ, òî ãåòåðîñêåäàñòè÷í³ñòü ïðèñóòíÿ.
Çàçíà÷èìî, ùî öåé òåñò íå ö³ëêîì íàä³éíèé äëÿ ïåðåâ³ðêè íà ãå-
òåðîñêåäàñòè÷í³ñòü. Îäíàê â³í äóæå ïðîñòèé ³ ÷àñòî âèêîðèñòîâóºòü-
ñÿ äëÿ ïåðøî¿ îö³íêè íàÿâíîñò³ ãåòåðîñêåäàñòè÷íîñò³ ìíîæèíè ñïî-
ñòåðåæåíü.

93
5.2.3. Òåñò Ãëåéñåðà
Ïåðåâ³ðêà íà ãåòåðîñêåäàñòè÷í³ñòü áàçóºòüñÿ íà ïîáóäîâ³ ðåãðå-
ñ³éíî¿ ôóíêö³¿, ùî õàðàêòåðèçóº çàëåæí³ñòü âåëè÷èíè çàëèøê³â çà ìî-
äóëåì â³ä ïîÿñíþþ÷î¿ çì³ííî¿ x
j
, ÿêà ìîæå çóìîâèòè çì³íó äèñïåðñ³¿
çàëèøê³â.
Àíàë³òè÷íà ôîðìà ðåãðåñ³éíèõ ôóíêö³é ìîæå ìàòè âèãëÿä
u
=
a
0
+a
1
x
j
,
u
=
a
0
+a
1
x
j
-1
,
u
=
a
0
+a
1
x
j
1/2
³ ò. ³í.
гøåííÿ ïðî â³äñóòí³ñòü ãåòåðîñêåäàñòè÷íîñò³ çàëèøê³â ïðèé-
ìàºòüñÿ íà îñíîâ³ çíà÷óùîñò³ êîåô³ö³ºíò³â a
0
³ a
1
. Ïåðåâàãà öüîãî ìå-
òîäó ïîëÿãຠâ ìîæëèâîñò³ ðîçð³çíÿòè âèïàäîê ÷èñòî¿ (a
0
=
0, a
1
≠
0)
³ çì³øàíî¿ (a
0
≠
0, a
1
≠
0) ãåòåðîñêåäàñòè÷íîñò³. Çàëåæíî â³ä öüîãî ïî-
òð³áíî âèêîðèñòîâóâàòè ð³çí³ ìàòðèö³ S.
Îñê³ëüêè ÿâèùå ãåòåðîñêåäàñòè÷íîñò³ ïîâÿçàíå ç òèì, ùî çì³íþ-
þòüñÿ äèñïåðñ³¿ çàëèøê³â, à êîâàð³àö³ÿ ì³æ íèìè â³äñóòíÿ, òî ìàòðè-
öÿ S ó ñï³ââ³äíîøåíí³
()Muu
′
=
2
u
S
σ
ìຠáóòè äîäàòíî âèçíà÷åíîþ é
ä³àãîíàëüíîþ.
Ïðèêëàä. Ïåðåâ³ðèòè ã³ïîòåçó ïðî â³äñóòí³ñòü ãåòåðîñêåäàñòè÷-
íîñò³ äëÿ ïîáóäîâè ìîäåë³, ÿêà õàðàêòåðèçóº çàëåæí³ñòü çàîùàäæåíü
â³ä äîõîä³â íàñåëåííÿ. Ñòàòèñòè÷í³ äàí³ íàâåäåíî â òàáëèö³.
гê Çàîùàäæåííÿ Äîõ³ä
1 1,36 14,87
2 1,2 14,4
3 1,7 13,8
4 1,84 15,6
5 2,1 15,94
6 1,12 16,9
7 1,89 17,7
8 2,3 18,67
9 2,5 18,04
10 1,17 19,5
11 1,9 21,4
12 1,95 22,7
13 2,87 25,7
14 2,6 27,18
15 1,75 28,9
16 1,96 29,45
17 1,4 30,07
18 2,99 30,2

94
Ðîçâÿçàííÿ. ²äåíòèô³êóºìî çì³íí³: y çàîùàäæåííÿ, x äîõ³ä.
Ñïåöèô³êóºìî ìîäåëü ó âèãëÿä³
01
,
ya axu
=+ +
01
,
y
aax
=+
äå è ñòîõàñòè÷íà ñêëàäîâà ìîäåë³.
Äëÿ ïåðåâ³ðêè ã³ïîòåçè ïðî â³äñóòí³ñòü ãåòåðîñêåäàñòè÷íîñò³ çà-
ëèøê³â ìîäåë³ çàñòîñóºìî ïàðàìåòðè÷íèé òåñò Ãîëüäôåëüäà Êâàíäòà.
1-é êðîê:
ñïîñòåðåæåííÿ âïîðÿäêóºìî çà çðîñòàííÿì çà âåëè÷èíîþ äîõîäó
(âåêòîð x)
, ÿêèé ìîæå ñïðè÷èíèòè çì³íó äèñïåðñ³¿ çàëèøê³â.
гê Çàîùàäæåííÿ Äîõ³ä
1 1,7 13,8
2 1,2 14,4
3 1,36 14,87
4 1,84 15,6
5 2,1 15,94
6 1,12 16,9
7 1,89 17,7
8 2,5 18,04
9 2,3 18,67
10 1,17 19,5
11 1,9 21,4
12 1,95 22,7
13 2,87 25,7
14 2,6 27,18
15 1,75 28,9
16 1,96 29,45
17 1,4 30,07
18 2,99 30,2
2-é êðîê:
â³äêèíåìî ñ ñïîñòåðåæåíü óñåðåäèí³ âåêòîðà âèõ³äíèõ äàíèõ, äå
4
15
n
c
=
, n ê³ëüê³ñòü åëåìåíò³â âåêòîðà x.
Îòæå,
418
4.
15
c
⋅
=≈

95
Îòðèìàºìî äâ³ ñóêóïíîñò³ ñïîñòåðåæåíü îáñÿãîì
18 4
7.
2
−
=
Ïåðøà ñóêóïí³ñòü ñïîñòåðåæåíü:
1 1,7 13,8
2 1,2 14,4
3 1,36 14,87
4 1,84 15,6
5 2,1 15,94
6 1,12 16,9
7 1,89 17,7
1 1,95 22,7
2 2,87 25,7
3 2,6 27,18
4 1,75 28,9
5 1,96 29,45
6 1,4 30,07
7 2,99 30,2
Äðóãà ñóêóïí³ñòü ñïîñòåðåæåíü:
3-é êðîê:
ïîáóäóºìî äâ³ ìîäåë³ íà îñíîâ³ çâè÷àéíîãî ÌÍÊ çà äâîìà ñòâî-
ðåíèìè ñóêóïíîñòÿìè ñïîñòåðåæåíü:
=+
1
0,7411 0,05514 ,
y
x
=−
2
2,9371 0,02595 .
yx
4-é êðîê:
çíàéäåìî ñóìó êâàäðàò³â çàëèøê³â S
1
³ S
2
çà ïåðøîþ ³ äðóãîþ ìî-
äåëÿìè:
111
0,8149,
tr
Suu
==
222
2,1628,
tr
Suu
==
äå u
1
³ u
2
çàëèøêè â³äïîâ³äíî çà ïåðøîþ ³ äðóãîþ ìîäåëÿìè.
5-é êðîê:
ðîçðàõóºìî êðèòåð³é
*
2
1
2,1628
2,654,
0,8149
S
F
S
== ≈
ÿêèé ó ðàç³ âèêî-
íàííÿ ã³ïîòåçè ïðî ãîìîñêåäàñòè÷í³ñòü â³äïîâ³äàòèìå F-ðîçïîä³ëó

96
ç
1
1
(
2
)
5,
2
nc m
−−
γ= =
1
2
(
2
)
5
2
nc m
−−
γ= =
ñòóïåíÿìè ñâîáîäè;
1
1;
mm
=+
çíà÷åííÿ êðèòåð³þ
*
F
ïîð³âíÿºìî ç òàáëè÷íèì çíà÷åííÿì F-êðè-
òåð³þ ïðè ð³âí³ çíà÷óùîñò³ α
=
0,05 ³ â³äïîâ³äíèõ ñòóïåíÿõ ñâîáîäè:
F
òàáë
=
F(0,05; 5)
=
5,05.
Îñê³ëüêè
*
òàáë
FF
≤
,
òî ãåòåðîñêåäàñòè÷í³ñòü â³äñóòíÿ. Îòæå,
ÌÍÊ-îö³íêè ïàðàìåòð³â ðåãðåñ³éíî¿ ìîäåë³ ìîæóòü çàñòîñîâóâàòèñÿ
äëÿ ïîäàëüøèõ äîñë³äæåíü.
5.3. Òðàíñôîðìóâàííÿ ïî÷àòêîâî¿ ìîäåë³
Ðîçãëÿíåìî ïèòàííÿ óñóíåííÿ ãåòåðîñêåäàñòè÷íîñò³ òðàíñôîðìó-
âàííÿì ïî÷àòêîâî¿ ìîäåë³.
Ïðèïóñòèìî, ùî çà ñòàòèñòè÷íèìè äàíèìè ïîáóäîâàíî ïî÷àòêî-
âó ðåãðåñ³éíó ìîäåëü
(,)yfxu
=
³ íà áàç³ áóäü-ÿêîãî òåñòó âñòàíîâëåíî íàÿâí³ñòü ãåòåðîñêåäàñòè÷íîñò³:
2
const.
ii
uu
D
=σ ≠
Äëÿ óñóíåííÿ ãåòåðîñêåäàñòè÷íîñò³ ïî÷àòêîâó ìîäåëü çì³íþþòü
(òðàíñôîðìóþòü) òàê, ùîá ïîìèëêè ìàëè ñòàëó äèñïåðñ³þ:
2
const.
ii
uu
D
=σ =
Òðàíñôîðìàö³ÿ ìîäåë³ çâîäèòüñÿ äî çì³íè ïî÷àòêîâî¿ ôîðìè ìî-
äåë³ ìåòîäîì, ÿêèé çàëåæèòü â³ä ñïåöèô³÷íî¿ ôîðìè ãåòåðîñêåäàñòè÷-
íîñò³, òîáòî â³ä ôîðìè çàëåæíîñò³ ì³æ äèñïåðñ³ÿìè çàëèøê³â ³ çíà-
÷åííÿìè íåçàëåæíèõ çì³ííèõ:
2
()
.
i
ui
x
σ=ϕ
(5.5)
Ðîçãëÿíåìî ìîæëèâ³ âèïàäêè òðàíñôîðìàö³¿ ìîäåë³ íà ïðèêëàä³
ïðîñòî¿ ë³í³éíî¿ ðåãðåñ³¿.
Íåõàé ïî÷àòêîâà ìîäåëü
01
ya axu
=+ +
, (5.6)
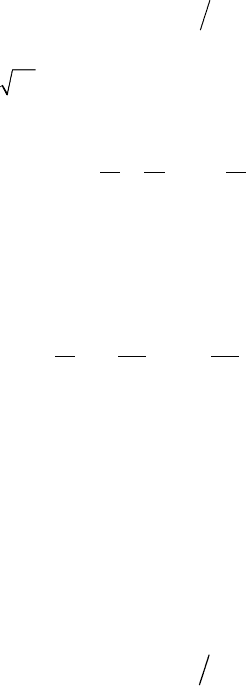
97
äå êîìïîíåíòè âèïàäêîâîãî âåêòîðà u ãåòåðîñêåäàñòè÷í³, àëå â³äïîâ³-
äàþòü ³íøèì êëàñè÷íèì ïðèïóùåííÿì ë³í³éíî¿ ðåãðåñ³¿.
Ðîçãëÿíåìî òàê³ âèïàäêè.
Âèïàäîê 1. Ïðèïóñòèìî, ùî ãåòåðîñêåäàñòè÷í³ñòü ìຠôîðìó
2222
,
i
ui
Mu k x
σ= =
(5.7)
äå k
=
const (òîáòî äèñïåðñ³ÿ çàëèøê³â çðîñòຠïðîïîðö³éíî äî x
2
).
²ç ïðèïóùåííÿ (5.7) âèïëèâàº
2
22
.
i
u
kx
=σ
Öå îçíà÷àº, ùî òðàíñôîðìàö³ÿ ìîäåë³ ïîëÿãຠâ ä³ëåíí³ ïî÷àòêî-
âî¿ ìîäåë³ íà
2
xx
=
.
Îòæå, òðàíñôîðìîâàíà ìîäåëü ìຠâèãëÿä
0
1
.
ii
ii i
ya u
a
xx x
=++
(5.8)
Çàçíà÷èìî, ùî ïàðàìåòð ïðè çì³íí³é 1/x
i
ó òðàíñôîðìîâàí³é ìî-
äåë³ º ïåðåòèíîì (â³ëüíèì ÷ëåíîì) ïî÷àòêîâî¿ ìîäåë³, òîä³ ÿê ïåðå-
òèí òðàíñôîðìîâàíî¿ ìîäåë³ º íàõèëîì ïî÷àòêîâî¿.
Ðîçãëÿíåìî
2
2
222
22
11
.
i
ii
i
ii
u
MMukxk
x
xx
== =
Îòæå, íîâà âèïàäêîâà âåëè÷èíà ìîäåë³ (5.8) ìຠñê³í÷åííó ñòàëó
äèñïåðñ³þ k
2
. Òàêèì ÷èíîì, ìîäåëü (5.8) ìຠãîìîñêåäàñòè÷íó âèïàä-
êîâó çì³ííó, ùî îçíà÷ຠïðàâîì³ðí³ñòü çàñòîñóâàííÿ êëàñè÷íîãî ÌÍÊ
äëÿ ðîçðàõóíêó íåâ³äîìèõ ïàðàìåòð³â òðàíñôîðìîâàíî¿ ìîäåë³ (5.8).
Âèïàäîê 2. Ïðèïóñòèìî, ùî ãåòåðîñêåäàñòè÷í³ñòü ìຠôîðìó
222
,
i
ui
Mu k x
σ= =
(5.9)
äå k
=
const (òîáòî äèñïåðñ³ÿ çàëèøê³â çðîñòຠïðîïîðö³éíî äî õ).
²ç ïðèïóùåííÿ (5.8) âèïëèâàº
22
.
i
u
kx
=σ
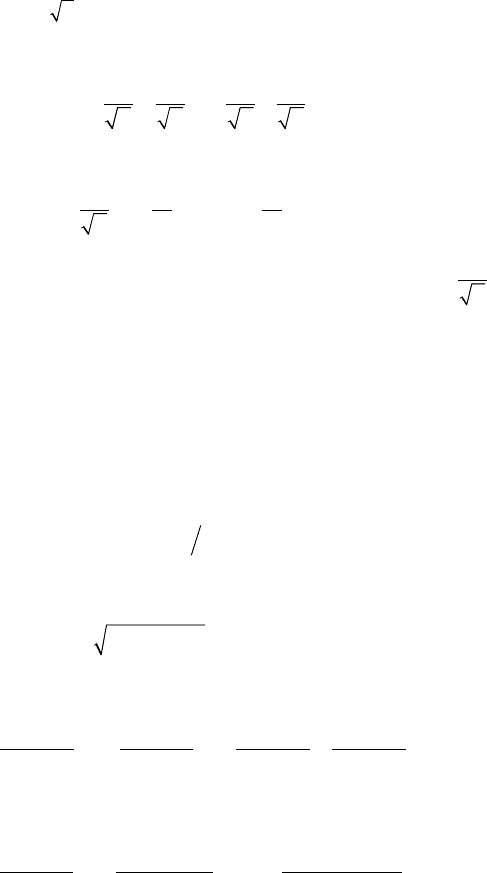
98
Öå îçíà÷àº, ùî äîïóñòèìà òðàíñôîðìàö³ÿ ïîëÿãຠâ ä³ëåíí³ ïî÷àò-
êîâî¿ ìîäåë³ íà
.x
Îòæå, òðàíñôîðìîâàíà ìîäåëü ìຠâèãëÿä
0
1
ya xu
a
xx xx
=+ +
. (5.10)
Ðîçãëÿíåìî
2
222
11
()
.
i
ii
ii
u
MMukxk
xx
x
===
Îòæå, äëÿ òðàíñôîðìîâàíî¿ ìîäåë³ âèïàäêîâà âåëè÷èíà
u
x
ãî-
ìîñêåäàñòè÷íà ç³ ñòàëîþ äèñïåðñ³ºþ k
2
. Öå îçíà÷àº, ùî, âèêîíàâøè
çàçíà÷åíå âèùå ïåðåòâîðåííÿ, ìè âèêëþ÷èëè ãåòåðîñêåäàñòè÷í³ñòü.
Âèïàäîê 3. Ïðèïóñòèìî, ùî ãåòåðîñêåäàñòè÷í³ñòü ìຠôîðìó
222 2
01
()
i
ui i
Mu k b b x
σ= = +
(5.11)
(äèñïåðñ³ÿ çðîñòຠïðîïîðö³éíî äî êâàäðàòà ë³í³éíî¿ ôóíêö³¿ â³ä x).
²ç ïðèïóùåííÿ (5.11) âèïëèâàº
2
22
01
()
i
ui
kbbx
=σ +
. (5.12)
Äîïóñòèìà òðàíñôîðìàö³ÿ ïîëÿãຠâ ä³ëåíí³ ïî÷àòêîâî¿ ìîäåë³ íà
2
01 01
()()
.
ii
bbx bbx
+=+
Îòæå, òðàíñôîðìîâàíà ìîäåëü ìຠâèãëÿä
01
01 01 01 01
1
.
iii
iiii
yxu
aa
bbx bbx bbxbbx
=++
++++
(5.13)
Ðîçãëÿíåìî
()
()
()
2
2
2
012
2
22
01
01 01
1
.
i
i
i
i
ii
kb bx
u
ÌMuk
bbx
bbx bbx
+
===
+
++
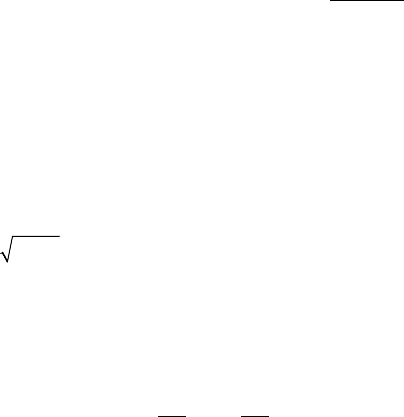
99
Îòæå, íîâà âèïàäêîâà âåëè÷èíà
01
i
i
u
bbx
+
º ãîìîñêåäàñòè÷íîþ ³ç
ñòàëîþ äèñïåðñ³ºþ k
2
.
Çàãàëüíèé âèïàäîê. Ïðèïóñòèìî, ùî ãåòåðîñêåäàñòè÷í³ñòü ìàº
ôîðìó
222
()
i
ui i
Mu k x
σ= =ϕ
, (5.14)
äå k
=
const,
()
i
x
ϕ
ôóíêö³ÿ â³ä x
i
.
Òðàíñôîðìàö³ÿ ïî÷àòêîâî¿ ìîäåë³ çä³éñíþºòüñÿ ä³ëåííÿì ¿¿ íà
()
i
x
ϕ
.
Çàçíà÷èìî, ùî òàêà òðàíñôîðìàö³ÿ åêâ³âàëåíòíà çàñòîñóâàííþ
çâàæåíîãî ìåòîäó íàéìåíøèõ êâàäðàò³â (ÇÌÍÊ), ÿêèé º îñîáëèâèì
âèïàäêîì óçàãàëüíåíîãî ìåòîäó íàéìåíøèõ êâàäðàò³â (ÓÌÍÊ). Ñóòü
ÇÌÍÊ ïîëÿãຠâ ì³í³ì³çàö³¿ çâàæåíî¿ ñóìè êâàäðàòè÷íèõ â³äõèëåíü:
()
2
2
01
22
11
1
min.
ii
nn
i
ii
uu
ii
u
y
aax
==
=−−→
σσ
∑∑
(5.15)
Çàçíà÷èìî òàêîæ, ùî ÇÌÍÊ, çàñòîñîâàíèé äî ïî÷àòêîâî¿ ìîäåë³,
äຠòàê³ ñàì³ ðåçóëüòàòè, ùî é ÌÍÊ, çàñòîñîâàíèé äî òðàíñôîðìîâà-
íî¿ ìîäåë³.
Òâåðäæåííÿ. Îö³íêè òðàíñôîðìîâàíî¿ ìîäåë³ ìàþòü ìåíøó äèñ-
ïåðñ³þ (åôåêòèâí³ø³), í³æ îö³íêè, îòðèìàí³ ³ç çàñòîñóâàííÿì ÌÍÊ
äî ïî÷àòêîâî¿ ìîäåë³.
Íàðåøò³, ïîòð³áíî ïàìÿòàòè, ùî ãåòåðîñêåäàñòè÷í³ñòü ìîæå ³ñíó-
âàòè çà ðàõóíîê íåâðàõîâàíèõ ôàêòîð³â (ïîãàíî¿ ñïåöèô³êàö³¿ ìîäåë³).
Ó öüîìó ðàç³ ìîæëèâèì ð³øåííÿì º âêëþ÷åííÿ íåâðàõîâàíèõ ôàê-
òîð³â ó ìîäåëü. Ñë³ïå çàñòîñóâàííÿ òðàíñôîðìàö³¿ (áåç àíàë³çó ïðè-
÷èí ãåòåðîñêåäàñòè÷íîñò³) çðîáèòü ãîìîñêåäàñòè÷íîþ âèïàäêîâó
çì³ííó, îäíàê îö³íêè ïàðàìåòð³â çàëèøàòüñÿ íåïðàâèëüíèìè ÷åðåç
íåâðàõóâàííÿ âàæëèâèõ ôàêòîð³â.
100
5.4. Îö³íþâàííÿ ïàðàìåòð³â áàãàòîôàêòîðíî¿
ðåãðåñ³éíî¿ ìîäåë³ íà îñíîâ³ óçàãàëüíåíîãî
ìåòîäó íàéìåíøèõ êâàäðàò³â
Ðîçãëÿíåìî äåòàëüí³øå çàãàëüíèé âèïàäîê îö³íþâàííÿ ïàðàìåòð³â
ìîäåë³ ç ãåòåðîñêåäàñòè÷íèìè çàëèøêàìè.
Çàïèøåìî óçàãàëüíåíó áàãàòîôàêòîðíó ðåãðåñ³éíó ìîäåëü ó ìàò-
ðè÷íîìó âèãëÿä³
,yXau
=+
(5.16)
äå ó âåêòîð-ñòîâïåöü çàëåæíî¿ çì³ííî¿ ðîçì³ðíîñò³ (n × 1);
X ìàòðèöÿ íåçàëåæíèõ çì³ííèõ ðîçì³ðíîñò³ (n × (m+ 1));
a âåêòîð-ñòîâïåöü íåâ³äîìèõ ïàðàìåòð³â ðîçì³ðíîñò³ ((m + 1) × 1);
u âåêòîð-ñòîâïåöü âèïàäêîâèõ ïîìèëîê ðîçì³ðíîñò³ (n × 1).
Íåõàé âèêîíóþòüñÿ âñ³ ïðèïóùåííÿ êëàñè÷íî¿ ë³í³éíî¿ áàãàòî-
ôàêòîðíî¿ ìîäåë³, çà âèíÿòêîì ïðèïóùåííÿ ïðî ãîìîñêåäàñòè÷í³ñòü
ïîõèáîê. ßêùî äî ìîäåë³ (5.16) çàñòîñóâàòè çâè÷àéíèé ÌÍÊ, îò-
ðèìàíà îö³íêà ïàðàìåòð³â áóäå íåçì³ùåíîþ, îáãðóíòîâàíîþ, îäíàê
íå åôåêòèâíîþ (íå ìຠíàéìåíøî¿ äèñïåðñ³¿ ñåðåä íåçì³ùåíèõ îö³-
íîê).
Çà íàÿâíîñò³ ãåòåðîñêåäàñòè÷íîñò³ äëÿ îö³íþâàííÿ ïàðàìåòð³â
ìîäåë³ äîö³ëüíî çàñòîñóâàòè óçàãàëüíåíèé ìåòîä íàéìåíøèõ êâàä-
ðàò³â (ìåòîä Åéòêåíà), âåêòîð îö³íþâàííÿ ÿêîãî ìຠâèãëÿä
−− −
′′
=
11 1
()
.
aXSXXSY
(5.17)
Âåêòîð a ì³ñòèòü íåçì³ùåíó ë³í³éíó îö³íêó ïàðàìåòð³â ìîäåë³, ÿêà
ìຠíàéìåíøó äèñïåðñ³þ ³ ìàòðèöþ êîâàð³àö³é:
−−
′
σ=σ
2211
() ( )
.
u
aXSX
Çàóâàæåííÿ. Äëÿ îòðèìàííÿ ÓÌÍÊ-îö³íîê íåîáõ³äíî çíàòè
êîâàð³àö³éíó ìàòðèöþ S âåêòîðà ïîõèáîê, ÿêà íà ïðàêòèö³ äóæå ð³äêî
â³äîìà. Òîìó ïðèðîäíî ñïåðøó îö³íèòè ìàòðèöþ S, à ïîò³ì çàñòîñó-
âàòè ¿¿ îö³íêó ó ôîðìóë³ (5.17). Öåé ï³äõ³ä º ñóòü óçàãàëüíåíîãî ìå-
òîäó íàéìåíøèõ êâàäðàò³â.
Âèçíà÷åííÿ ìàòðèö³ S. Îñê³ëüêè ÿâèùå ãåòåðîñêåäàñòè÷íîñò³
ïîâÿçàíå ëèøå ç òèì, ùî çì³íþþòüñÿ äèñïåðñ³¿ çàëèøê³â, à êîâà-
