Лещинський О.Л. Економетрія

Подождите немного. Документ загружается.

³ Y(³) K(i) L(³)

1 65,04 4,03 7,45

2 54,27 5,25 8,68

3 78,22 7,57 9,55

4 82,06 7,99 10,67

5 79,14 8,91 11,68

6 90,48 10,67 13,31

7 85,69 11,51 14,27

8 76,26 10,23 13,01

9 82,05 10,84 15,05

2. Çà ñòàòèñòè÷íèìè ïîêàçíèêàìè Y, K ³ L çà äåâÿòü ðîê³â ïðî-

àíàë³çóâàòè êëàñè÷íó ìîäåëü âèðîáíè÷î¿ ôóíêö³¿ Êîááà  Äóãëàñà,

ùî îïèñóº çàëåæí³ñòü ì³æ ïðîäóêòèâí³ñòþ ïðàö³

/yYL

òà ôîí-

äîîçáðîºí³ñòþ

/xKL

ç óðàõóâàííÿì âïëèâó òåõí³÷íîãî ïðîãðåñó

ó âèðîáíèöòâ³ ðåã³îíó, îö³íèâøè:

1) ïàðàìåòðè íåë³í³éíî¿ ìîäåë³;

2) êîåô³ö³ºíò äåòåðì³íàö³¿;

3) êîåô³ö³ºíò ìíîæèííî¿ êîðåëÿö³¿.

Ðîçä³ë 4. Ìóëüòèêîë³íåàðí³ñòü

4.1. Ïîíÿòòÿ ïðî ìóëüòèêîë³íåàðí³ñòü òà ¿¿

âïëèâ íà îö³íêó ïàðàìåòð³â ìîäåë³

Îäíà ç ïåðåäóìîâ çàñòîñóâàííÿ ìåòîäó íàéìåíøèõ êâàäðàò³â äî îö³-

íþâàííÿ ïàðàìåòð³â ë³í³éíèõ áàãàòîôàêòîðíèõ ìîäåëåé  â³äñóòí³ñòü

ë³í³éíèõ çâÿçê³â ì³æ íåçàëåæíèìè çì³ííèìè ìîäåë³. ßêùî òàê³ çâÿç-

êè ³ñíóþòü, òî öå ÿâèùå íàçèâàþòü ìóëüòèêîë³íåàðí³ñòþ.

Îçíà÷åííÿ 4.1. Ñóòü ìóëüòèêîë³íåàðíîñò³ ïîëÿãàº â òîìó, ùî â áà-

ãàòîôàêòîðí³é ðåãðåñ³éí³é ìîäåë³ äâ³ àáî á³ëüøå íåçàëåæíèõ çì³ííèõ

ïîâÿçàí³ ì³æ ñîáîþ ë³í³éíîþ çàëåæí³ñòþ àáî, ³íøèìè ñëîâàìè, ìàþòü

âèñîêèé ñòóï³íü êîðåëÿö³¿:

(1,).

→≠

Íàÿâí³ñòü ìóëüòèêîë³íåàðíîñò³ ñòâîðþº ïåâí³ ïðîáëåìè ïðè ðîç-

ðîáö³ ìîäåëåé. Íàñàìïåðåä, âèçíà÷íèê ìàòðèö³ ñïîñòåðåæåíü

íàáëèæàºòüñÿ äî íóëÿ, ³ îïåðàòîð îö³íþâàííÿ çà çâè÷àéíèì ÌÍÊ

ñòàº íàäçâè÷àéíî ÷óòëèâèé äî ïîõèáîê âèì³ðþâàíü ³ ïîõèáîê îá÷èñ-

ëåíü. Ïðè öüîìó ÌÍÊ-îö³íêè ìîæóòü ìàòè çíà÷íå çì³ùåííÿ â³äíîñ-

íî ä³éñíèõ îö³íîê óçàãàëüíåíî¿ ìîäåë³, à â äåÿêèõ âèïàäêàõ ìîæóòü

ñòàòè âçàãàë³ áåççì³ñòîâíèìè.

Ïåðåäóñ³ì ïîòð³áíî çðîçóì³òè ïðèðîäó ìóëüòèêîë³íåàðíîñò³.

Íàïðèêëàä, êîëè âèâ÷àºòüñÿ çàëåæí³ñòü ì³æ ö³íîþ àêö³¿, äèâ³äåí-

äàìè íà àêö³þ òà îòðèìàíèì ïðèáóòêîì íà àêö³þ, òî äèâ³äåíäè òà

îòðèìàíèé ïðèáóòîê íà îäíó àêö³þ ìàþòü âèñîêèé ñòóï³íü êîðåëÿö³¿.

²íøèìè ñëîâàìè, âèíèêàº ñèòóàö³ÿ, êîëè äâà êîë³íåàðíèõ ôàêòîðè

çì³íþþòüñÿ â îäíîìó íàïðÿìêó. Ó òàêîìó ðàç³ ìàéæå íåìîæëèâî

îö³íèòè âïëèâ êîæíîãî ç íèõ íà äîñë³äæóâàíèé ïîêàçíèê.

Çÿñóºìî, äî ÿêèõ íàñë³äê³â ìîæå ïðèçâåñòè ìóëüòèêîë³íåàðí³ñòü.

Öå îäíå ç íàéâàæëèâ³øèõ ïèòàíü, ÿêå ïîòð³áíî çðîçóì³òè ïðè ðîç-

ðîáö³ åêîíîìåòðè÷íèõ ìîäåëåé.

Ïðàêòè÷í³ íàñë³äêè ìóëüòèêîë³íåàðíîñò³:

• ìóëüòèêîë³íåàðí³ñòü íåçàëåæíèõ çì³ííèõ (ôàêòîð³â) ïðèçâî-

äèòü äî çì³ùåííÿ îö³íîê ïàðàìåòð³â ìîäåë³, ÿê³ ðîçðàõîâóþòüñÿ çà

ìåòîäîì íàéìåíøèõ êâàäðàò³â. Íà îñíîâ³ öèõ îö³íîê íåìîæëèâî çðî-

áèòè êîíêðåòí³ âèñíîâêè ïðî ðåçóëüòàòè âçàºìîçâÿçêó ì³æ ïîêàçíè-

êîì ³ ôàêòîðàìè;

• çá³ëüøåííÿ äèñïåðñ³¿ òà êîâàð³àö³¿ îö³íîê ïàðàìåòð³â, îá÷èñëå-

íèõ çà ìåòîäîì íàéìåíøèõ êâàäðàò³â.

Äëÿ ³ëþñòðàö³¿ ðîçãëÿíåìî äâîôàêòîðíó ðåãðåñ³éíó ìîäåëü

01122

ya ax ax u

=+ + +

òà ¿¿ âèá³ðêîâèé àíàëîã

01122

  

ya ax ax

=+ +

Äèñïåðñ³ÿ îö³íîê ïàðàìåòð³â



ìàº âèãëÿä



()

(

)( )

rxx

−−

∑

, (4.1)



()

(

)( )

rxx

−−

∑

, (4.2)

222

11 2 2



ñîv

(

)

(

)( )( )

rxxxx

−σ

−−−

∑∑

(4.3)

äå r  êîåô³ö³ºíò êîðåëÿö³¿ ì³æ õ

³ õ

Ç (4.1), (4.2) âèïëèâàº, ùî ÿêùî r çðîñòàº, òî



()

Da Da

òà-

êîæ çðîñòàþòü.

Ç (4.3) âèïëèâàº, ùî ÿêùî r çá³ëüøóºòüñÿ,



ñîv

(

)

çðîñòàº çà

àáñîëþòíîþ âåëè÷èíîþ. Ïðè÷îìó ïðè íàáëèæåíí³ äî ãðàíè÷íîãî çíà-

÷åííÿ öå çá³ëüøåííÿ ìàº åêñïîíåíö³àëüíèé õàðàêòåð.

• çá³ëüøåííÿ äîâ³ð÷îãî ³íòåðâàëó (îñê³ëüêè çá³ëüøóºòüñÿ ñåðåäí³é

êâàäðàò â³äõèëåííÿ ïàðàìåòð³â);

• íåçíà÷óù³ñòü t-ñòàòèñòèê.

(Îñê³ëüêè çíà÷åííÿ t-ñòàòèñòèêè Ñòüþäåíòà



, òî ó âèïàä-

êó ìóëüòèêîë³íåàðíîñò³



σ→∞

à îòæå,

→

Çàóâàæåííÿ. Ìóëüòèêîë³íåàðí³ñòü íå º ïðîáëåìîþ, ÿêùî ºäèíîþ

ìåòîþ ðåãðåñ³éíîãî àíàë³çó º ïðîãíîç (îñê³ëüêè ÷èì á³ëüøå çíà÷åí-

íÿ R

, òèì òî÷í³øèé ïðîãíîç). ßêùî ìåòîþ àíàë³çó º íå ïðîãíîç,

à ä³éñíå çíà÷åííÿ ïàðàìåòð³â, òî ìóëüòèêîë³íåàðí³ñòü ïåðåòâîðþºòü-

ñÿ íà ïðîáëåìó, îñê³ëüêè ¿¿ íàÿâí³ñòü ïðèçâîäèòü äî çíà÷íèõ ñòàí-

äàðòíèõ ïîõèáîê îö³íîê ïàðàìåòð³â.

4.2. Òåñòóâàííÿ íàÿâíîñò³ ìóëüòèêîë³íåàðíîñò³

ªäèíîãî ñïîñîáó âèçíà÷åííÿ ìóëüòèêîë³íåàðíîñò³, íà æàëü, íåìàº.

Çîâí³øí³ îçíàêè íàÿâíîñò³ ìóëüòèêîë³íåàðíîñò³ òàê³:

• âåëèêå çíà÷åííÿ R

³ íåçíà÷óù³ñòü t-ñòàòèñòèêè.

Íàÿâí³ñòü öèõ äâîõ ôàêòîð³â îäíî÷àñíî º êëàñè÷íîþ îçíàêîþ

ìóëüòèêîë³íåàðíîñò³.

Ç îäíîãî áîêó, íåçíà÷óù³ñòü t-ñòàòèñòèêè Ñòüþäåíòà îçíà÷àº, ùî

îäèí àáî á³ëüøå îö³íåíèõ ïàðàìåòð³â ñòàòèñòè÷íî íåçíà÷óùå

â³äð³çíÿþòüñÿ â³ä íóëÿ. Ç ³íøîãî áîêó, ÿêùî çíà÷åííÿ R

âåëèêå, ìè

ïðèéìàºìî ç âåëèêîþ éìîâ³ðí³ñòþ F-êðèòåð³é Ô³øåðà, ÿêèé â³äêè-

äàº íóëüîâó ã³ïîòåçó (Í

: a



0). Ñóïåðå÷í³ñòü ñâ³ä÷èòü

ïðî íàÿâí³ñòü ìóëüòèêîë³íåàðíîñò³;

• âåëèêå çíà÷åííÿ ïàðíèõ êîåô³ö³ºíò³â êîðåëÿö³¿.

ßêùî çíà÷åííÿ õî÷à á îäíîãî êîåô³ö³ºíòà êîðåëÿö³¿

0, 8,

≠

, òî ìóëüòèêîë³íåàðí³ñòü º ñåðéîçíîþ ïðîáëåìîþ.

Çàóâàæèìî, ùî âåëèêå çíà÷åííÿ ïàðíèõ êîåô³ö³ºíò³â êîðåëÿö³¿ 

äîñòàòíÿ, àëå íå íåîáõ³äíà óìîâà íàÿâíîñò³ ìóëüòèêîë³íåàðíîñò³.

Ìóëüòèêîë³íåàðí³ñòü ìîæå ìàòè ì³ñöå íàâ³òü ïðè â³äíîñíî íåâåëèêèõ

çíà÷åííÿõ ïàðíèõ êîåô³ö³ºíòàõ êîðåëÿö³¿ ó á³ëüø í³æ äâîôàêòîðí³é

ðåãðåñ³éí³é ìîäåë³.

Äëÿ âèçíà÷åííÿ ìóëüòèêîë³íåàðíîñò³ çäåá³ëüøîãî çàñòîñîâóþòü

òàê³ òåñòè:

• F-òåñò, çàïðîïîíîâàíèé Ãëîáåðîì ³ Ôàððàðîì (â³í ìàº é ³íøó

íàçâó: ïîáóäîâà äîïîì³æíî¿ ðåãðåñ³¿);

• õàðàêòåðèñòè÷í³ çíà÷åííÿ òà óìîâíèé ³íäåêñ.

Ðîçãëÿíåìî ¿õ á³ëüø äåòàëüíî.

Ïåðøèé ³ç íèõ áàçóºòüñÿ íà òîìó, ùî çà íàÿâíîñò³ ìóëüòèêîë³-

íåàðíîñò³ îäèí ÷è á³ëüøå ôàêòîð³â ïîâÿçàí³ ì³æ ñîáîþ ë³í³éíîþ àáî

ïðèáëèçíî ë³í³éíîþ çàëåæí³ñòþ. Îäíèì ³ç ñïîñîá³â âèçíà÷åííÿ

ù³ëüíîñò³ ðåãðåñ³éíîãî çâÿçêó º ïîáóäîâà ðåãðåñ³éíî¿ çàëåæíîñò³

êîæíîãî ôàêòîðà õ

ç óñ³ìà ³íøèìè ôàêòîðàìè. Òîìó F-òåñò ìàº ³íøó

íàçâó: ïîáóäîâà äîïîì³æíî¿ ðåãðåñ³¿. Îá÷èñëåííÿ â³äïîâ³äíîãî êîåô³ö³-

ºíòà äåòåðì³íàö³¿ äëÿ öüîãî äîïîì³æíîãî ðåãðåñ³éíîãî ð³âíÿííÿ òà

éîãî ïåðåâ³ðêà çà äîïîìîãîþ F-êðèòåð³þ äàþòü çìîãó âèÿâèòè ë³í³éí³

çâÿçêè ì³æ íåçàëåæíèìè çì³ííèìè.

Íåõàé

xxx x

 êîåô³ö³ºíò äåòåðì³íàö³¿ â ðåãðåñ³¿, ÿêà ïîâÿ-

çóº ôàêòîð õ

ç ³íøèìè ôàêòîðàìè. Òîä³ F-òåñò âèêîíóºòüñÿ òàê:

1) äëÿ êîæíîãî êîåô³ö³ºíòà äåòåðì³íàö³¿ ðîçðàõîâóºìî F

-â³ä-

íîøåííÿ:

()(

)

(

)( )

xxx x

Rnm

−

−−

(4.4)

äå n  ê³ëüê³ñòü ñïîñòåðåæåíü; m  ê³ëüê³ñòü ôàêòîð³â.

F-òåñò ïåðåâ³ðÿº ã³ïîòåçó H

xx x

ïðîòè ã³ïîòåçè H

xx x

≠

;

2) F

êð

çíàõîäèìî çà òàáëèöåþ F-ðîçïîä³ëó Ô³øåðà ç (m1) ³ (nm)

ñòóïåíÿìè ñâîáîäè ³ çàäàíèì ð³âíåì çíà÷óùîñò³;

3) ÿêùî F

> F

êð

, òî ã³ïîòåçó Í

â³äêèäàºìî (õ

 ìóëüòèêîë³íåàðíèé

ôàêòîð), ÿêùî F

< F

êð

, òî ã³ïîòåçó Í

ïðèéìàºìî (ôàêòîð õ

íå º ìóëü-

òèêîë³íåàðíèì).

Òåñò, ùî çàñòîñîâóº õàðàêòåðèñòè÷í³ çíà÷åííÿ (âëàñí³ ÷èñëà ìàòðèö³

ñïîñòåðåæåíü) òà óìîâíèé ³íäåêñ R (ùî îá÷èñëþºòüñÿ ÿê â³äíîøåííÿ

ìàêñèìàëüíîãî âëàñíîãî ÷èñëà ìàòðèö³ äî ¿¿ ì³í³ìàëüíîãî âëàñíîãî ÷èñ-

ëà), âèêîðèñòîâóºòüñÿ â ñó÷àñíèõ ñòàòèñòè÷íèõ ïàêåòàõ. Ìè íå ðîç-

ãëÿäàòèìåìî éîãî äåòàëüíî, áî öå ïîòðåáóº çàñòîñóâàííÿ àïàðàòó

òåîð³¿ ìàòðèöü.

Çàçíà÷èìî ëèøå, ùî çà öèì òåñòîì ðîçðàõîâóºòüñÿ íå ò³ëüêè óìîâíå

÷èñëî R, à é óìîâíèé ³íäåêñ

CI R

. ßêùî

100 1000R

≤≤

, ìóëüòèêî-

ë³íåàðí³ñòü ïîì³ðíà, ÿêùî R > 1000  âèñîêà. Àíàëîã³÷íî, ÿêùî

10 30CI

≤≤

, ìóëüòèêîë³íåàðí³ñòü ïîì³ðíà, ÿêùî CI > 0  âèñîêà.

Ìè ðîçãëÿíóëè ëèøå îñíîâí³ ìåòîäè òåñòóâàííÿ ìóëüòèêîë³íåàð-

íîñò³. Æîäåí ç íèõ íå º óí³âåðñàëüíèì. Óñ³ âîíè ìàþòü îäèí ñï³ëüíèé

íåäîë³ê: æîäåí ³ç íèõ íå ïðîâîäèòü ÷³òêî¿ ìåæ³ ì³æ òèì, ùî òðåáà

ââàæàòè ñóòòºâîþ ìóëüòèêîë³íåàðí³ñòþ, ÿêó íåîáõ³äíî âðàõîâóâà-

òè, ³ òèì, êîëè íåþ ìîæíà çíåõòóâàòè.

4.3. Àëãîðèòì Ôàððàðà  Ãëîáåðà

Íàéïîâí³øå äîñë³äèòè ìóëüòèêîë³íåàðí³ñòü äàº çìîãó àëãîðèòì

Ôàððàðà  Ãëîáåðà, ÿêèé çàñòîñîâóº òðè âèäè ñòàòèñòè÷íèõ êðèòåð³¿â

äëÿ âèÿâëåííÿ ìóëüòèêîë³íåàðíîñò³:

• óñüîãî ìàñèâó íåçàëåæíèõ çì³ííèõ (êðèòåð³é

);

• êîæíî¿ íåçàëåæíî¿ çì³ííî¿ ç óñ³ìà ³íøèìè (F-êðèòåð³é);

• êîæíî¿ ïàðè íåçàëåæíèõ çì³ííèõ (t-êðèòåð³é).

Ïîð³âíÿâøè ö³ êðèòåð³¿ ç ¿õ êðèòè÷íèìè çíà÷åííÿìè, ìîæíà çðî-

áèòè êîíêðåòí³ âèñíîâêè ùîäî íàÿâíîñò³ ÷è â³äñóòíîñò³ ìóëüòèêîë³-

íåàðíîñò³ íåçàëåæíèõ çì³ííèõ. Îïèøåìî öåé àëãîðèòì.

Ñêëàäåìî ïîêðîêîâèé àëãîðèòì Ôàððàðà  Ãëîáåðà.

1-é êðîê:

íîðìàë³çóâàòè çì³íí³ õ

, õ

, , õ

åêîíîìåòðè÷íî¿ ìîäåë³, îá÷èñ-

ëèâøè

()

−

äå n  ê³ëüê³ñòü ñïîñòåðåæåíü (i

1, 2, ..., n); m  ê³ëüê³ñòü íåçàëåæ-

íèõ çì³ííèõ (j

1, m);

 ñåðåäíÿ àðèôìåòè÷íà j-¿ íåçàëåæíî¿

çì³ííî¿;

 äèñïåðñ³ÿ j-¿ íåçàëåæíî¿ çì³ííî¿.

2-é êðîê:

íà îñíîâ³ ìàòðèö³

, åëåìåíòàìè ÿêî¿ º íîðìàë³çîâàí³ íåçàëåæí³

çì³íí³

, îá÷èñëèòè êîðåëÿö³éíó ìàòðèöþ (ìàòðèöþ ìîìåíò³â íîð-

ìàë³çîâàíî¿ ñèñòåìè íîðìàëüíèõ ð³âíÿíü):

12 1

21 2

1...

... ... ... ...

... 1

RXX







äå

 òðàíñïîíîâàíà ìàòðèöÿ

(åëåìåíòè ìàòðèö³ R õàðàêòå-

ðèçóþòü ù³ëüí³ñòü çâÿçêó îäí³º¿ íåçàëåæíî¿ çì³ííî¿ ç ³íøîþ);

 ïàðí³ êîåô³ö³ºíòè êîðåëÿö³¿.

Îäíàê íà îñíîâ³ ö³º¿ çàëåæíîñò³ íå ìîæíà ñòâåðäæóâàòè, ùî îò-

ðèìàíèé çâÿçîê º ÿâèùåì ìóëüòèêîë³íåàðíîñò³. ßêùî ä³àãîíàëüí³

åëåìåíòè ìàòðèö³ R íå äîð³âíþþòü îäèíèö³, òî íà ä³àãîíàë³ ö³º¿ ìàò-

ðèö³ ìè ïðîñòàâëÿºìî îäèíèö³, à äî ðåøòè åëåìåíò³â äîäàºìî ð³çíè-

öþ ì³æ îäèíèöåþ é çíà÷åííÿì ä³àãîíàëüíîãî åëåìåíòà.

3-é êðîê:

âèçíà÷èòè |R|  âèçíà÷íèê êîðåëÿö³éíî¿ ìàòðèö³ R;

îá÷èñëèòè êðèòåð³é

(

)

;

nm R



χ=− −− + ⋅





ïîð³âíÿòè çíà÷åííÿ

ç òàáëè÷íèì ïðè

(1)

−

ñòóïåíÿõ ñâî-

áîäè ³ ð³âí³ çíà÷óùîñò³ α (ÿêùî

òàáë

χχ

, òî â ìàñèâ³ íåçàëåæíèõ

çì³ííèõ ³ñíóº ìóëüòèêîë³íåàðí³ñòü).

4-é êðîê:

âèçíà÷èòè ìàòðèöþ ïîõèáîê:

11 12 1

21 22 2

1**1

...

()

... ... ... ...

...

mm mm

cc c

CR XX

cc c

−−





== =





5-é êðîê:

ðîçðàõóâàòè F-êðèòåð³¿:

(1)()

(1)

−−

−

äå ñ

 ä³àãîíàëüí³ åëåìåíòè ìàòðèö³ Ñ;

çíà÷åííÿ êðèòåð³¿â F

ïîð³âíÿòè ç òàáëè÷íèì ïðè (nm) ³ (m1)

ñòóïåíÿõ ñâîáîäè é ð³âí³ çíà÷óùîñò³ α (ÿêùî F

> F

òàáë

, òî â³äïîâ³äíà

k-òà íåçàëåæíà çì³ííà ìóëüòèêîë³íåàðíà ç ³íøèìè);

ðîçðàõóâàòè êîåô³ö³ºíòè äåòåðì³íàö³¿ äëÿ êîæíî¿ çì³ííî¿:

=−

6-é êðîê:

çíàéòè ÷àñòêîâ³ êîåô³ö³ºíòè êîðåëÿö³¿, ÿê³ õàðàêòåðèçóþòü

ù³ëüí³ñòü çâÿçêó ì³æ äâîìà çì³ííèìè çà óìîâè, ùî ³íø³ çì³íí³

, x

, ... , x

íå âïëèâàþòü íà öåé çâÿçîê (³ñíóâàííÿ ïàðíî¿ ìóëüòè-

êîë³íåàðíîñò³):

kk jj

−

äå ñ

 åëåìåíòè ìàòðèö³ Ñ, ùî ðîçì³ùåí³ â k-ìó ðÿäêó òà j-ìó

ñòîâïö³, k = 1, 2, ..., m; j = 1, 2, ..., m; ñ

³ ñ

 ä³àãîíàëüí³ åëåìåíòè

ìàòðèö³ Ñ.

Îäíàê ÿêùî ïîð³âíÿòè êîíêðåòí³ ÷èñëîâ³ çíà÷åííÿ ÷àñòêîâèõ

³ ïàðíèõ êîåô³ö³ºíò³â, òî ìîæíà ïîáà÷èòè, ùî ïåðø³ çíà÷íî ìåíø³,

í³æ îñòàíí³. Òîìó íà îñíîâ³ çíàííÿ ïàðíèõ êîåô³ö³ºíò³â êîðåëÿö³¿

âèñíîâîê ïðî ìóëüòèêîë³íåàðí³ñòü ðîáèòè íåìîæëèâî. Äëÿ öüîãî íå-

îáõ³äíî âèêîíàòè 7-é êðîê.

7-é êðîê:

ðîçðàõóâàòè t-êðèòåð³¿:

−

=⋅

−

;

çíà÷åííÿ êðèòåð³¿â t

ïîð³âíÿòè ç òàáëè÷íèìè ïðè (mn) ñòóïå-

íÿõ ñâîáîäè òà ð³âí³ çíà÷óùîñò³

; ÿêùî t

> t

òàáë

, òî ì³æ íåçàëåæ-

íèìè çì³ííèìè õ

³ õ

³ñíóº ìóëüòèêîë³íåàðí³ñòü.

Âèñíîâêè:

1. Ì³æ íåçàëåæíèìè çì³ííèìè ìîæå ³ñíóâàòè ë³í³éíà çàëåæí³ñòü,

îäíàê âîíà ìîæå é íå áóòè ÿâèùåì ìóëüòèêîë³íåàðíîñò³ çì³ííèõ,

à òîìó íå âïëèâàòèìå íà ê³ëüê³ñí³ îö³íêè ïàðàìåòð³â ìîäåë³, ðîçðà-

õîâàíèõ çà äîïîìîãîþ çâè÷àéíîãî ÌÍÊ.

2. ßêùî F

> F

òàáë

, òî õ

çàëåæèòü â³ä óñ³õ ³íøèõ íåçàëåæíèõ

çì³ííèõ ³ òðåáà âèð³øèòè ïèòàííÿ ïðî ¿¿ âèêëþ÷åííÿ ç ïåðåë³êó

çì³ííèõ.

3. ßêùî t

> t

òàáë

, òî õ

³ õ

ù³ëüíî ïîâÿçàí³ ì³æ ñîáîþ.

4. Àíàë³çóþ÷è F- i t-êðèòåð³¿, ðîáèìî âèñíîâîê, ÿêó ç³ çì³ííèõ

òðåáà âèêëþ÷èòè ç ìîäåë³ (çðîçóì³ëî, ÿêùî öå ìîæëèâî ç åêîíîì³êî-

ëîã³êî-òåîðåòè÷íèõ ì³ðêóâàíü).

5. ßêùî âèêîíàâøè ïï. 24, ìè íå äîñÿãëè ìåòè, òîáòî íå óñóíó-

ëè ìóëüòèêîë³íåàðí³ñòü, îö³íêó ïàðàìåòð³â ìîäåë³ ñë³ä îá÷èñëþâàòè

çà äîïîìîãîþ ³íøîãî ìåòîäó, íàïðèêëàä ìåòîäó ãîëîâíèõ êîìïîíåíò³â

(àáî îäí³º¿ ç éîãî ìîäèô³êàö³é).

Ïðèêëàä äîñë³äæåííÿ íàÿâíîñò³ ìóëüòèêîë³íåàðíîñò³

íà îñíîâ³ àëãîðèòìó Ôàððàðà  Ãëîáåðà

Ðîçãëÿíåìî äîñë³äæåííÿ âïëèâó íà åêîíîì³÷íèé ïîêàçíèê y  ðå-

àëüíå ñïîæèâàííÿ êðà¿íè (ó ìëðä ãðí.) òðüîõ ôàêòîð³â: x

 êóï³âë³ òà

îïëàòè òîâàð³â ³ ïîñëóã (ó ìëðä ãðí.), x

 óñ³õ çàîùàäæåíü â³ä çàãàëü-

íîãî ãðîøîâîãî äîõîäó (ó % â³ä çàãàëüíî¿ ñóìè äîõîäó), x

 ð³âíÿ ñòàâ-

êè ÏÄÂ (ó %). Íåîáõ³äíî ïåðåâ³ðèòè ôàêòîðè íà ìóëüòèêîë³íåàðí³ñòü.

Ðîçâÿçàííÿ.

1-é êðîê:

íîðìàë³çóºìî çì³íí³ õ

, õ

åêîíîìåòðè÷íî¿ ìîäåë³, îá÷èñëèâøè

()

ij j

−

äå n

20  ê³ëüê³ñòü ñïîñòåðåæåíü (³

1, 2, ..., n); m

3  ê³ëüê³ñòü íå-

çàëåæíèõ çì³ííèõ (j

1, m);

 ñåðåäíÿ àðèôìåòè÷íà j-¿ íåçàëåæ-

íî¿ çì³ííî¿:

9,3505;

18,874;

37,788;

 äèñïåðñ³ÿ j-¿ íåçàëåæíî¿ çì³ííî¿:

11,35297;

26,06648;

31,86169.

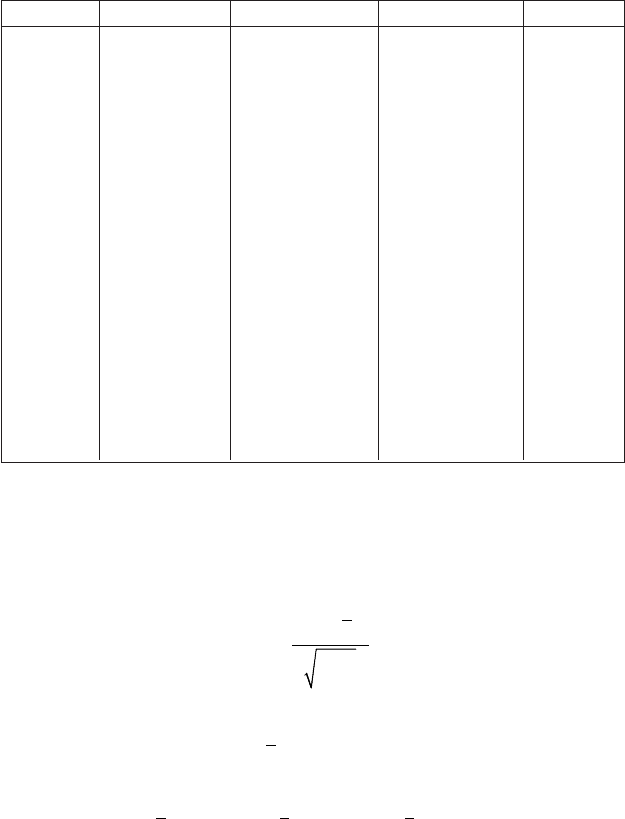
¹ ï/ï y(i) x

(i) x

(i)

1 25,74 4,69 11,97 29,23

2 25,34 5,64 13,43 29,35

3 31,26 6,26 12,92 33,40

4 33,50 6,99 14,74 30,97

5 32,30 6,36 14,64 32,92

6 38,90 7,60 17,10 37,27

7 41,58 7,12 15,63 30,97

8 48,02 6,81 15,35 33,58

9 43,30 8,67 15,85 35,62

10 51,78 7,83 18,05 34,99

11 52,14 7,84 17,24 39,34

12 54,94 8,85 20,52 41,50

13 59,18 9,61 19,18 45,58

14 62,22 10,67 19,03 41,08

15 63,62 11,04 21,45 40,54

16 65,01 11,85 22,25 42,75

17 67,78 12,94 24,75 43,89

18 71,45 14,24 25,03 41,95

19 75,24 15,67 27,87 44,06

20 77,38 16,33 30,486 46,77