Лекции - коллоидная химия
Подождите немного. Документ загружается.


91
χ
Ar
= –32,2·10
–30
см
3
;
Получаем
С = 0,77·10
45
ккал/(моль·см
6
)
Для обоих случаев адсорбции –
z
01
и z
02
:
U
01
= –1,82 ккал/моль;
U
02
= –2,44 ккал/моль.
2
1
z, Ǻ
U
дисп
0
-1
-2
43562
2
1
Рис. 7.9. Энергетические кривые для двух возможных вариантов адсорбции
аргона на графите.
Разница в энергетике
ΔU = 0,62 > RT (при 77 К среднекинетическая
энергия
= RT = 0,002·77 = 0,15 ккал/моль).
Т. е. адсорбция – локализованная: за счет теплового движения атом
аргона не может перейти из положения 2 в положение 1 (преодолеть барьер для
перехода из одного положения 2 в соседнее).
Экспериментальная теплота адсорбции
Q
эксп
= 2,2 ÷ 2,6 ккал/моль,
≈ (
U
01
+ U
02
)/2.
IV. Адсорбция сложных неполярных молекул
Рассмотрим адсорбцию насыщенных углеводородов C
n
H
2n+2
на базисной
грани графита.
Если ось молекулы углеводорода находится параллельно поверхности
графита, то энергия взаимодействия:
(
)
32
дисп CH CH
22UUnU
⎡⎤
=− + −
⎣⎦
U
дисп
= Q
а
(ккал/моль):
2 10
4
20
n
C
U
д
Рис. 7.10. Зависимость энергии адсорбции углеводородов от длины цепи.
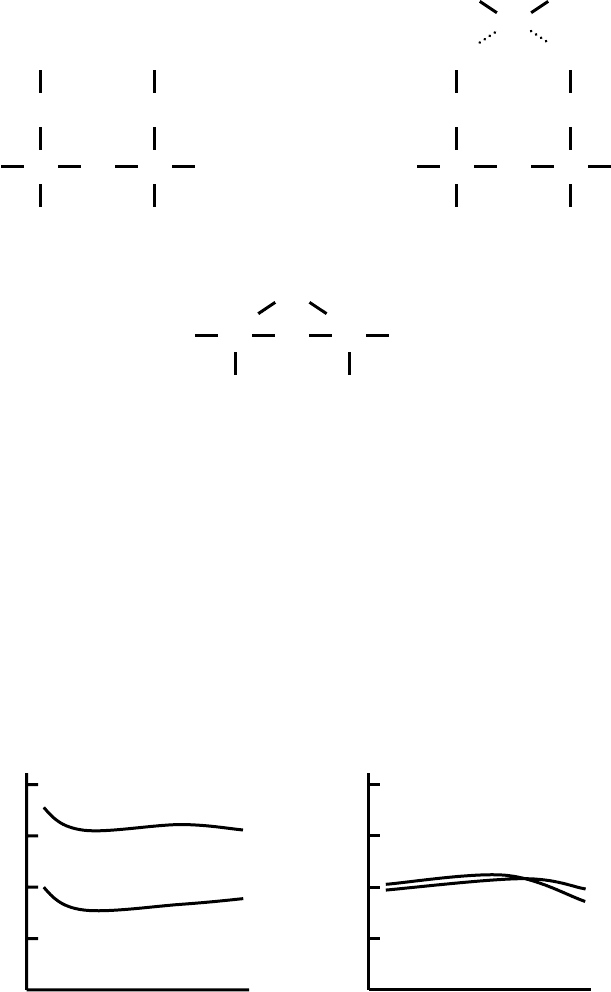
92
V. Адсорбция с образованием водородных связей
Рассмотрим адсорбцию воды на силикагеле.
Можно вычислить энергию водородной связи, проведя адсорбцию на
силикагеле до и после гидроксилирования:
Образование водородных связей можно обнаружить по смещению ИК
полос OH–групп.
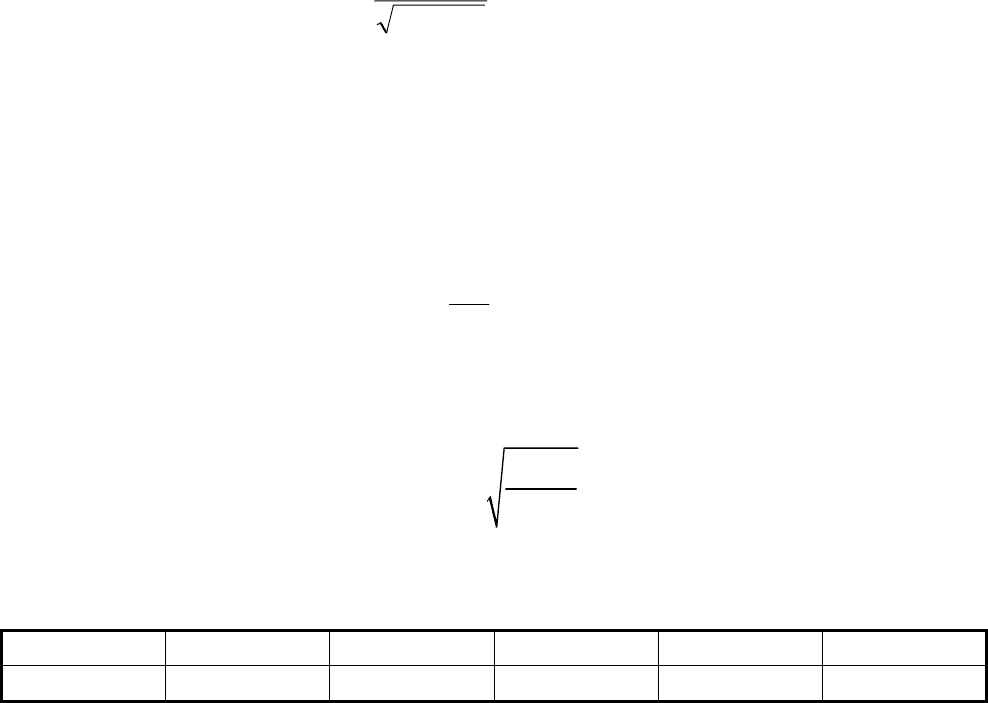
В другом примере рассмотрим адсорбцию сходных по природе веществ,
одно из которых способно образовывать водородную связь (диэтиловый эфир),
а другое – нет (н
-пентан). При адсорбции этих веществ на силикагеле, с
которым возможно образование водородной связи, видим, что теплота
адсорбции эфира примерно на 8 кДж/моль выше, чем в пентане. Для контроля,
при адсорбции на саже (нет возможности образования водородных связей), их
теплоты адсорбции примерно совпадают.
q
a
20
15
10
5
0
x
20
15
10
5
0
x
n-C
5
H
12
(C
2
H
5
)
2
O
n-C
5
H
12
(C
2
H
5
)
2
O
на силикагеле
на саже
Рис. 7.11. Дифференциальная теплота адсорбции н-пентана и диэтилового
эфира на силикагеле и на саже.
Si O
Si O
O
H
O
H
+ H
2
O → Si O SiO
O
H
O
H
O
HH
Si O SiO
O
дегидроксилированный
силикагель
93
7.2. Динамика процесса адсорбции.
При соударении с поверхностью, молекула адсорбата или упруго
ударится или задержится. За время задержки идет теплообмен адсорбата с
адсорбентом, увеличивается концентрация на поверхности.
Пребывать на поверхности молекула адсорбата будет до тех пор, пока она
не получит необходимой энергии за счет флуктуации теплового движения. Эта
необходимая энергия – энергии адсорбции.
Время пребывания на
поверхности – есть время адсорбции.
Устанавливается динамическое равновесие.
Основное уравнение:
τ
=
γ
n (7.34)
γ – адсорбция (молекул/см
2
);
τ – время адсорбции;
n – число молекул ударяющихся в секунду об один см
2
площади адсорбента
Согласно кинетической теории газов это число молекул равняется:
MRT
PN
n
A
π
=
2
(7.35)
Например если воздух имеет влажность 10% (
P = 1,75 мм.рт.ст.) и
температуре
t = 20°C, то число n составит 10
21
. Если площадь молекулы
A
0
= 10
-15
см
2
(адсорбция γ = 10
15
молекул/см
2
), тогда τ = 10
15
/10
21
= 10
-6
сек –
время установления равновесия (когда число ударяющихся молекул равно
числу удаляющихся).
Время адсорбции, очевидно, должно зависеть от температуры и теплоты
адсорбции. Согласно Френкелю (1924 г.):
⎟
⎠
⎞
⎜
⎝
⎛
⋅τ=τ
RT
Q
a
exp
0
(7.36)
где
τ
0
≈ 10
-13
с – период колебаний молекул адсорбата в направлении
перпендикулярном поверхности, близок к периоду колебаний атома в решетке;
Q
a
– молярная теплота адсорбции.
2/3
адсорбента 13
м
0
пл
4,75 10
M
T
−
τ=⋅
v
(7.37)
где v
м
– мольный объем адсорбента; T
пл
– температура плавления адсорбента.
В следующей таблице приведены времена адсорбции для разных
Q
a
:
Таблица 7.3
Q
a
1,5 10 20 30 147 (O
2
–W)
τ
10
-12
c 10
-6
c < 2 мин > 100 лет 10
90
лет
Два последних случая – необратимая адсорбция. Сорбированные
молекулы нельзя удалить никакой откачкой и равновесие практически не
установится.
94
Из уравнения (7.36) видно, что с увеличением температуры, время
адсорбции уменьшается, адсорбция
γ уменьшается (7.34), что означает быстрое
установление равновесия.
Таким образом для полного поглощения молекул адсорбата надо
понизить температуру, а для быстрого – увеличить.
95
8. ТЕОРИИ АДСОРБЦИИ НА ГРАНИЦЕ ТВЕРДОЕ ТЕЛО – ГАЗ
8.1. Эмпирическое уравнение Бедекера-Фрейндлиха (1902 г.)
1/n
K
P
Γ
=⋅
(8.1)
где P – равновесное давление газа в системе, K и n – постоянные.
С повышением температуры коэффициент
K должен уменьшаться, а 1/n –
увеличиваться. Эти константы можно найти графически по изотерме,
построенной в логарифмических координатах (уравнение прямой:
lg Г = lg
К + 1/n ⋅ lg P). Уравнение Бедекера-Фрейндлиха пригодно только для
интервала средних давлений, поскольку по сути – это уравнение параболы.
Показатель 1/
n для интервала средних равновесных давлений газа в системе для
адсорбции из газовой среды принимается равным в пределах 0,2
÷ 1, а для
адсорбции из растворов в пределах 0,1
÷ 0,5. Уравнение Фрейндлиха не
предполагает наличие на изотерме адсорбции участка насыщения. Изотермы
адсорбции в целом лучше описываются уравнением Лэнгмюра.
Уравнение применяется:
• для неоднородных поверхностей;
• в области среднего заполнения.
Рис. 8.1. Изотерма адсорбции по уравнению Бедекера-Фрейндлиха.
8.2. Теория Лэнгмюра (1915 г.)
Исходные положения теории:
1. адсорбция мономолекулярная;
2. нет взаимодействия адсорбат-адсорбат;
3. адсорбция локализована на активных центрах, нет миграции на поверхности;
4. активные центры энергетически эквивиалентны.
Пусть
θ – доля адсорбции, или доля занятой поверхности:
∞
γ
θ=
γ
(8.2)
∞
γ=θ⋅γ (8.3)
тогда (1 –
θ) – доля свободной поверхности
(
)
1 n
∞
γ= −θ ⋅ ⋅τ=θ⋅γ (8.4)
Г
P
96
1
2
nN
P
MRT
∞
θτ τ
=
=⋅
−θ γ
π
(8.5)
выражение (8.2) подставим в (8.5):
1
K
P
K
P
∞
γ=γ
+
(8.6)
– уравнение Лэнгмюра
.
Адсорбцию
γ в уравнении можно заменить и объемом адсорбата:
1
K
P
K
P
∞
=
+
vv (8.6а)
а) при
P → 0,
K
P
∞
=vv
б) с увеличением
P (при KP >> 1),
∞
=
vv
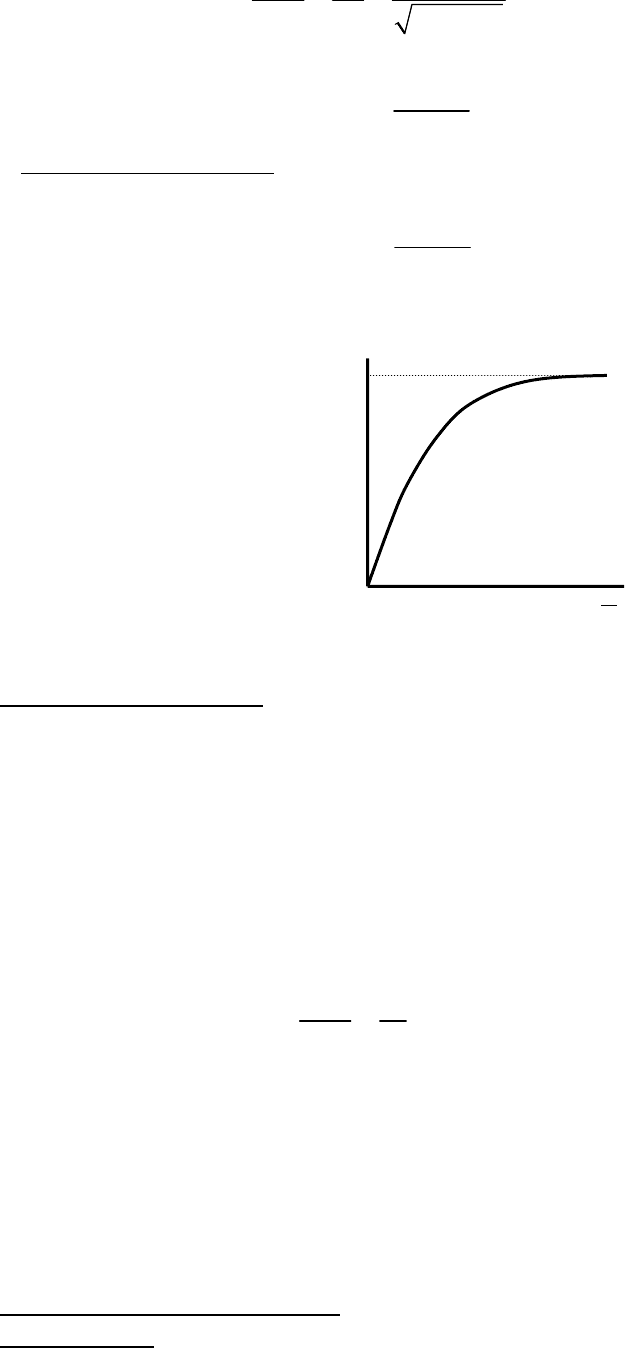
Рис. 8.2. Лэнгмюровская изотерма адсорбции.
Кинетический подход
Скорость процесса адсорбции будет равняться константе скорости,
помноженной на произведение давления адсорбата и доли свободной
поверхности:
()
адс 1
1kP=−θv (8.7)
скорость десорбции же будет зависеть только от доли занятой поверхности:
дес 2
k=θv (8.8)
При равновесии скорости адсорбции и десорбции сравняются, т. е.
(8.7) = (8.8), отсюда получаем:
1
2
1
k
PKP
k
θ
==
−θ
(8.9)
Полученное выражение (8.9) идентично выражению (8.5). Таким образом
константа Лэнгмюра
К имеет два смысла:
• константа равновесия;
• константа динамики адсорбции.
Так, зная константу Лэнгмюра имеем возможность найти время
адсорбции
τ и оценить теплоту адсорбции Q
а
.
Проверка теории Лэнгмюра.
Первый шаг:
v
P
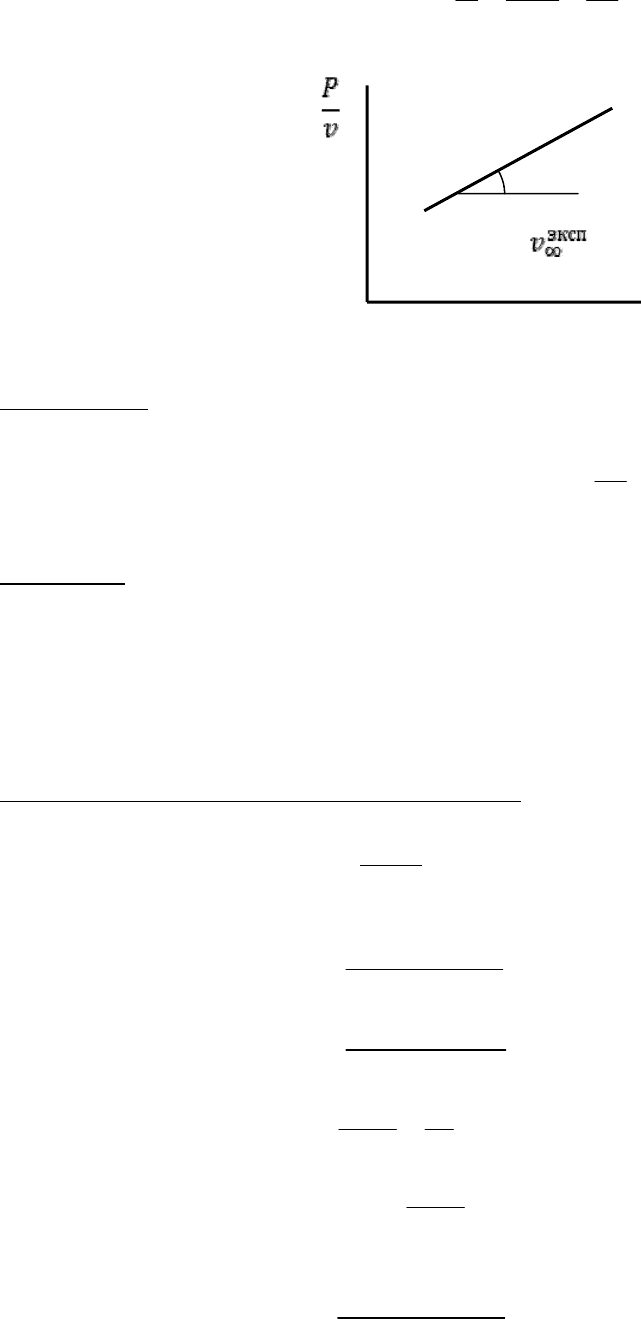
97
Преобразовав (8.6а) к виду
1PP
K
∞
∞
=+
vv v
, построим зависимость в
линейных координатах
Рис. 8.3. Проверка теории Лэнгмюра.
и по котангенсу угла наклона найдем предельный адсорбционный объем.
Второй шаг:
Экспериментально определив удельную площадь адсорбента, которая
связана с адсорбционным объемом (
эксп
уд 0
A
m
SNS
∞
=
v
v
) можем рассчитать
предельный адсорбционный объем и сравним с полученным первым способом.
Результат:
Предельный адсорбционный объем, рассчитанный по уравнению
Лэнгмюра составляет всего от 3 до 30% от объема, определенного через
удельную площадь. Это несовпадение обусловлено тем, что теория не
учитывает, что поверхность адсорбента неэквипотенциальна и газ
адсорбируется на активных центрах.
Условия применения уравнения Лэнгмюра:
1) для слабой хемосорбции с теплотой адсорбции
Q
а
≈ 10 ккал/моль
2) для физической адсорбции газов
(не паров!)
при малых
P; T > T
крит
.
3) для адсорбции из смеси газов (газ 1 и 2):
()
1
1
121
1
K
P
θ
=
−θ −θ
(8.10)
()
2
2
122
1
K
P
θ
=
−θ −θ
(8.11)
11 1
22 2
KP
KP
θ
=
θ
(8.12)
22
21
11
K
P
K
P
θ=θ (8.13)
(8.13) подставляем в (8.10):
11
1
11 2 2
1
KP
K
PKP
θ=
++
(8.14)
P
α
ctgα =

98
далее (8.12) подставив в (8.14) и в (8.11) получим:
22
2
11 2 2
1
KP
K
PKP
θ=
++
(8.15)
При P
1,2
= 0 снова возвращаемся к исходному уравнению Лэнгмюра.
4) Для энергетически неоднородной поверхности.
Если на поверхности есть участки с разной активностью, то:
1
i
i
i
i
K
P
K
P
∞
=
+
∑
vv (8.16)
– учет энергетической неоднородности поверхности.
Доказательство неоднородности.
Дифференциально-изотопный анализ:
1) пропускают над адсорбентом последовательно газы разного изотопного
состава;
2) десорбируют.
Изотопный состав десорбированного газа отличается от среднего, т. к.
газ, пропущенный первым, занял самые энергетически выгодные места.
Доля поверхности θ зависит от теплоты адсорбции.
При заполнении поверхности с энергетически неоднородными центрами:
/
/
e
1e
QRT
Q
QRT
KP
KP
−
−
⋅
θ=
+⋅
(8.17)
Суммарная адсорбция:
()
max
min
Q
Q
Q
QdQθ= θ ⋅ρ ⋅
∫
(8.18)
где ρ(Q) – функция распределения адсорбционных мест по теплотам
адсорбции.
Она может быть:
а) ρ(Q) = const = A, тогда
(
)
max
ln
A
RT K Pθ= ⋅ ⋅ (8.19)
– уравнение логарифмической изотермы адсорбции.
б)
(
)
e
mQ
QB
−
ρ=⋅ (B, m – постоянные), тогда:
1
'
n
B
Pθ= ⋅
(8.20)
получаем уравнение Бедекера-Фрейндлиха (т. е. объяснили теоретически).
8.3. Потенциальная теория Поляни (1915 г.)
Рассматривается полимолекулярная адсорбция на пористой поверхности:
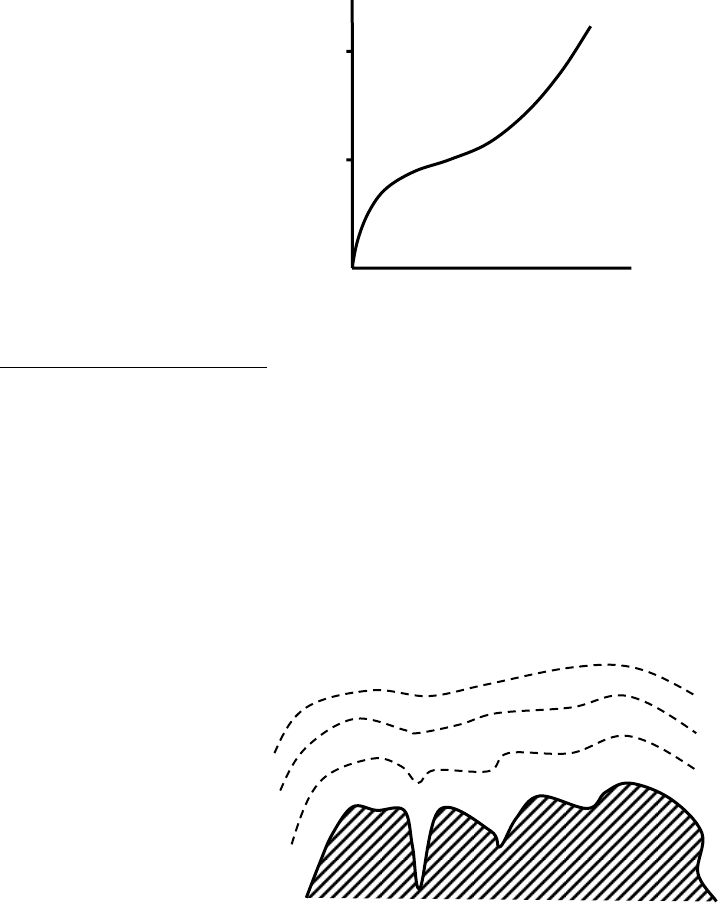
99
Рис. 8.4. Изотерма полимолекулярной адсорбции.
Исходные положения.
1. Адсорбция физическая (вандерваальсовая), нелокализованная,
полимолекулярная.
2. Нет взаимодействия адсорбат-адсорбат. Притяжение молекул адсорбата
поверхностью не зависит от наличия других молекул на поверхности.
– Давление пара непосредственно над поверхностью адсорбированной
жидкости не отличается от давления паров над обычной жидкостью.
3. Активные центры не рассматриваются. Адсорбционные силы исходят от
всей поверхности, создавая силовое
поле с потенциалом ε, убывающим по
мере удаления от поверхности.
Рис. 8.5. Эквипотенциальные поверхности.
– При адсорбции газов, их плотность в адсорбционном слое убывает по
нормали к поверхности;
– При адсорбции паров у поверхности образуется жидкий слой определенной
толщины, иначе на поверхности происходит фазовый переход (образуется
пленка жидкости).
4. ε ≠ f(T
). Увеличение десорбции объясняется увеличением интенсивности
теплового движения;
Параметрами теории являются адсорбционный потенциал ε и
адсорбционный объем
v (а не толщина адсорбционного слоя, т.к. ее сложно
определить). Задача теории – найти их взаимозависимость.
Адсорбционный потенциал ε – это работа перевода молекулы газа с
поверхности жидкого адсорбата в газовую фазу:
2
1
θ
P
/
P
s
ε
1
ε
0
ε
2
ε
3
v
1
v
2
v
3
100
ln
S
P
RT
P
ε= (8.21)
Адсорбционный объем
v находят по количеству адсорбированного
вещества:
x
d
=
v (8.22)
x – масса адсорбированного вещества, d – его плотность.
Для этого надо знать зависимость плотности от объема адсорбированного
вещества для нужной температуры.
Рис. 8.6. Зависимость плотности от адсорбционного объема.
1. T > T
кр.
(для идеального газа);
2. T ~ T
кр.
(по уравнению Ван-дер-Ваальса);
3. T < T
кр.
(d ≈ d
ж
) – для адсорбции паров.
Самый простой случай – адсорбция паров (плотность в адсорбционном
слое постоянна и равняется плотности жидкости).
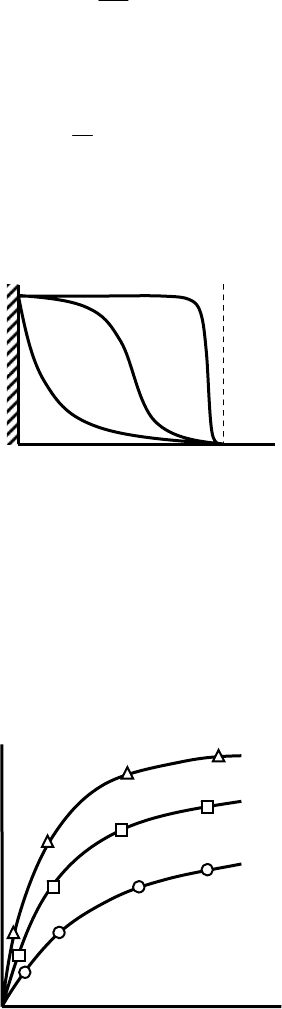
Экспериментально получаем обычные изотермы адсорбции:
Рис. 8.7. Изотермы адсорбции для построения зависимости ε –
v
(T
1
> T
2
> T
3
).
Далее пересчитываем в координаты ε от
v:
v
∞
газовая фаза
d
1
2
3
v
T
1
T
2
T
3
P
x
