Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Управление энергетическими системами. Часть1. Теория автоматического управления
Подождите немного. Документ загружается.


2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
79
Если вход и выход объекта – скалярные функции, то частот-
ная характеристика объекта определяется дробно-рациональной
функцией комплексного аргумента, которую можно рассматри-
вать как однопараметрическое семейство комплексных функций:
)(arg
)(
)()(
)()(
)(
1
10
1
10
ω
ω
ωω
ωω
ω
jWj
ejW
ajaja
bjbjb
jW
g
gg
g
gg
⋅=
+++
+++
=
−
−
.
Отношение Фурье-изображений входных и выходных сигналов
определяет
частотную характеристику, определяющую изме-
нение модуля и фазы выходного сигнала (как функцию часто-
ты) относительно входного сигнала
. Пусть входной сигнал яв-
ляется гармонической функцией
)sin()(
11
tAtu
ω
=
, а его Фурье-
изображение имеет вид
)]()([)()]([
11
1
ωωδωωδ
π
ω
+−−==
j
A
jutuF .
Полученные соотношения определяют реакцию объекта на
входное воздействие, которое представляется в форме:
),(
)(arg
)()()]([
ω
ω
ωω
ju
jWj
ejWjytyF ==
=
−
=
=
∫
+−−=
==
+−+
∞
∞−
−
j
ee
jWA
de
j
A
ejW
jyFy(t)
jWtjjWtj
tjjWj
2
)(
)]()([)(
2
1
)]([
))
1
(arg
1
())
1
(arg
1
(
11
11
1
)(arg
1
ωωωω
ωω
ω
ωωωδωωδ
π
ω
π
ω

80
.))(argsin()(
1111
ω
ω
ω
jWtjWA
+
=
Полученное выражение позволяет сформулировать сле-
дующее утверждение.
Утверждение 2.7.1. Если объект или система управления
являются устойчивыми, то установившаяся реакция на гармони-
ческое воздействие частоты
1
ω
является гармонической функцией
этой с амплитудой
)(
1
ω
jW
вх
A
вы
х
A
=
и относительным сдвигом
фаз:
)(arg
1
ω
jW=Ψ .
Таким образом, если входное воздействие
)sin()(
1
t
вх
Atu
ω
=
,
то выходная переменная определяется функцией
)sin()()(
11
Ψ
+
= tjW
вх
Aty
ω
ω
, где
)(
1
ω
Ψ
=
Ψ
- фазочастотная
функция, зависящая от частоты
1
ω
. Учитывая свойство зависимо-
сти о частоты амплитудной и фазовой частотных характеристик,
на практике используются амплитудно-частотная характеристика
(АЧХ) и фазочастотная характеристики (ФЧХ), которые опреде-
ляются равенствами:
,)(
)(
)(
ω
ω
ω
jW
вх
A
вых
A
A ==
),0[,)(arg)( ∞∈
=
Ψ
ω
ω
ω
j
W
.
При фиксированном значении ω величина, определяемая
функцией W(jω), отображается точкой на комплексной плоско-
сти. Зависимость комплексного числа (матрицы) W(jω) при изме-
нении ω от 0 до ∞, называют
годографом частотной характе-
ристики
или амплитудно-фазовой частотной характеристи-
кой
(АФЧХ) или соответствующих матриц.
На практике используются также:
логарифмическая ам-
плитудная частотная характеристика
(ЛАЧХ) объекта или
системы:

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
81
)(l
g
20)L(
ω
ω
A
=
,
логарифмическая фазовая частотная характеристика
(ЛФЧХ):
)(ar
g
)(
ω
ω
j
W
=
Ψ ,
которые строятся в функции аргумента-частоты в логарифмиче-
ском масштабе по оси ординат и оси абсцисс.
Частотные характеристики используются при анализе и син-
тезе линейных и нелинейных объектов и систем управления.
2.7.4. Связь между частотными и временными характе-
ристиками.
Пусть линейные объект или система управления
описываются частотной характеристикой W(jω), и в момент t=0
на входе системы имеется воздействие в виде δ-функции, т.е.
)()(
t
t
u
δ
= . Как было показано в п. 2.4.1, реакция y(t) на импульс-
ное воздействие есть импульсная переходная функция w(t). Вы-
числим ее спектральную характеристику, применив Фурье-
преобразование импульсной функции:
)()]([)(]|)([)]([
)()(
ω
δ
ω
δ
jWtFjWtyFtwF
ttu
=
=
=
=
,
поскольку
1)]([ =
t
F
δ
. Следовательно, комплексная частотная
характеристика (матрица) является спектральной характе-
ристикой импульсной переходной функции.
Справедливо обратное преобразование Фурье, опреде-
ляющее связь между импульсной переходной функцией (мат-
рицей) и передаточной функцией (матрицей)
:
∫
∞
∞
−
==
ω
ω
ω
π
ω
d
tj
ejWjWFtw
-
)(
2
1
)]([)(
1
.
Комплексная частотная характеристика позволяет вычислить пе-
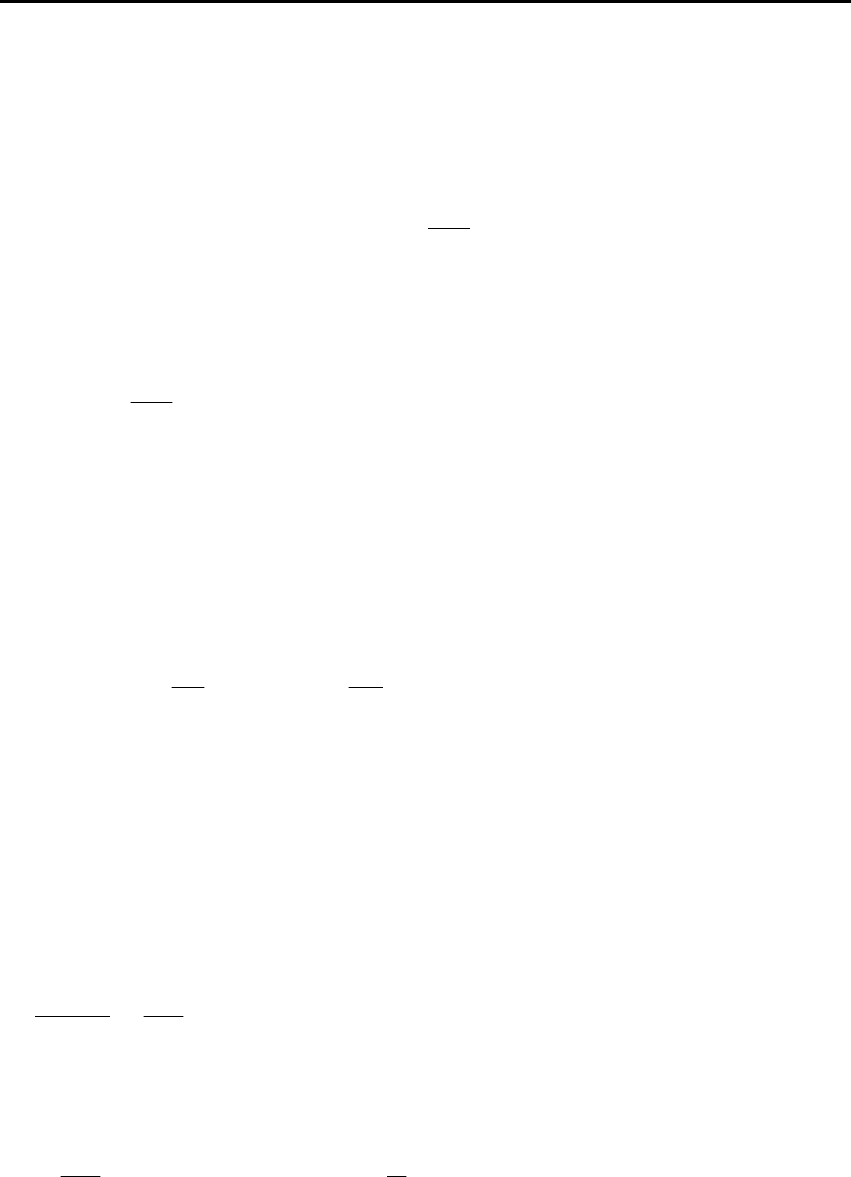
82
реходную функцию – реакцию системы на единичное входное
воздействие
. Спектральная характеристика как Фурье-
преобразование переходной функции определяется равенством:
⎥
⎦
⎤
⎢
⎣
⎡
+= )(
1
)()]([
ωδπ
ω
ω
j
jWthF
,
или
0,0)(;
0
)()(
1
)( <=
−
∫
∞
=
⎥
⎦
⎤
⎢
⎣
⎡
+ tthdt
tj
eth
j
jW
ω
ωδπ
ω
ω
.
Представим переходную функцию h(t) как реакцию объекта или
системы на единичное ступенчатое воздействие
с помощью об-
ратного Фурье-преобразования:
.0,)(
1
)(
2
1
)( >
∫
∞
∞−
ω
ω
⎥
⎦
⎤
⎢
⎣
⎡
ωδπ+
ω
ω
π
= td
tj
e
j
jWth
Известно, что умножение спектральной характеристики на jω эк-
вивалентно дифференцированию по времени оригинала во вре-
менной области. Поэтому справедливо следующее дифференци-
альное соотношение
[]
.)()(
2
)(
2
1
)(1)(
2
1)(
∫
∞
∞
−
+
∫
∞
∞−
=
=
∫
∞
∞−
+=
ω
ω
ωδωωω
ω
ω
π
ω
ω
ωδωπω
π
d
tj
ejW
j
d
tj
ejW
d
tj
ejjW
dt
thd
В силу «фильтрующего свойства δ-функции» второе слагаемое
в последнем равенстве равно нулю. В результате справедливо ра-
венство:
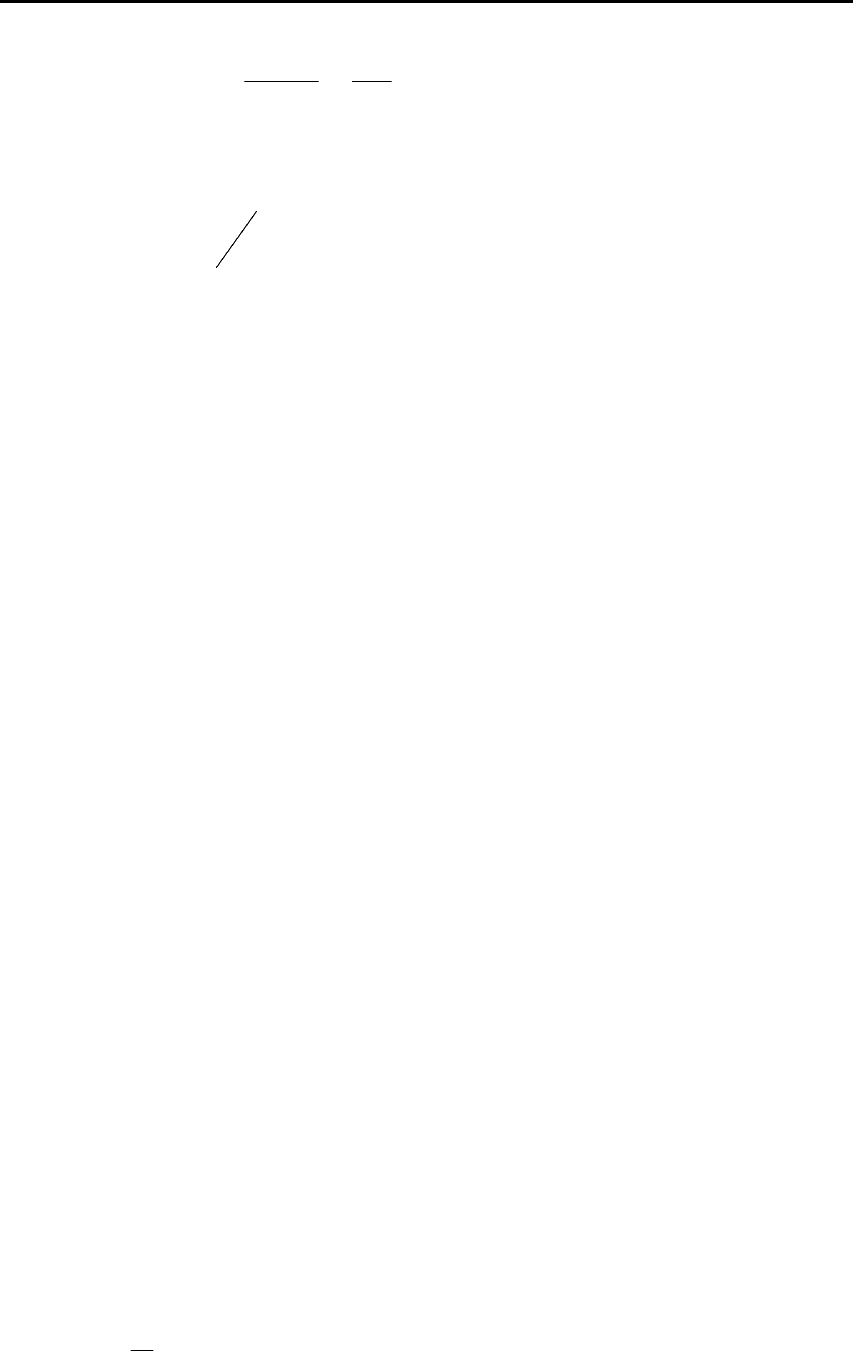
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
83
∫
∞
∞
−
=
ω
ω
ω
π
d
tj
ejW
dt
thd
)(
2
1)(
.
Следовательно, можно утверждать, что справедливо равен-
ство:
dt
tdh
tw
)(
)( =
, т.е. импульсная переходная функция является
производной по времени переходной функции как реакции объ-
екта или системы управления на единичное входное воздействие.
Таким образом,
импульсная переходная функция есть
производная по времени от переходной функции,
определяю-
щей реакцию системы на единичное воздействие в виде функции
Хевисайда.
2.8. Дискретное преобразование Фурье и частотные
характеристики дискретных объектов и систем
Введем в рассмотрение частотные характеристики дискрет-
ных объектов и систем управления с учетом квантования по вре-
мени, также характеризующие свойства объектов в зависимости
от одного параметра – частоты.
2.8.1. Постановка задачи. Пусть объект или система
управления описываются уравнениями (2.44). Требуется сформу-
лировать характеристики объектов и систем для анализа реакции
на периодические воздействия с помощью дискретного преобра-
зования Фурье для решетчатых функций.
2.8.2. Прямое и обратное дискретные преобразования
Фурье.
На основе «дискретного» преобразования Лапласа введем
дискретное преобразование Фурье.
Определение 2.8.1. Прямое дискретное преобразование
Фурье для решетчатых функций
следует из равенства (2.41)
при
ω
jq = :
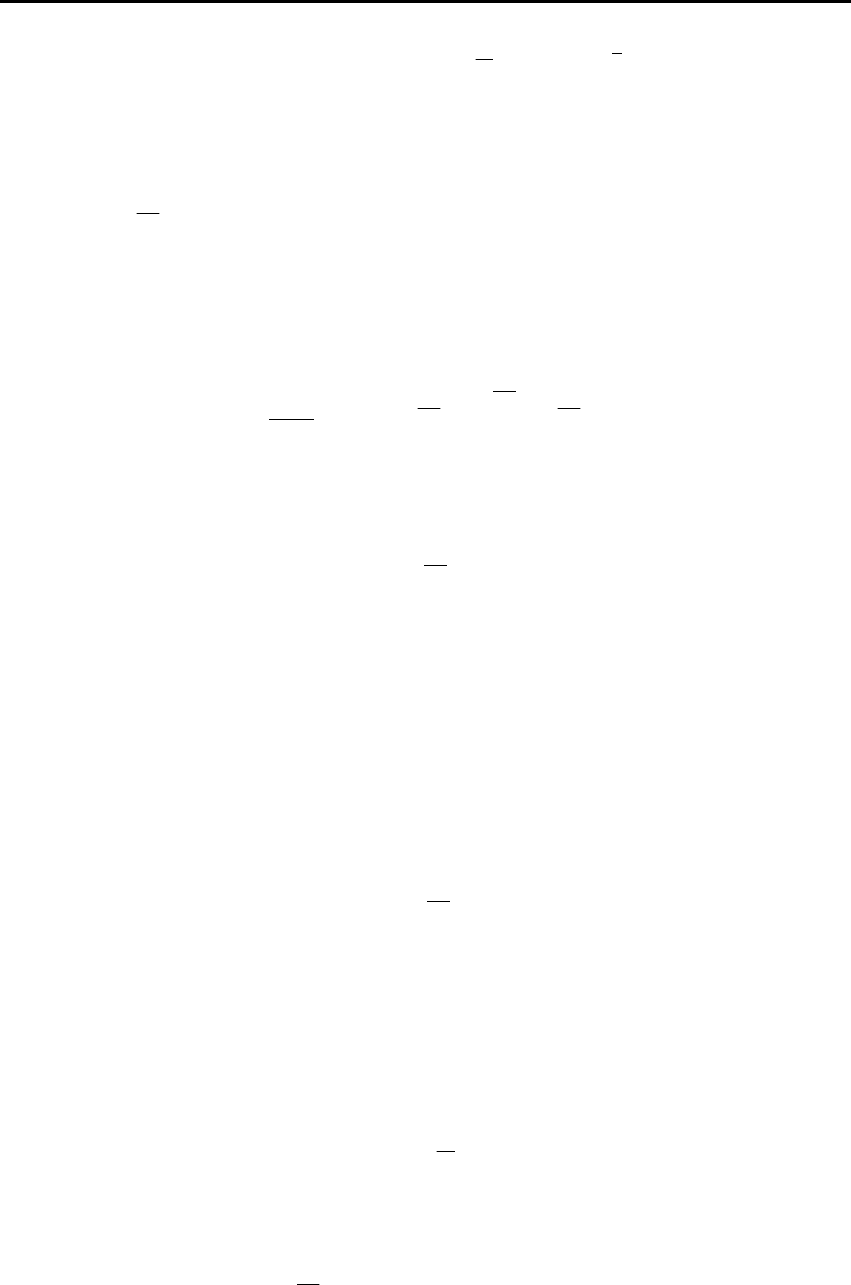
84
*
0
[] ( ) ,
jk
kk
k
DF f f j e f
ω
ω
∞
−
=
==
∑
(2.50)
где
)(kTf
k
f =
– дискретная функция (k = 0, 1, 2, ...); T – период
квантования;
T
⋅=
ω
ω
– относительная частота.
Определение 2.8.2. Обратное дискретное преобразование
Фурье
имеет вид:
∫
−
=
π
π
ω
ω
ω
π
.)(
2
1
*
d
kj
ejf
k
f
«Дискретные» Фурье-преобразования сигналов можно по-
лучить из табл. 2.2, положив
ω
jq
=
, поскольку это преобразова-
ние является частным случаем дискретного преобразования Лап-
ласа.
2.8.3. Частотные характеристики дискретных объектов и
систем.
Рассмотрим реакцию линейных дискретных устойчивых
объектов и систем автоматического управления на гармоническое
входное воздействие
)cos(
11
ϕ
ω
+
=
kAu
k
. (2.55)
Для определения реакции линейной дискретной системы на пе-
риодические воздействия расширим класс входных сигналов сис-
темы, выбрав в качестве входного воздействия функциюследую-
щего вида:
)
1
(
1
ϕ
ω
+
=
kj
k
eAf
. (2.56)
Очевидно, что это воздействие содержит воздействие вида (2.55),
поскольку
)(cosRe
11
ϕ
ω
+
= kAf
k
.
Дискретное изображение Фурье (DF-изображение) решет-

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
85
чатой функции типа (2.56) можно представить в силу определе-
ния данного изображения в следующей форме:
11
11
1
() ()
11
0
()
1
11
0
1
1
[] [ ]
(1 )
().
jk jk
qk
k
k
qj k qj
jj
k
j
jq q
DF f DF A e A e e
Ae e Ae e
Ae e e e
ωϕ ωϕ
ωω
ϕϕ
ω
ϕ
∞
++
−
=
∞
−+ −+
−
=
−
=
== =
==−=
=−
∑
∑
Для определения реакции воспользуемся моделью объекта
или системы управления в виде дискретной передаточной функ-
ции
)(/)()(
***
qQqPqW =
.
Дискретные Фурье-преобразования решетчатых функций
определятся путем применения обратного преобразования Фурье
к исходным изображениям. Оригиналы сигналов на выходе объ-
екта или системы определяются на основе теории вычетов теории
функции комплексной переменной:
=
∫
−
−
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
==
π
π
ω
ω
ω
π
ϕ
ω
ϕ
ω
d
kj
e
j
e
q
e
q
e
qW
j
eA
j
e
q
e
q
e
j
e
AqW
-
DFjy
-
DFy
k
1
1
1
1
*1*1
)(
*
2
)()]([
∑
=
=
−
−
=
l
qq
kq
e
j
e
q
e
q
e
qWs
j
eA
0
|
)1(
)(
*
Re
1
1
υ
υ
ω
ϕ
,
причем вычеты берутся в полюсах
l
qqq ...,,,
21
передаточной
функции и в точке
10
ω
jq = , определяемой входным сигналом

86
(2.56). Пусть )(
*
qW не имеет полюсов на мнимой оси. Рассмот-
рим эти вычеты. Вычет функции в точке
0
q равен:
.)(
)(
)(lim
|)(Re
1
1
*
1
1
*
1
1
1
*
kj
ejW
j
e
q
e
j
e
q
e
qk
e
qW
jq
j
e
q
e
qk
e
qWs
jq
ω
ω
ω
ω
ω
ω
ω
=
−
−
=
=
=
−
→
При вычислении вычетов в точках
l
qqq ,,,
21
надо учесть, что
полюсы могут быть простыми и кратными.
Вычет в простом
полюсе функции
)(
*
qW определяется следующим равенством:
() ()
(
)
()
()
()
11
1
**
*
*
Re lim
.
q
qk q
qk
q=q
jj
qq
qq
qk
q
j
eee
e
sW q W q
ee ee
Pqe
Qq e e
υ
υ
υ
υ
υ
ωω
υ
ω
υ
→
−
=
=
−−
=
−
Вычет в полюсе
υ
q кратности
υ
r описывается соотношением:
()
()
()
()
()
1
1
*
1
*
1
Re
1
lim .
1!
qk
q=q
j
q
r
q
qk q
r
rj
q
qq
q
e
sW q
ee
eee
d
Wq
r
ee
de
υ
υ
υ
υ
υ
υ
ω
ω
υ
−
−
→
=
−
⎡
⎤
−
⎢
⎥
=
⎢
⎥
−
−
⎢
⎥
⎣
⎦

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
8
7
Суммируя вычеты по всем полюсам, можно записать реакцию
дискретной системы управления на воздействие типа (2.56):
.
)!1(!
)()(
1
)(
1
0
11
1
*
)
1
(
1
∑
−−
∑
+
+==
=
−
−
=
−−
+
k
ikq
i
r
i
ir
j
kj
k
iri
ek
CeA
jWeAkTyy
υ
υ
υϕ
ϕ
ω
υ
υ
υ
ω
(2.57)
Если все полюсы простые, то оригинал определяется равенством:
∑
+=
=
+
k
kq
j
kj
k
eCeAjWeAy
1
.
1011
)
1
(
1
)()(
*
υ
υ
υϕ
ϕω
ωω
(2.58)
Поскольку действительные части полюсов
υ
q
отрицательны, что
связано с предположением устойчивости объектов, то с течением
времени вторые слагаемые (2.57), (2.58) стремятся к нулю, а пер-
вые слагаемые характеризуют установившийся процесс:
)(
*
)
1
(
1
1
ω
ϕω
jWeAy
kj
k
+
= .
Для исследования реакции объекта или системы на воздей-
ствие (2.55) требуется выделить вещественную часть сигнала
k
y :
))(
*
arg(cos)(
*
Re
1111
ωϕωω
jWkjWAyy
kk
++==
.
Определение 2.8.3. Функция
)(
*
arg*
)(
*
)(
ω
ωω
jWj
ejWjW =
называется
амплитудно-фазовой частотной характеристикой
(АФЧХ) дискретной системы
с квантованием по времени. Мо-
дуль АФЧХ
определяет изменение амплитуды входного сигнала,
а аргумент –
фазу выходного сигнала относительно входного
сигнала.

88
Дискретные системы имеют периодические частотные
характеристики
с периодом 2π, поскольку
)2()(
**
πωω
+= jWjW . Поэтому при использовании амплитуд-
но-фазовой частотной характеристики рассматривают ее значе-
ния только в интервале
]2,0[
π
ω
∈
. В терминах частотных харак-
теристик линейных дискретных объектов или систем управления
далее будут формулироваться критерии устойчивости.
2.9. Нелинейные математические модели
объектов и систем с сосредоточенными параметрами
Нелинейные математические модели описывают широкие
классы объектов и систем с сосредоточенными параметрами. Не-
линейные модели весьма разнообразны, однако в теории управ-
ления часто используются кусочно-линейные дифференциальные
или разностные уравнения состояния объектов и систем. Эти мо-
дели представляются обыкновенными
кусочно-линейными диф-
ференциальными или разностными уравнениями
для объектов
(систем) с сосредоточенными параметрами и типовыми звеньями.
2.9.1. Операторы типовых кусочно-линейных звеньев.
Конструктивной формой описания таких звеньев являются
ку-
сочно-линейные операторы.
Эти операторы позволяют описать
типовые нелинейности (табл. 2.3), которые можно определить на
классах функций непрерывного и дискретного времени.
Определение 2.9.1. Кусочно-линейные непрерывные опера-
торы определяются равенством
1
1
00
,,)( Rzqzzzbzq
p
i
ii
∈−++==
∑
=
ααϕ
. (2.59.а)
а разрывные операторы представляются в форме
1
00
1
() | |/( ), , .
p
ii i
i
qz z zzzzqzR
ψγβ β
=
==++ − − ∈
∑
(2.59.б)
