Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Управление энергетическими системами. Часть1. Теория автоматического управления

Подождите немного. Документ загружается.

1. ПРИНЦИПЫ ПОСТРОЕНИЯ И КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО

УПРАВЛЕНИЯ

1. ПРИНЦИПЫ ПОСТРОЕНИЯ И КЛАССИФИКАЦИЯ

СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Предмет теории автоматического управления состав-

ляют методы математического моделирования, анализа и

синтеза систем автоматического управления (САУ). САУ -

совокупность объекта управления (ОУ) и управляющего уст-

ройства (УУ), взаимодействующие на основе принципов

управления. Определена структура управления как целене-

правленного воздействия на объект.

1.1. Объекты управления

Объект управл

ения – это неизменяемая часть САУ. Рас-

смотрим примеры объектов, их структурные схемы (совокуп-

ность связанных элементов - звеньев) и цели управления.

Пример 1.1.1. Дифференциальные уравнения ОУ - электро-

энергетической системы (ЭЭС) конечной мощности, работающей

параллельно с ЭЭС бесконечной мощности, имеют вид:

y гэгг

TT p Tppku

ωωρϕ μϕω ω

+=−++ = +=−+





где (), (), (), ()ttptt

ϕμ

– отклонения частоты, угла ротора, мощ-

ности и нагрузки эквивалентного генератора от некоторого ста-

ционарного состояния;

эy

TkTT ,,,,

– параметры ОУ, u –

управление (управляющее воздействие) для изменения активной

мощности генератора. Структурная схема ОУ приведена на

рис. 1.1, где

ddt

= - оператор дифференцирования по времени,

а далее

s= - параметр преобразования Лапласа. Цели управле-

ния заданы целевыми неравенствами для частоты:

|() |

зад

ωσ

−≤, где

ад

- заданное значение частоты и допус-

тимая ошибка - отклонение от заданного значения по частоте.

Рис. 1.1. Структурная схема энергосистемы

Пример 1.1.2. Уравнения динамики ОУ - летательного ап-

парата (рис. 1.2) можно представить в форме:

1234

(),

( ), , / 57.3 ,

MM M MuMt

YYuYt n

ϑϑαα

αϑθανθρ

=++++

=++ =+ =

 





где

(), (), (), (), (), ()tttntutt

αθ ν

– отклонение углов тангажа,

атаки, наклона траектории, нормальная перегрузка, угол откло-

нения рулей высоты, скорость полета как функции времени, а

остальные величины – параметры объекта управления.

Рис. 1.2. К математической модели летательного аппарата

TpT +

1+pT

1−

1. ПРИНЦИПЫ ПОСТРОЕНИЯ И КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО

УПРАВЛЕНИЯ

Целью управления является достижение целевого условия

типа неравенства:

|() |tc

ϑϑ

−≤, что соответствует стабилизации

угла тангажа аппарата с помощью управляющих воздействий.

Пример 1.1.3. Уравнения, описывающие изменение

скорости двигателя постоянного тока имеют вид:

ωϕωωω

==++



kuTT

а соответствующая структурная схема, иллюстрирующая взаимо-

связь звеньев, приведена на рис. 1.3. В уравнениях и на рис. 1.3

Рис. 1.3. Структурная схема двигателя постоянного тока

использованы следующие обозначения переменных:

(), (), ()ttut

ωϕ

– отклонения скорости, угла и управления в ви-

де изменения напряжения. Цель управления состоит в обеспече-

нии целевого условия:

()

mint

−

→

, задающего цель управ-

ления в виде минимизации отклонения скорости от заданного

значения

с помощью синтезированных законов управления.

Рассмотренные объекты управления описываются обыкно-

венными дифференциальными уравнениями, которые могут быть

исходными для получения других видов математического описа-

ния, в частности, описаний в форме «вход-выход», «вход-

состояния-выход» (в непрерывном и дискретном времени), час-

тотной области, а также в других формах «временного» и «час-

тотного» описаний.

++ pTpT

u ω φ=y

1.2. Классификация и принципы создания систем

автоматического управ

ления

Управление – это целенаправленное воздействие на объ-

ект управления для достижения заданных целей. Управление

формируется управляющим устройством (УУ) в соответствии с

целями управления, типы которых определяются классами САУ.

1.2.1. Основные классы систем управления. Различают

основные классы САУ в зависимости от целей управления:

1. Системы стабилизации характеризуются наличием

внешних воздействий v(t), а це

ль управления заключается в под-

держании заданных значений координат – y(t) с помощью обрат-

ной связи, когда сигнал ошибки используется для формирования

управляющих воздействий на объект управления.

2. Системы программного управления содержат заданные

программы как функции времени – w(t), а цель управления – ор-

ганизация изменения выходных координат САУ по заданной про-

грамме.

3. Сле

дящие системы реализуют достижение цели управ-

ления – организация изменения координат y(t) по программе w(t)

с помощью обратной связи по отклонению от заданной програм-

мы изменения координат системы.

В зависимости от количества управляемых координат объ-

екта и управлений используются одномерные и многомерные

САУ. Современные САУ создаются с применением ЭВМ на эта-

пах пр

оектирования и формирования управляющих воздействий

на ОУ, что требует дискретизации процессов управления.

Структурная схема дискретной САУ с ЭВМ (рис. 1.4) реализует

управляющее устройство (УУ) основного контура (ОК) с помо-

щью ЭВМ, связанной с объектом аналого-цифровым (АЦП) и

цифро-аналоговым (ЦАП) преобразователями.

1. ПРИНЦИПЫ ПОСТРОЕНИЯ И КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО

УПРАВЛЕНИЯ

Рис. 1.4. Структурная схема дискретной САУ с объектом управления (ОУ)

и управляющим устройством (УУ)

Применение ЭВМ качественно изменяет законы управления

САУ в связи с алгоритмической формой задания законов про-

граммного управления, стабилизации и слежения, которая опре-

делила специфику качественного исследования. Это обстоятель-

ство требует математического аппарата для конструктивного

описания системы управления с ЭВМ. Использование ЭВМ по-

зволяет реализовать все основные принципы управления и обес-

печить достижение целей си

стем автоматического управления.

1.2.2. Основные классы, принципы и цели управления.

Различают следующие основные классы и принципы САУ,

структуры которых рассматриваются далее.

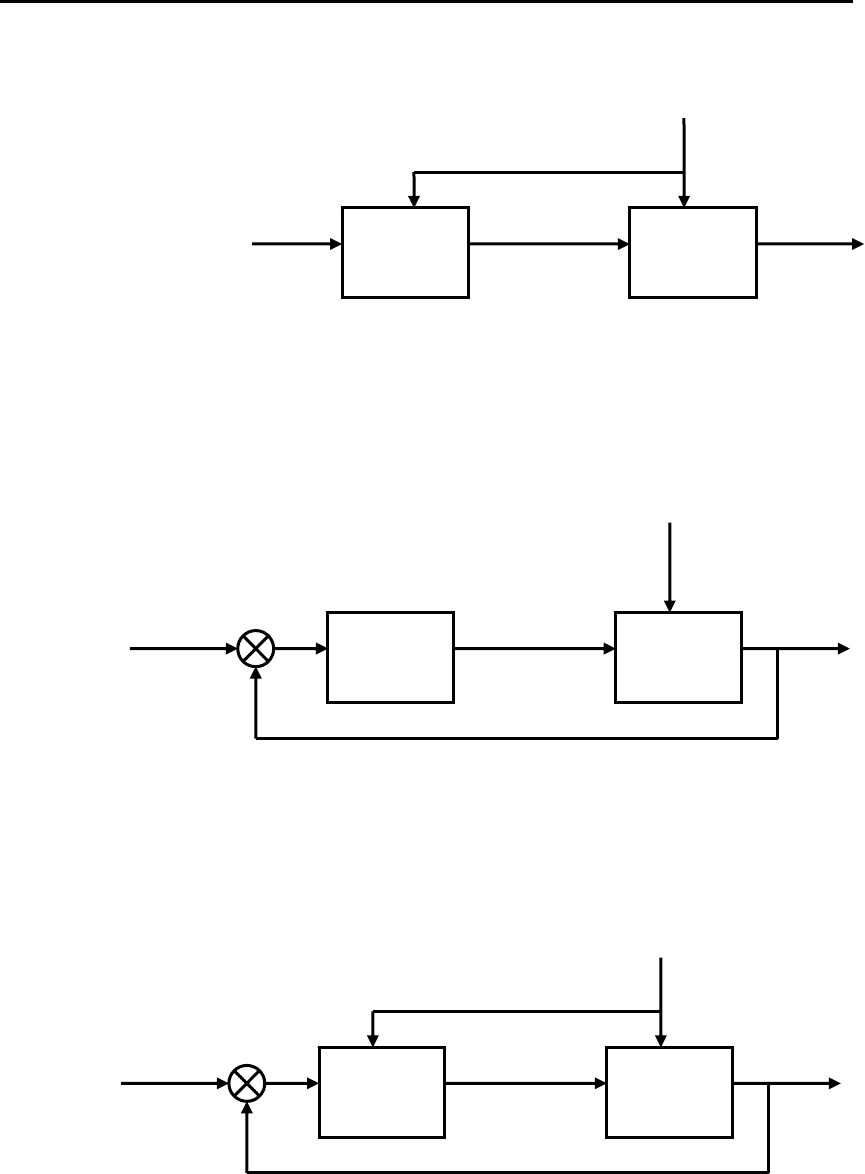
Разомкнутые САУ определяются соответствующей струк-

турной схемой (рис. 1.5.а), иллюстрирующей формирование

управлений только на основании информации о цели управления

и возмущении, а истинное значение управляемой координаты y(t)

ОУ

УУ ОК

АЦП

ЦАП

v(t)

(t)

u(t)

не контролируется. Этот классс САУ реализует принцип управ-

ления по возмущению.

Замкнутые САУ (рис. 1.5.б) формируются на основе прин-

ципа обратной связи. В замкнутых системах управления изме-

ряются отклонения управляемой координаты y(t) от заданного

значения w(t). Цель управления состоит в формировании управ-

лений, устраняющих ошибки:

)()()(

−

и реализуется

принцип управления по отклонению.

Комбинированные САУ (рис. 1.5.в) реализуют принципы

управления по возмущению и по отклонению.

Расширение функциональных возможностей САУ с управ-

ляющими устройствами с ЭВМ позволяет существенно увели-

чить возможности управления за счет перехода к модальному,

локально-оптимальному, оптимальному, адаптивному и робаст-

ному управлению как варианта адаптивного управления.

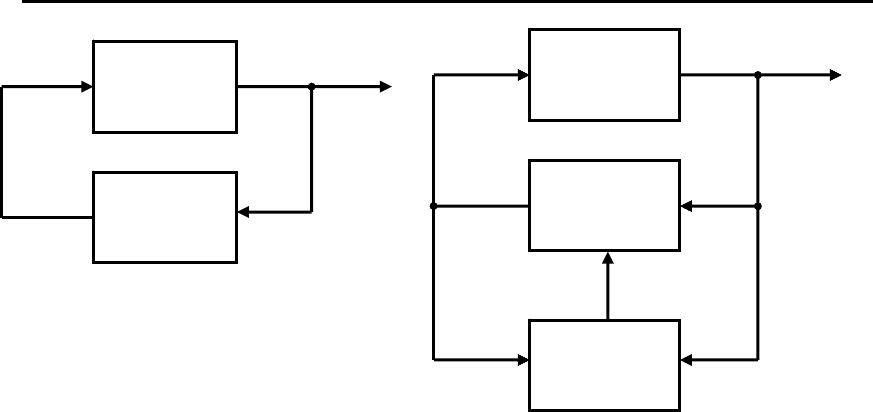
Структурные схемы САУ приведены на ри

с. 1.6 и 1.7. Схема

системы управления с управляющими устройствами сложного

типа (см. рис. 1.6) образуется объектом управления (ОУ) и УУ –

регулятором основного контура (РОК), для которого заданы це-

ли РОК.

Управление осуществляется при наличии или отсутствии

полной информации о координатах и параметрах объекта управ-

ления. При неполной инфор

мации о параметрах объекта управ-

ления в структуру САУ может включаться регулятор контура

адаптации (РКА), подстраивающего неизвестные параметры на

основе целевых условий РКА (см. рис. 1.7). При этом регулятор

основного контура формирует управления

)(

u в функции откло-

нений координат

)(

от заданных значений, а РКА, как правило,

формирует управления подстройкой параметров

, в непрерыв-

ном R

∈ или дискретном времени .

∈

1. ПРИНЦИПЫ ПОСТРОЕНИЯ И КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО

УПРАВЛЕНИЯ

Рис. 1.5. Структурные схемы разомкнутых, замкнутых и

комбинированных САУ

УУ ОУ

v(t)

w(t) u(t) y(t)

–

в)

УУ

ОУ

v(t)

w(t) u(t) y(t)

)

УУ ОУ

v(t)

w(t) u(t) y(t)

)

Рис.1.6. САУ с регулятором Рис.1.7. САУ с регуляторами

основного контура (РОК) основного контура (РОК) и

контура адаптации (РКА)

Системы управления с регулятором контура адаптации на-

зываются адаптивными САУ. Адаптивные САУ синтезируются

с применением методов идентификации, метода стохастической

аппроксимации, методом рекурретных целевых неравенств, ме-

тодом скоростного градиента, методом функций Ляпунова. Пере-

численные методы разработки РКА определяют соответствую-

щие целевые условия этого регулятора.

Общие принципы построения САУ реализуются на основе

математических мод

елей объектов, целей управления, мате-

матических формулировок задач управления с применением

моделей, принципов и целей. Это позволяет синтезировать и

реализовать алгоритмы управляющих устройств (регуляторов)

основного контура управления и контура адаптации.

РОК

ОУ

)(tu )(ty

РКА

РОК

ОУ

)(tu

)(ty

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ И

СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Системная характеристика линейных моделей объектов

и систем управления дана в виде совокупности взаимных пре-

образований моделей. Преобразование моделей выполняется

непрерывными и дискретными (прямыми и обратными) пре-

образованиями Лапласа и Фурье, на основе формулы Коши и

резольвенты линейного оператора систем. Приведены кусоч-

но-линейные моде

ли объектов управения и их свойства.

2.1. Классификация математических моделей

объектов и сист

ем

При решении задач автоматического управления использу-

ются различные математические модели объектов, систем авто-

матического управления (САУ) и их отдельных звеньев. Сущест-

венной характеристикой системы автоматического управления

являются типы сигналов, используемых при измерении и форми-

рования управляющего воздействия.

Если сигналы о состоянии объектов и управляющие воздей-

ствия являются непрерывными функциями времени, такие си

сте-

мы называются непрерывными САУ. Если аналогичные сигналы

в САУ формируются в дискретном времени, то координаты сис-

темы и управляющая функция (управление) являются дискрет-

ными функциями времени, а такие системы называются дис-

кретными САУ.

Непрерывные САУ описываются обыкновенными диффе-

ренциальными уравнениями или дифференциальными уравне-

ниями в частных производных. Дискретные САУ описываются

равнениями в конечных разностях. Дифференциальные и конеч-

но-разностные уравнения объектов и систем могут быть линей-

ными и нелинейными уравнениями. В соответствии с этим го-

ворят о линейных или нелинейных объектах и системах автома-

тического управления. Большое значение имеют специальные

классы нелинейных автоматических систем – кусочно-линейные

САУ, описываемые кусочно-линейными дифференциальными и

разностными уравнениями.

В дальнейшем большое внимание будет уделено линейным

объектам и системам. Будут рассмотрены уравнения объектов и

систем типа «вход–выход», «вход–состояния–выход», модели в

виде свертки, частотных характеристик (матриц частотных ха-

рактеристик) и передаточных функций (матриц передаточны

функций), взаимосвязи между которыми показаны на рис. 2.1. Из

данных рис. 2.1 можно сделать вывод о том, что ряд конкретных

математических моделей объектов и систем можно получить пу-

тем применения к их дифференциальным или разностным урав-

нениям интегральных или дискретных преобразований Лапласа

или Фурье.

Использование преобразования Лапласа дает возможность

ввести в рассмотрение уравнение свертки и изучать пе

редаточ-

ные функции САУ. С помощью преобразований Фурье могут

быть построены и изучены частотные характеристики непрерыв-

ных и дискретных САУ. Далее будут изучены связи между раз-

личными математическими моделями объектов и систем автома-

тического управления (см. рис. 2.1).

Для этого необходимо использовать ме

тоды теории функ-

ций комплексного переменного (ТФКП), формулу Коши для ре-

шения систем линейных уравнений, представленных в форме

«вход–состояние–выход» (уравнения состояния). Возможно так-

же применение общих методов для уравнений «вход–выход» для

полиномиальных моделей с правыми и левыми частями операто-

ров дифференцирования (полиномами от оператора дифференци-

рования) или раз

ностными операторами (полиномами от опера-

тора сдвига или оператора конечных разностей).